Intelligent Control and Automation, 2010, 1, 15-19
doi:10.4236/ica.201.11002 Published Online August 2010 (http://www.SciRP.org/journal/ica)
Optimal Control Strategy for a Fully Determined
HIV Model
Mohammad Shirazian1, Mohammad Hadi Farahi1,2
1Department of Applied Mathematics, Ferdowsi University of Mashhad, Mashhad, Iran
2The Center of Excellence in Modeling and Computations in Linear and Nonlinear Systems
Ferdowsi University of Mashhad, Mashhad, Iran
Received January 25, 2010; revised March 21, 2010; accepted June 22, 2010
Abstract
This paper shows how mathematical methods can be implemented to formulate guidelines for clinical testing
and monitoring of HIV/AIDS disease. First, a mathematical model for HIV infection is presented which the
measurement of the CD4+T cells and the viral load counts are needed to estimate all its parameters. Next,
through an analysis of model properties, the minimal number of measurement samples is obtained. In the
sequel, the effect of Reverse Transcriptase enzyme Inhibitor (RTI) on HIV progression is demonstrated by
using a control function. Also the total cost of treatment by this kind of drugs has been minimized. The nu-
merical results are obtained by a numerical method in discretization issue, called AVK.
Keywords: HIV/AIDS, Mathematical Modeling, System Identification, Control Theory, Immunotherapy
1. Introduction
Despite tremendous effort for mathematical modeling of
HIV/AIDS (for example, see [1-4]), estimation of model
parameters has not been attended a lot. For example, in
[2,5,6], only the virus clearance rate and the death rate of
infected CD4+T cells have been estimated. The impor-
tance of parameter estimation in models, is due to pre-
dicting “set-points” in the early infection stage for mak-
ing the desired treatment decisions (See [7]).
One of the objectives of this paper is presenting a re-
alistic model, i.e. the basic model of HIV, and estimating
all its parameters. It is necessary to mention that one can
identify all of the model parameters by using measured
output (For more details see [4]).
Another objective is to add a control function to the
identified basic model which plays the role of reverse
transcriptase enzyme inhibitor drug in disease progres-
sion.
In the sequel, the optimal control model of HIV will
be solved by a method in discretization issue, called
AVK.
Numerical results are obtained using mathematical
softwares, LINGO and MATLAB.
2. Translating Biological Knowledge to
Ordinary Differential Equations (ODE)
To make ODE’s from biological knowledge, first we
need some syntax. For example, if we denote the count
of uninfected and infected CD4+T helper cells, with a
and b, respectively, the syntax “0a” can be used to
present this biological descriptions: “Uninfected CD4+T
cells die” and the syntax “ab bb” can present:
“The reaction between two infected and uninfected CD4+T
cells produces two infected CD4+T cells”. Now, for
translating these syntaxes to the corresponding ODE’s,
we use Mass action law. This law says: “The rate of
change of products is proportional to the product of re-
actants concentration”. So if the syntax “ab c” is
obtained, according to the mass action law, we can write
ckab

, for k > 0, where dc
dt is denoted by c
. Two
other reactions in the previous syntax is dying a and
b reactants, while producing c. So we have also these
two ODE's as: akab


 and bkab
, for k > 0. Fi-
nally, the desired ODE, corresponding to the syntax
“ab c

” is

M. SHIRAZIAN ET AL.
16
,
,
.
ckab
akab
bkab






Obviously, the rate of change of a product is the sum
of changes from all reactions.
3. HIV Basic Model
The target cells of HIV infection are lymphocyte helper
cells, specially CD4+T cells. These cells become infected
and begin to produce free virions. The main fact about
HIV infection, is reducing the count of CD4+T cells,
which have an essential role in protecting body against
different pathogens. So it is important to understand the
dynamics of CD4+T cell count as a function of time. In
HIV infection basic model, three groups of molecules are
considered; Uninfected CD4+T cells (T), infected CD4+T
cells (I) and viral load (V). Biological descriptions, tran-
slation to reactions and corresponding ODE’s are pre-
sented in Table 1.
Now, according to Table 1 and Section 2, the com-
plete ODE model, which is sum of contributions from all
reactions, is as follows:
,
,
.
TsdT TV
ITVI
VkIcV


 





(1)
4. Properties of HIV Basic Model
There are two advantages to show the virous propagation
in HIV disease, by the basic model (1).
1) From medical point of view, one important subject
is the relative steady viral level during the asymptomatic
stage of an HIV infection. This level is called “set-point”.
When body reaches this level, immune system develops
HIV antibodies and begins to attempt to fight the virus.
The higher the viral load of the set point, the faster the
virus will progress to full blown AIDS (See [8]).
It can be shown that set-point is the amount of V, in
the equilibrium of virus depicted by the model (1), that is
*.
ks d
Vc



2) It can be seen that a model of such a simple nature
is able to adequately reflect the disease progression from
the initial infection to an asymptomatic stage after the
set-point is reached (See [9]).
5. Estimation of Models Parameters Using
Discretization
In this section, our aim is to estimate all parameters of
HIV basic model (1). Clinically all six variables in model
(1), can be measured. Since the cost of quantifying the
infected cells is much higher, we are going to omit vari-
able I, initially. For this, let 1 yT and 2 yV

. After
some calculations, model (1) can be changed to:
1121312
yyyy




 (2)
24252612
yyyyy




  (3)
where
2
3
4
5
6
1s
d
c
c
k



















 

.
The vector

defines a one-to-one map for 0


and c


. Therefore the identification of the original
parameters of (1) is equivalent to the identification of

.
It is known that for most HIV patients, 0


and
c


(See [7]). In this case, the following inverse map
can be defined:
Table 1. HIV basic model interactions.
Biological description Translation to reactionsReaction rate Translation to ODE
CD4+T cells production 0T
s
Ts

CD4+T cells natural death 0T d TdT

CD4+T cells become infected by virus TV IV



TTV
I
TV






Infected CD4+T cells death 0I

I
I



Virus replication in infected CD4+T cells
I
IV k VkI

Virus natural death 0
V c VcV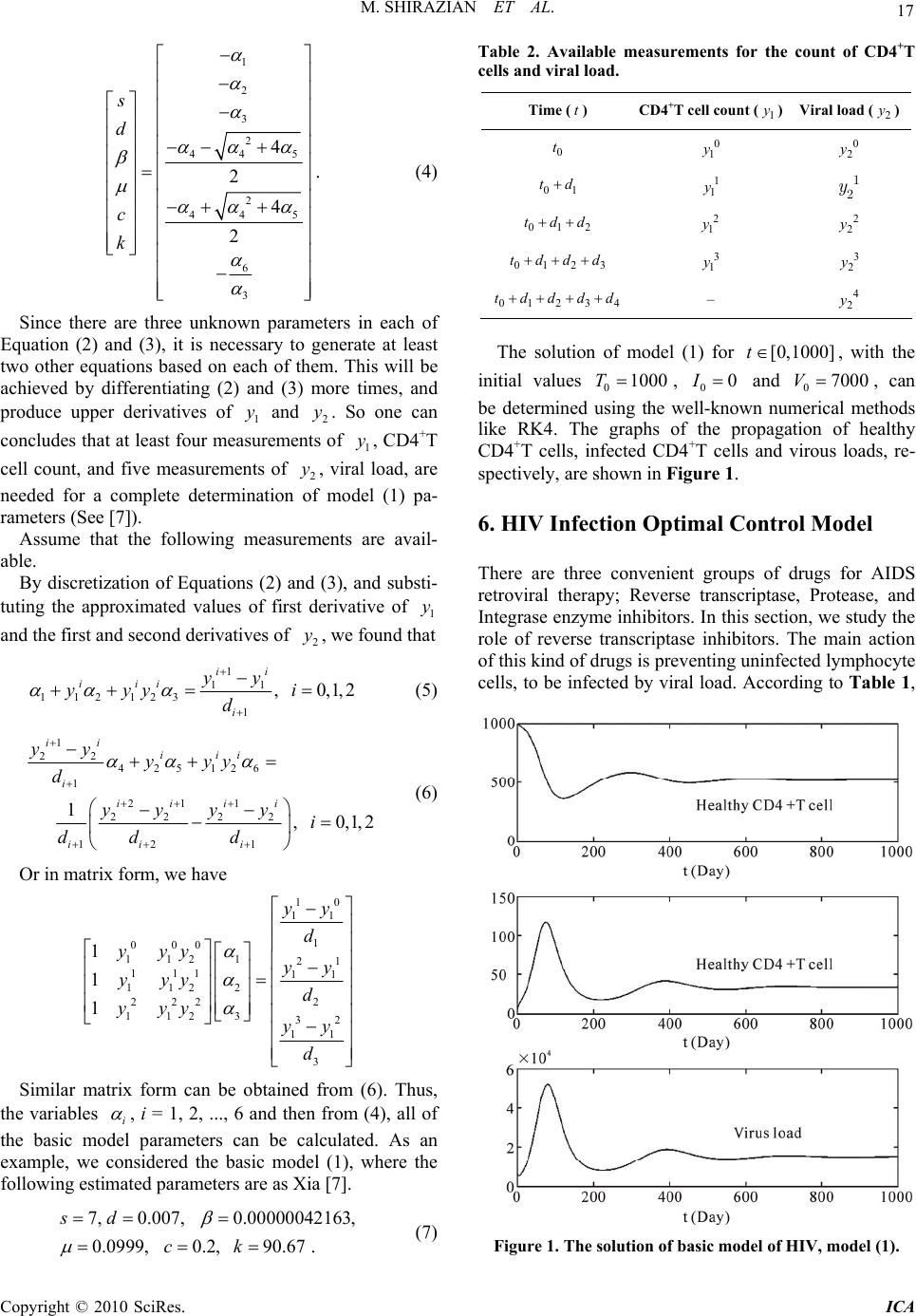


M. SHIRAZIAN ET AL.
17
1
2
3
2
44 5
2
44 5
6
3
4
2
4
2
s
d
c
k
















 

 
 
 
 

 
 
 
 
 

 
 


. (4)
Since there are three unknown parameters in each of
Equation (2) and (3), it is necessary to generate at least
two other equations based on each of them. This will be
achieved by differentiating (2) and (3) more times, and
produce upper derivatives of 1 y and 2 y. So one can
concludes that at least four measurements of 1 y, CD4+T
cell count, and five measurements of 2 y, viral load, are
needed for a complete determination of model (1) pa-
rameters (See [7]).
Assume that the following measurements are avail-
able.
By discretization of Equations (2) and (3), and substi-
tuting the approximated values of first derivative of 1 y
and the first and second derivatives of 2 y, we found that
1
11
112123
1
,0,1,2
ii
iii
i
yy
yyy i
d
 



  (5)
1
22
425126
1
21 1
2222
12 1
1,0,1,2
ii
iii
i
iiii
ii i
yy yyy
d
yyyy
i
dd d
 


 
 



 


(6)
Or in matrix form, we have
10
11
1
000
112121
111 11
1122
2 222
112 332
11
3
1
1
1
yy
d
yyy yy
yyy d
yyy
yy
d























Similar matrix form can be obtained from (6). Thus,
the variables i

, i = 1, 2, ..., 6 and then from (4), all of
the basic model parameters can be calculated. As an
example, we considered the basic model (1), where the
following estimated parameters are as Xia [7].
7, 0.007,0.00000042163,
0.0999,0.2,90.67 .
sd
ck


 
 (7)
Table 2. Available measurements for the count of CD4+T
cells and viral load.
Time (t) CD4+T cell count (1
y) Viral load (2 y)
0
t 0
1
y 0
2
y
01
td

1
1
y 1
2
y
012
tdd

 2
1
y 2
2
y
0123
tdd d

 3
1
y 3
2
y
01234
tdd dd

 – 4
2
y
The solution of model (1) for [0,1000]t, with the
initial values 01000T

, 00I and 07000V, can
be determined using the well-known numerical methods
like RK4. The graphs of the propagation of healthy
CD4+T cells, infected CD4+T cells and virous loads, re-
spectively, are shown in Figure 1.
6. HIV Infection Optimal Control Model
There are three convenient groups of drugs for AIDS
retroviral therapy; Reverse transcriptase, Protease, and
Integrase enzyme inhibitors. In this section, we study the
role of reverse transcriptase inhibitors. The main action
of this kind of drugs is preventing uninfected lymphocyte
cells, to be infected by viral load. According to Table 1,
Figure 1. The solution of basic model of HIV, model (1).

M. SHIRAZIAN ET AL.
18
this action is equivalent to the reaction TV IV.
So we control the first equation to prevent the transmis-
sion of uninfected cells to infected ones. This control
function is called ()ut, where 0()1ut. The most
drug efficiency is in the case 1u which means CD4+T
cells are not infected by viral load anymore. At the other
side, 0u is the case which the drug does not change
the disease progression. By above argument, the control
system is as:
(1 ),
(1 ),
.
TsdT TV u
ITVu I
VkIcV


 





(8)
Using [10], consider the objective functional to be de-
fined as:
 
0
2
1
,()
2
f
t
t
J
TuTtut dt 




 (9)
where 110

. Our goal is maximizing the objective
functional (9) subject to the control system (8); that is,
maximizing the total count of CD4+T cells and minimiz-
ing the costs of treatment by applying some RTI drugs.
The solution of this optimal control problem should be
calculated by numerical methods. We have used a special
discretization method, called AVK.
For a detailed explanation of this method, see [11].
In AVK method, for solving the optimal control prob-
lem,
 

0
Min,, ,
f
t
t
J
xu gxtuttdt (10)
Subject to:
 

 


0
00
,,, ,
,
f
ff
x
tfxtuttttt
xtxxtx








(11)
the following steps should be applied:
Step 1. Form the total error function 1 E as:
  
0
1,,,
f
t
t
Exuxt fxtuttdt

Step 2. Combine the total error function with the ob-
jective functional (10) as follows:
  

  

 
01
2
00
Min, ,
,,
subjectto :,
f
t
t
ff
gxtutt
x
tfxtuttdt
xtxxtx





 (12)
where nonnegative numbers 1

and 2

are two given
weights and 12
1

 .
Step 3. In order to control the error, add the following
constraint,


1,Exu
to the optimal control problem in Step 2. So the modified
optimal control problem (10)-(11) can be formulated as:
 





 

 
0
0
1
2
00
Min, ,
,,
subjectto :
,,
,
f
f
t
t
t
t
ff
gxtutt
x
tfxtuttdt
xtfxtuttdt
xtxxtx

 






(13)
Step 4. Calculate


i
ut by minimizing the optimal
control problem (13) using discretization method.
For example, if the norm function ., is norm 1, then
one can solve the following optimization problem:







0
1
21
0
1
0
1
1
0
Min ,,,,
subject to : ,,
,
n
iiii iii
h
n
iiii
h
ff
hgxutxfxut
hx
xtx xt
u
x
fxt












 (14)
where 0f
tt
hn

, 0i
ttih

, ()
ii
x
xt, ()
ii
uut

and 1
() ii
ii
x
x
xxt h



 for 0,1,., 1in
and n

.
Step 5. By the means of ()
i
ut for every i t, from
(11), it is easy to find ()
i
x
t, for any i, 0,1,., 1 in .
We use this technique to solve the control problem (8)
with the objective functional (9). The parameters used in
the basic control model (8) are exactly as (7). Assume
that the treatment begins when CD4+T cells reach their
minimum count, in the absence of drug.
According to Figure 1, (129) 363T is the mini-
mum count of CD4+T cells. So the treatment interval is
[129, 1000] day. Also, note that by Figure 1, at t = 129,
we have (129) 57I

and (129) 28860V.
Now, we divide [129, 1000] into n parts with length
h. The discretization form of (14) is:
 




12
1
0
2
000
1
Max 2
1
1
subjectto:,,0,01,0,1, 2,...,
363, 57,28860
n
ii
h
iiiii
iiiii
iii
iii i
hTu
TsdT TVu
ITVuI
VkIcV
TIVu in
TIV











 

 

 







M. SHIRAZIAN ET AL.
19
Figure 1. The solution of optimal control problem (8)-(9),
using AVK method.
where assumed 12
1
2
 .
The results of this optimization problem which ob-
tained by LINGO and MATLAB softwares for 200n

and 6
10 , are depicted in Figure 2.
7. Conclusions
In this paper, the parameter of the basic model of HIV/
AIDS is estimated only by measurement of the CD4+T
cells and the viral load count. Since the suggested mod-
els for HIV, or infectious diseases like consumption,
cholera, influenza and etc., have unknown parameters
which should be estimated, one can use the proposed
method in this paper to estimate the parameters of such
models.
One of the most important kinds of drug treatments for
HIV immunotherapy is assumed. One can investigate the
effects of other drugs, like Protease enzyme inhibitors in
preventing AIDS progression. In these cases, one can use
the described discretization method for solving such op-
timal control problems.
8. References
[1] D. Covert and D. Kirschner, “Revisiting Early Models of
the Host-Pathogen Interactions in HIV Infection,” Com-
ments Theoretical Biology, Vol. 5, No. 6, 2000, pp. 383-
411.
[2] M. A. Nowak and R.M. May, “Virus Dynamics: Mathe-
matical Principles of Immunology and Virology,” Oxford
University Press, New York, 2000.
[3] A. S. Perelson and P. W. Nelson, “Mathematical Analysis
of HIV-1 Dynamics in Vivo,” SIAM Review, Vol. 41, No.
1, 1999, pp. 3-44.
[4] W.-Y. Tan and H. Wu, “Deterministic and Stochastic
Models of AIDS Epidemics and HIV Infections with In-
tervention,” World Scientific, Singapore, 2005.
[5] M. A. Nowak and C. R. M. Bangham, “Population Dy-
namics of Immune Responses to Persistent Viruses,” Sci-
ence, Vol. 272, No. 5758, 1996, pp. 74-79.
[6] X. Wei, S. K. Ghosh, M. E. Taylor, V. A. Johnson, E. A.
Emini, P. Deutsch and J. D. Lifson, “Viral Dynamics in
HIV-1 Infection”, Nature, Vol. 273, No. 6510, 1995, pp.
117-122.
[7] X. Xia, “Estimation of HIV/AIDS parameters,” Auto-
matica, Vol. 39, No. 11, 2003, pp. 1983-1988.
[8] R. Pattman, M. Snow, P. Handy, K. N. Sankar and B.
Elawad, “Oxford Handbook of Genitourinary Medicine,
HIV and AIDS,” Oxford University Press, USA, 2005.
[9] X. Xia, “Modelling of HIV Infection: Vaccine Readiness,
Drug Effectiveness and Therapeutical Failures,” Journal
of Process Control, Vol. 17, No. 3, 2007, pp. 253-260.
[10] K. R. Fister and S. Lenhart, “Optimizing Chemotherapy
in an HIV Model,” Journal of Differential Equations, Vol.
1998, No. 32, 1998, pp. 1-12.
[11] K. P. Badakhshan and A. V. Kamyad, “Numerical Solu-
tion of Nonlinear Optimal Control Problems Using Non-
linear Programming,” Applied Mathematics and Compu-
tation, Vol. 187, No. 2, 2007, pp. 1511-1519.