 Journal of Intelligent Learning Systems and Applications, 2012, 4, 303-318 http://dx.doi.org/10.4236/jilsa.2012.44032 Published Online November 2012 (http://www.SciRP.org/journal/jilsa) 303 Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” José Luis Castillo Sequera, José Raúl Fernández del Castillo Diez, León Gonzalez Sotos Department of Computer Science, University of Alcala, Madrid, Spain. Email: jluis.castillo@uah.es, joseraul.castillo@uah.es, leon.gonzalez@uah.es Received May 16th, 2012; revised October 16th, 2012; accepted October 23rd, 2012 ABSTRACT In this paper, we show a clustering method supported on evolutionary algorithms with the paradigm of linear genetic programming. “The Straight-Line Programs (slp)”, which uses a data structure which will be useful to represent col- lections of documents. This data structure can be seen as a linear representation of programs, as well as representations in the form of graphs. It has been used as a theoretical model in Computer Algebra, and our purpose is to reuse it in a completely different context. In this case, we apply it to the field of grouping library collections through evolutionary algorithms. We show its efficiency with experimental data we got from traditional library collections. Keywords: Clustering; Genetic Algorithm; Data Mining; Straight Line Programs 1. Introduction Information Retrieval Systems (IRS) are a class of infor- mation systems concerned with databases composed of documents processing user queries, in order to facilitate access to relevant information. Many universities and public libraries use IRS to provide access to catalogs books, journals and other documents. In IRS, Cluster Analysis is the generic name for a wide variety of pro- cedures that can be used to create a classification of ob- jects and has been developed and used in many fields from social science to library and information science [1]. Document Clustering has attracted much interest in re- cent decades due to the relevance of the problem of find- ing the group that better describes a document. Genetic Algorithms (GA’s) are probabilistic search methods that apply natural selection for finding global optimum solution of optimization problems having fea- sible solutions [2]. In GA’s a population of strings (called chromosomes), which encodes candidate solu- tions (called individuals) to an optimization problem, evolves toward better solutions. The chromosomes are selected for reproduction under the action of crossover and mutation to form new population. The new popula- tion is evaluated and re-used genetic operators up to achieve an optimal solution. Evolution has proven to be a very powerful mechanism in finding good solutions to difficult problems. These concepts involve the preservation of the charac- teristics of the best exponents of a generation in the next generation; moreover one can introduce aleatory changes in the new generation composition by means of crossing over and mutation operations. This aleatory component prevents getting stuck into a local maximun from which you can not escape to reach a global maximun. This would represent one of the main advantages of genetic algorithm in opposition to the traditional search methods as the gradient method. Another advantage is its utility for real time applications, in spite of not providing the optimal solution to the problem it provides almost the better solution in a shorter time, including complex pro- blems to solve by traditional methods. The purpose of clustering is to divide a given group of objects in a number of groups (clusters). Once the opti- mization criterion is selected, the clustering problem is to provide an efficient algorithm in order to search the spa- ce of the all possible classifications and to find one on which the optimization function is minimized. Taking into account the quality of the solutions of GA in differ- ent types of fields and problems, it makes perfect sense to try to use it in clustering problems; also the flexibility associated with GA is one important aspect to bear in mind, because with the same genome representation and just by changing the fitness function one can have a dif- ferent algorithm. Furthermore, a slp consists of a finite sequence of computational assignments. Each assignment is obtained by applying some function (selected from given set) to a set of arguments that can be variables, constants or pre- computed results. The slp structure can describe complex computable functions using fewer amounts of computa- Copyright © 2012 SciRes. JILSA  Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” 304 tional resources than GP-trees. The key point for explain- ing this feature is the ability of slp’s for reusing previ- ously computed results during the evaluation process. Another advantage with respect to trees is that the slp structure can describe multivariate functions by selecting a number of assignments as the output set. Hence one single slp has the same representation capacity as a forest of trees. We study the practical performance of ad-hoc recombination operators for slp’s. and we apply the slp- based GP approach to solve clustering of documents. 1.1. slp Structure Straight line programs are commonly used for solving algebraic and geometric problems. An extensive study of the use of slp’s in this context can be found in [3]. The formal definition of slp’s we provide in this section is taken from [4]. Definition: Let 1,, n f 1in be a set of functions, where for each i, , each i has arity , and let be a set of terminals. i a 1,, m tt C The set satisfies that: with 1V,,tt m 1,, Vx x 1,, q Cc c is a finite set of variables and is a finite set of constants. A straight line program (slp) over these functions is a finite sequence of computational instructions , where each , The number of instructions l is the length of P. 1,, l PI I l 1, ,k 1i1 :,, ,, k km a tuk t 1i1 1 : ,, ,,,,for1 1 k km a tu k uk tu k Usually a slp will be identified with the set of variables ui introduced at each instruction, thus 1. Each of the nonterms variables ui can be considered as an expression over the set of terminals: 1,, l PI I ,, l Pu u 1,, m ttconstructed by a sequence of recursive com- positions from the set of functions 1,, n f. Following [4] we denote by slp the set of all slp’s over 11 ,, ,,, nm fftt 1,, n f,,t and . 1m Note 1: If we consider a slp P as a program code, for each instruction Ii, introducing a new variable that is not a term, then the numbers of these variables coincides with the number of instructions as well as the length of slp. Therefore, in the following we will denote a slp as . t 1,, l PI I 1,, l Pu u Each of the ui can be considered as a sub-slp on the set of terminals 1constructed as a sequence of recursive calls to evaluate functions ,, m tt 1,, n f. Example: Let F be the set of basic operations and let AND,ORF 12 ,,, Tdd d i PSLP the set of terminals. In this situation all slp that can be defined are polynomials in ,FT D variables with integer coefficients. 11 2 21 5 33 4 42 3 :AND :OR :AND (1) :OR Pu dd uud ud d uuu Then, the function is computed by evaluating the poly- nomial u4 1253 AND ORORANDdddd 4 d The next result computes the cardinal of the set 11 ,, ,,, ln slp fftt m , i.e. gives the amount of a given length slp l. This amount depends on the cardinal of the sets of functions and terminals. Note 2: All slp 1,, l Pu u on the sets of func- tions and terminals can be represented as a directed graph , p GVE. The set of vertices is 1l, where P’ contains all the terminals involved in computing. The set of edges E is constructed as follows: ,,u VP u For all k, 1kl , draw an edge for each , ki ua 1, , k ia. Note that P’ is the set of leaves of the graph GP and is a subset of terminals 1m. By example, the next graph shows the directed graph associated with the slp described in Equation (1) (See Figure 1). ,,tt 1.2. slp’s versus Trees Definition: Let 1,, l Pu u T a slp on the sets of functions and terminals. For each , we define the tree associated with non term variable as: 1,k l, k Label the root of the tree as Tk u k k Label the subtrees of , from left to right as: k T 1,, k TT In the case that i is a terminal, this is OR OR AND AND D3 D5 D4 D1 D2 Figure 1. Directed graph associated with the slp. Copyright © 2012 SciRes. JILSA  Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” 305 1,, i tt m then the tree i T will have a single node labeled i . The method for constructing the tree associated with a non-terminal variable k is a recursive process in each case calculated through subtrees. We can use this property to define a partial order as follows: T Definition: Let a slp on the sets of functions and terminals. We define the relation “<<” on it as the one which, for: 1,, l Pu u , ak 11 :,,and: ,, iai k ui fukf α With ik uu . If and only if 1,, . ak ui This relation “<<” is a partial order on the set of programs, in a similar way as the inclusion is a partial order in the power set of a given set. 1.3. Forest Associated with slp (See Figure 2) Let a slp on the sets of functions and terminals. We define the forest associated with P as the set of trees: is , where 1,, l Pu u ,, il T T ,, il is TTis the set of maximal elements of P respect to the partial order «. Example: Let the next slp on the set of functions and terms . 15 ,,Pu u AND, OR 4 d F 3 ,d 12 ,,Tdd 11 2 23 1 31 1 43 4 51 3 :OR :OR :OR :AND :OR Pu dd ud u uu u uu d uu u Then the set of maximal elements of P respect to the par- tial order « is 245 ,, uuuand the forest associ- ated with the slp P can be seen in the Figure 3. AND OR D4 OR OR OR D2 D1 D3 Figure 2. Example of slp with a set of functions and terms. 2 ≡ 4 ≡ 5 ≡ OR OR D3 D1 D2 AN OR D3 OR OR D2 D1 D2 D1 OR OR OR D2 D1 OR OR DDD D Figure 3. Forest associated with slp P. 2. Development of Evolutionary System for Document Clustering Our evolutionary system makes use of concepts of Ge- netic Algorithm (GA) [5,6], that allows to increase its potentiality and versatility. In our proposal, an individual is considered as a chromosome that adopts a proper length (depending on the number of documents). Here, the individual is represented by a binary tree structure grouping all documents in its leaves, where a document is more related to some other if they are in a nearest branch. These structures are formed by nodes. In our system, there are terminal and non-terminal nodes con- nected by edges. The terminal nodes (leaf nodes) are documents. Each terminal node contains the vector representation of a document (represented by its characteristic vector). Thus, each document in the collection has a single ter- minal node. Each non-terminal node contains the result of the function of adaptation (fitness) for the two re- maining nodes and the coordinates of the centroid of both. We apply the euclidean distance and the Pearson’s cor- relation coefficient simultaneously to evaluate the fitness of our algorithm. This function must be minimized in order to get the solution for the given crossing and mu- tation operators designed for the problem. The effects of different mutation and crossover rates had been compared. In this model documents are repre- sented by vector of terms that they are obtained with NZIPF method [7]. We use term vectors, obtained ap- plying a methodology of processing the documents [8] to obtain the best characteristic vectors, selected from the area defined by the use of the Zipf law [9] and the Goff- man Point [10,11]. Because we work with evolutionary algorithms, it needs the adjustment of several parameters that make strong effect on the results. Therefore we have to carefully de- fine the experimentation environment [12] and the data- set that we use in our tests. 2.1. Chromosome Representation An individual is a binary tree whose leaves are the docu- Copyright © 2012 SciRes. JILSA  Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” Copyright © 2012 SciRes. JILSA 306 tion we can show in Figure 4. ments to be grouped. Our chromosome is represented by a binary tree which is evaluated with a fitness based on a combination of distance and similarity measures, operat- ing in pairs of vectors. 2.2. Initial Population Let 1,, n ffa set of functions such that fi has arity ai for all i, 1≤ i ≤ n and let a set of terms as we introduced before. We describe the process for generating each of the slp initial population. 1,, m Tt t We call “global fitness” to fitness that corresponds to the non-terminal top level node (root node) and “partial fitness” the one obtained in the remaining non-terminal nodes. Therefore in the representation there are many “partial fitness” and a single “global fitness” for each individual (each tree). For the first non-terminal variable u1, select a function fj12 F randomly. For each argument 1 1, , iathis function fj1 randomly choose an element αi from the set of terms T. In general, for non-term variable uk, k > 1, also started choosing a function fjk F (from the set of given functions). The difference is now, for each argument i, 1 k ia , choose at random an element in the set 1,, kl Tu u . In practice, we code each of these structures by a string, in which the zeros (0) denote non-terminal nodes and non zeros substrings represent each document. Documents appears as an avatar (string) arranged be- tween the zeros, which in polish notation describes the tree. The string is traversed in “preorder ”. In practice, we must introduce an upper bound L for the length of the slp involved in the process of genetic programming. Therefore, the first step in the generation of each slp should consist of randomly selecting the length 1, ,lL. For example, we show two documentary collections, interpreted through a tour in preorder, as represented by strings 000A50420a$ which corresponds to the docu- ments [110,5,4,2,95,221] placed in a certain order (Fig- ure 4), or 000&Fh0300152 which corresponds to the documents [205,97,42,3,1,5,2] placed in a certain order (Figure 4). We have fixed 50 as the population’s size, so we have 50 different trees for each test. We generate the individu- als (chromosomes) in a random way. These chromoso- mes are called initial population that feed into genetic operator process [2,5]. The length of a chromosome de- pends on the number of documents in the documental database. Genetic operators generate a new population from the existing one, placing similar documents into a given groups (Figure 5). We should have all documents in our documental data base without repetition. This rep- resentation of the chromosome is a necessary condition for the algorithm. For the first document collection (first string): The character “A” is an avatar that corresponds to the docu- ment 110, the character “5” with the document 5, the character “4” with the document 4, the character “2” to document 2, the character “a” with the document 95, the character “$” with the document 221. For the second document collection (second string): The “&” character is an avatar that corresponds to the document 205, the character “F” with the document 97, the character “h” with the document 42, the character “3” with the document 3, the character “1” to document 1, the character “5” with the document 5 and the character “2” with the document 2. 2.3. Fitness Evaluation Each individual has a “global fitness” and each node has a “partial fitness”. We use two measures of the fitness Each of the strings is an individual, whose representa- 0 00 30 15 0 0 0 0 0 A 5 4 20 2 Strin : 000&Fh0300 152 0 h &F a $ * 3 4 2 9 *9 4 1 7 *4 5 8 7 * 12 11 8 7 * 9 7 1 8 * 9 11 7 8 *3 14 20 9 *13 11 20 19 *11 10 4 20 *13 15 12 9 *4 5 8 7 *9 7 1 8 0: No-terminal node * Ve ct o rs characterist *19 17 11 8 Strin : 000A50420a Figure 4. Tree representation of individuals in the system.  Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” 307 Documents Collections Method Processing of Vectors Characteristics Creation of the Initial F f Individual 1 Individual 2 Individua l N=50 F: Fitness global, f: Fitness local Di: Doc ument i Chromosome 1: 00506400123 Chromosome 2: 00401502036 f f D DD f D D D F f f Df DD Df D D F f f f D DD f D DD Chromosome 50: 00035400621 Figure 5: Initial population of individuals. function to calculate the distance and similarity between documents and to be able to form better clusters. Thus, the proposed fitness on the one hand try to maximize the similarity of documents and minimizing the distances between them, (see Table 1). where the α coefficient is the weight that balances the values of the distance (Euclidean) and of the value of similarity (α varies be- tween 0 and 1), ie the coefficient of the convex com- bination of the distance and the inverse of the similarity, and each di is represented by its characteristic vector. 2.4. Selection After we evaluate population’s fitness, the next step is chromosome selection. Selection embodies the principle of ‘survival of the fittest’. Satisfied fitness chromosomes are selected for reproduction, for it, we apply the method of selection of the tournament, using a tournament of 2, and we apply Elitism in each generation using the strat- egy called GAVAPS (Genetic variation in the size of the population) [2,13] using the concept of age and time of life, so that if an individual has better fitness will have more time to live. Therefore, this approach keeps elitism in subsequent generations. 2.5. Genetic Operator With the slp data structure can be implemented genetic operators used in the field of evolutionary computing, allowing its full potential, such as: 2.5.1. Propossed Crossover Operator with the Structure slp As slp is coded as a finite sequence of operations and individuals have the same length, classical crossover methods, such as cross at one point, two point crossover and the uniform crossover can be adapted to this data structure. Here are the details: Definition: Let 11 ,, Pu u and 21 ,, Pu u two slp with the same number of func- tions and terms. Then, the above crossover operators, act on these structures as follows: At one point: Since breaking point 1, ,iL, crossing at a point operating on the slp P1 and P2 pro- duces: 11 1 21 1 ,,, ,, ,,, ,, ii L iiL Pu uuu Pu uuu At two points: Given two break points , 1,,ij L with i < j crossing at two points operating on the slp P1 and P2 produces: 11 11 21 11 ,,, ,,,,, ,,, ,,,,, iijjL iijjL Pu uuuuu Pu uuuuu Uniform: Given a Boolean vector 1,, 0,1 L uniform cross operating on the slp P1 and P2 produces: 11 21 ,, ,,, L PvvPvv where for all 1, ,iL i i holds: If0thenand 1 thenand iiii iiii vu vu vu vu Although it is possible to apply any of the discussed crossover operators with slp structure, we had to develop a new crossover operator to avoid the possibility of having a given documents twice in an individual. Copyright © 2012 SciRes. JILSA  Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” 308 2.5.2. Crossover Operator Used We developed a crossover operator based on a crossover mask, which applies on the populations of individuals. First we selected two parent individuals by the method of the tournament, then we choose randomly one chromo- some and this chromosome is used to define the mask for the crossing. We call the “parent mask chosen”, the indi- vidual chromosome randomly chosen and “un chosen parent mask” the remaining one. At the beginning the new individual will have as ava- tar the chromosome of the chosen parent mask. Then, the crossing is made by examining the chromosomes gene by gene from both parents. If genes are a non-terminal node (node 0), we keep the gene that corresponds to the mask of the father elected to the new individual child. But if we find terminal nodes (documents) in both parents’ genes on the chromosomes, then we select the gene for the mask of the unselected parent, and this gene is sought and exchanged in the new individual with a correspond- ing gene of the mask of unelected father [14,15]. For example, if we have 5 documents and we have the fol- lowing chromosomes parents: 002105034 0 00 530214 The chromosome created after applying the crossing operator would be: 000130254 Then, the new individual will always have documents that are not repeated (Figure 6). 2.5.3. Mu t ation Operator The mutation operator is asexual and therefore acts on a single parent, making small random changes what will help to maintain diversity in the population that, other- wise, could tend to converge prematurely to a local opti- mum. Let 1,, n ff be a set of functions such that fi has arity ai for all i, 1≤ i ≤ n and let be a set of terms as we introduced before. The first step in applying the mutation slp to slp P is to select a non-terms variable ui P randomly. After than, we select ran- domly, one of the arguments of the function f 1,, m Tt t func- tions non-terms variable ui. For the final step, we replace the argument by one from the set cho- sen randomly. Formally, the slp mutation operation is de- scribed: 1,, il Tuu Let 1,, Pu u uf a slp on the set of functions and terms and let n 1,, i 1,, ki Tu u the variable non-termi- nal selected to be mutated, where f functions and . l Mutation of the slp P at point i occurs: ,where 111 ,, ,, ,, iii L Pu uuuu 11 1 11 ,,,,,, ,, ijjj jij uf Tuu n and both j and are randomly selected. Therefore, we use a mutation operator on nodes. This operator is implemented by selecting an individual in the population by the so-called method of the tournament, then randomly selects a pair of nodes of that individual. (If any of them is a terminal node). Then these nodes are exchanged, thus generating a new individual who could have a different tree structure. The new individual has the same base documents but placed in a different order. The mutation involves the alteration of the values of the chromosome depending on a rate of probability. Exam- ples of the use of this operator are depicted in Figures 7 and 8 respectively. 2.6. Stop Criteria Stop criteria is used to determine when the algorithm stops. When the fitness value has no changes during a given number of generations we consider that we got a good individual, representing relations between docu- ments. In any case the maximum number of generations is set to 4000. 3. Experiments and Results For the real tests we have used documents from the “Reuters 21578” collection [16], taking the distributions with greater dispersion of data (distribution 21, distribu- tion 2, distribution 20, distribution 8) and documents of the collection of editorials of the Spanish newspaper “El Mundo”. Reuters 21578 is a documentary collection, one of the “de facto” standards within the domain of automatic categorization of documents, used by numerous authors. We have also used the collection in Spanish of the edito- rials of the newspaper “El Mundo” from the years 2006 and 2007, which has been classified manually into the document processing stage. Thus from both collections have taken representative samples of groups of docu- ments. To verify the validity of our work, we used the distributions with higher dispersion. The comparative data is presented in Table 2. Samples were taken by selecting the documents from two categories of each documental collection, taking those categories that contain the greater quantity in docu- ments. For the collection of the editorials of the newspa- per “El Mundo”, we apply the same approach, using the main categories that it has the thesaurus Eurovoc [17]. It was necessary to carry out a manual classification previ- ously in each one of the editorials of the collection (1402 editorials). The Table 3 sample ordered the results ob- tained with the collection of the editorials alphabetically. Copyright © 2012 SciRes. JILSA 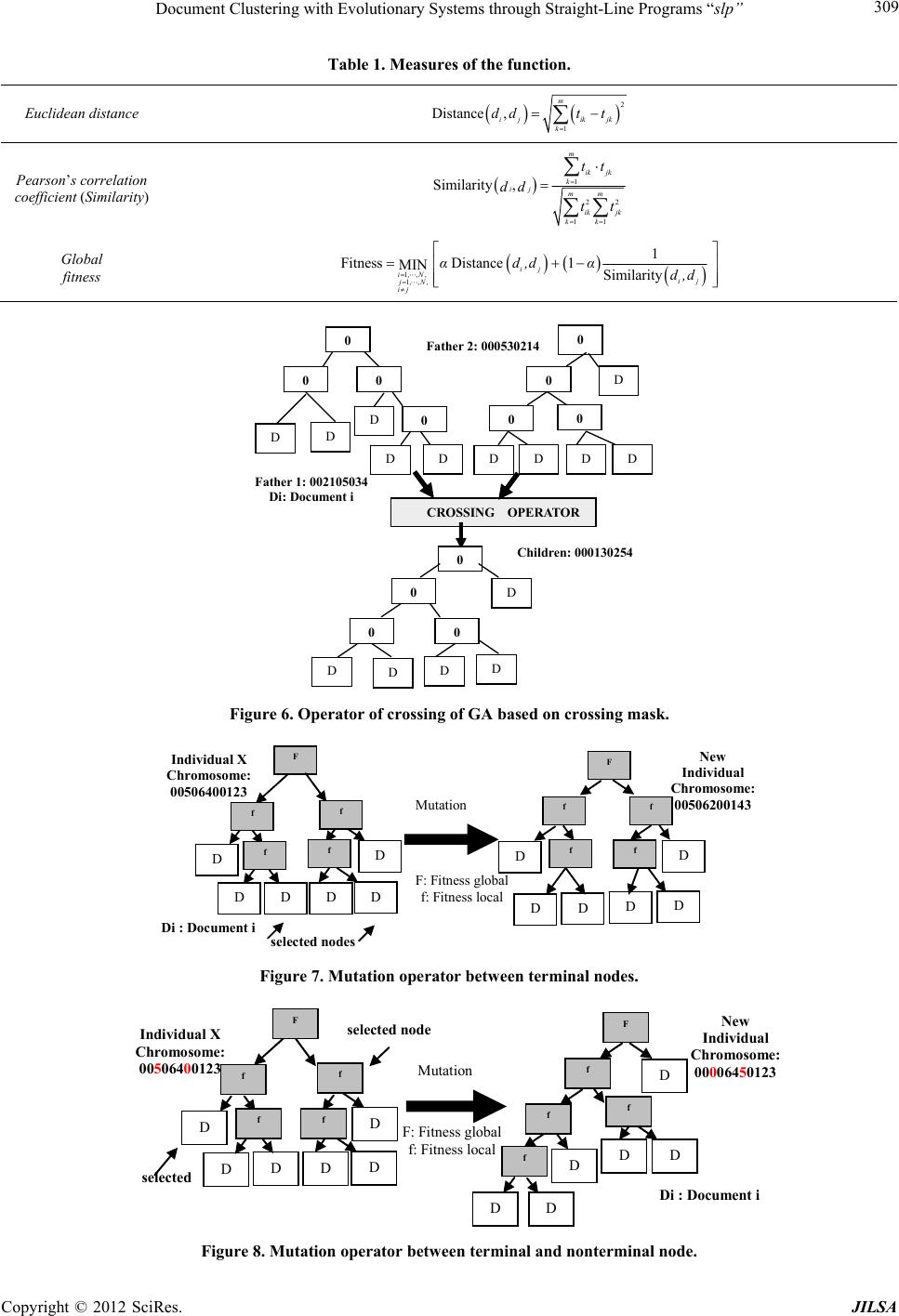 Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” Copyright © 2012 SciRes. JILSA 309 Table 1. Measures of the function. Euclidean distance 2 1 Distance , m ijikjk k ddtt Pearson’s correlation coefficient (Similarity) 1 22 11 Similarity , m ik jk k ij mm ik jk kk tt dd tt Global fitness 1, , , 1, , , 1 FitnessDistance 1 MIN Similarity ij iN ij jN ij αd,d α d,d 0 Father 2: 000530214 CROSSING OPERATOR Father 1: 002105034 Di: Document i Children: 000130254 DD D DDDDD D D DDDD D Figure 6. Operator of crossing of GA based on crossing mask. F: Fitness global f: Fitness local Mutation F Individual X Chromosome: 00506400123 D selected nodes New Individual Chromosome: 00506200143 D DD D DD DDDD D f f f f F f f f f Di : Document i Figure 7. Mutation operator between terminal nodes. F: Fitness global f: Fitness local Mutation New Individual Chromosome: 00006 504123 Individual Chromosome: 00 43 506 0012 F F f f f f f f f f D DDD D D D D DD D D selected node selected Di : Document i Figure 8. Mutation operator between terminal and nonterminal node. 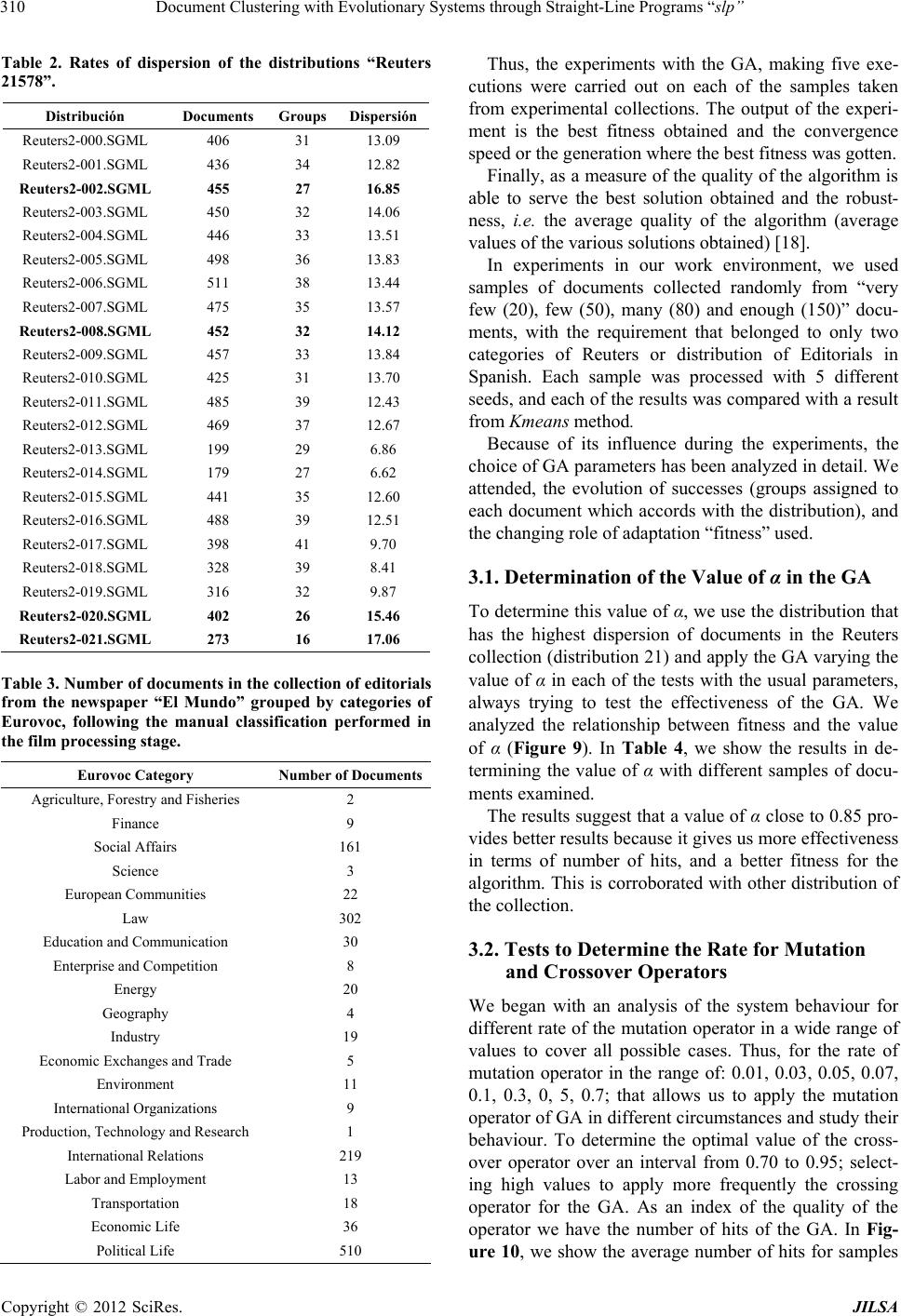 Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” 310 Table 2. Rates of dispersion of the distributions “Reuters 21578”. Distribución Documents Groups Dispersión Reuters2-000.SGML 406 31 13.09 Reuters2-001.SGML 436 34 12.82 Reuters2-002.SGML 455 27 16.85 Reuters2-003.SGML 450 32 14.06 Reuters2-004.SGML 446 33 13.51 Reuters2-005.SGML 498 36 13.83 Reuters2-006.SGML 511 38 13.44 Reuters2-007.SGML 475 35 13.57 Reuters2-008.SGML 452 32 14.12 Reuters2-009.SGML 457 33 13.84 Reuters2-010.SGML 425 31 13.70 Reuters2-011.SGML 485 39 12.43 Reuters2-012.SGML 469 37 12.67 Reuters2-013.SGML 199 29 6.86 Reuters2-014.SGML 179 27 6.62 Reuters2-015.SGML 441 35 12.60 Reuters2-016.SGML 488 39 12.51 Reuters2-017.SGML 398 41 9.70 Reuters2-018.SGML 328 39 8.41 Reuters2-019.SGML 316 32 9.87 Reuters2-020.SGML 402 26 15.46 Reuters2-021.SGML 273 16 17.06 Table 3. Number of documents in the collection of editorials from the newspaper “El Mundo” grouped by categories of Eurovoc, following the manual classification performed in the film processing stage. Eurovoc Category Number of Documents Agriculture, Forestry and Fisheries 2 Finance 9 Social Affairs 161 Science 3 European Communities 22 Law 302 Education and Communication 30 Enterprise and Competition 8 Energy 20 Geography 4 Industry 19 Economic Exchanges and Trade 5 Environment 11 International Organizations 9 Production, Technology and Research 1 International Relations 219 Labor and Employment 13 Transportation 18 Economic Life 36 Political Life 510 Thus, the experiments with the GA, making five exe- cutions were carried out on each of the samples taken from experimental collections. The output of the experi- ment is the best fitness obtained and the convergence speed or the generation where the best fitness was gotten. Finally, as a measure of the quality of the algorithm is able to serve the best solution obtained and the robust- ness, i.e. the average quality of the algorithm (average values of the various solutions obtained) [18]. In experiments in our work environment, we used samples of documents collected randomly from “very few (20), few (50), many (80) and enough (150)” docu- ments, with the requirement that belonged to only two categories of Reuters or distribution of Editorials in Spanish. Each sample was processed with 5 different seeds, and each of the results was compared with a result from Kmeans method. Because of its influence during the experiments, the choice of GA parameters has been analyzed in detail. We attended, the evolution of successes (groups assigned to each document which accords with the distribution), and the changing role of adaptation “fitness” used. 3.1. Determination of the Value of α in the GA To determine this value of α, we use the distribution that has the highest dispersion of documents in the Reuters collection (distribution 21) and apply the GA varying the value of α in each of the tests with the usual parameters, always trying to test the effectiveness of the GA. We analyzed the relationship between fitness and the value of α (Figure 9). In Table 4, we show the results in de- termining the value of α with different samples of docu- ments examined. The results suggest that a value of α close to 0.85 pro- vides better results because it gives us more effectiveness in terms of number of hits, and a better fitness for the algorithm. This is corroborated with other distribution of the collection. 3.2. Tests to Determine the Rate for Mutation and Crossover Operators We began with an analysis of the system behaviour for different rate of the mutation operator in a wide range of values to cover all possible cases. Thus, for the rate of mutation operator in the range of: 0.01, 0.03, 0.05, 0.07, 0.1, 0.3, 0, 5, 0.7; that allows us to apply the mutation operator of GA in different circumstances and study their behaviour. To determine the optimal value of the cross- over operator over an interval from 0.70 to 0.95; select- ing high values to apply more frequently the crossing operator for the GA. As an index of the quality of the operator we have the number of hits of the GA. In Fig- re 10, we show the average number of hits for samples u Copyright © 2012 SciRes. JILSA 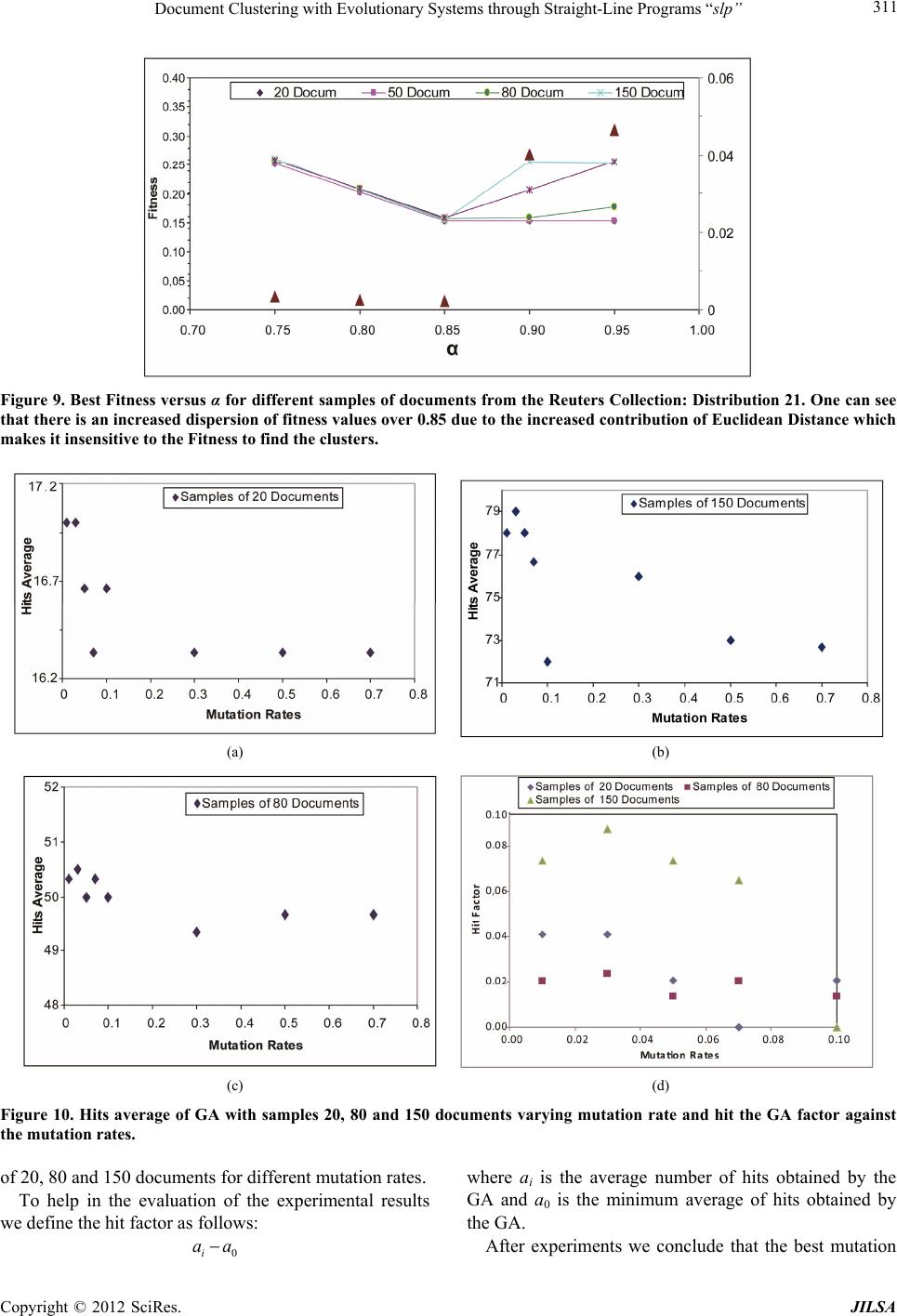 Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” 311 Figure 9. Best Fitness versus α for different samples of documents from the Reuters Collection: Distribution 21. One can see that there is an increased dispersion of fitness values over 0.85 due to the increased contribution of Euclidean Distance which makes it insensitive to the Fitness to find the clusters. (a) (b) (c) (d) Figure 10. Hits average of GA with samples 20, 80 and 150 documents varying mutation rate and hit the GA factor against the mutation rates. of 20, 80 and 150 documents for different mutation rates. To help in the evaluation of the experimental results we define the hit factor as follows: 0i aa where ai is the average number of hits obtained by the GA and a0 is the minimum average of hits obtained by the GA. A fter experiments we conclude that the best mutation Copyright © 2012 SciRes. JILSA 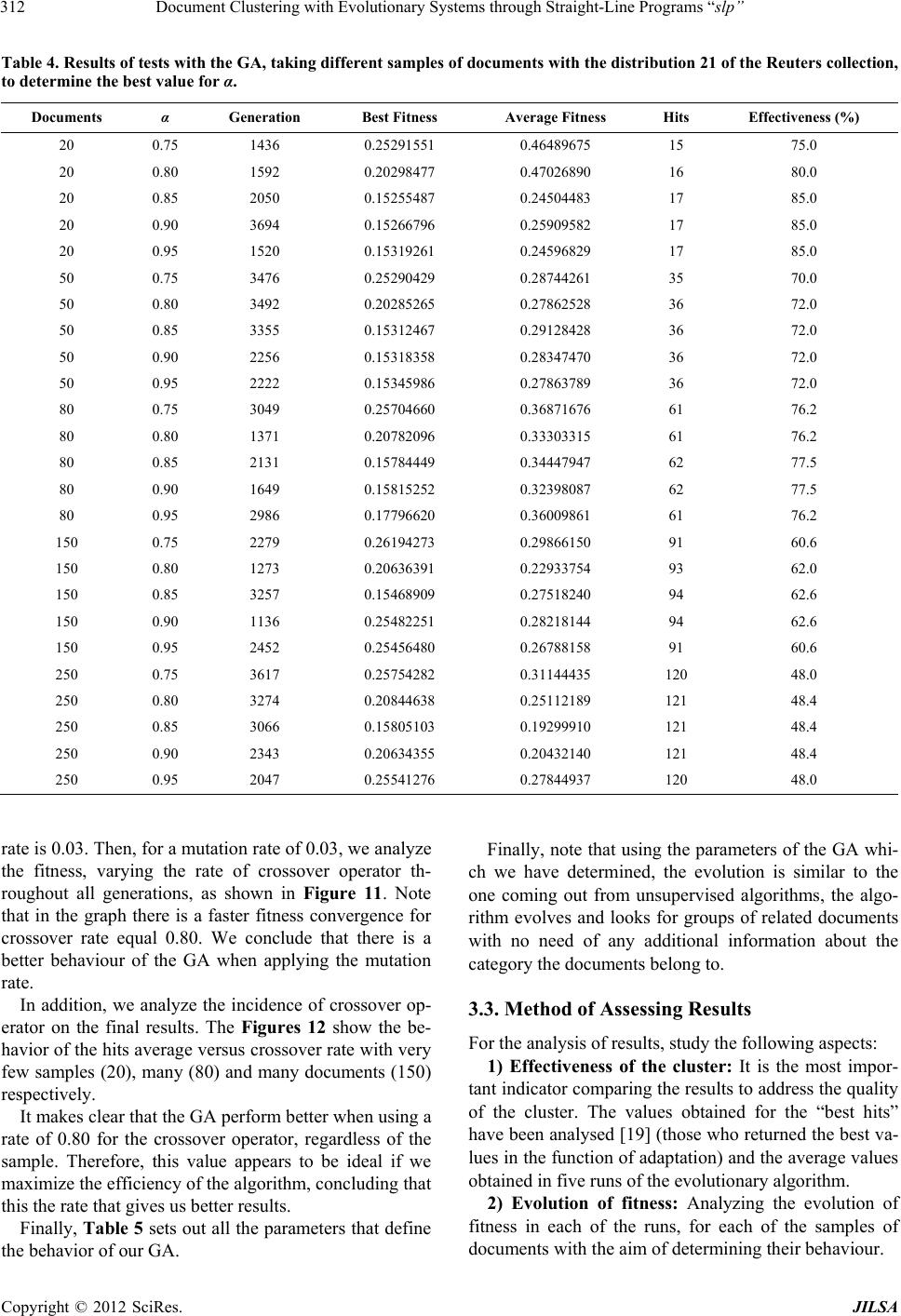 Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” 312 Table 4. Results of tests with the GA, taki ng different samples of documents with the distribution 21 of the Reuters collection, to determine the best value for α. Documents α Generation Best Fitness Average Fitness Hits Effectiveness (%) 20 0.75 1436 0.25291551 0.46489675 15 75.0 20 0.80 1592 0.20298477 0.47026890 16 80.0 20 0.85 2050 0.15255487 0.24504483 17 85.0 20 0.90 3694 0.15266796 0.25909582 17 85.0 20 0.95 1520 0.15319261 0.24596829 17 85.0 50 0.75 3476 0.25290429 0.28744261 35 70.0 50 0.80 3492 0.20285265 0.27862528 36 72.0 50 0.85 3355 0.15312467 0.29128428 36 72.0 50 0.90 2256 0.15318358 0.28347470 36 72.0 50 0.95 2222 0.15345986 0.27863789 36 72.0 80 0.75 3049 0.25704660 0.36871676 61 76.2 80 0.80 1371 0.20782096 0.33303315 61 76.2 80 0.85 2131 0.15784449 0.34447947 62 77.5 80 0.90 1649 0.15815252 0.32398087 62 77.5 80 0.95 2986 0.17796620 0.36009861 61 76.2 150 0.75 2279 0.26194273 0.29866150 91 60.6 150 0.80 1273 0.20636391 0.22933754 93 62.0 150 0.85 3257 0.15468909 0.27518240 94 62.6 150 0.90 1136 0.25482251 0.28218144 94 62.6 150 0.95 2452 0.25456480 0.26788158 91 60.6 250 0.75 3617 0.25754282 0.31144435 120 48.0 250 0.80 3274 0.20844638 0.25112189 121 48.4 250 0.85 3066 0.15805103 0.19299910 121 48.4 250 0.90 2343 0.20634355 0.20432140 121 48.4 250 0.95 2047 0.25541276 0.27844937 120 48.0 rate is 0.03. Then, for a mutation rate of 0.03, we analyze the fitness, varying the rate of crossover operator th- roughout all generations, as shown in Figure 11. Note that in the graph there is a faster fitness convergence for crossover rate equal 0.80. We conclude that there is a better behaviour of the GA when applying the mutation rate. In addition, we analyze the incidence of crossover op- erator on the final results. The Figures 12 show the be- havior of the hits average versus crossover rate with very few samples (20), many (80) and many documents (150) respectively. It makes clear that the GA perform better when using a rate of 0.80 for the crossover operator, regardless of the sample. Therefore, this value appears to be ideal if we maximize the efficiency of the algorithm, concluding that this the rate that gives us better results. Finally, Ta ble 5 sets out all the parameters that define the behavior of our GA. Finally, note that using the parameters of the GA whi- ch we have determined, the evolution is similar to the one coming out from unsupervised algorithms, the algo- rithm evolves and looks for groups of related documents with no need of any additional information about the category the documents belong to. 3.3. Method of Assessing Results For the analysis of results, study the following aspects: 1) Effectiveness of the cluster: It is the most impor- tant indicator comparing the results to address the quality of the cluster. The values obtained for the “best hits” have been analysed [19] (those who returned the best va- lues in the function of adaptation) and the average values obtained in five runs of the evolutionary algorithm. 2) Evolution of fitness: Analyzing the evolution of fitness in each of the runs, for each of the samples of documents with the aim of determining their behaviour. Copyright © 2012 SciRes. JILSA  Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” 313 3) Convergence of the algorithm: To ensure the ro- bustness of GA, we analyzed the mean convergence of the algorithm on all executions. In order to better compare the results, we introduced in the system parameters shown in Table 4 for all runs. In addition, all results are compared with those ob- tained by the Kmeans supervised clustering algorithm in optimal conditions. Therefore, all experiments that evalu- ated the quality of the evolutionary algorithm were made in advance knowing the actual results, varying for each test the number of documents to cluster, and taking groups of two known categories of documentary collec- tion. Thus, the results are always compared with real data obtained from the documentary process, being able to verify the efficiency of the GA [20]. In each run all the documents were processed by the evolving system with different seeds (5) that depended on the runtime system. In regard to Kmean s algorithm, it was executed with the same samples processed, passing as data the number of groups is desired, then also better compare the effective- ness the proposed algorithm against its performance in ideal conditions. 3.4. Better Results with Samples fro m Reuters Documents in the Collections (Collections in English) Analyzed the behaviour for the four distributions of Reu- ters collection, the tables below (Tables 6 and 7, Tables 8 and 9) show the best result and the average result for each sample. In the following graphs (Figures 13(a)-(d)), we show in percentage, the efficiency of the GA with different samples of documents in different distributions of the collection documents Reuters. 3.5. Better Results with Samples of Documents in the Collection of Publishers (Collections in Spanish) In Table 10, we perform the same treatment with the Table 5. Parameters considered for evolutionary system (GA). Parameters Values Population Size (Number of Trees) 50 Generations 4000 Tournament Size 2 Mutation Rate 0.03 Crossover Rate 0.80 Number of Documents Very Few (20), Few (50), Many (80), Enough Documents (150), and More Documents (250) Number of Terms Lemmatisers40 Coefficient α 0.85 Threshold Depth 7/10 Figure 11. Evolution of fitness by varying the rate of crossover operator GA for a fixed mutation rate equal to 0.03. It is seen that the values of crossover rate close to 0.80 improves the convergence of the GA. Copyright © 2012 SciRes. JILSA  Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” 314 (a) (b) (c) (d) Figure 12. Hits average of GA with samples 20, 80 and 150 documents varying crossover rate and hit the GA factor against the crossover rates. Table 6. Comparative results Evolutionary System with various samples of documents showing the best results and the aver- age results of evaluations with the “Distribution 2” of the Reuters 21578 collection. Distribution 2 Reuters Collection 1 Documents Categories: Acq y Earn Best Result Best Average Samples of Documents Fitness Effectiveness ConvergenceAverage FitnessDeviation Fitness Average Converg Kmeans Very Few documents (20 documents) 0.155447570 85% (18 hits) 886 0.15545476 0.00000828 1086 16.6 Few Documents (50 Documents) 0.156223280 94% (47 hits) 3051 0.15624280 0.00002329 2641 45.8 Many Documents (80 Documents) 0.159009400 89% (71 hits) 2500 0.15921181 0.00020587 2246 67.8 Enough Documents (150 Documents) 0.165013920 77% (115 hits)2342 0.16508519 0.00007452 2480 121.6 More Documents (246 Documents) 0.174112100 69% (170 hits)2203 0.17430502 0.00033602 2059 202.8 Spanish collection of documents from editorials of the “El Mundo” newspaper from the years 2006 and 2007. The following figures (Figures 14 and 15) show the effectiveness of the GA and the convergence of it. In the overall, our algorithm gives good results with both documentary collections. We can say that at the end of the evolution and using all the parameters studied and configured for the algorithm, we offer a high effective- ness to perform both clustering of documents. Thus, the algorithm is stable and robust, independently of the sam- Copyright © 2012 SciRes. JILSA  Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” 315 Table 7. Comparative results Evolutionary System with various samples of documents showing the best results and the aver- age results of evaluations with the “Distribution 8” of the Reuters 21578 collection. Distribution 8 Reuters Collection 2 Documents Categories: Acq y Earn Best Result Best Average Samples of documents Fitness Effectiveness ConvergenceAverage FitnessDeviation Fitness Average Converg.Kmeans Very Few documents (20 documents) 0.151163560 85% (17 hits) 555 0.15116356 0.00000000 679 15.8 Few Documents (50 Documents) 0.154856500 96% (48 hits) 1615 0.15485650 0.00000000 1334 43.8 Many Documents (80 Documents) 0.157073880 85% (68 hits) 746 0.15708362 0.00000898 1360 66.2 Enough Documentos (150 Documents) 0.162035070 69.3% (104 hits)1989 0.16242664 0.00033091 2283 117.6 More Documents (188 Documents) 0.163014600 68.63% (129 hits)2293 0.16334198 0.00027325 1773 140.6 Table 8. Comparative results Evolutionary System with various samples of documents showing the best results and the aver- age results of evaluations with the “Distribution 20” of the Reuters 21578 collection. Distribution 20 Reuters Collection 3 Documents Categories: Acq y EarnBest ResultBest Average Samples of Documents Fitness Effectiveness ConvergenceAverage FitnessDeviation Fitness Average ConvergKmeans Very Few Documents (20 Documents) 0.153027060 85% (17 hits) 1092 0.15321980 0.00018398 1108 16.8 Few Documents (50 Documents) 0.156198620 92% (46 hits) 2173 0.15666137 0.00030077 2635 44.8 Many Documents (80 Documents) 0.158069980 81.25% (65 hits)2196 0.15810383 0.00001884 1739 66.8 Enough Documents (108 Documents) 0.159031080 69.4% (75 hits)1437 0.15927630 0.00026701 2636 82.2 Table 9. Comparative results Evolutionary System with various samples of documents showing the best results and the aver- age results of evaluations with the “Distribution 21” of the Reuters 21578 collection. Distribution 21 Reuters Collection 4 Documents Categories: Acq y EarnBest ResultBest Average Samples of Documents Fitness EffectivenessConvergenceAverage FitnessDeviation Fitness Average ConvergKmeans Very Few Documents (20 Documents) 0.152048900 90% (18 hits) 1163 0.15206069 0.00001601 1165 17.8 Few Documents (50 Documents) 0.153006650 92% (46 hits) 2079 0.15304887 0.00004569 2736 45.6 Many Documents (80 Documents) 0.156029510 81% (65 hits) 2787 0.15637693 0.00025014 2810 66.4 Enough Documents (132 Documents) 0.157012180 70.4% (93 hits)3359 0.15720766 0.00024132 1980 98.6 ple or collections of documents used. The hit rate is very high in both collections of documents (having better ef- fectiveness in the collection Reuters). The results of combined fitness, are as good or better than the algorithm Kmeans. 4. Conclusions This work has done an extension of evolutionary algo- rithms, incorporating an slp data structure that improves the performance of the algorithm in its task of grouping documents. Considering the average results obtained on all samples in each of the used document collections, we see that good results are obtained, and it is feasible to extend and to design new data structures that can with- stand the usual genetic operators, in order to use them in optimization problems. This paper has proposed a so- lution, using an evolutionary system for the problem of clustering documents. The system has been studied in relation to the number of documents to be processed. Ex- periments show good performance for collections of less than 150 documents, with hits Kmeans above algorithm. hus, we found that the effectiveness of our algorithm T Copyright © 2012 SciRes. JILSA  Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” 316 (a) (b) (c) (d) Figure 13. (a) Comparison of percentages of effectiveness of GA and Kmeans with samples of documents from each of the major distributions of the Reuters collection (Distribution 2); (b) Comparison of percentages of effectiveness of GA and Kmeans with samples of documents from each of the major distributions of the Reuters collection (Distribution 8); (c) Com- parison of percentages of effectiveness of GA and Kmeans with samples of documents from each of the major distributions of the Reuters collection (Distribution 20);(d) Comparison of percentages of effectiveness of GA and Kmeans with samples of documents from each of the major distributions of the Reuters collection (Distribution 21). Copyright © 2012 SciRes. JILSA 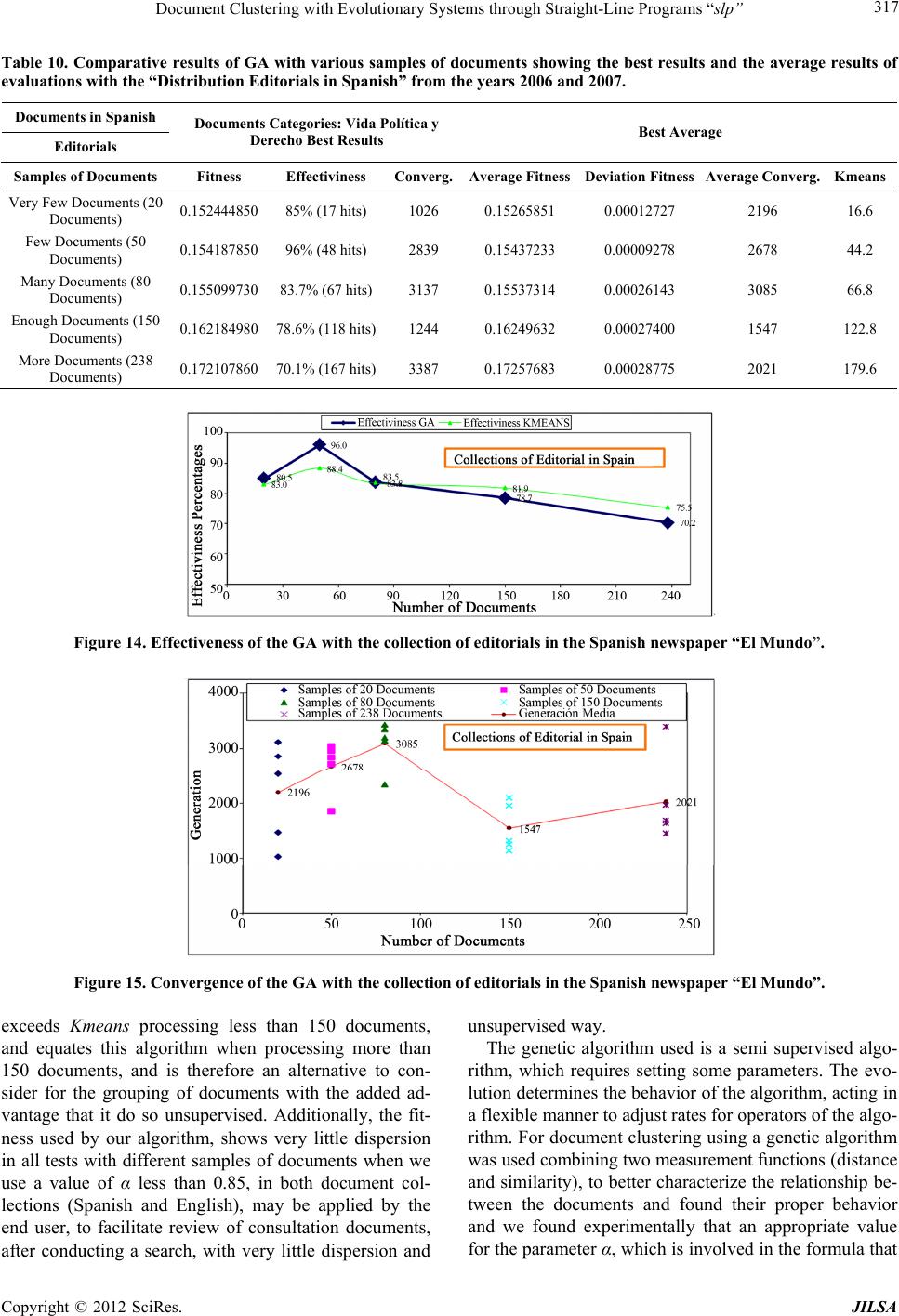 Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” 317 Table 10. Comparative results of GA with various samples of documents showing the best results and the average results of evaluations with the “Distribution Editorials in Spanish” from the years 2006 and 2007. Documents in Spanish Editorials Documents Categories: Vida Política y Derecho Best Results Best Average Samples of Documents Fitness Effectiviness Converg.Average FitnessDeviation Fitness Average Converg.Kmeans Very Few Documents (20 Documents) 0.152444850 85% (17 hits) 1026 0.15265851 0.00012727 2196 16.6 Few Documents (50 Documents) 0.154187850 96% (48 hits) 2839 0.15437233 0.00009278 2678 44.2 Many Documents (80 Documents) 0.155099730 83.7% (67 hits)3137 0.15537314 0.00026143 3085 66.8 Enough Documents (150 Documents) 0.162184980 78.6% (118 hits)1244 0.16249632 0.00027400 1547 122.8 More Documents (238 Documents) 0.172107860 70.1% (167 hits)3387 0.17257683 0.00028775 2021 179.6 Figure 14. Effectiveness of the GA with the collection of editorials in the Spanish newspaper “El Mundo”. Figure 15. Convergence of the GA with the collection of editorials in the Spanish newspaper “El Mundo”. exceeds Kmean s processing less than 150 documents, and equates this algorithm when processing more than 150 documents, and is therefore an alternative to con- sider for the grouping of documents with the added ad- vantage that it do so unsupervised. Additionally, the fit- ness used by our algorithm, shows very little dispersion in all tests with different samples of documents when we use a value of α less than 0.85, in both document col- lections (Spanish and English), may be applied by the end user, to facilitate review of consultation documents, after conducting a search, with very little dispersion and unsupervised way. The genetic algorithm used is a semi supervised algo- rithm, which requires setting some parameters. The evo- lution determines the behavior of the algorithm, acting in a flexible manner to adjust rates for operators of the algo- rithm. For document clustering using a genetic algorithm was used combining two measurement functions (distance and similarity), to better characterize the relationship be- tween the documents and found their proper behavior and we found experimentally that an appropriate value for the parameter α, which is involved in the formula that Copyright © 2012 SciRes. JILSA  Document Clustering with Evolutionary Systems through Straight-Line Programs “slp” 318 combines linearly and inverse distance metric of simi- larity of our fitness, has to take values close to 0.85. Ex- ceeded this value, the contribution of both metrics will gradually and cease to be adequate. We used a mutation rate equal to 0.03 along with a crossover rate of 0.80, to ensure that our results are better than the Km ean s algori- thm. Finally, we conclude that using an evolutionary ap- proach with appropriate parameters, is a preferable alter- native to traditional methods. 5. Acknowledgements We would like to thank Departament of Computer Sci- ence of University of Alcalá for its support and for pro- viding this research oportunity. Work done under project: VOA3Rr: Virtual Open Ac- cess Agriculture & Aquaculture Repository: Sharing Sci- entific and Scholarly Research related to Agriculture, Food, and Environment (CIP-ICT-PSP.2009.2.4: 250525- VOA-3R) REFERENCES [1] R. Baeza-Yates and B. Ribeiro Neto, “Modern Informa- tion Retrieval,” 2nd Edition, ACM Press Book Addison- Wesley, New York, 1999. [2] Z. Michalewicz, “Genetic Algorithms + Data Structures = Evolution Program,” Third Edition, Springer-Verlag, Ber- lin, 1999. [3] M. Aldaz, J. Heintz, G. Matera, J. L. Montaña and L. M. Pardo, “Time-Space Tradeoffs in Algebraic Complexity Theory,” Journal of Complexity, Vol. 16, No. 1, 1998, pp. 2-49. doi:10.1006/jcom.1999.0526 [4] C. L. Alonso, J. L. Montaña and J. Puente, “Straight Line Programs: A New Linear Genetic Programming Ap- proach,” Proceedings of the 20th International Confer- ence of the IEEE on Tools with Artificial Intelligence, ICTAI, Dayton, 3-5 November 2008, pp. 517-524. [5] D. Goldberg, “Genetic Algorithms in Search, Optimiza- tion and Machine Learning,” First Edition, AddisonWes- ley, 1989. [6] J. Koza, “Genetic Programming: On the Programming Computers by Means of Natural Selection,” Massachu- setts Institute of Technology, Cambridge, 1992. [7] J. L. Castillo, J. R. Fernández del Castillo and L. Gon- zález, “Feature Reduction for Document Clustering with NZIPF Method,” Proceedings of IADIS International Conference e-Society 2009, Barcelona, 25-28 February 2009, pp. 205-209. [8] J. L. Castillo, J. R. Fernández del Castillo and L. Gon- zález, “Methodology of Preprocessing of Documents for Systems of Recovery of Information,” Proceedings of IADIS International Conference, Information System 2008, Algarve, 9-11 April 2008, pp. 324-327. [9] G. K. Zipf, “Human Behavior and the Principle of Least Effort: An Introduction to Human Ecology,” Addison Wesley, Cambridge, 1949. [10] J. A. Moreiro González, “Applications from Content Ana- lysis of the Mathematical Theory of Information,” Jour- nal of Documentation, Vol. 5, 2002, pp. 273-286. [11] M. L. Pao, “Automatic Indexing Based on Goffman Tran- sition of Word Occurrences,” American society for In- formation Science. Meeting 40th Information Manage- ment in the 1980’s: Proceedings of the ASIS Annual Meeting, Chicago, 26 September-1 October 1977. [12] M. Berry and M. Castellanos, “Survey of Text Mining II,” Springer Verlag, London, 2008. doi:10.1007/978-1-84800-046-9 [13] J. Arabas, Z. Michalewicz Zbigniew and J. Mulawka “GAVaPs—A Genetic Algorithm with Varying Popula- tion Size,” Proceedings of the First Conference on Evolu- tionary Computation of the IEEE, orlando, 27-29 June 1994, pp. 73-79. [14] J. L. Castillo, J. R. Fernández del Castillo and L. Gon- zález, “Information Retrieval with Cluster Genetic,” Pro- ceedings of IADIS International Conference on Data Mi- ning, Amsterdam, 24-26 July 2008, pp. 77-81. [15] J. L. Castillo, J. R. Fernández del Castillo and L. Gon- zález, “Group Method of Documentary Collections using Genetic Algorithms,” Proceedings Part II of Distributed Computing, Artificial Intelligence, Bioinformatics, Soft Computing, and Ambient Assisted Living. 10th Interna- tional Work-Conference on Artificial Neural Network IWANN, Salamanca, 10-12 June 2009, pp. 992-1000. [16] L. Davis, “Reuters-21578 Text Categorization Test col- lection,” 1987. http://www.daviddlewis.com/resources/testcollections/reu ters21578/ [17] Eurovoc, “Eurovoc Thesaurus. Alphabetic Presentation Permuted,” Edition 4.2, Spanish Language, European Communities, 2006. [18] D. Olson and D. Delen, “Advanced Data Mining Tech- niques,” Springer-Verlag, Berlin, 2008. [19] A. M. Robertson and P. Willet, “Generation of Equifre- cuent Groups of Words Using a Genetic Algorithms,” Journal of Documentation, Vol. 50, No. 3, 1994, pp. 213- 232. [20] J. C. Bezdeck, “Genetic Algorithms Guided Clustering,” IEEE Proceedings of the First Conference on Evolution- ary Computation, Orlando, 27-29 June 1994, pp. 34-40. Copyright © 2012 SciRes. JILSA
|