Journal of Intelligent Learning Systems and Applications, 2012, 4, 255-265
http://dx.doi.org/10.4236/jilsa.2012.44026 Published Online November 2012 (http://www.SciRP.org/journal/jilsa)
255
Genetic Algorithms for Perceptual Codes Extraction
Mahmoud Ltaief, Sourour Njah, Hala Bezine, Adel M. Alimi
National School of Engineers, The University of Sfax, Sfax, Tunisia.
Received April 25th, 2012; revised July 11th, 2012; accepted July 18th, 2012
ABSTRACT
In this work a new technique for global perceptual codes (GPCs) extraction using genetic algorithms (GA) is presented.
GAs are employed to extract the GPCs in order to reduce the original number of features and to provide meaningful
representations of the original data. In this technique the GPCs are build from a certain combination of elementary per-
ceptual codes (EPCs) which are provided by the Beta-elliptic model for the generation of complex handwriting move-
ments. Indeed, in this model each script is modelled by a set of elliptic arcs. We associate to each arc an EPC. In the
proposed technique we defined four types of EPCs. The GPCs can be formed by many possible combinations of EPCs
depending on their number and types. So that, the problem of choosing the right combination for each GPC can be re-
garded as a global optimization problem which is treated in this work using the GAs. Several simulation examples are
presented to evaluate the interest and the efficiency of the proposed technique.
Keywords: Online Handwriting; Beta-Elliptic Model; Elementary Perceptual Codes; Global Perceptual Codes;
Genetic Algorithms
1. Introduction
Since the appearance of the computer, humankind has
always tried to give this machine the similar behavior.
He wanted to make it capable to read and to understand
automatically the handwriting. In order to do this task, it
is important to study the manner that we do it. The stud-
ies of psychologists try to have answers to these ques-
tions: How we can read and recognize words? How can
the reader pass from a set of features and curves to letters
and words? What are the detected primitives during the
process of reading?
Handwriting was developed a long time ago as a man-
ner to expand human memory and to facilitate commu-
nication [1,2]. Human are similar, they have a common
education but they produce a different handwritten styles.
Because written language is important, the understanding
of handwriting is important too. So far, several theories
and models have been proposed to study and to analyze
handwriting [3-6].
Reading a word is recognizing it. So, word recognition
implies the process of visual information, and its repre-
sentation at the linguistic level. Psychologists call lexical
access the process by which human associate the image
of the word with its meaning. Most lexical access models
take into account the orthographic (the way the word is
written) and the phonological aspects (the way the word
is pronounced) of the word [7,8]. Several reading and
writing models have been developed:
Pandemonium model (Selfridge, 1959): this model is
hierarchically composed of three levels containing re-
spectively: feature demons, cognitive demons and deci-
sion demons. These ones operate in parallel way. In order
to recognize a pattern, demons of the different levels are
activated [9-10].
Logogen model (Morton, 1969): it associates at every
logogen a threshold indicating the necessary activation
level to recognize the word partner [9,10].
Interactive Activation model (McClelland and Rumel-
hart, 1981): in this model, a connexion’s architecture of
three layers (primitive, letters and words), is hierarchi-
cally organized. The necessary time needed to recognize
one letter in a word is less than a time needed to recog-
nize letter in isolation position [8-10].
Marr’s model (Marr 1981): According to Marr: “Vi-
sion can be understood as an information processing task
which converts a numerical image representation into a
symbolic shape-oriented representation” [8,9,11].
In this paper, we present a new perceptual model
which is inspired from the McClelland and Rumelhart’s
reading model of the human system [12]. The underlying
idea is derived from studies of reading systems. In the
following section, we describe the proposed model. First
of all, we present the architecture and the steps which
compose this earlier. In section two we define the Beta-
elliptic model for the generation of complex handwriting
movements. Based on this previous model, an Elemen-

Genetic Algorithms for Perceptual Codes Extraction
256
tary Perceptual Codes (EPC) extractor is established
which is described in the third section. Forth section pre-
sents the Global Perceptual Codes (GPC) extractor using
genetic algorithms. In the last section we present the ex-
periments made to test the performance of the developed
system. Finally, we present some conclusions and further
works.
The Proposed Perceptual Model
The proposed model is interested to online handwriting.
The scripter writes on a digitizing tablet using a special
stylus. So that the user’s written scripts are captured as
they are being formed by sampling the pen’s (x,y) coor-
dinates at eventually spaced time intervals. The acquired
handwriting data are pre-processed. After that we use the
Beta elliptic model for the generation of handwriting
movements; in this step we obtain a matrix of parameters
which are used in the third step to extract the elementary
perceptual codes: the representation of a character is
made of four basic strokes, and a handwritten character is
generated by a combination of several strokes [13]. In the
last stage, we use genetic algorithms to extract the global
perceptual codes which are the combinations of different
EPCs sets.
The architecture of our proposed model is shown in
the following figure (Figure 1). Step 1: the pre-process-
ing of handwriting is done to have the best representation
of input data. The other steps will be described in the fol-
lowing part.
2. The Beta-Elliptic Model for the
Generation of Complex Handwriting
Movements
The beta-elliptic model is based on some assumptions:
Firstly, it considers that handwriting movement, like any
other highly skilled motor process, is partially program-
med in advance. Secondly, it supposes that movements
are represented and planned in the velocity domain since
the most widely accepted invariant in movement genera-
tion is the beta function of the velocity profiles. In its
simplest form, the model is based on the beta equation
where t0 is the starting time, t1 is
the ending time, p and q are intermediate parameters, as
shown in Equation (1). This equation describes the ve-
locity profile in the kinematics domain which is in turn
represented by an elliptic arc that characterizes the tra-
jectory in the static domain [14-17].

01
, , , , ,
c
tpqtt t 

 
01
010 1
01
01
,,,,,ift, t
0ifnot
Where :, , R
pq
c
cc
tt tt
tpqtt tt
tt tt
pqt t

 






(1)
1
c
pt qt
tpq



0
(2)
The curvilinear velocity is given by this equation:
 


12
2
dd ddVtx tyt
2
(3)
The Beta-parameters (tc, = t1  tc, p, q, H: Beta am-
plitude) are presented in the Figure 2.
The elliptic-parameters (x0, y
0, a, b, θ) describe the
static aspect of the handwriting movement; a: large axe
of ellipse, b: small axe of ellipse, and x0 and y0 corre-
spond to the coordinates of the ellipse centre O. The de-
viation angle θ is formed by the ellipse and the horizontal
axe, and it is obtained by the Equation (4) [16-18].


10
10
arctan yy gxx 
 






(4)
Pre-processing
Extraction of handwriting features
with the Beta-elliptic model
Extraction of Global Perceptual Codes (GPC) with genetic
algorithms
Analytic extraction of Elementary
Perceptual Codes (EPC)
Perceptual codified script
Data (x, y)
Figure 1. The architecture of the perceptual model.
Figure 2. The different Beta-parameters.

Genetic Algorithms for Perceptual Codes Extraction 257
Then for each ellipse arc we have ten parameters (t, p,
q, t0, t1, a, b, x0, y0, θ).
For each elementary perceptual code we affected three
variables which are: the code, the type (Shaft, valley,
Left oblique shaft and right oblique shaft) and the symbol
(see Table 1). These codes are used later to codify hand-
written scripts generated by the Beta-elliptic model.
Figure 3(a) presents the brute example of the Arabic
letter “” and the Figure 3(b) presents this letter
generated with the Beta-elliptic model.
3. Extraction of Elementary Perceptual
Codes
Basing on the Beta-elliptic model for the generation of
handwriting, each script is modeled by a series of elliptic
arcs. Each elliptic arc will be coded by a set of five pa-
rameters (respectively: a, b, x0, y0 and θ). With these pa-
rameters help, each script will be represented by a set of
strokes. The representation of a character is made by four
basic strokes, and a handwritten character was generated
by a combination of several strokes [13].
Depending on the ellipse deviation angle θ from the
horizontal, we subdivided the trigonometric circle into
eight equidistant intervals of length /4. Assuming the
trigonometric sense, we defined a positive part going
from 0 to  and a negative part going from 0 to . Ac-
cording to the orientation of ellipses we have identified
four types of strokes (see Figure 4). Each stroke has the
opportunity to belong to two separate intervals. The first
is the positive part of the trigonometric circle and the
second is the negative part. The stroke number two (Val-
ley), belongs to two intervals containing each one a posi-
tive and a negative part. It takes into account both sides
of the trigonometric circle (positive and negative) to in-
dicate the direction of writing which is consistent with
the trigonometric direction. The direction of writing gives
us the obligation to use two intervals (one in the negative
part of the trigonometric circle and the other in the posi-
tive part) for each stroke. This test provides a contribu-
tion to our model compared to the method of Freeman
giving discreet orientation for the entire strokes forming
the script and other models that do not take into account
the direction of the writing. These strokes still called
elementary perceptual codes (EPC).
(a) (b)
Figure 3. (a) The brute example of the Arabic letter “
The letter “” generated by elementary perceptual
codes (see Figure 5(a)) is composed by only one seg-
ment i.e. the writer wrote this script without lifting pen. It
is noted in the table below (see Figure 5(b)) that the
number of lines in the matrix of EPCs is proportional to
the number of segments making the script. The number
of columns of the matrix of EPCs indicates the number
of elementary perceptual codes making the letter “”.
Then each element of the matrix indicates the corre-
sponded code of the EPC. In our case the letter “” is
composed of twenty two EPCs.
1
3
4
22
34
1
‐7π/8
‐5π/8 ‐3π/8
‐π/8
π/8
3π/8
5π/8
7π/8
0
±pi
Figure 4. The Elementary Perceptual Codes EPC.
(a)
(b)
”; (b)
The Arabic letter “” generated with the Beta-elliptic
model.
Figure 5. (a) Generation of the letter “” with the EPCs; (b)
EPCs vector.

Genetic Algorithms for Perceptual Codes Extraction
258
The letter “D” generated with elementary perceptual
codes (Figure 6(a)) consists of two segments i.e. the
writer wrote the script with a lifted stylus. In the matrix
of EPCs each segment is represented by a column. If
segments of the same script did not have the same length
(number of EPCs) then in the matrix of EPCs we com-
plete the corresponding vacant boxes by zero as illus-
trated by the Figure 6(b) below.
The first segment of the letter “D” is composed by 4
EPCs and the second is composed by nine EPCs.
Relying on human vision we can not detect the ele-
mentary perceptual codes but we detect more general
features. The idea is to find a method for detecting global
features that constitute the script after gathering a num-
ber of elementary perceptual codes following basic crite-
ria. In our model we define a set of global features. These
features are called global perceptual codes (GPC).
4. Extraction of Global Perceptual Codes
In our model ten global perceptual codes GPCs are de-
fined varying from the shaft to the ain and different pos-
sibilities of combinations which differ in type and length.
The following table (see Table 2) presents the GPCs
with their different types, numbers, symbols and a few
Table 1. The elementary perceptual codes EPC.
Code Type Symbol
1 Shaft l
2 Valley 
3 Left oblique shaft /
4 Right oblique shaft \
(a)
(b)
Figure 6. (a) Generation of the letter “D ” with the EPCs; (b)
EPCs matrix.
Table 2. The global perceptual codes GPC.
CodeType Symbol Some examples of GPCs
1 Shaft |
{1 1 1 4}; {1 1 3 1 1}; {1 1
1 1 1 1}; {1 3 1 1 1 1 4}; ···
2 Valley  {2 2 4 2}; {2 2 2 2 2}; {2 2
3 2 2}; {2 3 2 2 3 2}; ···
3 Left oblique
shaft / {3 3 3 3}; {3 3 3 1 3}; {3 2 3 3 2}; {3 1 3 3 3 2}; ···
4 Right oblique
shaft \ {4 4 4 4}; {4 4 4 1}; {4 4 4 2}; {4 2 4 4 1 4}; ···
5
Right half
opening
occlusion

{3 1 4 2}; {2 2 3 1 3 1 1 2};
{2 2 1 1 3 2 4}; {3 3 1 4 2
2}; ···
6
Left half
opening
occlusion

{4 1 3 2}; {2 2 4 1 3 3 2};
{2 2 4 1 1 3 2 2}; {2 2 4 4 1
1 3 3 2}; ···
7
Up half
opening
occlusion
∪
{1 1 2 2 1 1}; {1 4 2 2 3 1};
{1 1 2 2 3 3 3}; {4 1 1 2 2 1
3 3}; ···
8
Down half
opening
occlusion

{1 3 2 1 1}; {1 1 3 2 1 1};
{1 1 3 2 4 4 4}; {1 1 4 2 2 3
1 1}; ···
9 Occlusion O
{1 3 4 1 3 4}; {3 2 4 3 2 4};
{1 3 2 4 1 3 2 4}; {2 3 1 4 2
3 1 4}; ···
10 Ain
{2 4 2 2 3 2}; {4 4 2 2 2 3
3}; {4 4 3 2 4 3 3}; {2 4 3 3
4 4 3 2}; ···
extraction criteria. It means a few sets of EPCs able to
build each GPC.
Referring to the Figure 7, we can note that there are
many possible combinations of elementary perceptual
codes that can form the GPCs which vary depending on
the number of EPCs and their types. Likewise for the
other global perceptual codes. Because of the variety of
combinations possibility concerning either the number or
the type of EPCs that form a GPC, a problem of choosing
the right combination for each GPC arises. This problem
of choice may therefore be regarded as a problem of
global optimization.
A set of GPCs can define the characteristic properties
of the symbols to be recognized and at the same time
make it possible to form a linguistic definition of a char-
acter or a word in a coded form. GPCs extraction is also
sometimes termed as data reduction, since it extracts the
required information from a huge amount of data and
thus reduces the processing time considerably if we
compare to the case when we use only the EPCs to define
the characteristic properties of the symbols to be recog-
nized. Considering the important variability of the matrix
length of the EPC which forms an unspecified GPC and
also the great number of possible combinations of the
EPCs associated with each GPC, we cannot use a deter-
ministic optimization method for the choice of the best
combination of the EPC and the fixing length of their

Genetic Algorithms for Perceptual Codes Extraction
259
GPC valley
.
.
.
.
.
22 43
2
2
2
2
2
2
3 22
2
2
GPC
Shaft
...
1
1
1
4
1
1
1
1
1
3
1
1
22
2
3
1
2
4
3
3
4
4
1
2 2
4
3
3
1
GPC right half
opening occlusion
…
4
2
3
3
1
2
4
2
2
4
3
3
1
4
1
3
3
4
4
2
2
3
4
GPC occlusion …
2
2
2
3
3
3
4
3
32
2
4
4
2
3
3
2 22
2
2
3
4
4
4
32
2 2
3…
GPC ain
Figure 7. Some examples of GPC.
matrix. Consequently, we propose the genetic algorithms
(GAs) as an indeterminist optimization technique.
The Figure 8 presents the architecture of the proposed
global perceptual codes extractor based on genetic algo-
rithms. Indeed, for each GPC we have developed a ge-
netic algorithm. Each one treats a matrix of elementary
perceptual codes and generates a set of GPCs forming the
initial script. The generated GPCs may contain redundan-
cies (i.e. GPCs that have the same location in the script)
or overlaps between some of them. To resolve theses pro-
blems we have proposed a refinement stage.
4.1. Genetic Algorithms
Genetic algorithms are a family of computational models
inspired by evolution. These algorithms encode a poten-
tial solution to a specific problem on a single chromo-
some and apply recombination operators to them so as to
preserve critical information. GAs are often viewed as
function optimizers, although the range of problems to
which GAs have been applied is quite broad. The major
reason for GAs popularity in various search and optimi-
zation problems is its global perspective, wide spread
applicability and inherent parallelism. GA starts with a
number of solutions known as population. These solu-
tions are represented using a string coding of fixed length.
After evaluating each chromosome using a fitness func-
tion and assigning a fitness value, three different opera-
tors—selection, crossover and mutation—are applied to
update the population. An iteration of these three opera-
tors is known as a generation. If a termination criterion is
not satisfied, this process repeats. This termination crite-
rion can be defined as reaching a predefined time limit or
number of generations or population convergence [19-
23].
The considered genetic algorithms have the following
properties:
4.1.1. Chromosome Representation
Unlike the traditional genetic algorithms (GAs) that adopt
binary bit strings to encode a chromosome, a more direct
representation is used in our model. As we can see in Fi-
gure 9 the chromosome is presented by a set of EPCs
which form a GPC.
4.1.2. Initialization of the Population
The initial population is randomly generated, with the
number of chromosomes is set at 100. The size of each
chromosome varies from 3 to n elementary perceptual
codes (with 3 is the minimum size of a GPC and n is the
maximum number of EPC forming a segment of the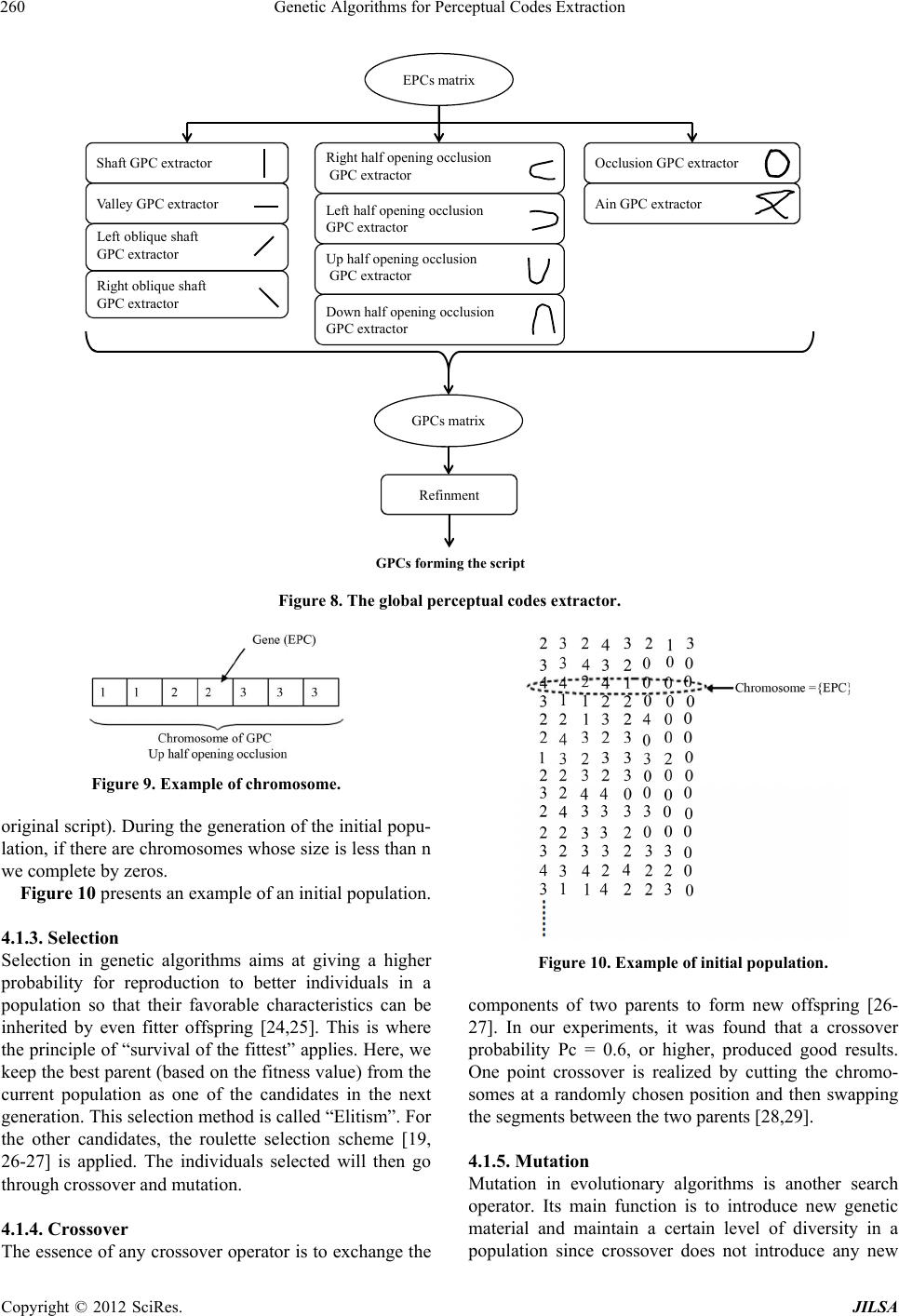

Genetic Algorithms for Perceptual Codes Extraction
260
GPCs matrix
Shaft GPC extractor
Valley GPC extractor
Left oblique shaft
GPC extractor
Right oblique shaft
GPC extractor
Right half opening occlusion
GPC extractor
Left half opening occlusion
GPC extractor
Up half opening occlusion
GPC extractor
Down half opening occlusion
GPC extractor
Occlusion GPC extractor
Ain GPC extractor
EPCs matrix
Refinment
GPCs forming the script
Figure 8. The global perceptual codes extractor.
Figure 9. Example of chromosome.
original script). During the generation of the initial popu-
lation, if there are chromosomes whose size is less than n
we complete by zeros.
Figure 10 presents an example of an initial population.
4.1.3. Selection
Selection in genetic algorithms aims at giving a higher
probability for reproduction to better individuals in a
population so that their favorable characteristics can be
inherited by even fitter offspring [24,25]. This is where
the principle of “survival of the fittest” applies. Here, we
keep the best parent (based on the fitness value) from the
current population as one of the candidates in the next
generation. This selection method is called “Elitism”. For
the other candidates, the roulette selection scheme [19,
26-27] is applied. The individuals selected will then go
through crossover and mutation.
4.1.4. Crossover
The essence of any crossover operator is to exchange the
Figure 10. Example of initial population.
components of two parents to form new offspring [26-
27]. In our experiments, it was found that a crossover
probability Pc = 0.6, or higher, produced good results.
One point crossover is realized by cutting the chromo-
somes at a randomly chosen position and then swapping
the segments between the two parents [28,29].
4.1.5. Mutation
Mutation in evolutionary algorithms is another search
operator. Its main function is to introduce new genetic
material and maintain a certain level of diversity in a
population since crossover does not introduce any new

Genetic Algorithms for Perceptual Codes Extraction 261
genetic material [28,29]. In our approach, the remaining
candidates of the next generation (after crossover) are
formed by the mutation operations.
4.1.6. Fitness Evaluation
In our model the value of the fitness evaluation is the per-
centage of correspondence between the elementary per-
ceptual codes that establish a chromosome and each part
of the script to be addressed.
The search for the existence of a GPC in a script (ma-
trix of EPCs) and the value of the fitness evaluation re-
quires: browse EPCs script by comparing them with the
first EPC of the required GPC. In Figure 11 and for re-
search of Right oblique shaft GPC we seek firstly it first
EPC, which is 4 (as shown in the figure). If we found the
first EPC of the GPC needed in the matrix of EPCs for-
ming the script, we safeguard the position of the first
EPC (in our example, the EPC 4) in the script EPCs ma-
trix as an initial position (pi = 13). Then we compare the
rest of EPCs of the required GPC with EPCs forming the
script from the initial position +1 (initial position + 1 =
position 14 in the Figure 11). If there is at least two suc-
cessive EPCs of the required GPC that have no corre-
spondents in the matrix of EPCs composing the script we
stop researching and we safeguard the final position
which is the last position of EPC found in the script
EPCs matrix. If the number of EPCs found is greater than
or equal to 3 EPCs (the smallest size of GPC) then we
retain the initial and final position of the GPC in the ma-
trix of EPCs, the code of GPC and the fitness value (see
Equation (10)).
EPC _ C
GPC
EPC
N
fN  (10)
where fGPC is the fitness value of the GPC, NEPC_C is the
number of EPCs which have a correspondence in the
matrix of EPCs composing the script and NEPC is the
number of EPCs forming the required GPC.
In Figure 11 we give an example of fitness calculation
for the GPC Right oblique shaft in the position 13 and
the GPC left oblique shaft in the position 3. In our exam-
ple we retain only the GPC Right oblique shaft with the
initial position (pi = 13), the final position (pf = 16) and
the fitness value which is equal to 4/5 (where 4 is the
number of EPCs of GPC Right oblique shaft which have
correspondences in EPCs matrix of the letter “”, and 5
is the size of this GPC (number of EPCs composing the
GPC Right oblique shaft)).
4.2. Extraction Criteria for the GPC
For the different GPCs already presented in Table 2 we
applied several extraction criteria. Among these criteria
there is a criterion which is applicable to all GPCs: we
should not find two or more consecutive EPCs in the
same GPC if they do not exist in the EPCs matrix form-
ing the script.
4.2.1. Extraction Criteria for the Simple GPCs
For all simple GPCs (Shaft, Valley, Left oblique shaft
and Right oblique Shaft) we use the same extraction cri-
terion.
In the first place we seek a series of EPCs of the same
type as the needed GPC. For example to extract the GPC
Right oblique shaft, we must seek a series of EPCs Right
oblique shaft. If there are two or more EPCs that are not
of the same type as the needed GPC or are not of the
same type as the EPCs forming the script, we stop sear-
ching, and the GPC is not considered. If the length of the
following EPCs found is greater than or equal to three,
we retain this suite as a GPC with the initial and final
positions in the script and the value of the fitness.
4.2.2. Extraction Criteria for the Complex GPCs
The GPCs considered as complex are the half occlusions,
the occlusions and the Ain. We will detail the extraction
methods for the Right opening occlusion and the Ain as
follows.
In the case of the GPC Right half opening occlusion
represented in Figure 12 and written from top to bottom,
it is necessary that these conditions must be verified:
 The first EPC is a valley or a Left oblique shaft,
 The last EPC is a valley or a Right oblique shaft,
 X0j < max (X0i, X0f),
 X0m< min (X0i, X0f),
 min (Y0i, Y0f) < Y0j < max (Y0i, Y0f).
where: (X0i, Y0i): the center coordinate of the ellipse
forming the first EPC, (X0f, Y0f) are the center coordinate
of the ellipse forming the last EPC, and


, jif, i: ini-
tial, f: final.
For the GPC ain represented in the figure below (Fig-
ure 13) we calculate the equations of the first EPC and
the last EPC in the tested GPC, and then we check if
there is intersection between the two EPCs (Pi: intersect-
tion point). Thus we look for the existence of two inflex-
ion points P1 and P2 where there is a sudden change of
the angle deviation of the EPCs forming the GPC. For
example, we have a set of EPCs Right oblique shaft and
a set of EPCs valley after the P1 point and a last set of
EPCs Left oblique shaft after point P2.
5. Refining
After the execution of the ten genetic algorithms (a ge-
netic algorithm for each GPC) we used a process of re-
finement of the results obtained after this execution.
In this stage we favor complex GPCs (Ain, Occlusion
an half occlusions) to simple GPC. In fact, we firstly d

Genetic Algorithms for Perceptual Codes Extraction
262
Figure 11. Search of GPC (Right oblique shaft and Left oblique shaft) in the EPCs matrix of the letter “”.
Shaft
Leftoblique shaft
Right oblique
shaft
Figure 12. Extraction of GPC Right half opening occlu-
sion. (a)
Up half opening
occlusion
(b)
Figure 13. Extraction of GPC Ain.
chose the GPCs Ain, Occlusion and subsequent half oc-
clusion GPCs (Left half occlusion, Right half occlusion,
Down half occlusion and Up half occlusion) and we
complete the simple GPCs (Shaft, valley, Left oblique
shaft and Right oblique shaft). Figures 14(a) and (b) re-
present the results of the letter “W” generated by the ex-
tractor of the global perceptual codes. For the first re-
sult, genetic algorithms generate continued following
GPCs: Shaft, Left oblique shaft, Right oblique shaft and
Left oblique shaft. For the second result genetic algori-
thms generate the following GPCs: two Up half opening
occlusion.
(b)
Figure 14. (a) First result for the GPCs forming the letter
“W”; (b) Second result for the GPCs forming the letter
“W”.
To determine the final set of GPCs forming the letter
“W”, we use the stage of refinement already introduced.
Knowing that the final refinement favors complex GPC
(Ain, Occlusion and half occlusions) compared to other
GPCs (Shaft, valley, Left oblique shaft and Right oblique

Genetic Algorithms for Perceptual Codes Extraction 263
shaft), the final result generated by the GPC extractor
(after refinement) is: two Up half opening occlusions.
6. Simulation Results
In the following part we present some examples of EPCs
extraction and then GPCs extraction. Figure 15(a) repre-
sents the generation of the capital letter “D” by EPCs.
The EPC extractor has detected 13 EPCs forming the
letter “D”. Using the EPCs as inputs, the GPC extractor
generated several GPCs building the letter “D”. A re-
finement stage is necessary to maintain the better ones
(GPC 1 = Shaft and GPC 6 = Left half opening occlusion)
(see Figure 15(b)). By the same way, the Arabic letter
“”, the French word “un” and the Arabic word “”
was generated by the EPCs (see respectively Figures
16(a), 17(a) and 18(a)), and then theses scripts (“”,
“un” and “”) was generated by the GPCs (see
respectively Figures 16(b) , 17(b) and 18(b)).
Referring the simulation examples, we can note the
reduction of the perceptual codes representing a script
using the GPCs comparing to case when the EPCs are
adopted. An other interesting advantage is that the use of
GPCs provides much more significant representation of
the script.
3
2
1
2
3
24
2
4
1
1
1
1
(a)
16
(b)
Figure 15: (a) Generation of the letter “D” with the EPCs;
(b) Generation of the letter “D” with the GPCs.
3
3
2
4
4
1
1
3
1
1
1
3
2
4
4
4
3
1
4
42
3
1
(a)
(a)
7
7
7
(b)
Figure 16. (a) Generation of the arabic letter “” with the
EPCs; (b) Generation of the arabic letter “” with the
GPCs.
3
3
3
1
1
1
1
1
1
1
1
3
3
2
4
2
3
3
3
2
4
1
1
3
3
1
1
1
4
4
2
4
1
1
1
4
(a)
(a)
38 81
7
(b)
Figure 17. (a) Generation of the word “un” with the EPCs;
(b) Generation of the word “un” with the GPCs.

Genetic Algorithms for Perceptual Codes Extraction
264
1
3
3
4
4
41
1
1
4
4
1
22
22
2
4
4
22
4
42
3
3
1
4
4
3
4
2
4
3
(a)
7
27
10
2
4
7
(b)
Figure 18. (a) Generation of the Arabic word “” with the
EPCs; (b) Generation of the Arabic word “” with the
GPCs.
7. Conclusions
In this paper, we present a new method of features ex-
traction of online handwriting. This method has attem-
pted to overcome the inherent ambiguities of handwriting
with the help of genetic algorithms. It was the difficult
part of the whole handwriting recognition system as the
features extraction had to be robust to cope up with the
handwriting variety and changes due to mood, health and
different writing styles.
To extract the GPCs of an online script we use the
Beta-elliptic model to modelise and to extract parameters
of handwriting. With the help of these parameters we de-
veloped an EPC extractor. For each elliptic arc and with
its deviation angle we define four types of EPCs. The
human visual sense is selectively activated in response to
global form. For this reason we developed a GPC ex-
tractor composed of ten GPCs. A GPC is a combination
of a set of EPCs according to well defined criteria. For
each GPC we used a genetic algorithm to optimize the
choice of a good combination (number and type of EPCs
composing the GPC) of EPCs. Finally a lot of proposi-
tion was giving by the GPC extractor to compose the
script. To choice the best and significant proposition a
stage of refinement was developed.
These GPCs can be used to develop a handwriting
recognition system.
REFERENCES
[1] E. Anquetil and G. Lorette, “Perceptual Model of Hand-
writing Drawing Application to the Handwriting Seg-
mentation Problem,” International Conference on Docu-
ment Analysis and Recognition, Ulm, 18-20 August 1997,
pp. 112-117.
[2] P. Viviani and N. Stucchi, “Biological Movements Look
Uniform: Evidence of Motor-Perceptual Interactions,”
Journal of Experimental Psychology: Human Perception
and Performance, Vol. 18, No. 3, 1992, pp. 603-623.
doi:10.1037/0096-1523.18.3.603
[3] D. Connell Scott, “On Line Handwritten Recognition
Using Multiple Pattern Class Models,” Ph.D. Thesis, Uni-
versité de Michigan state, East Lansing, 2000.
[4] A. L. Koerich, R. Sabourin and C. Y. Suen, “Large Vo-
cabulary Off-Line Handwriting Recognition: A Survey,”
Pattern Analytic Application, Vol. 6, No. 2, 2003, pp. 97-
121.
[5] A. Pavlidis, “36 Years on the Pattern Recognition Front,”
Pattern Recognition Letters, Vol. 24, No. 1-3, 2003, pp.
1-7. doi:10.1016/S0167-8655(02)00211-8
[6] R. Plamondon and S. N. Srihari, “On-Line and Off-Line
Handwriting Recognition: A Comprehensive Survey,”
IEEE Transaction on Pattern Analysis and Machine In-
telligence, Vol. 22, No. 1, 2000, pp. 63-84.
[7] M. Côté, E. Lecolinet, M. Cheriet and C. Y. Suen, “Auto-
matic Reading of Cursive Scripts Using a Reading Model
and Perceptual Concepts, The PERCEPTO System,” In-
ternational Journal on Document Analysis and Recogni-
tion, Vol. 1, No. 1, 1998, pp. 3-17.
doi:10.1007/s100320050002
[8] S. S. Maddouri, “A Neural Perceptual Model Combining
a Local and Global Vision for Arabic Handwritten Words
Recognition,” Ph.D. Thesis, National School of Engi-
neers of Tunis, Tunis, 2002.
[9] M. Côté, “The Use of Access Lexical Model and Percep-
tual Concepts for Image Recognition of Cursive Words,”
Ph.D. Thesis, TELECOM ParisTech, Paris, 1997.
[10] J. R. Pinales, “Recognition of Offline Cursive Handwrit-
ing Using Perceptual and Neural Models,” Ph.D. Thesis,
TELECOM ParisTech, Paris, 2001.
[11] D. Marr, “VISION: A Computational Investigation into
Human Representation and Processing of Visual Infor-
mation,” W. H. Freeman and Company, San Francisco,
1982, pp. 8-41.
[12] J. L. McClelland and D. E. Rumelhart, “Distributed
Memory and the Representation of General and Specific
Information,” Journal of Experimental Psychology: Ge-
neral, Vol. 114, No. 2, 1985, pp. 159-188.
doi:10.1037/0096-3445.114.2.159
[13] Y. Wada, Y. Koike, E. Bateson and M. Kawato, “A
Computational Model for Cursive Handwriting Based on
the Minimization Principle,” Proceeding of the 7th Con-
ference of the Advances in Neural Information Processing
Systems 6, Denver, 29 November-2 December 1993, pp.
727-734.
[14] M. A. Alimi, “Beta Neuro-Fuzzy Systems,” TASK Quar-
terly Journal, Vol. 7, No. 1, 2003, pp. 23-41.
[15] M. A. Alimi, “A Neuro-Fuzzy Approach to Recognize
Arabic Handwritten Characters,” International Confer-
ence on Neural Networks, Houston, 9-12 June 1997, pp.
1397-1400.
[16] H. Bezine, “Contribution to the Development of a Theory
of Handwritten Generation,” Ph.D. Thesis, National School
of Engineers of Sfax, Sfax, 2005.

Genetic Algorithms for Perceptual Codes Extraction
265
[17] H. Bezine, M. A. Alimi and N. Sherkat, “Generation and
Analysis of Handwriting Script with the Beta-Elliptic
Model,” Proceedings of the 9th International Workshop
on Frontiers in Handwriting Recognition, Tokyo, 26-29
October 2004, pp. 515-520. doi:10.1109/IWFHR.2004.45
[18] H. Bezine, M. Kefi and M. A. Alimi, “On the Beta-Ellip-
tic Model for the Control of the Human Arm Movement,”
International Journal of Pattern Recognition and Artifi-
cial Intelligence, Vol. 21, No. 1, 2007, pp. 5-19.
doi:10.1142/S0218001407005272
[19] F. L. Chung, T. C. Fu and R. W. P. Luk, “An Evolution-
ary Approach to Pattern-Based Time Series Segmenta-
tion,” IEEE Transactions on Evolutionary Computation,
Vol. 8, No. 5, 2004, pp. 471-489.
doi:10.1109/TEVC.2004.832863
[20] K. Deb, “Genetic Algorithm in Search and Optimization:
The Technique and Applications,” Proceedings of Inter-
national Workshop on Soft Computing and Intelligent
Systems, Calcutta, 12-13 January 1998, pp. 58-87.
[21] S. Forrest, R. E. Smith, B. Jakornik and A. S. et Perelson,
“Using Genetic Algorithms to Explore Pattern Recogni-
tion in the Immune System,” Evolutionary Computation,
Vol. 1, No. 3, 1993, pp. 191-211.
doi:10.1162/evco.1993.1.3.191
[22] C. Gagné and M. Parizeau, “Genetic Engineering of Hi-
erarchical Fuzzy Regional Representations for Handwrit-
ten Character Recognition,” International Journal on
Document Analysis and Recognition, Vol. 8, No. 4, 2006,
pp. 223-231. doi:10.1007/s10032-005-0005-6
[23] J. P. J. Alberto and C. P. C. Juan, “Genetic Algorithms
for Linear Feature Extraction,” Pattern Recognition Let-
ters, Vol. 27, No. 13, 2006, pp. 1508-1514.
doi:10.1016/j.patrec.2006.02.011
[24] M. S. William and A. D. J. Kenneth, “An Analysis of
Multipoint Crossover,” Proceedings of the First Work-
shop on Foundation of Genetic Algorithms, Bloomington,
15-18 July 1990, pp. 301-315.
[25] D. Delahaye, J. M. Alliot, M. Schoenauer and J. L. Farges,
“Genetic Algorithms for Partitioning Air Space,” Pro-
ceedings of the Tenth IEEE Conference on Artificial In-
telligence for Application, San Antonio, 1-4 March 1994,
pp. 291-297.
[26] G. Menier, “On-Line System of Reading and Writing
Cursive Handwriting: Continuous Analysis of Features
and Global Interpretation Optimized by Genetic Algo-
rithm,” Ph.D. Thesis, University Rennes 1, Rennes, 1995.
[27] H. L. Sai and K. L. Hak, “Playing Tic-Tac-Toe Using Ge-
netic Neural Network with Double Transfer Functions,”
Journal of Intelligent Learning Systems and Applications,
Vol. 3, No. 1, 2011, pp. 37-44.
doi:10.4236/jilsa.2011.31005
[28] S. Budi, A. B. Muhammad and E. W. Stefanus, “A Cross
Entropy-Genetic Algorithm for M-Machines No-Wait Job-
Shop Scheduling Problem,” Journal of Intelligent Learn-
ing Systems and Applications, Vol. 3, No. 3, 2011, pp.
171-180. doi:10.4236/jilsa.2011.33018
[29] Z. Bahadır and Ö. brahim, “An Improved Genetic Algo-
rithm for Crew Pairing Optimization,” Journal of Intelli-
gent Learning Systems and Applications, Vol. 4, No. 1,
2012, pp. 70-80. doi:10.4236/jilsa.2012.41007