J. Software Engineering & Applications, 2010, 3, 813-819
doi:10.4236/jsea.2010.38094 Published Online August 2010 (http://www.SciRP.org/journal/jsea)
813
Study of Integral Variable Structure Control
Method for Stability of SI Engine Idling Speed
Yang Zhang1, Nobuo Kurihara2
1Science Program in Mechanical Systems, Hachinohe Institute of Technology, Hachinohe, Japan; 2Graduate School of Engineering,
Hachinohe Institute of Technology, Hachinohe, Japan.
Received June 29th 2010; revised July 15th 2010; accepted July 30th 2010.
ABSTRACT
The intake air control system of a gasoline engine is a typical nonlinear system, and included among the adverse fac-
tors that always induce poor idle-speed control stability are dead time and disturbances in the intake air control proc-
ess. In this paper, to improve the responsiveness when idling with regard to disturbances, a mean-value engine model
(MVEM) with dead time was constructed as the control object, and the two servo structures of sliding mode control
(SMC) were studied for better idle control performance, especially in transient process of speed change. The simulation
results confirmed that under the constraint condition of control input, the robustness of idle speed control that is being
subjected to torque disturbances and noise disturbances can be greatly improved by use of the servo structure II.
Keywords: SI Engine, Idle Speed Control, Variable Structure, Integral Sliding Mode Control, Simulation
1. Introduction
Idle speed is the minimum operating speed of a combus-
tion engine. Most of the driving time of urban traffic
consists of periods when the engine is idling. Further-
more, if the idle speed can be reduced to 100 rpm (revo-
lutions per minute) by improving the control method,
fuel consumption will be reduced by 2 to 5%. Therefore,
significant fuel economy and emissions improvements
can be achieved by lowering the idle speed of an engine.
In order to achieve a relatively lower idle speed while at
the same time preventing the engine from stalling, it is
necessary to maintain a stable idle speed in the presence
of disturbances, both known disturbances (e.g. stationary
steering and evaporation-gas purges) and unknown.
The automotive engine is a typical nonlinear, time-
delay, time-varying parameter system. Recently there are
many studies that apply control theories such as LQG,
PID, adaptive control to idle-speed control [1,2]. In par-
ticular, because variable structure control is suitable for
systems that are linear or nonlinear, continual or discrete,
certain or uncertain, the application of sliding mode con-
trol is regarded as a solution to the problem of improving
idle-speed control. Nevertheless, there are some studies
is applying this theory [3-5]. However, idle-speed control
should be investigated practically; in other words, the
issues that typically constrain the application of SMC are
how to improve the transient process of an idle control
system and how to alleviate chattering, especially quasi-
sliding mode is used against chattering recently [6,7].
Consequently, in this paper, idle speed control was stud-
ied based on a non-linear gasoline engine model, and an
servo system of SMC was modified. As PID (propor-
tional–integral–derivative) controllers are usually used
for idle speed control in practical application, a PID con-
trol and sliding mode control (SMC) were employed to
improve idle-speed control. Several disturbances such as
torque and fuel disturbances were added into the engine
model to test the responsiveness and stability of three
control methods. Sudden start operation was also studied
during fuel disturbances. Moreover, an integral type of
control input instead of quasi-sliding mode is employed
for chattering alleviation. The system was simulated by
MATLAB/Simulink. According to the results of simula-
tions, the robustness of idle-speed control was improved
by using SMC.
2. Sliding Mode Control Design
SMC is a type of variable structure control in which the
dynamics of a nonlinear system are altered by the appli-
cation of a high-frequency switching control [8]. In other
words, SMC uses practically infinite gain to force the
trajectories of a dynamic system to slide along a re-
stricted sliding mode subspace. This is an important, ro-
bust control approach that provides an adaptive approach

Study of Integral Variable Structure Control Method for Stability of SI Engine Idling Speed 814
to dealing with parametric, uncertain parametric, and
uncertain disturbance systems. If a switching surface is
appropriately designed with desirable characteristics, the
system will exhibit desirable behavior when confined to
this switching surface. In order to achieve the target val-
ue, idle-speed control can be studied as a servo system.
Here, two servo systems using SMC were designed as
follows.
2.1 Servo System I Using SMC
Consider the system
x
Ax Bu

11 11 1
1
0
n
nn nnnn
xx aa
u
xa axb
  
  

  
  
  





(1)
1
yx
Where x is the state vector, y is the output, and u is the
scalar. To achieve a servo system, a new state z is in-
serted and a new input r as a target input is also neces-
sary. Accordingly, Equation (1) is extended as in Equa-
tion (2).
1
zrx
x
Ax BuEr




11111
1
01000 1
00 0
00
n
nnnnnn
zz
xaax
ur
xaaxb
 
















 


 

(2)
The switching surface is defined as
()
x
Sx


()
x
Sx



(3)
When the system is in sliding mode state, a dynamic
characteristic is exhibited. Firstly, taking into considera-
tion non-linear factors and uncertain disturbances, the
equivalent control for the SMC is usually employed.
Figure 1. Engine control system
eq nl
uu u

 (4)
As is well known, when the system is on the switching
surface, it maintains0




. Hence, by using Sx



,
substituting Equation (2) into Equation (3) gives the fol-
lowing:
0
eq
SxSAx SBuSEr


 
 (5)
1
()( )
eq
uSBSAxSEr


Here, 1 ()SB

can be used, but only when SB is the
nonsingular matrix, i.e. 0SB . So one part of the con-
trol input can be obtained, and another part nl
u is used
only for uncertain factors such as disturbances and
non-linear issues. In general, nl
u is designed as follows:
sgn( )
nl
uK


(6)
K is the switching gain, and. sgn( )

is the signal
function that can makes the system robust, but in the
same way it leads to chattering, which is undesirable.
Next, the parametric vector S in the switching surface
equation is required for deciding the existence of sliding
mode. There are a few methods for the S design. Pole
deployment (see Equation (7)) and the Riccati equation
(see Equation (8)) are usually employed.




1
x
IBSB SAxEr

 
 (7)
0
TT
PAAPPBB PQ
AAI





 (8)
0

 is assumed for the stability margin coefficient

.
T
SBP
Finally, according to Lyapunov’s second theorem on
stability, the reachability of sliding mode is assumed to
be proved.
sgn( )0V   

 
 (9)
where 0

 But in the theory of SMC, the two main
issues are the improvement of robustness with regard to
uncertain disturbances and the alleviation of chattering,
and these issues restrict the scope of application of SMC
to an extent.
2.2 Servo System II Using Modified SMC
In this section, to solve the two aforementioned problems,
the design method of SMC was modified. The structure
is shown in Figure 2.
The reader will remember the expansion servo system
described in Equation (2). Here another state variable
was used, and the derivative z
 of the target value and
the model output was inserted, which was expected to im-
prove the robustness of whichever engine control system

Study of Integral Variable Structure Control Method for Stability of SI Engine Idling Speed 815
Figure 2. Block diagram
is being used in the operating mode of holding a lower
idle speed or of a sudden start.
Equation (2) can be rewritten as follows:
'
x
AxBuErEr

12
1111211
2212222
12
000 0
001 0001
000 0
000 0
00 0
n
n
n
nnnnnnn
zHHHz
zz
xaaax
u
xaaax
xaaaxb
 
 

 
 

 
 
 
 
  
 
 




 

1
0
0
0
0
rr























(10)
1ii
H
a 1r zx  

 1r
zx




1r
zxdt  

The S in the hyper-plane was designed by using the
Riccati equation if and only if it has a solution. The
equivalent control input was solved by using Equation
(8). The alleviation of chattering was expected, but while
the smoothing function seems to alleviate or remove
chattering, it will in all probability weaken the robustness
of the system. As a result, the original signum function
was kept, and the authors hoped that gain K would
gradually get smaller so that chattering would be allevi-
ated with a lessening of switch gain K. For this purpose,
gain K was attained with the integration of the switching
function

[9]. Thus, gain K was higher when the sys-
tem was in reaching mode, and fell when the system was
in sliding mode. This not only alleviated chattering, but
also maintained the robustness of the system.


1
eqr r
uSBSAx SESE



  (11)
 
1
sgn 0
nl
uKSB K 

 (12)

00
tdt
   



When the integer 0

, 0

  and when 0


,
0  , it was assumed that the larger switching gain at
reaching mode will be alleviated.
Substituting (11), (12) into (9) gives

sgn 0VK K     
 (13)
The existence of the sliding mode and reachability is
proved based on Lyapunov’s second theorem on stability.
The modified servo control system of SMC was verified
by its application to idle speed control. The effect of
chattering alleviation is shown in Figure 3. The cSMC
denotes conventional SMC and the pSMC denotes modi-
fied SMC.
3. Application to Idling Speed Control
System
The control system of a spark-ignition engine (SI engine),
which was chosen as the target of this study on
idle-speed control is shown in Figure 1. The intake air
flow is adjusted to reach a certain engine speed by ad-
justing the angle and position of the electronic throttle.
The crank angle sensor detects the engine speed; and the
angle and position of the electronic throttle depend on the
controller in the engine control unit. Then the throttle
adjusts the amount of air supply to the cylinder. After
that fuel proportionate to the air flow is injected into the
cylinder. Thus, the torque produced by the combustion of
the fuel maintains a constant engine speed.
The idle-speed control system for the regulation of in-
take air flow is shown in Figure 4. The basic input is the
equivalent electronic throttle opening angle θ, which is
restricted within a finite opening scale and the controlled
output is engine speed Ne [rpm]. Because of the in-
versely-proportional relationship between the dead time
L and the engine speed Ne [rpm], the dead time is de-
rived from the feedback of the output of the system. In
view of the disturbances in an actual engine, three dis-
turbances are loaded into the engine model. Two distur-
bances, D1 and D2, are added as transitional disturbances
before and after the dead time, taking evaporative purge
and stationary steering into consideration. The measured
engine speed D3 is also added as a steady disturbance to
simulate the combustion fluctuation of an actual engine.
Figure 3. Non-linear control output by step response
Time [s]

Study of Integral Variable Structure Control Method for Stability of SI Engine Idling Speed 816
Figure 4. Model for idle-speed control
a) Intake air flow is in direct proportion to throttle an-
gle. Since the throttle is driven by the motor, it causes a
delay, the time constant

. K is the air flow conversion
factor; the input is θ and output is intake air flow
in
Q 
skg /, so that the state equation is
1
11
in in
K
QQ D 


 
 (14)
1
Dis the air leak and fuel purge disturbance.
b) In the manifold and cylinder, the input is in
Q and
the output is from manifold to cylinder intake air flow
o
Q,

mino
m
RT
PQQ
V

 (15)
120
cl e
om
VnN
QP
RT
 (16)
Equation (16) is substituted into Equation (15), there-
fore:
()
120
cl e
minm
m
VnN RT
PQ P
VRT

 (17)
m
V is the manifold volume; R is the air constant; T is
the temperature; and the cylinder pressure is assumed to
be equal to the manifold pressure.
c) In combustion, the engine torque e

is in direct
proportion to the cylinder intake air flow o Q, hence
60
s
L
eo
e
QZe
N


 (18)
Z is the comparison coefficient of unit conversion, and
the dead time is obtained by 1st order Padé approxi-
mant[10]. The state variable e
D is:
260
eoe
eo
Z
DQD
LN




 (19)
The dead time L is a function of engine speed, which
gives:
32 60
4e
LN

 (20)
Obtaining torque requires intake, compression and
combustion; hence the dead time is 3 strokes long. Equa-
tion (21) is obtained from Equations (16) and (19).
22
cl
ee m
ZnV
DP
JRT
  (21)
d) The engine inertia moment is J, the friction coeffi-
cient is Df, and the disturbance is D2. Then:

2
1
eeef
NNDD
J
  
 (22)
Equation (21) is substituted into Equation (22), there-
fore:
2
21
2
f
cl
eem e
D
ZnV
NDP ND
JJRTJJ
 
 (23)
The block diagram shown in Figure 2 is arrived at
based on the above equations. In addition, the equivalent
state space is:
x
Ax BuFd
yCx




(24)
emein
x
NPDQT




2
0
00
120
000
1000
f
cl
eo cl
mm
cl
D
ZnV
R
TL JJ
NnV
RT
VV
A
ZnV
RTL





























1
0
01
000 0
,,
000 0
10
0
T
J
BFC
K


 

 

 
 

 

 

 
 

4. Simulation
In order to confirm the robustness of the idle-speed con-
trol when disturbances are present, the system was simu-
lated using MATLAB/Simulink. The parameters of the
engine model in Figure 2 are set according to Table 1.
Firstly, the initial idle speed of the engine was 700 rpm,
but, taking into consideration the existence of distur-
bances such as fuel purges and the use of power windows,
a unit step input was added at 4 seconds for disturbance
(D1) that results from an evaporation-gas purge in the
fuel module and another unit step input was added at 12
seconds for disturbance (D2) that results from stationary
steering or other types of torque variations in the crank-
shaft module. The simulation results are shown in Figure
5.
Here cSMC represents a conventional SMC controller,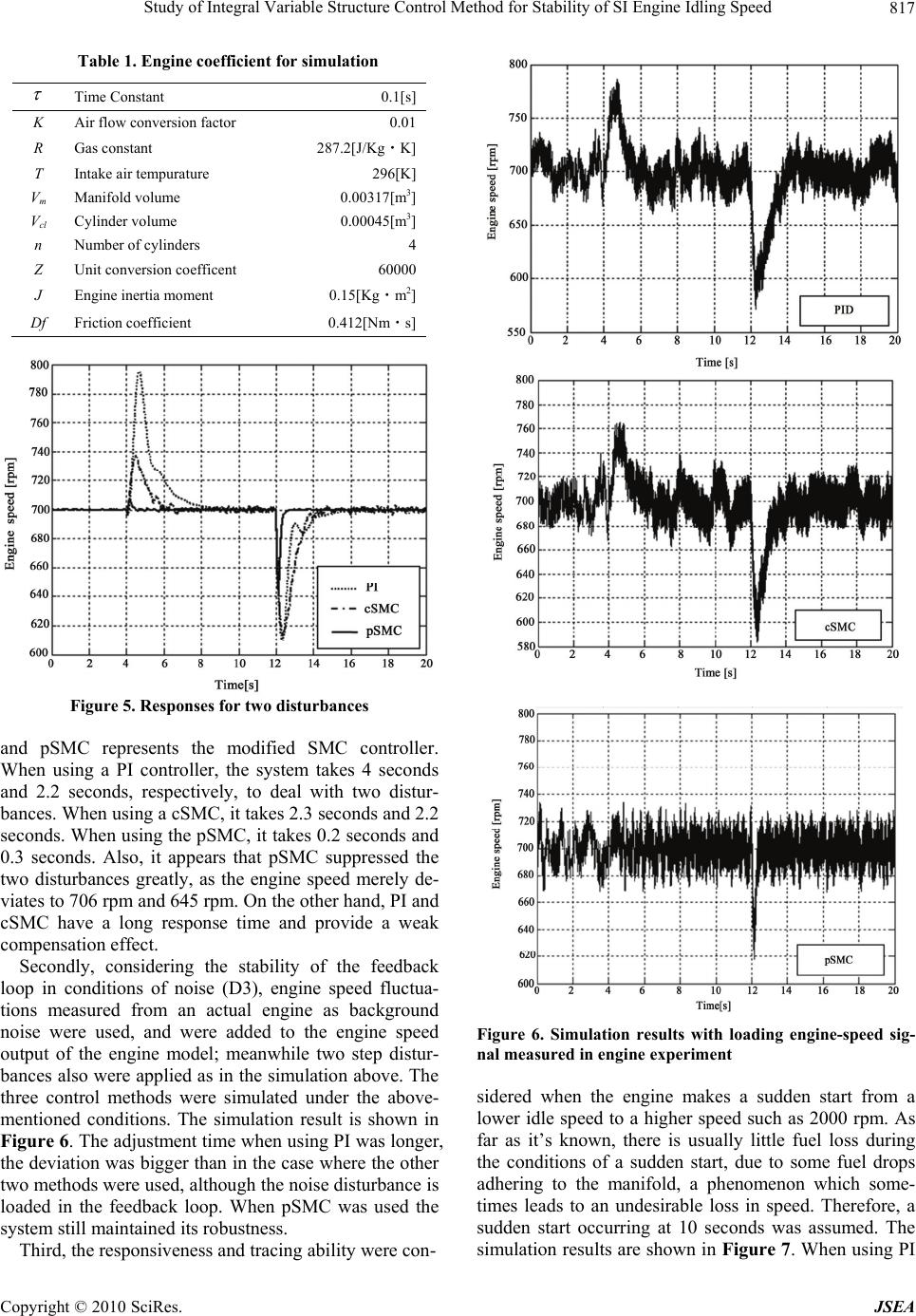

Study of Integral Variable Structure Control Method for Stability of SI Engine Idling Speed 817
Table 1. Engine coefficient for simulation

Time Constant 0.1[s]
K Air flow conversion factor 0.01
R Gas constant 287.2[J/Kg・K]
T Intake air tempurature 296[K]
Vm Manifold volume 0.00317[m3]
Vcl Cylinder volume 0.00045[m3]
n Number of cylinders 4
Z Unit conversion coefficent 60000
J Engine inertia moment 0.15[Kg・m2]
Df Friction coefficient 0.412[Nm・s]
Figure 5. Responses for two disturbances
and pSMC represents the modified SMC controller.
When using a PI controller, the system takes 4 seconds
and 2.2 seconds, respectively, to deal with two distur-
bances. When using a cSMC, it takes 2.3 seconds and 2.2
seconds. When using the pSMC, it takes 0.2 seconds and
0.3 seconds. Also, it appears that pSMC suppressed the
two disturbances greatly, as the engine speed merely de-
viates to 706 rpm and 645 rpm. On the other hand, PI and
cSMC have a long response time and provide a weak
compensation effect.
Secondly, considering the stability of the feedback
loop in conditions of noise (D3), engine speed fluctua-
tions measured from an actual engine as background
noise were used, and were added to the engine speed
output of the engine model; meanwhile two step distur-
bances also were applied as in the simulation above. The
three control methods were simulated under the above-
mentioned conditions. The simulation result is shown in
Figure 6. The adjustment time when using PI was longer,
the deviation was bigger than in the case where the other
two methods were used, although the noise disturbance is
loaded in the feedback loop. When pSMC was used the
system still maintained its robustness.
Third, the responsiveness and tracing ability were con-
Figure 6. Simulation results with loading engine-speed sig-
nal measured in engine experiment
sidered when the engine makes a sudden start from a
lower idle speed to a higher speed such as 2000 rpm. As
far as it’s known, there is usually little fuel loss during
the conditions of a sudden start, due to some fuel drops
adhering to the manifold, a phenomenon which some-
times leads to an undesirable loss in speed. Therefore, a
sudden start occurring at 10 seconds was assumed. The
simulation results are shown in Figure 7. When using PI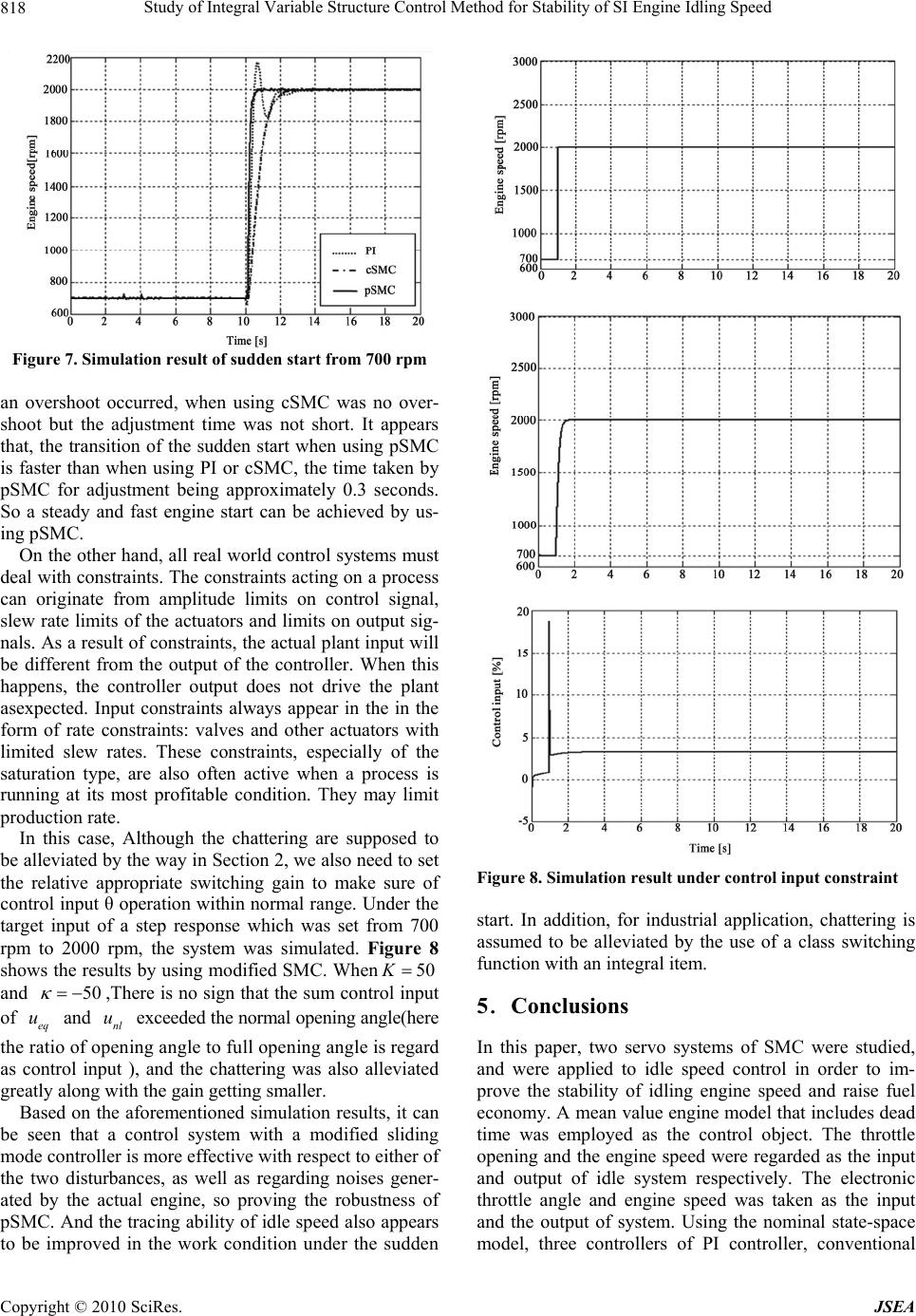

Study of Integral Variable Structure Control Method for Stability of SI Engine Idling Speed 818
Figure 7. Simulation result of sudden start from 700 rpm
an overshoot occurred, when using cSMC was no over-
shoot but the adjustment time was not short. It appears
that, the transition of the sudden start when using pSMC
is faster than when using PI or cSMC, the time taken by
pSMC for adjustment being approximately 0.3 seconds.
So a steady and fast engine start can be achieved by us-
ing pSMC.
On the other hand, all real world control systems must
deal with constraints. The constraints acting on a process
can originate from amplitude limits on control signal,
slew rate limits of the actuators and limits on output sig-
nals. As a result of constraints, the actual plant input will
be different from the output of the controller. When this
happens, the controller output does not drive the plant
asexpected. Input constraints always appear in the in the
form of rate constraints: valves and other actuators with
limited slew rates. These constraints, especially of the
saturation type, are also often active when a process is
running at its most profitable condition. They may limit
production rate.
In this case, Although the chattering are supposed to
be alleviated by the way in Section 2, we also need to set
the relative appropriate switching gain to make sure of
control input θ operation within normal range. Under the
target input of a step response which was set from 700
rpm to 2000 rpm, the system was simulated. Figure 8
shows the results by using modified SMC. When50K

and 50
  ,There is no sign that the sum control input
of eq u and nl u exceeded the normal opening angle(here
the ratio of opening angle to full opening angle is regard
as control input ), and the chattering was also alleviated
greatly along with the gain getting smaller.
Based on the aforementioned simulation results, it can
be seen that a control system with a modified sliding
mode controller is more effective with respect to either of
the two disturbances, as well as regarding noises gener-
ated by the actual engine, so proving the robustness of
pSMC. And the tracing ability of idle speed also appears
to be improved in the work condition under the sudden
Figure 8. Simulation result under control input constraint
start. In addition, for industrial application, chattering is
assumed to be alleviated by the use of a class switching
function with an integral item.
5．Conclusions
In this paper, two servo systems of SMC were studied,
and were applied to idle speed control in order to im-
prove the stability of idling engine speed and raise fuel
economy. A mean value engine model that includes dead
time was employed as the control object. The throttle
opening and the engine speed were regarded as the input
and output of idle system respectively. The electronic
throttle angle and engine speed was taken as the input
and the output of system. Using the nominal state-space
model, three controllers of PI controller, conventional

Study of Integral Variable Structure Control Method for Stability of SI Engine Idling Speed 819
SMC and modified SMC were constructed. Taking into
consideration actual engines, three disturbances D1, D2
and D3 were added in the author’s simulation, where, D1
and D2 were transition disturbances caused by sudden
operations, and D3 was a measured value of engine
speed fluctuation. The simulation results show excellent
responsiveness and stability when modified SMC was
used because it can shorten the transient process. Fur-
thermore, under the permission range of constraint con-
dition of control input, chattering which is regarded as an
obstacle to the application of SMC, was alleviated by
servo structure II.
REFERENCES
[1] F.-C. Hsieh and B.-C. Chen, “Adaptive Idle-speed Con-
trol for Spark-Ignition Engines,” SAE Paper, 2007-01-
1197.
[2] J. S. FU and N. Kurihara, “Intake Air Control of SI En-
gine Using Dead-Time Compensation,” SAE Paper,
2003-01-3267.
[3] B. Kwak and Y. J. Park, “Robust Vehicle Stability Con-
troller based on Multiple Sliding Mode Control,” SAE
Paper, 2001-01-1060.
[4] M. Kajitani and K. Nonami, “High Performance Idle-
speed Control Applying the Sliding Mode Control with H
Robust Hyperplane,” SAE Paper, 2001-01-0263.
[5] Y. Zhang, T. Koorikawa and N. Kurihara, “Evaluation of
Sliding Mode Idle-speed Control for SI Engines,” Japa-
nese Society of Automotive Engineers, Vol. 40, No. 4,
2009, pp. 997-1002.
[6] X. D. Li, T. W. S. Chow and J. K. L. Ho, “Quasi-Sliding
Mode Based Repetitive Control for Nonlinear Continu-
ous-Time Systems with Rejection of Periodic Distur-
bances,” Automatic Journal of IFAC, Vol. 45, No. 1,
2009, pp. 103-108.
[7] R. Ramos, D. Biel, E. Fossas and F. Guinjoan, “A
Fixed-Frequency Quasi-Sliding Control Algorithm: Ap-
plication to Power Inverters Design by means of FPGA
Implementation,” IEEE Transactions on Power Electron-
ics, Vol. 18, No. 1, 2003, pp. 344-355.
[8] V. I. Utkin, “Variable Structure Systems with Sliding
Modes,” IEEE Transactions on Automatic Control, Vol.
22, No. 1, 1977, pp. 212-222.
[9] J. I. Tahara, K. Tsuboi, T. Sawano and Y. Nagata, “An
Adaptive VSS Control Method with Integral Type
Switching Gain,” Proceedings of the IASTED Interna-
tional Conference Robotics and Applicatons, Tampa,
2001, pp. 106-111.
[10] O. J. M. Smith, “A Controller to Overcome Dead Time,”
Indian Scientist Association in Japan, Vol. 6, No. 2, 1959,
pp. 28-33.