J. Software Engineering & Applications, 2010, 3, 803-812
doi:10.4236/jsea.2010.38093 Published Online August 2010 (http://www.SciRP.org/journal/jsea)
803
Verifying Monoid and Group Morphisms over
Strongly Connected Algebraic Automata
Nazir Ahmad Zafar, Ajmal Hussain, Amir Ali
Faculty of Information Technology, University of Central Punjab, Lahore, Pakistan.
Received June 12th 2010; revised July 10th 2010; accepted July 15th 2010.
ABSTRACT
Automata theory has played an important role in theoretical computer science since last couple of decades. The alge-
braic automaton has emerged with several modern applications, for example, optimization of programs, design of mod-
el checkers, development of theorem provers because of having certain interesting properties and structures from alge-
braic theory of mathematics. Design of a complex system requires functionality and also needs to model its control be-
havior. Z notation has proved to be an effective tool for describing state space of a system and then defining operations
over it. Consequently, an integration of algebraic automata and Z will be a useful computer tool which can be used for
modeling of complex systems. In this paper, we have linked algebraic automata and Z defining a relationship between
fundamentals of these approaches which is refinement of our previous work. At first, we have described strongly con-
nected algebraic automata. Then homomorphism and its variants over strongly connected automata are specified. Next,
monoid endomorphisms and group automorphisms are formalized. Finally, equivalence of endomorphisms and auto-
morphisms under certain assumptions are described. The specification is analyzed and validated using Z/Eves toolset.
Keywords: Formal Methods, Z notation, Algebraic Automata, Validation and Verification
1. Introduction
Now a day, the complex and critical systems have shifted
from electro-mechanical systems to computerized syst-
ems. As a result, it requires controlling these systems by
computer software. When software is used in such com-
plex systems its failure may cause a huge loss in terms of
deaths, injuries or financial losses. Therefore, construc-
ting correct software is as important as its other counter-
parts including hardware and electro-mechanical systems
[1]. Formal methods are mathematical approaches used
for specification of properties of software and hardware
systems [2]. Using formal methods, we can describe a
mathematical model of a system and then it can be anal-
yzed and validated by computer tools such as model
checkers and theorem provers [3]. Current formal app-
roaches cannot be applied to develop a system using a
single formal technique and as a result its integration is
required with other traditional approaches. That is why
integration of approaches has become a well-researched
area [4-10]. There are a large variety of specification
techniques which are suitable for specific aspects in the
software development process. For example, Z, algebraic
techniques, VDM, RAISE and B are usually used for
defining data types while petri-nets, process algebra and
automata are best suited for modeling dynamic aspects of
systems [11]. Because of having well-defined mathe-
matical syntax and semantics of the formal techniques, it
is required to identify and link these approaches for
modeling of consistent, correct and complete computer-
ized systems.
There exists a lot of work on integration of approaches
but does not exist much work on formalization of graphi-
cal based notations. The work [12,13] of Dong et al. is
close to ours in which they have integrated Object Z and
Timed Automata. Another piece of good work is listed in
[14,15] in which R. L. Constable has given a constructive
formalization of some important concepts of automata
using Nuprl. A combination of Z with statecharts is given
in [9]. A relationship is investigated between Petri-nets
and Z in [16,17]. An integration of B and UML is given
in [18,19]. Wechler W. has introduced algebraic struc-
tures in fuzzy automata [20]. In [21], a treatment of fuzzy
automata and fuzzy language theory is given when the
set of possible values is a closed interval [0, 1]. Ito M. has
described formal languages and automata from the alge-
braic point of view in which the algebraic structures of
automata are investigated and then a kind of global the-
ory is treated [22]. Kaynar D. K et al. has presented a

Verifying Monoid and Group Morphisms over Strongly Connected Algebraic Automata 804
modeling framework of timed computing systems [23].
In [24], Godsil C. et al. has presented some ideas of alge-
braic graphs with an emphasis on current topics rather
than on classical structures of graphs.
Automata theory has proved to be a useful tool in
theoretical computer science since last couple of decades.
The algebraic automaton is an advanced form of auto-
mata which has very interesting properties and structures
from algebraic theory of mathematics. The applications
of algebraic theory of automata are not limited to com-
puters but are being seen in many other disciplines of
science and engineering, for example, representing cha-
racteristics of natural phenomena in biology [25] and
modeling of chemical systems using cellular automata
[26]. Another interesting application, in which a system
is described for synthesizing physics-based animation
programs based on hybrid automata, is presented in [27].
Because of having special algebraic characteristic, an
automaton can easily be extended to develop algebraic
automata.
In our previous work, some preliminary results on in-
tegration of algebraic automata and Z notation were pre-
sented in terms of a formal proof of equivalence in endo-
morphisms and automorphisms over strongly connected
automata [28,29]. Few inconsistencies and errors are
observed there which are presented after correction. For
example, the set of states in the strongly connected au-
tomata must be finite which was not described correc-
tly. The homomorphism was defined as a change in state
using schema structure which is now corrected to define
as a relationship between two different structures of
strongly connected automata. The similar corrections
have been made in defining endomorphism, isomorphism
and automorphism. Because all of these morphisms are
reused in defining monoids and groups therefore rest of
the specifications is refined accordingly. First, we have
given formal specification of strongly connected alge-
braic automaton and then homomorphism with its vari-
ants over the automata are formalized and generalized.
Next, monoid endomorphisms and group automorphisms
are described. Finally, a formal proof of their equiva-
lence is given under certain assumptions. The formal
models are analyzed and validated using Z/Eves toolset.
In Section 2, an overview of Z notation is given. In
Section 3, Formal models of morphisms over algebraic
automata are provided. In Section 4, an approach is pre-
sented to analyze the resultant formal models. Conclu-
sion and future work are discussed in Section 5.
2. An Introduction to Z Notation
Formal methods are approaches used for describing and
analyzing properties of software and hardware systems
[30]. There are several ways in which formal methods
may be classified. One frequently-made distinction is
between property oriented and model oriented methods
[31]. Property oriented approaches are used to describe
the operations defining their relationships. Property ori-
ented methods usually consist of two parts. The first one
is the signature part which is used for defining syntax of
an operation and the other one is an equations part used
for defining semantics of the operation by a set of axioms
called the rules. The OBJ language [32] and algebraic
specification of abstract data types [33] are examples of
property oriented methods. Model oriented methods are
used to construct a model of a system and then allows to
defining operations over it [34]. The Z is a model ori-
ented approach based on set theory and first order predi-
cate logic [35] used for specifying behavior of abstract
data types and sequential programs.
A brief overview of Z is given by taking a case from
the book “Using Z: specification, refinement and proof”
by Woodcock and Davies [36]. A programming interface
is taken as case study for file system. A list of operations
which is defined after defining the entire system is: 1)
read: used to read a piece of data from a file, 2) write:
used to write a piece of data to a file, 3) access: may
change the availability of a file for reading and writing
over the file of the system.
A file is represented as a schema using a relation be-
tween storage keys and data elements. Basic set types are
used for simple specification. The variables name, type,
keys and data elements of a file are represented as Name,
Type, Key and Data respectively in Z notation. An axio-
matic definition is used to define a variable null which is
used to prove that the type of a file cannot be null even
there are no contents on a file.
[Name, Type, Key, Data]; null: Type
A file consists of its contents and type which are spe-
cified by contents and type respectively. The schema
structure is usually used because of keeping specification
flexible and extensible. In the predicate part, an invariant
is described proving that the file type is non null even
there are no contents in it. As a file can associate a key
with at most one piece of a data and hence the relation
contents is assumed to be a partial function.

Verifying Monoid and Group Morphisms over Strongly Connected Algebraic Automata 805
The read operation is defined over the file to interro-
gate its state. A read operation requires an existing key as
input and provides the corresponding data as output. The
symbol  is used when there is no change in the state.
Now the structure  File means that the bindings of File
and File’ are of same type and equal in value. The deco-
rated file, File’, represents the next state of the file. In the
read operation, it is unchanged because the variable k? is
given as input and the output is returned to the variable
d!. The symbols ? and ! are used with input and output
variables respectively. In the predicate part of the schema,
first it is ensured that the input key k? is in the domain of
contents. Then the value of data against it is returned to
the output variable d!.
Another operation is defined to write contents over the
given file. The symbol  is used when there is a change
in the state. In the schema defined below, the structure
File gives a relationship between File and File’ repre-
senting that the bindings of File are changed. In this case,
the write operation defined below replaces the data
stored under an existing key and provides no output. The
old value of contents is updated with maplet k? d?.
The symbol

is an override operator used to replace
the previous value of a key with the new one in a given
function.

As a system may contain a number of files indexed
using a set of names and some of which might be open
hence it consists of two components namely collection of
files known to the system and set of files currently open.
The variable file is used as a partial function to associate
the file name and its contents. The variable open is of
type of power set of Name. The set of files which are
open must be a subset of set of total files as described
below in the schema.
As the open and close operations neither change name
of any file nor add and remove any file hence both are
the access operations. It may change the availability of a
file for reading or writing. In the schema FileAccess
given below, the variable n? is used to check if the file to
be accessed exist in the system. Further, it is also de-
scribed that the file is left unchanged.

Verifying Monoid and Group Morphisms over Strongly Connected Algebraic Automata 806
If we require creating another system with same pat-
tern but with different components, then renaming can be
used rather than creating the new system from the scratch.
Renaming is sometimes useful because in this way we
are able to introduce a different collection of variables
with the same pattern. For example, we might wish to in-
introduce variables n ewfile and newopen under the con-
straint of existing system System. In this case, the new
system NewSystem can be created in horizontal form by
defining: NewSystem System[newfile/file, newopen/
open] which is equivalent to the schema given below in
the vertical form.
3. Algebraic Automata and Morphisms
As we know that automata theory has become a basis in
the theoretical computer science because of its applica-
tions in modeling scientific and engineering problems
[37-40]. Algebraic automaton has some properties and
structures from algebraic theory of mathematics. The
algebraic automata have emerged with several modern
applications in computer science. Further, the applica-
tions of algebraic theory are not limited to computers but
are being seen in many other disciplines of science, e.g.,
representing chemical and physical phenomena in chem-
istry and biology. It is a well known fact that a given
automata may have different implementations and con-
sequently its time and space complexity must be different
which is one of the major issues in modeling using au-
tomata. Therefore it is required to describe the formal
specification of automata for its optimal implementation.
Formal models of algebraic automata are given in this
section. At first, formal description of some important
concepts of algebraic automata using Z is given. Homo-
morphism and its variants are described. Then, formal
description of monoid (group) on a set of endomor-
phisms (automorphisms) is presented. Finally an equiva-
lence of monoid endomorphisms and group automor-
phisms over strongly connected automata is described. It
is to be noted that the definitions used in this section are
based on the book “Algebraic Theory of Automata and
Languages” [22].
3.1 Strongly Connected Algebraic Automaton
A strongly connected automaton is a one for which if for
any two given states there exists a string s such that the
delta function connects these states through the string s.
A strongly connected algebraic automaton (SCAA) is a
5-tuple (Q, ∑, δ, T, Epsilon), where 1) Q is a finite non-
empty set of states, 2) ∑ is a finite set of alphabets, 3) δ
is a transition function which takes a state and a string
and produces a state, 4) T is a set of strings where each
string is based on set of alphabets and 5) Epsilon is a null
string. To formalize SCAA, Q and ∑ are denoted by S
and X respectively at an abstract level of specification [S,
X].
To describe a set of states for SCAA, a variable states
is introduced. Since, a given state q is of type Q therefore
states must be of type of power set of Q. For a set of al-
phabets, the variable alphabets is used which is of type
of power set of X. As we know that δ is a function be-
cause for each input (q, u), where q is a state and u is a
string there must be a unique state, which is image of (q,
u) under the transition function δ. Hence we can declare
δ as, S × seq X → S.
The delta function takes a state and a string as input
and produces the same state or new state as output. Be-
cause we need to compute the set of all the strings based
on the set of alphabets and hence the fourth variable is
used and denoted by strings which is of type of power set
of set of all the sequences, i.e., P(seq X). As we know
that a sequence can be empty and hence a fifth variable is
used representing it and is denoted by epsilon of type seq
X. The schema structure is used for composition because
it is very powerful at abstract level of specification and
helps in describing a good specification approach. All of
the above components are encapsulated and put in the
schema named as SCAA. The formal description of the
connected automaton is described.
Invariants: 1) The null string is an element of strings.
2) If the transition function takes a state and null string as
input, then it produces the same state. 3) For each (s,
(„aÒ^u)), where s is state, an alphabet and u is a string, the
delta function is defined as: delta (s, („aÒ ^ u)) = delta
((delta (s, „aÒ)), u). 4) For any two states q1 and q2, there
exists a string s such that: delta (q1, s) = q2.
3.2 Homomorphism and its Variants
The word homomorphism means “same shape” and is an
interesting concept because a similarity of structures can
be verified by it. It is a structure in abstract algebra
which preserves a mapping between two algebraic struc-
tures, for example, monoid, groups, rings, vector spaces.

Verifying Monoid and Group Morphisms over Strongly Connected Algebraic Automata 807
Now we give formal specification of it and its variants
over strongly connected automata. In [22], Ito M. has
given a concept of homomorphism and its variants over
algebraic automata.
Let A = (Q1, ∑1, δ1) and B = (Q2, ∑2, δ2) be two
strongly connected automata represented by SCAAa and
SCAAb respectively in Z. Let  be a mapping from Q1
into Q2. If  (δ1(q, x)) = δ2((q), x) holds for any q 
Q1 and x  ∑1, then  is called a homomorphism from
Q1 to Q2. The formal definitions of both the automata
are described by using the concept of renaming.
SCAAaSCAA[statesa/states, alphabetsa/alphabets,
stringsa/strings, deltaa/delta, epsilona/epsilon]
SCAAbSCAA[statesb/states, alphabetsb/alphabets,
stringsb/strings, deltab/delta, epsilonb/epsilon]
A formal definition of homomorphism from A into B
in terms of a schema is given below. It consists of three
components, i.e., SCAAa, SCAAa and row. The variable
row is a mapping from Q1 into Q2. The sets Q1 and Q2
are used for states of SCAAa and SCAAb respectively.
Invariants: 1) For every q in set of states and s in set
of strings of the first automata, if the mapping row satis-
fies the condition: row (deltaa (q, s)) = deltab ((row q), s)
then it conforms a homomorphism from automata SCAAa
into SCAAb.
If SCAAa = SCAAb in the homomorphism then it is
called an endomorphism. The mapping row is defined
from set of states S into itself. We have induced the for-
mal definition of endomorphism from the definition of
homomorphism because it is a special case of it.
Let us define the bijection over two given sets. Let X
and Y are two nonempty sets. A mapping  from X to Y
is called one to one if different elements of X have dif-
ferent images in Y. That is,  x1, x2  X; y  Y • (x1)

Verifying Monoid and Group Morphisms over Strongly Connected Algebraic Automata 808
= y and (x2) = y  x1 = x2. The mapping  is called
onto if each element of Y is an image of some element of
X. If a mapping is one to one and onto then it is called
bijective. If the mapping defined in case of homomorph-
ism is bijective from algebraic automata SCAAa to
SCAAb then it is called an isomorphism and the auto-
mata are said to be isomorphic. Formal description of
isomorphism from SCAAa to SCAAb is given below.
Invariants: 1) For all q1, q2 in set of states of SCAAa
and q in set of states of SCAAb, if images of q1 and q2
are same under the mapping row then the elements q1
and q2 must be same. 2) Each element of the set of states
of automata SCAAb is an image of some element of au-
tomata SCAAa under the mapping row.
If SCAAa = SCAAb then an isomorphism becomes an
automorphism. Its formal description is given below
along with its invariants which are not explained here
because it is a repetition as given above in the schema
Isomorph ism.
3.3 Formal Models of Monoid and Group
Morphisms
Let G be a nonempty set. The structure (G,*) under bi-
nary operation * is monoid if (i)  x, y  G, x*y  G, (ii)
 x, y, z  G, (x*y)*z = x*(y*z), that is associative
property is satisfied, (iii)  x  G, there exists an e  G
such that x*e = e * x = x, e is an identity of G.
Let us suppose that E(A) = set of all the endomor-
phisms over the strongly connected automata A. The for-
mal specification of E(A) in terms of the schema Endo-
morphisms is described below. Two variables are taken,
the first one, is a set of all endomorphisms which is of
type of power set of Endomorphism and is denoted by
endomorphisms and, the second one, is a binary opera-
tion denoted by boperation. It takes two endomorphisms
as input and produces a new endomorphism. The com-
ponents of Endomorphisms are defined in first part and
invariants in the second part of it. Now we verify that
E(A) is a monoid under binary operation defined above.

Verifying Monoid and Group Morphisms over Strongly Connected Algebraic Automata 809
The algebraic structure (G, *) is called a group if 1) it
is a monoid and 2) for any element x there exists y in G
such that x*y = y*x = e. That is the inverse of each ele-
ment of G exists. Let us suppose that G (A) = set of all
automorphisms. For its formal specification, three vari-
ables are assumed. The first one is a set of all automor-
phism of type of power set of Automorphism. The second
one is an identity element and the last one is binary op-
eration denoted by boperation. It takes two automor-
phisms as input and produces a new automorphism as an
output.
Invariant: The last one property verifies existence of
inverse of each element in set G (A). The first three
properties are same as in case of monoid endomorphisms
defined above.
Now we verify that the sets of endomorphisms and
automorphisms over strongly connected algebraic auto-
mata are same. This verification is done in terms of a
schema named as Equivalence. There are three inputs to
this schema which are Endomorphism , Endomorphisms
and Automorphisms. At first, it is described that set of all
endomorphisms are bijective and then it is checked that
the number of elements must be same in both of the
morphisms.
Invariant: 1) There is a one to one correspondence
between the set of Endomorphisms and Automorphisms.
2) Both the sets Endom orphisms and Automo rphi sms are
of same type. 3) The total number of elements in both the
morphisms are equal.
4. Model Analysis
As we know there does not exist any computer tool which
may guarantee about the correctness of a computer
model. That is why we believe that even the specification
is written, in any of the formal languages, it may contain
potential errors. These errors may range from syntax er-
rors to hazardous inconsistencies. The Z/Eves is one of
the most powerful tools which can be used for analyzing
the specification written in Z. It is integrated with various
facilities which provide rigorous analysis increasing con-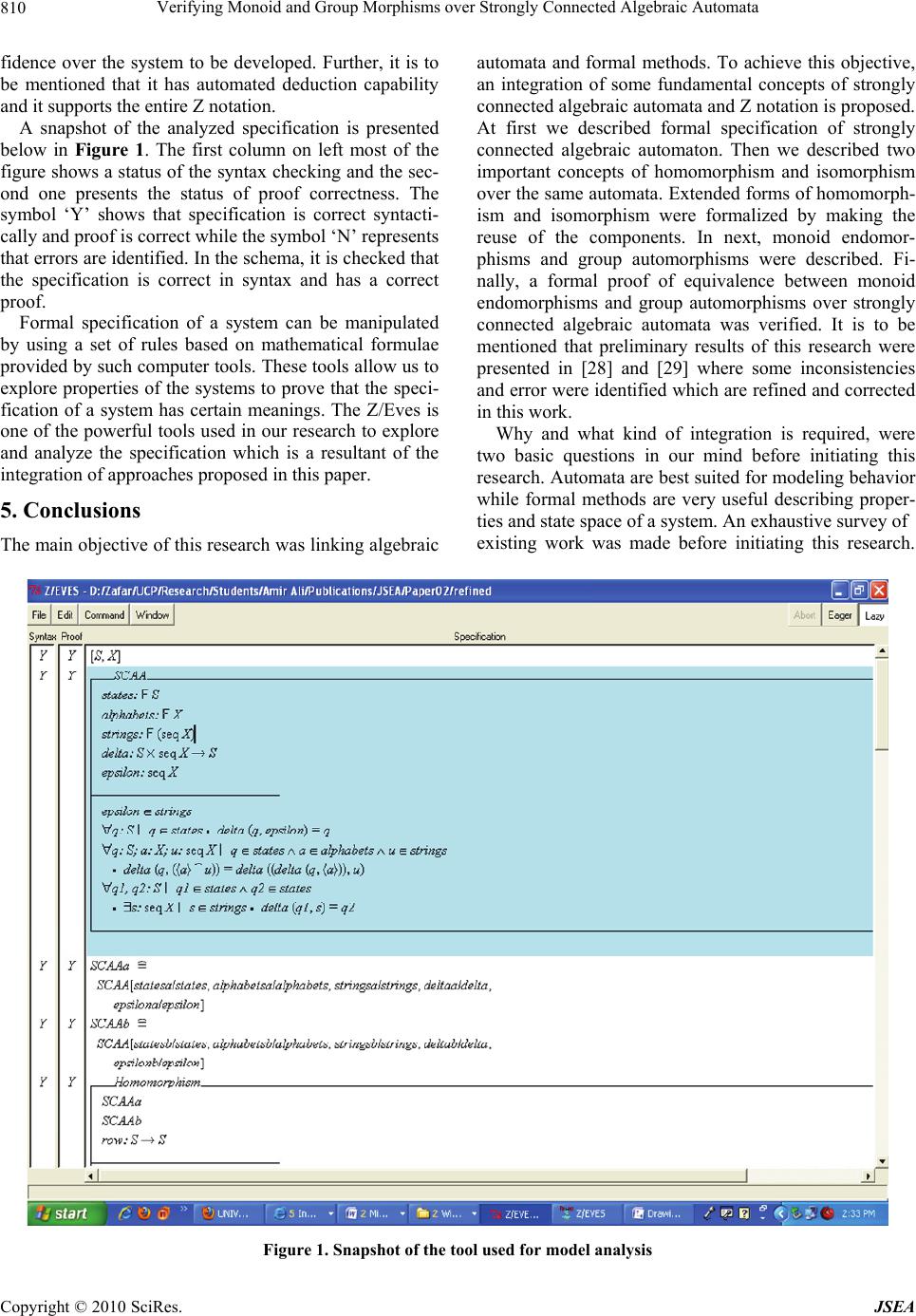

Verifying Monoid and Group Morphisms over Strongly Connected Algebraic Automata 810
fidence over the system to be developed. Further, it is to
be mentioned that it has automated deduction capability
and it supports the entire Z notation.
A snapshot of the analyzed specification is presented
below in Figure 1. The first column on left most of the
figure shows a status of the syntax checking and the sec-
ond one presents the status of proof correctness. The
symbol ‘Y’ shows that specification is correct syntacti-
cally and proof is correct while the symbol ‘N’ represents
that errors are identified. In the schema, it is checked that
the specification is correct in syntax and has a correct
proof.
Formal specification of a system can be manipulated
by using a set of rules based on mathematical formulae
provided by such computer tools. These tools allow us to
explore properties of the systems to prove that the speci-
fication of a system has certain meanings. The Z/Eves is
one of the powerful tools used in our research to explore
and analyze the specification which is a resultant of the
integration of approaches proposed in this paper.
5. Conclusions
The main objective of this research was linking algebraic
automata and formal methods. To achieve this objective,
an integration of some fundamental concepts of strongly
connected algebraic automata and Z notation is proposed.
At first we described formal specification of strongly
connected algebraic automaton. Then we described two
important concepts of homomorphism and isomorphism
over the same automata. Extended forms of homomorph-
ism and isomorphism were formalized by making the
reuse of the components. In next, monoid endomor-
phisms and group automorphisms were described. Fi-
nally, a formal proof of equivalence between monoid
endomorphisms and group automorphisms over strongly
connected algebraic automata was verified. It is to be
mentioned that preliminary results of this research were
presented in [28] and [29] where some inconsistencies
and error were identified which are refined and corrected
in this work.
Why and what kind of integration is required, were
two basic questions in our mind before initiating this
research. Automata are best suited for modeling behavior
while formal methods are very useful describing proper-
ties and state space of a system. An exhaustive survey of
existing work was made before initiating this research.
Figure 1. Snapshot of the tool used for model analysis

Verifying Monoid and Group Morphisms over Strongly Connected Algebraic Automata 811
Some interesting work [41-43] was found but our work
and approach are different because of abstract and con-
ceptual level integration of Z and algebraic automata. We
believe that this work will be useful in development of
integrated tools increasing their modeling power. It is to
be mentioned that most of the researchers have either
taken some examples in defining integration of ap-
proaches or addressed only some aspects. There is also a
lack of formalism which can be supported by computer
tools. Our work is different from others because we have
given a generic approach to link Z and algebraic auto-
mata which is verified by the Z/Eves toolset.
After integration, we have observed that a natural rela-
tionship exists between Z and algebraic automata. This
work is also important because formalizing graph based
notation is not easy as there has been little tradition of
formalization in it due to concreteness of graphs [44].
Our work is useful for researchers interested in integra-
tion of approaches. We believe that this research is also
useful because it is focused on general principles and
concepts and this integration can be used for modeling
systems after required reduction. The Z/Eves toolset
made it possible to capture the conceptual errors which
otherwise could not have been identified.
REFERENCES
[1] A. Hall, “Correctness by Construction: Integrating For-
mality into a Commercial Development Process,” Lecture
Notes in Computer Science, Springer, Vol. 2391, 2002, pp.
139-157.
[2] C. J. Burgess, “The Role of Formal Methods in Software
Engineering Education and Industry,” Technical Report:
CS-EXT-1995-045, University of Bristol, Bristol, 1995.
[3] B. A. L. Gwandu and D. J. Creasey, “The Importance of
Formal Specification in the Design of Hardware Systems,”
School of Electron & Electrical Engineering, Birmingham
University, Birmingham, 1994.
[4] H. A. Gabbar, “Fundamentals of Formal Methods,” Mod-
ern Formal Methods and Applications, Springer Nether-
lands, 2006.
[5] E. A. Boiten, et al., “Integrated Formal Methods (IFM
04),” Springer, Canterbury, 2004.
[6] J. Davies and J. Gibbons, “Integrated Formal Methods
(IFM07),” UK, Springer, 2007.
[7] J. Romijn, G. Smith and J. V. D. Pol, “Integrated Formal
Methods (IFM 05),” Springer, Eindhoven, 2005.
[8] K. Araki, A. Galloway and K. Taguchi, “Integrated For-
mal Methods (IFM99),” Springer, York, 1999.
[9] R. Bussow and W. Grieskamp, “A Modular Framework
for Integration of Heterogeneous Notations and Tools,”
Integrated Formal Methods (IFM 99), Springer-Verlag,
York, 1999, pp. 211-230.
[10] W. Grieskamp, T. Santen and B. Stoddart, “Integrated
Formal Methods,” Springer, Dagstuhl Castle, 2000.
[11] T. B. Raymond, “Integrating Formal Methods by Unifying
Abstractions,” Lecture Notes in Computer Science,
Springer, Vol. 2999, 2004, pp. 441-460.
[12] J. S. Dong, R. Duke and P. Hao, “Integrating Object-Z
with Timed Automata,” 12th IEEE International Confer-
ence on Engineering Complex Computer Systems, Auck-
land, 2005, pp. 488-497.
[13] S. Dong, et al., “Timed Patterns: TCOZ to Timed Auto-
mata,” 6th International Conference on Formal Engineer-
ing Methods, Seattle, 2004, pp. 483-498.
[14] R. L. Constable, et al., “Formalizing Automata II: Decid-
able Properties,” Cornell University, New York, 1997.
[15] R. L. Constable, et al., “Constructively Formalizing Au-
tomata Theory,” Foundations of Computing Series, MIT
Press, Cambridge, 2000.
[16] X. He, “Pz Nets a Formal Method Integrating Petri Nets
with Z,” Information & Software Technology, Vol. 43, No.
1, 2001, pp. 1-18.
[17] M. Heiner and M. Heisel, “Modeling Safety Critical Sys-
tems with Z and Petri Nets,” International Conference on
Computer Safety, Reliability and Security, Springer, Lec-
ture Notes In Computer Science, Toulouse, Vol. 1698,
1999, pp. 361-374.
[18] H. Leading and J. Souquieres, “Integration of UML and B
Specification Techniques: Systematic Transformation
from OCL Expressions into B,” Asia-Pacific Software En-
gineering Conference, Gold Coast, 2002, pp. 495-504.
[19] H. Leading and J. Souquieres, “Integration of UML Views
using B Notation,” Proceeding of Workshop on Integra-
tion and Transformation of UML Models, Málaga, 2002.
[20] W. Wechler, “The Concept of Fuzziness in Automata and
Language Theory,” Akademic-Verlag, Berlin, 1978.
[21] N. M. John and S. M. Davender, “Fuzzy Automata and
Languages: Theory and Applications,” Chapman & Hall,
CRC, USA, 2002.
[22] M. Ito, “Algebraic Theory of Automata and Languages,”
World Scientific Publishing, Singapore, 2004.
[23] D. K. Kaynar and N. Lynchn, “The Theory of Timed I/O
Automata,” Morgan & Claypool, 2006.
[24] C. Godsil and G. Royle, “Algebraic Graph Theory,”
Springer, New York, 2001.
[25] Z. Aleksic, “From Biology to Computation,” IOS Press
Publishers, IOS Press, Amsterdam, 1993.
[26] L. B. Kier, P. G. Seybold and C. K. Cheng, “Modeling
Chemical Systems Using Cellular Automata,” Springer,
New York, 2005.
[27] T. Ellman, “Specification and Synthesis of Hybrid Auto-
mata for Physics-based Animation,” Automated Software
Engineering, Vol. 13, No. 3, 2006, pp. 395-418.
[28] N. A. Zafar, A. Hussain and A. Ali, “Refinement: Formal
Proof of Equivalence in Endomorphisms and Automor-
phisms over Strongly Connected Automata,” Journal of
Software Engineering and Applications, Vol. 2, No. 2,
2009, pp. 77-85.
[29] N. A. Zafar, A. Hussain and A. Ali, “Formal Proof of

Verifying Monoid and Group Morphisms over Strongly Connected Algebraic Automata 812
Equivalence in Endomorphisms and Automorphisms over
Strongly Connected Automata,” Proceedings of the 2008
International Conference on Computer Science and Soft-
ware Engineering, Wuhan, Vol. 2, 2008, pp. 792-795.
[30] D. P. Tuan, “Computing with Words in Formal Methods,”
University of Canberra, Canberra, Australia, 2000.
[31] M. Conrad and D. Hötzer, “Selective Integration of For-
mal Methods in Development of Electronic Control
Units,” Proceedings of the 2nd IEEE International Con-
ference on Formal Engineering Methods, Brisbane, 1998,
pp.144-155.
[32] M. Brendan and J. S. Dong, “Blending Object-Z and
Timed CSP: An Introduction to TCOZ,” Proceedings of
the 20th International Conference on Software Engineer-
ing, Kyoto, 1998, pp. 95-104.
[33] A. T. Nakagawa, et al., “Cafe an Industrial-Strength Alge-
braic Formal Method,” Elsevier Science & Technology,
Amsterdam, 2000.
[34] J. V. Guttag and J. J. Horning, “The Algebraic Specifica-
tion of Abstract Data Types,” Acta Informatica, Springer
Berlin, Vol. 10, No. 1, 2004, pp. 27-52.
[35] J. M. Spivey, “The Z Notation: A Reference Manual,”
International Series in Computer Science, Prentice Hall,
1989.
[36] J. M. Wing, “A Specifier: Introduction to Formal Meth-
ods,” IEEE Computer, Vol. 23, No. 9, 1990, pp. 8-24.
[37] J. Woodcock and J. Davies, “Using Z: Specification, Re-
finement and Proof,” Prentice Hall, International Series in
Computer Science, 1996.
[38] J. A. Anderson, “Automata Theory with Modern Applica-
tions,” Cambridge University Press, Cambridge, 2006.
[39] L. L. Claudio, et al., “Applications of Finite Automata
Representing Large Vocabularies,” Software Practice &
Experience, Vol. 23, No. 1, 1993, pp. 15-30.
[40] Y. V. Moshe, “Nontraditional Applications of Automata
Theory,” Proceedings of the International Conference on
Theoretical Aspects of Computer Software, Lecture Notes
in Computer Science, Vol. 789, Sendai, 1994, pp. 575-597.
[41] D. I. A. Cohen, “Introduction to Computer Theory,” 2nd
Edition, John Wiley & Sons Inc., New York, 1996.
[42] J. P. Bowen, “Formal Specification and Documentation
Using Z: A Case Study Approach,” International Thomson
Computer Press, London, 1996.
[43] S. A. Vilkomir and J. P. Bowen, “Formalization of Soft-
ware Testing Criterion,” South Bank University, London,
2001.
[44] C. T. Chou, “A Formal Theory of Undirected Graphs in
Higher Order Logic,” Proceeding of 7th International
Workshop on Higher Order Logic, Lecture Notes in Com-
puter Science, Valletta, Vol. 859, 1994, pp. 144-157.