Paper Menu >>
Journal Menu >>
 p J. So f tware E doi:10.4236/js e Copyright © 2 0 Effici e Tran s Stand Mohamed N 1German Univ e Alexandria, Eg y Email: mrizkal l Received Janu a ABSTRA C I n this paper, dard is prop o denote the ro w on the standa r complexities o tional compl e other provid e With lower c o quality-dema n p roposed fast Keywords: Fa 1. Introdu c NOWDAYS t p roducts and f life activities i daily necessa r and surveilla n video streami n (HD) product dards organiz a The Internat i which is an o applications a n for low bit r a H.262, H.263 the Internatio n more focused the MPEG se r tures. The M MPEG-2 and In [4], the DCT is revea E n g ineerin g & e a.2010.38091 P 0 10 SciRes. e nt Fa s form a ard N asr Hagga g e rsity at Cairo N y pt; 3Purdue Sc h l @iupui.edu a ry 21st, 2010; r e C T efficient one- d o sed. Based o n w /column per m r d matrix, the o f the propose d e xity reductio n e s more comp u o mplexity and n ding video c o algorithm is s a st Algorithm, c tion t he demand f o f aster digital v i s increasing. T r y needs, like v n ce, up to our n g, digital ca m s [1,2]. There a tions driving i onal Teleco m o rganization f o n d has create d a te video tele p and H.264 [ 3 n al Standards on consumer r ies standards M PEG standa MPEG-4 [1-3 ] 16 × 16 2-D m led, using the Applications , P ublished Onli n st Mu l a tion f o g 1 , Mohame d N ew Cairo City , C h ool of Engine e e vised June 30th d imensional ( n the symmetr i m utations and efficient fast 1 d fast in te ger t n one of the p u tational com p better transfo r o ding comput a s uitable to acc e HDTV, H.265 o r higher qual i v ideo applicati T hese deman d v ideo confere n entertainment m eras, and all have been t w the definition m munications o cused on tel e d the series of H p hony. These 3 ]. The other Organization applications a for compress i rd series in c ] . m atrix for the decompositi o , 2010, 3, 784- n e August 2010 ( l tiplic a o r the d El-Sharka w C airo, Egypt; 2 E e ring and Techn o , 2010; accepte d 1-D) f ast inte g i c property o f the matrix de c 1 -D integer tr a t ransform are p roposed algo r p lexity reduct i r mation quali t a tions. On th e e lerate the vi d , ICT, Order- 1 i ty digital vid e ons in our dai d s start from o u n cing, televisi o , iPods, inter n high definiti o w o primary sta n of video codi n Union (IT U e communicati o H .26x standar d include H.26 organization (ISO), which a nd has defin e i ng moving pi c lude MPEG- H.265 standa r o n and the mo d 795 ( http://www.Sc i a tion F 1-D D w y 2 , Gamal F E gypt Japan Un i o logy, Indianap o d July 5th, 2010. g er transform f the integer t r c ompositions, a a nsform algor i smaller than t r ithms provid e i on while mai t y, the first pr o e other hand, w d eo coding co m 1 6 Transform, e o ly u r o n n et o n n - n g. U ), o n d s 1, is is e d c- 1, r d d - ificatio n duce t w compl e to mak i The tion 2, standa r efficie n H.265 factori z these p analysi tween t thod is al com p done i n sion. 2. Re v the The H. i RP.org/journal /j F ree I n CT o f F ahmy 1 , Ma h i versity of Scie n o lis, USA. algorithms o f r ansform mat r a long with usi n i thms are dev e t hose of the di r e s transforma t ntaining alm o o posed fast al g w ith the signi f m putations. Video Codin g n techniques u w o proposed a e xity of the al i ng it multipli c rest of this p a review of the r d is describe d n t fast intege r standard are i n z ations. Then p roposed algo r s and compa r t he proposed f shown. In Se c p lexity done i n Section 4 is d v iew of the H.265 Sta n 265 is the ne w /j sea) n te g er f the H h er Rizkall a n ce and Techno l f the DCT mat r ix and the m a n g the dyadic s e loped. There fo r ect method. I n t ion quality i m o st the same t r g orithm is sui t f icant lower c g u sed in [5-8], a lgorithm that gorithm impl e c ation-free. a per is organi z integer transf o d . In Section r transform a l n troduced wit h the computa t r ithms are di s r ison of tran s f ast algorithm s c tion 5, comp a i n Section 3 a d iscussed. Fin a Integer T r n dard w est yet to b e .265 a 1 l ogy Borg Al A r r ix for the H . 2 a trix operatio n s ymmetry mo d fo re, the comp u n addition to c m provement, w r ansformation t able to accel e c omplexity, th e this paper w will aim to re e mentation in z ed as follows . o rmation for t h 3, the two p l gorithms for h the propose d t ional comple x s cussed. In S e s formation qu a s and the ori g a rison of com p a nd quality e v a lly, we give a r ansformat i e released sta n JSEA r ab, 2 65 stan- n s, which d ification u tational c ompu t a- w hile the quality. e rate the e second ill int r o- duce the addition . In Sec- h e H.265 p roposed the 2-D d matrix x ities of e ction 4, a lity be- g inal m e- p utation- v aluation a conclu- i on for n dard for  Efficient Fast Multiplication Free Integer Transformation for the 1-D DCT of the H.265 Standard Copyright © 2010 SciRes. JSEA 785 high definition video processing. From [4], the matrix of the 2-D 16 × 16 integer cosine transformation for the H.265 standard is shown in Equation (1). The matrix elements in Equation (1) shows that there is symmetric properties between the left side and right side of the matrix, this property will be exp loited using matrix decomposition in order to this matrix into the product of sparse matrices in the next section. 3232 32 32 32 32 32 32 32 32 32 32 32 32 32 32 454340352921134413 21 29 35 40 43 45 4438259925 38 44 44 38 2599253844 4329421 40 45 35 131335454021429 43 421717 42 42 171742421717 42 42 171742 40435 43 1329452121 45 29134335440 389442525449 3838 9442525449 38 35 21 434451340 29294013 454432135 323232 3232 3232 3232 3232 3232 3232 32 294013 45443 2135 3521 43445 1340 29 2544938 389442525 44938 38944 25 2145 2913 43 35440 40435 43 1329 45 21 1742 42 1717 42 42 1717 42 42 1717 42 42 17 1335 45 40 21429 43 43 29421 40 45 35 13 925 38 44 44 38 259925 38 44 44 38 259 413 21 29 35 40 43 45 45 43 40 35 29 21 134 (1) 3. Proposed Algorithms In this section, two proposed algorithm for efficient fast multiplication-free for the H.265 standard are presented. The proposed algorithms are done using a combination of Modified Integer Cosine Transformation, matrix de- composition and dyadic symmetry. The common part in the complexity reduction is discussed first, then each algorithm is presented individually and its complexity is calculated with it. The aim of the proposed algorithms is to reduce the computational complexities, which are refe- rred to as the numbers of additions and shift operations as much as possiblewhile maintaining reasonable error margin. The DCT matrix for the H.265 is given as T in Equation (1). The symmetric property of the transformation matrix is exploited to decompose it into the product of two sparse matrices. so the transformation matrix in Equation 1 can be rewritten in Equation (2) [5,8]. 1T TTP (2) 323232323232323200000000 00000000413212935404345 4438259925384400000000 00000000133545402142943 421717424217174200000000 00000000214529134335440 3894425254493800000000 00000000294013454432135 323232323232323200000000 00000000352143445134029 2544938389442500000000 00000000404354313294521 174242171742421700000000 00000000432942140453513 9253844443825900000000 00000000454340352921134  Efficient Fast Multiplication Free Integer Transformation for the 1-D DCT of the H.265 Standard Copyright © 2010 SciRes. JSEA 786 1 0 0 0 0 0 0 000000001 0 1 0 0 0 0 0 000000010 0 0 1 0 0 0 0 000000100 0 0 0 1 0 0 0 000001000 0 0 0 0 1 0 0 000010000 0 0 0 0 0 1 0 000100000 0 0 0 0 0 0 1 001000000 0 0 0 0 0 0 0 110000000 0 0 0 0 0 0 0110000000 000000 1 0 01000000 00000 1 00 00100000 0000 1 000 00010000 000 1 0000 00001000 00 1 00000 00000100 0 1 000000 00000010 10 0 0 0 0 0 000000001 Where Trr TPT (3) 1000000000000000 0000000010000000 0100000000000000 0000000001000000 0010000000000000 0000000000100000 0001000000000000 0000000000010000 0000100000000000 0000000000001000 0000010000000000 0000000000000100 0000001000000000 0000000000000010 0000000100000000 0000000000000001 and 323232323232323200000000 4438259925384400000000 421717424217174200000000 3894425254493800000000 323232323232323200000000 2544938389442500000000 174242171742421700000000 9253844443825900000000 00000000413212935404345 00000000133545402142943 00000000214529134335440 00000000294013454432135 00000000352143445134029 00000000404354313294521 00000000432942140453513 00000000454340352921134  Efficient Fast Multiplication Free Integer Transformation for the 1-D DCT of the H.265 Standard Copyright © 2010 SciRes. JSEA 787 The function of P1 is the post-process matrix for the input data to the matrix multiplication, and the post- process only uses the additions and subtracts. The com- putational complexities of P1 are 16 additions. In Equa- tion (2), the elements of TT are scattered; the rearrange- ment of the elements in TT is required to group the ele- ments of TT into two 8 × 8 independent matrices. Pr is a pre-process matrix that permutes the rows of T, so that it is rewritten as in Equation (3) [5,8]. As shown in Equation (3 ), the matrix Pr can be used as a pre-process matrix. Pr doesn’t have any complexity at all while serving the purpose of rearranging TT into Tr where the matrix can be easily represented as the direct sum of its two non-zero areas. The result of the direct sum is shown in Equation (4). 00 11r TT T (4) Where 00 32323232 32323232 44 382599253844 42 1717424217 1742 389442525449 38 32 3232323232 3232 25 44 938389 4425 174242 171742 4217 9 2538 444438259 T And 11 4 13212935404345 13 354540 21429 43 214529 134335440 294013 454432135 352143445 134029 404354313294521 43 29421 4045 3513 45434035 2921134 T The computation of T00 can be called the computation of the even frequency part in the transform matrix, and the computation of T11 can be called the computation of the odd frequency part in the transform matrix [5]. In Equation (4), the integers of matrix T00 have the symmetry property, using matrix decomposition T00 can be expressed as the product of the three sparse matrices R1, T0 and R2 as was done with the original matrix T [4,7]. The result of the decomposition for T00 is shown in Equation (5). 000 1r TRTR (5) Where 10000000 00001000 01000000 00000100 00100000 00000010 00010000 00000001 r R 0 32 3232320000 42 1717420000 323232 320000 1742 42170000 00 0 09253844 000 02544938 00003894425 000 0443825 9 T And 1 10000001 01000010 00100100 00011000 000 11000 00 100100 01000010 10000001 R As shown in the above equation, R1 can be implemented using additions and subtractions only and have a com- plexity of 8 additions, while Rr doesn’t have any com- plexity at all [5], as for T0 it can be expressed by the di- rect sum of matrices T0E and T0O, as shown in Equation (6). 00 0 E O TT T (6) Where 0 32 323232 42 171742 323232 32 1742 4217 E T 0 9 253844 25 44938 389 4425 4438 259 O T The symmetry of the matrix T0E can be further exploited using matrix decomposition to decompose the matrix into  Efficient Fast Multiplication Free Integer Transformation for the 1-D DCT of the H.265 Standard Copyright © 2010 SciRes. JSEA 788 the product of sparse matrices U1 and U2 [5], as shown in Equation (7). 012E TUU (7) Where 1 32 3200 001742 32 32 00 004217 U And 2 1001 0110 0110 1001 U In Equation (7), U2 can be implemented using addi- tions and subtractions only and have a complexity of 4 additions, while U1 can be implemented using 10 addi- tions and 10 shifts. This would sum up to a complexity of 14 addition and 10 shift operations for Equation (7) [5]. Although there is no symmetry present in matrix T0O, the matrix addition can be used to segment the matrix into two matrices with more value coherence in their elements, as shown in Equation (8). 001O TKK (8) Where 0 9 244036 24 36940 409 3624 3640 249 K And 1 0128 1802 208 1 8210 K After using the matrix addition, K0 can be simplified using matrix decomposition into the product of matrices K2 and K3. The result of the decomposition for K0 is shown in Equation (9). 023 KKK (9) Where 2 1004 0140 04 10 40 01 K And 3 98 80 80 98 890 8 0889 K As shown in the above equation; K1 can be implement- ted using additions and shifts only and have a complexity of 8 additions and 8 shifts, the addition between K1 and the product of K2 and K3 has a complexity of 4 additions, As for the matrix K2 it have a complexity of 4 additions and 4 shifts, while on the other hand K3 have a complex- ity of 12 additions and 4 shifts. This in the end sums the complexity of T0O to 28 additions and 16 shifts [5,6]. All of the above decomposition and summation sum the complexity of T00 to 66 additions and 32 shifts [5,6]. Turning to matrix T11 which represents the computa- tion of the odd frequency part, the matrix as shown in Equation (10), doesn't have the symmetric property within its elements, in order to be able to decompose this matrix the modification techniques will be used. For the decomposition of this matrix two proposed algorithms will be presented in this paper. 3.1 Proposed Algorithm 1 For Proposed Algorithm 1, the odd frequency modified integer cosine transformation matrix based on the dyadic symmetry concept used by Wai-Kuen Cham in [8] is obtained by modifying the positions of the elements in the matrix to provide the matrix basic vectors with or- thogonality regardless of the matrix elements values [8]. The matrix T11 and the modified matrix are shown in Equation (10) below. 11 1mod TT∶ (10) Where 11 4 13212935404345 13 354540 21429 43 214529 134335440 294013 454432135 352143445 134029 404354313294521 43 29421 4045 3513 45434035 2921134 T and 1mod 413212935404345 35 40 4345413 2129 21 2941343 4535 40 454340352921134 4345 354021 29413 134292140 354543 292113445434035 40354543 1342921 T Replacing T11 with T1mod as the new odd frequency transformation matrix [8], this matrix can be segmented into two matrices with more value coherence in their  Efficient Fast Multiplication Free Integer Transformation for the 1-D DCT of the H.265 Standard Copyright © 2010 SciRes. JSEA 789 elements as was done in the matrix T00O, as shown in Equation (11). 1mod1 2mm TTT (11) Where 1 4 16243236444444 36 44 4444416 2432 24 3241644443644 44 4444 3632 24164 44 4436442432416 16 4322444364444 3224 16444 444436 44 36444416432 24 m T and 2 0333141 1 14110333 330 31114 11413330 11 143 303 30 334111 33301141 41 1 13033 m T In Equation (11), the segment Tm1 from the matrix ad- dition segmentation done on the matrix T1mod has sym- metric properties; hence it can be further simplified using matrix decomposition algorithm into the product of three sparse matrices [8]. The result of this matrix decomposi- tion is shown in Equation (12). 1123 4 m TMMM (12) Where 1 20 11 1310 31110201 1310102 1 010131 12 1132010 1 1110 201 3 02011131 102311 10 M 2 00001 101 00110010 01010010 01100010 0 1110000 10000 10 1 10 0 010 0 1 10001100 M and 3 11201020 201120 10 2 100 1120 110 20102 0 21 1 0201 12001 102 00 21 20 11 00120211 M As shown from the equation above; M1 can be imple- mented using additions and shifts only and have a com- plexity of 48 additions and 8 shifts, while M2 can be im- plemented using only additions and have a complexity of 16 additions, As for the matrix M3 it have a complexity of 32 additions and 8 shifts. This in the end sums the complexity of Tm1 to 96 additions and 40 shifts [8]. On the other hand, Tm2 can be implemented using additions and shifts only, and has a complexity of 72 additions and 8 shifts [5,6,8]. By using equations from Equation (2) to Equation (12), the efficient fast multiplication-free integer transforma- tion for the 2-D DCT matrix for the H.265 standard for proposed algorithm 1 is given as shown in Equation (13). 121 231 . rr TP RUUKKKR 1123 1 4 m TMMM P (13) 3.2 Proposed Algorithm 2 In the proposed algorithm presented in this section the same complexity reduction and decomposition tech- niques will be done, the difference will be that in the odd frequencies matrix in the step done in Equation (10) in- stead of only using dyadic symmetry to rearrange the elements of the matrix, a modification in values of the elements will be done so that it matches the matrix Tm1 in Equation (11). The resultant odd frequency matrix is given in Equation (14). 11 1mod2 TT∶ (14) Where 1mod2 4 16243236444444 36 44 44 44416 24 32 24 3241644 4436 44 44 4444 3632 24164 4444 364424 32416 16 4322444364444 3224164 444444 36 44 3644 4416432 24 T The odd frequency matrix for proposed algorithm 2 T1mod2 can be decomposed for complexity reduction in 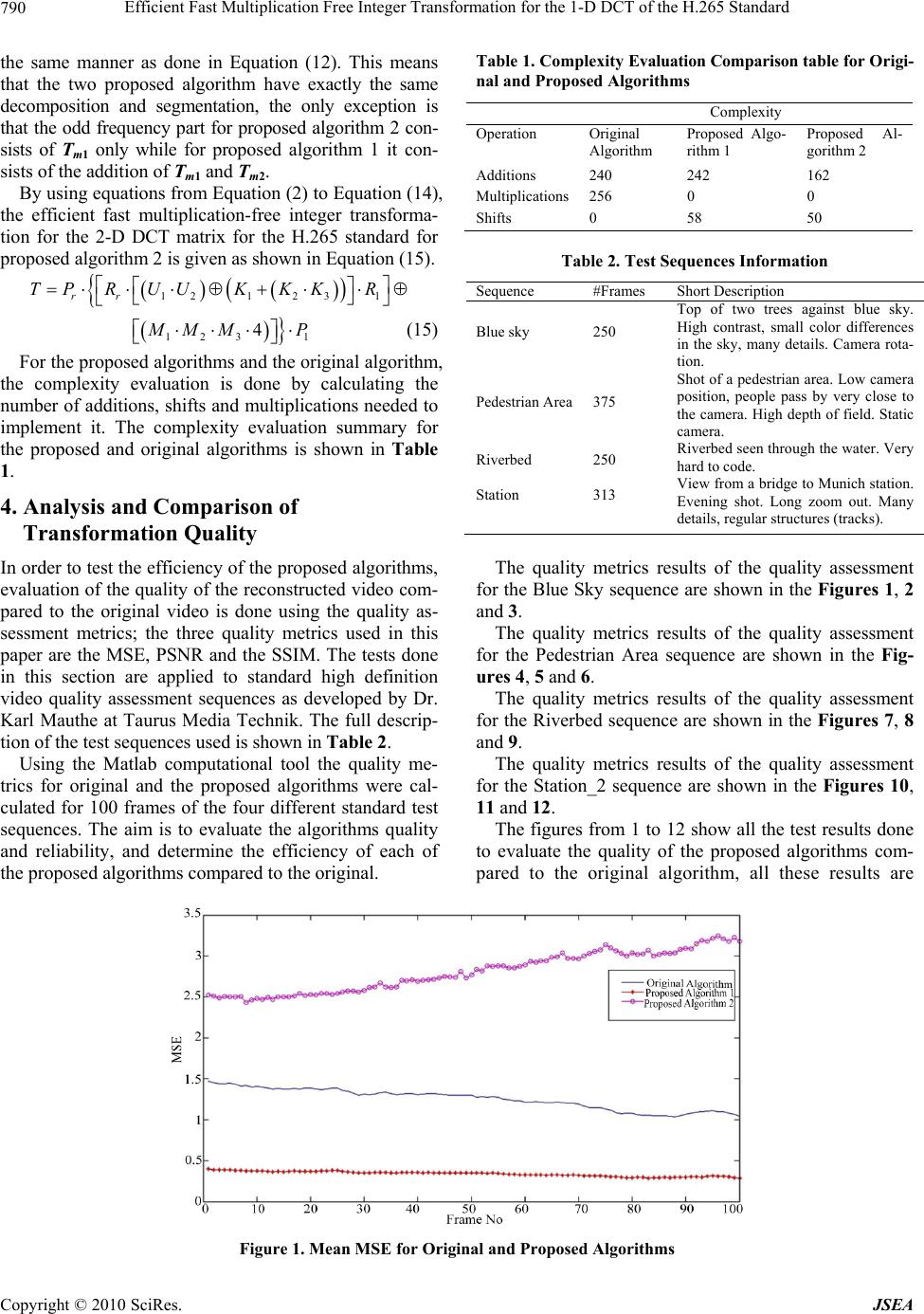 Efficient Fast Multiplication Free Integer Transformation for the 1-D DCT of the H.265 Standard Copyright © 2010 SciRes. JSEA 790 the same manner as done in Equation (12). This means that the two proposed algorithm have exactly the same decomposition and segmentation, the only exception is that the odd frequency part for proposed algorithm 2 con- sists of Tm1 only while for proposed algorithm 1 it con- sists of the addition of Tm1 and Tm2. By using equations from Equation (2) to Equation (14), the efficient fast multiplication-free integer transforma- tion for the 2-D DCT matrix for the H.265 standard for proposed algorithm 2 is given as shown in Equation (15). 121 231rr TP R UUKKKR 123 1 4 M MM P (15) For the proposed algorithms and th e original algor ithm, the complexity evaluation is done by calculating the number of additions, shifts and multiplications needed to implement it. The complexity evaluation summary for the proposed and original algorithms is shown in Table 1. 4. Analysis and Comparison of Transformation Quality In order to test the efficiency of the proposed algor ithms, evaluation of the quality of the reconstructed video com- pared to the original video is done using the quality as- sessment metrics; the three quality metrics used in this paper are the MSE, PSNR and the SSIM. The tests done in this section are applied to standard high definition video quality assessment sequences as developed by Dr. Karl Mauthe at Taurus Media Technik. The full descrip- tion of the test sequences used is shown in Table 2. Using the Matlab computational tool the quality me- trics for original and the proposed algorithms were cal- culated for 100 frames of the four different standard test sequences. The aim is to evaluate the algorithms quality and reliability, and determine the efficiency of each of the proposed algorithms compared to the original. Table 1. Complexity Evaluation Comparison table for Origi- nal and Proposed Algorithms Complexity Operation Original Algorithm Proposed Algo- rithm 1 Proposed Al- gorithm 2 Additions 240 242 162 Multiplications256 0 0 Shifts 0 58 50 Table 2. Test Sequences Information Sequence #Frames Short Description Blue sky 250 Top of two trees against blue sky. High contrast, small color differences in the sky, many details. Camera rota- tion. Pedestrian Area375 Shot of a pedestrian area. Low camera position, people pass by very close to the camera. High depth of field. Static camera. Riverbed 250 Riverbed seen through the water. Very hard to code. Station 313 View from a bridge to Munich station. Evening shot. Long zoom out. Many details, regular structures (tracks). The quality metrics results of the quality assessment for the Blue Sky sequence are shown in the Figures 1, 2 and 3. The quality metrics results of the quality assessment for the Pedestrian Area sequence are shown in the Fig- ures 4, 5 and 6. The quality metrics results of the quality assessment for the Riverbed sequence are shown in the Figures 7, 8 and 9. The quality metrics results of the quality assessment for the Station_2 sequence are shown in the Figures 10, 11 and 12. The figures from 1 to 12 show all the test results done to evaluate the quality of the proposed algorithms com- pared to the original algorithm, all these results are Figure 1. Mean MSE for Original and Proposed Algorithms 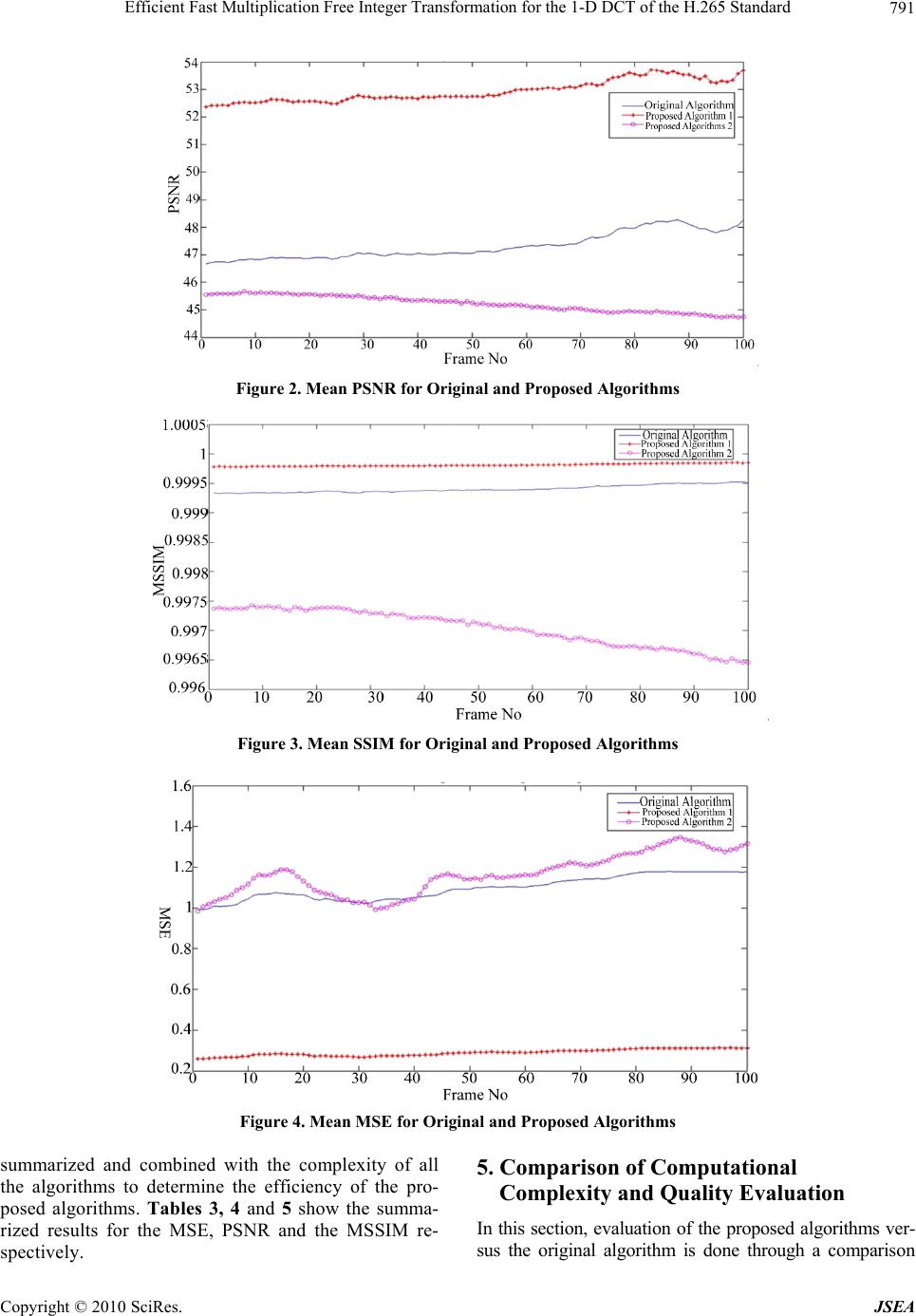 Efficient Fast Multiplication Free Integer Transformation for the 1-D DCT of the H.265 Standard Copyright © 2010 SciRes. JSEA 791 Figure 2. Mean PSNR for Original and Proposed Algorithms Figure 3. Mean SSIM for Original and Proposed Algorithms Figure 4. Mean MSE for Original and Proposed Algorithms summarized and combined with the complexity of all the algorithms to determine the efficiency of the pro- posed algorithms. Tables 3, 4 and 5 show the summa- rized results for the MSE, PSNR and the MSSIM re- spectively. 5. Comparison of Computational Complexity and Quality Evaluation In this section, evaluation of the proposed algorithms ver- sus the original algorithm is done through a comparison 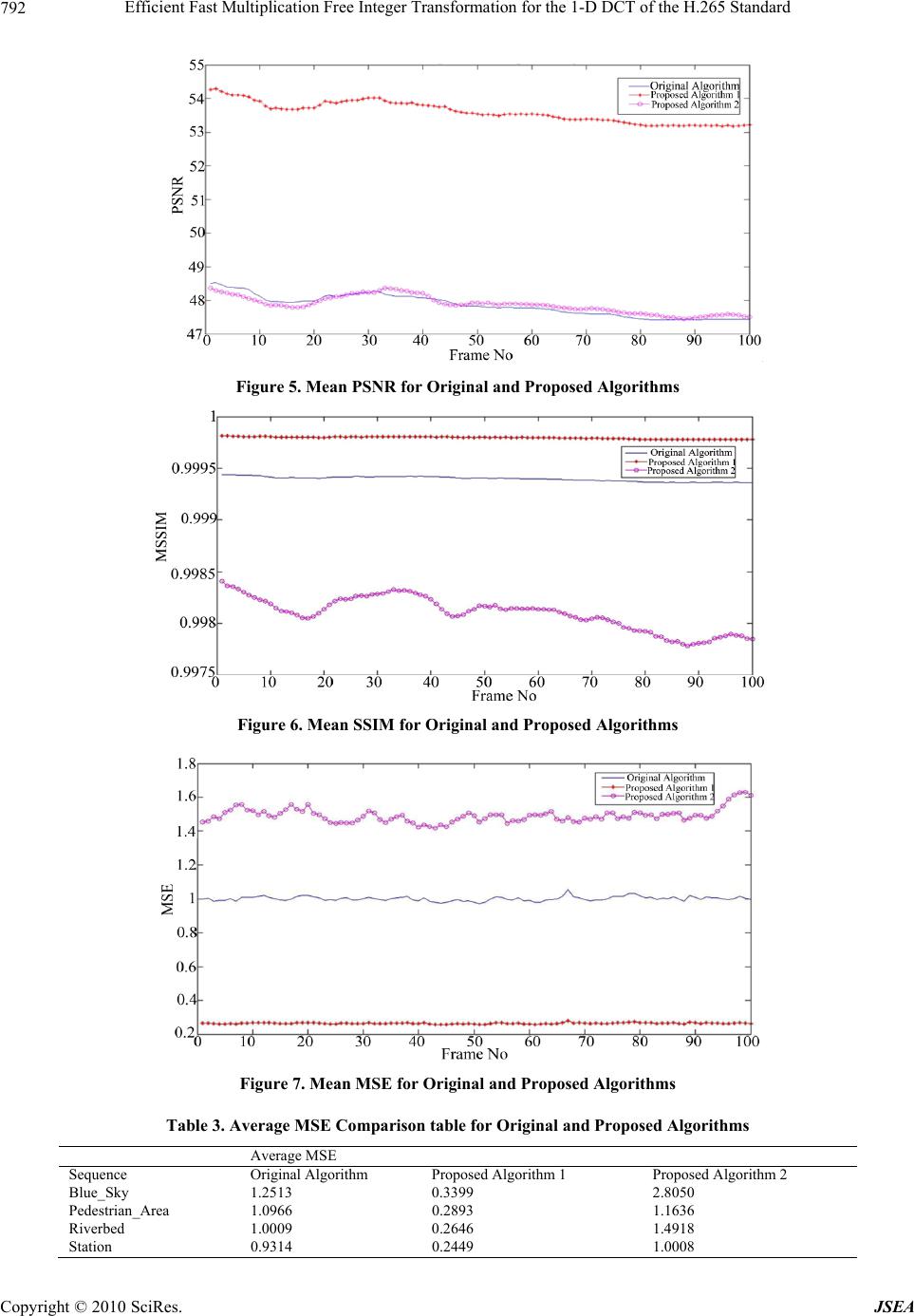 Efficient Fast Multiplication Free Integer Transformation for the 1-D DCT of the H.265 Standard Copyright © 2010 SciRes. JSEA 792 Figure 5. Mean PSNR for Original and Proposed Algorithms Figure 6. Mean SSIM for Original and Proposed Algorithms Figure 7. Mean MSE for Original and Proposed Algorithms Table 3. Average MSE Comparison table for Original and Proposed Algorithms Average MSE Sequence Original Algorithm Proposed Algorithm 1 Proposed Algorithm 2 Blue_Sky 1.2513 0.3399 2.8050 Pedestrian_Area 1.0966 0.2893 1.1636 Riverbed 1.0009 0.2646 1.4918 Station 0.9314 0.2449 1.0008 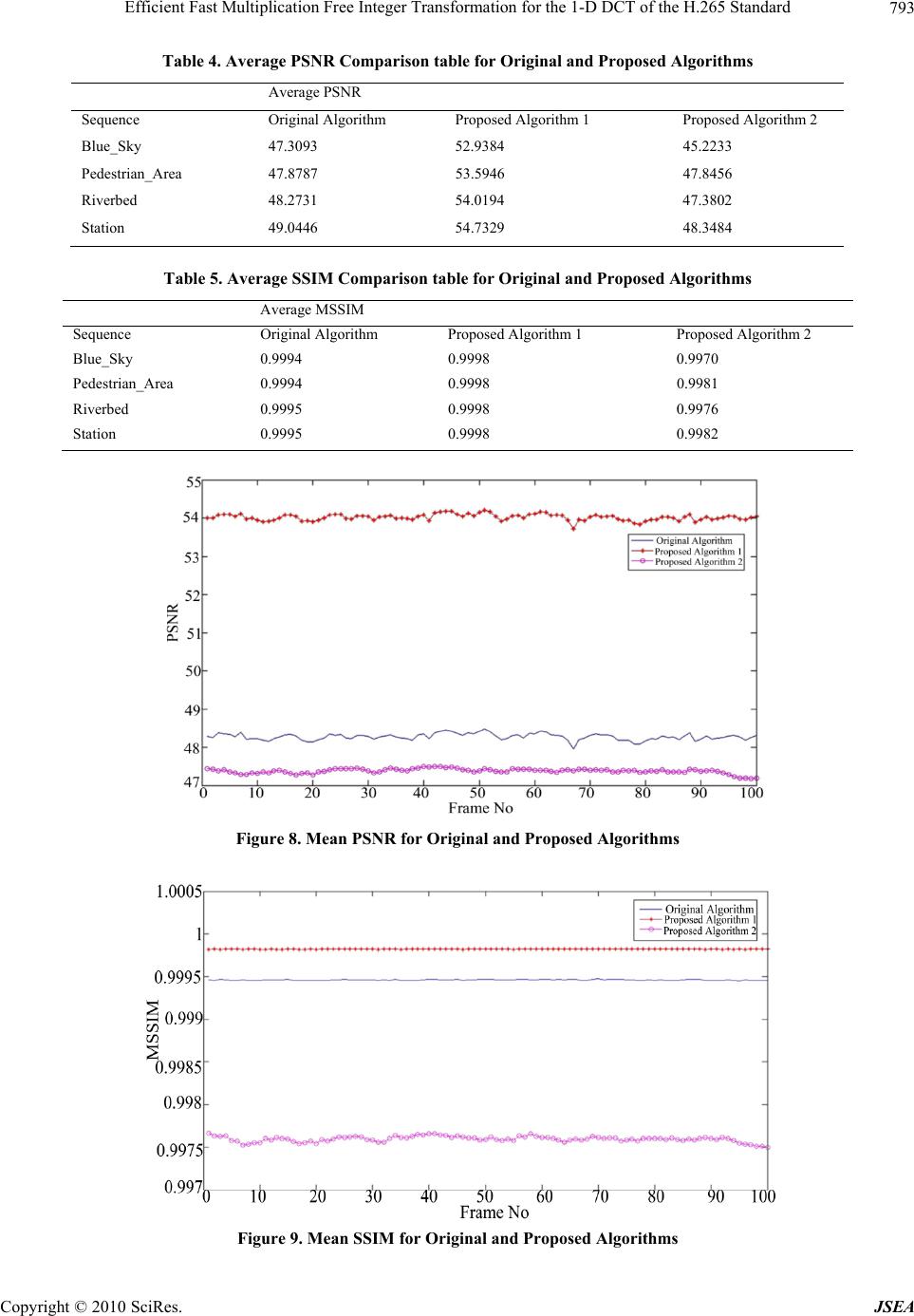 Efficient Fast Multiplication Free Integer Transformation for the 1-D DCT of the H.265 Standard Copyright © 2010 SciRes. JSEA 793 Table 4. Average PSNR Comparison table for Original and Proposed Algorithms Average PSNR Sequence Original Algorithm Proposed Algorithm 1 Proposed Algorithm 2 Blue_Sky 47.3093 52.9384 45.2233 Pedestrian_Area 47.8787 53.5946 47.8456 Riverbed 48.2731 54.0194 47.3802 Station 49.0446 54.7329 48.3484 Table 5. Average SSIM Comparison table for Original and Proposed Algorithms Average MSSIM Sequence Original Algorithm Proposed Algorithm 1 Proposed Algorithm 2 Blue_Sky 0.9994 0.9998 0.9970 Pedestrian_Area 0.9994 0.9998 0.9981 Riverbed 0.9995 0.9998 0.9976 Station 0.9995 0.9998 0.9982 Figure 8. Mean PSNR for Original and Proposed Algorithms Figure 9. Mean SSIM for Original and Proposed Algorithms  Efficient Fast Multiplication Free Integer Transformation for the 1-D DCT of the H.265 Standard Copyright © 2010 SciRes. JSEA 794 Figure 10. Mean MSE for Original and Proposed Algorithms Figure 11. Mean PSNR for Original and Proposed Algorithms Figure 12. Mean SSIM for Original and Proposed Algorithms  Efficient Fast Multiplication Free Integer Transformation for the 1-D DCT of the H.265 Standard Copyright © 2010 SciRes. JSEA 795 between the results of Section 3 and Section 4. In terms of quality assessment Table 3 clearly shows the advantage of Proposed Algorithm 1 over Proposed Algorithm 2 and even the Original algorithm as it was able to achieve the smallest values for the MSE index over 4 different test sequences. Table 4 backs the results shown in Table 3, and also shows that the different in quality measured by the PSNR index between the ori- ginnal algorithm and Proposed Algorithm 2 is not high, which means that both achieve comparable qualities [9]. Table 5 shows that according to a more (HVS) based index, Proposed Algorithm 1 still achieve the best result with the original algorithm coming in second place, and proposed algorithm achieving lower structural similarity than both. However the values in this table indicate that the results for the three algorithms are all almost in the same range, and achieve what is considered high struc- tural similarity. These improved results achieved by the proposed algorithms compared to the original one are due to applying the dyadic symmetry on the transforma- tion matrix odd-frequency part which makes the trans- formation matrix as a whole symmetric and hence elimi- nates the transformation error as the product of the transformation matrix multiplied by its transpose will yield an identity matrix. As for the complexity point of view, taking into con- sideration that multiplications are the process in terms of complexity and hardware followed by additions and fi- nally shifts. Table 1 clearly shows the superiority of proposed Algorithm 2 over the other two algorithms in terms of less complexity, and emphasis the fact that both of the proposed algorithms are multiplication-free, also the table shows that proposed Algorithm 1 is far less complex than the original algorithm, although it requires two more additions than the original algorithm, it has no multiplications and small number of shifts. Finally form all the results obtained in this section, it can be concluded that the proposed Algorithm 1 achieves the highest quality in encoding and decoding while main- taining less complexity than the original algorithm, which means that it would be suitable for quality-oriented appli- cations, however on the other hand proposed Algorithm 2 achieves the dramatically less complexity than the origi- nal algorithm without having any noticeable or detectable quality degradation, which makes this algorithm suitable for speed or hardware oriented applications. 6. Conclusions A new 16 × 16 DCT matrix was recently introduced for the highly anticipated H.265 standard, this DCT matrix is developed for high definition videos encoding and de- coding, the aim is to make them less complex and faster for video communication and transmission, like in high definition broadcasting and storage. Two new algorithms were proposed in this paper. The first technique is a quality oriented algorithm while offering multiplica- tion-free complexity. The second algorithm is a com- plexity and speed oriented algorithm while maintaining almost the same quality offered by the original algorithm. The aim of proposing an efficient fast 1-D algorithm for this DCT matrix is to reduce the complexity and hence the hardware and increase the speed of computa- tion to meet the constantly improving demands in the fields of communication and transmission. Quality As- sessment Tests were carried out and the quality metrics MSE, PSNR and SSIM were calculated to evaluate the performance of the pro posed algorithms compared to the original one. The test results showed that the first pro- posed algorithm offers better quality, objective and sub- jective, while offering less complexity and multiplica- tion-free computation. While the second proposed algo- rithm offers almost the same quality, objective and sub- jective, while offering much less complexity and multip- lication-free computation than the original algorithm and the first proposed one. REFERENCES [1] J.-B. Lee and H. Kalva, “The VC-1 and H.264 Video Compression Standards for Broadband Video Services,” Springer, New York, 2008. [2] I. E. G. Richardson, “H. 264/MPEG-4 Part 10: Overview,” 7 October 2002. http://www.vcodex.com/files/h264_over- view_orig.pdf [3] T. Wiegand, G. J. Sullivan, G. Bjøntegaard and A. Luthra, “Overview of the H.264/AVC Video Coding Standard,” IEEE Actions on Circuits and Systems for Video Tech- nology, Vol. 13, No. 7, July 2003, pp. 560-576. [4] C.-P. Fan and G.-A. Su, “Efficient Fast 1-D 8x8 Inverse Integer Transform for VC-1 Application,” IEEE Transac- tions on Circuits and Systems for Video Technology, Vol. 19, No. 4, 2009, pp. 584-590. [5] C.-P. Fanm, G.-A. Su, “Efficient Low-Cost Sharing De- sign of Fast 1-D Inverse Integer Transform Algorithms for H.264/AVC and VC-1,” IEEE Signal Processing Let- ters, Vol. 15, 2008, pp. 926-929. [6] W.-K. Cham, “Development of Integer Cosine Transfor- mation by the Principle of Dyadic Symmetry,” IEEE Proceedings, Vol. 136, No. 4, August 1989, pp. 276-282. [7] J. Dong, K. N. Ngan, C.-K. Fong and W.-K. Cham, “2D Order-16 Integer Transfor ms for HD Video Codi ng,” IEEE Transactions on Circuits and Systems for Video Technolo- gy, Vol. 19, No. 10, October 2009, pp. 1463-1474 [8] J. Dong, “Transform Error Introduced by Non-Orthogo- nality,” 27 April 2009. http://www.h265.net/index.php?s= dct [9] Z. Wang, A. C. Bovik, H. R. Sheikh and E. P. Simoncelli, “Image Quality Assessment: From Error Visibility to Structural Similarity,” IEEE Transactions on Image Processing, Vol. 13, No. 4, April 2004, pp. 600-612. |

