Energy and Power En gineering, 2010, 2, 196-202
doi:10.4236/epe.2010.23029 Published Online August 2010 (http://www.SciRP.org/journal/epe)
Multi-Bias Model for Power Diode Using a Very High
Description Language
Hassene Mnif, Montassar Najari, Hekmet Samet, Nouri Masmoudi
National Sch o ol of En gi neering of Sfax , LETI Laboratory, Sfax, Tunisia
Received May 3, 2010; revised June 12, 2010; accepted July 16, 2010
Abstract
This study focused on the determination and analysis of an accurate analytical model for PIN diode under
different bias conditions. This approach employs analytically derived expressions including the variation of
the depletion regions in the device to make the used model available over a wide range of testing conditions
without remake the parameters extraction procedure. The validity of the proposed extraction procedure has
been verified by the very good agreement between simulated and measured current and voltage waveforms
reverse recovery at different range of the operation conditions. The model is developed and simulated with
the VHDL-AMS language under Ansoft Simplorer® Environment.
Keywords: Power PIN Diode, VHDL-AMS, Modeling, High Injection, Parameter Extraction
1. Introduction
Design of integrated power systems requires prototype-
less approaches. Accurate simulations are necessary for
analysis and verification purposes. Simulation relies on
component models and associated parameters.
Most of the power PIN diode models provided by the
literature are not valid for a mutli-bias simulation be-
cause of their limitation to accurately describe the de-
vice’s physical rules.
One of these physical limitations can be due to sup-
posing a fixed depletion region width which is the case
of several studies [1]. In [2], the power PIN diode model
includes three empirical and non physical equations to
escape the extraction procedure when using the model
for multi-bias conditions.
In this study, the developed power PIN diode model
supposes that the width of the intrinsic bulk region is a
function of reverse applied voltage as it’s reported by
Neudeck and Streetman [3].
Our study is structured as follows. In Section 2, a de-
tailed presentation of a new moving boundary diffusion
model for the power PIN diodes is made. Section 3 treats
the test bench circuit and demonstrates a first comparison
with experimental data. Section 4 investigates on the
influence of the parasitic inductance in simulation result
and the improvement of simulated test circuit by the cor-
rection of this parasitic inductance value. Finally, Section
6 gives some conclusions and future study.
All the operations (implementation, extraction, optimi-
zation …) are made under the free mixed signal simula-
tor “Simplorer-sv 7.0” by Ansoft®.
2. PIN Diode Model Description
As it is reported in [2], the model is formulated for a P+-
IN+ type diode based on the Lauritzen power diode
model [1]. Lauritzen and Al.’s model is based on a sys-
tematic technique for analytical modeling; the lumped-
charge modeling technique (LC) developed by Linvill [4].
Figure 1 shows the charge distribution in a conducting
pin diode under forward conduction.
The charge distribution in the i-region is assigned to
four charge storage nodes following the lumped model
approach developed by Linvill [4] with:
Figure 1. Charge distribution profile in diode forward
conduction [1].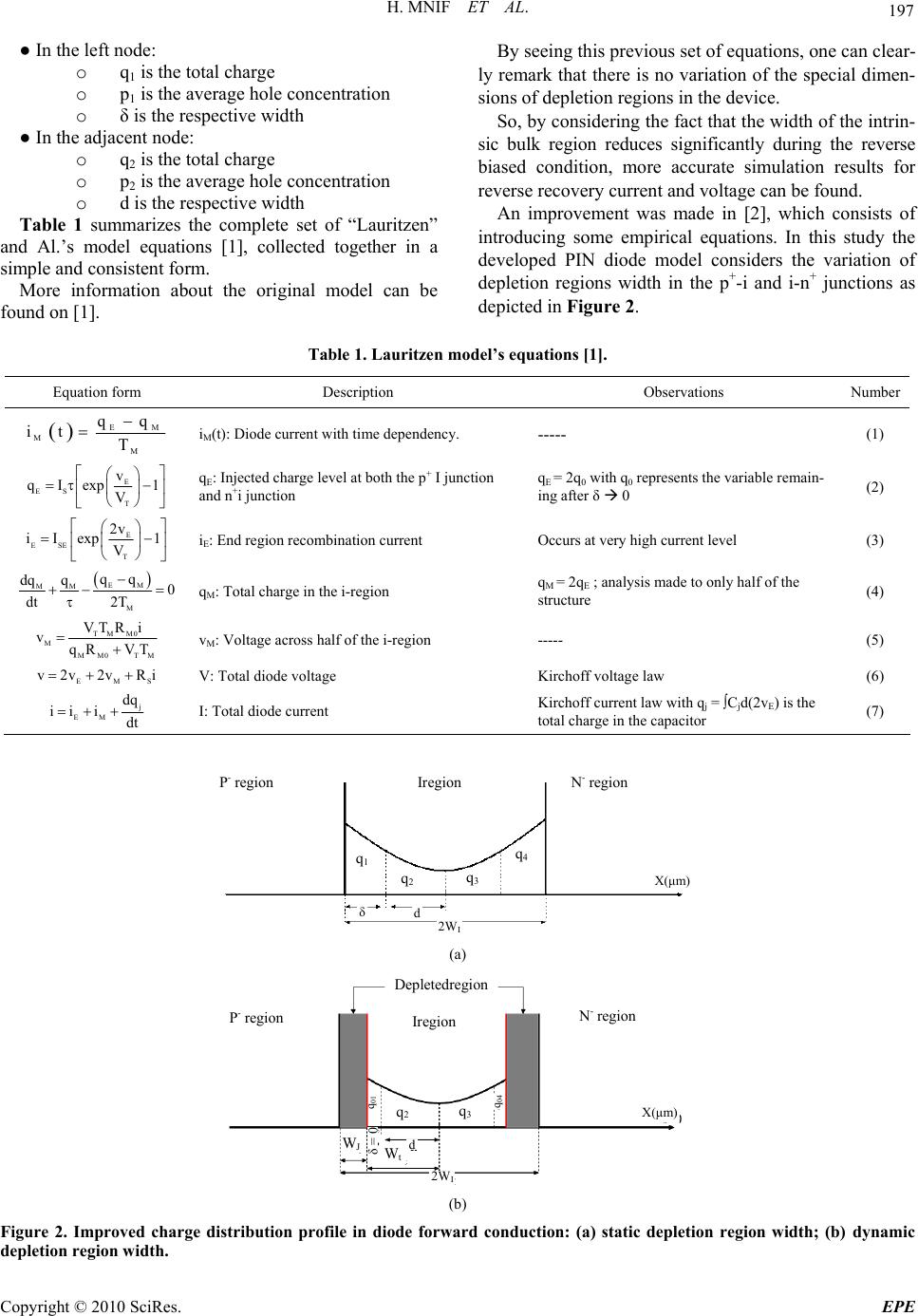

H. MNIF ET AL.
197
● In the left node:
o q1 is the total charge
o p1 is the average hole concentration
o δ is the respective width
● In the adjacent node:
o q2 is the total charge
o p2 is the average hole concentration
o d is the respective width
Table 1 summarizes the complete set of “Lauritzen”
and Al.’s model equations [1], collected together in a
simple and consistent form.
More information about the original model can be
found on [1].
By seeing this previous set of equations, one can clear-
ly remark that there is no variation of the special dimen-
sions of depletion regions in the device.
So, by considering the fact that the width of the intrin-
sic bulk region reduces significantly during the reverse
biased condition, more accurate simulation results for
reverse recovery current and voltage can be found.
An improvement was made in [2], which consists of
introducing some empirical equations. In this study the
developed PIN diode model considers the variation of
depletion regions width in the p+-i and i-n+ junctions as
depicted in Figure 2.
Table 1. Lauritzen model’s equations [1].
Equation form Description Observations Number

EM
M
M
qq
it T

 iM(t): Diode current with time dependency. ----- (1)
E
ES
T
v
qIexp 1
V
 
 
 


qE: Injected charge level at both the p+ I junction
and n+i junction
qE = 2q0 with q0 represents the variable remain-
ing after δ  0 (2)
E
ESE
T
2v
iIexp 1
V



 


iE: End region recombination current Occurs at very high current level (3)

EM MM
M
qq
dq q0
dt 2T

 
 qM: Total charge in the i-region qM = 2qE ; analysis made to only half of the
structure (4)
TM M0
M
MM0 TM
VT Ri
vqR VT  vM: Voltage across half of the i-region ----- (5)
EMS
v2v 2vRi V: Total diode voltage Kirchoff voltage law (6)
j
EM
dq
ii idt  I: Total diode current Kirchoff current law with qj = ∫Cjd(2vE) is the
total charge in the capacitor (7)
Ire gi o n
N
-
regionP
-
region
q
1
q
2
q
3
q
4
d
δ
2W
I
X(μm)
(a)
Ire gi on
N
-
region
P
-
region
W
J
q
2
q
3
q
01
d
δ = 0
2W
I
X(μm)
W
t
Depletedregion
q
04
(b)
Figure 2. Improved charge distribution profile in diode forward conduction: (a) static depletion region width; (b) dynamic
depletion region width.

H. MNIF ET AL.
198
3. A Moving Boundary Diffusion Model
In fact, by applying a reverse potential and due to the as-
ymmetrically doped junction, the junction region exte-
nds primarily into the less doped intrinsic side. The half
width of the dynamic intrinsic bulk region Wt can be
calculated as:
Wt = WI – WJ (8)
in which WI is the half physical intrinsic region.
Unlike the low injection phenomenon, the junction-
depletion width WJ variation effects under the high in-
jection phenomenon can be written as [5]:

12
Sbi A
J
diode
I
sat
2VV
Wi
qN qAv












(9)
where:
εs = The silicon permittivity;
NI = The doping level of the bulk region;
q = The electron charge;
Vbi, VA = Respectively the bult-in potential and the
applied voltage to the junction;
idiode = The total current under the device;
A = The device active area;
vsat = The carrier saturation velocity.
By adding this new concept to Najjari’s and Al. Model
[2], many parameters, especially the carrier transit time, will
be affected and it’s crucial to investigate on this.
Transit time TM: As it’s reported in Table 1, to cal-
culate the diode current due to carriers injected to the
i-region by the two junctions, i.e. p+/i and i/n+ junctions,
the carrier transit time must be defined. So, by varying
the depletion region width in the power PIN diode model
with respect to the two (8) and (9), the carrier transit time
TM will be varied and the following equation is crucial
for establishing this relation:
2
t
M
a
(W )
T4D  (10)
with Da is the ambipolar diffusion constant defined by:
np
aT
np
D2 U

 (11)
So, the set of equations in Table 1 will be affected by
this new concept and this variation of the depletion re-
gion with respect to the applied bias on the device will
be considered in our new formulation of the power di-
ode model.
In addition to the nine classical Lauritzen and Al.’s
model parameters (τ, TM, ISE, IS, Cj0, RS, m, ФB and RM0),
three new parameters describing the moving boundary
effect are added, i.e. (WI, NI and τrr). The new improved
model has the following VHDL-AMS structure, Figure 3.
4. New Model’s Parameters Discussion
In this section, an investigation about the new model par-
ameters (WI, NI and τrr) influence will be done.
After writing the VHDL-AMS code for this power
PIN diode model, the device is simulated under the cir-
cuit simulator Simplorer from Ansoft.
The same switching cell used in [2] is considered like
it’s shown in Figure 4.
The switching cell main operating conditions are the
forward current IF and the reverse voltage VR. These
conditions are imposed by a current and a voltage source
respectively. The “IRF740” transistor is a fast NMOS
type. The parasitic inductance Lm has to be estimated
carefully since it controls the current rate to some extent.
In Section 4, we will discuss how to fix the value of this
parasitic capacitance in the right way.
In order to avoid damaging the device, generally,
due to the voltage overshoot, a RC-snubber was placed
in parallel with the diode. Because of the small values
of the snubber resistance and capacitance, the varia-
tion in component values with respect to temperature
change could be neglected in so far as these variations
might alter the diode switching waveforms [6].
Since the diode turn-off behavior is of more concern
to engineers than the turn-on because of the important
energy losses, only the experimental results for diode
turn-off are performed.
V
R
W
I
I
F
N
I
tau
Turn-off
characteristics
PIN VHDL-AMS
model
Figure 3. New VHDL-AMS power PIN diode structure.
C
R
D
V
diode
V
R
R
G
L
m
V
G
I
diode
I
F
IRF 740
Figure 4. Principal circuit for the measurements.

H. MNIF ET AL.
199
4.1. Influence of the Half Physical Intrinsic Region
Width WI
Under this turn-off state, we perform a simulation of the
device with different values of the physical intrinsic re-
gion width WI and we capture the curves of the forward
current, IF and the reverse voltage, VR.
Figure 5 shows that with increasing WI, we give per-
mission to the device to accumulate more charge under
the on-state. When switched to the off-state, the device
gets more time to evacuate these accumulated charges, so
we can see a higher maximal reverse voltage and current.
4.2. Influence of the Doping Level NI
Figure 6 shows that with increasing the doping profile
NI in the device, the device gives more important values
of reverse voltage and current. This can be explained by
the fact that the depletion region width WJ becomes
higher and so, injected charges rise more and more.
4.3. Influence of the Carrier Life Time τ
With respect to the following equation of the reverse re-
covery time τRR [2]:
M
RR
M
T
T

  (12)
The plot of Figure 7 is established with supposing a
constant transit time set to 22ns. This plotted function is
growing-up with increasing the carrier life time τ, i.e.,
the reverse recovery time τRR is growing-up.
In fact, carriers injected to the bulk region recombine
less and they have more chances to reach the side con-
tacts of the device. So in the turn-off state, the device
gives higher values of reverse voltage and current which
is mentioned in Figure 8.
4.4. Comparison with Experimental Data
The model parameters for the power diode are estimated
T
i
me
(
n sec
)
5.00
2.50
0
–2.50
–5.00
–7.50
–10.00
–12.50
–15.00
D
i
o
d
e current
(
A
)
25.0 50.0 66.7 83.3 100.0 125.0
W
1
= 34.10
-4
cm
W
1
= 34, 5.10
-4
cm
W
1
= 35.10
-4
cm
Figure 5. Influence of the intrinsic region width WI on the
diode current turn off characteristic.
T
i
me
(
n sec
)
5.00
0
–5.00
–10.00
–15.00
–20.00
–25.00
–30.00
D
i
o
d
e current
(
A
)
25.0 40.0 60.0 80.0 100.0 120.0 150.0
N
1
= 3.10
14
cm
-3
N
1
= 3, 5.10
1
4
cm
-
3
N
1
= 4.10
14
cm
-3
Figure 6. Influence of the intrinsic region doping NI on the
diode current turn off characteristic.
τRR
(
n sec
)
–2.6 × 10
-8
–2.8 × 10
-8
-3 × 10
-8
–3.2 × 10
-8
–3.4 × 10
-8
–3.6 × 10
-8
–3.8 × 10
-8
τRR
(
n sec
)
5 × 10
-8
10 × 10
-8
1.5 × 10
-7
2 × 10
-7
Figure 7. Variation of the reverse recovery time τRR in re-
spect to the carrier life time τ.
T
i
me
(
n sec
)
5.00
2.50
0
–2.50
–5.00
–7.50
–10.00
–12.50
–15.00
D
i
o
d
e current
(A)
40.0 50.0 62.5 75.0 87.5 100.0 120.0
τ = 100 n sec
τ = 200 n sec
τ = 400 n sec
Figure 8. Influence of the carrier life time τ on the diode
current turn off characteristic.

H. MNIF ET AL.
200
using the same parameter extraction procedure described
in [2] at reverse recovery condition. The Table 2 gives a
summary of these model parameters values for the
BYT12P600 power diode [7] which are valid for all op-
eration conditions.
Figure 9 illustrates a comparison of the measured and
the simulated voltage and current waveforms for reverse
recovery on three different operating conditions: a) VR =
60V and IF = 10A, b) VR = 70V and IF = 2.05A, c) VR =
120V and IF = 10A. The two simulated curves are re-
spectively the simulation result of model [2] and the im-
proved model developed in this study.
These previous Figures 9(a), (b) and (c) show a good
agreement between simulation and experimental results
except at the end of turn-off where oscillations appear.
These oscillations at the end of the reverse recovery
voltage waveforms are due to residual phenomena and
are very difficult to simulate. However, the effect of
these oscillations is not very interesting in design appli-
cations [8].
In this figure, the agreement is good enough about the
current (IRM and RR) but not so good about the voltage.
On the other hand, the estimation of the stray induc-
tance in the switching loop of the circuit is critical for
modeling the switching process.
One cause of error is due to the current and voltage
probes. In fact, as stated in [8], probes interact with the
device under test, create delays due to propagation in the
cable and worst of all degrade the signal due to distortion
in the probes and the cables. The overall accuracy of the
extraction procedure requires the probe effects to be
taken into account in simulation.
Simulated forward current curve for the model cited in
[2] for IF = 2A and VR = 120A presents an error on the
slope compared with the measurement forward current
curves. In fact, textbooks [9,10] detail that the diode cur-
rent slope is approximated by di/dt = –VR/Lm at the begin-
ning of the reverse recovery, inside a switching cell circuit
where a unique wiring parasitic inductance is considered.
For this reason, an improvement on the parasitic test-
bench inductance was made in this work. The next sec-
tion will treat this part.
4.5. Parasitic Test Bench Inductance Investigation
For estimating the behavior of the device in circuit simu-
lation, a complete model of the wiring influence is requi-
red which demands the development of a parasitic induc-
tive matrix [8]. For more simplicity and short simulation
time, in this study, a simple model for this wiring para-
sitic is formulated. This simulated test bench inductance
improvement is based on the extracted values of Lm (see
test bench circuit, Figure 4) from the measured turn-off
characteristics according to the following relation:
R
m
V
di
dt L
 (13)
Figure 10 presents the variation of this test bench
parasitic inductance extracted from the measured turn-off
characteristics for 3 different test conditions. To capture
this inductance influence on the simulated switching cell,
a 2nd order polynomial fitting equation is introduced to
predict its right value:
RR
m2 10
FF
VV
La a a
II
 


 
  (14)
With a2, a1 et a0 are fitting parameters set to:
a2 = 0.0268.109 [HA/V]
a1 = 1.3582.109 [HA/V]
a0 = 103.19.109 [HA/V]
This equation is added to simulated test bench circuit via
a VHDL-AMS entity in substitution of the fixed inductance.
Figure 9(c) shows the correction of the slope on the
simulated current curves compared to measurement.
5. Conclusions
A physical improvement is made for a power diode lump-
ed-charge model which consists of varying the width of
the intrinsic bulk region with respect to the reverse ap-
plied voltage and current variations. A second improve-
ment is made to the simulated test-bench circuit to esti-
mate the right value of the parasitic inductance value.
The new model is described in VHDL-AMS language
and has been implemented in the SIMPLORER simulator.
A good agreement is observed between the new model
simulated data and measured data. The results of this
improved model are verified with a wide range of oper-
ating conditions.
This model can be extended by including the selfhea-
ting effect which can greatly affect the turn off charac-
teristics and the device performance.
Table 2. New model’s parameters list.
Parameter
symbol description Parameter value Unity
WI Bulk region width 37.6 µm
NI Doping level of the
I-region 3.12 × 1014 cm3
 carriers lifetime 103.5 n sec
TM carriers transit time Equation 10 n sec
IS Saturation current 2.78 × 1024 A
RM0 Initial resistance 500 Ω
ISE Recombination current 45.7386 × 109A
Cj0 Junction capacitance 2.2281 nF
RS Serial resistance 15.7632 mΩ
m Gradient coefficient 430.9960 × 103--
ФB Bult-in potential 5.9294 mV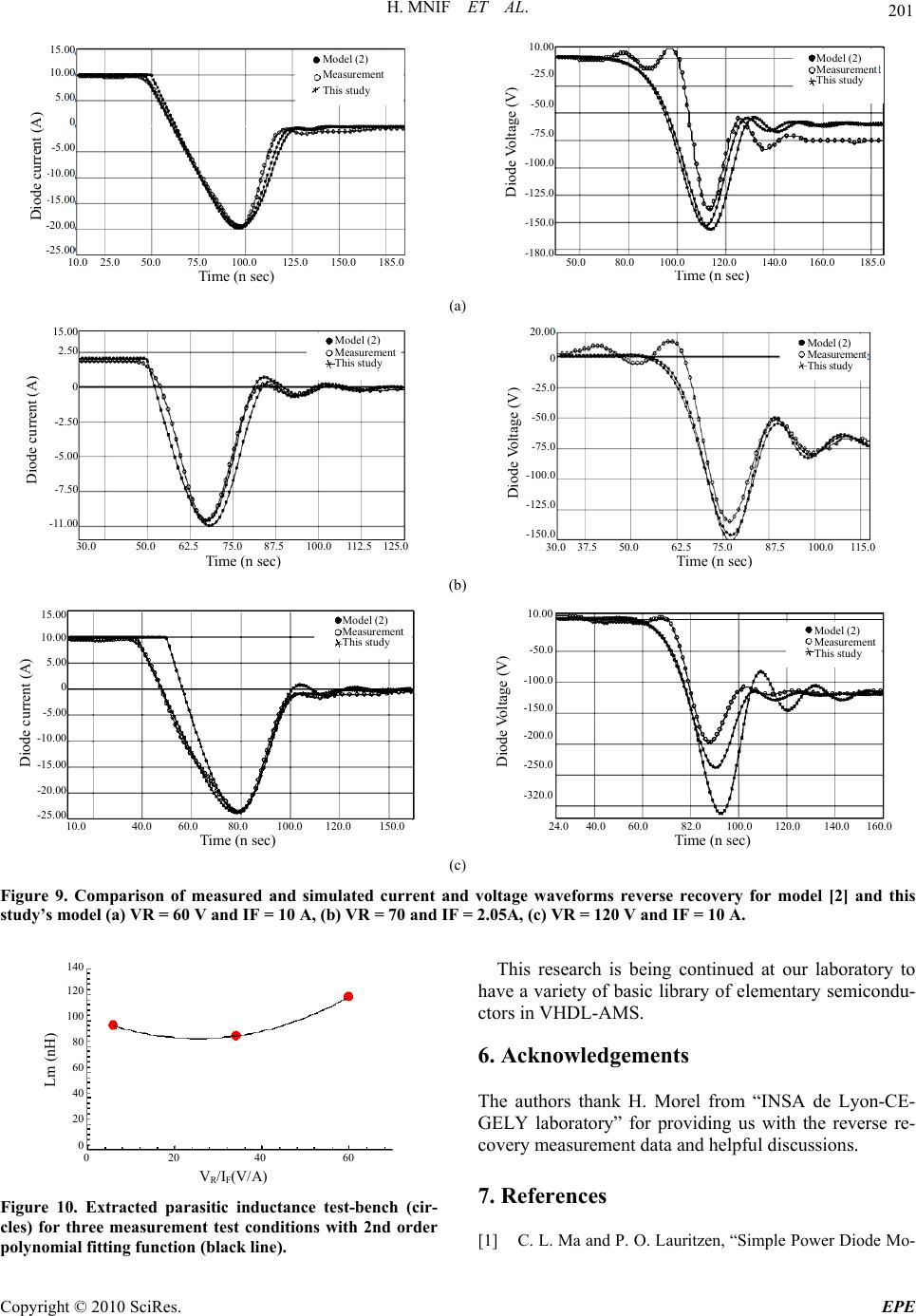

H. MNIF ET AL.
201
T
i
me
(
n sec
)
15.00
10.00
5.00
0
-5.00
-10.00
-15.00
-20.00
-25.00
D
i
o
d
e current
(
A
)
10.0 25.0 50.0 75.0 100.0 125.0 150.0 185.0
Model (2)
Measurement
This stud
y
T
i
me
(
n sec
)
10.00
-25.0
-50.0
-75.0
-100.0
-125.0
-150.0
-180.0
D
i
o
d
e Vo
l
tage
(
V
)
50.0 80.0 100.0 120.0 140.0 160.0 185.0
Model (2)
Measurement
This study
(a)
T
i
me
(
n sec
)
15.00
2.50
0
-2.50
-5.00
-7.50
-11.00
Di
o
d
e current
(A)
30.0 50.0 62.5 75.0 87.5 100.0 112.5 125.0
Model (2)
Measurement
This study
T
i
me
(
n sec
)
20.00
0
-25.0
-50.0
-75.0
-100.0
-125.0
-150.0
Di
o
d
e
V
o
l
tage
(
V
)
30.0 37.5 50.0 62.5 75.0 87.5 100.0 115.0
Model (2)
Measurement
This study
(b)
T
i
me
(
n sec
)
15.00
10.00
5.00
0
-5.00
-10.00
-15.00
-20.00
-25.00
D
i
o
d
e current
(
A
)
10.0 40.0 60.0 80.0 100.0 120.0 150.0
Model (2)
Measurement
This study
T
i
me
(
n sec
)
10.00
-50.0
-100.0
-150.0
-200.0
-250.0
-320.0
D
i
o
d
e Vo
l
tage
(
V
)
24.0 40.0 60.0 82.0 100.0 120.0 140.0 160.0
Model (2)
Measurement
This study
(c)
Figure 9. Comparison of measured and simulated current and voltage waveforms reverse recovery for model [2] and this
study’s model (a) VR = 60 V and IF = 10 A, (b) VR = 70 and IF = 2.05A, (c) VR = 120 V and IF = 10 A.
V
R
/
I
F
(
V
/
A
)
140
120
100
80
60
40
20
0
Lm
(
nH
)
0 20 40 60
Figure 10. Extracted parasitic inductance test-bench (cir-
cles) for three measurement test conditions with 2nd order
polynomial fitting function (black line).
This research is being continued at our laboratory to
have a variety of basic library of elementary semicondu-
ctors in VHDL-AMS.
6. Acknowledgements
The authors thank H. Morel from “INSA de Lyon-CE-
GELY laboratory” for providing us with the reverse re-
covery measurement data and helpful discussions.
7. References
[1] C. L. Ma and P. O. Lauritzen, “Simple Power Diode Mo-

H. MNIF ET AL.
202
del with Forward and Reverse Recovery,” IEEE Transac-
tions on Power Electronics, Vol. 8, No. 4, 1993, pp. 342-
346.
[2] M. Najjari, H. Mnif, H. Samet and N. Masmoudi, “New
Modeling of the Power Diode Using the VHDL-AMS
Language,” The European Physical Journal Applied Phy-
sics, Vol. 4, No. 1, 2008, pp. 1-11.
[3] H. Zhang and J. A. Pappas, “A Moving Boundary Diffu-
sion Model for PIN Diodes,” IEEE Transactions on Mag-
net, Vol. 37, No. 1, 2001, pp. 406-410.
[4] P. Antognetti and G. Massobrio, “Semiconductor Device
Modeling with SPICE,” MCGraw-Hill Inc, New York,
1988.
[5] C. L. Ma and P. O. Lauritzen, “Modeling of Diodes with
the Lumped-charge Modeling Technique,” IEEE Trans-
actions on Power Electronics, Vol. 12, No. 3, 1997, pp.
398-405.
[6] K. X. A. Caiafa, E. Santi, J. L. Hudgins and P. R. Palmer,
“Parameter Extraction for a Power Diode Circuit Simu-
lator Model Including Temperature Dependent Effects,”
17th Annual IEEE Applied Power Electronics Conference
and Exposition, Dallas, March 2002, pp. 452-458.
[7] BYT12 600 Datasheet, “Datasheet Archive,” 1998. http://
www.datasheetArchive.com
[8] H. Garrab, B. Allard, H. Morel, K. Ammous, S. Ghedira,
et al., “On the Extraction of PiN Diode Design Parame-
ters for Validation of Integrated Power Converter,” IEEE
Transactions on Power Electronics, Monastir, Vol. 20,
No. 3, May 2005, pp. 660-670.
[9] N. Mohan, T. M. Undeland and W. R. Robbins, “Power
Electronics: Converters, Applications and Design,” 2nd
Edition, John Wiley & Sons, New York, 1995.
[10] R.W. Erickson and D. Maksimovic, “Fundamentals of
Power Electronics,” 2nd Edition, Kluwer Academic
Pulishers, Berlin, 2001.