Open Journal of Discrete Mathematics, 2012, 2, 149-155
http://dx.doi.org/10.4236/ojdm.2012.24030 Published Online October 2012 (http://www.SciRP.org/journal/ojdm)
H- and H2-Cordial Labeling of Some Graphs
Freeda Selvanayagom, Robinson S. Chellathurai
Department of Mathematics, Scott Christian College, Nagercoil, India
Received July 31, 2012; revised September 3, 2012; accepted September 25, 2012
ABSTRACT
In this paper we prove that the join of two path graphs, two cycle graphs, Ladder graph and the tensor product 2n PP

are H2-cordial labeling . Fur ther w e prov e that the join of two wheel graphs Wn and Wm, admits a H-
cordial labeling.

0mod4nm

0,1
0,1
Keywords: H-Cordial; H2-Cordial; Join of Two Graphs
1. Introduction
All graphs considered here are finite, simple and undi-
rected. The origin of graph labelings can be attributed to
Rosa. Several types of graph labeling have been investi-
gated both from a purely combinatorial perspective as
well as from an application point of view. Any graph
labeling will have the following three common charac-
teristics. A set of numbers from which vertex labels are
chosen, number of vertices of G having label i
under f. = number of edges of G having label i
under f*.

f
vi

f
ei
The concept of cordial labeling was introduced by I.
Cahit, who called a graph G is cordial if there is a vertex
labeling such that the induced label-
 
:fvG
 

ing defined by
:fEG

 
f
xyf xfy
, for all edges


x
yEG and
with the following inequalities holding
 
01
ff
vv1 and
 
01
ff
ee1.
In [1] introduced the co ncept of H-cordial labelin g. [1]
calls a graph H-cordial if it is possible to label the edges
with the numbers from the set


1, 1 in such a way that,
for some k, at each vertex v the sum of the labels on the
edges incident with v is either k or –k and the inequalities
 
1
ff
vk vk and


11
ff
ee1 are also
satisfied where


vi


and e(j) are respectively, the
number of vertices labeled with i and the number of
edges labeled with j. He calls a graph Hn-cordial if it is
possible to label the edges with the numbers from the set
in such a way that at each vertex v, the
sum of the labels on the edges incid ent with v is in the set
and the inequalities

1, 2,,n 

1, 2,,n 



1
ff
vi vi
and
 
1i
1in

.
In [1]roved that is H-Cordial if and only if n >
2 p,nn
k
nd and “n” is even; a,,
mn
kmn is H-cordial if and
only if


1mod4n, m is even and m > 2, n > 2.
In [2] provn is H-Cordial if and only if 0n ed that k

or


3mod4 and 3n

.
Wordial if and only if n is odd. kn
Hn is H-cis not
2-cordial if


1mod4n. Also [2] proved that every
wheel has an H-corling.
In [3] several variations of graph labeling such as
gra
2
1 1
dial labe
ceful, bigraceful, harmonious, cordial, equitable, hum-
ming etc. have been introduced by several authors. For
definitions and terminologies in graph theory we refer to
[4].
1.1. Definition: The j oin G = G1 + G2 of grap h G1 and
G2 with disjoint point sets V1 and V2 and edge sets E1 and
E2 denoted by G = G1 + G2 is the graph union 12 GG
together with all the edges joining v1, v2. If G1 is (p,q)
graph and G2 is (p2,q2) graph then G1 + G2 is (p1 + p2, q1
+ q2 + p1 + p2).
1.2. Definition: Let G1 = (V1, E1) and G2 = (V2, E2) be
two graphs. The Cartesian product of G1 and G2 which is
denoted by 12
GG

is the graph with vertex set v = v1 ×
v2 consisting of vertices


 
12 12
,, ,Vuuuvvvu 
and v are adjacent in 1
GG
2

wheuv and u2
adjacent to v2 or u1 adjacent to v1 and

22
uv.
1.3. Definition: The tensor product 1 GG G of
gr ith disjoint point
never = 1
2
and
1
aphs G1 and G2 w sets
edge sets E1 and E2 is the graph with vertex set 12
VV
v1 and v2

such that (u1, u2) is adjacent to (v1, v2) whenever


11 1
,uv E

and


22 2
,uv E. If 1 is (p1, q1 G) gra ph
and G2 is (paph, then
in of tw
2, q2) gr12
G is a (P1P2, 2q1q2).
pesults on
G
stigated somIn this par we have invee re H-
and H2-cordial labeling for joo graphs, Cartesian
ff
 are also satisfied for each i with ei e
C
opyright © 2012 SciRes. OJDM

S. FREEDA, R. S. CHELLATHURAI 150
pr
oin of two path graphs P and Pm
beling whe.
he ee
se
1
The edge matrix of Pn + Pm is givenn Table 1.
In view of the above labeling pattern we give the poof
as
h graphs P3 and P2.
the edge label matrix of P3 + P is given by
1
v
oduct and tensor product of some graphs.
2. Main Results 1
v
2.1. Theorem: The j
admits a H-cordial lan n

1, 2mod4nm
2
Proof: Let 12 , ,,n vv v and 12 , , ,m uu u are the
two vertex sets of the path graphsdg Pn and Pm. T
of Pn and Pm
t E1 and E2 iunion together
with all the edges joining the vertex sets vi and ui,
1, 2 ,,in.
Define the edge labeling
s the graph

:fEG
 
1,
i
follows:
1) When

1mod4nm
Consider the join of two pat
Using Table 12
2
3
v
v
12
uu
1 1
1 1
1 1
1 1








1
with respect to the above labeling total number of verti-
ces labeled with
11
1


1,1,2
s
ss

 and 2
s

 are given by

14
f
vn,

14
f
vn,

23
f
vn and
.

24
f
vn



1122
fff f
vvv v 1, differ by one.
The total number of edges labeled with 1,1,2
s
ss


and 2
s
  are given by
  
11
1, 1, 2(2)
2
ff
nn
ee ee

 0
2
ff

 


1122
ff
eefeef 1, differ byne.
Hence the join of two path graphs P3
H2-cordial labeling.
graphs P4 and P2.
U, the edge label maix of P + P is given by
vvv
o
and P2 admits a
2) When

2mod4nm
Consider the join of two path
sing Table 1tr 4 2
Table 1. Edge matrix of Pn + Pm.
1
2
n
v
v

12
m uu u
11 12 1
21 222
12
1212 231
,
m
m
nn n
mm
vu vu vu
vu vuvu
vu vuvu
uuuu uuuu










 


m
12
12 23
1
,
nn
vv vv
vv


2
3
4
v
v
v
12
1 1
1 1
1 1
1 1
1 1
uu
















1
In view of the above labeling pattern the total number
of edges labeled with
11
11
1



1,1,2
s
ss


 and 2
s

 are given
by








12,12,220
f
enene 0,e
ff f
 








1122
fff f
eee e0 by zero.
The total number of vertices labeled with
, differ

1,1,2
s
ss



and 2
s


are given by






14,14,25
ff f
nvnv nv

  and


25
f
vn

.






11220
fff f
v vvv

 
, differ by zo.
Thus in each cases we have
er






11221
fff f
vv vv

  and






11221
fff f
eee e

 .
Hence the jo of two path graphs P4 and P2 admits a
H2-cordial labeling of graphs.
In Figure 1 illustrates the H-cordial lab
Ages receive the label +1
and the other six edges receive the . The in-
duced vertex labels are given in the figure.
2.2. Theorem: The join of two cycle graphs Cn and Cm
ad
in
2
mong the twelve edges, six edeling on P4 + P2.
label 1
mits a H2-cordial labeling when
P
4 :
V
1
V
2
V
3
V
4
1 -1 -
1
P
2 :
U
1
1 U
2
-1 1 2 -1 -2 -1 -1
V
1
V
2
V
3
V
4
-1
-1 1
11
-1
-1 1
11
U
1
U
2
1
Figure 1. H2-cordial labeling on P4 + P2.

S. FREEDA, R. S. CHELLATHURAI 151

1, 3mod 4,,3nm nm  .
Proof: Let and are the
vertex set of cmedge sets
E1 and E2of cnwith all
the edges joi and
We note that
12
, ,,n vv v
ycles cn and c
is the graph union
ning the vert
12
, , ,m uu u
respectively. The
and cm together
ex sets 12
, ,vv,n v
12
, , ,m uu u.

12
VGp p and

12 12
.EGq qpp
Define 1
The edge matrix table of
 
:1,fEG.
nm
cc

is given in Table 2.
In view of the above labelin we give the proof
as follows.
Case (1) when
Consid.
Using Table 2 the edge lable matrix of c3 and c4 is
gi

11
f the above labeling pattern the total number
of
g pattern

3mod4,, 3nm nm .
er the join of two cycle graphs c3 and c4
ven by
1
v
1234
1 1 1 1
1
uuuu




2
v
3
v 1



1 1 1
1 1 1
11 11 11 11



 
11
1

In view o
edges labeled with 1,1,2
s
ss
 
nd 2 a
s

 a re given by
   
12
1, 1, 20, 20.
2
ff ff
nn
ee ee

 
2
 


11ee er 221
fff f
e e , diffby one.
The total number vertices labeled with 1,1,2
s
ss


and 2
s
  are given by
 


15,15,2
ff f
vnvnv n 5 and

26
f
vn.



1122
fff f
vvv v 1, diffeby one.
Thus in each cases we have
r



1122
fff f
vvv v 1 and



11221
fff f
eee e .
Hence the join of traphs cd c4 admits a

wo cycle g3 an
H2-cordial labeling.
Table 2. Edge matrix of cn +
v






12 1
,n vv vv
cm.
11 31
21222 32
12
12 1122311
u
vu
, ,,
m
m
nn nm
m
vu
vu vuvu
vu vuvu
uu uuuu uuuuuu










 


2
n
v
v

123
11 12
v
m
uuu u
vu vu

m
m
11
,
nnn
vv v v


m
12 23
, vv vv
Case (2) when


4, ,3nm1modnm

.
Consider the d c4.
Using Table 2 the edge label matrix of + c4 is give n by
join of two cycle graphs c5 an
c5
1
v
1234
1
uuuu



2
3
4
5
v
v
v
v
1 1 1
1 1 1 1
1 1 1 1
1 1 1 1

 
 


11 11 11 11


1 1 1 1










 
11
In view of the above labeling pattern the total number
of edges labeled with
11
11
11



11
1,1,2
s
ss


 and 2
s

 a re given by
   
1,
2
2
ff
11nn
1 ,20.
ff
ee ee
2
 







11220
fff f
eee e

 , differ by zero.
1,1,2
s
ss


 The total number of vertices labeled with
and 2
s


are given by




17,1
ff
vnv n7






26,2
ff
vnv n7








1122
fff f
vvv v1

 , differ by one.
Thus in each cases we have






1122
fff f
vvv v1

  and






11 21
ff
ee e2
f f
e

 .
Hence the join of two cycle graphs c5 and c4 admits a
H2-cordial labeling.
In Figure 2 illustrates the H2-cordial
Ce the label
ourteen edges receive the label
labeling on C5 +
4. Among the 29 edges, fifteen edges receiv
+1 and the remaining f
1

. The induced vertex labels are given in the figure.
2.3. Theorem : The join of two wheel graphs W and
Wm admits a H-cordial labeling whenn


0mod4nm
,u are the ver-
.
Proof: Let and
tex set of thph W
an gether with all
the edges joinivertex set d
at
12
, ,,n vv v
e wheel gra
ng the
m
u. We note th
12
, ,uu
n and Wm.
n and Wm to
12
, ,vv

m
The edge set E1
d E2 is the graph union of W,n
v an
12
, , ,uu12 VGp p and


12 1
EGq qpp 2 .
Define




:1,1fEG
The edge matrix is given in.
In the view of the above labeling pattern we give the
proof as follows:
when
Tabl e 3


0mod4nm
Consider the join of two wheel graphs W and W. U
4 4
g Table 3 the edge label matrix of W4 + W4 is given by
s-
in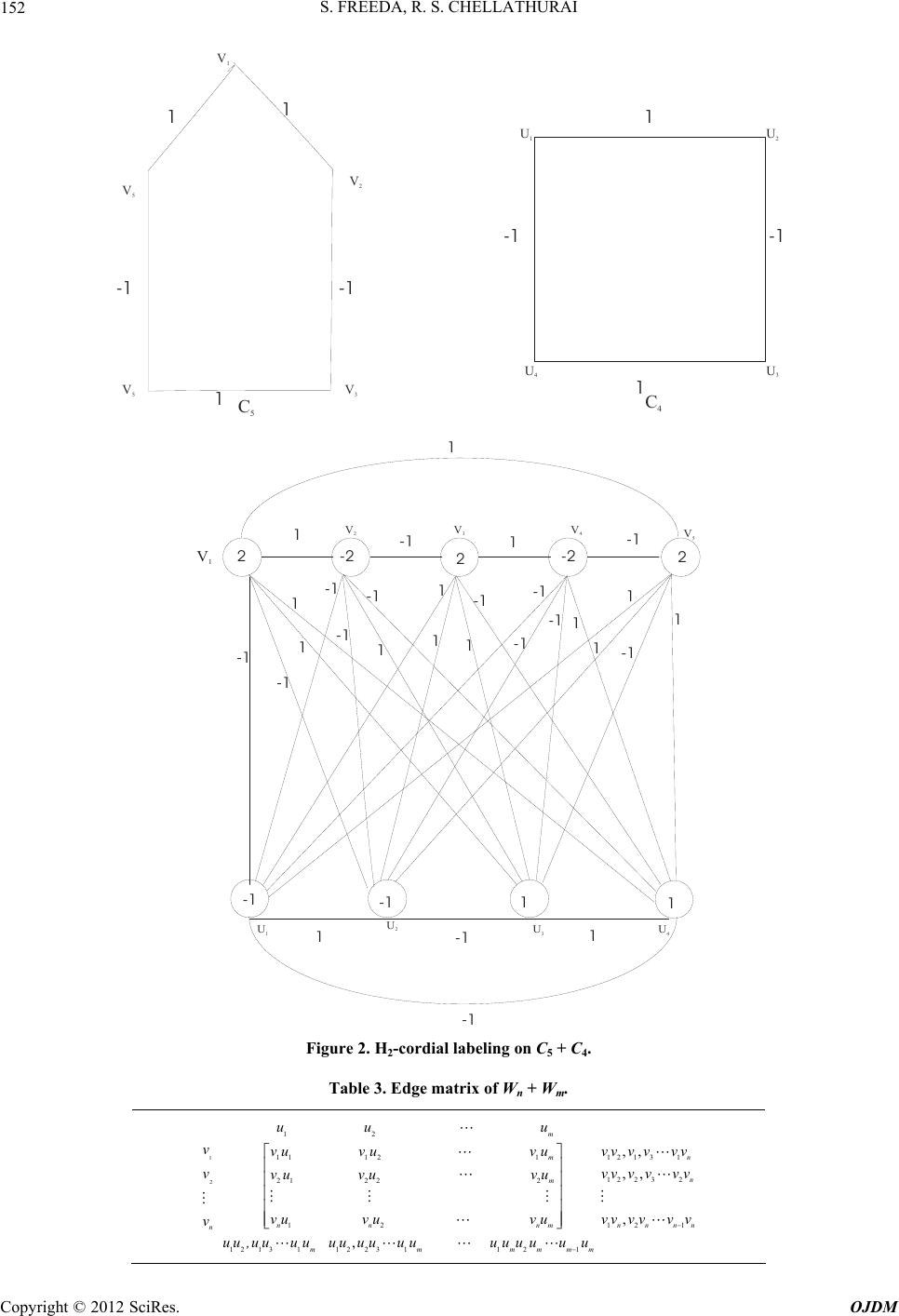

S. FREEDA, R. S. CHELLATHURAI 152
V
1
V
5
11
V
2
U
1
-1 -1
V
5
V
3
C
5
U
4
U
3
U
1
-1 -1
1C
4
1
2
V
1
U
1
U
2
U
3
U
4
22
1-1 1
-1 -1 11
1
-1
-2 2-2
1-1 1-1
V
2
V
3
V
4
V
5
-1
-1
1
1
-1
-1
1
-1 1
11
-1 -1
-1
-1 1
1
1-1
1
Figure 2. H2-cordial labeling on C5 + C4.
Table 3. Edge matrix of Wn + Wm.
v1213 1
,, n
n
vvv vvv
1
2
n
v
v

12
11 121
21 222
12
12 13112231121
,
m
m
m
nn nm
mmmm
uuu
vu vu vu
vu vuvu
vu vu vu
uu, uuuuuuu uuu uuuuuu











 


mm
12 2 32
121
,,
,
n
nnn
v vvv vv
vv vvv v





S. FREEDA, R. S. CHELLATHURAI 153
v
4
1
In view of the above labeling pattern we give the proof
as follows.
The total number of edges labeled with
1
2
3
4
v
v
v
123
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
111
uuuu










 111 111 1 11 
1 1
111
111
111



1
s
 and 1
s


are given by

12
f
en,


12
f
en
 
11
ff
ee0, differ by zero. Thtal num
of vertices labeled with
e tober
1
s
 and 1
s
  are gien by v

12
f
vn and

12
f
vn
 
110 , differ by
ff
vv zer
Thus in each cases we have
o.

11
ff
vv1 and
 
111
ff
e.
Hence the join of two wheel graphs w4 and w4 admits a
H-
e
rin 4 +
he twenty
ceive the label +1 an
figure.
2.4 Theorem: known as ladder
gra .
where n is
and
cordial labeling.
In Figure 3 illustrates the H-codial labelg on W
W4. Among trtee eight edges, foun edges re-
d the other fourteen edges receive
the label 1. The induced vertex labels are shown in the
2n
PP (also
ven n
n
L
ph) is H2-Cordial labeling for e
Proof: Let G be the graph even
i2n
PP
and

1, 2
ij
VG Vnj  be the
vertices of G.


1, 2,,
We note that

2VGn and

32EG n.
Define
 
:1,1fEG as follows
Case (1) When

0mod4n
For 1, 1n ik

11
,1
ik
fvv 
For 1,nikn

1fvv 
For 1,ik
11
,
ik
1n

2, 2
,1
ik
fv v
For n1,ik n
n
2) when

2, 2
,1
ik
fv v
For 11in 

12
,1
ii
fvv 
For 1ni

12
,1
ii
fvv 
Case (
For

2mod4n
2n1,ik

11
,1
ik
fvv 
-1
-1
1
1-1
1
V
2
V
3
V
4
V
1
W
4
-1
1
-1
-1 1
1
U
2
U
3
U
4
U
1
W
4
1
V
1
V
2
1
1
-1 1
V
3
-1
V
4
-
1
-1
-1 -1
1
-1
11
-1 1
-1
-1
1
1
1
-1
1
-1 -11
U
1
U
2
U
3
U
4
-1 1
1
-1 1
-1-1
-1 -111
Figure 3. H-cordial labeling on W4 + W4.


22
,1
ik
fv v

For n2,nik




11
,1
ik
fvv




22
,1
ik
fv v


12in

 For


12
,1
ii
fvv



S. FREEDA, R. S. CHELLATHURAI 154
For n
In view of the above defined labeling pattern we give
the proof as follo ws.
The total number of edges labeled with
2,ni

12
,1
ii
fvv 
1,1,2
s
ss



and 2
s

 are given by


12
f
en

12
f
en ,
0
 
22
f

.
 

f
ee
 


1122
fff f
e e 
The total number of vertices labeled with
0
, differ by zero.
ee
1
s
and 1
s


,
2
s
 and 2
s

 are given by







1 142;
242,24
ff
ff
vv n
vnvn

   2.



1122
fff f
vvv v 0
differ by zero.
Thus in each cases we have
 


1122
fff f
vvv v  1
  
1122
fff f
eee e  1
Hence the ladder graph 2n PP

admits a H2- cordia
labeling.
In Fig ling on
. Among the ten edges, five edges receive the la-
nd otherfive edges receive the label
l
ure 4 illustrates the H2-cordial labe
42

bel +1 a
PP 1

. The
in vertex labels are shown in the figure.
2.5 Theorem: The tensor product is H2-cor-
dial labeling.
Proof: Let G be e graph and
be the verti-
ote that
duced
2n
PP
th 2n PP
and 1j

,G

1 2,,,2
ij
Vuv in
ces of G.
We n

2VGn and

22EGn
ne 1 two cases are to be con-
sidere
Defi 

G
 
:1,fE
d.
V
42
V
41
-1
V
31
V
32
V
22
21
V
-1
1
V
V
11 12
-1
-2 -2
-1 -1
-1 -
11
1
11
22
11
242
Case
Figure 4. H-cordial labeling on P × P.
(1). When n is even
For 1in



1,if1mod 2i 



112
,1, if1 mod
ii
fu vuv i
 
2


For 1in



2i
fu v


11
1,if1mod 2
,1, if2
i
i
uv i

 






When n is odd

1 mod
Case (2)
For 1in


For



112
1,if1, 3mod4
,1,if0,2mod 4
ii
i
fuvuv i

 

 


1in


In view of the above defined labeling pattern we give
the proof as follo ws.
The total number of edges labeled with



211
1,if1, 3mod 4
,1,if0,2 mod4
ii
i
fuvuv i

  




1,1,2
s
ss



are given by

12
f
en

12
f
en
and 2
s


,




220
ff
ee


.






1122
fff f
e e0ee

 
The total number of vertices labeled with
, differ by zero.
1 ,1 ,2
s
ss



and 2
s


are given by






 
1 182;
242,24
ff
ff
vv n
vnvn

  2.
UV
11
UV
12
UV
21
UV
41
UV
22
UV
12
UV
42
-1
-1
-1
1
1
- 1
-2 2
-2
-2 2
1
Figure 5. Hrdial labeling on P P2.
31
2
UV
UV
51
-1 UV
52
1-1
2-co
1
1
4

S. FREEDA, R. S. CHELLATHURAI 155



1122
fff f
vvv v  0differ by zero.
Thus in each cases we have
 


112
ff f
vv v 21
f
v 
  
11221
fff f
eee e 
Hence the tensor product 2n
PP admits a H2-cordial
beling.
In Figure 5 illustrates the H2-cordial labeling on
. Among the eight edges four edges receive the
nd the other four edges receive the label
la
52
PP
label +1 a1

.
The induced vertex labels are shown in the figure.
3. Concluding Remarks
Here we investigate H- and H2-cordial labeling for join
of path graphs, cycle graphs, wheel graphs, Cartesian
product and tensor product. Similar re
riv and in the context of dif-
fere opn area of research.
REFERENCES
[1] hs,” Bu
inatorics and Its Applications, Vol. 18, 1996, pp.
[2] M
[3] J. A. Gallian, “A Dynamic Survey of Graph Labeling,”
ombinations, Vol. 18, 2011.
sults can be de-
ed for other graph families
nt graph labeling problem is ane
I. Cahit, “H-Cordial Graplletin of the Institute of
Comb
87-101.
. Ghebleh and R. Khoeilar, “A Note on ‘H-Cordial
Graphs,’” Bulletin of the Institute of Combinatorics and
Its Applications, Vol. 31, 2001, pp. 60-68.
The Electronics Journal of C
[4] D. B. West, “Introduction to Graph Theory,” Prentice-
Hall of India Pvt. Ltd., Delhi, 2001.