Open Journal of Discrete Mathematics, 2012, 2, 119-124
http://dx.doi.org/10.4236/ojdm.2012.24023 Published Online October 2012 (http://www.SciRP.org/journal/ojdm)
A Non-Conventional Coloring of the Edges of a Graph
Sándor Szabó
Department of Applied Mathematics, Institute of Mathematics and Informatics,
University of Pécs, Pécs, Hungary
Received August 15, 2012; revised September 3, 2012; accepted September 15, 2012
ABSTRACT
Coloring the nodes of a graph is a commonly used technique to speed up clique search algorithms. Coloring the edges
of the graph as a preconditioning method can also be used to speed up computations. In this paper we will show that an
unconventional coloring scheme of the edges leads to an NP-complete problem when one intends to determine the op-
timal number of colors.
Keywords: Maximum Clique; Coloring the Vertices of a Graph; Coloring the Edges of Graph; NP-Complete Problems
1. Introduction
Let be a finite simple graph. This means that
has finitely many nodes, that is,

GV,E

GV is finite. Fur-
ther does not have any double edge or loop. In this
special case an edge of can be identified with a two
element subset of . As a consequence the set of edges
of G is a family of two element subsets of . A
subgraph of G is called a clique if two distinct nodes
of are always adjacent in G. A clique with
nodes is simply called a -clique. The number of nodes
of a clique is sometimes referred as the size of the clique.
A 1-clique inGis a vertex of . A 2-clique inis an
edge in . A 3-clique in is sometimes referred as a
triangle in . A -clique in is called a maximal
clique if it is not a subgraph of any -clique in .
A k-clique in is defined to be a maximum clique if
does not contain any
G


GG
G
G
k
V
k
E
G
V
G
k
G
G
G

G

k

1k

1

-clique. The graph
may have several maximum cliques. However, each
maximum clique in has the same number of nodes.
This well defined number is called the clique size of
and it is denoted by .
G
G
G

G 
Determining the size of a maximum clique in a given
graph is an important problem in applied and pure dis-
crete mathematics. A number of selected applications are
presented in [1] and [2]. It was recognized in [3] that the
efficiency of the clique search algorithms can be cru-
cially improved by coloring and rearranging the nodes of
the tested graph. In [4] instead of coloring the nodes a
technique based on dynamic programming was used
successfully. In [5] another coloring idea was presented.
This time the edges of the graph were colored. Numerical
evidence shows that the edge coloring provides sharper
upper bounds for the clique size than the node coloring.
However, the improved upper bound comes for a higher
computational cost.
We color the nodes of a finite simple graph


GV,E
using colors. We assume that the coloring satisfies the
following conditions: 1) Each node of receives ex-
actly one color; 2) Adjacent nodes in never receive
the same color. We will call this an type coloring of
the nodes of with
kG
G
L
G
k
colors. The letter refers to
the expression legal coloring. We may use the numbers
as colors. The coloring can be defined by a map
L
1, ,k


,:1,
f
vk which is onto. Provided that




,
12
vv
1
v
2
ff v


,vv imply that v1 and v2 are not ad- jacent for each 12 V

.
We color the edges of a finite simple graph


GV,E
using colors. We suppose that for the coloring the
next two conditions hold: 1) Each edge of receives
exactly one color; 2) If
kG
,,,
x
yuv are nodes of a 4-cli-
que in G, then the edges


,
x
y
k
and

cannot
have the same color. We will call this a type coloring
of the edges of with colors. In a conversation
Bogdán Zaválnij proposed this edge coloring scheme.
The letter comes from the name Bogdán. The color-

,uv
B
G
B
ing can be described by a map

:1,,

g
Ek that is
onto. We require that



  
,,

,
g
xyg uv and




,,xy uv

 imply that ,,,
x
yuv

,,,
are not nodes
of a 4-clique in for each

G
x
yuvG
E
.
Problem 1. Given a finite simple graph and given
a positive integer . Decide if the edges of have
type coloring using k colors.
k G
B
The smaller is the number of colors for which the
edges of have a type coloring the more useable is
the coloring in connection with clique search. The main
k
G B
result of this paper is that Problem 1 is NP-complete for
C
opyright © 2012 SciRes. OJDM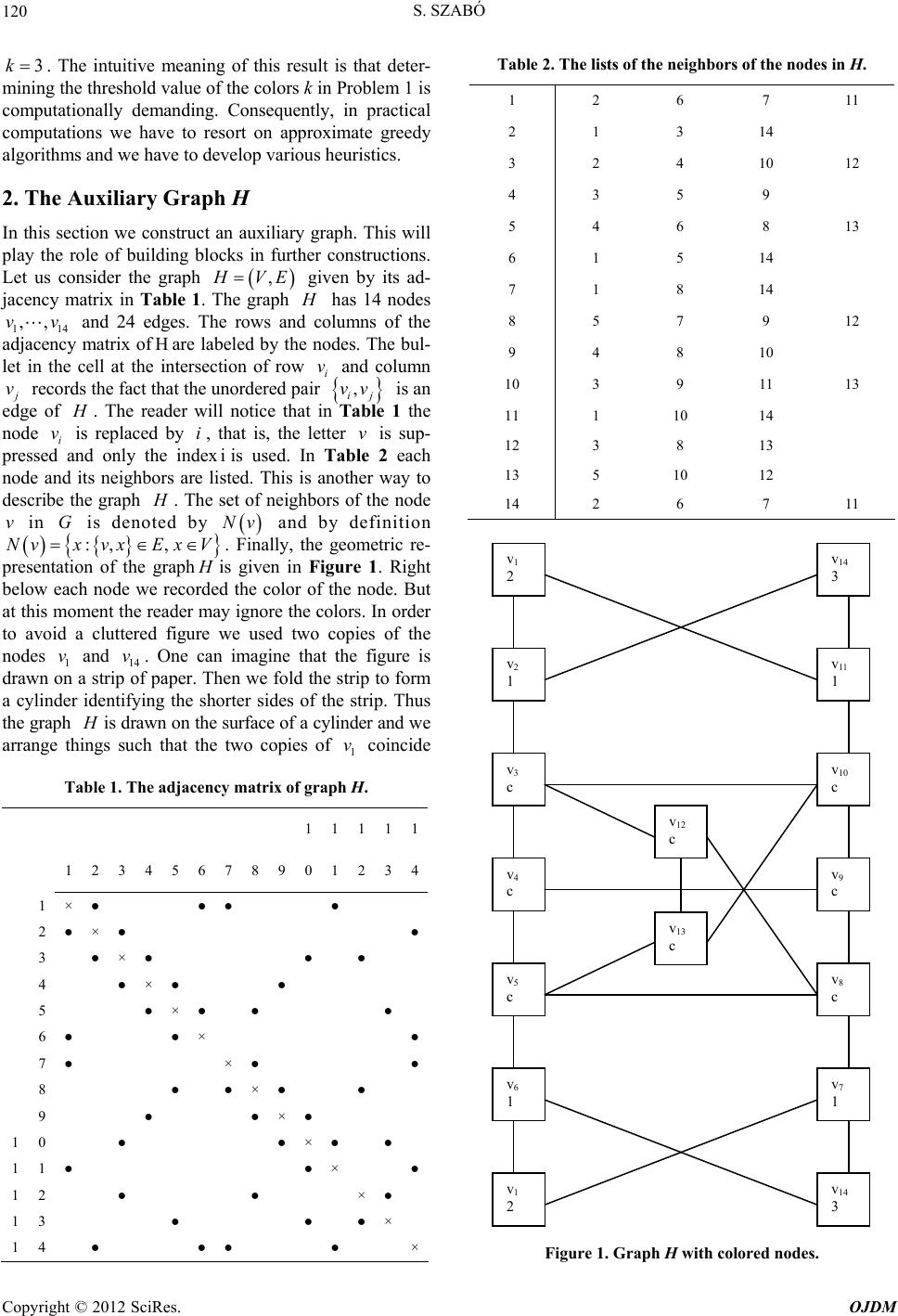

S. SZABÓ 120
Table 2. The lists of the neighbors of the nodes in H.
3k. The intuitive meaning of this result is that deter-
mining the threshold value of the colors k in Problem 1 is
computationally demanding. Consequently, in practical
computations we have to resort on approximate greedy
algorithms and we have to develop various heuristics.
1 2 6 7
2. The Auxiliary Graph H
In this section we construct an auxiliary graph. This will
play the role of building blocks in further constructions.
Let us consider the graph

,

H
VE given by its ad-
jacency matrix in Table 1. The graph
H
has 14 nodes
114
and 24 edges. The rows and columns of the
adjacency matrix ofare labeled by the nodes. The bul-
let in the cell at the intersection of row i and column
,,vv
Hv
j
v records the fact that the unordered pair is an
edge of

,
ij
vv

H
. The reader will notice that in Table 1 the
node i is replaced by , that is, the letter is sup-
pressed and only the indexis used. In Table 2 each
node and its neighbors are listed. This is another way to
describe the graph
v iv
i
H
. The set of neighbors of the node
in is denoted by and by definition
. Finally, the geometric re-
presentation of the graph
vG

Nv

Nv

V
  
:,vx x,Ex
H
is given in Figure 1. Right
below each node we recorded the color of the node. But
at this moment the reader may ignore the colors. In order
to avoid a cluttered figure we used two copies of the
nodes 1 and 14 . One can imagine that the figure is
drawn on a strip of paper. Then we fold the strip to form
a cylinder identifying the shorter sides of the strip. Thus
the graph
v v
H
is drawn on the surface of a cylinder and we
arrange things such that the two copies of coincide
1
v
Table 1. The adjacency matrix of graph H.
1 1 111
1 2 3 4 5 6 7 8 9 0 1 2 3 4
1 × ● ● ● ●
2 ● × ● ●
3 ● × ● ● ●
4 ● × ● ●
5 ● × ● ● ●
6 ● ● × ●
7 ●
×● ●
8 ● ●× ● ●
9 ● ● × ●
1 0 ● ● × ● ●
1 1 ●
● × ●
1 2 ● ● ×●
1
3 ● ● ●×
1 4 ● ● ● ● ×
11
2 1 3 14
3 2 4 10 12
4 3 5 9
5 4 6 8 13
6 1 5 14
7 1 8 14
8 5 7 9 12
9 4 8 10
10 3 9 11 13
11 1 10 14
12 3 8 13
13 5 10 12
14 2 6 7 11
v
1
2
v
14
3
v
2
1
v
11
1
v
10
c
v
3
c
v
9
c
v
4
c
v
8
c
v
5
c
v
7
1
v
6
1
v
14
3
v
1
2
v
12
c
v
13
c
Figure 1. Graph H with colored nodes.

S. SZABÓ 121
and also the two copies of 14 coincide. The properties
of the graph
v
H
we will use later are spelled out for-
mally as a proposition.
Proposition 1. (1) The graph
H
does not contain any
3-clique. (2) In an type coloring of the nodes of
L
H
with 3 colors the nodes 1
v and 14 must receive the
same color. (3) The nodes of
v
H
do have an type
coloring with 3 colors.
L
Proof. The statements of the proposition can be veri-
fied by simple inspections. Here is how the inspection
goes in connection with statement (1). Pick the bullet in
the cell at the intersection of row and column 2
v.
This bullet represents the edge

12
. Scanning the
rows and of the adjacency matrix we can see
that 2
. This means that the edge
12
cannot be a side of any triangle in
1
v
,vv

1
v
Nv

2
v

1
Nv
 


,vv
H
. Then
repeat the argument for all the 24 edges of
H
.
In order to prove the statement (2) let us assume on the
contrary that there is an L type coloring


:1,2,fV3
of the nodes of
H
such that 14

1
 
f
vfv
3


14
fv 
. We may
assume that and since this is
only a matter of rearranging the colors 1, 2, 3 among
each other. Note that

1
fv 2

1
f
v and

11

f
v

fv
must be equal
to 1. From this it follows that and

2,3
3
. A similar argument gives that
 
10 2,3fv 
 
,

67
f
vfv
must be equal to 1 and



52,3fv ,
 
82,3fv. This portion of the reasoning can be fol-
lowed in Figure 1. We distinguish four cases listed in
Table 3. Let us consider case 1. As

32fv

and
, it follows that

82fv 


12 1fv  must hold. Simi-
larly, must hold. But 12
v and 13 are ad-
jacent nodes inand so we get the contradiction that
12 13

13
fv 
 
1
H

v
f
vf

53fv 
v
. The situation is illustrated in Figure 2.
Let us consider case 2. From and
, it follows that

32fv 


41fv 
v must hold. Simi- larly, must hold. But 4 and 9 are adja-
cent nodes in

9
fv 1v
H
and so we get the contradiction that



4

9
f
vfv. Each of the remaining cases can be han-
dled in an analogous way. The reasoning can be followed
in Figure 3.
The statement (3) can be proved by exhibiting a re-
quired coloring. This is done in Figure 4.
3. The Auxiliary Graph K
Using the graph
H
we construct a new graph
K
. Let
Table 3. The cases.
case f(v3) f(v10) f(v5) f(v8)
1 2 3 2 3
2 2 3 3 2
3 3 2 2 3
4 3 2 3 2
v
3
2
v
10
3
v
4
c
v
5
2
v
9
c
v
8
3
v
12
1
v
13
1
Figure 2. Case 1.
v
3
2
v
10
3
v
4
1
v
5
3
v
9
1
v
8
2
v
12
c
v
13
c
Figure 3. Case 2.
114
,,
x
x, 114 be pair-wise distinct points. These
will be the nodes of . We connect the nodes
,,yy
Ki
x
and
i for each y,1ii14

. The edge

,
ii

x
y of and
the node of
K
i
v
H
correspond to each other mutually.
The edges


,
ii
x
y ,1 14ii


K
form a matching in
In other words these edges do not have any common end
points and their end points give all the nodes of . We
will call these edges of primary edges. We will call
all the other edges of secondary edges. If i and
K.
K
v K
j
v are adjacent nodes in
H
, then we add the following
edges to .
K


,
ij
x
x


,
ij
x
y (1)

,
ij
yx

,
ij
yy

Figure 5 illustrates the construction. If i and v
j
v
are not adjacent nodes in H, then we do not add any new
edge to
K
. The new graph
K
has



421 28


nodes and






1424 4

110 edges.
To the node i of H we assigned the edge v


,
ij
x
y
of . To the edge K


,
ij
vv of
H
we assigned the
4-clique in K whose nodes are jj ,,
ii ,
x
yxy . Collapsing
the nodes i
x
and
j
y to one point the edges (1) col-
lapse to an edge and from we get back an isomor- K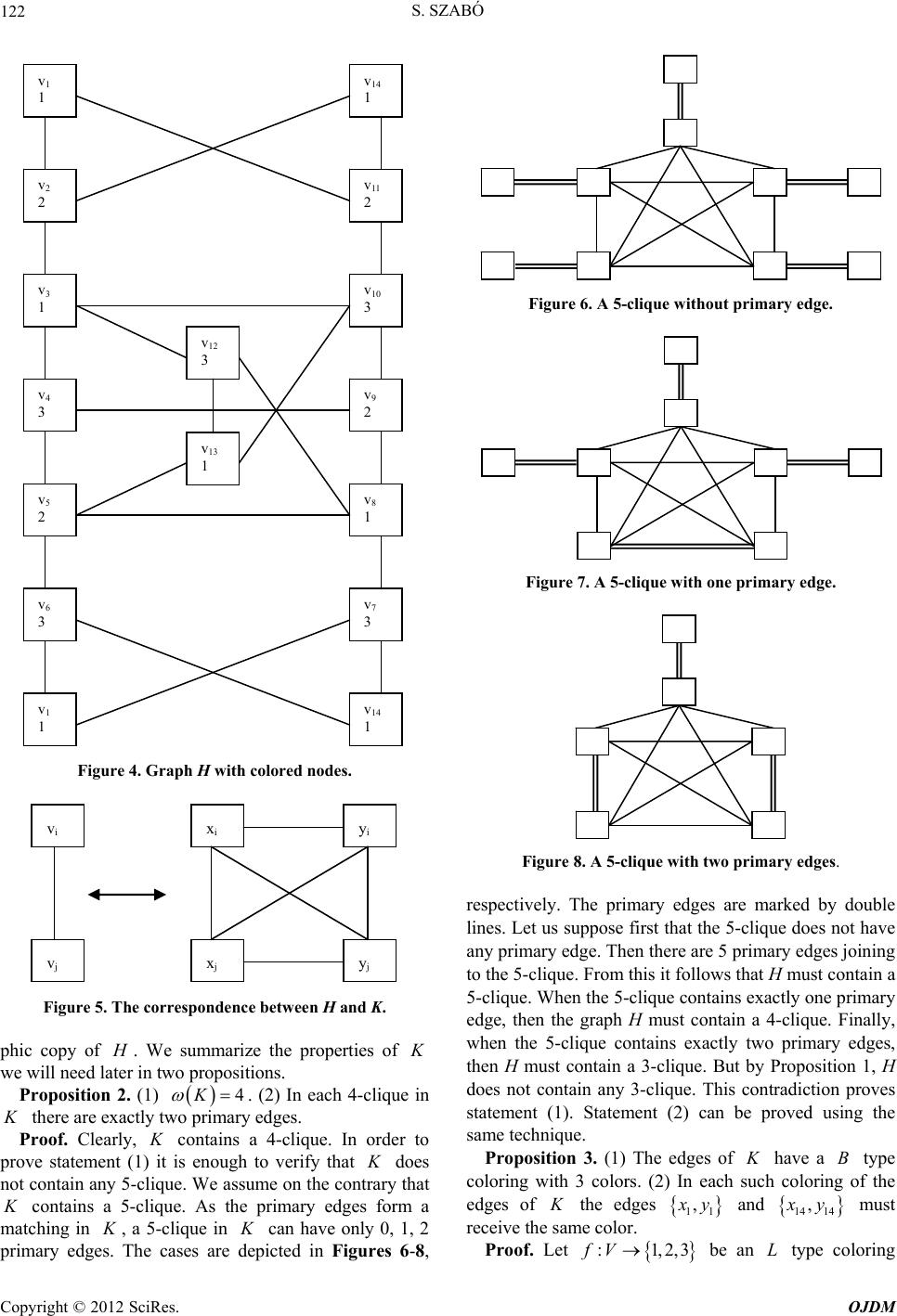

S. SZABÓ 122
v
1
1
v
14
1
v
2
2
v
11
2
v
10
3
v
3
1
v
9
2
v
4
3
v
8
1
v
5
2
v
7
3
v
6
3
v
14
1
v
1
1
v
12
3
v
13
1
Figure 4. Graph H with colored nodes.
y
j
v
i
v
j
x
i
y
i
x
j
Figure 5. The correspondence between H and K.
phic copy of
H
. We summarize the properties of
K
we will need later in two propositions.
Proposition 2. (1)

4K 

. (2) In each 4-clique in
K
there are exactly two primary edges.
Proof. Clearly,
K
contains a 4-clique. In order to
prove statement (1) it is enough to verify that
K
does
not contain any 5-clique. We assume on the contrary that
K
contains a 5-clique. As the primary edges form a
matching in
K
, a 5-clique in
K
can have only 0, 1, 2
primary edges. The cases are depicted in Figures 6-8,
Figure 6. A 5-clique without primary edge.
Figure 7. A 5-clique with one primary edge.
Figure 8. A 5-clique with two primary edges.
respectively. The primary edges are marked by double
lines. Let us suppose first that the 5-clique does not have
any primary edge. Then there are 5 primary edges joining
to the 5-clique. From this it follows that H must contain a
5-clique. When the 5-clique contains exactly one primary
edge, then the graph H must contain a 4-clique. Finally,
when the 5-clique contains exactly two primary edges,
then H must contain a 3-clique. But by Proposition 1, H
does not contain any 3-clique. This contradiction proves
statement (1). Statement (2) can be proved using the
same technique.
Proposition 3. (1) The edges of have a type
coloring with 3 colors. (2) In each such coloring of the
edges of the edges
K B
K


11
,
x
y and

14 14
,

x
y must
receive the same color.
Proof. Let


:1,2,fV3 be an type coloring L

S. SZABÓ 123
of the nodes of

,

H
VE. By Proposition 1, such col-
oring exists. Using
f
we can construct a type col-
oring of the edges of
B

1,2,3:gF

,

K
WF

. We
can achieve this by setting



,
ii
g
xy to be equal to
i

f
v. If and
i
v
j
v are adjacent nodes in
H
, then
the nodes ,,,
iij j
x
yxy

j
are nodes of a 4-clique in .
K
Now

i
f
vfv and so





j

ii j

,,
g
xy


,
ii
g xy.
The remaining four edges of the 4-clique we color in the
following way. Set
g
xy ,


,
ij


g
xy to be
equal to

i

f
v and set




,
ij
g
yx ,


,
ij

g
yy to
be equal to

j
f
v. A routine inspection shows that the
edges of the 4-clique whose nodes are iij j , ,,
x
yx
B

:1,2gF
1,
y
K
K

,3
have atype coloring with 3 colors. (The reader will
notice that in fact we used only 2 colors to color the
nodes of the 4-clique.) This coloring procedure can be
repeated for each 4-clique in which has exactly two
primary edges. By Proposition 2, each 4-clique in
has exactly two primary edges and so each edge of
is colored. Therefore the edges of have a type
coloring with 3 colors. This proves statement (1).
B

:1,2
K
K
:fV
In order to prove statement (2) let be
a type coloring of the edges of K. Using g we can
construct an L type coloring


2,3
B
fV

i

,3 of the nodes of H. Simply we set
f
v

i
f
v to be equal to



,
ij
g
xy .
4. The Auxiliary Graph L
Let

,

K
WF



,

be an isomorphic copy of
K
WF
K
 such that the sets and W are disjoint.
Using and
W
K



14 14
,xy
K
we construct a new graph by
adding the following edges to .
L


14
yy
L


14 14
,,,yx



14 14
,,xx

14
,

(2)
Figure 9 illustrates the construction. These edges con-
nect the graphs and
K
. The resulting graph is de-
noted by L. The graph L has


22

856 nodes and

4

2 110 

L

224 

edges. The properties of the
graph we will need later are spelled out in the next
x
14
(x
14
)′
y
14
(y
14
)′
Figure 9. Connecting the graphs K and K′.
proposition.
Proposition 4. (1) The edges of have type col-
oring with 3 colors. (2) In such a coloring of the edges of
the edges
L B
L


11
,x
y
and

14 ,x14
y
cannot receive the
same color.
Proof. By Proposition 3, the edges of
K
have a
type coloring with 3 colors. In such a coloring of the
edges of
B
K
the edges


11
,
x
y and


14 ,14
x
y must
receive the same color. Because the colors of the edges
can be exchanged among each other freely we may in
fact prescribe the colors of these edges. Similarly, the
edges of
K

have a type coloring with 3 colors. In
the coloring of the edges of
B
K
 the colors of the edges
 


11
,xy

 and
 


14 14
,xy
 must be equal. Again
the color of these edges can be prescribed. Because of the
presence of the edges (2) the edges

14 14
,

x
y and
 


14 14
,xy

 must receive distinct colors.
5. The Main Result
We are ready to prove the main result of this paper.
Theorem 1. Problem 1 is NP-complete for 3k

.
Proof. Let


,GVE
L
be a finite simple graph. Us-
ing we construct a new graph which
satisfies the following two requirements: 1) If the nodes
of have an type coloring using 3 colors, then the
edges of
G
G

,GVE



G

have a type coloring using 3 colors; 2)
If the edges of
B
G

have a type coloring with 3 col-
ors, then the nodes of G have an type coloring
with 3 colors.
BL
Let be all the vertices of G. This means that
1,, n
vv


1,, n
v
i
v
Vv . We assign two points i and i to
the node for each
w z
,1iin


i
z
. We choose the points
1, 1 to be pair-wise distinct. We con-
nect the nodes i and . In other words
,,n wwz,,
n
wz


ii
wz, is
an edge of G for each ,1iin

. For each
,,1ijijn

 we consider an isomorphic copy


,,,
,
ijijij
LWF of the auxiliary graph


,LWF. If
i
v and
j
v
G are adjacent nodes in , then we insert
to
G
,i
Lj

such that the edge of

,
ii
wz G

is iden-
tified with the edge


L
,,1 ,,1
,
ij ij
xy of . Further the
,ij
edge


,
j
j
wz of G

is identified with the edge

,,1 ,,1
,
ij ij
xy







of . If and
,ij
Li v
j
v are not adja-
cent in , then we do not add any new node or new
edge to
G
G

.
We may say that the graph is a blown up version
of the graph . Each node of is replaced by two
connected nodes in
G
G G
G

. Further an isomorphic copy of
the graph plays the role of each edge of in GL G

.

S. SZABÓ 124
One can collapse the nodes and of G
i
wi z

to one
point. If

and
  
,
ii
wz ,
j
j
wz are connected with an
isomorphic copy ,ij
of , then one can collapse
to a single edge. In this way one recovers the graph
from the graph .
L
G
L,ij LG
Let us suppose first that the nodes of


,GVE

E

. We


3

,V

have an type coloring . We define
an edge coloring :g G


set
 
L
,
ii

1: ,2,

2,3 of
fV

1,E


g
wz be equal to

to

i
f
vi v and . If
j
v
e adjacent nodes in G, then in the way we have seen
in the proof of Proposition 4 we can extend the coloring
of the edges


,,1 ,,1
,,
i iijij
wzx y and
ar

h ee graph
Thus the edges of a
tha is a
ty


,,1 ,,1
,,
i iijij
wz xy




to eac
have
t
dge
:1
of th
type coloring as

,2,3
,ij
L.
clai
G B
med in statement (1).
Let us suppose next gE
B
pe coloring of the edges of


,GV
coloring
E

. We define a


:1,2,3fV of tG by setting

i
he nodes of
f
v to


,
be equal toii
g
wz . We claim that

fv and ijat i v and

fv
ij imply th
j
v are
des in In order to proe the claim let
us assume on the contrary that


i
fv fv, ij
not adjacent noG. v
j

and the nodes i
v,
j
v are adjacent in ro


G

,,
. By Pposi-
tion 4,
  
,,1 ,,1,,1,,1ijijijij
gx yg xy









g giv
holds.
On the other hand the definitiohrines tn of te colohat





,,fvg wzg xy . Similarly, by the
,, ,1iii i1 ,ij
,,1i

j
,1i


definition of the coloring

m
we get the contradiction
 

,,




,iii jj
fvg wzgxy



. Fro this



ij
f
vfv
ld recall t
graph a
. This
o th
nd su
proves
the proof onoue result
th
6. The Derived Graph
ple ppose
pa

From we construct a new graph . The
nodes of
G

,UF

are the edges of , that is, UGE

. Two
distinct nodes


,
x
y and

of  are connected

,uv




,,uvxy

statement (2).
To completee sh
at the problem of deciding if the nodes a given simple
graph have a L type coloring with 3 colors is an NP-
complete problem. Proofs of this well-known result can
be found for example in [6,7].
Let

,GVE be a finite sim
that find a B type coloring of the edges of
G. A possible interpretation of the main result of this
per is that determining the optimal number of colors is
a computationally demanding problem. In practical com-
putations we should be content with suboptimal values of
the number of colors.
we want to
in Γ if  and ,,,
x
yuv are not nodes
of a 4-clique in . In the lack of established terminal-
ogy we call  the derived graph of G. The essential con-
nection between G and
G

is the following result.
Proposition 5. The nodes of have an type col-
oring with k colors if and only if the edges of have a
type coloring with k colors.
LG
B
The reader will not have any difficulty to check the
veracity of the proposition. The result makes possible to
apply all the greedy coloring techniques developed for
coloring the nodes of a graph. When the graph has n
nodes it may have
G


2
On
G
G
edges. For instance when
has 4000 nodes, then may have 10 millions edges. In
this case the adjacency matrix of does not fit into the
memory of an ordinary computer. Thus one should
compute the entries of the adjacency matrix from the
adjacency matrix of during the coloring algorithm.
The most commonly used greedy coloring of the nodes
of a graph takes
G



2
On steps. Applying this technique
to the derived graph we get an algorithm whose compu-
tational complexity is


4
On . The author has carried
out a large scale numerical experiment with this algo-
rithm. The results are encouraging.
REFERENCES
[1] I. M. Bomze, M. Budinich, P. M. Pardalos and M. Pelillo,
“The Maximum Clique Problem,” In: D.-Z. Du and P. M.
Pardalos, Eds., Handbook of Combinatorial Optimization,
Kluwer Academic Pubisher, Dordrecht, 1999, pp. 1-74.
[2] D. Kumlander, “Some Practical Algorithms to Solve the
Maximal Clique Problem,” Ph.D. Thesis, Tallin Univer-
sity of Technology, Tallinn, 2005.
[3] R. Carraghan and P. M. Pardalos, “An Exact Algorithm
for the Maximum Clique Problem,” Operation Research
Letters, Vol. 9, No. 6, 1990, pp. 375-382.
doi:10.1016/0167-6377(90)90057-C
[4] P. R. J. Östergård, “A Fast Algorithm for the Maximum
Clique Problem,” Discrete Applied Mathematics, Vol. 120,
No. 1-3, 2002, pp. 197-207.
doi:10.1016/S0166-218X(01)00290-6
[5] S. Szabó, “Parallel Algorithms for Finding Cliques in a
Graph,” Journal of Physics: Conference Series, Vol. 268,
No. 1, 2011, Article ID: 012030.
doi:10.1088/1742-6596/268/1/012030
[6] M. R. Garey and S. Johnson, “Computers and Intractabil-
ity: A Guide to the Theory of NP-completeness,” Free-
man, New York, 2003.
[7] C. H. Papadimitriou, “Computational Complexity,” Ad-
dison-Wesley Publishing Co. Inc., Boston, 1994.