Energy and Power Engineering, 2010, 2, 154-160
doi:10.4236/epe.2010.23023 Published Online August 2010 (http://www.SciRP.org/journal/epe)
Classification of Power Quality Disturbances Using
Wavelet Packet Energy Entropy and LS-SVM
Ming Zhang, Kaicheng Li, Yisheng Hu
College of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan, China
Received April 11, 2010; revised May 22, 2010; accepted June 27, 2010
Abstract
The power quality (PQ) signals are traditionally analyzed in the time-domain by skilled engineers. However,
PQ disturbances may not always be obvious in the original time-domain signal. Fourier analysis transforms
signals into frequency domain, but has the disadvantage that time characteristics will become unobvious.
Wavelet analysis, which provides both time and frequency information, can overcome this limitation. In this
paper, there were two stages in analyzing PQ signals: feature extraction and disturbances classification. To
extract features from PQ signals, wavelet packet transform (WPT) was first applied and feature vectors were
constructed from wavelet packet log-energy entropy of different nodes. Least square support vector ma-
chines (LS-SVM) was applied to these feature vectors to classify PQ disturbances. Simulation results show
that the proposed method possesses high recognition rate, so it is suitable to the monitoring and classifying
system for PQ disturbances.
Keywords: Power Quality (PQ), Wavelet Packet Transform (WPT), Wavelet Packet Log-Energy Entropy,
Least Square Support Vector Machines (LS-SVM)
1. Introduction
The deregulation polices in electric power systems re-
sults in the absolute necessity to quantify power quality
(PQ). This fact highlights the need for an effective rec-
ognition technique capable of detecting and classifying
the PQ disturbances. Traditionally PQ recordings are
analyzed in the time-domain by skilled engineers. How-
ever, PQ disturbances may not always be obvious in the
original time-domain signal. One of the traditional signal
processing techniques called Fourier transform provides
information in frequency-domain but it does have limita-
tions. One crucial limitation is that a Fourier coefficient
represents a component that lasts for all time. This makes
Fourier analysis less suitable for non-stationary signals.
Wavelet analysis, which provides both time and fre-
quency information, can overcome this limitation. Unlike
the Fourier transforms, the wavelet transform has a fully
scalable window, which allows a more accurate local
description and separation of signal characteristics [1].
The wavelet transform has been applied to the wide
range of PQ signals analysis: feature extraction [2], noise
reduction [3], and data compression [4]. Recently, The
identification of PQ disturbances is often based on artifi-
cial neural network (ANN) [5], fuzzy method (FL) [6],
expert system (ES) [7], support vector machines (SVM)
[8], and hidden Markov model (HMM) [9]. Many of the
studies proposed in the literature present that these tech-
niques can use feature vectors derived from disturbance
waveforms to classify PQ disturbances.
The types of PQ disturbances include the sag, inter-
ruption, swell, harmonic, notch, oscillatory transient
(Osc. transient) and impulsive transient (Imp. transient)
(see Figure 1) [10]. In this paper, the combined tech-
nique of wavelet packet transform (WPT) and least
square support vector machines (LS-SVM) for PQ dis-
turbances recognition is presented. Decision making is
performed in two stages: feature extraction and LS-SVM
as a classifier. Figure 2 shows the block diagram of the
classification system. The details of each stage are de-
scribed in the next sections. High accuracies were
achieved by using the LS-SVM trained on the wavelet
packet log-energy entropy of different nodes.
The rest of this paper is organized as follows. In Sec-
tion 2, the feature extraction by WPT is explained. In
Section 3, brief review of the LS-SVM with the mini-
mum output coding (MOC) technique is presented.
In Section 4, the results of classification of the LS-
SVM trained on wavelet packet log-energy entropy to

M. ZHANG ET AL.
155
Figure 1. Power quality disturbance waveforms: (a) Normal
signal; (b) Sag; (c) Interruption; (d) Swell; (e) Harmonic; (f)
Notch; (g) Oscillatory transient; (h) Impulsive transient.
Figure 2. Block diagram of the classification system.
the studied PQ disturbance signals are presented. Finally,
conclusions are given in Section 5.
2. Feature Extraction Using WPT
The purpose of the feature extraction process is to select
and retain relevant information from original signals.
The WPT was first applied to decompose the original PQ
signals into frequency bands. One of the advantages of
the WPT is that it is able to decompose signals at various
resolutions, which allows accurate feature extraction fro-
m non-stationary signals like PQ disturbances. The fea-
tures of signals, such as wavelet packet energy entropy,
were then extracted from these decomposed signals as
feature vectors.
The wavelet transform decomposes a signal into a set
of basic functions called wavelets. These basic functions
are obtained by dilations, contractions and shifts of a
unique function called wavelet prototype. Continuous
wavelets are functions generated functions generated
from one single function by dilations and translations of
a unique admissible mother wavelet )(tψ:
)(
1
)(
,a
bt
a
t
ba
−
=ψψ (1)
where 0,, ≠ℜ∈ aba are the scale and translation
parameters, respectively, and
t
is the time. The func-
tion set ()(
,t ba
ψ) is called wavelet family. It is common
to employ both wavelet and scaling functions in the
transform representation. In general, the scale and shift
parameters of the discrete wavelet family are given by
=
a
j a0 and j akbb 00 =, where
j
and k are inte-
gers. The function family with discretized parameters
becomes:
)()( 0
2/
0, kbtaat j
j
kj−= −
−ψψ (2)
where )(
,t kj
ψis called the discrete wavelet transform
(DWT) basis.
DWT analyzes the signal at different frequency bands,
with different resolutions by decomposing the signal into
a coarse approximation and detail information. DWT em-
ploys two sets of functions called scaling functions )(tϕ
and wavelet functions )(
t
ψ
, which associated with low-
pass and high-pass filters, respectively. The original sig-
nal )(
t
x
can be decomposed to:
∑∑∑ =
+= J
jjk k
jk
k
tkdtkctx jj 1 )()()()()( ψϕ (3)
where
j
is the level number of the wavelet decomposi-
tion,
J
j
,,2,1
L
=
with J the time of the wavelet de-
composition. j c and j d are the approximation coeffi-
cients and detail coefficients of )(
t
x
, respectively.
Because the information in higher frequency compo-
nents is important, the frequency resolution of DWT may

M. ZHANG ET AL.
156
not be fine enough to extract pertinent frequency infor-
mation about the signal. The necessary frequency resolu-
tion may be achieved by using WPT, an extension of the
DWT. In the WPT, the wavelet detail at each level is, in
addition to decomposition of only the wavelet approxi-
mation in the regular wavelet analysis, further decom-
posed in to its own approximation and detail components.
By this process, some lower frequency contents leaked in
the wavelet details at the previous level can be further
sifted out at the current level and also the frequency res-
olution for signal analysis increases. As a result, the
WPT may provide better accuracy in both higher and
lower frequency components of the signal.
Figure 3 shows the wavelet packet decomposition tree
for three levels (3
=
J). For each level of decomposition
the signal is filtered into approximate information of the
signals (lower frequency component) and detail informa-
tion (higher frequency component). If this procedure is
repeated J times, a filter bank is created with J filters.
To evaluate the importance of the wavelet packet com-
ponents to a signal, the concept of entropy is often ap-
plied in signal processing and there are various defini-
tions of entropy in the literature. Among them, two rep-
resentative ones are used in the present article, i.e. the
energy entropy and the Shannon entropy. The wavelet
packet energy entropy at a particular node n in the wave-
let packet tree of a signal is a special case of p = 2 of the
p-norm entropy, defined as
)1(
,≥= ∑pwcEnt p
kknn (4)
where
kn
wc ,denotes the wavelet packet coefficients cor-
responding to node n at time k. It was demonstrated that
the wavelet packet energy has more potential for use in
signal classification as compared to the wavelet packet
coefficients alone. The wavelet packet energy represents
energy stored in a particular frequency band and is
mainly used in this study to extract the dominant fre-
quency components of the signal.
The Shannon energy entropy and relative Shannon en-
ergy entropy are defined respectively as [11]
Figure 3. Wavelet packet decomposition tree.
∑
−=
kknknn wcwcEnts )log( 2.
2. (5)
nnornn EntsEntsREnts _
/= (6)
where nnor Ents _ is the Shannon energy entropy of the
normal signal corresponding to node n.
In this paper, one of the commonly used entropy, log-
energy entropy is also defined as
∑
=
kknn wcEntl )log(2. (7)
The relative log-energy entropy is proposed as
nnornn EntlEntlREntl _
/= (8)
where nnor Entl _ is the log-energy entropy of the normal
signal corresponding to node n.
3. LS-SVM
The second stage is the disturbances classification. Sup-
port vector machine (SVM) can avoid the problems of
over learning, dimension disaster and local minimum in
the classical study method, and is applied in many classi-
fication problems successfully [8,11]. According to the
practice, [12] advanced by J. A. K. Suyken can overcome
the disadvantage of slow training velocity in the large
scale problem, as LS-SVM algorithm translates the qua-
dratic optimization problem into that of solving linear
equation set. Although a wide range of classifiers are
available, we use LS-SVM in this paper.
We consider a training set of N data points
{
}
kk yx,,
N
k,,2,1
L
=, where n
k
xℜ∈ is the input data,
ℜ
∈
k
y
is the thk
−
output data, the SVM constructs a deci-
sion function that is represented by:
bxwxy T+=)( (9)
where the dimension of w is not specified. It means that
it can be infinitely dimensional. The separating hyper-
plane that creates the maximum distance between the
plane and the nearest data is called as the optimal sepa-
rating hyperplane as shown in Figure 4.
In LS-SVM for the function estimation the following
optimization problem can be given
∑
=
+= N
kk
T
LS
ebw eCwwebwJ
1
2
2
1
2
1
,, ),,(min (10)
subject to the equality constraints
Nkebxwykk
T
k,...,1, =++= (11)
where k e are slack variables and C is a positive real
constant. One defines the Lagrangian
∑
=
−++−= N
kkkk
T
kLS yebxwJebwL
1
)();,,( αα (12)

M. ZHANG ET AL.
157
w
m2 =
1
wxb
+=+
0
wxb
+=
1
wxb
+=−
w
m
Figure 4. Optimal separating hyper plane.
with Lagrange multipliers k α. The conditions for opti-
mality are
1
1
0
00
0
00
k
k
N
kk
k
N
k
k
kk
T
kkk
Lwx
w
L
b
Le
e
Lwxbey
α
α
αγ
α
=
=

∂
=→=

∂


∂
=→=


∂


∂
=→=

∂

∂

=→++−=
∂

∑
∑ (13)
for
N
k
,
,
2
,
1
L
=
. It can be written immediately as the
solution to the following set of linear equations:
00
0
000
00
0
T
w
b
γ
−




−


=


−






IX
I1
IIIe
α
Y
X1I
r
r
(14)
with ],...,[X 1N xx=, ],...,[Y1N yy=, ]1,...,1[1=
r
,
=
e
1
[,...,]
N
ee
and ],...,[α1N αα=. The solution is finally
given by






=














+
−
−Yα
IXX1
100
1
b
T
T
γ
r
r
(15)
with k
kkxw
∑
=α, Ce kk /α=. The support values
k
α are proportional now to the errors at the data points.
So far we explained the linear case. SVM’s with
polynomials, splines, radial basis function networks, or
multilayer perceptrons as kernels are obtained after map-
ping the input data into a higher dimensional space by
)( k xφ, where )(
⋅
φ
: h
n nℜ→ℜ. The number h
n does
not have to be specified because of the application of
Mercer’s condition, which means that
)()(),( j
T
kjk xxxxK φφ= (16)
can be imposed for these kernels. Finally, the nonlinear
function takes the form:
bxxKxy N
kkk+= ∑ =1
),()(α (17)
where the parameters k α, b follow from (15) after
replacing j
T
kxx by ),(jk xxK .
Multi-class classification was realized by the combi-
nation of LS-SVM classifiers with the minimum output
coding (MOC) technique. In the MOC technique, up to
m
2
log (where m is the number of classes) LS-SVM clas-
sifiers were trained, and each of them aimed to separate a
different combination of classes. There were eight
classes (normal signal, sag, interruption, swell, harmonic,
notch, oscillatory transient and impulsive transient) in
this study, so three classifiers were necessary to differen-
tiate them. The coding was defined by the codebook
represented by a matrix, where the columns represent the
different classes, and the rows indicate the results of the
binary classifiers. The multi-class classifier output code
for a pattern is a combination of targets of these three
classifiers. In this study, the eight classes were encoded
in the following codebook of minimum output coding:
T
codebook
CCCCCCCC










−−−−
−−−−
−−−−
=
11111111
11111111
11111111
87654321
where 8,7,6,5,4,3,2,1
C
and
C
C
C
C
C
C
C
are normal
signal, sag, interruption, swell, harmonic, notch, oscilla-
tory transient and impulsive transient, respectively.
4. Simulation Analysis
To test classification results for PQ disturbances, the
testing samples of these PQ disturbances have been gen-
erated using algebraic equations [14]. The advantage of
using algebraic equations for evaluation is the flexibility
of adjusting signal noise contents as well as various
waveform parameters such as the disturbance occurrence
time, harmonic contents, sag depth, etc.
These disturbance waveforms are generated at a sam-
pling rate of 256 samples/cycle for a total of 2560 points
(10 cycles). In order to create different disturbance cases,
some unique parameters such as starting time, magnitude,
duration, frequency, and damping are allowed to change
randomly. The random generation of signals is helpful
for the testing of the classification more reliable since
none of these attributes is fixed for real distribution sys-

M. ZHANG ET AL.
158
tem disturbances.
Using wavelet packet decomposition, each signal shown
above was decomposed to level 3. The wavelet ‘Daub4’
was selected because it is more adequate for classifica-
tion of PQ disturbances [13]. The wavelet packet energy
entropy of different nodes of the decomposed signals
were calculated, which could be used to identify the type
of PQ disturbances. The performances of difference wave-
let packet energy entropy for feature sets are shown in
Figure 5. From above Figure 5, we can conclude that
relative log-energy entropy is more effective than tradi-
tional relative Shannon energy entropy, which can am-
plify the errors among the feature vectors. These features
consist of 8-dimension feature space.
In this paper, we construct a LS-SVM by using radial
basis function (RBF) as kernel function in LS-SVM pro-
posed above.
)
2
exp(),( 2
2
σ
ji
ji
xx
xxK − −= (18)
where
σ
is the width of the kernel.
For training the SVMs with RBF kernel functions, one
has to predetermine the
σ
values. The optimal or near
optimal
σ
values can only be ascertained after trying
out several, or even many values. Beside this, the choice
of C parameter in the SVM is very critical in order to
have a properly trained SVM. The SVM has to be trained
for different C values until to have the best result.
From the Figure 6, It is found that the near optimal val-
ues are 1
2=σ and 4
=
C.
node
(a)
×
10
5
node
(b)
×
10
4
node
(c)
node
(d)
Figure 5. Performance comparison of difference wavelet energy entropy of the waveforms in Figure 1: (a) Wavelet packet
Shannon energy entropy; (b) Relative wavelet packet Shannon energy entropy; (c) Wavelet packet log-energy entropy; (d)
Relative wavelet packet log-energy entropy.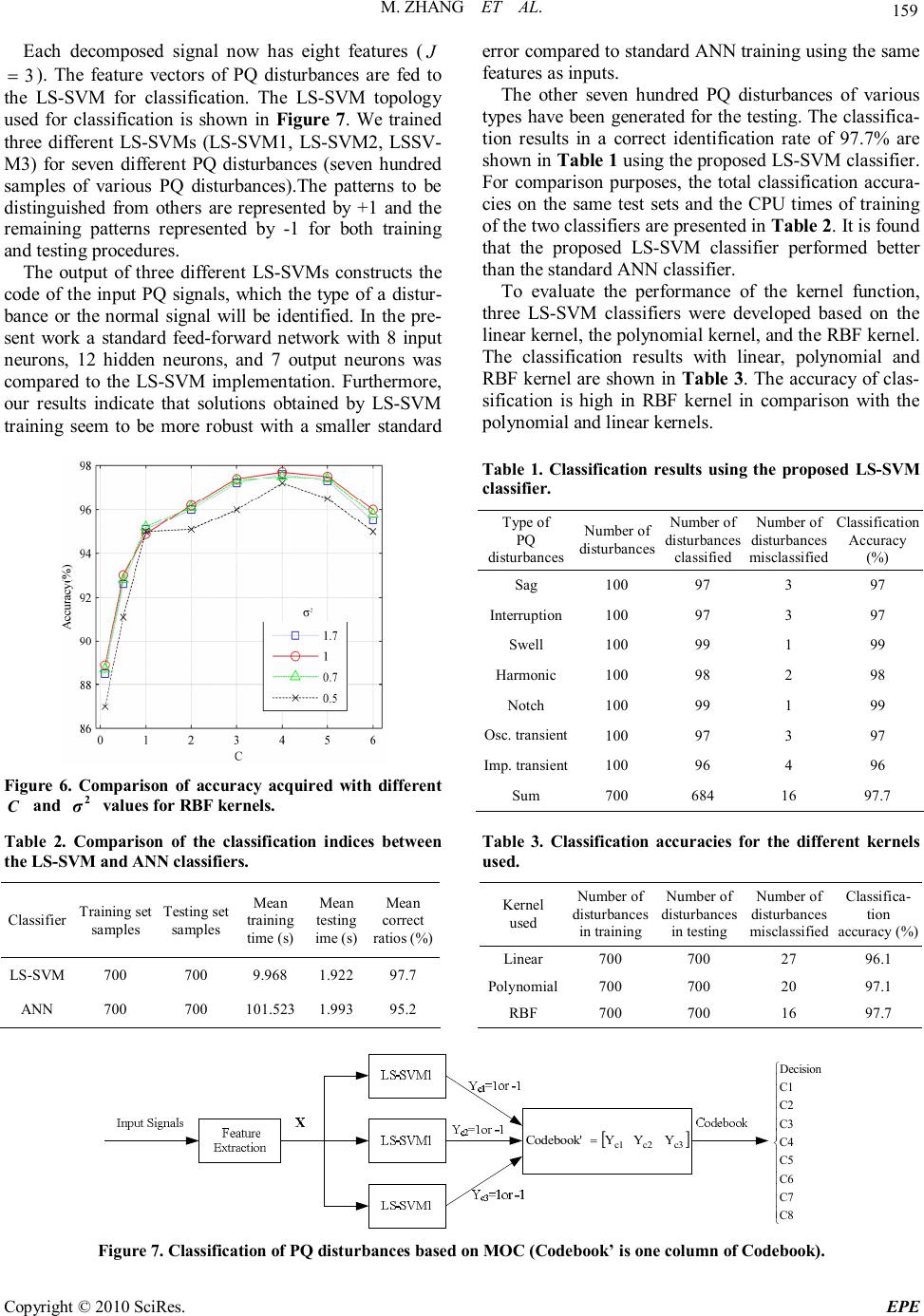

M. ZHANG ET AL.
159
Each decomposed signal now has eight features (J
3
=
). The feature vectors of PQ disturbances are fed to
the LS-SVM for classification. The LS-SVM topology
used for classification is shown in Figure 7. We trained
three different LS-SVMs (LS-SVM1, LS-SVM2, LSSV-
M3) for seven different PQ disturbances (seven hundred
samples of various PQ disturbances).The patterns to be
distinguished from others are represented by +1 and the
remaining patterns represented by -1 for both training
and testing procedures.
The output of three different LS-SVMs constructs the
code of the input PQ signals, which the type of a distur-
bance or the normal signal will be identified. In the pre-
sent work a standard feed-forward network with 8 input
neurons, 12 hidden neurons, and 7 output neurons was
compared to the LS-SVM implementation. Furthermore,
our results indicate that solutions obtained by LS-SVM
training seem to be more robust with a smaller standard
error compared to standard ANN training using the same
features as inputs.
The other seven hundred PQ disturbances of various
types have been generated for the testing. The classifica-
tion results in a correct identification rate of 97.7% are
shown in Table 1 using the proposed LS-SVM classifier.
For comparison purposes, the total classification accura-
cies on the same test sets and the CPU times of training
of the two classifiers are presented in Table 2. It is found
that the proposed LS-SVM classifier performed better
than the standard ANN classifier.
To evaluate the performance of the kernel function,
three LS-SVM classifiers were developed based on the
linear kernel, the polynomial kernel, and the RBF kernel.
The classification results with linear, polynomial and
RBF kernel are shown in Table 3. The accuracy of clas-
sification is high in RBF kernel in comparison with the
polynomial and linear kernels.
Figure 6. Comparison of accuracy acquired with different
C and
2
σ
values for RBF kernels.
Table 1. Classification results using the proposed LS-SVM
classifier.
Type of
PQ
disturbances
Number of
disturbances
Number of
disturbances
classified
Number of
disturbances
misclassified
Classification
Accuracy
(%)
Sag 100 97 3 97
Interruption 100 97 3 97
Swell 100 99 1 99
Harmonic 100 98 2 98
Notch 100 99 1 99
Osc. transient 100 97 3 97
Imp. transient 100 96 4 96
Sum 700 684 16 97.7
Table 2. Comparison of the classification indices between
the LS-SVM and ANN classifiers.
Classifier
Training set
samples Testing set samples
Mean
training
time (s)
Mean
testing
ime (s)
Mean
correct
ratios (%)
LS-SVM 700 700 9.968 1.922 97.7
ANN 700 700 101.523 1.993 95.2
Table 3. Classification accuracies for the different kernels
used.
Kernel
used
Number of
disturbances
in training
Number of
disturbances
in testing
Number of
disturbances
misclassified
Classifica-
tion
accuracy (%)
Linear 700 700 27 96.1
Polynomial 700 700 20 97.1
RBF 700 700 16 97.7
[
]
c3c2c1
YYYCodebook' =















C8
C7
C6
C5
C4
C3
C2
C1
Decision
Figure 7. Classification of PQ disturbances based on MOC (Codebook’ is one column of Codebook).

M. ZHANG ET AL.
160
5. Conclusions
In this paper, an attempt has been made to extract effici-
ent features of the PQ disturbances using WPT and to
classify the disturbances using LS-SVM with the MOC
technique. It is also found that relative wavelet packet
log-energy entropy is considered as feature vectors, wh-
ich are suitable for classification of PQ disturbances. For
comparison different classifiers, the LS-SVM and ANN
classifiers were implemented to deal with the same class-
ification. The classification accuracies and the CPU tim-
es of training showed that the LS-SVM classifier produc-
es considerably better performance than that of the ANN
classifier.
6. Acknowledgements
The authors would like to thank to the support of Wuhan
Xinlian Science and Technology Ltd.
7. References
[1] S. Mallat, “A Wavelet Tour of Signal Processing,” Aca-
demic Press, San Diego, California, 1998.
[2] S. Santoso, E. J .Powers and P. Hofman, “Power Quality
Assessment via Wavelet Transform Analysis,” IEEE
Transaction on Power Delivery, Vol. 11, No. 2, 1996, pp.
924-930.
[3] H. T. Yang and C. C. Liao, “A De-Noising Scheme for
Enhancing Wavelet-Based Power Quality Monitoring
System,” IEEE Transaction on Power Delivery, Vol. 16,
No. 3, 2001, pp. 353-360.
[4] S. Santoso, E. J. Powers and W. M. Grady, “Power Qual-
ity Disturbance Data Compression Using Wavelet Trans-
form Methods,” IEEE Transaction on Power Delivery,
Vol. 12, No. 3, 1997, pp. 1250-1257.
[5] A. K. Ghosh and D. L. Lubkeman, “The Classification of
Power System Disturbance Waveforms Using a Neural
Network Approach,” IEEE Transaction on Power Deliv-
ery, Vol. 10, No. 1, 1995, pp. 109-115.
[6] T. X. Zhu, S. K. Tso and K. L. Lo, “Wavelet-Based
Fuzzy Reasoning Approach to Power Quality Distur-
bance Recognition,” IEEE Transaction on Power Deliv-
ery, Vol. 19, No. 4, 2004, pp. 1928-1935.
[7] M. B. I. Reaz, F. Choong, M. S. Sulaiman, F. Mohd-
Yasin and M. Kamada, “Expert System for Power Qual-
ity Disturbance Classifier,” IEEE Transaction on Power
Delivery, Vol. 22, No. 3, 2007, pp. 1979-1988.
[8] P. Janik and T. Lobos, “Automated Classification of
Power Quality Disturbances Using SVM and RBF Net-
works,” IEEE Transaction on Power Delivery, Vol. 21,
No. 3, 2006, pp. 1663-1669.
[9] J. Chung, E. J. Powers, W. M. Grady and S. C. Bhatt,
“Power Disturbance Classifier Using a Rule-Based
Method and Wavelet Packet-Based Hidden Markov
Model, ” IEEE Transaction on Power Delivery, Vol. 17,
No. 1, 2002, pp. 233-241.
[10] IEEE Recommended Practice for Monitoring Electric
Power Quality, IEEE Standards Description: 1159-1995,
2009.
[11] G. S. Hu, F. F. Zhu and Z. Ren, “Power Quality Distur-
bance Identification Using Wavelet Packet Energy En-
tropy and Weighted Support Vector Machines,” Expert
Systems with Applications, Vol. 35, No. 1-2, 2008, pp.
143-149.
[12] J. A. K. Suykens and J. Vandewalle, “Least Squares Sup-
port Vector Machine Classifiers,” Neural Processing Let-
ter , Vol. 9, No. 3, 1999, pp. 293-300.
[13] N. S. D. Brito, B. A. Souza and F. A. C. Pires, “Daube-
chies Wavelets in Quality of Electrical Power,” 8th In-
ternational Conference on Harmonics and Quality of
Power , Athens, 14-18 October 1998, pp. 511-515.
[14] T. K. Abdel-Galil, M. Kamel, A. M. Youssef, E. F.
El-Saadany and M. M. A. Salama, “Power Quality Dis-
turbance Classification Using the Inductive Inference
Approach,” IEEE Transaction on Power Delivery, Vol.
19, No. 4, 2004, pp. 1812-1818.