Paper Menu >>
Journal Menu >>
 Energy and Power Engineering, 2010, 2, 137-142 doi:10.4236/epe.2010.23020 Published Online August 2010 (http://www.SciRP.org/journal/epe) Copyright © 2010 SciRes. EPE Draw of Infinite Energy from Space and Negations of Two Important Laws Fusui Liu Department of Physics, Beijing University, Beijing, China E-mail: fsliu@pku.edu.cn Received February 25, 2010; revised April 15 , 2010; accepted June 12, 2010 Abstract This paper shows that energy of 105 ton of oil can be obtained from space by fs (fermtosecond) eletromag- netic pulse technique in one second and one cm3 without any loss. This paper shows that the energy conser- vation law and Fermi golden rule should be negatived in some cases. The negation of Fermi golden rule has important influences on many fields based on quantum mechanics. For example, the present knowledge on the charge distribution in atomic nucleus might be wrong completely. This paper emphasizes that the propo- sition on introducing the concept of the energy support ability in space will cause a series of unimaginable discoveries, and, therefore is of epoch-making significance. This paper gives indirect experimental verifica- tions for the necessity of introducing the concept of energy support ability in space, and suggests a very sim- ple experiment to show directly that the energy conservation law and Fermi golden rule should be negatived in some cases. Keywords: Energy Conservation Law, Fermi Golden Rule, Fermtosecond Technique 1. Introduction In the calculations for the probability of transition to con- tinuous spectrum all textbooks of quantum mechanics make the following four assumptions [1-11]. 1) The tran- sition matrix element and the density of states are an energy constant, and the transition rate does not depend on time, which is called Fermi golden rule; 2) The transi- tion probability is determined only by the height of the first peak in curve of the energy density of transition probability; 3) The width of the first peak is determined by the energy uncertainty principle; 4) It is easy to see that the first peak is of property of energy conservation, and the second peak is not of property of energy conser- vation. However, considering that (height of second peak) /(height of second peak) = 0.06, the second peak and more higher order peaks are neglected i.e., the energy nonconservation in transition process does not been con- sidered. We strongly doubt the correctness of the above four assumptions, based on the following considerations. 1) It is obvious that there is no verification for the correctness of neglecting the energy variations of the transition ma- trix element and density of states in any cases. However, they are strongly energy-dependent in some cases; 2) There is no verification for the correctness of the time independence of transition rate in any cases; 3) Actually, the formula of transition probability is derived without using the energy uncertainty principle. Therefore, the explanation for the width of the first peak in terms of energy uncertainty principle is utterly unjustifiable; 4) The second peak and others of energy nonconservation should not been neglected in any cases. We should try to increase the height of the second peak and others. If we can, then mankind can have infinite energy without any loss in terms of energy nonconservation. This paper makes exact calculations for the transition probability, and obtains many important discoveries, which are stated in Sections 2, 3 and 4. Some discussions are given in Section 5. Our conclusions are listed in Se- ction 6. 2. Draw of Infinite Energy from Space and Negation of Energy Conservation Law in Some Cases For the convenience of statement, at first we study the elementary theory of photoeffect. Let us consider a hydr- ogen atom in ground state. The Hamiltonian H is H = H0 + H'. |m > is the state vector of discrete spectrum of H =  F. S. LIU Copyright © 2010 SciRes. EPE 138 H0. |k > is the state vector of continuous spectrum of H = H0. B is the domain of |k >. H' is the Hamiltonian of ele- ctron of hydrogen atom in electromagnetic field. H' is [1] H' = ercos(θ) E0 (eiωt' +e iωt') = H" (e iωt' +e iωt'), (1) where r is the position vector of electron, θ is the angle between field and r. Assume that the duration time of field is between 0 and t0. The probability of transition from state |m > to one state |k >, Wm→k, at t ≥ t0 due to absorption of a photon is [1] 22 0 2 1 4||''|| sin() 2 () 2 km mk km kH mt Wh (2) where )2/()( 2mk k and m is the mass of electron. For simplicity, we consider the boundary absorption of hydrogen atom in ground state. In this case m 6.13 eV. The energy density of transition probabi- lity from state |m> to any state |k > with energy between k E and kk dEE per unit solid angle at 0 tt due to absorption of a photon , k dEm W, is [1] )( ||''||4 2 2 kdEm E mHk Wk k k k dE t 2 0 2 2 1 sin , (3) where )( k E is the density of states, and it is [1] dd ELm E k ksin 8 2 1 )( 33 2 1 3 2 3 2 1 , (4) where ddsin is solid angle. <r|m> = 2/1 0)( a exp )/(0 ar, and 0 a is Bohr radius [1]. <r|k> = ex p 2/3 L (ik.r) [1]. After simple derivation we have kdm dW k 4 2 5 2 1 2 2 5 7 0 2 0 2 2 cos128 maEe . 2 sin ) 2 1( 2 0 2 2 1 6 2 0 k k k k k kd t ma (5) From Equation (5) we know that k dm W is propor- tional to I . 2 0 2 2 1 617 2 sin )10396.21( k k k k k t I II k k k. )10396.21( 2 1 617 IIIII . . (6) In the now available calculations the energy-depen- dent factor I I I is taken to be an energy constant which is equal to the energy determined by the center of the first peak in the curve of factor I I versus k , all en- ergy variations come from the factor I I, and, therefore, the energy variation of k dm W comes only from the factor I I [1-11]. If we use the fs electromagnetic pulse technique, then 15 010 t second. Figure 1 gives the curve of II versus f, where k hf 15 102. From Figure 1 we see that (height of the first peak)/(height of second peak) = 0.06. The previous general points of view are that the second peak of energy nonconservation can be neglected because it is too small. That the center of the first peak is at 0 k means energy conservation, and the width of the first peak comes from energy uncer- tainty principle [1,2]. However, if we take 0 k , which is determined by the center of the first peak in Fi- gure 1, then 0 III , which means 0 k dm W i.e., the transition of boundary absorption of electron of hy- drogen atom is exactly prohibited. It is obvious that this prohibition does not fit the experiments, and is com- pletely wrong. Therefore, we have to consider the energy variation of the factor I I I . The curve of )( IIIIII versus f is shown in Figure 2. From Figure 2 we see that the transition of boundary absorption can happen because I I I I I does not always equal to zero. The curve in Fi- gure 2 does not have any connection with energy uncer- tainty principle (By the way, here we should mention f (10 15 Hz) 0 1 2 3 1.0 =0.5 0.0 Figure 1. Theoretical curve of II versus f (1015 Hz). If the energy variation of III is neglected, as usually be done in all quantum mechanics books, then II is proportional to frequency density of transition probability k dωm W. 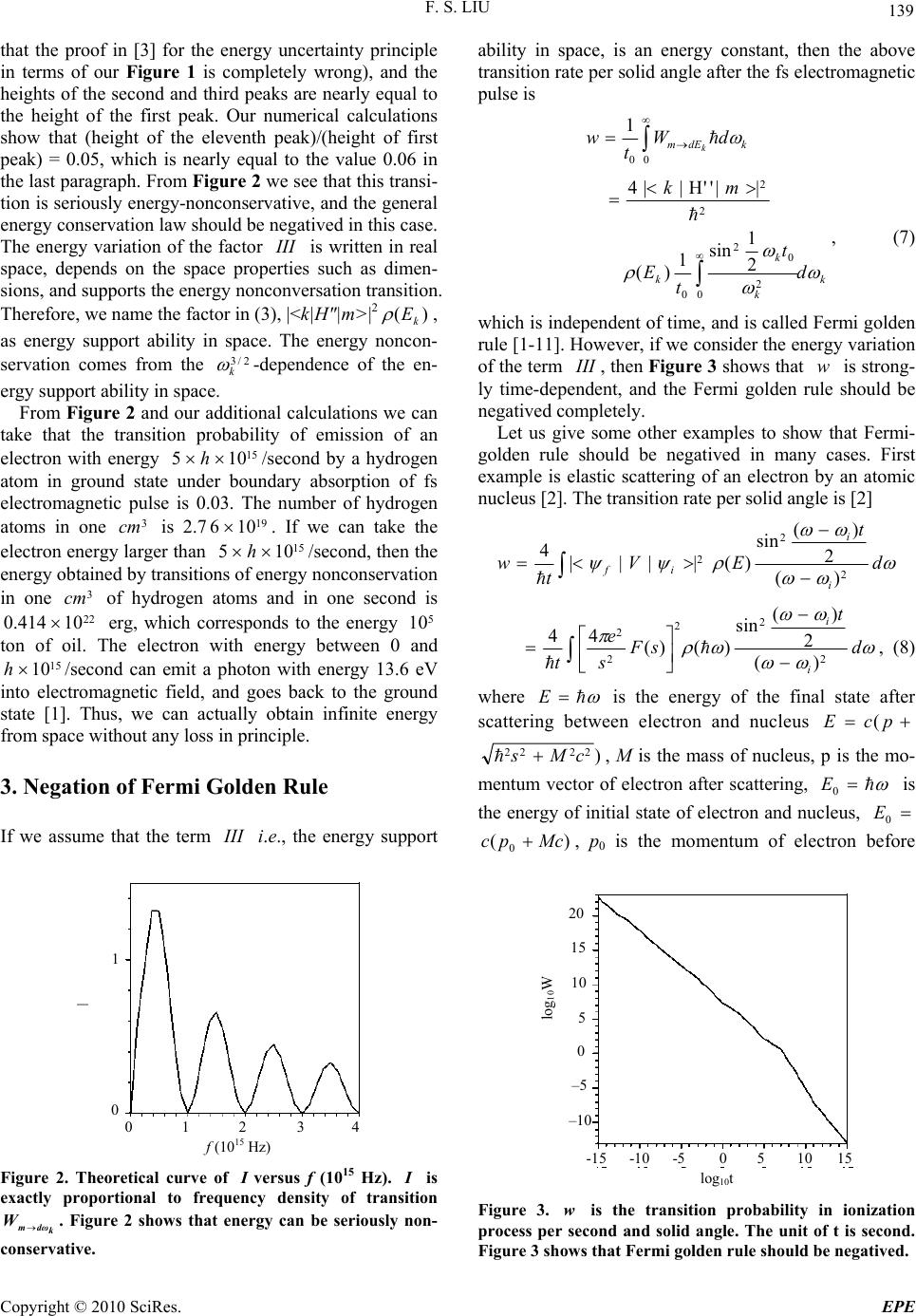 F. S. LIU Copyright © 2010 SciRes. EPE 139 that the proof in [3] for the energy uncertainty principle in terms of our Figure 1 is completely wrong), and the heights of the second and third peaks are nearly equal to the height of the first peak. Our numerical calculations show that (height of the eleventh peak)/(height of first peak) = 0.05, which is nearly equal to the value 0.06 in the last paragraph. From Figure 2 we see that this transi- tion is seriously energy-nonconservative, and the general energy conservation law should be negatived in this case. The energy variation of the factor I I I is written in real space, depends on the space properties such as dimen- sions, and supports the energy nonconversation transition. Therefore, we name the factor in (3), |<k|H"|m>|2)( k E , as energy support ability in space. The energy noncon- servation comes from the 2/3 k -dependence of the en- ergy support ability in space. From Figure 2 and our additional calculations we can take that the transition probability of emission of an electron with energy 15 105 h/second by a hydrogen atom in ground state under boundary absorption of fs electromagnetic pulse is 0.03. The number of hydrogen atoms in one 3 cm is 2.719 106 . If we can take the electron energy larger than 15 105 h/second, then the energy obtained by transitions of energy nonconservation in one 3 cm of hydrogen atoms and in one second is 22 10414.0 erg, which corresponds to the energy 5 10 ton of oil. The electron with energy between 0 and 15 10h/second can emit a photon with energy 13.6 eV into electromagnetic field, and goes back to the ground state [1]. Thus, we can actually obtain infinite energy from space without any loss in principle. 3. Negation of Fermi Golden Rule If we assume that the term I I I i.e., the energy support f ( 10 15 Hz ) 0 1 2 3 4 - 0 1 Figure 2. Theoretical curve of Iversus f (1015 Hz). I is exactly proportional to frequency density of transition k dωm W. Figure 2 shows that energy can be seriously non- conservative. ability in space, is an energy constant, then the above transition rate per solid angle after the fs electromagnetic pulse is 0 0 1 kdEmdW t wk k k k kd t t E mk 0 2 0 2 0 2 2 2 1 sin 1 )( ||''||4 , (7) which is independent of time, and is called Fermi golden rule [1-11]. However, if we consider the energy variation of the term I I I , then Figure 3 shows that w is strong- ly time-dependent, and the Fermi golden rule should be negatived completely. Let us give some other examples to show that Fermi- golden rule should be negatived in many cases. First example is elastic scattering of an electron by an atomic nucleus [2]. The transition rate per solid angle is [2] d t EV t w i i if 2 2 2 )( 2 )( sin )(|||| 4 d t sF s e ti i 2 2 2 2 2 )( 2 )( sin )()( 44 , (8) where E is the energy of the final state after scattering between electron and nucleus pcE ( ) 2222 cMs , M is the mass of nucleus, p is the mo- mentum vector of electron after scattering, 0 E is the energy of initial state of electron and nucleus, 0 E )( 0Mcpc , p0 is the momentum of electron before log 10 t -15 -10 -5 0 5 10 15 20 15 10 5 0 – 5 – 10 log 10 W Figure 3. w is the transition probability in ionization process per second and solid angle. The unit of t is second. Figure 3 shows that Fermi golden rule should be negatived. 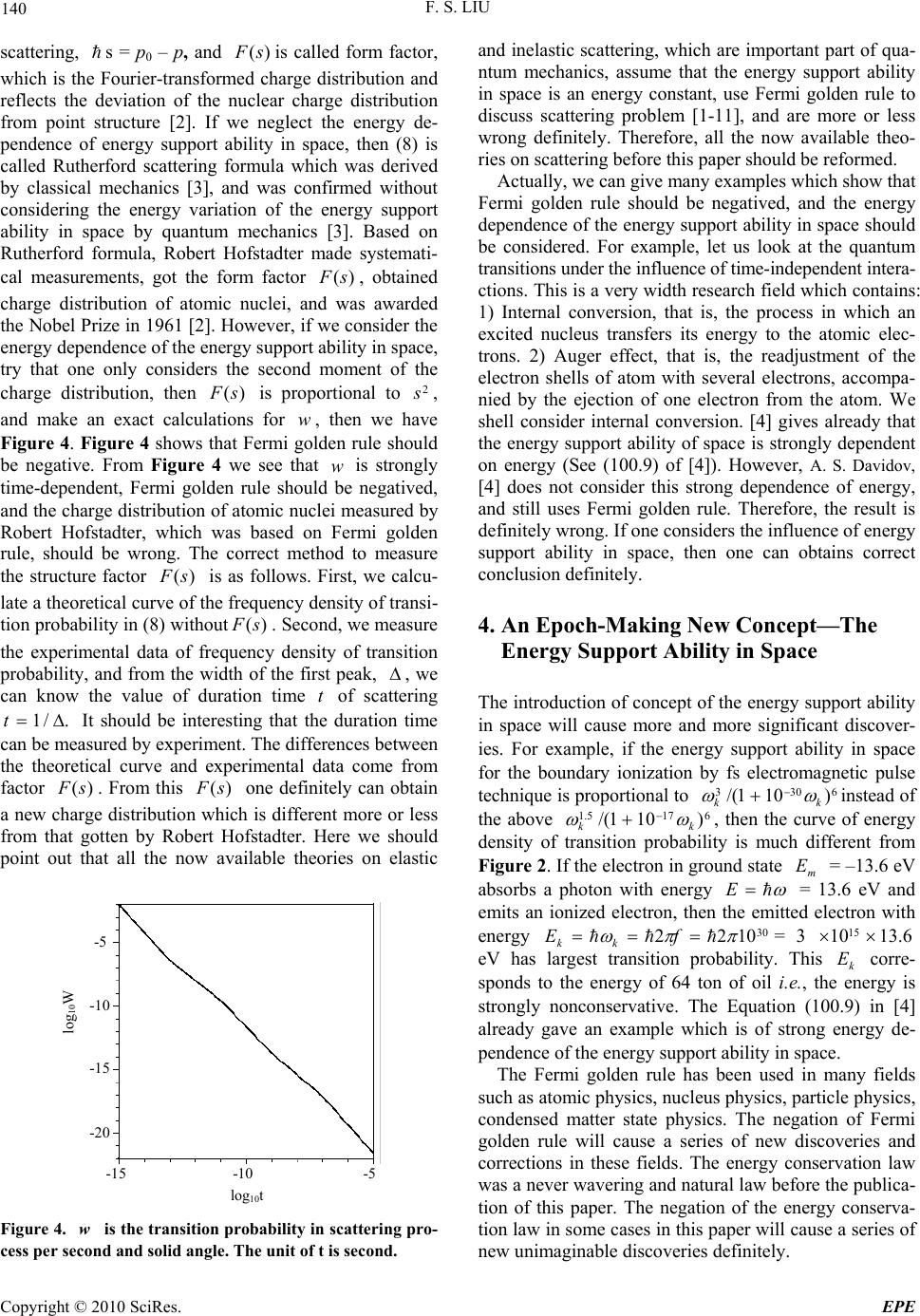 F. S. LIU Copyright © 2010 SciRes. EPE 140 scattering, s = p0 – p, and )(sF is called form factor, which is the Fourier-transformed charge distribution and reflects the deviation of the nuclear charge distribution from point structure [2]. If we neglect the energy de- pendence of energy support ability in space, then (8) is called Rutherford scattering formula which was derived by classical mechanics [3], and was confirmed without considering the energy variation of the energy support ability in space by quantum mechanics [3]. Based on Rutherford formula, Robert Hofstadter made systemati- cal measurements, got the form factor )(sF , obtained charge distribution of atomic nuclei, and was awarded the Nobel Prize in 1961 [2]. However, if we consider the energy dependence of the energy support ability in space, try that one only considers the second moment of the charge distribution, then )( sF is proportional to 2 s, and make an exact calculations for w, then we have Figure 4. Figure 4 shows that Fermi golden rule should be negative. From Figure 4 we see that w is strongly time-dependent, Fermi golden rule should be negatived, and the charge distribution of atomic nuclei measured by Robert Hofstadter, which was based on Fermi golden rule, should be wrong. The correct method to measure the structure factor )(sF is as follows. First, we calcu- late a theoretical curve of the frequency density of transi- tion probability in (8) without)(sF . Second, we measure the experimental data of frequency density of transition probability, and from the width of the first peak, , we can know the value of duration time t of scattering ./1t It should be interesting that the duration time can be measured by experiment. The differences between the theoretical curve and experimental data come from factor )( sF . From this )(sF one definitely can obtain a new charge distribution which is different more or less from that gotten by Robert Hofstadter. Here we should point out that all the now available theories on elastic log 10 t -15 -10 -5 -5 -10 log 10 W -15 -20 Figure 4. w is the transition probability in scattering pro- cess per second and solid angle. The unit of t is second. and inelastic scattering, which are important part of qua- ntum mechanics, assume that the energy support ability in space is an energy constant, use Fermi golden rule to discuss scattering problem [1-11], and are more or less wrong definitely. Therefore, all the now available theo- ries on scattering before this paper should be reformed. Actually, we can give many examples which show that Fermi golden rule should be negatived, and the energy dependence of the energy support ability in space should be considered. For example, let us look at the quantum transitions under the influence of time-independent intera- ctions. This is a very width research field which contains: 1) Internal conversion, that is, the process in which an excited nucleus transfers its energy to the atomic elec- trons. 2) Auger effect, that is, the readjustment of the electron shells of atom with several electrons, accompa- nied by the ejection of one electron from the atom. We shell consider internal conversion. [4] gives already that the energy support ability of space is strongly dependent on energy (See (100.9) of [4]). However, A. S. Davidov, [4] does not consider this strong dependence of energy, and still uses Fermi golden rule. Therefore, the result is definitely wrong. If one considers the influence of energy support ability in space, then one can obtains correct conclusion definitely. 4. An Epoch-Making New Concept—The Energy Support Ability in Space The introduction of concept of the energy support ability in space will cause more and more significant discover- ies. For example, if the energy support ability in space for the boundary ionization by fs electromagnetic pulse technique is proportional to 6303 )101/( kk instead of the above 6175.1 )101/( kk , then the curve of energy density of transition probability is much different from Figure 2. If the electron in ground state m E = –13.6 eV absorbs a photon with energy E = 13.6 eV and emits an ionized electron, then the emitted electron with energy 30 1022 f Ekk = 3 6.131015 eV has largest transition probability. This k E corre- sponds to the energy of 64 ton of oil i.e., the energy is strongly nonconservative. The Equation (100.9) in [4] already gave an example which is of strong energy de- pendence of the energy support ability in space. The Fermi golden rule has been used in many fields such as atomic physics, nucleus physics, particle physics, condensed matter state physics. The negation of Fermi golden rule will cause a series of new discoveries and corrections in these fields. The energy conservation law was a never wavering and natural law before the publica- tion of this paper. The negation of the energy conserva- tion law in some cases in this paper will cause a series of new unimaginable discoveries definitely.  F. S. LIU Copyright © 2010 SciRes. EPE 141 5. Discussion Although all results in Sections 2, 3 and 4 come just from exact calculations of transition probability, many readers still do not believe their correctness. Let us give some indirect experimental verifications for the correct- ness of considering the energy dependence of the energy support ability in space. First, let us consider the study on relaxation process which is an ancient project more than 100 years. The KWW empirical law is that the re- laxation function is KWW _ exp( t/) . 1 KWW is only for a few materials, and for 90% of materials 0 KWW < 1. [14-17] show that if we consider the energy dependence of the energy support ability in space, then 1 KWW . Second, [18-20] show that if we consider the energy dependence of the energy support ability in space, then cold fusion can occur, and the result of experimental observations for the cold fusion is true. Reference [3] and Section 3 of this paper point out that the Rutherford scattering formula, which was based on classical mechanics, and the Mott-Gorden scattering formula, which was based on quantum mechanics and neglecting the energy variation of the energy support ability in space, are the same. This fact tells us that the energy variation of the energy support ability in space includes quantum effect, and, therefore, it can not been neglected. If we neglect it, then classical and quantum mechanics give the same result. A simple direct experimental verification on the ne- cessity of introducing the concept of energy support abil- ity in space is to obtain the experimental data corre- sponding to Figure 2. 6. Conclusions From our exact derivations and numerical calculations in Sections 2, 3 and 4 we obtain the following conclusions. 1) It is absolutely necessary to consider the energy de- pendences of the transition matrix element and the den- sity of states in transition and scattering processes. However, all the now available theories on the transition and scattering processes do not consider these energy dependences, and, therefore, should be revised. 2) The general energy conservation law should be negatived in some cases. 3) It is possible to obtain infinite energy from space without any loss. 4) The Fermi golden rule should be negatived in some cases because that the ap- proximation of neglecting the energy dependence of the energy support ability in space is reasonable only in a few cases. 5) The transition process does not have any connection with energy uncertainty principle. 6) The concept on the energy support ability in space will be- come an important new concept. 7) Section 3 points out that the duration time of scattering between electron and nucleus can be measured by experiment. 8) The current standard model of cosmology, or Big Bang model, has been receiving wider and wider attention since the dis- covery of cosmic background radiation at 2.73 K. The observable facts upon which the standard model is based are, in fact, very few [10]. This paper shows that the en- ergy support ability in space is only determined by the structure of space, and, therefore, it can always supply energy without any loss i.e., the energy is infinite in cosmology. Because energy can become mass, the mass in the cosmology is also infinite. The cosmology being of infinite energy and mass can not collapse, should have infinite lifetime, and the Big Bang model can not be cor- rect. 9) The present theory to estimate the energy in cosmology is as follows. If all the energy in cosmology is 1, then the energy of galaxy is 4/100, the energy of dark mass is 23/100, and the energy of dark energy is 73/100. It is obvious that this estimation is based on the energy finiteness of cosmology. This paper concludes that the above estimation for the energy distribution in cosmology is wrong because the energy in cosmology is infinite. 10) G. Amelino-Camelia [21] pointed out that combing general relativity with quantum mechanics is the last hundle to be overcome in the “quantum revolu- tion”. One of the most exciting approaches to the unifi- cation of general relativity and quantum mechanics is the idea of a space-time that is itself quantized, for example, replacing the space-time continuum with a collection of isolated points. This paper shows that the energy support ability in space depends on the structure of space. Therefore, the energy support ability in space can be used to judge any proposed model of space structure. 11) B. R. Martin [13] pointed out that the observable quanti- ties in nuclear and particle physics are cross-sections and decay rates. However, we should note that the formulas to calculate the two quantities are used Fermi golden rule. This paper shows that Fermi golden rule should be nega- tived, especially, in the calculations of cross-sections. Therefore, many conclusions coming from the two quan- tities might be wrong. 7. References [1] L. I. Schiff, “Quantum Mechanics,” McGraw-Hill Book Company, New York, 1968. [2] W. Greiner, “Quantum Mechanics: An Introduction,” 3rd Edition, Springer-Verlag Belin Heidelberg, New York, 1994. [3] L. D. Landau and E. M. Lifshitz, “Quantum Mechanics: Non-Relativistic theory,” Pergamon Press, Oxford, 1958. [4] A. S. Davidov, “Quantum Mechanics,” 2nd Edition, Per- gamon Press, Oxford, 1976. [5] B. R. Desai, “Quantum Mechanics,” Cambridge Univer- sity, Cambridge, 2010. [6] E. R. Bittner, “Quantum Dynamics: Applications in Bio-  F. S. LIU Copyright © 2010 SciRes. EPE 142 logical and Materials Systems,” Taylor and Francis/CRC Press, New York, 2010. [7] R. L. Liboff, “Introductory Quantum Mechanics,” Addi- son-Wesley, New York, 2003. [8] K. T. Hecht, “Quantum Mechanics,” Springer-Verlag, New York, 2000. [9] A. I. M. Rae, “Quantum Mechanics,” Taylor and Francis, New York, 2008. [10] E. Elbaz, “Quantum: The Quantum Theory of Particles, Fields, and Cosmology,” Springer, New York, 1998. [11] J. J. Sakurai and S. F. Tuan, “Modern Quantum Mechani- cs,” Addison-Wesley, New York, 1994. [12] S. L. Kakani and S. Kakani, “Nuclear and Particle Phy- sics,” Anshan, Kent, 2008. [13] B. R. Martin, “Nuclear and Particle Physics,” 2nd Edition, John Wisley and Sons Ltd, West Eussex, 2009. [14] F. S. Liu and C. Wen, “Dynamics of Continuous-Time Random Walk, Fractional Time Dispersion, and Frac- tional Exponential Time Relaxation,” Physical Review B (Condensed Matter), Vol. 40, No. 10, 1989, pp. 7091- 7095. [15] F. S. Liu and W. F. Chen, “A New Universal Theory of Non-Exponential Relaxation,” Journal Physics D: App- lied Physics, Vol. 27, No. 4, 1994, pp. 845-847. [16] F. S. Liu, K. D. Peng and W. F. Chen, “Departure from Fermi Golden Rule,” International Journal of Theoretical Physics, Vol. 40, No. 11, 2001, pp. 2037-2043. [17] F. S. Liu and W. F. Chen, “Necessity of Exact Calcula- tion for Transition Probability,” Communications in Theoretical Physics, Beijing, Vol. 39, No. 2, 2003, pp. 209-211. [18] F. S. Liu and W. F. Chen, “Phonon-Induced Hopping Rate Enhancement in the Pd-D System,” Journal of Phy- sics: Condensed Matter, Vol. 15, No. 29, 2003, pp. 4995- 5000. [19] F. S. Liu, Y. M. Hou and W. F. Chen, “Theory of Fusion during Acoustic Cavitation in ODC63 Liquid,” Journal of Condensed Matter Nuclear Science, Vol. 1, No. 1, 2007, pp. 142-147. [20] F. S. Liu and W. F. Chen, “The Effect of Phonon-Induced Hopping Enhancement and Exact Theory of Cold Fu- sion,” Communications in Theoretical Physics. Vol. 23, No. 2, 1995, pp. 241-244. [21] G. Amelino-Camelia, “Quantums Theory’s Last Chal- lenge,” Nature (London), Vol. 408, No. 6813, 2000, pp. 661-664. |

