Circuits and Systems
Vol.07 No.04(2016), Article ID:66112,18 pages
10.4236/cs.2016.74038
State Space Modeling and Implementation of a New Transformer Based Multilevel Inverter Topology with Reduced Switch Count
R. Gandhi Raj1, S. Palani2, H. Habeebullah Sait1
1Department of Electrical and Electronics Engineering, Anna University, BIT Campus, Tiruchirappalli, India
2Department of Electronics and Communication Engineering, Sudharsan Engineering College, Pudukottai, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 March 2016; accepted 25 April 2016; published 28 April 2016
ABSTRACT
This paper presents a new transformer based multilevel inverter, with a novel pulse width modulation scheme to achieve seven-level inverter output voltage. The proposed inverter switching pattern consists of three fundamental frequency sinusoidal reference signals with an offset value, and one high frequency triangular carrier signal. This switching scheme has been implemented using an 8-bit Xilinx SPARTAN-3E field programmable gate array based controller. In addition, the state space model of the proposed inverter is developed. The significant features of the proposed topology are: reduction of the power switch count and the gate drive power supply unit, the provision of a galvanic isolation between load and sources by a centre tap transformer. An exhaustive comparison has been made of the existing multilevel inverter topologies and the proposed topology. The performances of the proposed topology with resistive, resistive-inductive loads are simulated in a MATLAB environment and validated experimentally on a laboratory prototype.
Keywords:
Centre Tap Transformer, Field Programmable Gate Array (FPGA), Multilevel Inverter (MLI), Pulse Width Modulation (PWM), State Space Model

1. Introduction
Recently, multilevel inverters have been receiving increasing attention, because of their many features: it has higher voltage operating capability, reduced rate of change of voltage (dv/dt), lower common mode voltages, reduced harmonic content, near sinusoidal voltage and current, smaller output filter. Multilevel inverters are considered as one of the industrial solutions for high dynamic performance and power quality demanding applications [1] [2] . The basic configurations of multilevel inverters are a Diode Clamped Multilevel Inverter (DCMLI), a Flying Capacitor Multilevel Inverter (FCMLI) and a Cascaded H-Bridge Multilevel Inverter (CHB- MLI). The above said topologies use a different mechanism for providing the stepped output voltage. The Diode clamped MLI, which suffers from voltage unbalancing problem in series connected capacitors, requires more number of clamping diodes and also creates the problem of circuit intricacy. The flying Capacitor multilevel inverter requires more number of large size capacitors, thereby making it bigger in size and costlier, and moreover, the regulation of voltage in each capacitor is complicated with a single input DC source. The Cascaded H-bridge inverter is more popular because of its modularity and controllability. If there is a fault in any one H-Bridge cell, the other unit can be operated without affecting the entire system. However, the main drawback of CHBMLI is that, it requires more number of isolated DC voltage sources for each module and requires more number of switches when the number of output voltage level increases [3] - [5] . In recent years, to overcome the aforementioned problems, several topologies have been presented [6] - [15] . These topologies have utilized less power electronic switches and gate driver circuits, however the number of switches still can be reduced. Recently, to increase the number of voltage levels, multilevel inverters with coupled inductors or transformer have been proposed [16] - [19] .
In [16] , a cascaded transformer type multilevel inverter topology has been presented. It uses a single isolated dc voltage source, eight power switches and two cascaded single phase transformer for producing nine level ac output voltages. The major disadvantage of the topology is that, it requires more number of switches, can generate only 3n level of output voltage and the turns ratio of the secondary winding of the transformer plays a role to generate n-level of the output voltage, consequently making the system bulky in size and expensive. A single source cascaded transformers reduced switch multilevel inverter (CTRSI) has been presented in [17] . It utilized eight power switches, three transformers with a single isolated dc voltage source, for making seven-level output voltage. This topology can not only generate 3n level of output voltage, but can generate any level of output voltage. But the major drawbacks of this topology are the requirement of more number of power switches and transformers on the output side, which will increase the volume of the system and cost. A transformer based symmetrical and asymmetrical cascaded multilevel inverter has been proposed in [18] . They utilize four bidirectional power switches, four unidirectional power switches and four transformers with a single input dc voltage source, for obtaining seven-level output voltage. The drawbacks of this topology are the requirement of bidirectional power switches and more number of transformers on the output side, which make the system realization and practical implementation difficult. The transformer-based single phase seven-level inverter topology is proposed in [19] , uses a single DC voltage source with six power switches to generate seven-level voltage. In this topology, both primary and secondary winding is directly connected to the input dc voltage source through power switches. The problem of this topology is, there is no galvanic isolation between input dc voltage source and ac load, which affects the reliability of the system. From the above discussion, it is concluded that, the main disadvantages of MLI are excessive number of power switches, more gate driver circuits resulting in increased cost, and complex control circuits, which limit their applications. Therefore, reducing the number of power switching devices is the main intent of the proposed work.
The present work focuses on transformer based new multilevel inverter topology, which is composed of three isolated DC voltage sources, five power switches and one single phase centre tap transformer to generate seven- level output voltage. The inverter structure uses a novel pulse width modulation (PWM) switching pattern to produce controlled output voltage. The proposed topology has salient inherent features such as a galvanic isolation between an input dc source and output load, which enhance the reliability of the inverter. This topology can be recommended for power conditioning devices and renewable energy power generation systems. A computer aided simulation and experimental results are used to justify the proposed topology and to show the validity of the presented inverter structure for real time applications.
This paper is organized as follows: Section 2 presents the structure and details of the mode of operation of the proposed inverter, with mathematical formulations. Section 3 describes the novel switching scheme for the proposed inverter. Section 4 presents the state space model of the proposed topology. Section 5 discusses the simulation and experimental results of the proposed inverter. Section 6 presents the comparison of the proposed topology with the classical and recent topologies. Finally, Section 7 concludes the paper based on the simulation and experimental results.
2. Proposed Inverter Topology
The proposed single-phase seven-level inverter comprises three equal value of dc sources, five unidirectional power switches, and a centre tap transformer as shown in Figure 1.
For symmetrical mode of operation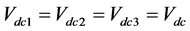 . The proposed inverter can produce seven output voltage levels of Vdc, 2Vdc, 3Vdc, 0, −Vdc, −2Vdc, −3Vdc from the constant input dc voltage sources. The switches S1, S2 and S3 determine the level of the output voltage, and the switches S4 and S5 decide the polarity of the output voltage. The number of output voltage levels (NSTEP), the required number of IGBTs (NIGBT), for the proposed topology is computed from the following equations.
. The proposed inverter can produce seven output voltage levels of Vdc, 2Vdc, 3Vdc, 0, −Vdc, −2Vdc, −3Vdc from the constant input dc voltage sources. The switches S1, S2 and S3 determine the level of the output voltage, and the switches S4 and S5 decide the polarity of the output voltage. The number of output voltage levels (NSTEP), the required number of IGBTs (NIGBT), for the proposed topology is computed from the following equations.
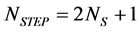 (1)
(1)
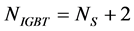 (2)
(2)
where, Ns is the number of sources. Here, the number of sources decides the output voltage level.
Figure 2 indicates the typical seven-level inverter output voltage waveform for understanding the operation of the proposed inverter. The switching state of the proposed inverter is such that at any instant of time, two power switches are in the conducting state and the other devices are in the non- conducting state. The switches S4 and S5 are operating in the fundamental frequency, and the other switches are operating at 1 kHz. This indicates that the proposed inverter has a reduction in conduction and switching losses, which results in an increase in the effi- ciency of the proposed inverter. To understand the operation of the proposed inverter, the following modes are
Figure 1. Circuit diagram of the proposed transformer based seven-level inverter topology.
Figure 2. Typical stepped seven-level inverter output voltage waveform.
explained using seven switching states, as shown in Figures 3(a)-(g). Here, the red line represents the conduction path of the current flow. The required seven levels of output voltage are generated as follows.




Figure 3. Switching combination required to generate seven-level output voltage (a)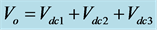 ; (b)
; (b)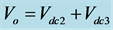 ; (c)
; (c)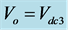 ; (d)
; (d)



・ Mode 1: Output Voltage of
Figure 3(a) shows the switching state resulting in an output voltage of
・ Mode 2: Output Voltage of
Figure 3(b) depicts the switching state delivering an output voltage of
・ Mode 3: Output Voltage of (+Vdc3)
Figure 3(c) illustrates the switching state generating an output voltage of Vdc3. When switches S1 and S4 are kept ON, source (Vdc3) supplies energy to the load. The load current flows from terminal a to b, and the voltage across the load terminals are +Vdc.
・ Mode 4: Zero Output Voltage (0)
Figure 3(d) illustrates the switching state generating an output voltage of zero. This level is produced by keeping switch S5 and body diode of S4 is ON and all other controlled switches OFF. The primary winding of the centre tap transformer is short circuited, and the voltage applied to the load is zero.
・ Mode 5: Output Voltage of (−Vdc3)
Figure 3(e) shows the switching state generating an output voltage of −Vdc3. When switches S1 and S5 are kept ON, source (Vdc3) supplies energy to the load. The load current flows from terminal b to a and the voltage across the load are −Vdc.
・ Mode 6: Output Voltage of
Figure 3(f) depicts the switching state generating an output voltage of

・ Mode 7: Output Voltage of
Figure 3(g) indicates the switching state generating an output voltage of

Mathematical Formulation
The mathematical formulation for the proposed inverter is as follows: Let Bj be a switching function corresponding to switch Sj (j = 1 to n) defined as [7] ,

The inverter output voltage 


where 
The following equations give the instantaneous inverter output voltage and current of the proposed inverter,


3. Novel Switching Scheme for the Proposed Inverter
The proposed switching scheme utilizes fundamental frequency (50 Hz) of three unidirectional sinusoidal waves as reference signal with offset voltage, and one triangular carrier signal of 1 kHz. The reference signals have the same amplitude and frequency and are in phase with an offset value that is equivalent to the amplitude of the carrier signal. By comparing each reference signal with a carrier signal, a control signal is produced for switching a device in the proposed MLI.
Figure 4 depicts the novel modulation scheme for the proposed inverter. The switching pattern proposed in [15] , requires more number of logic gates because, the pulse pattern of the positive cycle and negative cycle is different, so it will create complexity in the control circuit. However, the proposed topology uses a symmetrical pulse pattern for both positive and negative cycle in each controlled switch. The switching signal S4 is derived by comparing reference signal (Vref1) with zero and S5 is obtained from inverting signal of S4. The pulse pattern for S1 is arrived by comparing Vref1, Vref2 with Vcarrier and the pulse pattern for S2 is derived by comparing Vref2, Vref3 with Vcarrier. Similarly, the pulse pattern for S3 is arrived by comparing Vref3 with Vcarrier. Here, it is seen that, the level modulated switches S1, S2, S3 operate at switching frequency of 1 KHz (carrier frequency) and polarity modulated switches S4 and S5 operate at fundamental frequency (reference frequency) of 50Hz. The switching interval for the seven-level inverter is represented by seven modes as follows:
Mode 1:
Mode 2:
Mode 3:
Mode 4:
Mode 5:
Mode 6:
Mode 7:
According to the amplitude of the reference signal, the operational interval of each mode varies within a definite period. The angles 

Figure 4. Simulated novel switching pattern for the proposed inverter.
Table 1. Switching State for Proposed MLI.
about the output voltage according to the switching state of the ON/OFF condition.
The amplitude modulation (Ma) of the proposed seven-level inverter can be calculated as follows,

where Vref is the amplitude of the sinusoidal signal, and Vcarrier is the amplitude of the triangular signal. The level of the inverter output voltage changes with the modulation index.
(9)
The Equation (9) gives the information about the level of the inverter based on the value of the modulation index (Ma).
4. State Space Model of the Proposed Multilevel Inverter
A state space model of a system consists of state equation and output equation. The state equation of a system is a function of state variables and inputs as defined by Equation (10). The state equation is a set of variables which describes the system at any instant of time. The output equation of the system is a function of state variables and outputs defined by Equation (11). The state space representation provides a convenient way to model and analyze the many input many output (MIMO) systems. The state model of the system defined as [20] [21]


The output voltage of the inverter circuit is the secondary voltage across the load. To facilitate the analysis of the circuit, the secondary impedance and the load impedance are referred to the primary winding as shown in Figure 5 with a load impedance of


Figure 5. Proposed inverter with physical transformer referred to primary.

where, 


Control signal,

The state variable of the circuit are the source current is, the magnetizing current im and the output current io. Equations (12), (13), (14) are rewritten as,



Substitute Equation (20) into Equations (19) and (21)


From Equations (20), (22) and (23) the state space model of the inverter circuit is formulated as,

Equation (24) gives the state equation of the proposed inverter. Division of the Equation (24) by the fundamental frequency, result in normalized state equation of the system.

where 


5. Investigation of the Simulation and Experimental Results
The simulation and experimental hardware results are presented to verify the validation of the proposed transformer based multilevel inverter. A computer-aided simulation has been carried out to validate the performance of proposed seven-level inverter with R and R-L Load using MATLAB/Simulink environment. Figure 6 shows the simulink model of the proposed 7-level inverter. The simulink model consists of IGBTs, and centre tap transformer with R-L load. The switching signal for the inverter is generated by comparing the single triangular signal with three unidirectional offset sinusoidal signals, which is presented in control signal generation block. In this study, the proposed inverter produces a maximum voltage of 60 V, 50-Hz output waveform from three equal DC input voltage of 20 V. Here, both R and R-L loads with the values of 150 Ω and 240 mH are considered for simulation and experimental investigation.
To validate the proposed topology, a prototype of the single phase seven-level inverter is developed in the laboratory. The photograph of the setup is shown in Figure 7. The IGBTs utilized in the prototype is H15R1203 with internal anti parallel diodes. The PWM controller scheme is implemented through Xilinx Spartan-3E XC3S100E FPGA. The gating signal from the controller is fed to the IGBTs through isolated gate driver (IC-
Figure 6. Simulink model of the proposed transformer based seven-level inverter.
Figure 7. Photograph of the Experimental setup.
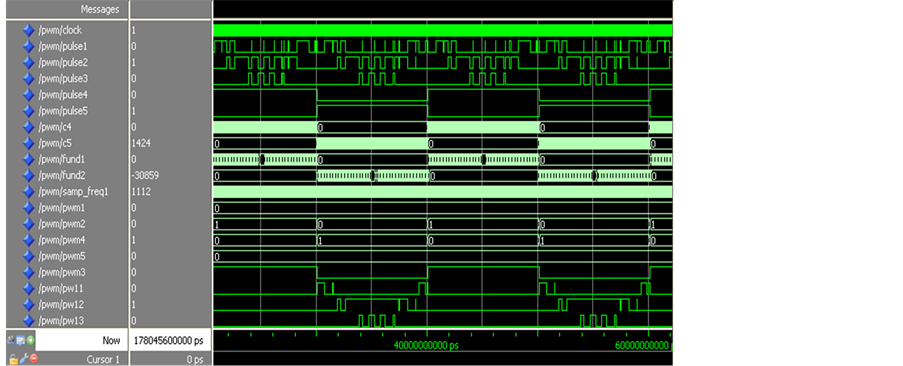
TLP250) circuits. The generation of PWM waveform for the proposed inverter through Xilinx is shown in Figure 8. The switching signals generated by the FPGA controller is used for trigger the IGBTs of the proposed multilevel inverter.
Figure 9 and Figure 10 illustrate the simulated and experimental gating signal for the proposed multilevel inverter. From these figures it can be observed that the level modulated switches (S1, S2, S3) are operated at a high frequency and polarity changed switches (S4, S5) are operated at a fundamental frequency. Figure 11 and Figure 12 show the simulation and experimental results of the voltage stress across each switching devices. It can be concluded that, the voltage across each switch varies depending on the position of the switches. The PIV value will decide the voltage blocking capability of switch utilized in the inverter circuits. The simulated and experimental output voltage and current waveform for R and R-L load obtained at the inverter terminal is shown in Figure 13, Figure 14 and Figure 15, Figure 16 respectively. The load voltage and current waveforms obtained experimentally in accord with respective simulation results. Hence, this topology along with the proposed control algorithm can be a good choice for inverter circuits. The experimental results are used to justify the simulation results and theoretical analysis of the proposed multilevel inverter. Figure 17 shows the simulated voltage harmonic spectrum of the proposed inverter with R-L load. The total harmonic distortion of the seven- level PWM output voltage is 18.27%. Figure 18 shows the experimental harmonic content of the proposed inverter with R-L load. From experimental, the total harmonic distortion of the seven-level PWM output voltage is 20.17%.
6. Comparative Study
To make clear the understanding of the evolution of the transformer based multilevel inverter structures are presented in Figure 19. The main motivation of this work is development of transformer based multilevel inverter with reduced number of components. As shown in Figure 20(a), the proposed topology requires fewer numbers of power switches than other topologies. For example, for a seven-level inverter, the presented inverter utilizes 5 power switches. However, other structures utilized more number of power switches than proposed topology. Figure 20(b) shows the comparison of the gate drivers with other structures. For example, for a seven-level inverter, the presented inverter utilizes 5 gate drivers. However, in the cascaded H-bridge multilevel inverter 12 gate drivers are required. Reduction of the gate drivers reduces the overall implementation cost, circuit complexity and increases the system reliability.
Another decisive factor to assess the performance of the multilevel inverters is the number of on-state switches. Figure 20(c) depicts the comparison of the numbers of on-state switches with proposed topology and topology presented in [17] - [19] , CHBMLI. In proposed topology, to attain any level of output voltage only 2 power switches are ON condition so that conduction loss is less which increases its efficiency. Whereas the other topologies use more number of on-state switches to attain same level of output voltage. Moreover, the proposed topology requires only one centre tap transformer to attain any level of output voltage as compared to other topologies which is shown in Figure 20(d). The summarized characteristics of the proposed inverter and the
Figure 8. Generation of PWM waveform for the proposed inverter using Xilinx.
Figure 9. Simulated pulse pattern from a novel switching scheme for the proposed inverter.

Figure 10. Experimental Pulse pattern from novel switching scheme for Proposed Inverter (a) Pulse for Switch S1, S2 and S3; (b) Pulse for Switch S4 and S5. (x axis: 2.22 ms/div, y axis: 5 V/div).
Figure 11. Simulation of voltage stress across each switching devices.





Figure 12. Experimental result of voltage stress across each switching devices (a) Voltage stress across switch S1; (b) Voltage stress across switch S2; (c) Voltage stress across switch S3; (d) Voltage stress across S4; (e) Voltage stress across S5. (x axis:10 ms/div, y axis: 2 V/div by 1:10 probe).
Figure 13. Simulated inverter output voltage and current waveform for R load.
Figure 14. Experimental Inverter Output Voltage and Current waveform for R load. (x axis: 5 ms/div, y axis: 30 V/div and 0.5 A/div).
structure presented in [17] - [19] , CHBMLI for m-level are given in Table 2. Moreover, to elucidate the comparison, the number of components required for seven-level output voltage is given in Table 3. It is concluded that, the component comparison of the proposed topology and the other recent topologies, indicates the superiority of the proposed inverter.
7. Conclusion
In this paper, a prototype model of transformer based seven-level inverter has been implemented with a novel
Figure 15. Simulated inverter output voltage and current for R-L load.
Figure 16. Experimental inverter output voltage and current for R-L load. (x axis: 3.33 ms/div, y axis: 30 V/div and 0.5 A/div).
PWM switching technique using FPGA controller. The state space model of the proposed inverter has been developed. The proposed multilevel inverter utilizes five power switches and one centre tap transformer to generate seven-level output voltage. The working nature of the proposed topology, mathematical formulation and a novel PWM technique have been analyzed in detail. This work has been compared with the classical and recent MLIs. Based on the comparative study, it is confirmed that the proposed MLI utilized the minimum number of switching devices with gate drive circuits, and the on-state switches through the current path are also reduced. In
Figure 17. Simulated voltage harmonic spectrum of the proposed inverter with R-L load (without filter).
Figure 18. Experimental harmonic content of the proposed inverter with R-L load (without filter).
Table 2. Comparison of proposed inverter with other inverters.




Figure 19. Circuit configuration of the different multilevel inverter topology. (a) Conventional CHBMLI; (b) Proposed Topology in [16] ; (c) Proposed Topology in [17] ; (d) Proposed Topology in [18] ; (e) Proposed Topology in [19] .


Figure 20. Comparison of the proposed topology with topology presented in [17] - [19] and conventional CHBMLI. (a) Number of Power Switches; (b) Number of Gate Drives; (c) Number of on-state switches; (d) Number of Transformers.
Table 3. Comparison of proposed inverter with other inverter for 7-level.
order to validate the operation and performance of the proposed inverter, the MATLAB simulation and the experimental prototype model are developed and tested with unity and a lagging power factor loads.
Cite this paper
R. Gandhi Raj,S. Palani,H. Habeebullah Sait, (2016) State Space Modeling and Implementation of a New Transformer Based Multilevel Inverter Topology with Reduced Switch Count. Circuits and Systems,07,446-463. doi: 10.4236/cs.2016.74038
References
- 1. Lai, J.S. and Peng, F.Z. (1996) Multilevel Converters—A New Breed of Power Converters. IEEE Transactions on Industry Applications, 32, 509-517.
http://dx.doi.org/10.1109/28.502161 - 2. Rodriguez, J., Lai, J.S. and Peng, F.Z. (2002) Multilevel Inverters: A Survey of Topologies, Controls, Applications. IEEE Transactions on Industrial Electronics, 49, 724-738.
http://dx.doi.org/10.1109/TIE.2002.801052 - 3. Rodriguez, J., Franquelo, L.G., Kouro, S., Leon, J.I., Portillo, R.C., Prats, M.A.M. and Perez, M.A. (2009) Multilevel Converters: An Enabling Technology for High Power Applications. Proceedings of the IEEE, 97, 1786-1817.
http://dx.doi.org/10.1109/JPROC.2009.2030235 - 4. Malinowski, M., Gopakumar, K., Rodriguez, J. and Perez, M.A. (2010) A Survey on Cascaded Multilevel Inverters. IEEE Transactions on Industrial Electronics, 57, 2197-2206.
http://dx.doi.org/10.1109/TIE.2009.2030767 - 5. Kouro, S., Malinowski, M., Gopakumar, K., Pou, J., Franquelo, L., Wu, B., Rodriguez, J., Perez, M.A. and Leon, J. (2010) Recent Advances and Industrial Applications of Multilevel Converters. IEEE Transactions on Industrial Electronics, 57, 2553-2580.
http://dx.doi.org/10.1109/TIE.2010.2049719 - 6. Oskuee, M.R.J., Salary, E. and Ravadanegh, S.N. (2015) Creative Design of Symmetric Multilevel Converter to Enhance the Circuit’s Performance. IET Power Electronics, 8, 96-102. http://dx.doi.org/10.1049/iet-pel.2013.0752
- 7. Gupta, K.K. and Jain, S. (2014) A Novel Multilevel Inverter Based on Switched DC Sources. IEEE Transactions on Industrial Electronics, 61, 3269-3278.
http://dx.doi.org/10.1109/TIE.2013.2282606 - 8. Najafi, E. and Yatim, A.H.M. (2012) Design and Implementation of a New Multilevel Inverter Topology. IEEE Transactions on Industrial Electronics, 59, 4148-4154.
http://dx.doi.org/10.1109/TIE.2011.2176691 - 9. Ajami, A., Oskuee, M.R.J., Mokhberdoran, A. and Van den Bossche, A. (2014) Developed Cascaded Multilevel Inverter Topology to Minimize the Number of Circuit Devices and Voltage Stresses of Switches. IET Power Electronics, 7, 459-466.
http://dx.doi.org/10.1049/iet-pel.2013.0080 - 10. Alishah, R.S., Nazarpour, D., Hosseini, S.H. and Sabahi, M. (2014) Novel Topologies for Symmetric, Asymmetric and Cascade Switched-Diode Multilevel Converter with Minimum Number of Power Electronic Components. IEEE Trans- actions on Industrial Electronics, 61, 5300-5310.
http://dx.doi.org/10.1109/TIE.2013.2297300 - 11. Mokhberdoran, A. and Ajami, A. (2014) Symmetric and Asymmetric Design and Implementation of New Cascaded Multilevel Inverter Topology. IEEE Transactions on Power Electronics, 29, 6712-6724.
http://dx.doi.org/10.1109/TPEL.2014.2302873 - 12. Babaei, E., Alilu, S. and Laali, S. (2014) A New General Topology for Cascaded Multilevel Inverters With Reduced Number of Components Based on Developed H-Bridge. IEEE Transactions on Industrial Electronics, 61, 3932-3939.
http://dx.doi.org/10.1109/TIE.2013.2286561 - 13. Kangarlu, M.F. and Babaei, E. (2013) A Generalized Cascaded Multilevel Inverter Using Series Connection of Submultilevel Inverters. IEEE Transactions on Power Electronics, 28, 625-636.
http://dx.doi.org/10.1109/TPEL.2012.2203339 - 14. Hinago, Y. and Koizumi, H. (2012) A Switched-Capacitor Inverter Using Series/Parallel Conversion with Inductive load. IEEE Transactions on Industrial Electronics, 59, 878-887.
http://dx.doi.org/10.1109/TIE.2011.2158768 - 15. Rahim, N.A., Chaniago, K. and Selvaraj, J. (2011) Single-Phase Seven-Level Grid-Connected Inverter for Photovoltaic System. IEEE Transactions on Industrial Electronics, 58, 2435-2443.
http://dx.doi.org/10.1109/TIE.2010.2064278 - 16. Park, S.J., Kang, F.S., Cho, S.E., Moon, C.J. and Nam, H.K. (2005) A Novel Switching Strategy for Improving Modularity and Manufacturability of Cascaded-Transformer-Based Multilevel Inverters. Electric Power Systems Research, 74, 409-416.
http://dx.doi.org/10.1016/j.epsr.2005.01.005 - 17. Banaei, M.R., Khounjahan, H. and Salary, E. (2012) Single-Source Cascaded Transformers Multilevel Inverter with Reduced Number of Switches. IET Power Electronics, 5, 1748-1753.
http://dx.doi.org/10.1049/iet-pel.2011.0431 - 18. Farakhor, A., Ahrabi, R.R., Ardi, H. and Ravadanegh, S.N. (2015) Symmetric and Asymmetric Transformer Based Cascaded Multilevel Inverter with Minimum Number of Components. IET Power Electronics, 8, 1052-1060.
http://dx.doi.org/10.1049/iet-pel.2014.0378 - 19. Gandomi, A.A., Saeidabadi, S., Hosseini, S.H. and Babaei, E. (2015) Transformer-Based Inverter with Reduced Number of Switches for Renewable Energy Applications. IET Power Electronics, 8, 1875-1884.
http://dx.doi.org/10.1049/iet-pel.2014.0768 - 20. Ogata, K. (1997) Modern Control Engineering. 3rd Edition, Prentice Hall, Upper Saddle River.
- 21. Shaffer, R (2007) Fundamentals of Power Electronics with MATLAB. Charles River Media, Boston.