Journal of Modern Physics
Vol.06 No.11(2015), Article ID:60001,5 pages
10.4236/jmp.2015.611171
Some Elucidations of the Theory on Revised Quantum Electrodynamics
Bo Lehnert
Alfvén Laboratory, Royal Institute of Technology, Stockholm, Sweden
Email: bo.lehnert@ee.kth.se
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 July 2015; accepted 25 September 2015; published 28 September 2015
ABSTRACT
A theory elaborated by the author on revised quantum electrodynamics (RQED) is elucidated in a condensed form on special important points. The latter concerns the basic electromagnetic field equations in a vacuum state, the connection of this state with the Zero Point Energy (ZPE), the procedure of quantization, steady states of particle models, the concept of the individual photon, and examples on experimental support of the theory.
Keywords:
Quantum Electrodynamics, Zero Point Energy, Standard Model and Beyond

1. Introduction
A revised quantum electrodynamic theory (RQED) on the vacuum state has earlier been elaborated by the author, as described in a monograph [1] and in a number of associated publications. The present paper has the purpose of being complementary to this work, and to elucidate it in a condensed form on special important points being characteristic of and only available by RQED.
2. Points of Consideration
2.1. The Conventional Electromagnetic Field Equations
The conventional electromagnetic field equations have been used as a guideline and basis for proper inter- pretation, also of a quantum electrodynamical approach as stated by Schiff [2] among others. There are then strong restrictions imposed through the symmetry of the electric and magnetic field strengths E and B due to a vanishing electric field divergence divE, in the Standard Model of a vacuum state of empty space. These restrictions are hardly removed by an added quantization process, as also being supported in the following Section 2.4 of this paper. Thereby the corresponding solutions lead to models of particles and wave packets which have no integrated rest mass, electric charge, or angular momentum (spin) [1] . Even in cases where there are local contributions to a spin, its total integrated value still vanishes, such as in a model of the individual photon. These statements are also in accordance with that of Quigg [3] which implies that the symmetry of the conventional field equations does not permit masses for leptons and quarks.
2.2. The Zero Point Energy
The vacuum is however not a state of empty space. The solutions of the harmonic oscillator do not only lead to the Planck electromagnetic wave energy, but also to a lowest nonzero energy of one-half quantum per state, i.e. the Zero Point Energy (ZPE). The vacuum state therefore includes fluctuations part of which also carry electric charges, as pointed out by Abbott [4] . An example of these fluctuations has been given by Casimir [5] who predicted that two metal plates will attract each other when being sufficiently close together. This Casimir force was first confirmed experimentally by Lamoreaux [6] . It reveals the existence of a real macroscopic pressure and energy density originating from the photon-like fluctuations of the ZPE.
The low-frequency part of the ZPE fluctuations has thus to be accepted as an experimental fact, but there exists a problem with their high-frequency part. As demonstrated by Terletskii [7] , Milonni [8] , and Loudon [9] among others, conventional theory results in a spectrum having infinite total (integrated) energy density. This is an unacceptable result, both from the physical point of view and due to the fact that the underlying analysis is underdetermined, i.e. in not having defined a total energy of the system, and in treating the infinite number of included states with the same statistical probability, even being equal to the unacceptable value of unity. Consequently, several investigators such as Riess and Turner [10] and Heitler [11] have thrown doubts upon this approach.
To overcome these difficulties, the author [12] - [14] has proposed the ensemble of ZPE modes to be subject to a separate treatment, also being applicable at the temperature T = 0. Such a treatment has to be self-consistent, in having a given and finite total energy density, and being conducted in the standard way of an ensemble of ZPE photons of frequency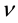 , populating the available states in statistical equilibrium with a probability not being equal to unity but to a Boltzmann factor
, populating the available states in statistical equilibrium with a probability not being equal to unity but to a Boltzmann factor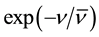 . Here
. Here 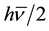 is the average and finite member energy of the ensemble. This leads to a physically acceptable and finite total pressure of the ZPE “photons”.
is the average and finite member energy of the ensemble. This leads to a physically acceptable and finite total pressure of the ZPE “photons”.
2.3. The Extended Electromagnetic Field Equations
The restrictions and shortcomings of the conventional field equations governing the vacuum state can be eliminated by including the ZPE effects into the theoretical foundation, thereby breaking the symmetry between E and B, and introducing an extra source term. To preserve the Lorentz and gauge invariance at the same time, this is done by including a four-current 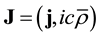 in the vacuum, with j as the corresponding three-space current density and
in the vacuum, with j as the corresponding three-space current density and 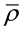 as the related electric charge density. This form of J is reconcilable with the corres- ponding standard form of Maxwell's equations with sources due to a current density j and a charge density
as the related electric charge density. This form of J is reconcilable with the corres- ponding standard form of Maxwell's equations with sources due to a current density j and a charge density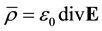 .
.
Since J has to vanish when there is no charge density, the final form of the four-current density becomes [1]
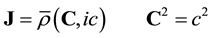 (1)
(1)
where c is a velocity vector having a modulus equal to the velocity constant c of light. In three-space the extended electromagnetic field equations of the vacuum state then become
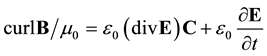 (2)
(2)
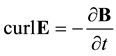 (3)
(3)
 (4)
(4)
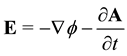 (5)
(5)
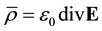 (6)
(6)
where 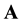 and
and 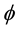 are the magnetic and electrostatic potentials. Here the first term of the right-hand side of Equation (2) and Equation (6) represent the new features of RQED. They introduce fundamental changes in the resulting analysis. These added effects disappear with the electric charge density, in what case we are back to the restricted and symmetric theory of Maxwell’s equations for an empty vacuum state.
are the magnetic and electrostatic potentials. Here the first term of the right-hand side of Equation (2) and Equation (6) represent the new features of RQED. They introduce fundamental changes in the resulting analysis. These added effects disappear with the electric charge density, in what case we are back to the restricted and symmetric theory of Maxwell’s equations for an empty vacuum state.
The nonzero electric field divergence of Equation (6) acts here somewhat like a “hidden” variable, removing the condition . This enhances the available degrees of freedom, thus making it possible to impose necessary quantum conditions of a self-consistent analysis. It may also be added that the hypothesis of a nonzero electric field divergence becomes conceptually acceptable even without the present ZPE interpretation. It has then to be observed that the total average electric charge of the universe appears to be zero.
. This enhances the available degrees of freedom, thus making it possible to impose necessary quantum conditions of a self-consistent analysis. It may also be added that the hypothesis of a nonzero electric field divergence becomes conceptually acceptable even without the present ZPE interpretation. It has then to be observed that the total average electric charge of the universe appears to be zero.
The solutions which come out of Equations (1)-(6) for models of particles and waves include nonzero integrated rest masses, net electric charges, and spin. There are thus configurations with nonzero local electric charge density which after spatial integration result both in nonzero and zero net electric charge, at the same time as both the local and integrated energy densities and corresponding masses become nonzero and finite.
2.4. Quantization
To convert the present approach into a quantized electrodynamic theory, the quantum conditions could be included into the deductions already from the outset. Here we shall instead make a short-cut and simplification, by first determining the general solutions of the basic field equations, and then imposing relevant quantum conditions. This is at least justified by the fact that a quantization of the general electrodynamic field equations merely results into the same equations in which the potentials and currents are replaced by their expectation values as shown by Heitler [11] . Such a way in handling the quantization should therefore not be too far from the truth, e.g. by using the most probable trajectories and states in a first approximation. The final results of the theory are then obtained after imposing a number of quantum conditions, such as those concerning energy, magnetic moment, and spin.
Here we finally notice that the conventional symmetric field equations for an empty vacuum space lead to imposed restrictions which therefore cannot be removed by quantization.
2.5. Steady States
A characteristic feature of RQED, not being available from conventional theory on the vacuum, is the steady states obtained from Equations (1)-(6) in the case of no explicit time dependence. This leads to models for particles being at rest. In the case of spatially limited axisymmetric configurations, spherical coordinates are then introduced, and the magnetic and electrostatic potentials as well as the charge density can all be derived from a generating function [1] . When the latter becomes separable into the product of a radial and polar part, particle-like configurations with net electric charge arise from a divergent radial part and a polar part with top- bottom symmetry. In the remaining cases the configurations have no integrated net electric charge.
2.5.1. Particle Configurations with Net Electric Charge
For a divergent radial part models can thus be elaborated in a spherical frame of coordinates 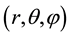 of an axisymmetric state of the electron, muon, and tauon [1] which all have been observed to have an electric charge equal to the elementary value
of an axisymmetric state of the electron, muon, and tauon [1] which all have been observed to have an electric charge equal to the elementary value 

where

with




where 
2.5.2. Particle Configurations with Vanishing Net Electric Charge
For a convergent radial part models can be elaborated for neutral particles, i.e. those with vanishing net integrated charge. This case does not require a revised renormalization procedure, and it is associated with a finite and defined characteristic radial dimension.
One example is given by the Z boson considered by the author [15] [16] . Here a mass of 91 GeV yields a characteristic radius in the range of 


The particle discovered at CERN [17] [18] is unstable, has vanishing electric charge and spin, and a rest mass of 125 GeV, not being specified by the theory of Higgs [19] . It is generally believed to be a confirmation of the boson proposed by Higgs. Thereby Quigg [3] has pointed out that the Higgs is perhaps not a truly fundamental particle, but is built out of as yet unobserved constituents to form a composite particle. According to the author [15] [16] such a particle can be formed by superimposing two Z boson solutions with opposite spin directions, thus having no intrinsic magnetic field and being purely electrostatic and highly unstable. With the observed masses, 91 and 125 GeV, of the Z boson and the detected particle at CERN, the characteristic radius of the composite particle should be in the range of 

At this stage it may be argued that this composite particle solution is not the particle observed at CERN, and that the latter also has been considered in terms of interactions with the quarks of other elementary particles. This leads to two points of discussion:
1) It may be questioned if there can exist two non-identical particles which still behave like “twins”, in possessing the same basic properties of vanishing charge and spin as well as rest masses of the same order of magnitude.
2) The present theory has so far been directed towards individual and free particles. Interaction with bound particles such as quarks, and the related strong forces, have not been considered. But in principle such consi- derations could equally well become applicable to the present composite model.
2.6. The Individual Photon
According to experimental experience, the individual photon is limited in its transverse directions, and it has a nonzero spin. This implies that a physically relevant photon model should have the form of a wave or wave packet of preserved and limited shape, propagating in an undamped way in a defined direction. A single plane wave has infinite spatial extensions and no spin, and is therefore hardly suitable for an individual photon model. This is instead the case of a cylindrical configuration.
Starting from the basic Equations (1)-(6), the velocity vector then has the form

in a cylindrical frame. For normal propagating modes varying as 


Here the phase and group velocities are both equal to v. In terms of a generating function, the fields E and B are obtained from the basic equations. The normal modes are then superimposed into an axisymmetric wave packet of narrow line width, having a main wave number 
and a frequency



and there is an equivalent “rest mass”

being associated with the transverse velocity component of C in Equation (10), and with a spin of the magnitude

These results are summarized as follows [1] [12] :
1) A nonzero spin does not have to be added to the system as an extra ad hoc assumption, but becomes an integrated property obtained from the field equations.
2) The concept of Lorentz invariance is extended to apply not only to a plane wave, but also to a cylindrical one. This is done by replacing the scalar velocity c by the velocity vector C.
3) The existence of a nonzero spin is obtained at the expense of a slight reduction in the velocity v of propagation, from c to
4) For relevant radial extensions of an axisymmetric wave packet, this reduction becomes extremely small. It is first appearing in the ninth or tenth decimal of v, as given by Equation (12).
5) A nonzero spin is related to a nonzero “rest mass”. But the latter does only need to become extremely small to satisfy relevant conditions on the present photon model.
6) The radial extensions of the photon model become limited. In its turn, this results in such properties as needle radiation and a combined wave-particle behaviour, as well as in increased understanding of the photoelectric effect and two-slit experiments.
3. Concluding Remarks
The present RQED approach is likely to lead to several new possibilities within fundamental physics, being beyond the theories of the Standard Model, Dirac, and Higgs, and including more applications. Examples of consistency with experimental facts are as follows:
1) The present field equations result in steady particle models having nonzero electric charge, mass, and spin.
2) The electron is point-charge-like and has very small radial extensions.
3) The deduced minimum electric charge agrees with the observed elementary charge within an uncertainty of only a few percent.
4) The charged leptons are prevented by the included magnetic field from “exploding” under the action of their electrostatic eigenforce.
5) The deduced characteristic radial extension of the Z boson agrees with its so far estimated order of magnitude.
6) The composite unstable and electrostatic particle obtained from the present theory has at least the same basic properties of vanishing charge, vanishing spin, and order-of-magnitude mass as that detected at CERN.
7) The model of the individual photon has a nonzero spin. It also contributes to the understanding of the wave-particle nature, needle radiation, the photoelectric effect, and of two-slit experiments.
The future will show what is relevant and not relevant of these considerations.
Cite this paper
BoLehnert, (2015) Some Elucidations of the Theory on Revised Quantum Electrodynamics. Journal of Modern Physics,06,1695-1700. doi: 10.4236/jmp.2015.611171
References
- 1. Lehnert, B. (2013) Revised Quantum Electrodynamics. Nova Science Publications, Inc., New York.
- 2. Schiff, L. (1949) Quantum Mechanics. McGraw-Hill Book Comp., Inc., New York-Toronto-London.
- 3. Quigg, C. (2008) Scientific American, 298, 46-53.
http://dx.doi.org/10.1038/scientificamerican0208-46 - 4. Abbott, L. (1988) Scientific American, 258, 106-113.
http://dx.doi.org/10.1038/scientificamerican0588-106 - 5. Casimir, H.B.G. (1948) Proc. Ned. Akad. Wet., 51, 793-795.
- 6. Lamoreaux, S.K. (1997) Physical Review Letters, 78, 5-8.
http://dx.doi.org/10.1103/PhysRevLett.78.5 - 7. Terletskii, Yu.D. (1971) Statistical Physics. North-Holland Publishing Comp., Amsterdam, London.
- 8. Milonni, P.W. (1994) The Quantum Vacuum. American Press Inc., Harcourt Brace and Company, Boston, San Diego, New York, London, Sydney, Tokyo and Toronto.
- 9. Loudon, R. (2000) The Quantum Theory of Light. Third Edition, Oxford University Press.
- 10. Riess, A.G. and Turner, M.S. (2004) Scientific American, 50-55.
http://dx.doi.org/10.1038/scientificamerican0204-62 - 11. Heitler, W. (1954) The Quantum Theory of Radiation. Third Edition, Clarendon Press, Oxford, 57, 409.
- 12. Lehnert, B. (2013) Journal of Plasma Physics, 79, 327-334.
http://dx.doi.org/10.1017/s0022377812001055 - 13. Lehnert, B. (2014) Journal of Electromagnetic Analysis and Applications, 6, 319-327.
http://dx.doi.org/10.4236/jemaa.2014.610032 - 14. Lehnert, B. (2015) Journal of Modern Physics, 6, 448-452.
http://dx.doi.org/10.4236/jmp.2015.64048 - 15. Lehnert, B. (2013) Progress in Physics, 3, 31-32.
- 16. Lehnert, B. (2014) Progress in Physics, 10, 5-7.
- 17. Aad, G., et al. (2012) Physics Letters, B716, 1-29.
http://dx.doi.org/10.1016/j.physletb.2012.08.020 - 18. Chatrchyan, S., et al. (2012) Physics Letters, B716, 30-61.
http://dx.doi.org/10.1016/j.physletb.2012.08.021 - 19. Higgs, P.W. (1966) Physical Review, 154, 1156-1168.
http://dx.doi.org/10.1103/physrev.145.1156


