Journal of Modern Physics
Vol.3 No.9A(2012), Article ID:37076,3 pages DOI:10.4236/jmp.2012.329167
The Machian Origin of the Centrifugal Force
Department of Physics, University of Pisa and I.N.F.N., Pisa, Italy
Email: christ@df.unipi.it
Received June 20, 2012; revised July 19, 2012; accepted July 28, 2012
Keywords: Centrifugal Force; Mach’s Principle
ABSTRACT
A derivation of the centrifugal force from an effective vector formulation of gravitation is attempted. The centrifugal force appears to be due to a relativistic effect of the counter-rotating Universe. Gravitomagnetic energy effects, a million times stronger than the self-energy effects responsible for curvature in the GR language, would thus produce the centrifugal acceleration. The Machian picture, already successful in the case of the Coriolis force, gets an additional circumstantial support.
1. Introduction
In spite of centennial speculations [1,2], a satisfactory, at least semiquantitative, solution of the problem of relative rotational motion is, in our opinion, still lacking.
Is the rotation of, say, the earth with respect to the rest of the Universe equivalent to a counter rotation of the latter?
Further arguments in favor of this logically stringent position have been put forward more recently by Sciama [3], who however has not gone farther than stressing the analogy of gravitomagnetic with magnetic forces, thus making plausible such an origin in the case of the Coriolis force.
This has been proven by us in [4].
General relativity (GR) does not address the problem at all, since in its privileged frame of reference (“the precession takes place with respect to the inertial frame, which is generally believed to be defined by the distant extragalactic nebulae, the so called “fixed stars” [5]) no mention is made of the rest of the Universe.
According to [6] also “Ironically, though GR was intended to be based on relational concepts, contrary to its name it still contains absolute elements. This is already expressed in the calculation of the advance of Mercury’s perihelion, which is referred to a coordinate system.”
The aim of the present paper is to extend the considerations already used in [4] to account for the Coriolis force, to predict unavoidably the form of the centrifugal force and to show that its coefficient is, within the present Universe estimates, compatible with the canonical value.
The essential points will be:
1) the proportionality between the gravitomagnetic field of a rotating mass distribution and its angular velocity and their dimensional equivalence;
2) the expression of the gravitomagnetic energy density;
3) the kinematical relation among quantities in inertial and rotating frames by which the centrifugal acceleration can be linked to the gravitomagnetic field (our final equation).
2. The Centrifugal Force from the Counter Rotating Universe
In two recent works of ours [4,7], a set of effective vector equations for low velocity weak field gravitation has been derived from special relativity and shown to predict in simple terms the quadrupole gravitational radiation as well as geodetic precession, frame dragging and the gravitational clock effect.
Numerous NR reductions of GR for the same conditions have been recently appeared [11-15] confirming the soundness of such an approach.
Most important, in respect to the matter we are addressing here, the Coriolis force (since the equivalence principle is explicitly used we will speak indifferently of force and acceleration) has been shown to play a crucial role in the abovementioned stationary processes and the role of the (rest of the) Universe to be crucial in explaining the observed effects.
Indeed the gravitomagnetic (GM) force of a rotating mass M at a distance R on a test mass m reads
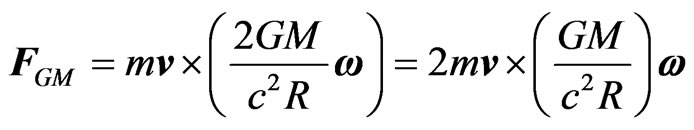 (1)
(1)
which can be compared to the expression for the Coriolis force
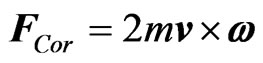 (2)
(2)
Thus, when applied to the Universe, if
 (3)
(3)
and this relation compares favourably with present day estimates as well as with other theoretical considerations [9,10] , it follows that
 (4)
(4)
The relevant point in this argument is that in the relative rotation, the magnetic field generated by distant layers of matter goes as 1/R i.e. the same behaviour of radiation, rather than the usual 1/R2 of Newtonian forces. Therefore a relative more important role even of distant stars is a matter of fact.
Thus the physical origin of the Coriolis force seems to get a semiquantitative confirmation.
Let us pass over to the centrifugal force with some additional remarks.
Now whereas a gravitomagnetic origin of a Coriolis force might seem reasonable (effect of counterrotating masses on a moving one), at first sight it might seem puzzling the effect of the same counterrotating masses on a mass in its rest frame. As it has been pedagogically underlined in [7] however a mass at rest experiences a force from the relativistic effects (i.e. O(v2/c2)) of moving ones (even if this is customarily expressed as magnetic force).
And indeed the relativistic origin of the effect is evident from the proportionality coefficient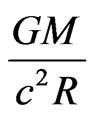 !
!
The essential point in the previous considerations is that a rotating matter distribution produces a gravitomagnetic field h proportional to the angular velocity of rotation ω
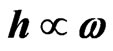
 (5)
(5)
the proportionality coefficient depending of course on the geometry (loop, spherical shell, etc.). In other words a gravitomagnetic field produced by moving masses is dimensionally equivalent to an angular velocity.
This has a profound physical meaning. We know that the T ≠ 0 cosmic background radiation, essentially coincident with the fixed stars system, represents the privileged inertial reference frame. However in terms of relative motion the fact that the rotation of the Universe, as seen from us, be determined by the properties of the other masses (MU and RU) renders physical what seemed just a kinematical affair.
Therefore if the previous relation between h and ω holds true, just a two-fold application of the kinematical relation for operators
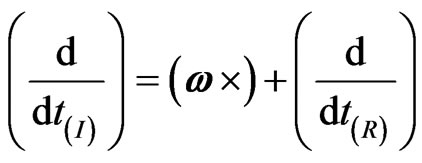 (6)
(6)
(where the suffixes refer respectively to the inertial (I) and rotating (R) frames) yields for the acceleration of the radius vector r the additional centrifugal acceleration.
Let us give some additional arguments.
Consider a symmetric spherical rotating shell.
Its mass (energy and mass are used indifferently) density reads [7]
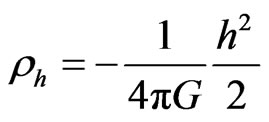 (7)
(7)
The Coriolis force has been accounted for by a gravitomagnetic field where for the contribution of the Universe the same expression obtained for a mass loop (the orbiting earth) where 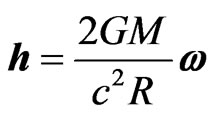 has been used. On the contrary if one considers spherical symmetry, in the interior the constant gravitomagnetic field (see e.g. [8]) is
has been used. On the contrary if one considers spherical symmetry, in the interior the constant gravitomagnetic field (see e.g. [8]) is
 . If we use the value 2 which reproduces the Coriolis force, then from the expression of the field energy
. If we use the value 2 which reproduces the Coriolis force, then from the expression of the field energy 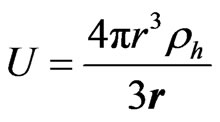 one gets
one gets
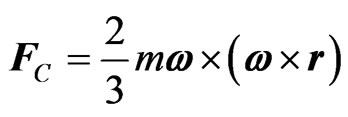 (8)
(8)
a centrifugal force due to the negative energy density.
This result is noteworthy in many respects.
First the centrifugal force is a relativistic effect!
Second, the correct dimensional requirement for the acceleration comes from a (subtle?) interplay between the expression for the mass density and that for the field, which makes the desired ω2 factor unavoidable. Moreover the gravitational constant G only enters through the standard weak field formula in brackets.
The coefficients, upon whose evaluation many criticisms might apply, is remarkably close to one.
In this respect let us once more underline how even two drastically different density expressions like ρ ≈ constant and ρ ≈ 1/r2 which implements the black hole possibility, yield for the self energy the two very close coefficients 3/5 and 1 respectively. Thus even if our evaluation of the total Universe contribution by simply substituting its values is surely questionable, the semiquantitative agreement can hardly be regarded as fortuitous.
The reason why only gravitomagnetic forces act is obvious: within a symmetric spherical shell the static gravitoelectric effects cancel out because of the symmetry, whereas the magnetic ones, constant in R, are different from zero and along ω.
The fact that no retardation for magnetic terms is present, depends on our choice of the gauge, as explained in [7], see also [16].
3. Conclusions
The fact that only relative rotations have a physical significance has thus been substantiated, both as regards the expression of the centrifugal force as well as its actual value.
Some more comments are in order.
It is not superfluous to underline the similarities and differences with the case of orbiting satellites [4]. There for the gyroscopes in free fall around the earth the effect of the Universe rotation provided only part of the effect (essentially 1/2) the other being due to the earth rotation. Here of course only the former contributes both for moving objects (Coriolis on the earth) and for masses at rest (centrifugal). Thus this double constraint gives us some more confidence in a non accidental agreement.
Therefore it is really rewarding to have such an interesting link between local and global properties of the Universe and probably a deeper understanding of gravitoelectric effects (self energy or space time curvature where only the earth constituents are involved) and of the gravitomagnetic ones (much bigger centrifugal acceleration determined by the Universe).
In conclusion Berkeley-Mach’s [1,2] thinking enters quite rightly our picture of the Universe through the pre-
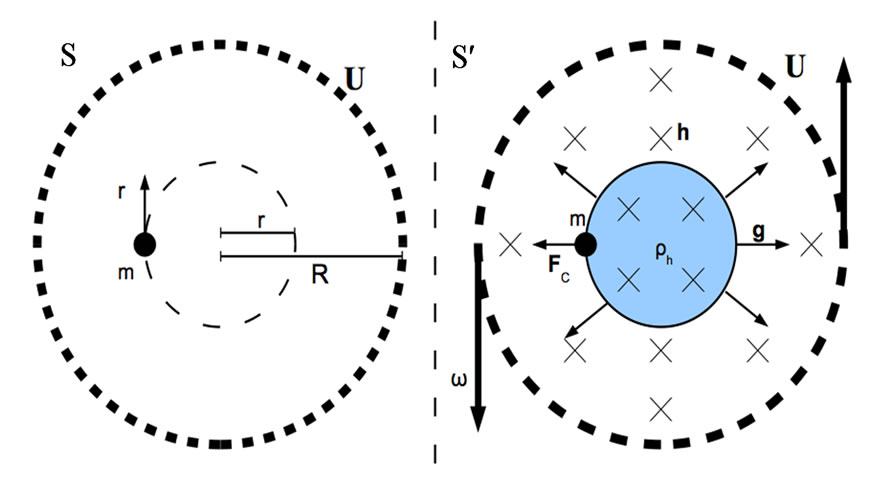
Figure 1. A mass m rotates in the fixed Universe frame S at a distance r from the center. From the mass rest frame S' the Universe is seen to counter rotate, generating a gravitomagnetic field h ∝ ω and a gravitomagnetic field density which causes the “fictitious” centrifugal force. As a particular case our mass is at the surface of the earth and the whole Universe contributes to the repulsion. Thus for the Earth one has the fascinating fact of a gravitoelectric self energy (space curvature) effect of O(10–9) with respect to g, and of a much bigger gravitomagnetic influence, due to its rotation (or better to the counter rotation of the Universe), of O(10−3). Also in the former case self energy acts “centrifugally” so as to diminish g.
diction, in addition to the Coriolis, also of the “fictitious” centrifugal force as “real ones”!
4. Acknowledgements
It is a pleasure to thank C. Bonati, G. Cicogna and G. Morchio for a critical reading of the manuscript and for helpful comments.
REFERENCES
- B. De Motu, “Berkeley’s Philosophical Writings,” Collier, New York, 1974.
- E. Mach, “Space and Geometry,” Open Court Publishing, Chicago, 1906.
- D. W. Sciama, “The Unity of the Universe,” Faber and Faber, London, 1959.
- P. Christillin and L. Barattini, “The Machian Contribution of the Universe to Geodetic Precession, Frame Dragging and Gravitational Clock Effect,” arXiv:1206.4593v1 [physics.gen-ph], 2012.
- L. I. Schiff, “Motion of a Gyroscope According to Einstein’s Theory,” Proceedings of the National Academy of Sciences, Vol. 46, 1960, pp. 871-882. doi:10.1073/pnas.46.6.871
- H. Lichtenegger and B. Mashoon, “Mach’s Principle,” arXiv:physics/0407078 [physics.hist-ph].
- P. Christillin and L. Barattini, “Gravitomagnetic Forces and Quadrupole Gravitational Radiation from Special Relativity,” arXiv:1205.3514v1, 2012.
- D. J. Griffiths, “Introduction to Electrodynamics,” Pearson, San Francisco, 2008, p. 234
- P. Christillin, “Spooky Black Holes: Gravitational SelfEnergy and Space Curvature,” EPJ Plus, Vol. 126, 2011, p. 48.
- P. Christillin, “Speakable and Unspeakable in Cosmology: Dark Matter vs. Gravitational Self-Energies. Hubble’s Constant the Cosmological Term and All That,” EPJ Plus, Vol. 126, 2011, p. 88.
- R. P. Lano “Gravitational Meissner Effect,” 1996. arXiv:hep-th/9603077
- D. Bedford and P. Krumm, “On Relativistic Gravitation,” American Journal of Physic, Vol. 53, No. 9, 1985, p. 889. doi:10.1119/1.14358
- H. Kolbenstvedt, “Gravomagnetism in Special Relativity,” American Journal of Physics, Vol. 56, No. 6, 1988, p. 523. doi:10.1119/1.15544
- B. Mashhoon, et al., “Gravitomagnetism and the Clock Effect,” arXiv:gr-qc/991202, 1999.
- M. Agop et al., “On Gravitational Shielding in Electromagnetic Fields,” arXiv:gr-qc/9911011.
- R. P. Feynman, “Lectures on Gravitation,” Penguin Books, London, p. 40.

