Journal of Modern Physics
Vol.3 No.8(2012), Article ID:21695,11 pages DOI:10.4236/jmp.2012.38110
Electronic Structure with Rovibrational and Dipole Moment Study of the NiO Molecule
1Faculty of Science, Beirut Arab University, Riad El Solh, Beirut, Lebanon
2Khalifa University, Sharjah, UAE
Email: *fkorek@yahoo.com
Received June 10, 2012; revised July 9, 2012; accepted July 31, 2012
Keywords: ab Initio Calculation; NiO Molecule; Potential Energy Curves; Spectroscopic Constants; Dipole Moment; Rovibrational Calculation
ABSTRACT
The potential energy curves have been investigated for the 40 lowest electronic states in the  representation below 25,000 cm–1 of the molecule NiO via CASSCF, MRCI (single and double excitation with Davidson correction) and CASPT2 methods. The harmonic frequency
representation below 25,000 cm–1 of the molecule NiO via CASSCF, MRCI (single and double excitation with Davidson correction) and CASPT2 methods. The harmonic frequency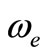 , the internuclear distance re, the rotational constant Be, the electronic energy with respect to the ground state Te, and the permanent dipole moment
, the internuclear distance re, the rotational constant Be, the electronic energy with respect to the ground state Te, and the permanent dipole moment 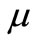 have been calculated. By using the canonical functions approach, the eigenvalues Ev, the rotational constant Bv and the abscissas of the turning points rmin and rmax have been calculated for the considered electronic states up to the vibration level v = 12. Eleven electronic states have been studied theoretically here for the first time. The comparison of these values to the theoretical and experimental results available in literature shows a very good agreement.
have been calculated. By using the canonical functions approach, the eigenvalues Ev, the rotational constant Bv and the abscissas of the turning points rmin and rmax have been calculated for the considered electronic states up to the vibration level v = 12. Eleven electronic states have been studied theoretically here for the first time. The comparison of these values to the theoretical and experimental results available in literature shows a very good agreement.
1. Introduction
The metal oxide NiO shows complicated electronic spectra because of the presence of large number of electronic states derived from several low-lying configurations but it gives a systematic example of chemical bonding, which depends on the relative energy between the 3d orbital of the metal and the 2p orbital of oxygen [1,2]. The transition metal oxides have interesting applications in many fields such as materials application and the oxidation of metal surfaces. Among these compounds the NiO molecule which is considered as a prototype of ionic crystals, it is classified as a Mott-Hubbard insulator of very low conductivity. The conductivity of nanostructred NiO was found to be enhanced by six to eight orders of magnitude over those of NiO single crystals [3-10]. The magnetic properties of different sizes of NiO nanoparticles reveal the presence of superparamagnetism as evidenced by the increasing magnetization with decreasing size as well as the magnetic hysteresis at low temperatures. Nanomagnetism promises have applications in magnetic storage with nanomagnetic particles, improved battery lifetimes and also quantum computing [11-14]. The nanoarticles formed by the NiO molecule have many applications in electronics, optical, electro-optical devices and photocatalytic reaction. Despite this importance of the nickel oxide NiO, this molecule has been studied experimenttally and theoretically [15-35] where a limited number of electronic states have been obtained with the corresponding molecular constants. The theoretical calculation of the NiO molecule is an extreme computational challenge because of the degeneracy of several energetically low-lying excited states and the open d, p, and s shells. The presence of the d shell implies large multiplicities which are split by spin-orbit interaction. The components of the spin and the many states perturb each other. The prediction and assignment of the electronic configuration in the ground and excited states and the description of the bonding may often be difficult.
Based on our previous theoretical calculation [36-45], the important connection between energy relations of solids and molecules [46], and stimulated by the lack of theoretical calculation of excited electronic states with the existence of preliminary experimental and theoretical data, we performed an ab initio study of the low-lying electronic states of the molecule NiO below 25,000 cm–1. In this work, we investigate the potential energy curves (PECs), the electric dipole moment and spectroscopic constants for the 40 2s+1Λ(±) low-lying electronic states of this molecule obtained by MRCI and RSPT2 calculations. Taking advantage of the electronic structure of the investigated electronic states of the NiO molecule and by using the canonical functions approach [47], the eigenvalues Ev, the rotational constant Bv and the abscissas of the turning points rmin and rmax have been calculated for several vibrational levels of the considered electronic states.
2. Computational Approach
2.1. Ab Initio Calculation
The PECs of the lowest-lying electronic states of the NiO molecule have been investigated via CASSCF and CASPT2 methods. The MRCI calculations (single and double excitations with Davidson corrections) were performed. The Nickel atom is treated as a system with 10 inner electrons taken into account using the basis LANL2DZECP [48] for s, p and d functions. The 8 electrons of the oxygen atom are considered using the DGauss-a2-Xfit [49] basis set including s, p and d functions. Among the 26 electrons explicitly considered for the NiO molecule (18 electrons for Ni and 8 for O), 14 inner electrons were frozen in subsequent calculations so that 12 valence electrons were explicitly treated. This calculation has been performed via the computational chemistry program MOLPRO [50] taking advantage of the graphical user interface GABEDIT [51].
In the representation 2s+1Λ(±), 40 electronic states have been investigated for 46 internuclear distances in the range 1.331 Å ≤ r ≤ 2.681 Å by using the MRCI and RSPT2 calculations. The potential energy curves for the singlet and triplet states, obtained by MRCI calculation, are given in Figures 1-4.
The spectroscopic constants such as the vibration harmonic constant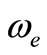 , the internuclear distance at equilibrium re, the rotational constant Be and the electronic transition energy with respect to the ground state Te have been calculated by fitting the energy values around the equilibrium position to a polynomial in terms of the internuclear distance. These values are given in Table 1 together with the available data in the literature either theoretical or experimental.
, the internuclear distance at equilibrium re, the rotational constant Be and the electronic transition energy with respect to the ground state Te have been calculated by fitting the energy values around the equilibrium position to a polynomial in terms of the internuclear distance. These values are given in Table 1 together with the available data in the literature either theoretical or experimental.
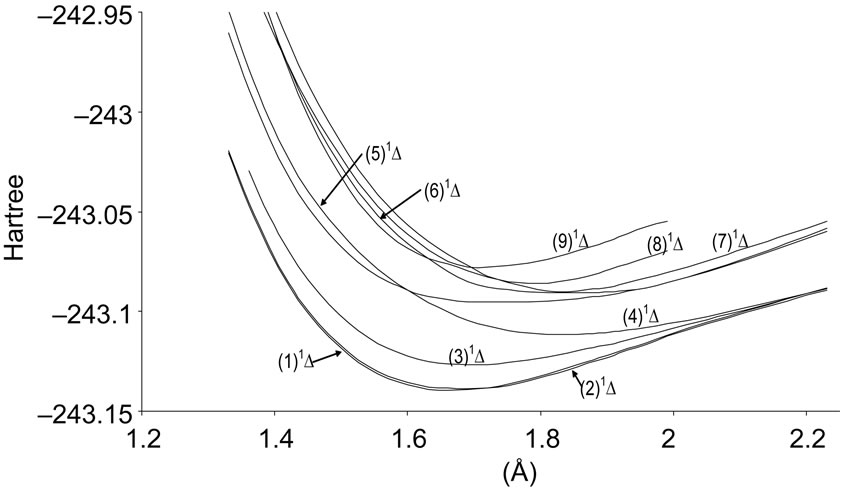
Figure 1. Potential energy curves of the lowest singlet 1D and 1S states of the molecule NiO.
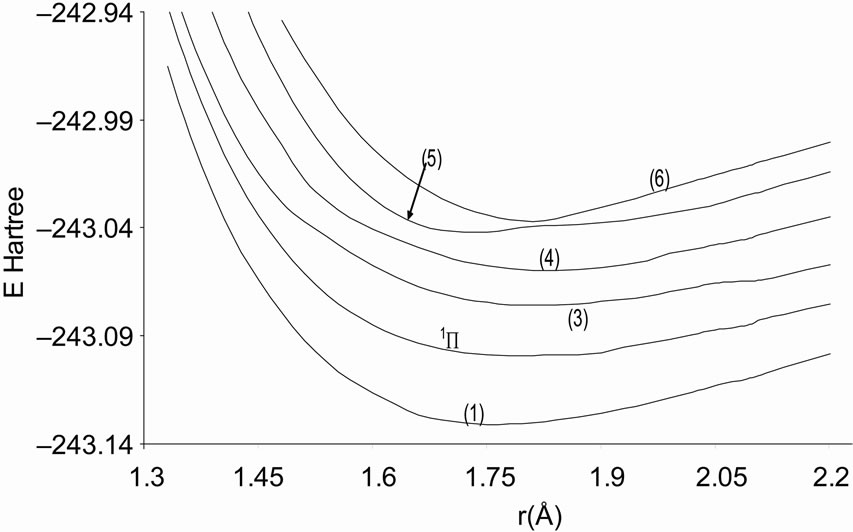
Figure 2. Potential energy curves of the lowest singlet 1P states of the molecule NiO.
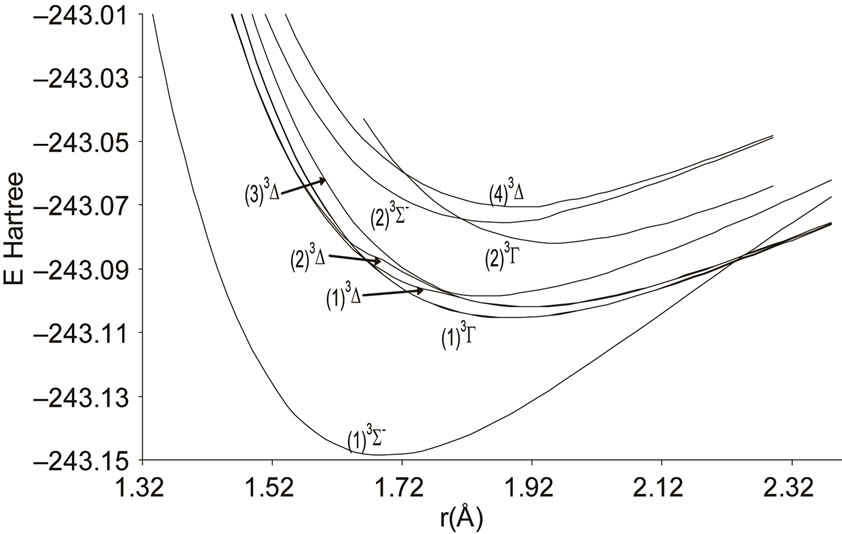
Figure 3. Potential energy curves of the lowest triplet 3S-, 3D and 3G states the molecule NiO.

Figure 4. Potential energy curves of the lowest triplet 3P and 3F states of the molecule NiO.
An overlap between the 3d and 4s orbitals of the Ni atom and the 2p orbitals of the oxygen atom lead to the formation of the molecular orbitals of the molecule NiO. The ground state of this molecule is confirmed theoreticcally and experimentally to be a3S– [1,16-23,34-35, 52-58], its electronic configuration can approximately described as 8σ2 3π4 1δ4 9σ2 4π2. The 9σ and 4π orbitals are antibonding, the 1δ orbital is nonbonding, and the
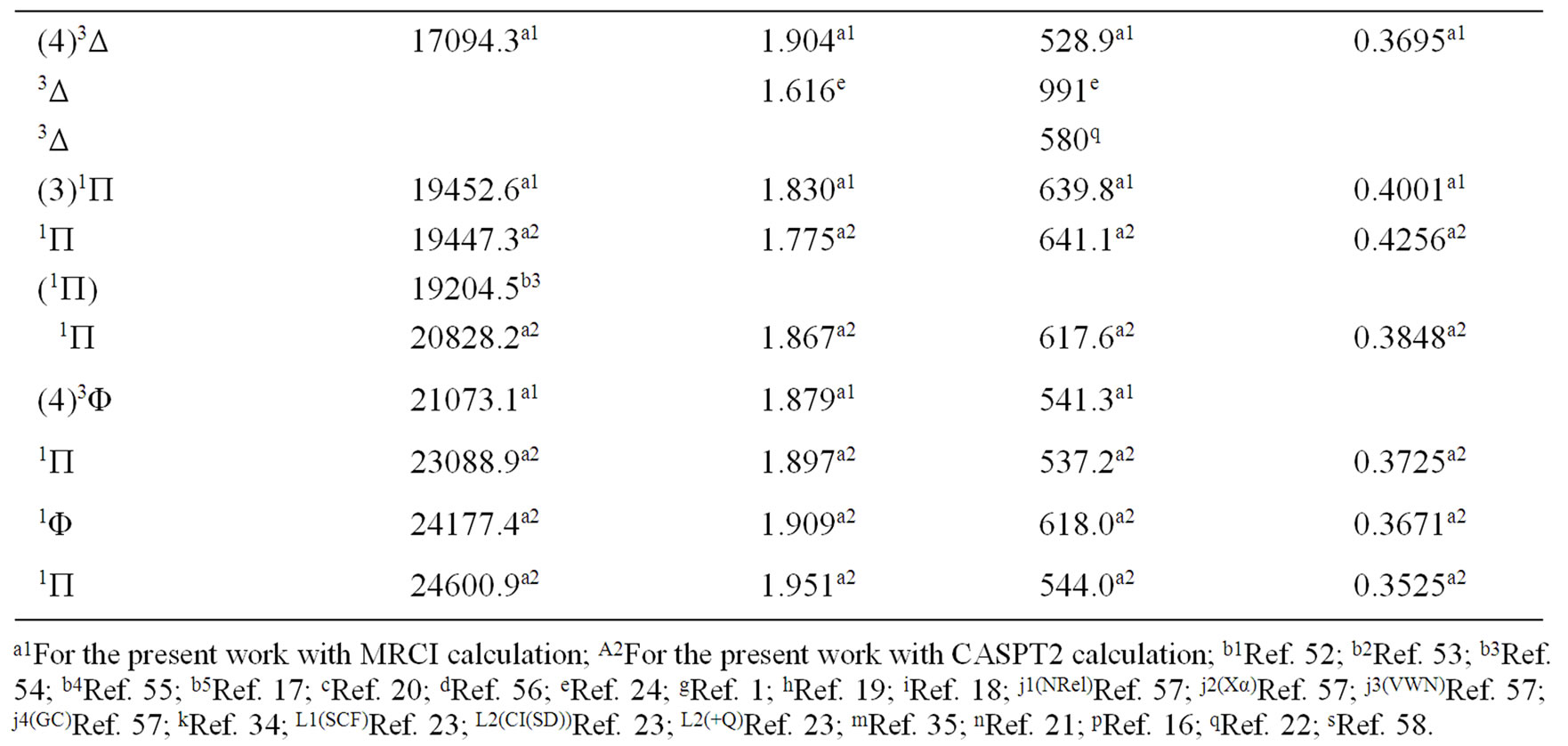

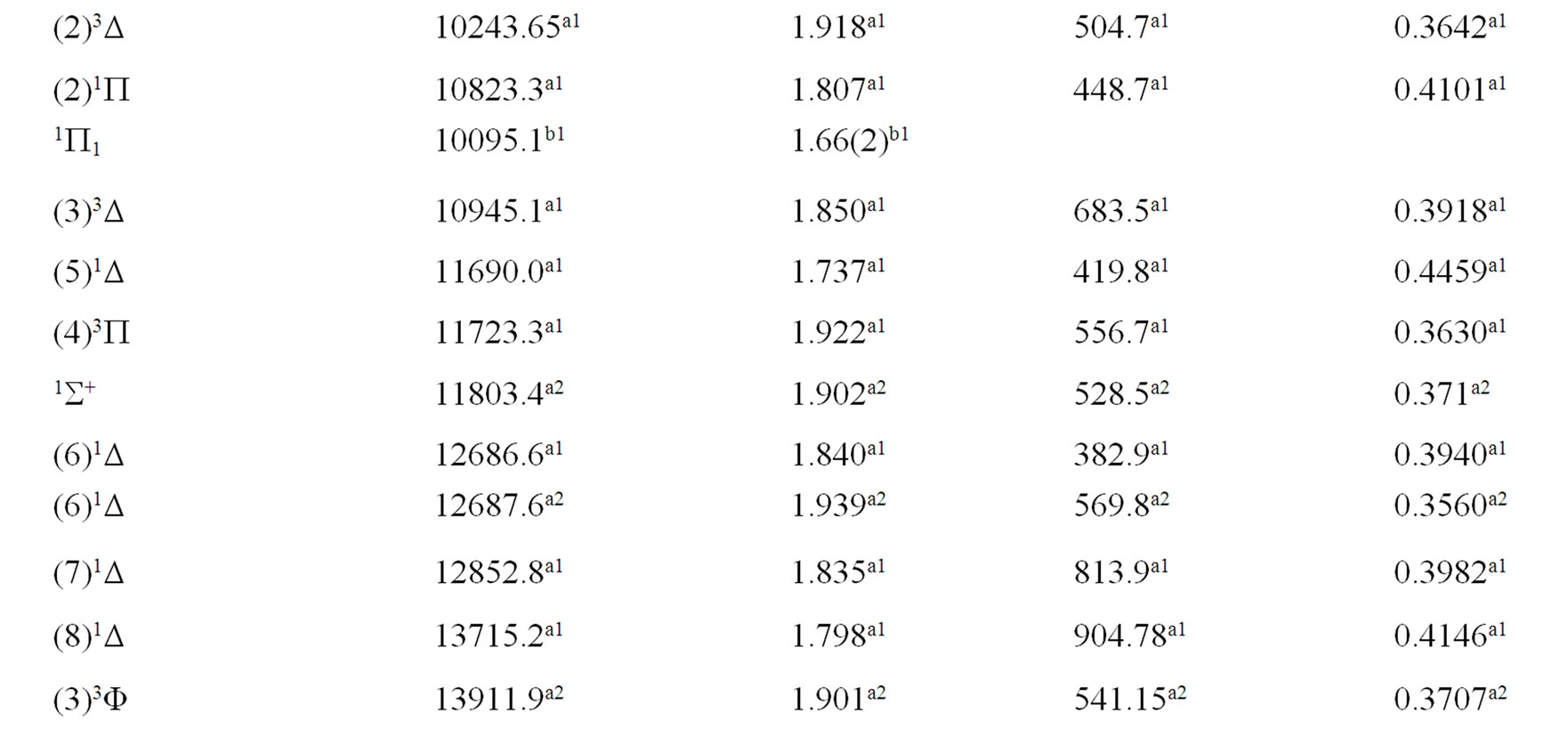
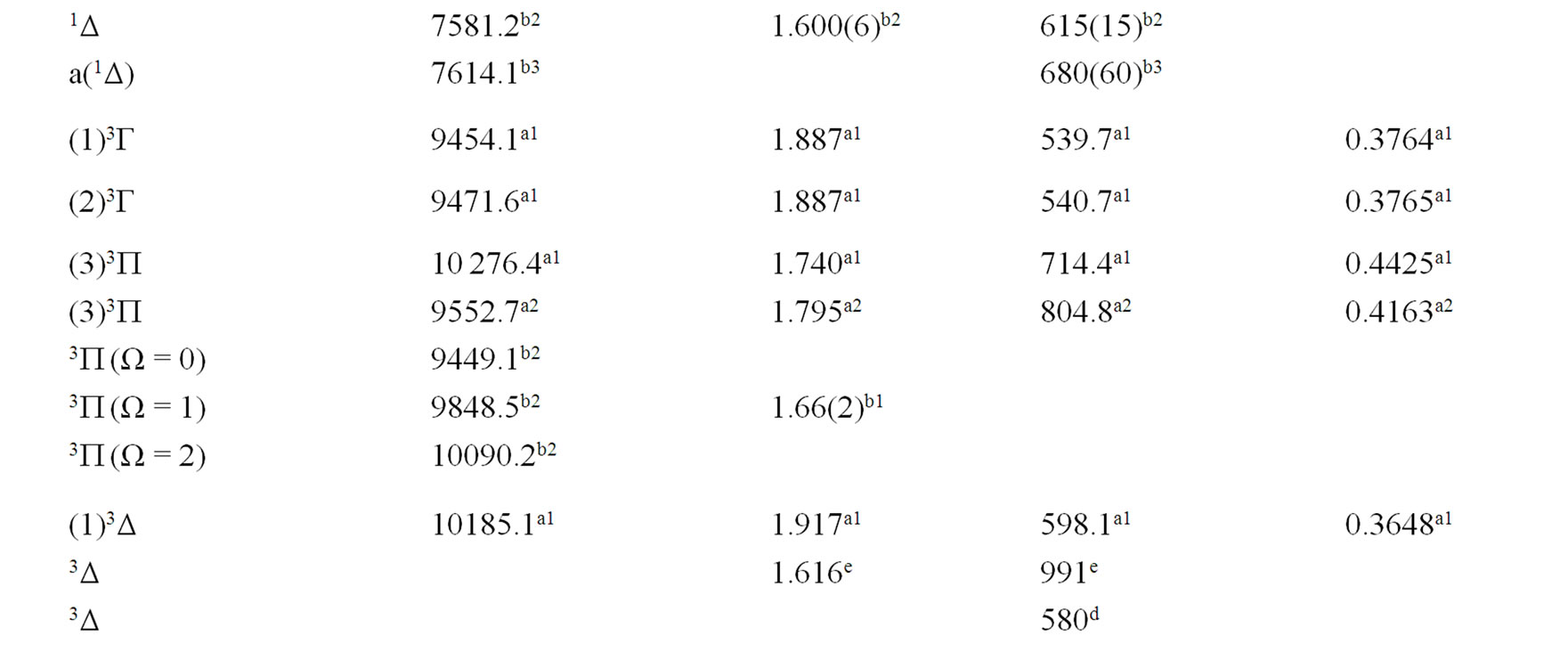


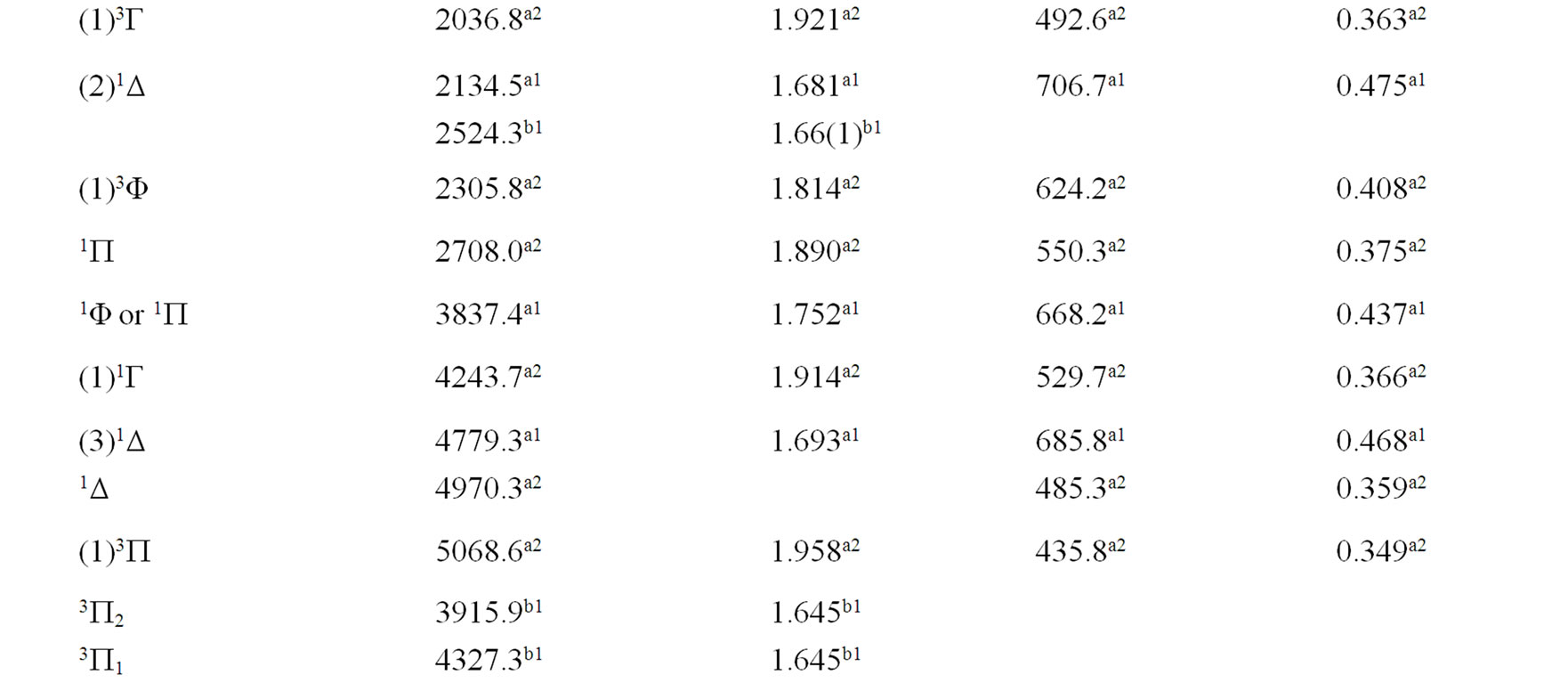

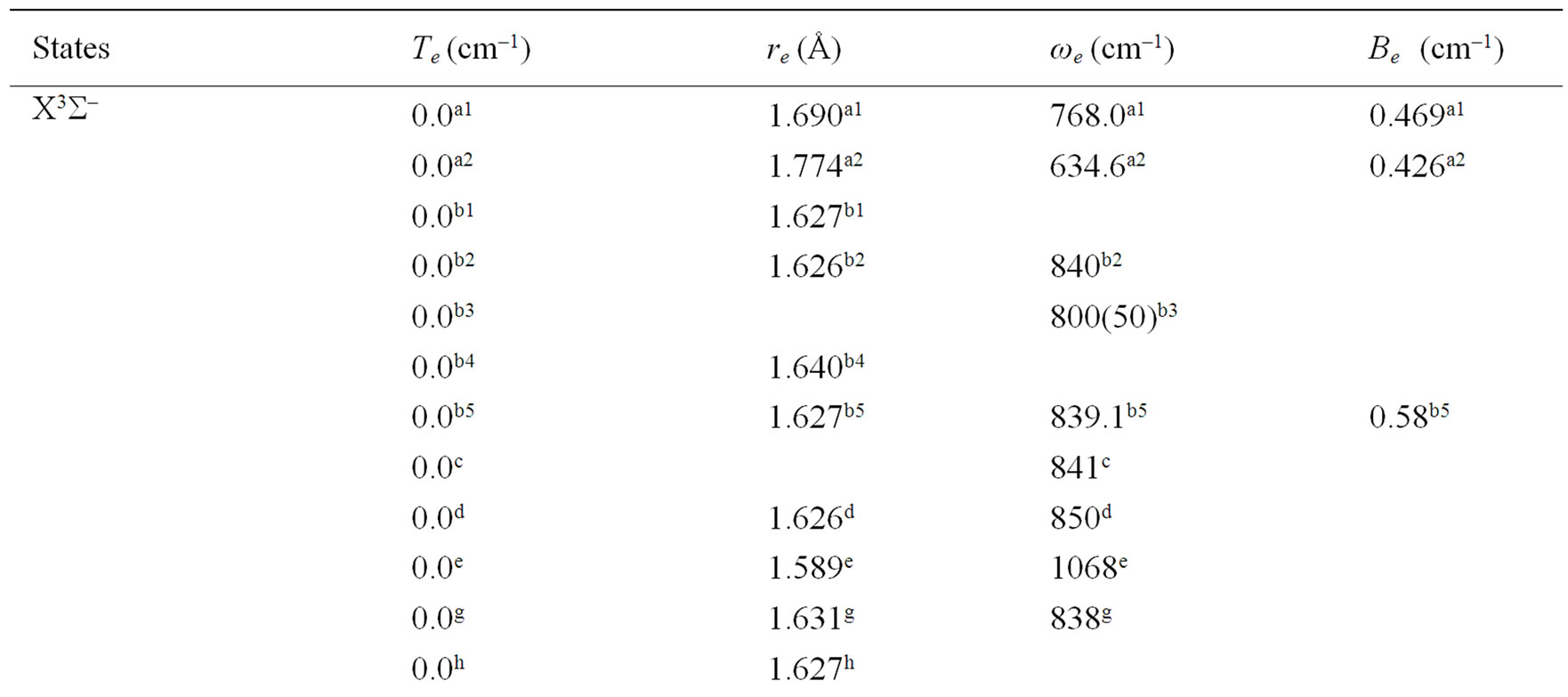
Table 1. Spectroscopic constants for the electronic states of the molecule NiO.
remaining orbitals are bonding [53]. The electronic structure of all the open shell 3d oxide are dominated by M2+O2– zero-order character at low energy, while the NiO molecule has the chance to be represented by Ni+O– atomic-ion-in-molecule model [18]. Our calculated values of the internuclear distance re and the vibrational harmonic constant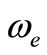 , for the ground state, by using the MRCI calculation, are in very good agreement with the experimental values in literature with the relative differences 2.7% (Ref. [34]) < Δre/re < 3.8% (Ref. [53]) and 4% (Ref. [53]) <
, for the ground state, by using the MRCI calculation, are in very good agreement with the experimental values in literature with the relative differences 2.7% (Ref. [34]) < Δre/re < 3.8% (Ref. [53]) and 4% (Ref. [53]) < 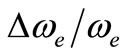 < 8.5% (Ref. [18]) respectively. These relative differences become larger by using the CASPT2 method where 7.3% (Ref. [34]) < Δre/re < 8.3% (Ref. [53]) and 20.6% (Ref. [54]) <
< 8.5% (Ref. [18]) respectively. These relative differences become larger by using the CASPT2 method where 7.3% (Ref. [34]) < Δre/re < 8.3% (Ref. [53]) and 20.6% (Ref. [54]) < 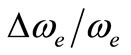 < 24.4% (Ref. [18]), but the value of
< 24.4% (Ref. [18]), but the value of 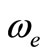 given by Huber and Herzberg [35] is in very good agreement with our value calculated by CASPT2 method where
given by Huber and Herzberg [35] is in very good agreement with our value calculated by CASPT2 method where  = 3% and bad agreement with the value calculated by the MRCI method with
= 3% and bad agreement with the value calculated by the MRCI method with 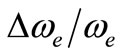 = 20%. By comparing our calculated values of re with those calculated theoretically in literature we obtained a very good agreement with relative differences 3.8% (Ref. [56]) < Δre/re < 5.6% (Ref. [23]) and 0.5% (Ref. [23]) < Δre/re < 8.3% (Ref. [56]) calculated by MRCI and CASPT2 respectively, while the theoretical values of
= 20%. By comparing our calculated values of re with those calculated theoretically in literature we obtained a very good agreement with relative differences 3.8% (Ref. [56]) < Δre/re < 5.6% (Ref. [23]) and 0.5% (Ref. [23]) < Δre/re < 8.3% (Ref. [56]) calculated by MRCI and CASPT2 respectively, while the theoretical values of 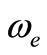 calculated in literature varies between 748 and 1068 cm–1 and our values are in agreement with the lower value.
calculated in literature varies between 748 and 1068 cm–1 and our values are in agreement with the lower value.
A large number of low-lying electronic states, many with very high spin multiplicity, of 3d metal oxides are produced by the unpaired electrons, therefore strong state mixing results in spectroscopy which implies difficult theoretical calculation. Another dimension of complexity can be added originating for the large nuclear spin and magnetic moment of the nuclei with odd atomic number. The first excited state of the NiO molecules has long been a matter of controversy. The theoretical calculation of Bauschlicher Jr. and collaborators [21,22,56] and that of Bakalbassis et al. [24] found that the first excited state of this molecule is 3P. Moravec and jarrold [53] and Wu and Wang [54] confirmed experimentally that 3P is the first excited state. For Ram and Bernath [19] and Freidman-Hill and Field [18] this 3P state is located experimentally above the ground state X3S– at 4330 and 4293 cm–1 respectively. From the photoelectron spectroscopy technique, Ramond et al. located the 3P2 and 3P1 at 3916 and 4327 cm–1 respectively [52]. By a theoretical calculation, Walch and Goddard [20] predicted that the first excited state is 1P rather than 3P and located this state at 6000 cm–1 above the ground state X3S–. This prediction of Walch and Goddard [20] for the first excited state 1Δ is in agreement with the present work but our 3P state is located at 5068.6 cm–1 above the ground state. Moreover between the first excited state (1)1Δ and the (1)3P we found the 4 new singlet electronic states (1)1Δ, (2)1Δ, 1Φ or 1P and (3)1Δ by using MRCI calculation and the 2 new triplet electronic states (1)3Γ, (1)3Φ, and the 3 new singlet electronic states 1P (1)1Γ and 1Δ by using RSPT2 calculation. The agreement between the 2 ways of calculation is only for the last state 1Δ. Ramond et al. [52] investigated an electronic state at 2525 cm–1 between X3S– and 3P2 states without assigning the nature of this state. By comparing the data of this state with our calculated values, one can find that, it is either (2)1Δ or (1)3Φ.
Also without assigning the name of the state, Ramond et al. [52] detected the energy 5230.6 cm–1 above the 3P1, this energy is in very good agreement with the energy of our calculated (2)3Φ state with the relative differences ΔTe/Te = 0.8% and Δre/re = 5%. Between the values of energy 7659.2 cm–1 < Te < 8788.4 cm–1, Ramond et al. [52] suggested to these values an assignment to one of the three states 3Φi, 3Δi and 3Pi. By comparing this data to our calculated values in the present work (Table 1), the assignment to the states 3ΦI and 3ΔI are excluded since Te((2)3Φ = 5271.9 cm–1), Te((3)3Φ = 13911.9 cm–1), Te((1)3Δ = 10185.1 cm–1), and Te((2)3Δ = 10243.65 cm–1), therefore the only possible assignment is (2)3P. These values of energy obtained by Ramond et al. [52] can fit also with the energy of the state (4)1Δ in Table 1, but since this state is not suggested by the authors, this assignment is excluded in the present work. The same authors [52] obtained experimentally for the state 1P the energy Te = 10095.1 cm–1 which fits with our calculated value of the state (2)1P with the relative difference ΔTe/Te = 6.7%.
The values of the energy Te of the states 3Φ2,3,4 and 1Δ obtained experimentally by Moravec and Jarrold [53] are respectively in good agreement and assignment with the (2)3Φ and (4)1Δ of the present work. Our calculated value of 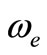 for the state (4)1Δ is in good agreement with that measured by Moravec and Jarrold [53] with relative difference
for the state (4)1Δ is in good agreement with that measured by Moravec and Jarrold [53] with relative difference 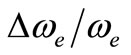 = 5.4%. The 3P1,2,3 states detected by Moravec and Jarrold [53] are in good agreement and assignment with the (3)3P of the present work (Table 1).
= 5.4%. The 3P1,2,3 states detected by Moravec and Jarrold [53] are in good agreement and assignment with the (3)3P of the present work (Table 1).
The assignment of the three states a(1Δ), b(1S+) and c(1∏) detected experimentally by Wu and Wang [54] are in very good agreement with our assignment of the states (4)1Δ, 1S+ and (3)1P with the relative differences ΔTe/Te (a(1Δ)) = 6%, ΔTe/Te (b(1S+)) = 0.5%, ΔTe/Te (c(1P)) = 1.3% respectively. Baushlicher Jr. [21] calculated the nearest 1S+ state at 8340 cm–1 above the 3S– which is in disagreement with our calculated value and those of Wu and Wang [54]. The MRCI calculated values of Te, in the present work, for the (2)3Φ and (3)3Φ states are respectively 5271.9 and 13911.9 cm–1, therefore the possible assignment of the B(3Φ) state, where Te = 10025.7 cm–1, investigated by Wu and Wang [54] is the (3)3Φ (Table 1). The calculated values of re and  by bakalbassiss et al. [24] for the states 3Δ and 1S+, which are fitting with our (4)3Δ and 1S+, are in disagreement with the values calculated in the present work, while there are good agreements between our data and those of Bauschlicher Jr. and Maitre [56] for the values of re for these states with the relative differences Δre/re(3Δ) = 9% and Δre/re(1S+) = 5%.
by bakalbassiss et al. [24] for the states 3Δ and 1S+, which are fitting with our (4)3Δ and 1S+, are in disagreement with the values calculated in the present work, while there are good agreements between our data and those of Bauschlicher Jr. and Maitre [56] for the values of re for these states with the relative differences Δre/re(3Δ) = 9% and Δre/re(1S+) = 5%.
The 3S– at 16,000 cm–1 predicted by Friedman-Hill and Field [18] is in very good agreement with the (2)3S– state calculated in the present work with the relative difference ΔTe/Te = 0.3%. The detected 3P state by Walch and Goddard [20] at ≈6000 cm–1 fits with our assignment of the state (2)3P where the relative difference in energy ΔTe/Te = 12%. The comparison of our results with the most recent investigation on the molecule NiO [58] shows an excellent agreement with our results for the state 3S–, but our assumption for the energies 19452.6 cm–1 and 19447.3 cm–1 are in agreement with that given by Wu and Wang [54]. Because of the breakdown of the Born-Oppenheimer approximation at the crossing and avoided crossing of the potential energy curves near the minimum of the potential energy curves there is no calculation of the spectroscopic constants of other calculated electronic states where the potential energy curves are given in Figures 1-4.
The electric dipole moment is an effective gauge of the ionic characters; it is helping for understanding the macroscopic properties of imperfect gases, liquids and solids and is of great utility in the construction of molecular orbital. The expectation value of this operator is sensitive primarily to the nature of the least energetic and most chemically relevant valence electrons. To understand the ionic behavior of the excited electronic states we have presented in Figures 5-8 the adiabatic permanent dipole moment for the investigated electronic states in the range of the considered internuclear distance. It was seen that the variation of the adiabatic dipole moment is very important in the vicinity of the avoided crossings and the position of the peaks corresponds to the positions of these avoided crossings of the adiabatic curves. Each time an adiabatic state loses its ionic character, it becomes neutral and the corresponding dipole moment tends towards zero. One can notice the fit between the positions of the intersections of the permanent dipole moment curves and the position of the avoided crossings of the corresponding potential energy curves for the following states (4)1Δ/(5)1Δ (6)1Δ/(7)1Δ and (1)3Δ/(3)3Δ at 1.631 Å, 1.812 Å and 1.811 Å respectively. These fittings confirm the validity and the accuracy of the investigated data in the present work on the molecule NiO.

Figure 5. Permanent dipole moment curves of the lowest singlet 1D and 1S states of the molecule NiO.
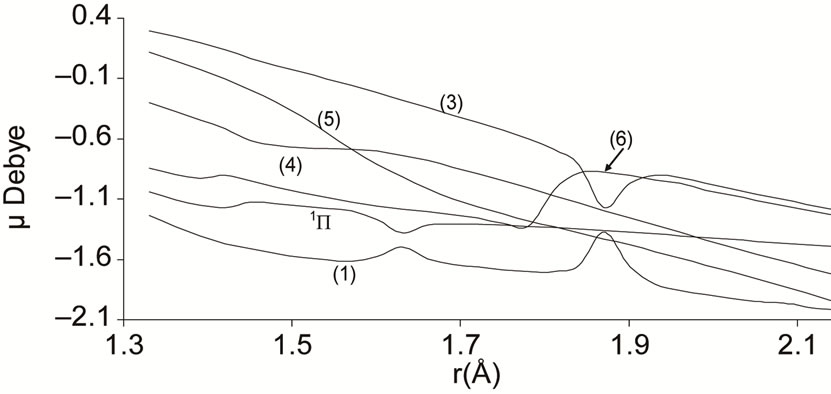
Figure 6. Permanent dipole moment curves of the lowest singlet 1P states of the molecule NiO.

Figure 7. Permanent dipole moment curves of the lowest singlet 3S-, 3D and 3G states of the molecule NiO.
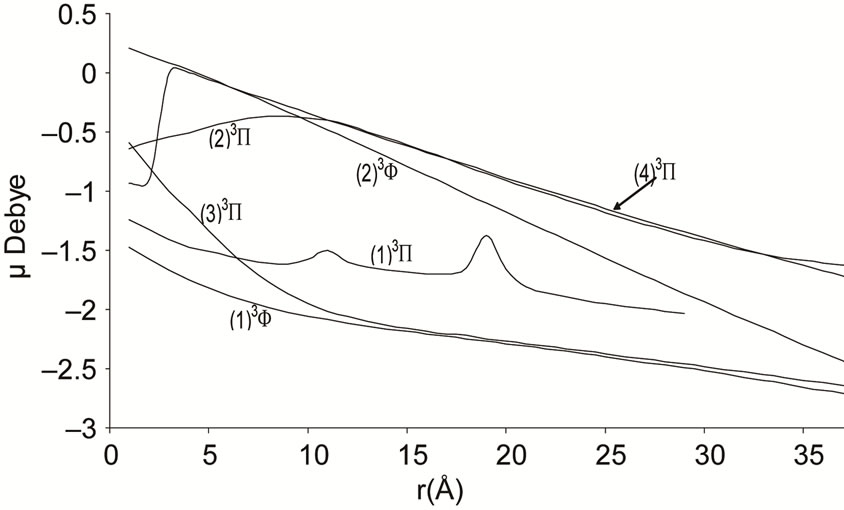
Figure 8. Permanent dipole moment curves of the lowest triplet 3P and 3F states of the molecule NiO.
2.2. The Vibration-Rotation Calculation
Within the Born-Oppenheimer approximation, the vibration rotation motion of a diatomic molecule in a given electronic state is governed by the radial Schrödinger equation
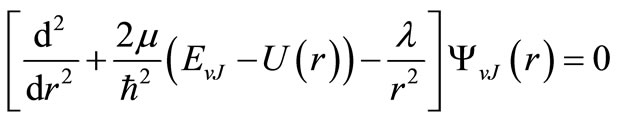 (1)
(1)
where r is the internuclear distance, v and J are respecttively the vibrational and rotational quantum numbers, 
 and
and 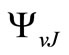 are respectively the eigenvalue and the eigenfunction of this equation. In the perturbation theory these functions can be expanded as
are respectively the eigenvalue and the eigenfunction of this equation. In the perturbation theory these functions can be expanded as
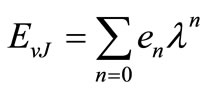 (2)
(2)
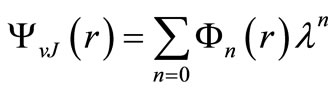 (3)
(3)
with e0 = Ev, e1 = Bv, e2 = –Dv, f0 is the pure vibration wave function and fn its rotational corrections. By replacing Equations (2) and (3) into Equation (1) and since this equation is satisfied for any value of l, one can write [47,59-63]
 (4)
(4)
 (5a)
(5a)
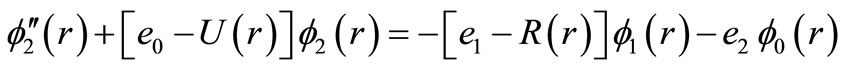 (5b)
(5b)
···
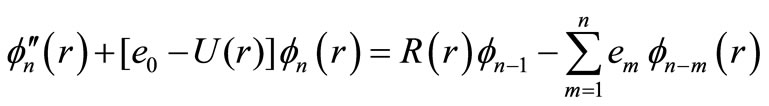 (5n)
(5n)
where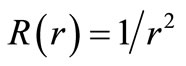 , the first equation is the pure vibrational Schrödinger equation and the remaining equations are called the rotational Schrödinger equations. One may project Equations (7) onto f0 and find
, the first equation is the pure vibrational Schrödinger equation and the remaining equations are called the rotational Schrödinger equations. One may project Equations (7) onto f0 and find
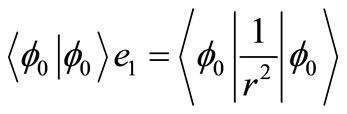 (6a)
(6a)
 (6b)
(6b)
···
 (6n)
(6n)
Once e0 is calculated from Equation (4), e1, e2, e3··· can be obtained by using alternatively Equations (5) and (6). By using the canonical functions approach [47] and the cubic spline interpolation between each two consecutive points of the PECs obtained from the ab initio calculation of the NiO molecule, the eigenvalue Ev, the rotational constant Bv, the distortion constant Dv, and the abscissas of the turning point rmin and rmax have been calculated up to the vibrational levels v = 12 for the investigated electronic states in the present work. These values for the state X1∑+ and the (2)3Φ (as illustration) are given in Table 2. The comparison of the investigated values of Bv and Dv in literature [18,19,25] with our calculated values for these states showed a good agreement with relative difference ΔBv/Bv ≈ 8% for v = 0, 1 and ΔDv/Dv equal 7.5% and 2.4 % respectively for v = 1 and v = 2.
3. Conclusion
In the present work, the ab initio investigation for the 40 low-lying singlet and triplet electronic states of the NiO molecule has been performed via CAS-SCF/MRCI and CASPT2 methods. The potential energy and the dipole moment curves have been determined along with the spectroscopic constants Te, re,  , and the rotational constant Be for the lowest-lying electronic states. The comparison of our results, for different states, with those obtained experimentally and theoretically shows a good agreement. By using the canonical functions approach [47,59-63], the eigenvalue Ev, the rotational constant Bv,
, and the rotational constant Be for the lowest-lying electronic states. The comparison of our results, for different states, with those obtained experimentally and theoretically shows a good agreement. By using the canonical functions approach [47,59-63], the eigenvalue Ev, the rotational constant Bv,
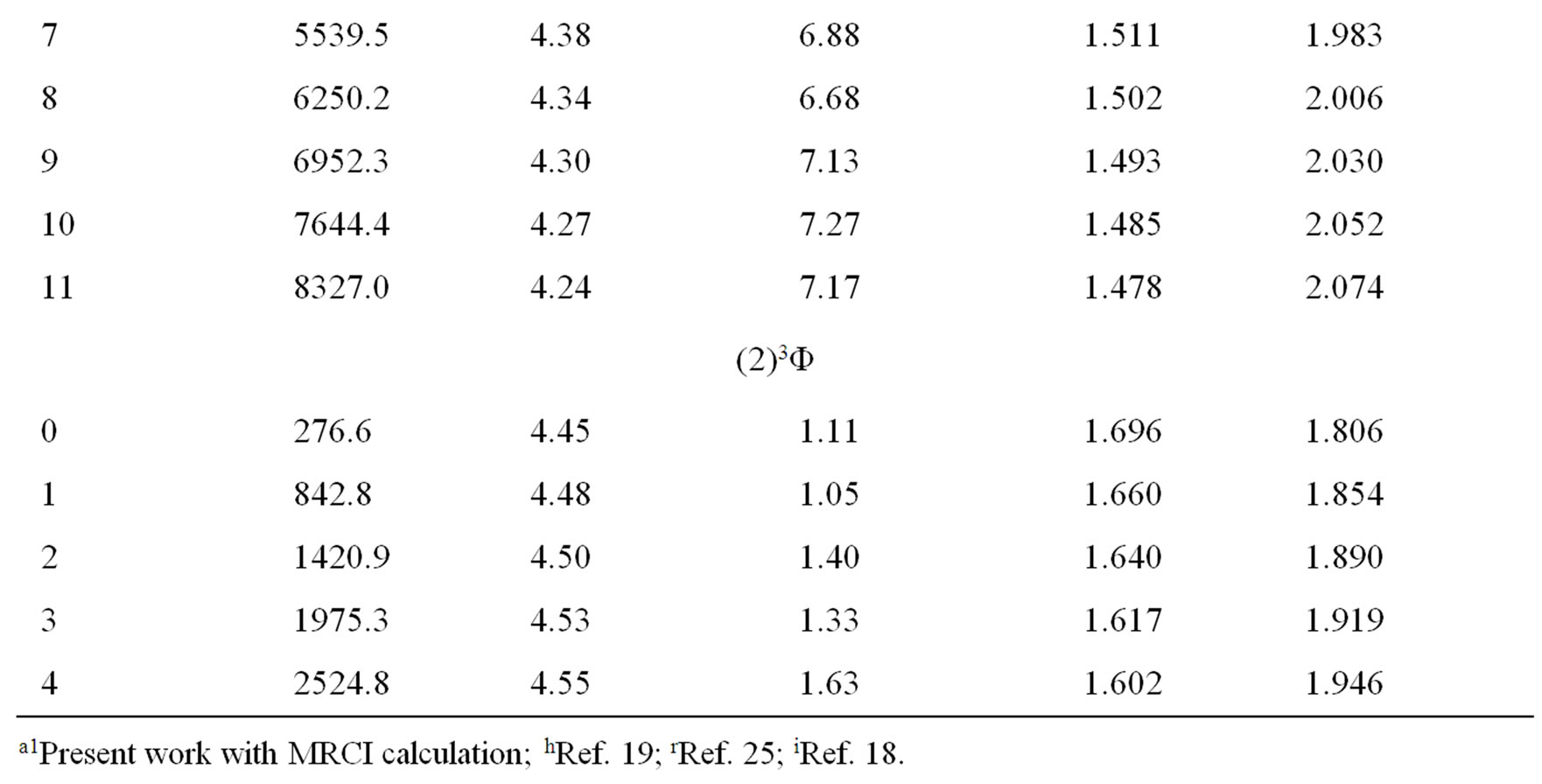
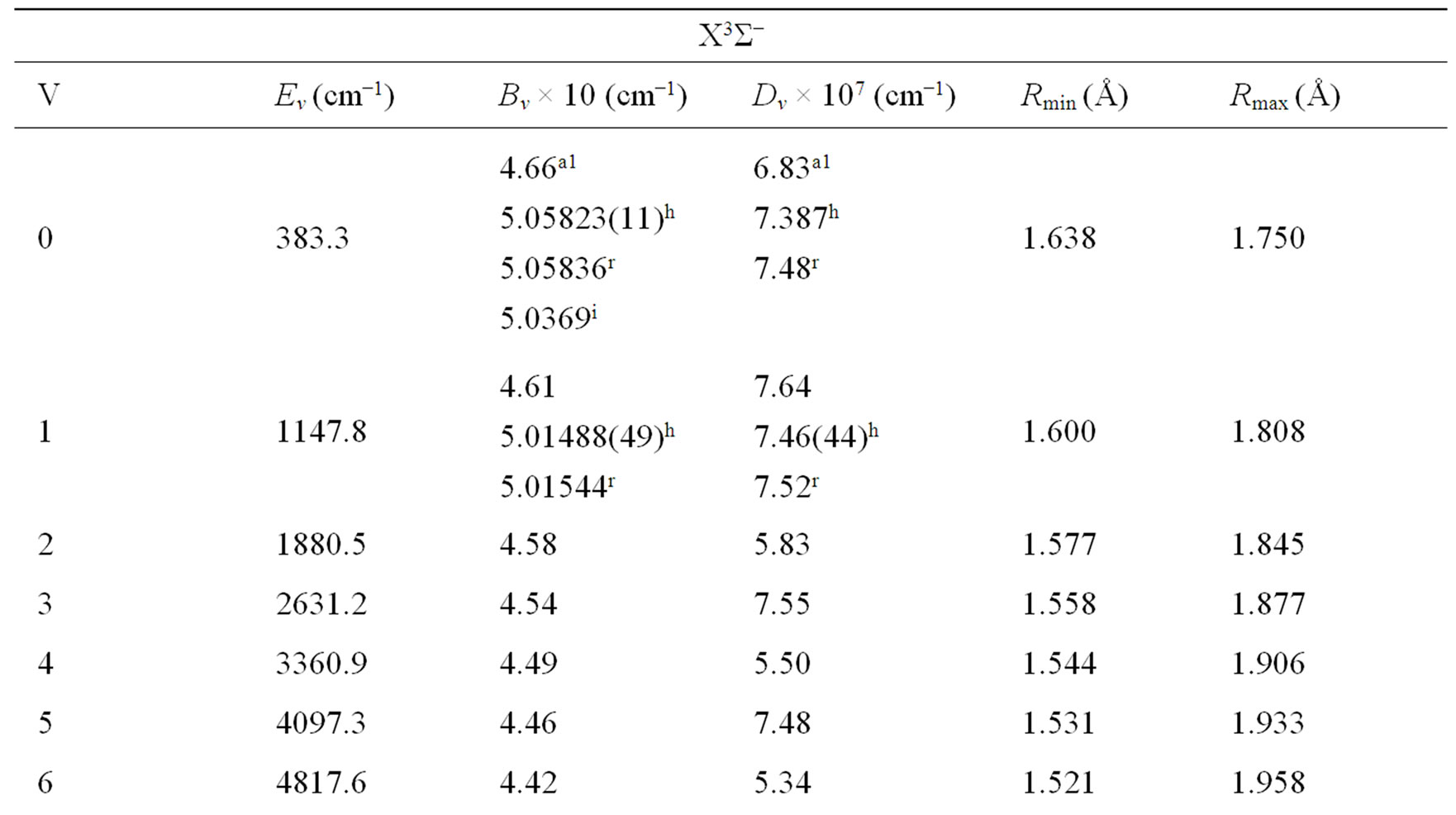
Table 2. Rovibrational calculation of the X3Σ– and (2)3Φ of the molecule NiO.
and the abscissas of the turning points rmin and rmax have been calculated up to the vibrational level v = 12. Eleven electronic states have been investigated in the present work for the first time.
REFERENCES
- A. J. Merer, “Spectroscopy of the Diatomic 3d Transition Metal Oxides,” Annual Review of Physical Chemistry, Vol. 40, 1989, pp. 407-438. doi:10.1146/annurev.pc.40.100189.002203
- R. W. Field, D. P. Baldwin, E. J. Hill, M. Li and M. C. McCarthy, “Spectroscopy Beyond Molecular Constants,” Spectrochimica Acta Part A: Molecular Spectroscopy, Vol. 45, No. 1, 1989, pp. 75-89. doi:10.1016/S0584-8539(89)80090-X
- F. J. Morin, “Electrical Properties of NiO,” Physical Review, Vol. 93, No. 6, 1954, pp. 1199-1204.
- D. Adler and J. Feinleib, “Electrical and Optical Properties of Narrow-Band Materials,” Physical Review B, Vol. 2, No. 8, 1970, pp. 3112-3134.
- A. J. Bosman and H. J. Van Daal, “Small-polaron versus Band Conduction in Some Transition-Metal Oxides,” Advances in Physics, Vol. 19, No. 77, 1970, pp. 1-117. doi:10.1080/00018737000101071
- P. Pushparajah and S. Radhakrishna, “Transparent conducting Lithium-Doped Nickel Oxide Thin Films by Spray Pyrolysis Technique,” Journal of Materials Science, Vol. 32, No. 11, 1997, pp. 3001-3006. doi:10.1023/A:1018657424566
- A. J. Bosman and Crrevecoeur, “Mechanism of the Electrical Conduction in Li-Doped NiO,” Physical Review, Vol. 144, No. 2, 1965, pp. 763-770.
- S. Van Houten, “Semiconduction in LixNi1−xO,” Journal of Physics and Chemistry of Solids, Vol. 17, No. 1-2, 1960, pp. 7-17. doi:10.1016/0022-3697(60)90169-4
- R. R. Heikes and W. D. Johnston, “Mechanism of Conduction in Li—Substituted Transition Metal Oxides,” Journal of Chemical Physics, Vol. 26, No. 3, 1957, pp. 582-588. doi:10.1063/1.1743350
- P. Lunkenheimer, A. Loidl, C. R. Ottermann and K. Bange, “Correlated barrier hopping in NiO films,” Physical Review B, Vol. 44, No. 11, 1991, pp. 5927-5930.
- S. A. Makhlouf, F. T. Parker, F. E. Spada and A. E. Berkowitz, “Magnetic anomalies in NiO nanoparticles,” Journal of Applied Physics, Vol. 81, No. 8, 1997, pp. 5561-5564. doi:10.1063/1.364661
- J. T. Richardson, D. I. Yiagas, B. Turk, K. Forster and M. V. Twigg, “Origin of superparamagnetism in Nickel Oxide,” Journal of Applied Physics, Vol. 70, No. 11, 1991, pp. 6977-6983. doi:10.1063/1.349826
- F. Bødker, M. F. Hansen, C. B. Koch and S. Mørup, “Particle interaction effects in antiferromagnetic NiO nanoparticles,” Journal of Magnetism and Magnetic Materials, Vol. 221, No. 1-2, 2000, pp. 32-36. doi:10.1016/S0304-8853(00)00392-9
- R. H. Kodama, S. A. Makhlouf and A. E. Berkowitz, “Finite Size Effects in Antiferromagnetic NiO Nanoparticles,” Physical Review Letters, Vol. 79, No. 7, 1997, pp. 1393-1396.
- B. Rosen, “Spectra of Diatomic Oxides by the Method of Exploded Wire,” Nature, Vol. 156, 1945, pp. 570-570. doi:10.1038/156570a0
- D. W. Green, G. T. Reedy and J. G. Kay, “Matrix-Isolated FeO, NiO, and CoO Ground-State Vibrational Frequencies,” Journal of Molecular Spectroscopy, Vol. 78, No. 2, 1979, pp. 257-266. doi:10.1016/0022-2852(79)90005-5
- V. I. Srdanov and D. O. Harris, “Laser Spectroscopy of NiO: the 3S− ground State,” Journal of Chemical Physics, Vol. 89, No. 5, 1988, pp. 2748-2753. doi:10.1063/1.455711
- E. J. Friedman-Hill and R.W. Field, “Analysis of the [16.0]3S−-X3S− and [16.0]S−-[4.3]3Пi band systems of the NiO Molecule,” Journal of Molecular Spectroscopy, Vol. 155, 1992, pp. 259-276. doi:10.1016/0022-2852(92)90516-Q
- R. S. Ram and P. F. Bernath, “Fourier Transform Infrared Emission Spectroscopy of a New A3Пi-X3S− System of NiO,” Journal of Molecular Spectroscopy, Vol. 155, 1992, pp. 315-325. doi:10.1016/0022-2852(92)90520-X
- S. P. Walch and W. A. Goddard III, “Electronic states of the Nickel Oxide Molecule,” Journal of the American Chemical Society, Vol. 100, No. 5, 1978, pp. 1338-1348. doi:10.1021/ja00473a002
- C. W. Bauschlicher Jr., “On the similarity of the bonding NiS and NiO,” Chemical Physics, Vol. 93, 1985, pp. 399- 404. doi:10.1016/0301-0104(85)87004-X
- C. W. Bauschlicher Jr., C. J. Nelin and P. S. Bagus, “Transition metal oxides: CrO, MoO, NiO, PdO, AgO,” Journal of Chemical Physics, Vol. 82, No. 7, 1985, pp. 3265-3277. doi:10.1063/1.448224
- M. Dolg, U. Wedig, H. Stoll and H. Preuss, “ab initi Pseudopotential Study of the First Row Transition Metal Monoxide and Iron Monohydride,“ Journal of Chemical Physics, Vol. 86, No. 4, 1987, pp. 2123-2131. doi:10.1063/1.452110
- E. G. Bakalbassis, M. D. Stiakaki, A. C. Tsipis and C. A. Tsipis, “Ground and Low-Lying Excited State Properties of the First-Row Transition-Metal Oxide Diatomics Calculated by an improved ASED-MO model,” Chemical Physics, Vol. 205, No. 3, 1996, pp. 389-399. doi:10.1016/0301-0104(95)00417-3
- K. Namiki and S. Saito, “Microwave spectrum of the NiO radical in the X3S−-state,” Chemical Physics Letters, Vol. 252, No. 5-6, 1996, pp. 343-347. doi:10.1016/0009-2614(96)00195-9
- H. Y. H. Chan, S. Zou and M. J. Weaver, “Mechanistic Differences between Electrochemical and Gas-Phase Thermal Oxidation of Platinum-Group Transition Metals as Discerned by Surface-Enhanced Raman Spectroscopy,” Journal of Physical Chemistry B, Vol. 103, No. 50, 1999, pp. 11141-11151. doi:10.1021/jp992500o
- T. Sasaki, N. Koshizaki and K. M. Beck, “Comparison of Pt/TiO2 nanocomposite Films Prepared by sputtering and Pulsed Laser Deposition,” Applied Physics A: Materials Science & Processing, Vol. 69, No. 7, 1999, pp. S771- S774. doi:10.1007/s003390051526
- L. Maya, L. Riester, T. Thundat and C. S. Yust, “Characterization of Sputtered Amorphous Platinum Dioxide Films,” Journal of Applied Physics, Vol. 84, No. 11, 1998, pp. 6382-6387. doi:10.1063/1.368883
- O. L. Shcheka, N. V. Dobrodey and T. B. Emelina, “Quantum Chemical Study of Catalysts Based on oxides of Transition Metals,” International Journal of Quantum Chemistry, Vol. 50, No. 3, 1994, pp. 181-188. doi:10.1002/qua.560500303
- G. Boschloo and A. Hagfeldt, “Spectroelectrochemistry of Nanostructured NiO,” Journal of Physical Chemistry B, Vol. 105, No. 15, 2001, pp. 3039-3044. doi:10.1021/jp003499s
- S. C. Su, J. N. Carstens and A. T. Bell, “A Study of the Dynamics of Pd Oxidation and PdO Reduction by H2 and CH4,” Journal of Catalysis, Vol. 176, No. 1, 1998, pp. 125-135. doi:10.1006/jcat.1998.2028
- V. Biju and M. Abdul Khadar, “Dielectric properties of nanostructured nickel oxide,” Journal of Materials Science, Vol.38, 2003, pp. 4055-4063. doi:10.1023/A:1026131103898
- J. R. Mc Bride, G. W. Graham, C. R. Peters and W. H. Weber, “Growth and characterization of reactively sputtered thin—film Platinum Oxides,” Journal of Applied Physics, Vol. 69, No. 3, 1991, pp. 1596-1605. doi:10.1063/1.347255
- A. Citra, G. V. Chertihin and L. Andrews, “Reactions of Laser-Ablated Nickel Atoms with Dioxygen. Infrared Spectra and Density Functional Calculations of Nickel Oxides NiO, ONiO, Ni2O2, and Ni2O3, Superoxide NiOO, Peroxide Ni(O2), and Higher Complexes in Solid Argon,” Journal of Physical Chemistry A, Vol. 101, No. 17, 1997, pp. 3109-3118. doi:10.1021/jp970019x
- K. P. Huber and G. Herzberg, “Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecules,” Van Nostrand Reinhold, New York, 1979.
- Saleh N. Abdul Al, Mahmoud Korek and Abdul Rahman Allouche, “Theoretical Electronic Structure of the lowest-Lying States of the YI molecule,” Chemical Physics, Vol. 308, No. 1-2, 2005, pp. 1-6. doi:10.1016/j.chemphys.2004.07.032
- M. Korek, Y. A. Moghrabi and A. R. Allouche, “Theoretical calculation of the Excited States of the KCs Molecule Including the Spin-Orbit Interaction,” Journal of Chemical Physics, Vol. 124, No. 9, 2006, Article ID: 094309. doi:10.1063/1.2173239
- M. Korek, S. Bleik and A. R. Allouche, “Theoretical calculation of the Low Laying Electronic States of the molecule NaCs with Spin-Orbit Effect,“ Journal of Chemical Physics, Vol. 126, No. 12, 2007, Article ID: 124313. doi:10.1063/1.2710257
- F. Taher-Mansour, A. R. Allouche and M. Korek, “Theoretical Electronic Structure of the Lowest-Lying States of ScCl molecule below 22,500 cm−1,” Journal of Molecular Spectroscopy, Vol. 248, No. 1, 2008, pp. 61-65. doi:10.1016/j.jms.2007.11.012
- M. Korek, S. Kontar, F. Taher-Mansour and A. R. Allouche, “Theoretical Electronic Structure of the molecule ScI,” International Journal of Quantum Chemistry, Vol. 109, No. 2, 2009, pp. 236-242. doi:10.1002/qua.21779
- M. Korek, S. Al-Shawa and G. A. Younes, “Theoretical calculation of the Electronic Structure of the molecule LiRb Including the Spin-Orbit Interaction,” Journal of Molecular Structure: THEOCHEM, Vol. 899, No. 1-3, 2009, pp. 25-31. doi:10.1016/j.theochem.2008.12.006
- M. Korek and S. N. Abdul-Al, “Rovibrational study and Dipole Moment Calculation of the molecule YF with Spin-Orbit Interaction,” Chemical Physics, Vol. 355, No. 2-3, 2009, pp. 130-134. doi:10.1016/j.chemphys.2008.11.022
- A. Hamdan, M. Korek, “Theoretical calculation of the Low-Lying Sextet Electronic States of CrF molecule,” Chemical Physics, Vol. 369, No. 1, 2010, pp. 13-18. doi:10.1016/j.chemphys.2010.01.023
- A. Hamdan, and M. Korek, “Theoretical calculation of the Low-Lying Quartet States of the CrF molecule,” Canadian Journal of Chemistry, Vol. 89, No. 10, 2011, pp. 1304-13011. doi:10.1139/v11-082
- A. Hamdan and M. Korek, “Theoretical study with vibration-rotation and Dipole Moment Calculations of Quartet States of the CrCl molecule,” International Journal of Quantum Chemistry, Vol. 111, No. 12, 2011, pp. 2960-2965. doi:10.1002/qua.22602
- J. R. Smith, H. Schlosser, W. Leaf, J. Ferrante and J. H. Rose, “Connection Between Energy Relations of Solids and Molecules,” Physic Review A, Vol. 39, 1989, pp. 514- 517.
- M. Korek, “A One Directional Shooting Method for the computation of Diatomic Centrifugal Distortion Constants,” Computer Physics Communications, Vol. 119, No. 2-3, 1999, pp. 169-178. doi:10.1016/S0010-4655(98)00180-5
- W. R. Wadt, P. J. Hay, “Ab initio Effective Core Potentials for Molecular Calculations. Potentials for the Transition Metal Atoms Sc to Hg,” Journal of Chemical Physics, Vol. 82, No. 1, 1985, pp. 270-284. doi:10.1063/1.448799
- N. Godbout, D. R. Salahub, J. Andzelm and E. Wimmer, “Optimization of Gaussian-Type Basis Sets for Local Spin Density Functional Calculations. Part I. Boron through neon, Optimization Technique and validation,” Canadian Journal of Chemistry, Vol. 70, No. 2, 1992, pp. 560-571. doi:10.1139/v92-079
- H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, P. Celani, T. Korona, G. Rauhut, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, C. Hampel, G. Hetzer, A. W. Lloyd, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklaß, P. Palmieri, R. Pitzer, U. Schumann, H. Stoll, A. J. Stone, R. Tarroni and T. Thorsteinsson, “MOLPRO is a package of ab initio programs.” http://www.molpro.net/info/molpro2006.1/molpro_manual
- A. R. Allouche, “Gabedit—A graphical user interface for Computational Chemistry Softwares,” Journal of Computational Chemistry, Vol. 32, No. 1, 2011, pp. 174-182. doi:10.1002/jcc.21600
- T. M. Ramond, G. E. Davico, F. Hellberg, F. Svedberg, P. Salén, P. Söderqvist and W. C. Lineberger, “Photoelectron Spectroscopy of Nickel, Palladium, and Platinum Oxide Anions,” Journal of Molecular Spectroscopy, Vol. 216, No. 1, 2002, pp. 1-14. doi:10.1006/jmsp.2002.8669
- V. D. Moravec and C. C. Jarrold, “Study of the LowLying States of NiO− and NIO Using Anion Photoelectron Spectroscopy,” Journal of Chemical Physics, Vol. 108, No. 5, 1998, pp. 1804-18011. doi:10.1063/1.475557
- H. Wu and L. S. Wang, “A study of Nickel Monoxide (NiO), Nickel Dioxide (ONiO), and Ni(O2) complex by Anion Photoelectron Spectroscopy,” Journal of Chemical Physics, Vol. 107, No. 1, 1997, pp. 16-21. doi:10.1063/1.474362
- O. Gropen, U. Wahlgren and L. Pettersson, “Effective core Potential Calculation on Small Molecules Containing Transition Metal Atoms,” Chemical Physics, Vol. 66, 1982, pp. 459-464. doi:10.1016/0301-0104(82)88047-6
- C. W. Bauschlicher Jr. and P. Maitre, “Theoretical study of the First Transition Row Oxides and Sulfides,” Theoretica Chimica Acta, Vol. 90, No. 2-3, 1995, pp. 189- 203. doi:10.1007/BF01113847
- S. C. Chung, S. Krüger, G. Pacchioni and N. Rösch, “Relativistic effects in the Electronic Structure of the Monoxides Andmonocarbonyls of Ni, Pd, and Pt: Local and Gradient-Corrected Density Functional Calculations,” Journal of Chemical Physics, Vol. 102, 1995, pp. 3693- 3701. doi:10.1063/1.468551
- R. L. Gattinger, E. J. Llewellyn and W. F. J. Evans, “Chemiluminescent NiO Emissions: Band Systems and Spectral Simulation,” Canadian Journal of Physics, Vol. 89, No 8, 2011, pp. 869-874. doi:10.1139/p11-068
- M. Korek and H. Kobeissi, “Diatomic Centrifugal Distortion Constants for a RKR potential: The Canonical Functions Method,” Journal of Molecular Spectroscopy, Vol. 145, No. 2, 1991, pp. 448-450. doi:10.1016/0022-2852(91)90131-S
- A. El-Hajj, H. Kobeissi and M. Korek, “SSM: a set of subprograms for Calculating Eigenvalues for a Diatomic Molecule Using a Simplified Shooting Method,” Computer Physics Communications, Vol. 74, No. 2, 1992, pp. 297-302. doi:10.1016/0010-4655(93)90099-X
- M. Korek and H. Kobeissi, “Highly accurate diatomic Centrifugal Distortion Constants for High Orders and High Levels,” Journal of Computational Chemistry, Vol. 13, No. 9, 1992, pp. 1103-1108. doi:10.1002/jcc.540130909
- H. Kobeissi and M. Korek, “One Compact Analytic Expression of the Diatomic Centrifugal Distortion Constants to Any Order,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 26, No. 3, 1993, pp. L35-L37. doi:10.1088/0953-4075/26/3/001
- M. Korek and H. Kobeissi, “Diatomic Centrifugal Distortion Constants for Large Orders at Any Level: Application to the
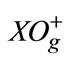 -I2 state,” Canadian Journal of Chemistry, Vol. 71, No. 3, 1993, pp. 313-317. doi:10.1139/v93-046
-I2 state,” Canadian Journal of Chemistry, Vol. 71, No. 3, 1993, pp. 313-317. doi:10.1139/v93-046
NOTES
*Corresponding author.

