Applied Mathematics
Vol.05 No.10(2014), Article ID:46891,5 pages
10.4236/am.2014.510154
An Improved Algorithm for the Solution of Generalized Burger-Fishers Equation
Morufu Oyedunsi Olayiwola1,2
1Department of Mathematical and Physical Sciences, Faculty of Basic & Applied Sciences, College of Science, Engineering & Technology, Osun State University, Osogbo, Nigeria
2Information Management & Technology Centre, Office of the Vice-Chancellor, Osun State University, Osogbo, Nigeria
Email: olayiwola.oyedunsi@uniosun.edu.ng
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 April 2014; revised 20 May 2014; accepted 28 May 2014
ABSTRACT
In this paper, an improved algorithm for the solution of Generalized Burger-Fisher’s Equation is presented. A Maple code is generated for the algorithm and simulated. It was observed that the algorithm gives the solution with less computation. The solution gives a better result when compared with the numerical solutions in the existing literature.
Keywords:
Algorithm, PDE, MVIM, Generalized Burger-Fisher’s Equation

1. Introduction
Generalized Burger-Fisher equation, being a nonlinear partial differential equation, is of great importance for describing the interaction between reaction mechanisms, convection effects, and diffusion transports. Since there exists no general technique for finding analytical solution of nonlinear diffusion equations so far, numerical solutions of nonlinear equations are of great importance in physical problems.
Many researchers [1] -[13] have used various numerical methods to solve Generalized Burger-Fisher. Recently Javidi [10] used modified pseudospectral method for generalized Burger’s-Fisher equation. Kaya [2] introduced a numerical simulation of the generalized Burger’s-Fisher equation. Ismail [8] presented a restructive pade approximation for the solution of the generalized Burger’s-Fisher equation. Hassan et al. [3] studied Adomian Decomposition Method (ADM) for generalized Burger’s-Huxley and Burger’s-Fisher equations.
Unlike some previous methods that used various transformations and several iterations, we present a new Modified Variational Iteration Method (MVIM) for the numerical solutions of generalized Burger-Fisher equation.
In Table 1, the results of MVIM were compared with those of ADM and VIM when
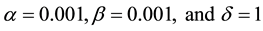 .
.
In Table 2, we compared MVIM, ADM and VIM results for 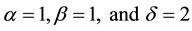 while in Table 3 the results are compared for
while in Table 3 the results are compared for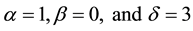 .
.
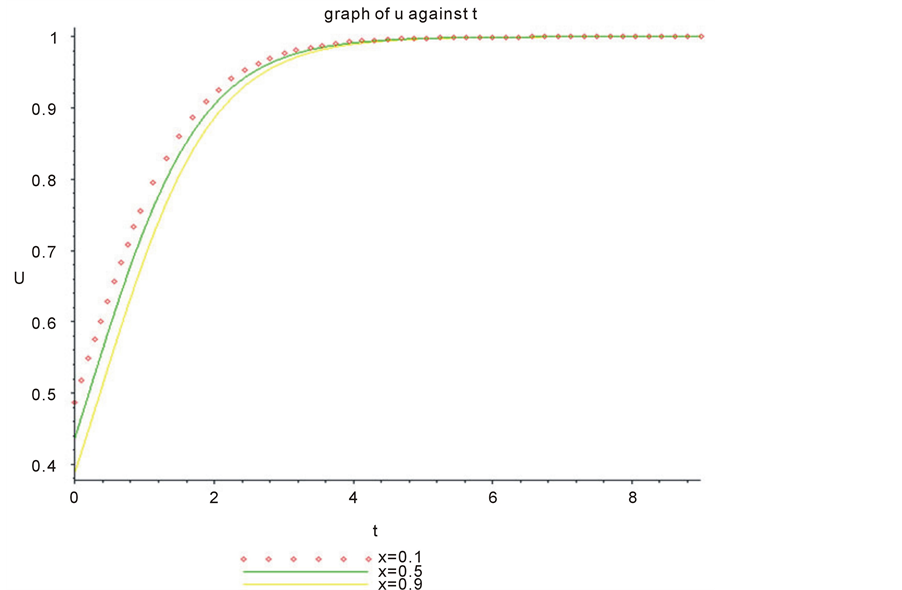
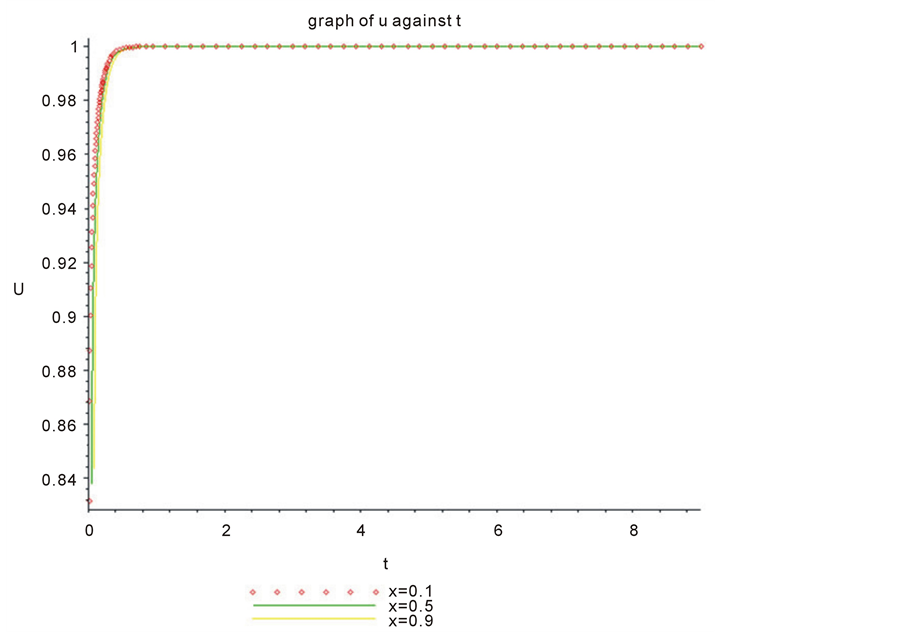
Figure 1 and Figure 2 show the graphical representation of gBF for various values of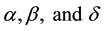 .
.
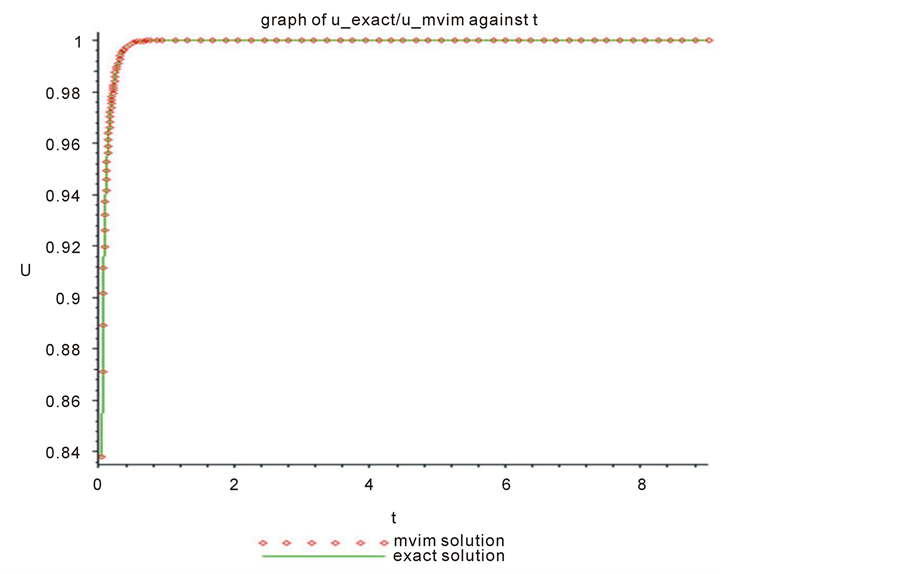
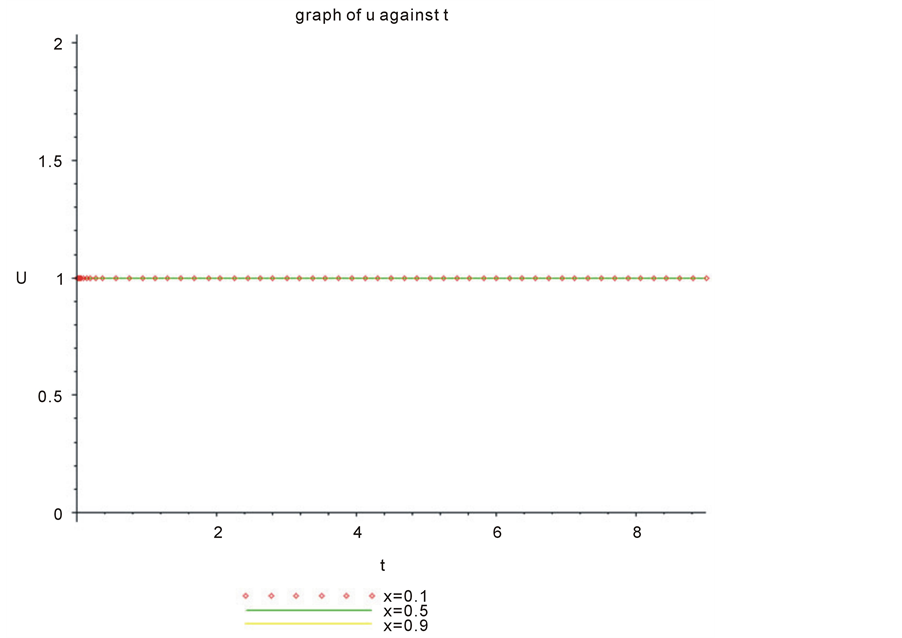
Figure 3 shows the graph of exact solution and MVIM solution. Figure 4 also represents graph of gBF when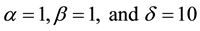 .
.
2. Modified Variational Iteration Method (MVIM)
The idea of variational iteration can be traced to Inokuti [9] . The variational iteration method was proposed by J.-H. He [4] - [7] , In this paper, a Modified Variational Iteration Method proposed by Olayiwola [11] - [14] is
Table 1. The Absolute error for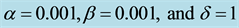 .
.
Table 2. The Absolute error for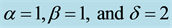 .
.
Table 3. The Absolute error for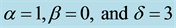 .
.
Figure 1. Graph of Burger-Fisher for .
.
Figure 2. Graph of gBF when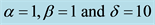 .
.
Figure 3. Graph of Exact /MVIM against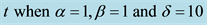
Figure 4. Graph of gBF when
presented for the solution of the generalized Burger-Fisher equation.
To illustrate the basic concept of the MVIM, we consider the following general nonlinear partial differential equation:
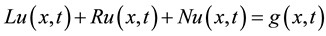
where L is a linear time derivative operator, R is a linear operator which has partial derivative with respect to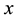
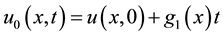
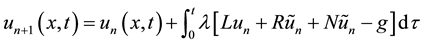
where 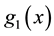

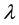
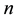
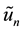
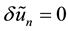
3. MVIM for the Solution of Generalized Burger-Fisher Equation
The following generalized Burger-Fisher (gBF) equation problems arising in various field of science is considered.
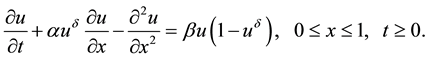
with the initial condition
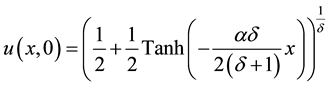
And the boundary conditions
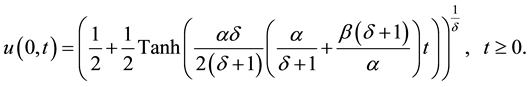
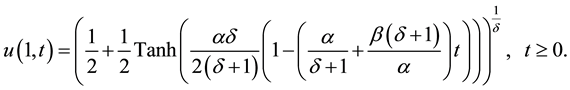
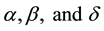
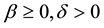
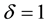
We used Maple to code (1.1 - 1.2) for the solution of (1.3 - 1.6) and the following results were obtained after one iteration:
When 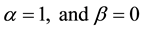
4. Results and Discussion
Tables 1-3 shows that the MVIM is the best approximant when compared with VIM and ADM. Figure 2 is the graph of Exact solution for the generalized Burger-fisher when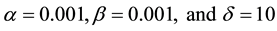
Figure 3 compares the graph of Exact with the MVIM. It is also to be noted that both graphs of Burger-Fisher and generalized Burger-Fisher as shown in Figure 1 and Figure 3, respectively, justify the conclusion that the two equations approaches the same steady state. However, as 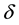
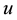
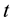
5. Conclusions
There are some important points to note here. First, the MVIM provides the solutions in terms of convergent series with easily computable components. Second, it is clear and remarkable that approximate solutions using MVIM are in good agreement. Third, the MVIM technique requires less computational work than many existing approaches. The MVIM was used in a direct way without using linearization, perturbation or restrictive assumptions.
The MVIM provides more realistic series solutions, very high accuracy, fast transformation and possibility of implementation of algorithm. The Algorithm makes it easier for the system to predict the next series.
References
- Goyal, A., Alka, R.G. and Kumar, C.N. (2011) Solitary Wave Solutions for Burgers-Fisher type Equations with Variable Coefficients. WASET, 60, 1742-1746.
- Kaya, D. and El-Sayed, S.M. (2004) A Numerical Simulation and Explicit Solutions of the Generalized Berger-Fisher Equation. Applied Mathematics and Computation, 152, 403-413. http://dx.doi.org/10.1016/S0096-3003(03)00565-4
- Ismail, H.N.A., Raslam, K. and Abd Rabboh, A.A. (2004) Adomian Decomposition Method for Generalized Burger’s- Huxley and Burger’s-Fisher Equation. Applied Mathematics and Computation, 159, 291-301. http://dx.doi.org/10.1016/j.amc.2003.10.050
- He, J.-H. (2000) Variational Iteration Method for Autonomous Ordinary Differential System. Applied Mathematics and Computation, 114, 115-123. http://dx.doi.org/10.1016/S0096-3003(99)00104-6
- He, J.-H. (1999) Variational Iteration Method―A Kind of Non-Linear Analytical Technique: Some Examples. International Journal of Non-Linear Mechanics, 34, 699-708. http://dx.doi.org/10.1016/S0020-7462(98)00048-1
- He, J.-H. (1998) Approximate Analytical Solution for Seepage Flow with Fractional Derivatives in Porous Media. Computer Methods in Applied Mechanics and Engineering, 167, 57-68. http://dx.doi.org/10.1016/S0045-7825(98)00108-X
- He, J.-H. (1998) Approximate Solution of Nonlinear Differential Equations with Convolution Product Nonlinearities. Computer Methods in Applied Mechanics and Engineering, 167, 69-73. http://dx.doi.org/10.1016/S0045-7825(98)00109-1
- Ismail, H.N.A. and Rabboh, A.A.A. (2004) A Restrictive Pade Approximation for the Solution of the Generalized Fisher and Berger-Fisher Equation. Applied Mathematics and Computation, 154, 203-210. http://dx.doi.org/10.1016/S0096-3003(03)00703-3
- Inokuti, M. (1978) General Use of the Lagrange Multiplier in Nonlinear Mathematical Physics. In: Nemat Nasser, S., Ed., Variational Method in the Mechanics of Solid, Pergamon Press, Oxford, 156-162.
- Javidi, M. (2006) Modified Pseudospectral Method for generalized Burger’s-Fisher Equation. International Mathematical Forum, 1, 1555-1564.
- Olayiwola, M.O., Gbolagade, A.W. and Akinpelu, F.O. (2011) An Efficient Algorithm for Solving the Nonlinear PDE. International Journal of Scientific and Engineering Research, 2, 1-10.
- Olayiwola, M.O., Gbolagade, A.W. and Adesanya, A.O. (2010) An Efficient Algorithm for Solving the Telegraph Equation. Journal of the Nigerian Association of Mathematical Physics, 16, 199-204.
- Olayiwola, M.O., Gbolagade, A.W. and Adesanya, A.O. (2010) Solving Variable Coefficient Fourth-Order Parabolic Equation by Modified initial guess Variational Iteration Method. Journal of the Nigerian Association of Mathematical Physics, 16, 205-210.
- Olayiwola, M.O., Akinpelu, F.O. and Gbolagade, A.W. (2012) Modified Variational Iteration Method for the Solution of a Class of Differential Equations. American Journal of Computational and Applied Mathematics, 2, 228-231. http://dx.doi.org/10.5923/j.ajcam.20120205.05