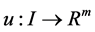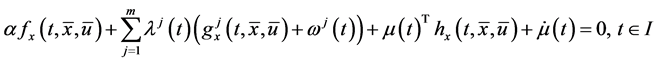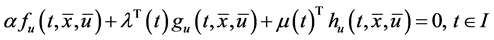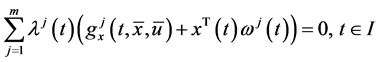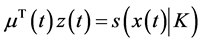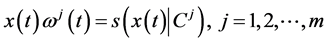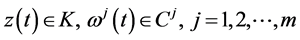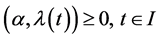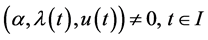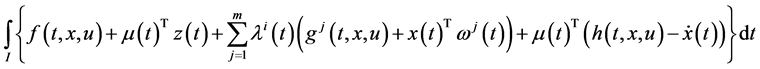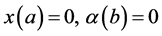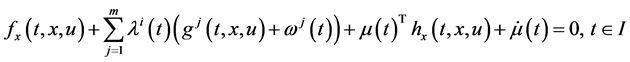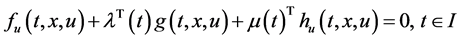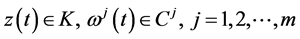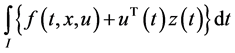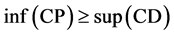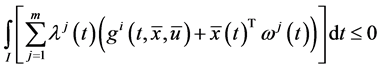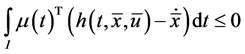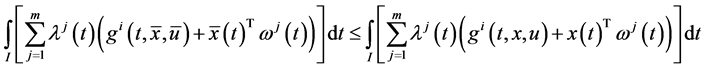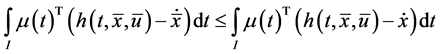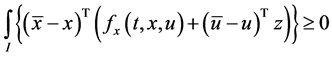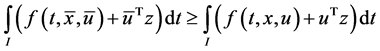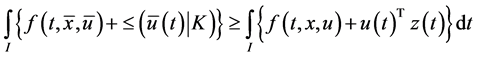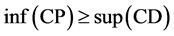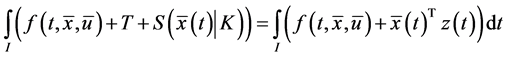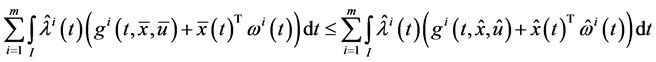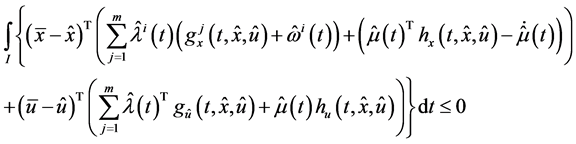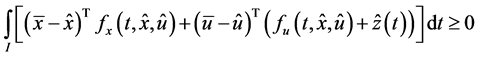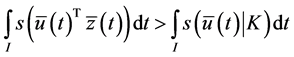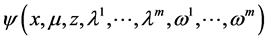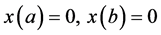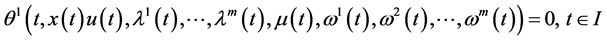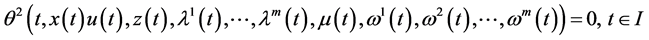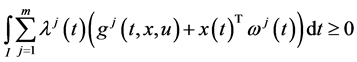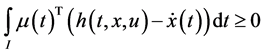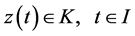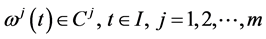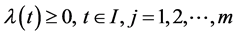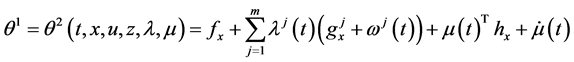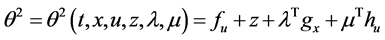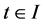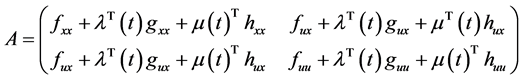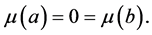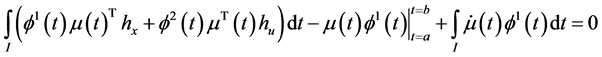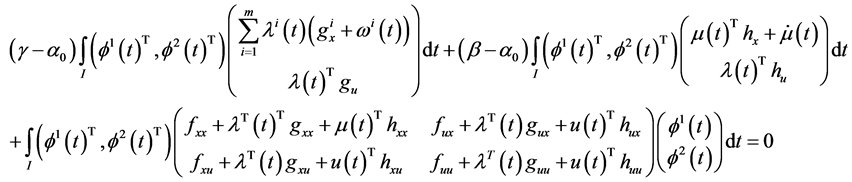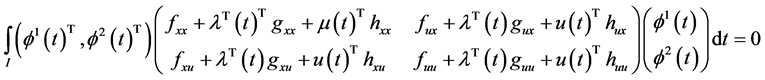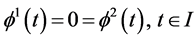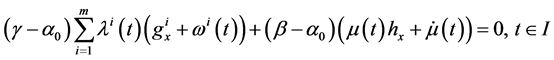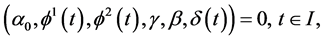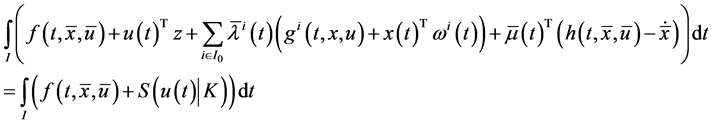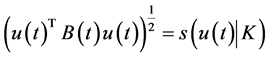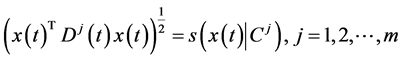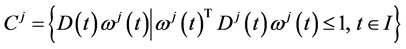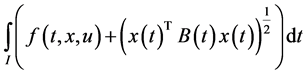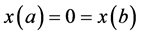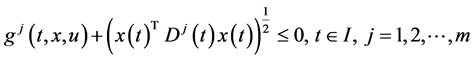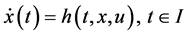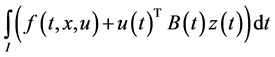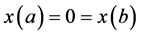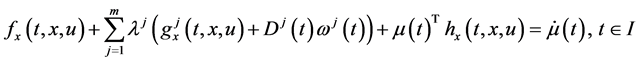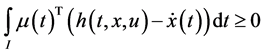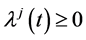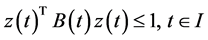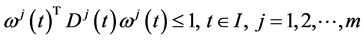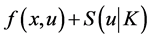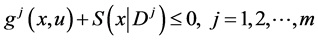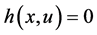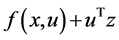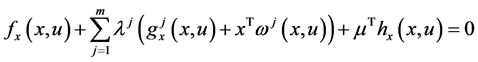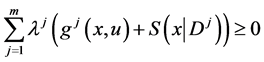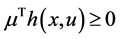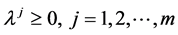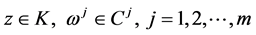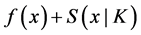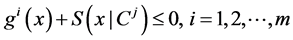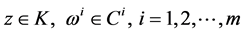Applied Mathematics
Vol.05 No.21(2014), Article ID:52592,11 pages
10.4236/am.2014.521330
Duality for a Control Problem Involving Support Functions
I. Husain1, Abdul Raoof Shah2, Rishi K. Pandey1
1Department of Mathematics, Jaypee University of Engineering and Technology, Guna, India
2Department of Statistics, University of Kashmir, Srinagar, India
Email: ihusain11@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 September 2014; revised 12 October 2014; accepted 8 November 2014
ABSTRACT
Mond-Weir type duality for control problem with support functions is investigated under generalized convexity conditions. Special cases are derived. A relationship between our results and those of nonlinear programming problem containing support functions is outlined.
Keywords:
Control Problem, Support Function, Generalize Convexity, Converse Duality, Nonlinear Programming

1. Introduction and Preliminaries
Consider the following control problem containing support functions introduced by Husain et al. [1]
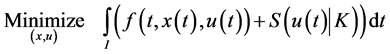
subject to
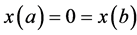 (1)
(1)
 (2)
(2)
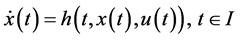 (3)
(3)
where
1) 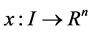 is a differentiable state vector function with its derivative
is a differentiable state vector function with its derivative 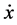 and
and 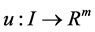 is a smooth control vector function.
is a smooth control vector function.
2) 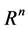 denotes an n-dimensional Euclidean space and
denotes an n-dimensional Euclidean space and 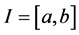 is a real interval.
is a real interval.
3) ,
, 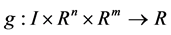 and
and 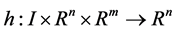 are continuously differentiable.
are continuously differentiable.
4)  and
and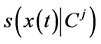 ,
, 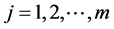 are the support function of the compact set K and
are the support function of the compact set K and  respectively.
respectively.
Denote the partial derivatives of f where by ft, fx and ft,
where superscript denote the vector components. Similarly we have ht, hx, hu and gt, gx, gu. X is the space of continuously differentiable state functions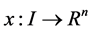

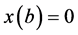
the norm 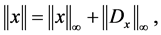
having the uniform norm 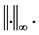
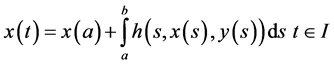
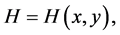
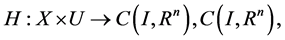
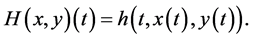
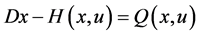
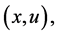
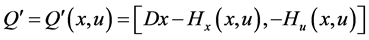
Proposition 1. (Fritz John Condition): If 


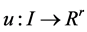
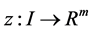
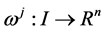
As in [3] , Husain et al. [1] pointed out if the optimal solution for (CP) is normal, then the Fritz john type optimal conditions reduce to the following Karush-Kuhn-Tucker optimal conditions.
Proposition 2. If 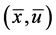
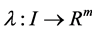
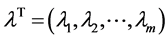



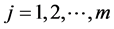
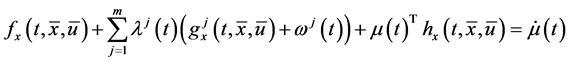

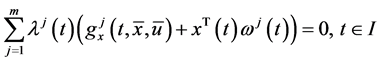
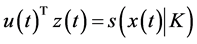
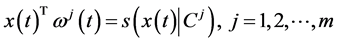
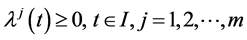

Using the Karush-Kuhn-Tucker type optimality condition given in Proposition 2, Husain et al. [1] presented the following Wolfe type dual to the control problem (CP) and proved usual duality theorem under the pseudo-
convexity of 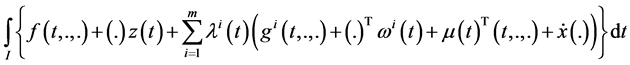
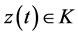

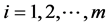
(WCD): Maximize
subject to
We review some well known facts about a support function for easy reference. Let 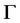
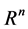


A support function, being convex and everywhere finite, has a subdifferential in the sense of convex analysis, that is, there exists 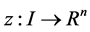
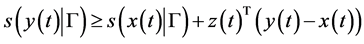
ferential of 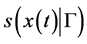
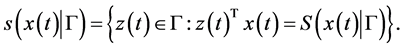

cone at a point 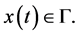
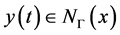
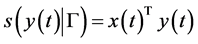
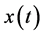
In order to relax the pseudoconvexity in [1] , Mond-Weir type dual to (CP) is constructed and various duality theorems are derived. Particular cases are deduced and it is also indicated that our results can be considered as the dynamic generalization of the duality results for nonlinear programming problem with support functions.
2. Mond-Weir Type Duality
We propose the following Mond-Weir type dual (M-WCD) to the control problem (CP):
Dual (M-WCD): Maximize
subject to
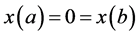
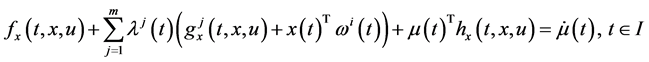
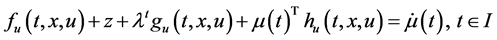

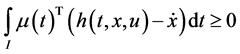
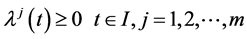
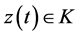
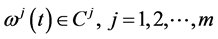
Theorem 1. (Weak Duality): Assume that
(A1): 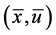
(A2): 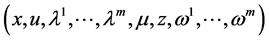
(A3): 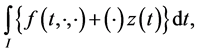
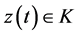
(A4): 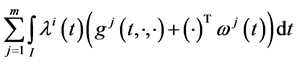
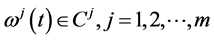
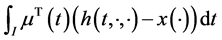
Then
Proof: Since 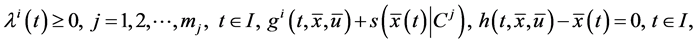
and
Combining these inequalities with (14) and (15) respectively, we have
and
These, because of the hypothesis (A4) yields
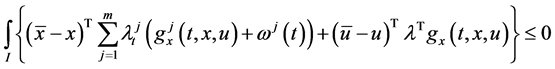
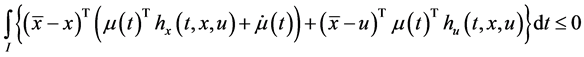
Combining (19) and (20) and then using (12) and (13), we have
This, due to the pseudoconvexity of 
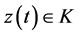
Since 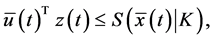
yielding
Theorem 2. (Strong Duality): If 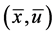

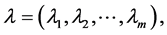
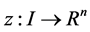
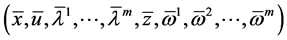
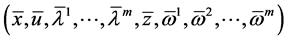
Proof: Since 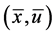
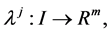
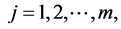
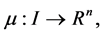
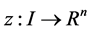
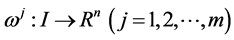
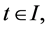
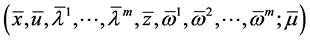
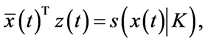
The equality of the objective functionals of the problems (CP) and (M-WCD) follows. This along with the hypotheses of Theorem 1, the optimality of 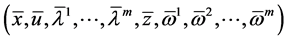
The following gives the Mangasarian type strict converse duality theorem:
Theorem 3. (Strict Converse Duality): Assume that
(A1): 
(A2): 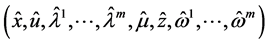
(A3): 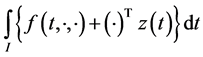

(A4): 
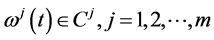
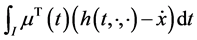
Then 
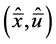
Proof: Assume that 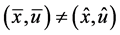

(CP). By Theorem 2 there exist 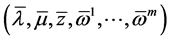
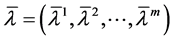
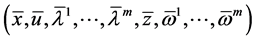
Thus

Since 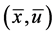
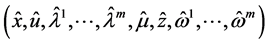
and
These, because of the hypothesis (A4) imply the merged inequality
This, by using the equality constraints (12) and (13) of (M-WCD) gives
By the hypothesis (A2), this implies
(using (21)). Consequently, we have
Since 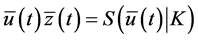
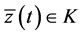
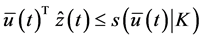
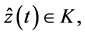
This cannot happen. Hence
3. Converse Duality
The problem (M-WCD) can be written as the follows:
Maximize:
subject to
where
Consider 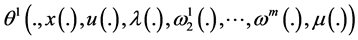
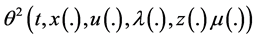
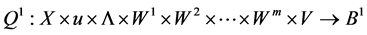
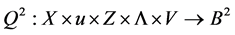
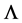
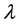
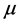

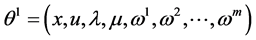
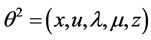
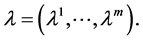
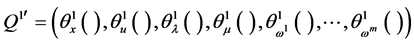
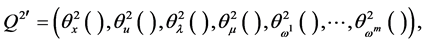
Theorem 4. (Converse Duality): Assume that
(A1): 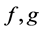
(A2): 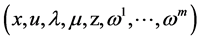
(A3): 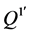
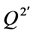
(A4): 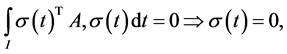

(A5): 1) The gradient vectors 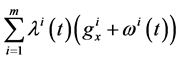
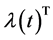
2) The gradient vectors 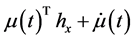
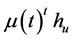
(A6):
Proof: Since 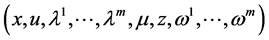

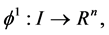
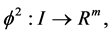
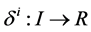
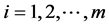
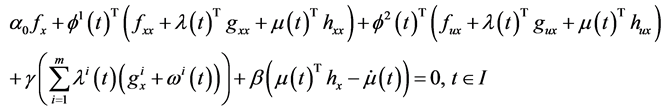
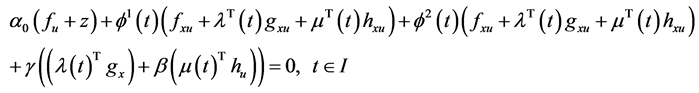
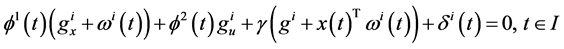
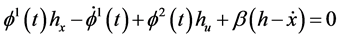
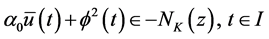
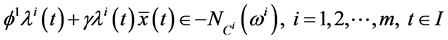
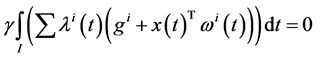
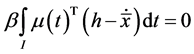
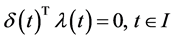
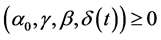

Multiplying (24) by 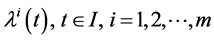
which can be written as,
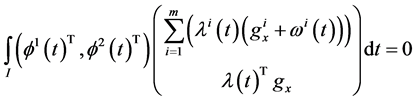
Multiplying (25) by 
This implies
or
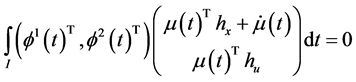
Using the equality constraints (12) and (13) of the problem (M-WCD) in (22) and (23), we have
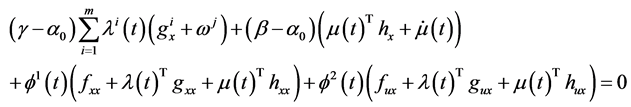
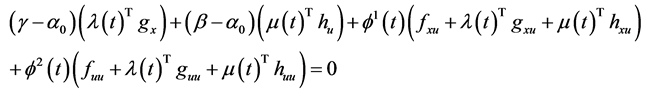
Combining (35) and (36), we have
This by premultiplying by 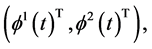
Using (33) and (34), we have
This because of hypothesis (A4) implies
Using 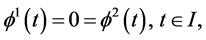
This, because of hypothesis (A5) implies
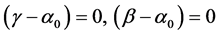
Assume 
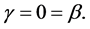
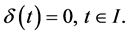
contradicting (32). Hence 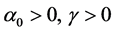
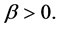
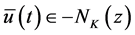
yielding 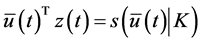
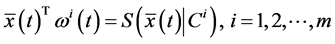
From (24), we have
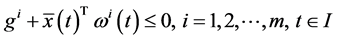
and

From (25), we have
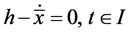
and

The feasibility of 
Consider
(by using 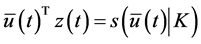
This along with the generalized convexity hypotheses implies that 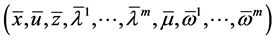
4. Special Cases
Let for 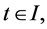
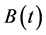
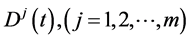
where
and
where
Replacing the support function by their corresponding square root of a quadratic form, we have:
Primal (CP0): Minimize
subject to
(M-WCD0): Maximize
subject to
The above pair of nondifferentiable dual control problem has not been explicitly reported in the literature but the duality amongst (CP0) and (M-WCD0) readily follows on the lines of the analysis of the preceding section.
5. Related Nonlinear Programming Problems
If the time dependency of the problem (CP) and (M-WCD) is removed, then these problems reduce to the following problem (NP), its Mond-Weir dual (M-WND):
Primal (NP0): Minimize
subject to
Dual (M-WND0): Maximize
subject to
The above nonlinear programming problems with support functions do not appear in the literature. However, if 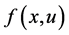
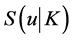

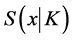
(P1): Minimize
subject to
(M-WCD): Maximize
subject to
6. Conclusion
Mond-Weir type duality for a control problem having support functions is studied under generalized convexity assumptions. Special cases are deduced. The linkage between the results of this research and those of nonlinear programming problem with support functions is indicated. The problem of this research can be revisited in multiobjective setting.
Cite this paper
I. Husain,Abdul Raoof Shah,Rishi K. Pandey, (2014) Duality for a Control Problem Involving Support Functions. Applied Mathematics,05,3525-3535. doi: 10.4236/am.2014.521330
References
- 1. Husain, I., Ahmad, A. and Shah, A.R. (2014) On a Control Problem with Support Functions. (Submitted for Publication)
- 2. Craven, B.D. (1978) Mathematical Programming and Control Theory. Chapman and Hall, Landon.
http://dx.doi.org/10.1007/978-94-009-5796-1 - 3. Mond, B. and Hanson, M. (1968) Duality for Control Problem. SIAM Journal on Control, 6, 114-120.
http://dx.doi.org/10.1137/0306009 - 4. Husain, I., Abha and Jabeen, Z. (2002) On Nonlinear Programming with Support Function. Journal of Applied Mathematics and Computing, 10, 83-99.