Psychology
Vol.09 No.04(2018), Article ID:84339,20 pages
10.4236/psych.2018.94054
A Consideration on Emotional Topology: Verbal Data Processing and Representation Applied to Athlete Statements
Koichiro Aoki1,2*, Hiroyuki Hirahara1, Chieko Kato2, Kensei Tsuchida2
1Graduate School of Science and Engineering, Saitama University, Saitama, Japan
2Department of Information Sciences and Arts, Toyo University, Saitama, Japan
Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 27, 2018; Accepted: April 27, 2018; Published: April 30, 2018
ABSTRACT
In order to analyze emotional state and movement for desirable life, we considered a topological analysis of mind for the representative people whom were, in this case, athletes. The utterances were acquired from online articles that included statements they made during interviews. The sampled data was processed with TF-IDF, BLSOM, and fuzzy clustering technique. The resultant mapping provides a typical emotional state and movement in the extracted axes so that one can discuss the athletes’ psychological transition on this map. The proposed procedure was significantly effective at presenting the player’s emotional interest and motivation.
Keywords:
Psychological Measurement and Evaluation, Topological Mapping, Verbal Data Processing and Representation, Self-Organizing Maps (SOM), Fuzzy Cluster Analysis

1. Introduction
1.1. Background of the Present Study
States of mind demonstrate significant variation, so their diagnoses are an incredible task for researchers. In order to perceive an individual’s state of mind, many visualization techniques have been developed in science, engineering, medicine, and other fields. In the present paper, we will discuss a visualization technique with which to represent mental states and motions. Since emotion has no entity, the representation technique requires technical knowledge to analogize relationships between an event and emotion. In extant literature, we are able to find some pioneer studies on the general representation relating to art, culture, education, and psychology, and so on, such as the pattern variation of literature ( Inami et al., 2013 ), the relations in a human group ( Namekawa et al., 2014 ), and the counseling record and the characterization of personality (Heliang et al., 2014) . Traditionally, an individual mind has been inspected and evaluated by psychology experts in each particular field. A specially developed visualization technique in each category has been adapted to diagnostics to communicate knowledge among psychology experts, or the professional and the layperson. In this paper, we will discuss an emotional topology with a unique visualization method that employs mathematical analysis to recognize an individual’s emotional states, emotion, and changes.
Now, in the realm of psychological support, the process of resolving or preventing psychological problems and facilitating recovery from mental illness often requires accurate recognition of individuals’ mental state. According to recent developments in culture and thought, as well as the drastic progression in communication protocol, the psychological states of individuals represent a variety of forms and diverse styles. Therefore, we must comprehend and digest complex problems and anxieties. A client’s accurate psychological assessment is vital for third parties to provide mental support that accounts for individual cases and diverse, complex, challenges.
These previous assessments have been performed according to the policy of the researchers and the situation of each object. The psychological assessment protocol should be selected depending on the methodology of each research field. Here, the common protocols that have been used in previous research are as follows: 1) case event information collection, 2) information analysis and support planning, 3) change identification and treatment improvement ( Arai & Shoji, 2014 ). For protocol 1), we used to adopt some methods, such as an interview, an observation, or psychological tests, and so on, so that the data regarding the psychological state and characteristics of the client could be acquired. In this process, it is necessary not only to conduct the surveys using questionnaires, but also to collect the data widely by focusing on a client’s utterances through an interview in order to clarify the problems and psychological features for each individual.
In addition, in qualitative assessments and surveys including interviews, advanced expertise is required to collect, analyze, and evaluate effective data. Therefore, psychological counselors bear heavy burdens in facing the difficulty of sharing a common recognition between the clients and counselors about the evidence of the assessment. Nowadays, since we perform such assessments by involving different experts and teams, a systematic protocol should be developed with identification regarding recognition for the client’s situation by experts and non-experts alike. For this sake, quantitative analysis should be applied to qualitative data, such as utterances in an interview, to extract essential property. Thus, effective visualization of the clients’ characteristics is an inevitable process for intuitive recognition.
1.2. Proposal of the Present Study
The present study was conducted with quantitative analysis by using a text mining on the utterances of objectives in an interview-based article that appeared on the internet. Based on the utterances of the targets in the interview, we tried to quantify the psychological state of each person. In the present study, an interesting technique has been proposed to visualize the relevance and time sequence of multidimensional data, via transformation into two dimensions by combining self-organizing maps (SOM; Kohonen, 1995 ; Kanaya et al., 2001 ). Such an approach is a nonlinear analysis method with unsupervised learning and fuzzy cluster analysis, which is effective as a processing tool to quantify an ambiguity that is inherently included in natural language processing ( Shinkai, 2008 ).
1.3. Previous Studies
1.3.1. Text Mining with Verbal Analysis
First, let us describe text mining with verbal analysis. This technique is well known as a method of applying quantitative analysis on text data (e.g., a speech, description, newspaper article, novel sentences, and other types of communication). The vector space method ( Salton et al., 1975 ) is known as an attractive technique for searching and classifying the documents. By using this method, the individual documents are characterized with vectors (the frequency at which keywords appear as specific phrases included in the document, which are referred to as document vectors in this study), and retrieval and classification is possible. Now, since the number of keywords corresponds to the dimension of the vector (i.e., the number of components), the document vectors usually constitute multidimensional vector data. In order to classify and cluster such multidimensional data, a suitable technique has been used to reduce the dimension, such as latent semantic indexing (LSI; Deerwester et al., 1990 ), principal component analysis, factor analysis, and so on. These analyses make it possible to reduce a high-dimensional document vector to a low-dimensional space so that we can obtain a representation with two- or three-dimensional charts to provide as an overview of our understanding. Such processing is very effective and fruitful, whereas an essential information loss is inevitably involved. In addition, since the document vectors that are quantified by text mining in interviewing, etc., are fundamentally qualitative data, we cannot expect a linear correlation and should suppose a more complicated correlation structure.
For this reason, we propose an effective combination of SOM and fuzzy cluster analysis. SOM is a nonlinear analysis method that makes it possible to visualize the classified result on a two-dimensional plane. An important advantage of SOM is that the data can be analyzed while maintaining the topological order of data in a multidimensional space. In addition, by classifying the data on the two-dimensional map that is obtained as the output result, there is a possibility of interpreting the psychological state indicated for each individual and extracting a primary emotional axis for psychological evaluation.
1.3.2. Evaluation of Axes of Emotion
The previous studies ( Wundt, 1924 ; Russell, 1980) revealed that emotions, as a transient psychological state, are divided into two- or three-dimensional axes (i.e., “pleasure-displeasure” and “activation-deactivation” or “tension-relaxation” and “excitement-depression”). Sakairi et al. (2013) reported that the psychological scale based on these evaluation axes, as shown in Figure 1, was a useful way to quantitatively describe the psychological state of the subject and its time sequential change. As shown in previous research, a psychological metric for measuring emotions is introduced and the measurement results using the scale are reduced by factor analysis. Following this analysis, two- or three-dimensional evaluation axes have been extracted as an important general factor in emotion. Then, we can use them as an index to capture the difference of emotions occurring between different groups and the time sequential change in emotion.
In the present study, psychological features indicated by verbal data are quantified and analyzed with multidimensional document vectors. Now, a novel processing procedure has been proposed, in which the psychological state evaluation axis is not only restricted in the above two- or three-dimensional space, but it also represents the emotional base axes obtained by SOM. Consequently, the evaluated axis for psychological state will be determined from the distribution and transition of output data, which is deduced with SOM analysis. Therefore, we can expect an effective and efficient communication in exchanging the information about the psychological state or transient change of the subject between the investigators.
1.3.3. Psychological Evaluation of Athletes
As the first trial, we adopt this process to the utterances delivered by the athletes
Figure 1. Core affect and two-dimensional mood scale.
who are at the pinnacle of in some athletic field. With the analysis proposed in this study, we quantified the psychological state of individual athletes and visually expressed the transition. Actually, sports performance requires the acquisition of physical skills, technical skills, and mental skills to control psychological state. Athletes who engage in physical training need to understand their own physical condition in order to know what physical factors they should improve. For athletes to face mental training, it is necessary to understand the skills they possess or are missing, and also to understand the psychological state according the circumstances (e.g., by conducting an interview or questionnaire assessment). We developed an evaluation index of athletes’ psychological-competitive ability by using a questionnaire and confirmed the effectiveness of that approach ( Aoki et al., 2017 ). An analysis of athletes’ utterances in interviews is expected to clarify their psychological characteristics in more detail. Thus, there is significant meaning in the analysis on athletes’ utterances in the interview so that we visualize their psychological characteristics and share common recognition about them with the athletes themselves, coaches, managers, and so on.
In an attempt to visualize the psychological state of the sports group, we can apply the findings from the study by Takemura et al. (2014) , in which they performed SOM clustering based on the mental and physical features of each player on a rugby team. In the study, the relationship between physical and psychological features and personal attributes (e.g., positions, regulars, and substitutes) has been analyzed based on the result of clustering. However, it cannot cover an evaluation method relating to an individual psychological state that is based on certain criteria and method to visualize the transition. As an attempt to note a time sequential variation of the psychological state of the group and individual, Kobayashi et al. (2016) distributed a psychological scale questionnaire among a basketball team and visualized the result of each player in the two-dimensional coordinate plane.
Kobayashi et al.’s (2016) study described the effective visualization by using a two-dimensional plane in which the psychological changes of both groups and individuals can be visually grasped. In the present study, the use of SOM makes it possible for us to make such changes visible from the aspect that set the transition of phase. Consequently, we can realize an effective information transmission or communication that grasps the state and transition in the psychological phase space.
2. Processing for Emotional Topology
2.1. Concept of Processing Protocol
To analyze and visualize the verbal data, we proposed the following procedure as shown in Figure 2. The objects of analysis in the current inspection are athlete statements that are presented online. We will not aim to collect the verbal data directly from an athlete because we would like to treat naturally stated verbal data that they were not conscious of inspection. In the second step, the modal
Figure 2. Processing flow for emotional topology representation.
words will be selected from the collected words. The modal words will significantly reflect the psychological state of the subject, so the researcher should deliberately choose them. In the third step, the frequency of modal words (TF: term frequency) is counted, then the inverse document frequency (IDF) is calculated from the data. The significance of TF and IDF in the present processing is slightly different from the previous studies. The reason will be explained at a later point.
The next step has two processes, SOM and fuzzy cluster analyses. The input vectors for both types of processes are TF-IDF data. In fuzzy cluster analysis, assessment is focused on the representative vector in the SOM output layer, then the clustering of neurons, which constitutes the output layer, is performed with the representative vectors. Consequently, we can get the coordinates that are classified by using individual utterances and the area division on the output layer. In the last step, we will discuss the topological characteristics based on the coordinates, thus the features of clients (athletes) are obtained via psychological diagnostics.
2.2. Verbal Data Processing
2.2.1. Collection of Verbal Data
Articles in Japanese that contain interviews with athletes in swimming, baseball, golf, and so on, including Olympians and Paralympians, were collected as the source of data. The corresponding terms were obtained from these sources. In this process, the unit of data is an “utterance,” which is one paragraph in the interview statements. We can obtain several utterances for each athlete, and ultimately the source of data is constructed with utterances, , where , from interview articles.
2.2.2. Selection of Modal Words
As a preliminary language processing tool, morphological analysis by TTM ( Matsumura & Miura, 2009 ) was adopted on the source of data. In such analysis, the original source was fragmented into morphemes (i.e., some minimum units, such as a noun, verb, adjective, adverb, conjunction, and so on); that is, decomposing the utterances into the morphemes. Through this processing, 4418 sorts of morphemes were extracted from U. After the decomposition, 20 top-ranked words , where , were selected as modal words. Appearance frequency data of each modal word was obtained for ( and ).
2.2.3. Application of TF-DFs
We newly defined the TF-DF algorithm for quantitative evaluation. In this method, term frequency (TF, Luhn, 1957 ) and document frequency (DF) instead of inverse document frequency (IDF, Spärck Jones, 1972 ) are adopted and they imply the probability of a word appearance and a weight coefficient of the word over the documents, respectively. Thus, TF-DF involves a metric of frequency with weight for the word. The arithmetic equations are as follows:
(1)
(2)
(3)
Here, represents a total number of modal words in each utterance , and is a ratio of appearance of in . The variable is a total utterance number including . From the above, , which is the product of and , indicates the weight coefficient of each modal word in .
The TF-IDF method is considered to be effective at distinguishing various documents by emphasizing on differences between them. In contrast, the TF-DF method can cluster documents by weighting common words and increasing similarity between them. Because of that, we used the TF-DF method for weighting the appearance frequency data in consideration of fuzzy cluster analysis in the present study.
2.3. Verbal Data Representation
2.3.1. Self-Organizing Maps
SOM, a neural network algorithm proposed by Kohonen (1995) , is an effective technique for nonlinear mapping that converts multidimensional data into a low-dimensional space. This mapping consists of a two-layered structure as an input layer and an output layer (competitive layer). Usually, the output layer is two-dimensional, such as a grid or lattice. Each lattice is called a neuron, and vector data (representative vector) with a certain dimension is associated with the input data or vector, which is also allocated on each neuron.
In a usual SOM algorithm, each input vector is compared with all representative vectors, and a neuron (lattice) of which a representative vector has the smallest norm from the input vector is assigned as the winner neuron. As a result, the input vectors are classified into the output layer so that the input vectors with similar features are mapped on the neuron. Through some iteration, the representative vector is updated in such a manner as to approach the input vector. Such sequential self-learning-type algorithm causes the closer correlation between the representative vector and the input vector.
Now, we are able to find a variety of algorithms in SOM. Some algorithms are developed to make a cluster and extract the features in a good manner; however, some of them depend on the initial input vector distribution. Such dependency is not preferable for our task, so we adopted the batch-learning type of SOM (Batch Learning SOM: BLSOM). We used a BLSOM analysis program “BLSOMviewer”, which was created by Kanaya et al. (2001) . The details of this analysis are described below.
1) Setting the initial value of representative vector
In order to assign the initial value of a representative vector into each neuron of the output layer, a principal component analysis was carried out with the input vectors ( ), which is defined as follows.
(4)
Here, we used a reduced expression H for 20 of the i-components of h.
Eigenvectors and , the first and second principal components, and standard deviations and of the first and second principal component were obtained from this analysis. Using these values, the initial values of the representative vector, , where , is calculated with the next equation ( Kanaya et al., 2001 ).
(5)
(6)
(7)
where is the average of the input vector over . and are ceiling functions to give the smallest integer greater than or equal to x, and floor function to give the largest integer less than or equal to x, respectively.
2) Redistribution of input vectors
Each input vector is allocated to a suitable neuron, which is the smallest norm between the representative and input vectors in a 20-dimensional Euclidean space (i.e., which used to be called the winner neuron). In such a way, the input vector is redistributed in the map, then the representative vector is updated with input vectors. The sequence is as follows:
For j-th input vector,
, suppose that the representative vector,
, has the smallest Euclidean distance (i.e., norm in the modal words space, here a 20-dimension space). Thus, all of the vector elements
will be distributed into the space, 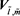 , which fulfills the following equations. The variable
, which fulfills the following equations. The variable  is the following learning parameter indicating the neighbor region of the winning neuron. It decreases as the iteration of learning increases.
is the following learning parameter indicating the neighbor region of the winning neuron. It decreases as the iteration of learning increases.
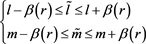 (8)
(8)
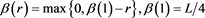 (9)
(9)
Here, r is the iteration number, which is incremented at each step of redistribution of input vectors, and the representative vectors are updated.
3) Update of representative vector
In order to assign the initial value of the representative vector into each neuron of the output layer, a principal component analysis has been carried out with the input vectors  (
( ), which is defined as follows.
), which is defined as follows.
After classification of all of the input vectors, the representative vector will be updated according to the following equation.
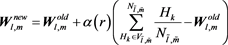 (10)
(10)
 (11)
(11)
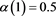 and
and  (12)
(12)
Here,  is called a learning rate coefficient, so it is a parameter for determining the convergence in updating the representative vector
is called a learning rate coefficient, so it is a parameter for determining the convergence in updating the representative vector . T is the iteration of learning.
. T is the iteration of learning. 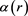 also decreases as the iteration of learning increases, thus the representative vector gradually converges to the optimum value.
also decreases as the iteration of learning increases, thus the representative vector gradually converges to the optimum value.
2.3.2. Fuzzy Cluster Analysis
Here we treat the representative vector as the representative matrix . The representative matrix
. The representative matrix  expresses a characteristic pattern about the emotional distribution. To extract the features of
expresses a characteristic pattern about the emotional distribution. To extract the features of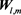 , fuzzy cluster analysis was conducted. In normal cluster analysis, it is assumed that an object belongs to one cluster (hard clustering), whereas fuzzy cluster analysis assumes that an object ambiguously belongs to any specific cluster. By using this concept, we can find the common properties among the objects that have multidimensional components. First of all, we shall calculate the correlation between all pairs of elements of
, fuzzy cluster analysis was conducted. In normal cluster analysis, it is assumed that an object belongs to one cluster (hard clustering), whereas fuzzy cluster analysis assumes that an object ambiguously belongs to any specific cluster. By using this concept, we can find the common properties among the objects that have multidimensional components. First of all, we shall calculate the correlation between all pairs of elements of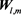



where 



Here, function-Max indicates the maximum value among each element product, which corresponds to the logical sum of regular reachability matrix calculus. After 

2.3.3. Visualization of Wl,m and Hj
As the result with BLSOM analysis, the representative matrix 


3. Result and Discussion
3.1. Calculation of Input Vector Hj
In this paper, we collected a total of 60 articles of NC = 60 players (one article per player) through web contents. Each article includes 5 - 20 utterances, so we obtained NU = 736 utterances from 60 player’s articles. The set of all utterances U was decomposed by TTM, so 4418 sorts of morphemes were generated. Through the frequency analysis, NM = 20 modal words, 


After estimating 



3.2. Clustering of Hj
Since the output of the analysis is that 






Now, we shall show some results if the threshold was changed to obtain a suitable clustering. After the processing of a reachability matrix, we obtained the following map. Figure 3(a) shows the color contour map of
According to the above processing, we can obtain various clusters by changing and considering the similarity R. Figure 4 shows several examples illustrating the clustering of



Now, we should determine a suitable set of clusters from these classifications. For adequate diagnosis, we selected a 10-cluster categorization with R = 0.79, in which we can see uniformly scattered clusters more than the others. In Figure 4,
Table 1. Modal words, Mi.


Figure 3. (a) Correlation distribution of 

Figure 4. Several clustersr of 
we can find an interesting categorization in this clustering. The results of 5, 6, 7, 8, 10, and 13 clusters are demonstrated according to R = 0.68, 0.73, 0.74, 0.78, 0.79 and 0.81, respectively. The numbers of clustered 


3.3. Psychological Interpretation of Wl,m
Before discussing the characteristics of 10 clusters in Figure 5 and Figure 6, we present a histogram of the vector components of 

The map is extracted again, as shown in Figure 7, with some additional features since a major modal word in each cluster has been tagged. Referring to these words, at a glance we can conceive positive and negative expression clusters; that is, CLs 6 and 7 are dominant with negative words and are located at the upper region, whereas the others are positive. CLs 8-10 present especially positive and rewarding emotional terms. In order to psychologically interpret this mapping, let us consider the kinematic similarity in emotion (i.e., the state of mind). The kinetics is used to expressing coordinates’ velocity and acceleration.
Figure 5. Vector components of 
Figure 6. Vector components of 
In addition to this principal, our emotion should be described dynamically with a state and motion. Namely, the state will be denoted in scalar and the motion in vector. Here, we will try to express the emotional transition with coordinates and vectors in the SOM table.
According to BLSOM analysis, we introduced some major axes in the map. Here, the solid arrows indicate scalar coordinates and dashed arrows portray vector coordinates. As shown in this mapping, we can find “displeasure” and “pleasure” states in the upper row and right column, and “active,” “tense,” and “ebullient” states in the bottom row. Furthermore, considering the transition between those state, “deactivation and activation,” “fighting spirit,” and “spontaneity” vectors are automatically discovered. The definition is not unique, of course, so one can find another interpretation instead of the present expression. Now, we will propose an effective expression, as shown in Figure 7, to understand the emotional state and transition for the athletes. As the template for the recognition of the present athlete’s emotional behavior, we will discuss the player’s psychological emotion in the final section.
Figure 7. Emotional characterization with 10 clustering.
3.4. Utterance Transition for Exemplary Players
In this section, we will discuss the emotional behavior according to the utterance transition for some players. Figures 8(a)-(c) show the sample mapping of exemplary players. In this analysis, we will not mention the properties of a player, such as his/her sports events, category, and so on.
Figure 8(a) shows the emotional transition of player #33. The circled number indicates the serial number of his/her utterance in the articles. Following the trajectory, one can see that the psychological change along the activation/deactivation axis dominates his/her subjects. The appropriate change is characterized in the refrain of modal word, such as “win” or “goal,” in utterances. The activation vector indicated by player #33 is closely related to his/her extrinsic motivation, which is proposed by Deci & Ryan (1985) ; that is, these words do not imply an emotional interest or fun about sport itself, but an irrelevant benefit as a substantial reward. Player #33 also indicates an almost constant transition on the map, thus a consistent attitude toward his/her competition, which may be encouraged by the extrinsic motivation.
Figure 8(b) shows a transition within player #47. The trajectory shows a departure within the displeasure zone. Seven out of twelve input vectors of this player are classified into CLs 6 and 7 on the output layer, which means that



Figure 8. Emotional transition of some sample players. (a) Player # 33; (b) Player # 47; (c) Player # 54.
his/her utterances often include negative words such as “bad,” “hard,” and so on. Other vectors are classified into CLs 4 and 5, which are related to activation and a fighting spirit. However, this player repeatedly shows the emotional transition to CLs 6 and 7. Therefore, his/her increase in a fighting spirit can be associated with the feeling of displeasure.
Figure 8(c) shows a transition of player #54. This player exhibits the emotional transition to CLs 8 and 9, which means his/her utterances sometimes include positive words such as “happy,” “enjoy,” and so on. This tendency also indicates his/her feeling of pleasure and attitude of spontaneity toward competition; that is, intrinsic motivation, which is proposed by Deci & Ryan (1985) . It is presumed that player #54 is simply blessed with an enjoyment for his/her sport.
4. Concluding Remarks
For the effective comprehension of emotional state and transition, an analysis procedure and recognition protocol has been proposed by using athletes’ interviews. The verbal data was decomposed with morphological analysis into some units such as morphemes, words, and utterances. From those data, by extracting major words, TF-IDF was estimated at first. After BLSOM and fuzzy cluster analysis, consequently, we obtained an emotional state and transition for individual interview articles. The following conclusion has been presented in this paper.
1) In order to determine the emotional mapping, the representative vector obtained by BLSOM is a very effective way to reveal the emotional coordinates. Furthermore, the combination with BLSOM and fuzzy cluster analysis gives more apparent discipline for psychological consideration.
2) Based on the present clustering technique, one can obtain the state and vector axes in emotion. Thus, the topological interpretation is available for the utterances of some subjects. In this paper, athletes’ interviews have been analyzed, and then 10 clusters and four axes of states and three principal vectors have been efficiently introduced.
3) In the present sampling from online interview articles, we tried to assess the athletes’ emotional state and movement by adopting the proposed protocol. We can recognize a representative pattern in their emotional transition, so the effectiveness of the present protocol is demonstrated.
4) The protocol in the present study can be utilized for the psychological assessment of clients or patients by means of processing of verbal data. The accumulation of analyzing data enables us to make a standard emotional axis and visualize a time sequential change. The present protocol will be applied to emotional assessments in a variety of general fields beyond athletics.
Cite this paper
Aoki, K., Hirahara, H., Kato, C., & Tsuchida, K. (2018). A Consideration on Emotional Topology: Verbal Data Processing and Representation Applied to Athlete Statements. Psychology, 9, 876-895. https://doi.org/10.4236/psych.2018.94054
References
- 1. Aoki, K., Uehara, M., Kato, C., & Hirahara, H. (2017). Evaluation of Rugby Players’ Psychological-Competitive Ability by Utilizing the Analytic Hierarchy Process. Open Journal of Social Sciences, 4, 103-117. [Paper reference 1]
- 2. Arai, M., & Shoji, I. (2014). Research of Assessment Process by Clinical Psychologists Focusing on Clinical Cases of Children and Adolescents: A Review. Japanese Journal of Counseling Science, 47, 11-19. [Paper reference 1]
- 3. Deci, E. L., & Ryan, R. M. (1985). Intrinsic Motivation and Self-Determination in Human Behavior. New York: Plenum. https://doi.org/10.1007/978-1-4899-2271-7 [Paper reference 2]
- 4. Deerwester, S., Dumais, S. T., Furnas, G. W., Landauer, T. K., & Harshman, R. (1990). Indexing by Latent Semantic Analysis. Journal of the Association for Information Science and Technology, 41, 391-407. https://doi.org/10.1002/(SICI)1097-4571(199009)41:6<391::AID-ASI1>3.0.CO;2-9 [Paper reference 1]
- 5. Heliang, Z., Kato, C., & Tsuchida, K. (2014). An Application of 3D Spiral Visualization to the Psychological Data. Transactions of Visualization Society of Japan, 34, 2-7. [Paper reference 1]
- 6. Inami, M., Saito, M., Horii, K., Hosoi, H., Yamagata, T., Fujisawa, N. et al. (2013). Visualization of “The Tale of Genji”. Transactions of Visualization Society of Japan, 33, 97-107. [Paper reference 1]
- 7. Kanaya, S., Kinouchi, M., Abe, T., Kudo, Y., Yamada, Y., Nishi, T. et al. (2001). Analysis of Codon Usage Diversity for Bacterial Genes with a Self-Organizing Map (SOM): Characterization of Horizontally Transferred Genes with Emphasis on the E. coli O157 Genome. Gene, 276, 89-99. https://doi.org/10.1016/S0378-1119(01)00673-4 [Paper reference 3]
- 8. Kobayashi, M., Uchida, R., & Tsuchiya, H. (2016). Proposal for a Framework Assessing the Psychological State of Sports Group: Two-Dimensional Approach from the Collective Efficacy and Group Cohesion. Japan Journal of Physical Education, Health and Sport Sciences, 61, 245-255. [Paper reference 2]
- 9. Kohonen, T. (1995). Self-Organizing Maps. In Springer Series in Information Sciences (Vol. 30). Berlin, Heidelberg, New York: Springer. [Paper reference 2]
- 10. Luhn, H. P. (1957). A Statistical Approach to Mechanized Encoding and Searching of Literary Information. IBM Journal of Research and Development, 1, 309-317. https://doi.org/10.1147/rd.14.0309 [Paper reference 1]
- 11. Matsumura, M., & Miura, A. (2009). Text Mining for Humanities and Social Sciences. Seishin Shobo. [Paper reference 1]
- 12. Namekawa, M., Shiono, Y., & Satoh, A. (2014). Visualization of Fuzzy Graph Model for Human Relations. Transactions of Visualization Society of Japan, 34, 26-30. [Paper reference 1]
- 13. Russell, J. A. (1980). A Circumplex Model of Affect. Journal of Personality and Social Psychology, 39, 1161-1178. https://doi.org/10.1037/h0077714 [Paper reference 1]
- 14. Sakairi, Y., Nakatsuka, K., & Shimizu, T. (2013). Development of the Two-Dimensional Mood Scale for Self-Monitoring and Self-Regulation of Momentary Mood States. Japanese Psychological Research, 55, 338-349. [Paper reference 1]
- 15. Salton, G., Wong, A., & Yang, C. S. (1975). A Vector Space Model for Automatic Indexing. Communications of the ACM, 18, 613-620. https://doi.org/10.1145/361219.361220 [Paper reference 1]
- 16. Shinkai, K. (2008). Fuzzy Cluster Analysis and Its Evaluation Method. Biomedical Fuzzy and human Sciences, 13, 3-9. [Paper reference 1]
- 17. Sparck Jones, K. (1972). A Statistical Interpretation of Term Specificity and Its Application in Retrieval. Journal of Documentation, 28, 11-21. https://doi.org/10.1108/eb026526 [Paper reference 1]
- 18. Takemura, Y., Yokoyama, M., Omori, S., & Shimosaka, R. (2014). Evaluation and Analysis of Relationship and Individual Role Adaptation for Team Sports Using SOM. Soft Computing in Artificial Intelligence, 270, 93-106. https://doi.org/10.1007/978-3-319-05515-2_9 [Paper reference 1]
- 19. Wundt, W. (1924). An Introduction to Psychology. London: Allen & Unwin. [Paper reference 1]
Nomenclature



NC: number of clients (or articles) = 60
NM: number of modal words = 20
NU: total number of utterances
NW: total number of words = 21007
R: similarity



c: client number,














i: modal words number,
j: utterance number,
l, m: SOM dimension, 






















