Theoretical Economics Letters
Vol.2 No.5(2012), Article ID:25924,6 pages DOI:10.4236/tel.2012.25100
A Decomposition of the Atkinson Index through the Shapley Value
Faculty of Economics, Autonomous University of San Luis Potosí, San Luis Potosí, México
Email: joss.sanchez@uaslp.mx, vick_tor_2000@hotmail.com
Received September 17, 2012; revised October 19, 2012; accepted November 20, 2012
Keywords: Atkinson Index; Shapley Value; Opportunity Inequality
ABSTRACT
This paper studies the economic inequality as a phenomenon resulting from two variables: The variable of responsibility which depends on the agents’ performance in the economy, and the variable of opportunity which is independent of the individuals’ performance in the economy. Identifying the contribution of the inequality of opportunity in the total inequality as the problem to be measured, we propose a decomposition of the Atkinson inequality index, by using one of the central solution concepts of cooperative game theory, called the Shapley value.
1. Introduction
“Social equality is an extremely complex notion” (Sen [1]). Walking on the streets of any city with a free market economic system, observing the behaviors and characteristics of the people, we find that economic inequality is a totally natural and usual aspect. The existence of such inequality is totally intuitive, because the citizens play economic activities with different characteristics of human capital and therefore they get different remunerations. If the problem of economic inequality were thought from this point of view, then there would be no need for questions or concernings at all, since it would only be a consequence of the individual decisions made by citizens, given their preferences. But if the economic inequality is very large, would be hard to believe that there are agents that would take decisions which would lead them to take certain spots of the economic structure, or worse, in an extreme case, to death for the lack of resources to survive; which tells us that the inequality is not necessarily a consequence of the different rational agents decisions. It is also important to mention that there is a close relationship between the rebellions propensity or fluctuations of insecurity in a population, and the economic inequality that this presents. Inequality must be therefore measured, because it is a strong indicator of the economic situation and could also describe more aspects of a defined territory or population. Following the current social welfare functions theory in Bergson-Samuelson [2], which defines that welfare must be based on the utility of the agents, breaking with the concept of welfare of Pareto which has no power of discrimination and therefore no useful judgment to the measure of this problem (see for instance Sen [1]). In order to rank welfare functions, Atkinson [3] assumes increasing, concave and equal functions of utility among the individuals and establishes some desirable characteristics1 that this ranking should have. He also looks for a measure of the total inequality which respects such ranking and based in this he defines the equaly distributed equivalent level of income, or the level of income per head which if equally distributed would give the same level of social welfare as the present distribution, and using this concept he defines an inequality index. Levy et al. [4] found this index as the only one that satisfies some desire properties in order to give a health benefits analysis. So in this work we will use this measurement to get the inequality of a given income distribution.
Inequality is an aspect that has been treated and observed throughout human history. Awakening the interest of the society, and humanitarian feelings, this topic has originated some spirit of solidarity and total apathy. Trying to focus on the income inequality problem, and explaining it as a result of two variables (responsibility and opportunity), the present work arises.
Following the welfare economics theory, that looks to provide a judgment criteria for a given income distribution, and using one of the main concepts of the cooperative games theory, which has been used to decompose inequality indices; and considering that economic inequality is not necessarily a result of the agents’ rational actions, we address the following questions: Given a level of economic inequality in a population1) How much inequality is due to the difference in opportunitiy for the population? and 2) How much inequality is due to their decisions?
This paper provides an identification of the contribution of the inequality of opportunity in the total inequality as the problem to be measured, we propose a decomposition of the Atkinson inequality index, by using one of the central solution concepts of cooperative game theory, called the Shapley value. With this we explain the participation of each of these variables in the total inequality for a given income distribution.
The application of the Shapley value algorithm to decompose inequality and poverty measures has been proposed by Shorrocks [5] and by Sastre and Trannoy [6] for inequality measures. We propose a modified application of the Shapley value which takes into account a multiplicative class of indices expressed in equality terms.
The paper is organized as follows. We first recall the main basic features of games in characteristic function form and Atkinson index. The equality of opportunity model is introduced in Section 3, taken out from Peragine [7]. In Section 4 we propose a decomposition of the Atkinson index, using the Shapley value to find the participation of the total inequality explanatory factors. Finally, Section 6 concludes.
2. Framework
In this section we provide some concepts and notation related to 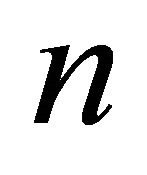 -person-person games in characteristic function form, as well as a brief subsection of preliminaries related to the Atkinson index.
-person-person games in characteristic function form, as well as a brief subsection of preliminaries related to the Atkinson index.
2.1. Games in Characteristic Function Form
By an n-person game2 in characteristic function form, in what follows just a game, we mean a pair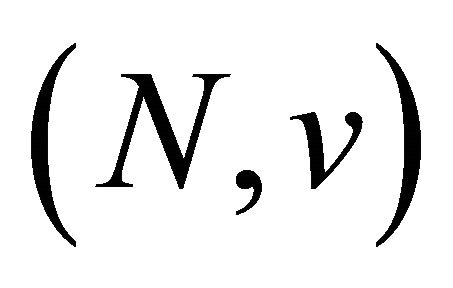 , where
, where 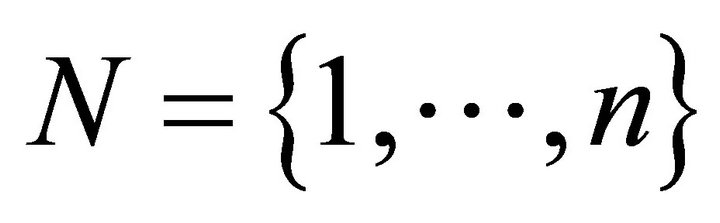 is a finite set of players and
is a finite set of players and 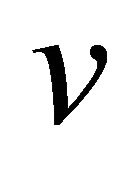 is a function
is a function 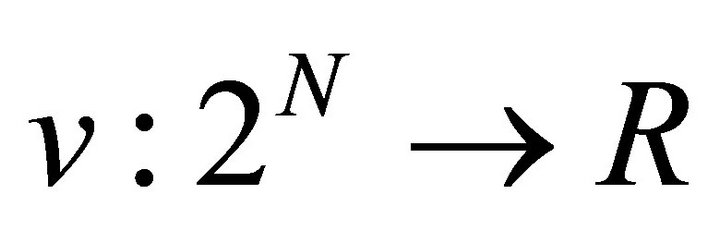 with the property that
with the property that 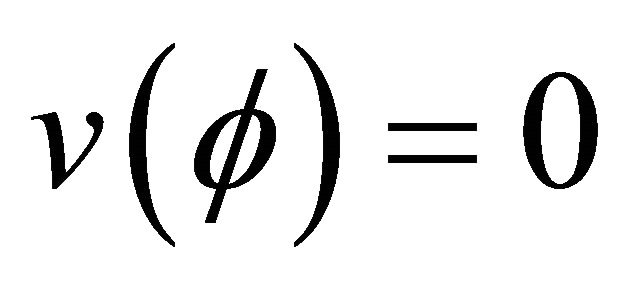 (
(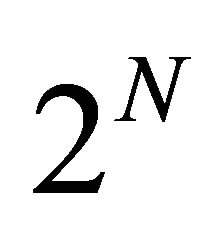 denotes the set of subsets of
denotes the set of subsets of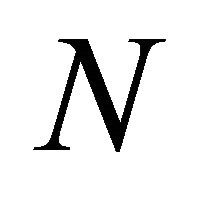 ). We usually refer to subsets
). We usually refer to subsets 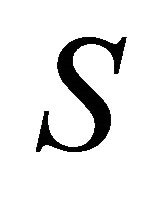 of
of 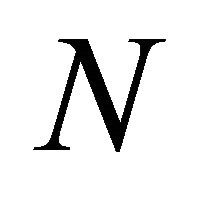 as coalitions and to the number
as coalitions and to the number 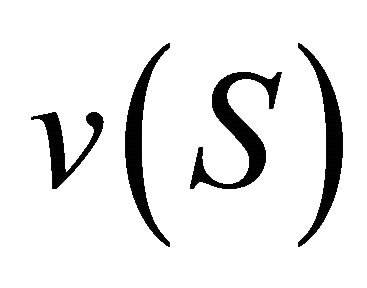 as the worth of
as the worth of . There are several interpretations for
. There are several interpretations for , it depends on what people want to model.
, it depends on what people want to model.
We denote by  the set of all games with a fixed set of players
the set of all games with a fixed set of players , i.e.,
, i.e.,
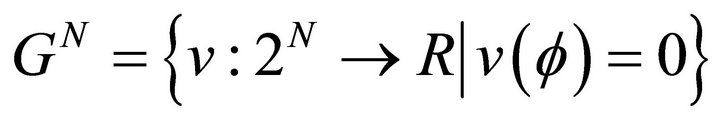
Given 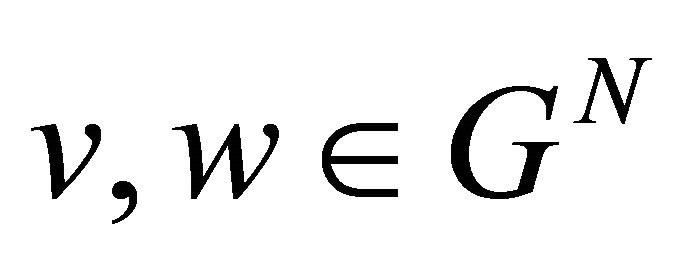 and
and , we define the sum and the product,
, we define the sum and the product,  and
and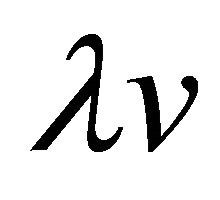 , in
, in 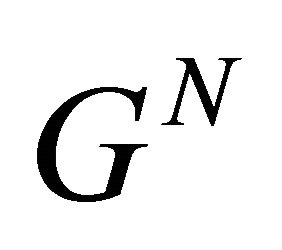 in the usual form, i.e.,
in the usual form, i.e.,

It is easy to verify that 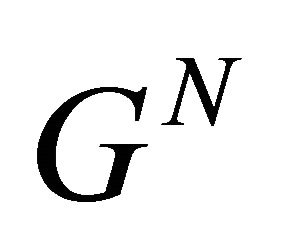 is a vector space with these operations.
is a vector space with these operations.
Next, we define some axioms which are common in the cooperative game theory frame-work.
Axiom 1 (Linearity) The solution  is linear if
is linear if 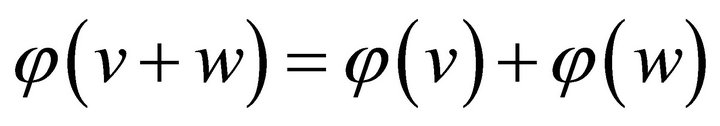 and
and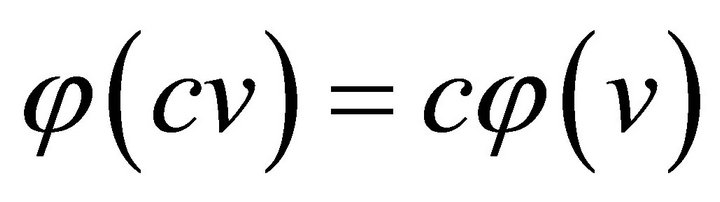 , for all
, for all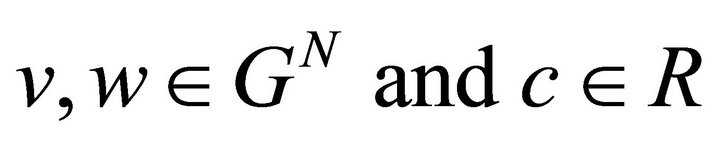 .
.
Let us consider the group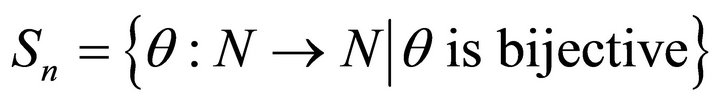 , the group of permutations of the set of players. For every
, the group of permutations of the set of players. For every 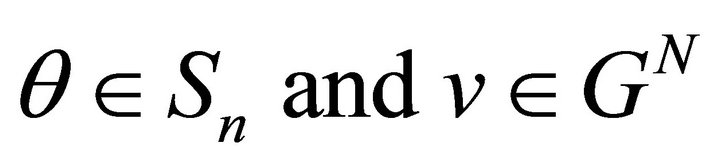 we define another game
we define another game 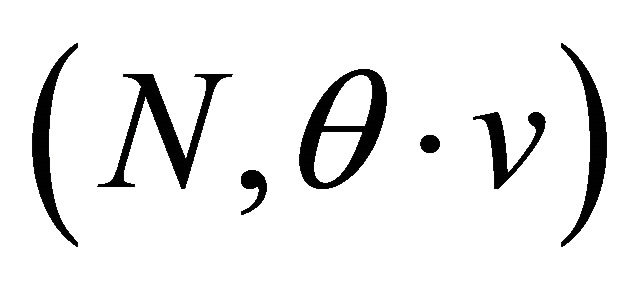 as follows
as follows
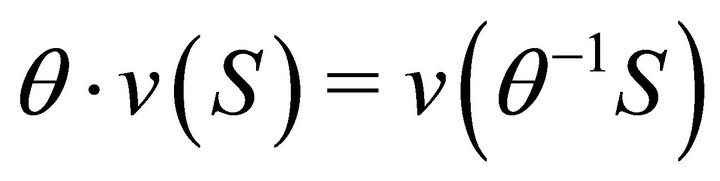
Axiom 2 (Symmetry) The solution  is said to be symmetric if and only if
is said to be symmetric if and only if 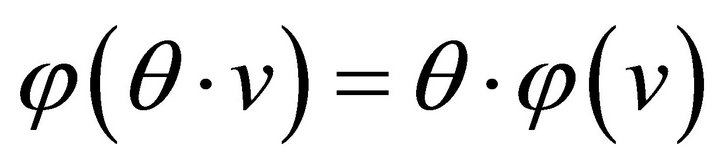 for every
for every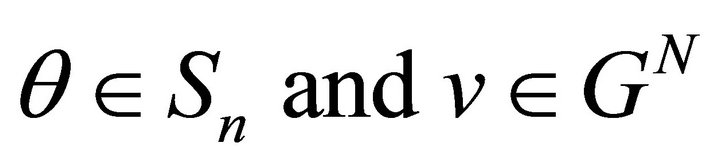 .
.
The player  is said to be a null player in the game
is said to be a null player in the game  if
if 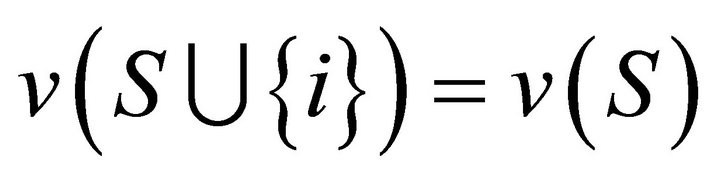 for every
for every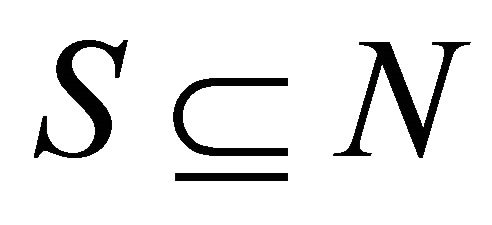 . The nullity axiom requests that every dummy player in
. The nullity axiom requests that every dummy player in 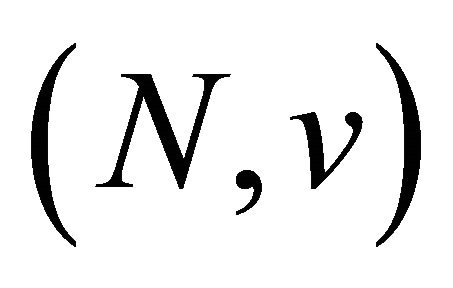 gets a zero payoff.
gets a zero payoff.
Axiom 3 (Nullity) If the player  is a null player in
is a null player in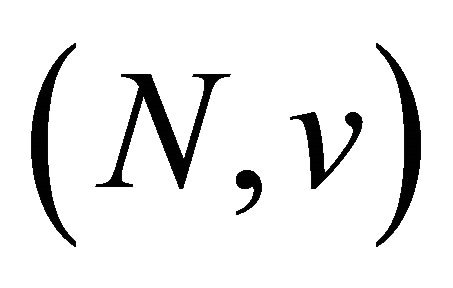 , then
, then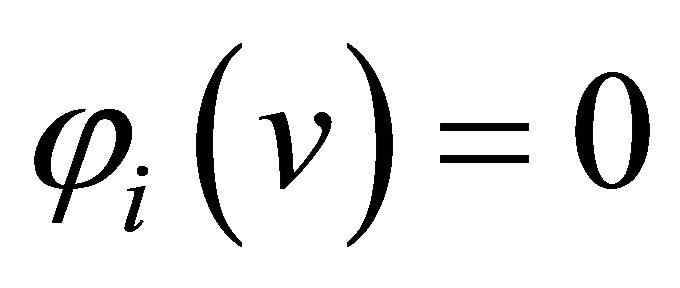 .
.
Axiom 4 (Efficiency) The solution  satisfies the efficiency axiom if and only if
satisfies the efficiency axiom if and only if 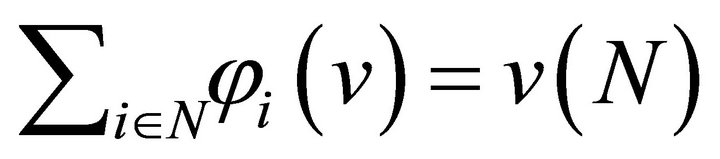 for every
for every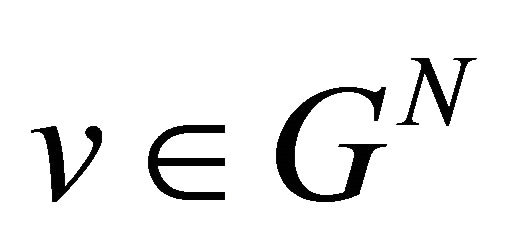 .
.
Theorem 5 (Shapley [9]) There exists a unique solution 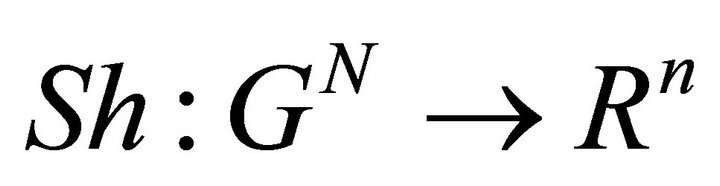 that satisfies linearity, symmetry, nullity and efficiency axioms. Furthermore it is given by
that satisfies linearity, symmetry, nullity and efficiency axioms. Furthermore it is given by
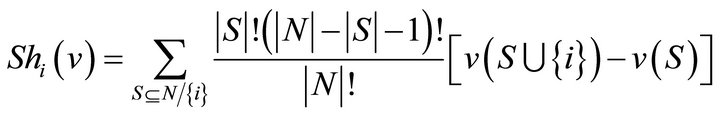
2.2. The Atkinson Index
Atkinson [3] defines the equally distributed equivalent level of income, 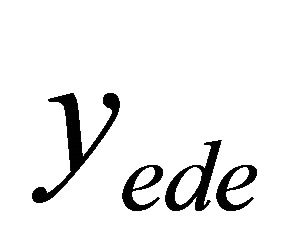 , which is the per capita income level that distributed among the population in an egalitarian way, presents the welfare level of the given income distribution. That is, the level of income per head which if equally distributed would give the same level of social welfare as the present distribution, so
, which is the per capita income level that distributed among the population in an egalitarian way, presents the welfare level of the given income distribution. That is, the level of income per head which if equally distributed would give the same level of social welfare as the present distribution, so 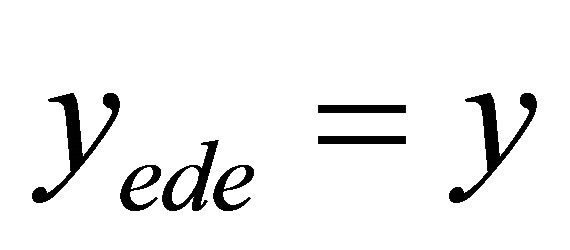 if
if 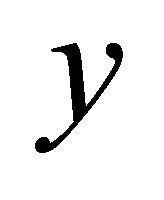 satisfies
satisfies

where 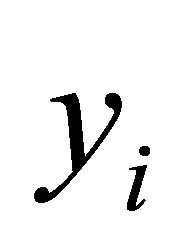 is the income level of the person
is the income level of the person ,
,  is a linear or concave utility function, and
is a linear or concave utility function, and  is the number of agents in the economy, and from it Atkinson defines the measure of inequality
is the number of agents in the economy, and from it Atkinson defines the measure of inequality

or 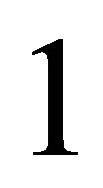 minus the ratio of the equally distributed equivalent level of income to the mean
minus the ratio of the equally distributed equivalent level of income to the mean  of the actual distribution. If
of the actual distribution. If 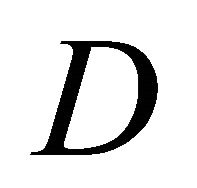 falls, then the distribution has become more equal—we would require a higher level of equally distributed income (relative to the mean) to achieve the same level of social welfare as the actual distribution. The measure
falls, then the distribution has become more equal—we would require a higher level of equally distributed income (relative to the mean) to achieve the same level of social welfare as the actual distribution. The measure 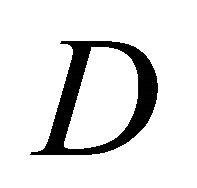 has, of course, the convenient property of lying between
has, of course, the convenient property of lying between 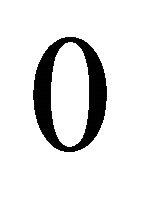 (complete equality) and
(complete equality) and 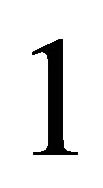 (complete inequality).
(complete inequality).
Consider a society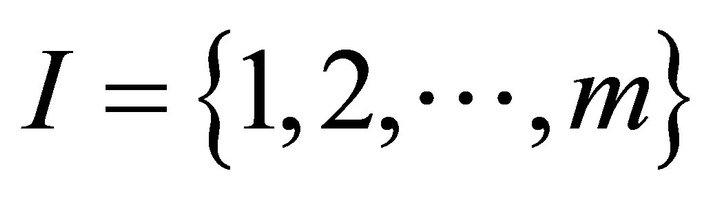 , where their incomes are given by the vector
, where their incomes are given by the vector . The Atkinson’s equality index of the distribution
. The Atkinson’s equality index of the distribution 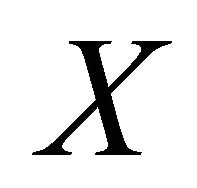 according to the value of parameter
according to the value of parameter 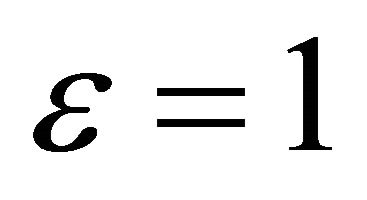 is by Atkinson [3]3:
is by Atkinson [3]3:
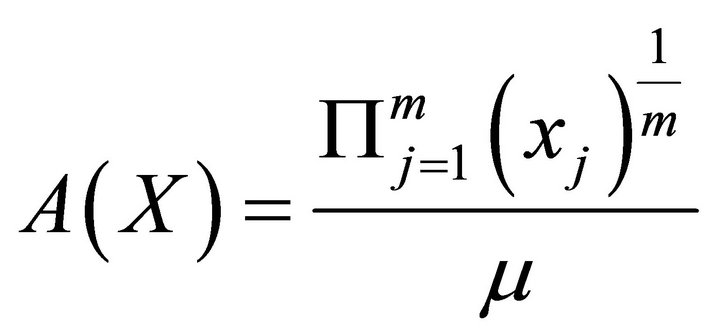
where 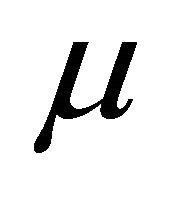 denotes the mean of the values in the income vector
denotes the mean of the values in the income vector .
.
3. The Model
The model will be based on the one proposed by Peragine [7], which focuses on the individuals economic opportunities differences, as a welfare ranking criteria for different income distributions.
We consider a society  with
with  individuals, each individual’s income
individuals, each individual’s income 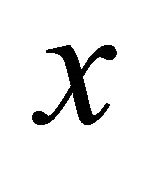 is causally determined by two kinds of factors: Factors beyond the individual control, represented by a person’s opportunity set
is causally determined by two kinds of factors: Factors beyond the individual control, represented by a person’s opportunity set  and factors for which the individual is fully responsible, represented by a scalar variable
and factors for which the individual is fully responsible, represented by a scalar variable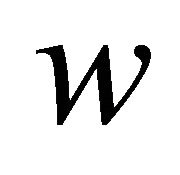 : Income
: Income 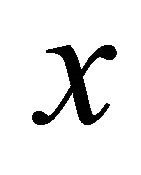 is supposed to be continuously distributed, with cumulative distribution function
is supposed to be continuously distributed, with cumulative distribution function  and
and , where
, where  is the maximum individual income. A person’s opportunity set
is the maximum individual income. A person’s opportunity set  is observable, and we denote by
is observable, and we denote by 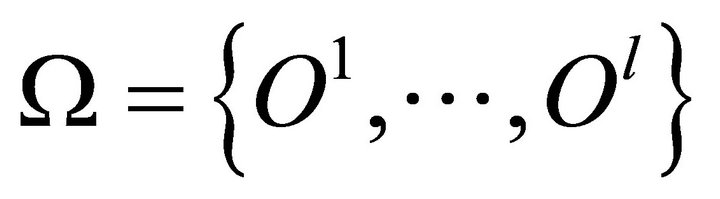 the set of all possible opportunity sets, considered to be finite. We assume that there is a general political agreement on the following ordering over all possible opportunity sets, assumed to be antisymmetric:
the set of all possible opportunity sets, considered to be finite. We assume that there is a general political agreement on the following ordering over all possible opportunity sets, assumed to be antisymmetric:
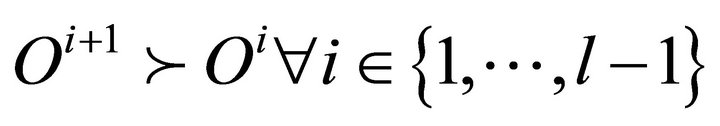
The responsibility variable  is unobservable and individuals have the same degree of access to the set
is unobservable and individuals have the same degree of access to the set ,
,  , of all possible values of the responsibility variable.
, of all possible values of the responsibility variable.
The individual income  is then given by
is then given by
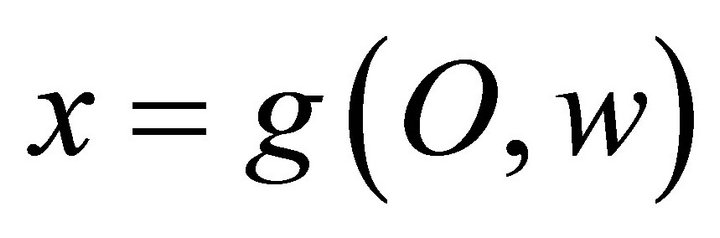
where 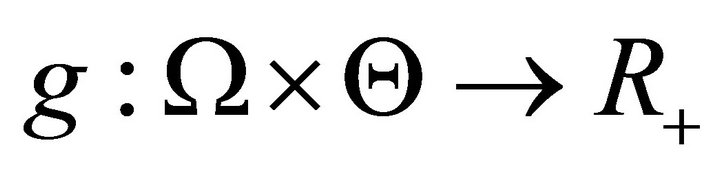 is a function that assigns individual incomes to combinations of responsibility and opportunities.
is a function that assigns individual incomes to combinations of responsibility and opportunities.
Now, there is a partition the population into types, where each type denotes the subset of the total population having the same opportunity set: Type  is defined as the set of individuals whose opportunity set is
is defined as the set of individuals whose opportunity set is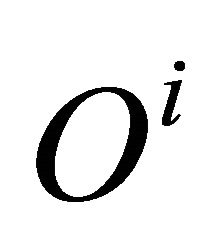 , and is denoted by
, and is denoted by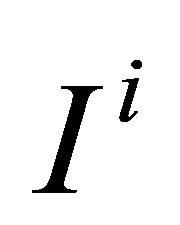 . We denote by
. We denote by  the set of income distributions. For any
the set of income distributions. For any , within each type
, within each type  there will be a distribution of income
there will be a distribution of income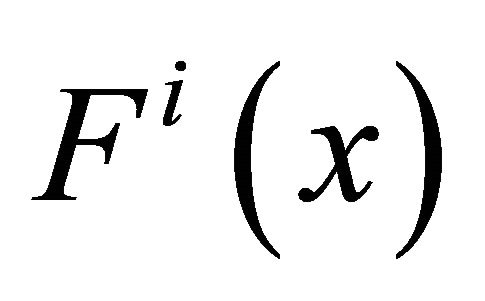 , with density function
, with density function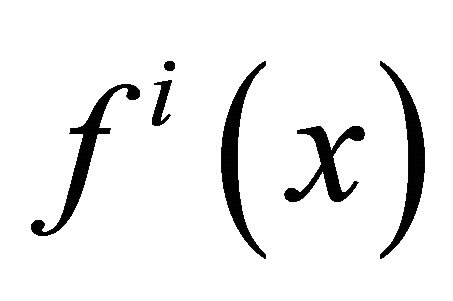 .
.
Consider any individual 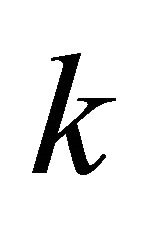 who is endowed with opportunity
who is endowed with opportunity 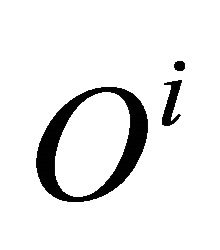 and, after exercising responsibility
and, after exercising responsibility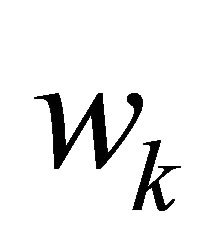 , ends up with ex-post income
, ends up with ex-post income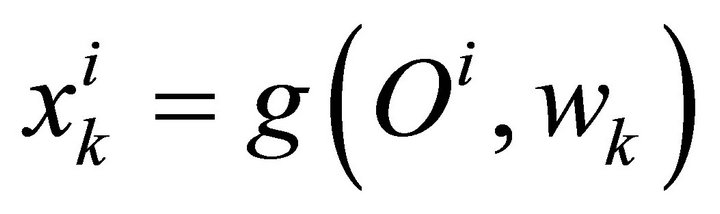 . Denoting by
. Denoting by 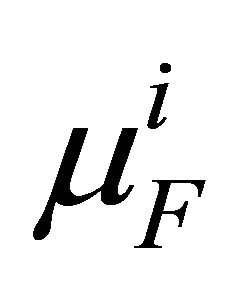 the mean income of type
the mean income of type , defined as
, defined as
 and by
and by 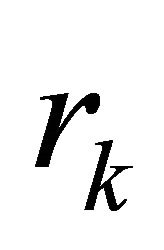 the residual terms, such that, within each type
the residual terms, such that, within each type ,
, 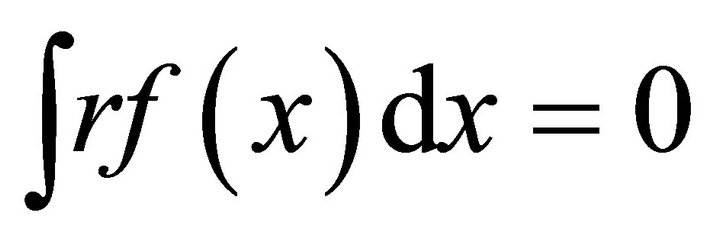 , we can write the income level of individual
, we can write the income level of individual 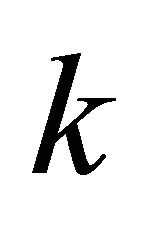 in type
in type  as
as

Now, consider that income differences between the individuals within the same type will only be because of differences on their responsibility. On the other hand, it seems reasonable to interpret the average income reached within each type, as a characteristic of the type itself; that is to say that the average income is determined, within each type, by the common endowment of opportunity.
Formally:
Assumption 1
1)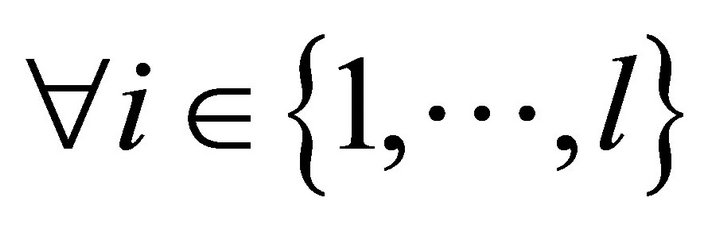 ,
, 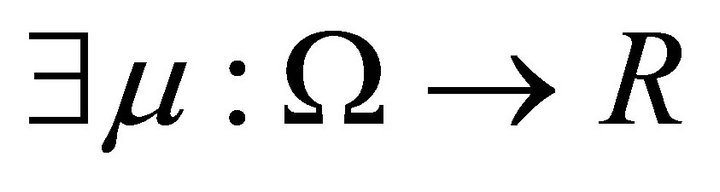 such that
such that
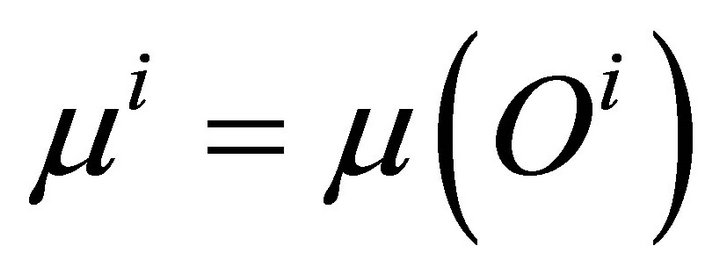 ;
;
2)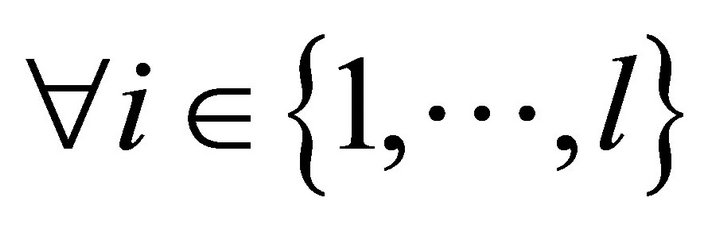 ,
, 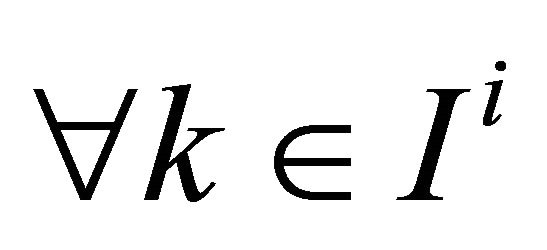 ,
, 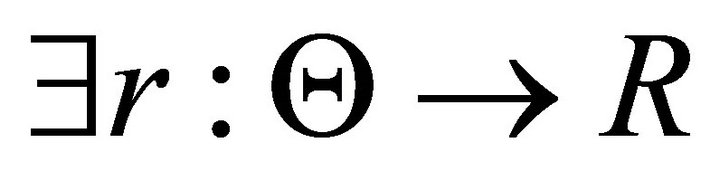 such that
such that  .
.
This assumption implies that the individual income is additively separable in responsible and non-responsible factors. From this we can say that the income average of each type depends on the opportunity, so since all of the individuals inside of  had the same opportunity
had the same opportunity  then we could say that their average income will indicate the part of the income which all of them could get. And therefore the rest of the income will be explained by a residual term which depends on the performance of the individuals in the economy (responsibility variable).
then we could say that their average income will indicate the part of the income which all of them could get. And therefore the rest of the income will be explained by a residual term which depends on the performance of the individuals in the economy (responsibility variable).
Assumption 2
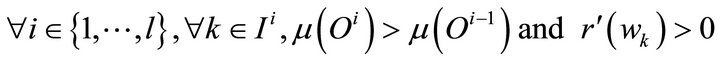
This assumption implies that the type means are ordered according to the opportunities order. Notice that the assumption also implies that the residual term increases with the responsibility variable.
4. The Decomposition
Decomposition analysis provides help in the difficult task of explaining how different factors affect an income distribution.
In the context of difference in opportunities and responsibility by the agents, where the opportunities are the set of circumstances in which agents are developed, and the responsibility refers to the efforts and actions of agents for income generation, we identify the inequality caused by the difference in opportunities as a problem, and not the one caused by the performance of the agents. Lets see it from the productivity point of view, if we face some income inequality that only depends on the performance of the agents, there will be no reason to complain at all, because we could say that every one gets what they deserve and if some individual wants to increase his income, then he would have to increase his performance, however if we start giving people a different payback depending in some other aspect such as an opportunity level, this could disincentive productivity because the agents could lose the opportunity of getting what they first wanted. Since we would like to preserve or increase productivity incentives in the economy, we try to highlight the difference in opportunities roll in the total income inequality, with this we could measure the size of such issue and therefore give a more complete analysis about an income distribution. So what we try to explain is: given a level of inequality is, how much inequality is caused due to the difference in opportunities? and, how much inequality is caused due to the variable of responsibility? In other words, this section seeks to find the level of participation of these variables in the total inequality and facilitate the analysis and measurement of the inequality in opportunities problem for a given population. To answer these questions we will use the approach of the Shapley value, looking for the advantages already set out in the coalitional games section.
To decompose the Atkinson index we will assume that the cardinality is equal between each type (in a case of homogenous type partitions), i.e. 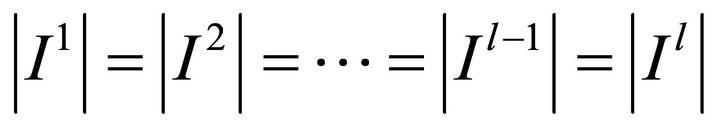 and we define the following profiles:
and we define the following profiles:
1) The original income distribution:

2) Each agent gets the average of their type; this payoff vector shows the opportunity differences, because of the assumption that establishes the types averages dependency only on the opportunity level:
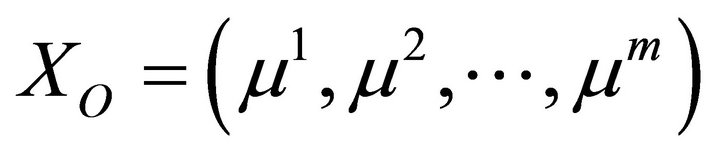
where 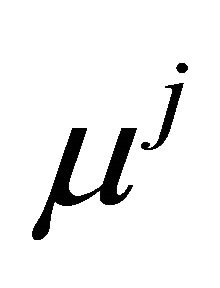 denotes the income mean of the opportunity set where
denotes the income mean of the opportunity set where  belongs.
belongs.
3) A payoff vector which is a payment reescalation such that all types have the general mean (or same opportunity), showing the responsibility difference:
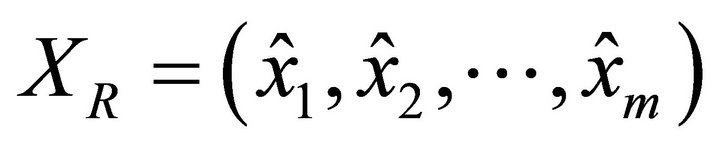
where 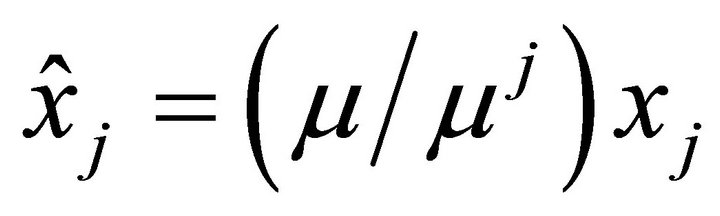 and
and 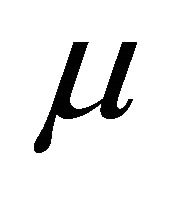 being the income mean of the original distribution
being the income mean of the original distribution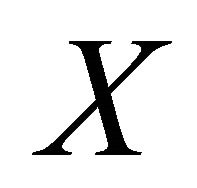 .
.
Now, we reach the decomposition by getting the marginal contribution of the income level determining variables (opportunity and responsibility) to the total inequality, to be able to assign the average of their marginal contributions. The last part of this process gets done by computing the Shapley value of a certain game, such that we can know the contribution of each variable.
Considering that the total inequality of the original income is given by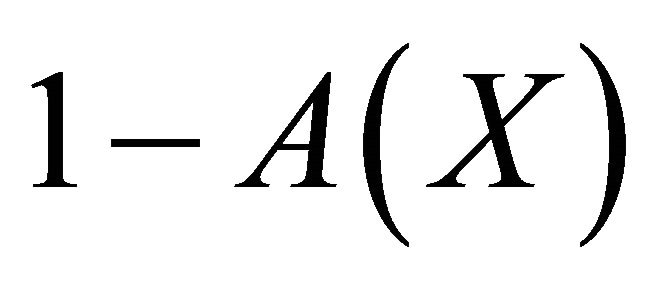 , we can take advantage of the efficiency property in the Shapley value, since we can establish the exact participation of the factors in the exact total inequality.
, we can take advantage of the efficiency property in the Shapley value, since we can establish the exact participation of the factors in the exact total inequality.
Formally, there are two players or factors 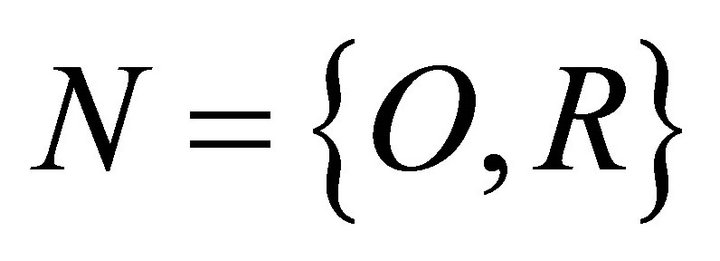 influencing the inequality (denoting the factors of opportunity and responsibility, respectively); so the worth of the grand coalition is
influencing the inequality (denoting the factors of opportunity and responsibility, respectively); so the worth of the grand coalition is 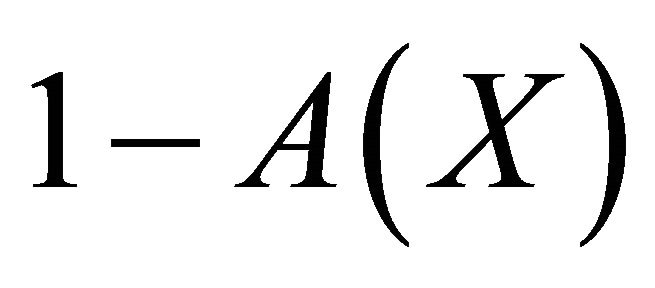 and it will be the amount to be distributed among the players
and it will be the amount to be distributed among the players  and
and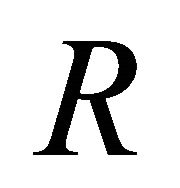 , which are the profiles that exhibit the difference in opportunities
, which are the profiles that exhibit the difference in opportunities 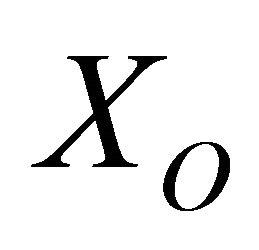 and in responsibility
and in responsibility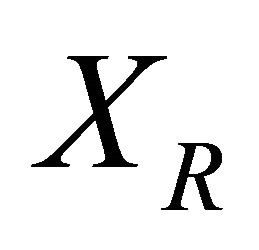 .
.
So the game has the next characteristic function:

The next table shows the marginal contributions for the previous game and the Shapley value for it:

Example 6 Let  be the income distribution of a given population that presents two types of opportunity
be the income distribution of a given population that presents two types of opportunity  and
and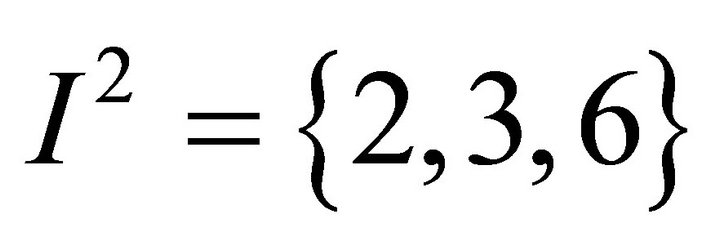 . Notice that the mean for types
. Notice that the mean for types 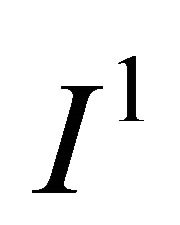 and
and 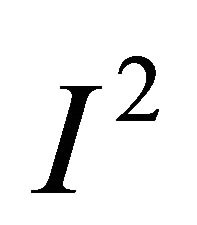 are
are 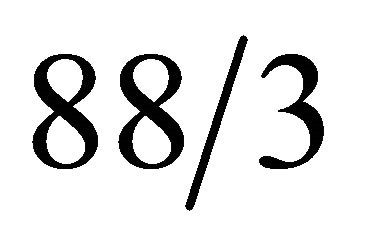 and
and , respectively. Now, as an illustration,
, respectively. Now, as an illustration,
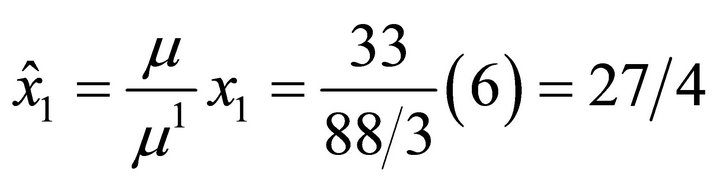 . Then, in sumary:
. Then, in sumary:

where,
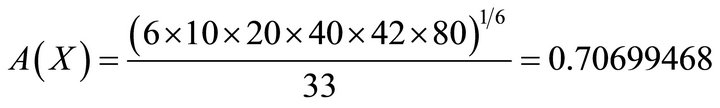
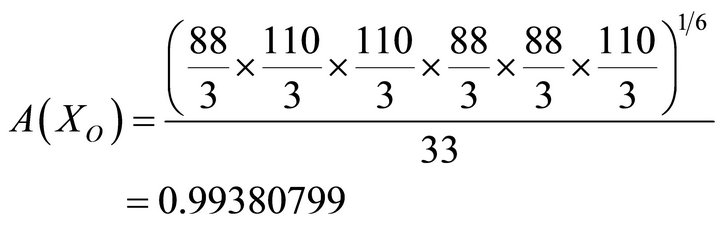

And the game is given by
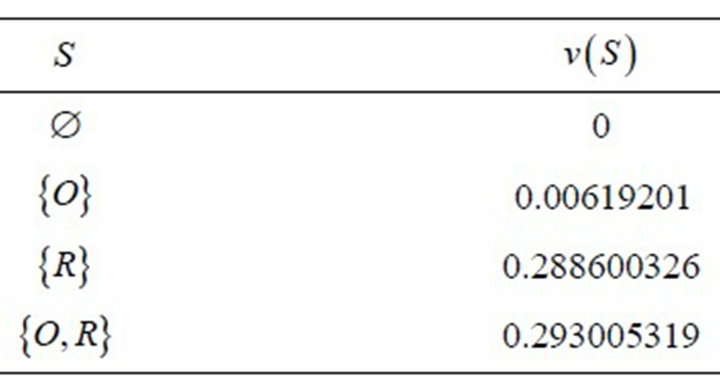
where for example,
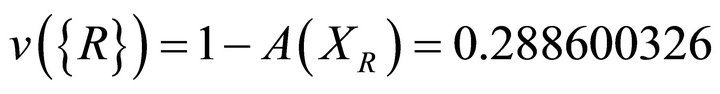
Finally,
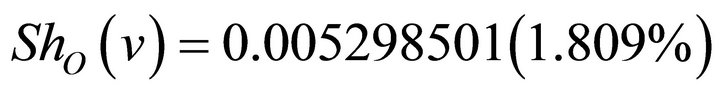

Now we have answer our two questions by giving the participation level of each variable in the total income inequality.
Remark 7 We previously assumed that there was the same number of people in each opportunity type. To get a more realistic decomposition (considering the possibility of heterogeneous partitions), we must change the reescalation made in the profile that shows the difference in responsibility (3):
3’. Once again, this vector represents the differences in the variable of responsibility, because all of the types will have the general mean:
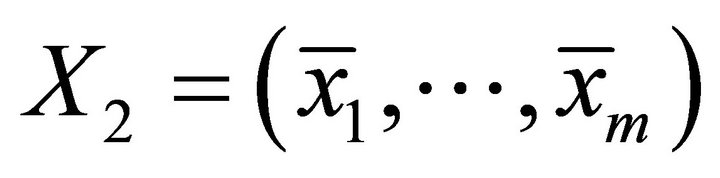
where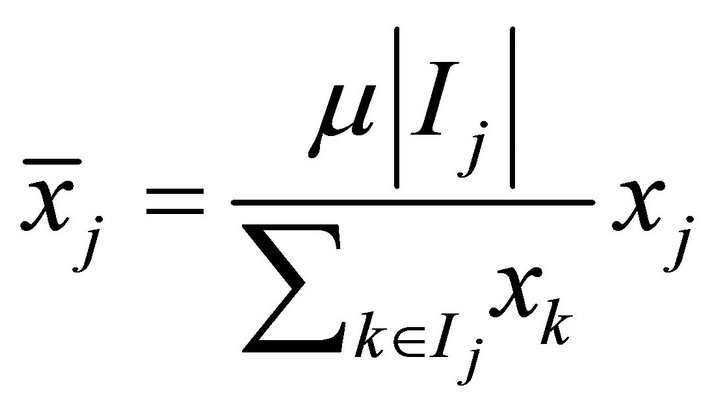 , denoting by
, denoting by  the opportunity set where
the opportunity set where  belongs.
belongs.
Example 8 Somewhere in the world there exists a society of 21 people that grew up under different conditions, since not all of them had the money to afford different services or to do human capital investment. The income vector for this people is given by

and there are five opportunity types for the individuals,
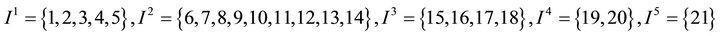
this based on the services they were endowed. Given this data, now it is possible to compute the Atkinson index decomposition. The game is given by

Finally,

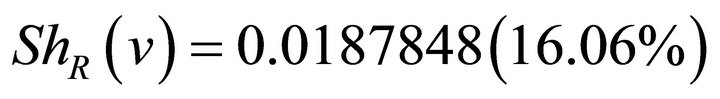
And we have a greater participation of the difference in opportunity level occupying more than 80% of the total income inequality.
5. Concluding Remarks
Despite the fact that economic inequality has always been treated with seriousness, not all inequality is necessarily a problem. The context of equal opportunities, allows us to understand how far should we get in the compensation of economic differences. And thus takes us to a less drastic, but more strategic solutions design.
The use of the cooperative game theory, allows us to get an idea about allocations or assignments, that use the axiomatic way, with strongly natural and intuitive criteria. So the use of the Shapley value that complies with its already seen four axioms, is convincing for the realization of the inequality index decomposition.
The measurement of inequality is intended to search for the improvement of social conditions, because it tries to rank the distribution functions in terms of social welfare, so in the decomposition, can be used as a criteria because it can be used to rank income distribution functions with the same inequality level but different contribution of the opportunities variable.
The decomposition of the inequality index is very useful to rule out the views that consider the treatment of economic inequality as a policy that disincentives productivity; i.e., an incentive to decrease the responsibility variable, because it defines the problem to be treated, and seeks to set aside the inequality caused by economic productivity. Therefore, operating from the framework of the difference in opportunities, we can forget about so many debates and controversy caused by the inequality treatment, highlighting the ground for the development of more effective policies that seek to solve the problem in concrete and encourage a population’s productivity.
6. Acknowledgements
J. Sánchez-Pérez acknowledges support from CONACYT research grant 130515. V. Rosas-Martínez acknowledges support from CONACYT grant 17665. We also wish to thank the editor and an anonymous referee. All possible remaining errors and short-comings are still ours.
REFERENCES
- A. K. Sen, “The Economic Inequality,” Fondo de Cultura Económica, Mexico City, 2001.
- A. Bergson-Samuelson, “A Reformulation of Certain Aspects of Welfare Economics,” Journal of Economics, Vol. 52, No. 2, 1938, pp. 310-334. doi:10.2307/1881737
- A. B. Atkinson, “On the Measurement of Inequality,” Journal of Economic Theory, Vol. 2, No. 3, 1970, pp. 244- 263.
- J. Levy, S. Chemerynski and J. Tuchmann, “Incorporating Concepts of Inequality and Inequity into Health Benefits Analysis,” International Journal for Equity in Health, Vol. 5, 2006, p. 2.
- A. F. Shorrocks, “Decomposition Procedures for Distributional Analysis: A Unified Framework Based on the Shapley Value,” University of Essex, Colchester, UK.
- M. Sastre and A. Trannoy, “Shapley Inequality Decomposition by Factor Components: Some Methodological Issues,” Journal of Economics, Vol. 9, No. 1, 2002, pp. 51-90. doi:10.1007/BF03052500
- V. Peragine, “Measuring and Implementing Equality of Opportunity for Income,” Social Choice and Welfare, Vol. 22, No. 1, 2004, pp. 187-210. doi:10.1007/s00355-003-0282-2
- T. Driessen, “Cooperative Games, Solutions and Applications,” Springer-Verlag, Dordrecht, 1988.
- L. S. Shapley, “A Value for n-person Games,” In: H. W. Kuhn and A. W. Tucker, Eds., Annals of Mathematic Studies, Princeton University Press, Princeton, 1953, pp. 307-317.
- M. C. Lasso de la Vega and A. M. Urrutia, “A New Factorial Decomposition for the Atkinson Measure,” Economics Bulletin, Vol. 4, No. 29, 2003, pp. 1-12.
NOTES
1Such as the Daltons’ principle of transfers (see Atkinson [3]).
2For a brief revision of the concepts of cooperative games that are mentioned here, see Driessen [8].
3Defined also in Lasso de la Vega and Urrutia [10].

