 Journal of Software Engineering and Applications, 2012, 5, 752-763 http://dx.doi.org/10.4236/jsea.2012.510088 Published Online October 2012 (http://www.SciRP.org/journal/jsea) Lossless Image Compression Technique Using Combination Methods A. Alarabeyyat1, S. Al-Hashemi1, T. Khdour1, M. Hjouj Btoush1, S. Bani-Ahmad1, R. Al-Hashemi2 1Prince Abdulah Bin Gazi Faculty of Information Technology, Al-Balqa Applied University, Salt, Jordan; 2The Computer Informa- tion Systems Department, College of Information Technology, Al-Hussein Bin Talal University, Ma’an, Jordan. Email: alarabeyat@bau.edu.jo, sarah_85_199@yahoo.com, khdour@bau.edu.jo, m.hjouj@bau.edu.jo, sulieman@bau.edu.jo, rafiq_alhashimy@yahoo.com Received May 8th, 2012; revised June 10th, 2012; accepted June 22nd, 2012 ABSTRACT The development of multimedia and digital imaging has led to high quantity of data required to represent modern im- agery. This requires large disk space for storage, and long time for transmission over computer networks, and these two are relatively expensive. These factors prove the need for images compression. Image compression addresses the prob- lem of reducing the amount of space required to represent a digital image yielding a compact representation of an image, and thereby reducing the image storage/transmission time requirements. The key idea here is to remove redundancy of data presented within an image to reduce its size without affecting the essential information of it. We are concerned with lossless image compression in this paper. Our proposed approach is a mix of a number of already existing tech- niques. Our approach works as follows: first, we apply the well-known Lempel-Ziv-Welch (LZW) algorithm on the image in hand. What comes out of the first step is forward to the second step where the Bose, Chaudhuri and Hoc- quenghem (BCH) error correction and detected algorithm is used. To improve the compression ratio, the proposed ap- proach applies the BCH algorithms repeatedly until “inflation” is detected. The experimental results show that the pro- posed algorithm could achieve an excellent compression ratio without losing data when compared to the standard com- pression algorithms. Keywords: Image Compression; LZW; BCH 1. Introduction Image applications are widely used, driven by recent ad- vances in the technology and breakthroughs in the price and performance of the hardware and the firmware. This leads to an enormous increase in the storage space and the transmitting time required for images. This empha- sizes the need to provide efficient and effective image compression techniques. In this paper we provide a method which is capable of compressing images without degrading its quality. This is achieved through minimizing the number of bits re- quired to represent each pixel. This, in return, reduces the amount of memory required to store images and facili- tates transmitting image in less time. Image compression techniques fall into two categories: lossless or lossy image compression. Choosing which of these two categories depends on the application and on the compression degree required [1,2]. Lossless image compression is used to compress im- ages in critical applications as it allows the exact original image to be reconstructed from the compressed one with- out any loss of the image data. Lossy image compression, on the other hand, suffers from the loss of some data. Thus, repeatedly compressing and decompressing an image results in poor quality of image. An advantage of this technique is that it allows for higher compression ratio than the lossless [3,4]. Compression is achieved by removing one or more of the three basic data redundancies: 1) Coding redundancy, which is presented when less than optimal code words are used; 2) Interpixel redundancy, which results from correla- tions between the pixels of an image; 3) Psychovisual redundancy, which is due to data that are ignored by the human visual system [5]. So, image compression becomes a solution to many imaging applications that require a vast amount of data to represent the images, such as document imaging mana- gement systems, facsimile transmission, image archiving, remote sensing, medical imaging, entertainment, HDTV, broadcasting, education and video teleconferencing [6]. One major difficulty that faces lossless image comp- ression is how to protect the quality of the image in a Copyright © 2012 SciRes. JSEA  Lossless Image Compression Technique Using Combination Methods 753 way that the decompressed image appears identical to the original one. In this paper we are concerned with lossless image compression based on LZW and BCH algorithms, which compresses different types of image formats. The proposed method repeats the compression three times in order to increase the compression ratio. The proposed method is an implementation of the loss- less image compression. The steps of our approach are as follows: first, we perform a preprocessing step to convert the image in hand into binary. Next, we apply the LZW algorithm on the image to compress. In this step, the codes from 0 to 255 represent 1-character sequences consisting of the corresponding 8-bit character, and the codes from 256 through 4095 are created in a dictionary for sequences encountered in the data as it is encoded. The code for the sequence (without that character) is emited, and a new code (for the sequence with that char- acter) is added to the dictionary [7]. Finally, we use the BCH algorithm to increase image compression ratio. An error correction method is used in this step where we store the normal data and first parity data in a memory cell array, the normal data and first parity data form BCH encoded data. We also generate the second parity data from the stored normal data. To check for errors, we compare the first parity data with the second parity data as in [8,9]. Notice that we repeat compressing by the BCH algo- rithm until the required level of compression is achieved. The method of decompression is done in reversible order that produces image identical to original one. 2. Literature Review A large number of data compression algorithms have been developed and used throughout the years. Some of which are of general use, i.e., can be used to compress files of different types (e.g., text files, image files, video files, etc.). Others are developed to compress efficiently a par- ticular type of files. It has been realized that, according to the representation form of the data at which the compres- sion process is performed, below is reviewing some of the literature review in this field. In [10], the authors present lossless image compress- ion with four modular components: pixel sequence, pre- diction, error modeling, and coding. They used two meth- ods that clearly separate the four modular components. These method are called Multi-Level Progressive Meth- od (MLP), and Partial Precision Matching Method (PPMM) for lossless compression, both involving linear predic- tions, modeling prediction errors by estimating the vari- ance of a Laplace distribution (symmetric exponential), and coding using arithmetic coding applied to pre-com- puted distributions [10]. In [11], a composite modeling method (hybrid com- pression algorithm for binary image) is used to reduce the number of data coded by arithmetic coding, which code the uniform areas with less computation and apply arithmetic coding to the areas. The image block is classi- fied into three categories: all-white, all-black, and mixed, then image processed 16 rows at a time, which is then operated by two global and local stages [11]. In [12], the authors propose an algorithm that works by applying a reversible transformation on the fourteen commonly used files of the Calgary Compression Corpus. It does not process its input sequentially, but instead pro- cesses a block of texts as a single unit, to form a new block that contains the same characters, but is easier to compress by simple compression algorithms, group char- acters together based on their contexts. This technique makes use of the context on only one side of each char- acter so that the probability of finding a character closer to another instance of the same character is increased substantially. The transformation does not itself com- press the data, but reorder it to make it easy to compress with simple algorithms such as move-to-front coding in combination with Huffman or arithmetic coding [12]. In [13], the authors present Lossless grayscale image compression method—TMW—is based on the use of linear predictors and implicit segmentation. The compression process is split into an analysis step and a coding step. In the analysis step, a set of linear predictors and other pa- rameters suitable for the image are calculated in the analysis step in a way that minimizes the length of the encoded image which is included in the compressed file and subsequently used for the coding step. To do the ac- tual encoding, obviously, the chosen parameter set has to be considered as a part of the encoded image and has to be stored or transmitted alongside with the result of the Coding Stage [13]. In [14], the authors propose a lossless compression scheme for binary images which consists of a novel en- coding algorithm and uses a new edge tracking algorithm. The proposed scheme consists of two major steps: the first step encodes binary image data using the proposed encoding method that encodes image data to only char- acteristic vector information of objects in image by using a new edge tracing method. Unlike the existing approaches, our method encodes information of edge lines obtained using the modified edge tracing method instead of di- rectly encoding whole image data. The second is com- pressing the encoded image Huffman and Lempel-Ziv- Welch (LZW) [14]. In [15], the author presents an algorithm for lossless binary image compression which consists of two modules, called Two Modules Based Algorithm (TMBA), the first module: direct redundancy exploitation and the second: improved arithmetic coding [15]. In [16], a two-dimensional dictionary-based on lossless image compression scheme for grayscale images is Copyright © 2012 SciRes. JSEA  Lossless Image Compression Technique Using Combination Methods Copyright © 2012 SciRes. JSEA 754 This paper uses the adaptive bit-level text compression schema based on humming code data compression used in [19]. Our schema consists of six steps repeated to in- crease image compression rate. The compression ratio is found by multiplying the compression ratio for each loop, and are referred to this schema by HCDC (K) where (K) represents the number of repetition [19]. introduced. The proposed scheme reduces a correlation in image data by finding two-dimensional blocks of pix- els that are approximately matched throughout the data and replacing them with short codewords. In [16], the two-dimensional Lempel-Ziv image com- pression scheme (denoted GS-2D-LZ) is proposed. This scheme is designed to take advantage of the two-dimen- sional correlations in the image data. It relies on three different compression strategies, namely: two-dimensional block matching, prediction, and statistical encoding. In [20], the authors presented a lossless image com- pression based on BCH combined with Huffman algo- rithm [20]. In [17], the authors presented a lossless image com- pression method that is based on Multiple-Table’s Arith- metic Coding (MTAC) method to encode a gray-level image, first classifies the data and then encodes each cluster of data using a distinct code table. The MTAC method employs a median edge detector (MED) to re- duce the entropy rate of f. The gray levels of two adjacent pixels in an image are usually similar. A base-switching transformation approach is then used to reduce the spatial redundancy of the image. The gray levels of some pixels in an image are more common than those of others. Fi- nally, the arithmetic encoding method is applied to re- duce the coding redundancy of the image [17]. 3. The Proposed Method The objective of the proposed method in this paper is to design an efficient and effective lossless image compres- sion scheme. This section deals with the design of a loss- less image compression method. The proposed method is based on LZW algorithm and the BCH algorithm an error correcting technique, in order to improve the compres- sion ratio of the image comparing to other compression techniques in the literature review. Later, we will explain the methodology that will be used in details and the ar- chitecture of the proposed method. The proposed method is a lossless image compression scheme which is applied to all types of image based on LZW algorithm that reduce the repeated value in image and BCH codes that detect/correct the errors. The BCH algorithm works by adding extra bits called parity bits, whose role is to verify the correctness of the original message sent to the receiver so, the system in this paper benefit from this feature. This method of BCH convert blocks of size k to n by adding parity bits, depending on the size of the message k, which is encoded into a code word of the length n. The proposed method is shown below in Figure 1. In [18], the authors used a lossless method of image compression and decompression is proposed. It uses a simple coding technique called Huffman coding. A soft- ware algorithm has been developed and implemented to compress and decompress the given image using Huff- man coding techniques in a MATLAB platform. They concern with compressing images by reducing the num- ber of bits per pixel required to represent it, and to de- crease the transmission time for images transmission. The image is reconstructed back by decoding it using Huff- man codes [18]. Figure 1. Proposed image compression approach.  Lossless Image Compression Technique Using Combination Methods 755 3.1. Lempel-Ziv-Welch (LZW) The compression system improves the compression of the image through the implementation of LZW algorithm. First, the entered image is converted to the gray scale and then converted from decimal to binary to be a suitable form to be compressed. The algorithm builds a data dic- tionary (also called a translation table or string table) of data occurring in an uncompressed data stream. Patterns of data are identified in the data stream and are matched to entries in the dictionary. If the patterns are not present in the dictionary, a code phrase is created based on the data content of that pattern, and it is stored in the dic- tionary. The phrase is then written to the compressed output stream. When a reoccurrence of a pattern is iden- tified in the data, the phrase of the pattern already stored in the dictionary is written to the output. 3.2. Bose, Chaudhuri and Hocquenghem (BCH) The binary input image is firstly divided into blocks of size 7 bits each; only 7 bits needed to represent in each byte, 128 value in total, while eighth bits represent sign of the number (most significant bit) that don’t affect the total value of blocks, and converts it to a galoris field to be accepted as an input to the BCH. Each block is de- coded using BCH decoder, then is checked if it is a valid codeword or not. The BCH decoder converts the valid block to 4 bits. The proposed method adds 1 as an indi- cator for the valid codeword to an extra file called (map), otherwise if it is not a codeword, it remains 7 and adds 0 to the same file. The benefit of the extra file (map) is that it is used as the key for image decompression in order to distinguish between compressed blocks and the not com- pressed ones (codeword or not). After the image is compressed, the file (map) is com- pressed by RLE to decrease its size, and then it is attached to the header of the image. This step is iterated three times, the BCH decoding repeat three times to improve the compression ratio; we stopped repeating this algo- rithm at three times after done experiment; conclude that if we try to decode more it will affect the other perform- ance factor that leads to increase time needed for com- pression, and the map file becomes large in each time we decode by BCH so it leads to the problem of increase the size of image, which opposes the objective of this paper to reduce the image size. Below is an example of the compressed image: Example: Next is an example of the proposed system compres- sion stage. In this example a segment of the image is demonstrated using the proposed algorithm. First of all it converts the decimal values into binary, compresses it by LZW and then divides it into blocks of 7 bits A = Original 30237524416070 249 149 133149 The block is compressed by LZW algorithm and the output is: 31238534516171 250 150 134150 Now it is converting to Binary and divided to 7 bit each: 0110100 1 0 1 1 00 0 0101101 0 0 1 0 101 1111111 0 0 0 1 010 0001011 0 1 1 0 100 1010110 0 0 1 1 101 1111111 0 0 0 After dividing the image into blocks of 7 bits, the sys- tem implements the BCH code that checks each block if it is a codeword or not by matching the block with 16 standards codeword in the BCH. The first iteration shows that we found four codewords. This block is compressed by using BCH algorithm which is converted to blocks of 4 bit each. 1 0 1 1 0 0 0 > 1000 1 1 1 1 1 1 1 > 1111 0 0 0 1 0 1 1 > 1011 1 1 1 1 1 1 1 > 1111 When implementing the BCH algorithm, the file (Map 1) initializes. If the block is a codeword, it is added to the file 1 and adds 0 if the block is a non-codeword. In this example Map 1 is: Map 1 = 0 1 0 0 1 0 0 0 1 0 1 This operation is repeated three times. The file (Map 3, Map 2, and Map 1) is compressed by RLE before attach- ing to the header of the image to gain more compression ratio. 3.3. Compression Algorithm Steps The proposed method compression the original image by implements a number of steps Figure 2 represents the flowchart of the proposed method. The algorithm steps are: Input: image (f) Output: compressed file Begin Initialize parameters SET round to zero READ image (f) Convert (f) to gray scale SET A = ( ) // set empty value to matrix A A = image (f) Bn = convert matrix A into binary Initial matrix Map 1, Map 2, Map 3 to store parity bits Copyright © 2012 SciRes. JSEA  Lossless Image Compression Technique Using Combination Methods 756 Figure 2. Algorithm 1. Encoding algorithm. Copyright © 2012 SciRes. JSEA  Lossless Image Compression Technique Using Combination Methods 757 Out1 = Compress matrix by LZW algorithm function norm 2l zw (Bn); Convert matrix compress by LZW into binary Set N = 7, k = 4 WHILE (there is a codeword) and (round ≤3) xxx = the size of the (Out 1) remd = matrix size mod N; div = matrix size /N; FOR i = 1 to xxx-remd step N FOR R = i to iN1 divide the image into blocks of size 7 save into pa- rameter msg = out 1 [R] END FOR R c2 = convert (msg) to Galoris field; origin = c2 d2 = decoding by BCH decoder (bchdec (c2, n, k,)) c2 = Encode by BCH encoder for test bchenc (d2, n, k) IF (c2 == origin) THEN // original message parameter INCREMENT the parameter test (the number of cod- eword found) by 1; add the compressed block d2 to the matrix CmprsImg add 1 to the map[round] matrix ELSE add the original block (origin) to the matrix CmprsImg add 0 to the map[round] matrix ENDIF END FOR i Pad and Add remd bits to the matrix CmprsImg and encode it Final map file = map [round] to reuse map file in the iteration FOR stp = 1 to 3 Compress map by RLE encoder and put in parameter map_RLE [stp] = RLE (map [stp]) END FOR stp INCREMENT round by 1 ENDWHILE END 3.4. Decompression It is reversible steps to the compression stage to recon- struct the images. At first the system decompress the attach file (map) by RLE decoder because we depend on its values to know which block in the compress image is a code word to be decompressed. That means if the value of the map file is 1, then it reads 4 bit block from the compressed image which means it’s a codeword then decompressed by BCH encoder. If the value is 0, it reads the 7 bit block from the compressed image which means that it is not a codeword. This operation is repeated three times, after that the output from BCH is decompressed using LZW algorithm. The below example explains these steps. Example: Read the map file after decompressing it by RLE algo- rithm. 0 0 0 1 0 0 1 0 0 0 Depending on the value of the map file, in the posi- tions 4 and 7, the value is 1 which means that the system will read 4 bit from the compressed image. This means that a codeword and by compressing it by BCH, it recon- structs 7 bit from 16 codewords valid in BCH that match it, and the remained value of the file is 0. This mean it a non codeword reads 7 bit from the compressed image. The compressed image is: 1 1 0 0 0 0 0 1 1 1 1 1 1 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 1 0 1 0 0 0 0 1 1 1 0 0 1 1 0 0 Decompression procedure shown in the Figure 3 is implemented to find the original image from the com- pressed image and it is performed as follows: Input: compressed image, attach file mapi Output: original image Begin Initial parameter SET P = ( ) // set empty value to matrix P SET j = 1 SET n = 7 SET k = 4 SET round = 3 // number of iteration Rle_matrix = RLE decoder (mapi) WHILE round > 0 FOR i = 0 to length of (Rle_matrix) IF Rle_matrix [i] = 1 THEN encode by BCH FOR s = j to jk1 encode compress image by BCH encoder and put in parameter (c2) c2 = bchenc (CmprsImg (s)), n, k) INCREMENT j by 4 add c2 to matrix p ENDFOR s ELSE //block is not compress then read it as it FOR s1 = j to jn1 add uncompress block from CmprsImg [s1] to matrix p INCREMENT j by 7 ENDFOR s1 ENDIF Copyright © 2012 SciRes. JSEA 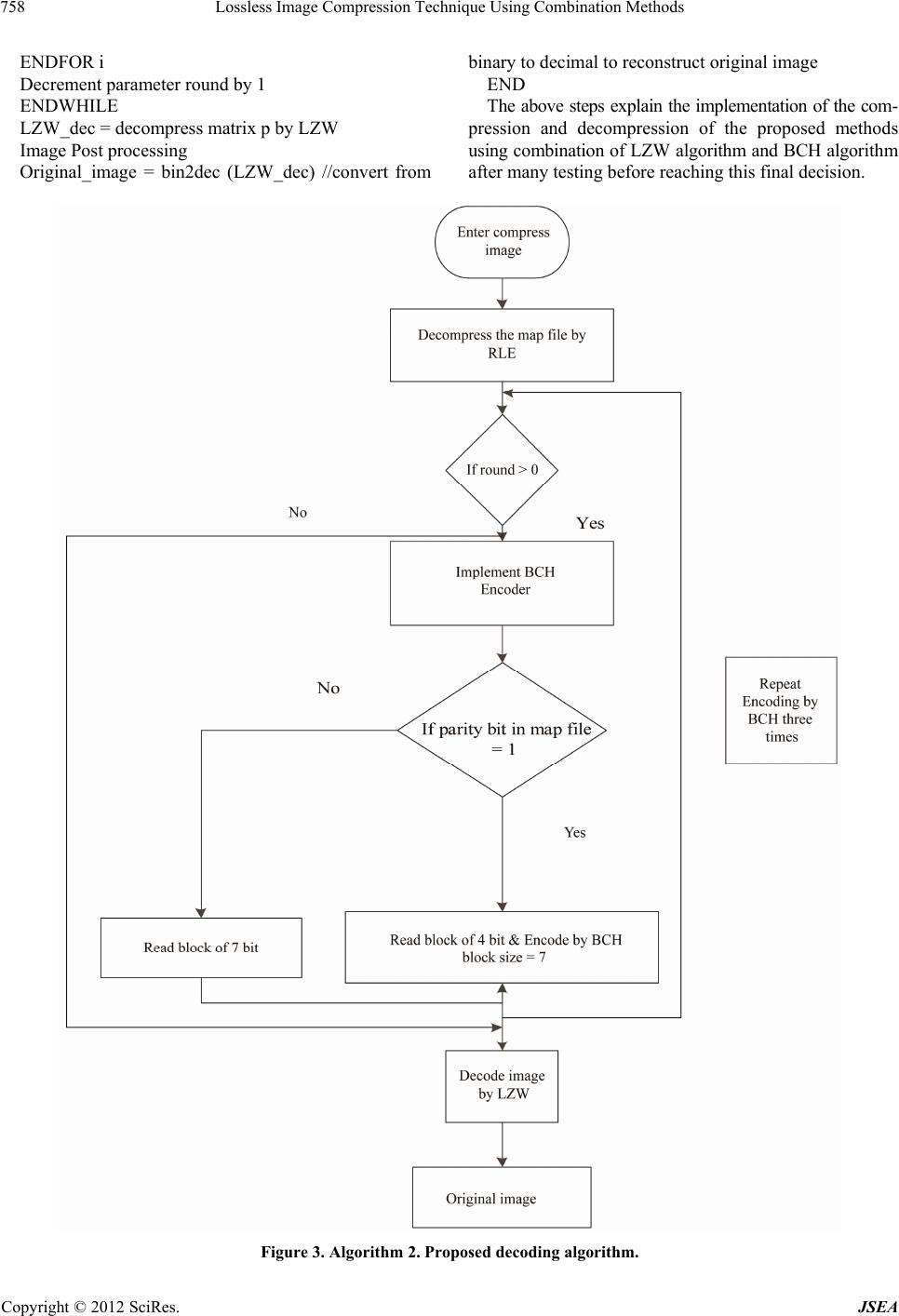 Lossless Image Compression Technique Using Combination Methods 758 ENDFOR i Decrement parameter round by 1 ENDWHILE LZW_dec = decompress matrix p by LZW Image Post processing Original_image = bin2dec (LZW_dec) //convert from binary to decimal to reconstruct original image END The above steps explain the implementation of the com- pression and decompression of the proposed methods using combination of LZW algorithm and BCH algorithm after many testing before reaching this final decision. Figure 3. Algorithm 2. Proposed decoding algorithm. Copyright © 2012 SciRes. JSEA  Lossless Image Compression Technique Using Combination Methods 759 ENDFOR i Decrement parameter round by 1 ENDWHILE LZW_dec = decompress matrix p by LZW Image Post processing Original_image = bin2dec (LZW_dec) //convert from binary to decimal to reconstruct original image END The above steps explain the implementation of the com- pression and decompression of the proposed methods using combination of LZW algorithm and BCH algorithm after many testing before reaching this final decision. The next section shows the result from using this me- thod by using MatLab platform; calculating the compres- sion ratio by using this equation: r Coriginal sizecompress size Use the same dataset and the same size to compare between proposed method and LZW, RLE, Huffman, and then compare it depending on the bit that needs to repre- sent each pixel according to the equation below: r BPP1 C8 Or by use the following equation: 0 r Cc qS S (q) Is the number of bit represent each pixel in uncom- pressed image, (S0) the size of the original data and (Sc) the size of the compressed data. Also compare it with the standards of the compression technique, and finally explain the test (the codeword found in image) comparing it with the original size of the image in bit. 3.5. Result and Discussion In order to evaluate the compression performance of our proposed method, we compared the proposed method in this paper with other standard lossless image compres- sion schemes in the literature review. At first, the com- parison is based on the compression ratio, and the second is based on a bit per pixel. Lossless images compression lets the images to oc- cupy less space. In lossless compression, no data are lost during the process, which means that it protects the quality of the image. Decompression process restores the ori- ginal image without losing essential data. The tested im- ages used during compression are stored in GIF, PNG, JPG, and Tiff formats that are all compressed automati- cally by the proposed method. Hardware used: PC, proc- essor Intel® core™ i3 CPU, hard size: 200 GB, RAM 2.00 GB, Software using Windows 7 ultimate Operating Sys- tem, and MatLab Version 7.5. 0.342 R (2007b). Analyzes and discusses the results obtained in per- forming the LZW and BCH algorithms discussed above on the set of images. The proposed system uses the set of images that are commonly used in image processing (air- plane, baboon, F-18, Lina, and peppers, etc.) as a test set. The proposed method has been tested on different image sizes. The simulation result is compared with RLE, Huffman and LZW. The results show that the proposed method has higher compression ratio than the standard compression algo- rithm mentioned above. The results based on the com- pression ratio shown in Tables 1 and 2 show the com- pression based on bit per pixel. The above results show that the compression by the proposed system is the best compared to the results of Table 1. Compression with typical compression methods based on compression ratio w hich divide original image size by size of compressed image. Image RLE LZW HUFF LZW & BCH Airplane 1.2162 1.6052 1.1857 1.8193 Barbara 1.0871 1.2894 1.4187 1.461 Lenna 1.0892 1.3811 1.0795 1.5719 U3 1.0098 1.0098 1.1009 1.1406 Peppers2 1.0969 1.3311 1.4187 1.5095 Gold-hill 1.1149 1.3812 1.0749 1.572 Zelda28_tif 1.0701 1.3925 1.1017 1.57 Boat 1.1023 1.3893 1.1192 1.5637 house28.tiff 1.1867 1.4515 1.1039 1.6493 F-128.jpg 2.1014 2.5747 1.4219 2.9018 Camera.jpg 1.1441 1.483 1.1285 1.6779 Woman blonde 1.0701 1.4074 1.1145 1.5953 Walk bridge 1.0398 1.2212 1.0475 1.3845 Pirate 1.064 1.3462 1.0911 1.5249 Lake 1.0875 1.3151 1.0633 1.4949 Living room 1.0629 1.3425 1.0845 1.5186 Woman darkhair 1.1333 1.5197 1.0964 1.7234 Mini-fenn0043 1.1337 1.571 1.2339 1.7763 AVG 1.156111 1.445106 1.160267 1.636383 Copyright © 2012 SciRes. JSEA  Lossless Image Compression Technique Using Combination Methods 760 Table 2. Compression results of images in bit/pixel. Image RLE LZW HUFF LZW & BCH Airplane 6.577865 4.983803 6.747069 4.397766 Barbara 7.359028 6.204436 5.638965 5.47622 Lenna 7.34484 5.792484 7.410838 5.090454 U3 7.92236 7.92236 7.266782 7.038986 Peppers2 7.293281 6.010066 5.638965 5.300354 Goldhill 7.175531 5.792065 7.442553 5.089417 Zelda28_tif 7.475936 5.745062 7.261505 5.096191 Boat 7.257552 5.758295 7.147963 5.116516 House28.tiff 6.741383 5.511539 7.247033 4.851074 F-128.jpg 3.806985 3.107158 5.626274 2.9018 Camera.jpg 6.992396 5.394471 7.089056 4.768494 Woman_Blonde 7.475937 5.68424 7.178107 5.015198 Walkbridge 7.693787 6.550934 7.637232 5.778625 Pirate 7.518797 5.942653 7.33205 5.24707 Lake 7.356322 6.083188 7.523747 5.352234 Livingroom 7.526578 5.959032 7.376671 5.268677 Woman_darkhair 7.059031 5.264197 7.296607 4.642334 Mini-fenn0043 7.056541 5.092298 6.483508 4.504769 AVG 7.090786 5.711016 6.963607 5.05201 compressing the image by using RLE algorithm, LZW algorithm or Huffman algorithm. Here in Figure 4, we illustrate the comparison based on compression ratio between the proposed algorithm (BCH and LZW) and the standard image compression algorithms (RLE, Huffman and LZW) which can be dis- tinguished by color. And Figure 5 explains the size of original image compared with image after compressed by the standard image compression algorithm and the pro- posed method. Table 2 shows the results of the compres- sion based on bit per pixel rate for the proposed method, and the standards compression algorithm. Figure 6 explains the result of the above Tab le 2. 3.6. Discussion In this section we show the efficiency of the proposed system which uses MatLab to implement the algorithm. In order to demonstrate the compression performance of the proposed method, we compared it with some repre- sentative lossless image compression techniques on the set of ISO test images that were made available to the proposer that were shown in the first column in all tables. Table 1 lists compression ratio results of the tested images which calculated depend on size of original im- age to the size of image after compression; the second column of this table lists the compression ratio result from compress image by the RLE algorithm. Column three and four list the compression ratio result from compress by LZW and Huffman algorithms respectively while the last column lists the compression ratio achieved by the proposed method. In addition the average compression ratio of each method after applied on all tested images (RLE 1.2017, LZW 1.4808, Huffman 1.195782 and BCH and, LZW the average is 1.676091). The average of com- pression ratio on tested images based on the proposed method is the best ratio achieved, this mean image size is reduced more when compressed by using combination method LZW and BCH compared to the standards of lossless compression algorithm, and Figure 2 can clear the view of the proposed method that has higher compres- sion ratio than the RLE, LZW and Huffman. Figure 3 displays the original image size and the size of image after compressed by each RLE, LZW, Huffman and compress by the proposed method which show it had the less image size which achieves the goal of this paper to utilize storage need to store the image and therefore, re- duce time for transmission. The second comparison depends on bit per pixel shown in Table 2. The goal of the image compression is to re- duce the size as much as possible, while maintaining the image quality. Smaller files use less space to store, so it is better to have fewer bits need to represent in each pixel. The table tests the same image sets and explains the pro- posed method that needs fewer numbers of bit per pixel than the other standard image compression and the ave- rage bit per pixel of all tested images are 6.904287, Copyright © 2012 SciRes. JSEA 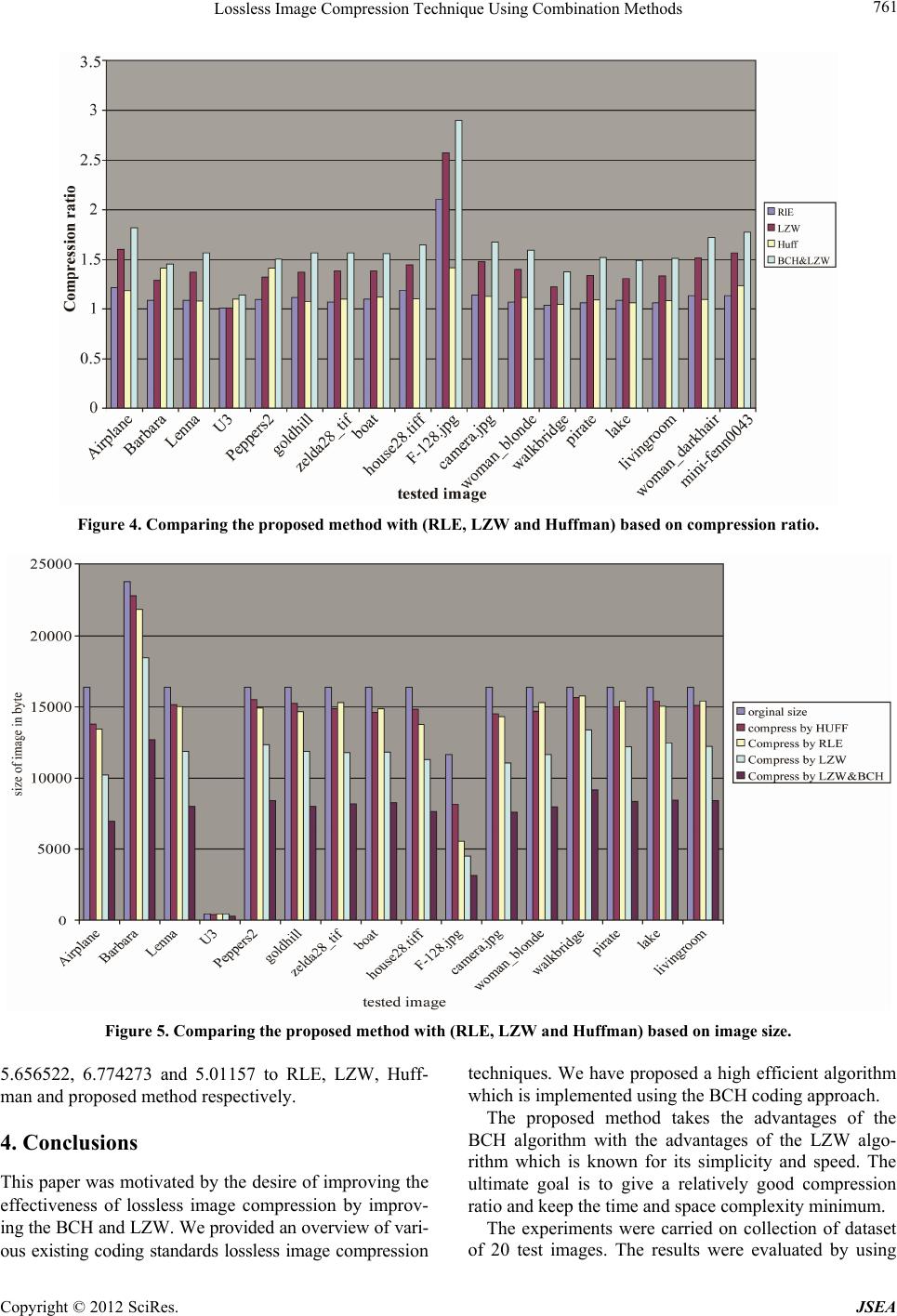 Lossless Image Compression Technique Using Combination Methods 761 Figure 4. Comparing the proposed method with (RLE, LZW and Huffman) based on compression ratio. Figure 5. Comparing the proposed method with (RLE, LZW and Huffman) based on image size. 5.656522, 6.774273 and 5.01157 to RLE, LZW, Huff- man and proposed method respectively. 4. Conclusions This paper was motivated by the desire of improving the effectiveness of lossless image compression by improv- ing the BCH and LZW. We provided an overview of vari- ous existing coding standards lossless image compression techniques. We have proposed a high efficient algorithm which is implemented using the BCH coding approach. The proposed method takes the advantages of the BCH algorithm with the advantages of the LZW algo- rithm which is known for its simplicity and speed. The ultimate goal is to give a relatively good compression ratio and keep the time and space complexity minimum. The experiments were carried on collection of dataset of 20 test images. The resultvaluated by using s were e Copyright © 2012 SciRes. JSEA  Lossless Image Compression Technique Using Combination Methods 762 Figure 6. Comparing the proposed method with (RLE, LZW and Huffman) based on bit per pixel. compression ratio and bits per pixel. The experimental results show that the proposed algorithm improves the compression of images comparing compared with the RLE, Huffman and LZW algorithms, the proposed method ave- rage compression ratio is 1.636383, which is better than the standard lossless image compression. 5. Future Work In this paper, we develop a method for improve image compression based on BCH and LZW. We suggest for future work to use BCH with another compression me- thod and that enable to repeat the compression more than three times, and to investigate how to provide a high compression ratio for given images and to find an algo- rithm that decrease file (map). The experiment dataset in this paper was somehow limited so applying the deve- loped methods on a larger dataset could be a subject for future research and finally extending the work to the video compression is also very interesting, Video data is basi- cally a three-dimensional array of color pixels, that con- tains spatial and temporal redundancy. Similarities can thus be encoded by registering differences within a frame (spatial), and/or between frames (temporal) where data frame is a set of all pixels that correspond to a single time moment. Basically, a frame is the same as a still picture. Spatial encoding in video compression is performed by taking advantage of the fact that the human eye is unable to distinguish small differences in color as easily as it can perceive changes in brightness, so that very similar areas of color can be “averaged out” in a similar way to JPEG images. With temporal compression only the changes from one frame to the next are encoded as often a large num- ber of the pixels will be the same on a series of frames. REFERENCES [1] R. C. Gonzalez, R. E. Woods and S. L. Eddins, “Digital Image Processing Using MATLAB,” Pearson Prentice Hall, Upper Saddle River, 2003. [2] K. D. Sonal, “Study of Various Image Compression Tech- niques,” Proceedings of COIT, RIMT Institute of Engi- neering & Technology, Pacific, 2000, pp. 799-803. [3] M. Rabbani and W. P. Jones, “Digital Image Compres- sion Techniques,” SPIE, Washington. doi:10.1117/3.34917 [4] D. Shapira and A. Daptardar, “Adapting the Knuth-Mor- ris-Pratt Algorithm for Pattern Matching in Huffman En- coded Texts,” Information Processing and Management, Vol. 42, No. 2, 2006, pp. 429-439. doi:10.1016/j.ipm.2005.02.003 [5] H. Zha, “Progressive Lossless Image Compression Using Image Decomposition and Context Quantization,” Master Thesis, University of Waterloo, Waterloo. [6] W. Walczak, “Fractal Compression of Medical Images,” Master Thesis, School of Engineering Blekinge Institute of Technology, Sweden. [7] R. Rajeswari and R. Rajesh, “WBMP Compression,” In- ternational Journal of Wisdom Based Computing, Vol. 1, No. 2, 2011. doi:10.1109/ICIIP.2011.6108930 [8] M. Poolakkaparambil, J. Mathew, A. M. Jabir, D. K. Pradhan and S. P. Mohanty, “BCH Code Based Multiple Bit Error Correction in Finite Field Multiplier Circuits,” Copyright © 2012 SciRes. JSEA  Lossless Image Compression Technique Using Combination Methods 763 Proceedings of the 12th International Symposium on Q ua l - ity Electronic Design (ISQED), Santa Clara, 14-16 March 2011, pp. 1-6. doi:10.1109/ISQED.2011.5770792 [9] B. Ranjan, “Information Theory, Coding and Cryptogra- phy,” 2nd Edition, McGraw-Hill Book Company, India, 2008. [10] P. G. Howard and V. J. Scott, “New Method for Lossless Image Compression Using Arithmetic Coding,” Informa- tion Processing & Management, Vol. 28, No. 6, 1992, pp. 749-763. doi:10.1016/0306-4573(92)90066-9 [11] P. Franti, “A Fast and Efficient Compression Method for Binary Image,” 1993. [12] M. Burrows and D. J. Wheeler, “A Block-Sorting Loss- less Data Compression Algorithm,” Systems Research Center, Vol. 22, No. 5, 1994, pp. [13] B. Meyer and P. Tischer, “TMW—A New Method for Lossless Image Compression,” Australia, 1997. [14] M. F. Talu and İ. Türkoğlu, “Hybrid Lossless Compres- sion Method for Binary Images,” University of Firat, Ela- zig, Turkey, 2003. [15] L. Zhou, “A New Highly Efficient Algorithm for Lossless Binary Image Compression,” Master Thesis, University of Northern British Columbia, Prince George, 2004. [16] N. J. Brittain and M. R. El-Sakka, “Grayscale True Two- Dimensional Dictionary-Based Image Compression,” Jour- nal of Visual Communication and Image Representation, Vol. 18, No. 1, pp. 35-44. [17] R.-C. Chen, P.-Y. Pai, Y.-K. Chan and C.-C. Chang, “Lossless Image Compression Based on Multiple-Tables Arithmetic Coding,” Mathematical Problems in Engi- neering, Vol. 2009, 2009, Article ID: 128317. doi:10.1155/2009/128317 [18] J. H. Pujar and L. M. Kadlaskar, “A New Lossless Me- thod of Image Compression and Decompression Using Huffman Coding Technique,” Journal of Theoretical and Applied Information Technology, Vol. 15, No. 1, 2010. [19] H. Bahadili and A. Rababa’a, “A Bit-Level Text Com- pression Scheme Based on the HCDC Algorithm,” Inter- national Journal of Computers and Applications, Vol. 32, No. 3, 2010. [20] R. Al-Hashemi and I. Kamal, “A New Lossless Image Compression Technique Based on Bose,” International Journal of Software Engineering and Its Applications, Vol. 5, No. 3, 2011, pp. 15-22. Copyright © 2012 SciRes. JSEA
|