 World Journal of Mechanics, 2012, 2, 272-279 doi:10.4236/wjm.2012.25033 Published Online October 2012 (http://www.SciRP.org/journal/wjm) Natural Convection Flow and Heat Transfer Enhancement of a Nanofluid past a Truncated Cone with Magnetic Field Effect Sameh E. Ahmed, A. Mahdy Mathematics Department, Faculty of Science, South Valley University, Qena, Egypt Email: sameh_sci_math@yahoo.com, mahdy4@yahoo.com Received August 2, 2012; revised September 1, 2012; accepted September 12, 2012 ABSTRACT A nonsimilarity analysis is per formed to investigate the laminar , free convection boundar y layer flow over a permeable isothermal truncated cone in the presence of a transverse magnetic field effect. A suitable set of dimensionless variables is used and non-similar equations governing the problem are obtained. Fourth order Runge-Kutta with shooting tech- nique is employed for the numerical solution of the obtained equations. Different water-based nanofluids containing Cu, Ag, CuO, Al2O3, and TiO2 are taken into consideration. The effects of pertinent parameters such as the solid volume fraction of nanoparticles, and magnetic field parameter have been investigated. Furthermore, different models of nan- ofluid based on different formulas for thermal conductivity and dynamic viscosity on the flow and heat transfer charac- teristics are discussed. Various comparisons with previously published work for the case of a vertical plate are per- formed and the results are found to be in excellent agreement. Keywords: Nanofluid; Truncated Cone; Magnetic Field; Natural Convection; Non-Similarity Solution 1. Introduction As it is well known that the natural convection phenom- ena arise in nature as well as in industries. Therefore, laminar free-convection boundary-layer flow of an elec- trically conducting fluid in the presence of a magnetic field has been investigated by many researchers due to its frequent encounter in industrial and technological appli- cations. For instance, Lin and Chen [1] have studied mixed convection on a vertical plate for fluids on any Prandtl number. The laminar natural convection over a slender vertical frustum of a cone has been reported by Na and Chiou [2,3]. Chamkha [4] investigated the lami- nar, coupled heat and mass transfer by natural convective boundary layer flow over a permeable isothermal trun- cated cone in the presence of magnetic field Raptis and Singh [5] have solved the problem of hydromagnetic natural convection flow past an accelerated vertical plate. Kao [6] has reported on the local nonsimilarity solution for laminar natural convection adjacent to a vertical sur- face. Na [7] has considered natural convective flow past a nonisothermal vertical flat plate and reported a nu- merical solution. The laminar natural convection from a nonisothermal cone was analyzed by Roy [8] and Hering and Grosh [9]. An approximate method of solution for the overall heat transfer from vertical cones in laminar natural convection was reported by Alamgir [10]. Takhar and Ram [11] have studied magneto-hydrodynamic natural convection flow of water through a porous me- dium. On the other hand, nanofluids have been widely used in industry, because of the growing use of these smart fluids. Many studies [12-17] explained that nanofluids clearly exhibit enhanced thermal conductivity, which goes up with increasing volumetric fraction of nanoparti- cles. Nanofluid concept is utilized to describe a fluid in which nanometer-sized particles are suspended in con- ventional heat transfer basic fluids. Conventional heat transfer fluids, including oil, water, and ethylene glycol mixture are poor heat transfer fluids, since the thermal conductivity of these flu ids play an important role on the heat transfer coefficient between the heat transfer me- dium and the heat transfer surface. Therefore, numerous methods have been taken to improve the thermal conduc- tivity of these fluids by suspending nano/micro or lar- ger -sized particle materials in liquids [18]. Choi et al. [19] showed that the addition of a small amount (less than 1% by volume) of nanoparticles to convention al heat transfer liquids increased the thermal co nductivity of the fluid up to approximately two times. Mahdy and Sameh [20] re- ported numerical analysis for laminar free convection over a vertical wavy surface embedded in a porous me- dium saturated with a nanofluid. Khan and Pop [21] in- Copyright © 2012 SciRes. WJM  S. E. AHMED, A. MAHDY 273 vestigated numerically the problem of laminar fluid flow resulting from the stretching of a flat surface in a nan- ofluid. The used model for the nanofluid incorporated the effects of Brownian motion and thermophoresis. Hojjat et al. [22] investigated experimentally laminar convec- tion heat transfer behavior of three different types of nanofluids flowing through a uniformly heated horizontal circular tube. Nanofluids were made by dispersion of Al2O3, CuO, and TiO2 nanoparticles in an aqueous solu- tion of carboxymethyl cellulose (CMC). All nanofluids as well as the base fluid exhibited shear-thinning behave- ior. The goal of the present investigation is to find nu- merical solutions for the problem of boundary layer flow and heat transfer characteristics utilizing nanofluids past a truncated cone in the presence of a transverse magnetic field effect. The effects due to uncertainties of thermal conductivity and dynamic viscosity have been under- taken and discussed. 2. Analysis of the Problem We consider steady state, laminar, and heat transfer by natural convection, boundary layer flow of an electrically conducting and optically dense fluid about a truncated permeable cone with a half angle as shown in Fig- ure 1. The fluid is a water based nanofluid containing different types of nanoparticles such as Copper Cu, Sil- ver Ag, Alumina Al2O3, Copper oxide CuO and Titanate TiO2. It is assumed that the base fluid and the nanoparti- cles are in thermal equilibrium and no slip occurs be- tween them. The thermo physical properties of the nan- ofluid are given in Table 1 as [23,24]. In addition, the origin of the coordinate system is placed at the vertex of the full cone where represents the distance along the Figure 1. Physical model and coordinate system. Table 1. Thermo-physic al properties of water and nanopar - ticles [23,24]. 3 kgm r 11 Jkg K p c 11 Wm K k 51 x10 K b H2O 997.1 4179 0.6130 21.0 Cu 8933 385.0 401.00 1.67 CuO 3620 531.8 76.500 1.80 Ag 10500 235.0 429.00 1.89 Al2O33970 765.0 40.000 0.85 TiO2 4250 686.2 8.9538 0.90 cone and represents the distance normal to the sur- face of the cone. The cone surface is maintained at a constant temperature w while the ambient temperature far away from the surface of the cone is assumed to be uniform. A uniform magnetic field is applied in the -direction normal to the flow direction. The magnetic Reynolds number is assumed to be small so that the in- duced magnetic field is neglected. In addition, the Hall effect and the electric field are assumed negligible. The small magnetic Reynolds number assumption uncouples the Navier Stokes equations from Maxwell’s equations. By invoking all of the boundary layer and Boussineq, the governing equations for this investigation can be written as y TT y 0 ru ru xy (1) 2 2 2 cos n fnf f n TT A uu u u Bgu xy y (2) 2 2 pnf nf TT cu xy k y T (3) The proper boundary and ambient conditions for this problem can be written as 0, ,0t a,,0 a t w uv TT u y TyT (4) where, and v are the velocity components along the axes u and , respectively, is the radius of the truncated cone, y r , B are the fluid electrical conductivity, magnetic induction. nf is the effective density of the nanofluid, nf is the effective dynamic viscosity of the nanofluid, is the temperature of the nanofluid, nf T is the thermal expansion of the nanofluid, is the ac- celeration due to gravity. Now, for nanofluids, let us in- troducing the expression for nf , and c pnf nf of the nanofluid as Copyright © 2012 SciRes. WJM  S. E. AHMED, A. MAHDY Copyright © 2012 SciRes. WJM 274 , , 1 1 1 nf p fs pnf p s nff s ccc (5) 12 14 , 31 14 4 fr f Gr ufUf x Gr f vf x f (7) On the other hand, effective thermal conductivity can be incorporated from the following expression: 11 1 sf f nf f sffs knkn kk kk knk kk s Substituting Equations (6) and (7) into Equations (2) and (3) yields the following nonsimilar dimensionless equations: 2 2 11 1 13 214 nf s sff f g fMf fff ff ff (8) where is the empirical shape factor for the nanopar- ticle. In particular, for spherical shaped nanopar- ticles and n 3 n 32n for cylindrical ones, Table 2 shows four models of nanofluid based on different formulas for thermal conductivity and dynamic viscosity. Furthermore, is the solid volume fraction, is the dynamic vis- cosity of the base fluid, and are the thermal expansion coefficients of the base fluid and nanoparticle, respectively, and are the densities of the base fluid and nanoparticle, respectively, nf is the thermal conductivity and nf is the heat capacity of the nanofluid, k p c k and k are the thermal conductivities of the base fluid and nanoparticle, respectively. The gov- erning equations and boundary conditions can be made dimensionless by introducing the stream function such that 3 14 Pr 1 f p nf s pf c c f f kk (9) 0:0, 1 :0,0 ff f (10) ,rru yx where a prime denotes partial differentiation with respect to and and using the following dimensionless variables 34 2 20 2,Pr , fwf g fx f gTTx B GrM Gr 1/4 1/4 0 00 ,, (,), (,) wf xxx y Gr xx x TT f TT rGr (6) are the Grashof number, Prandtl number and square of the Hartmann number. Table 2. Models of nanofluid based on different formulas for thermal conductivity and dynamic viscosity. Model Shape of nanoparticles Thermal conductivity Dynamic viscosity I Spherical 22 2 sf fs nf f sf fs kk kk kk kk kk 2.5 1 nf f II Spherical 22 2 sf fs nf f sf fs kk kk kk kk kk 2 1 7.3123 nf f III Cylindrical (nanotubes) 0.5 0.5 0.5 sf fs nf f sffs kk kk kk kkkk 2.5 1 nf f IV Cylindrical (nanotubes) 0.5 0.5 0.5 sf fs nf f sffs kk kk kk kkkk 2 1 7.3123 nf f  S. E. AHMED, A. MAHDY 275 The quantities of physical interest are the local skin friction coefficient C and the rate of heat transfer that expressed in terms of local Nusselt number Nu and these are given by 2 2, ww fx fw fr xq CNu kT T U (11) where the skin friction w and the heat transfer from the sheet are given by w q 0 , wnfw nf y u qk y 0y T y (12) Applying the non-dimensional transformations (5), one obtain 1 4 1 4 2,0 ,0 nf fx f nf xx f CGrf k Nu Grk , (13) 3. Numerical Procedure The numerical algorithm used to solve the dimens ionless equations (8) and (9) with the boundary conditions (10) is based on the well-known fourth order Runge-Kutta integration scheme. In the current technique, the differ- ence between the forward and backward values of de- pendent variables should be zero for a true solution. The procedure uses a generalized Newton method to reduce these differences to zero, by calculating corrections to the estimated boundary values. This process is repeated it- eratively until convergence is obtained to as specified accuracy. This method was found to be suitable and gave results that are very close to the results obtained in Refs. [4,25,26]. Table 3 shows comparison of values of 0,0f and 0,0 for various values of Pr for pure fluid. As it is observed, there is an excellent agreement with the earlier publish ed results. 4. Results and Discussion Steady state two-dimensional laminar magneto-hydro- dynamics natural convection flow and heat transfer of a nanofluid past a truncated cone has been studied nu- merically. Parametric studies of the influence of various parameters such as finite volume fraction (00.15 ), magnetic field parameter (0 g), different formu- las of dynamic viscosity ratio (5M nf f ) and thermal conductivity ratio (nf f kk) on the fluid flow and heat transfer have been performed. In all the obtained results, pure water with Pr 7 has been used as a base nan- ofluid. Figures 2 and 3 display the effects of solid vol- ume fraction on the local skin friction coefficient and the rate of heat transfer for Cu-water nanofluid using model I. It is found that, increasing in solid volume fraction re- sults in an increase in rate of heat transfer and a reduction in local skin friction coefficient. In fact, high values of causes the fluid becomes more viscous. As results, the natural convection is reduced which causes the fluid flows is very slowly. This velocity reduction causes an increase in thermal boundary layer thickness, which in turn, increases the rate of heat transfer and decreases the local Nusselt number. The main objective from adding nanoparticles to the classical fluid is enhancing the rate of heat transfer for such fluids, so it is necessary to explain which the best model can be used to reach to this goal. In Figures 4 and 5, a comparison among different formulas for nanofluid dynamic viscosity and nanofluid thermal conductivity was performed at 0.08 and. These formulas 1 g M Table 3. Comparison of values of f0,0 and 0,0 for various values of Pr for pure fluid. 0,0f 0,0 Pr [25] [26] [4] present [25] [26] [4] present 0.0001 1.4998 - 1.4997 1.49906 0.0060 - 0.0059 0.00598 0.001 1.4728 - 1.4727 1.47299 0.0189 - 0.0188 0.01859 0.01 1.3968 - 1.3965 1.38941 0.0570 - 0.0574 0.05738 0.1 1.2144 1.2104 1.2151 1.20918 0.1629 0.1637 0.1630 0.16312 1.0 0.9084 0.9081 0.9081 0.90813 0.4012 0.4009 0.4015 0.40131 10.0 0.5927 0.5930 0.5927 0.59268 0.8266 0.8266 0.8274 0.82664 100.0 0.3539 0.3564 0.3558 0.35557 1.5493 1.5495 1.5503 1.54928 1000.0 0.2049 - 0.2049 0.20468 2.8035 - 2.8044 2.80099 10000.0 0.1161 - 0.1161 0.11669 5.0127 - 5.0131 5.02900 Copyright © 2012 SciRes. WJM 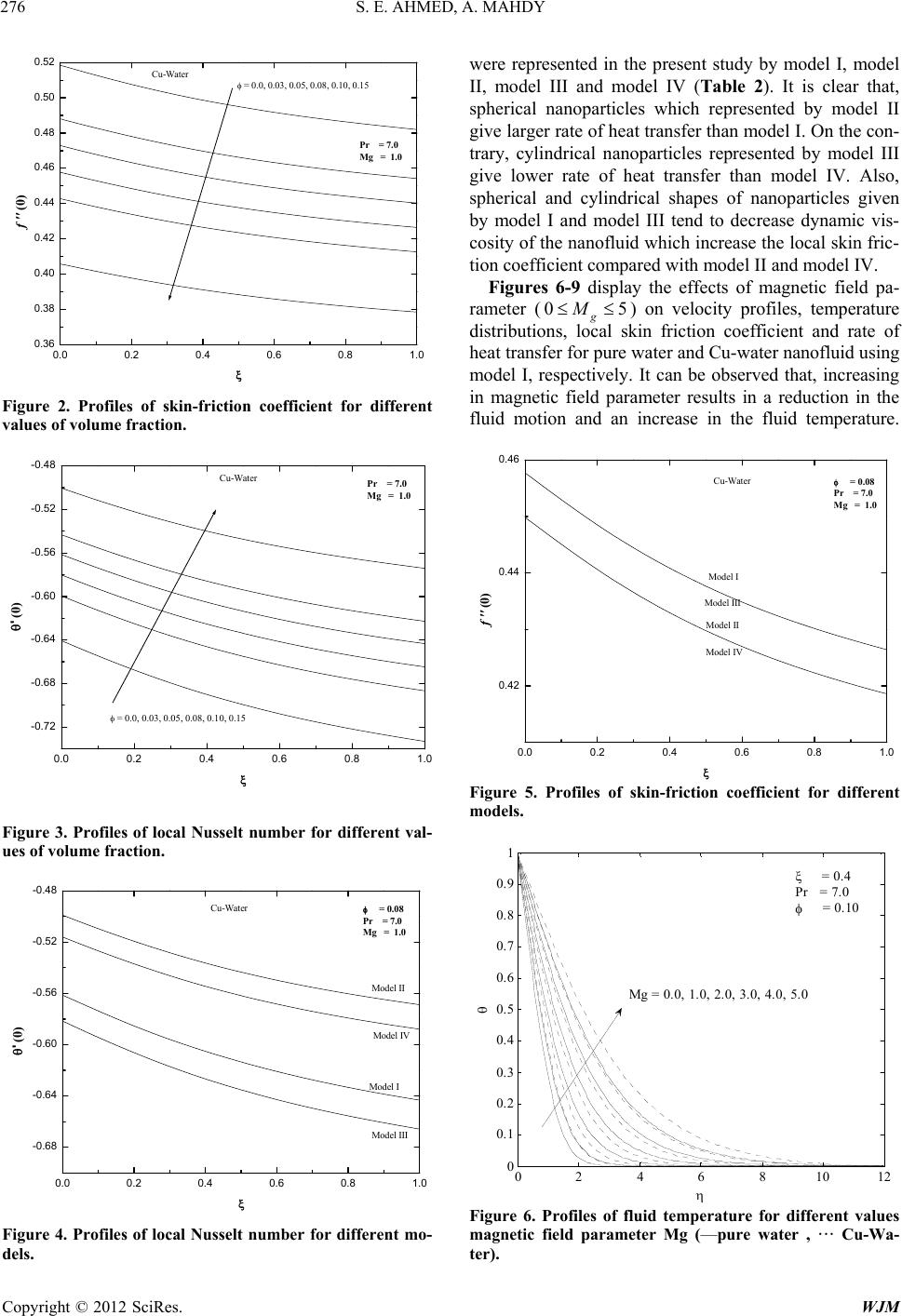 S. E. AHMED, A. MAHDY 276 0.0 0.2 0.4 0.6 0.8 1.0 0.36 0.38 0.40 0.42 0.44 0.46 0.48 0.50 0.52 = 0.0, 0.03, 0.05 , 0. 08, 0.10, 0. 15 Pr = 7.0 Mg = 1.0 Cu-Water f '' (0) Figure 2. Profiles of skin-friction coefficient for different values of volume fraction. 0.0 0.2 0.4 0.6 0.8 1.0 -0.72 -0.68 -0.64 -0.60 -0.56 -0.52 -0.48 = 0.0, 0. 03, 0.05, 0. 08, 0.10, 0.1 5 Cu-Water Pr = 7.0 Mg = 1.0 ' (0) Figure 3. Profiles of local Nusselt number for different val- ues of volume fraction. 0.00.20.40.60.81 -0.68 -0.64 -0.60 -0.56 -0.52 -0.48 .0 Model IV Model II Model I Model III Cu-Water = 0.08 Pr = 7.0 Mg = 1.0 ' (0) Figure 4. Profiles of local Nusselt number for different mo- dels. were represented in the present study by model I, model II, model III and model IV (Table 2). It is clear that, spherical nanoparticles which represented by model II give larger rate of heat transfer than model I. On the con- trary, cylindrical nanoparticles represented by model III give lower rate of heat transfer than model IV. Also, spherical and cylindrical shapes of nanoparticles given by model I and model III tend to decrease dynamic vis- cosity of the nanofluid which increase the local sk in fric- tion coefficient compared with model II and model IV. Figures 6-9 display the effects of magnetic field pa- rameter (0 g5M ) on velocity profiles, temperature distributions, local skin friction coefficient and rate of heat transfer for pure water and Cu-water nanofluid using model I, respectively. It can be observed that, increasing in magnetic field parameter results in a reduction in the fluid motion and an increase in the fluid temperature. 0.0 0.2 0.40.6 0.8 1.0 0.42 0.44 0.46 Model III Model IV Model II Model I = 0.08 Pr = 7.0 Mg = 1.0 Cu-Water f '' (0) Figure 5. Profiles of skin-friction coefficient for different models. 02 46810 12 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Mg = 0.0, 1. 0, 2 . 0, 3. 0, 4. 0, 5. 0 = 0.4 Pr = 7.0 = 0.10 Figure 6. Profiles of fluid temperature for different values magnetic field parameter Mg (—pure water , ··· Cu-Wa- ter). Copyright © 2012 SciRes. WJM  S. E. AHMED, A. MAHDY 277 02 46 81012 0 0. 05 0. 1 0. 15 0. 2 0. 25 f ' Mg = 0. 0, 1. 0, 2. 0, 3. 0, 4. 0, 5. 0 = 0.4 Mg = 1.0 = 0.10 Figure 7. Velocity profiles for different values magnetic field parameter Mg (—pure water , ··· Cu-Water). 0.0 0.2 0.4 0.6 0.8 1.0 0.2 0.3 0.4 0.5 0.6 Pure water Cu-W ater Mg = 0.0, 1.0, 2.0, 3.0, 4.0, 5.0 Cu-Water = 0.08 Pr = 7.0 f '' (0) Figure 8. Profiles of skin-friction coefficient for different values of magnetic field Mg. 0.0 0.2 0.4 0.6 0.8 1.0 -0.8 -0.7 -0.6 -0.5 -0.4 -0.3 -0.2 Pure water Cu-Water Cu-Water = 0.08 Pr = 7.0 Mg = 0.0, 1.0, 2.0, 3.0, 4.0, 5.0 ' (0) This can be attributed to the existence of magnetic field within the flow region which causes a force called Lor- entz force. This force works opposite to the flow direc- tion and it resists the flow. This reduction leads to de- creases the local skin friction coefficient and increases the boundary layer thickn ess which in turn, increases the rate of heat transfer as well. Figures 10 and 11 show the profiles of fluid velocity and fluid temperature for pure water (0 ), Cu-water, CuO-water, Al2O3-water, Ag-water and TiO2-water nano- fluid with (0.08 ) related with Model I at 1 g M and 0.4 . The results show that, the fluid motion becomes very slowly by adding Al2O3 nanoparticles. However, the CuO-nanoparticles give faster motion for nanofluid than other nanoparticles. On the other hand, the high value of thermal conductivity of Ag (Table 1) causes to decrease the fluid temperature whereas, the TiO2 nanoparticles leads to increase the fluid temperature. The behaviors of velocity and temperatures mentioned above have opposite effects on behaviors of local skin friction coefficient and rate of heat transfer. It can be noticed from Figures 12 and 13 which depicted the pro- files of local skin friction coefficient and rate of heat transfer for different nanoparticles, respectively, that, TiO2-water nanofluid has a high value of skin friction while the CuO-water nanofluid has a lower value of it. In addition, the high rate of heat transfer can be obtained by adding Ag-nanoparticles and TiO2 nanoparticles give a lower value of it. The mean responsible of these effects is the values of thermal conductivity for such nanoparticles (Table 1). Similar behaviors are observed by Rana and Bhargava [27] which make sure that the present results are more accurate. 5. Conclusion In this paper, the problems of MHD natural convection 02 46 810 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 Figure 9. Profiles of local nusselt number for different val- ues of magnetic field Mg. f ' 0.8 11.2 1.4 0.15 0.155 0.16 0.165 f ' Pr =7.0 Mg = 1 .0 = 0.4 = 0. 08 Al2O3, TiO2, Ag, Cu, CuO Figure 10. Velocity profiles for different nanoparticles. Copyright © 2012 SciRes. WJM 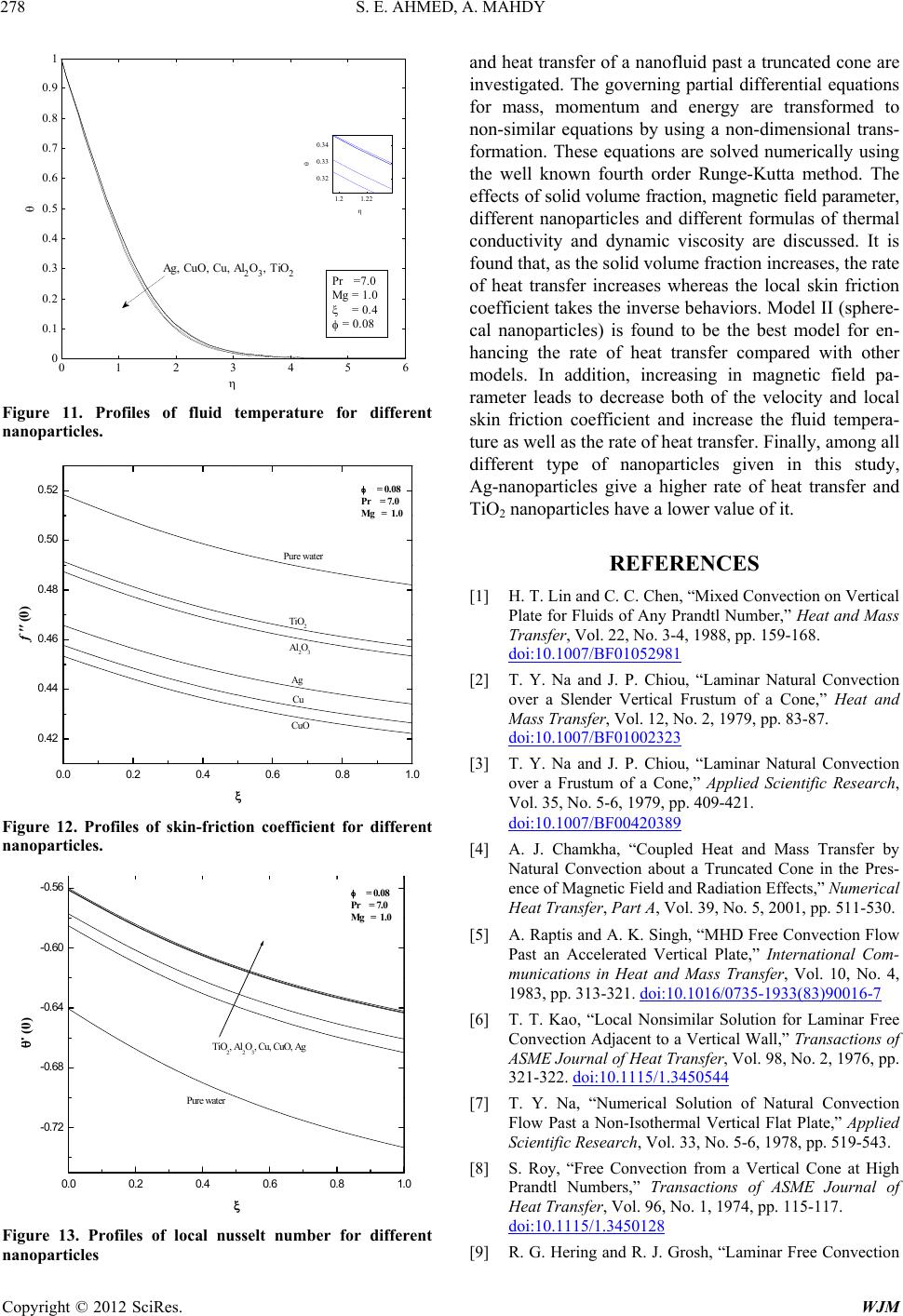 S. E. AHMED, A. MAHDY 278 0 12 34 56 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.2 1.22 0.32 0.33 0.34 Pr =7.0 Mg = 1. 0 = 0.4 = 0. 08 Ag, CuO, Cu, Al 2 O 3 , TiO 2 Fi t nanoparticles. gure 11. Profiles of fluid temperature for differen 0.0 0.2 0.4 0.6 0.8 1.0 0.42 0.44 0.46 0.48 0.50 0.52 = 0.08 Pr = 7 .0 Mg = 1 .0 CuO Cu Ag Al 2O3 TiO2 Pure w a ter f '' (0) Figure 12. Profiles of skin-friction coefficient for different nanoparticles. 0.0 0.2 0.4 0.6 0.8 1.0 -0.72 -0.68 -0.64 -0.60 -0.56 = 0.08 P r = 7 .0 M g = 1 .0 TiO2, Al2O3, C u , C u O, A g Pure water igure 13. Profiles of local nusselt number for diffe ticles and heat transfer of a nanofluid past a truncated cone are investigated. The governing partial differential equations for mass, momentum and energy are transformed to non-similar equations by using a non-dimensional trans- formation. These equations are solved numerically using the well known fourth order Runge-Kutta method. The eff ec ts of solid volume fraction, magnetic field parame ter, different nanoparticles and different formulas of thermal conductivity and dynamic viscosity are discussed. It is found that, as the solid volume fraction increases, the rate of heat transfer increases whereas the local skin friction coefficient takes the inverse behaviors. Model II (sphere- cal nanoparticles) is found to be the best model for en- hancing the rate of heat transfer compared with other models. In addition, increasing in magnetic field F nanopar rent pa- rameter leads to decrease both of the velocity and local skin friction coefficient and increase the fluid tempera- ture as well as the rate of heat transfer. Finally, among all different type of nanoparticles given in this study, Ag-nanoparticles give a higher rate of heat transfer and TiO2 nanoparticles have a lower value of it. REFERENCES [1] H. T. Lin and C. C. Chen, “Mixed Convection on Vertical Plate for Fluids of Any Prandtl Number,” Heat and Mass Transfer, Vol. 22, No. 3-4, 1988, pp. 159-168. doi:10.1007/BF01052981 [2] T. Y. Na and J. P. Chiou, “Laminar Natural Convection over a Slender Vertical Frustum of a Cone,” Heat and Mass Transfer, Vol. 12, No. 2, 1979, pp. 83-87. doi:10.1007/BF01002323 [3] T. Y. Na and J. P. Chiou, “Laminar Natural Convection over a Frustum of a Cone,” Applied Scientific Research, Vol. 35, No. 5-6, 1979, pp. 409-421. doi:10.1007/BF00420389 [4] A. J. Chamkha, “Coupled Heat and Mass Transfer by Natural Convection about a Truncated Cone in the Pres- ence of Magnetic Field and Radiation Effects,” Numerical Heat Transfer, Part A, Vol. 39, No. 5, 2001, pp. 511-530. [5] A. Raptis and A. K. Singhection Flow Past an Accelernational Com- , “MHD Free Conv erated Vertical Plate,” Int munications in Heat and Mass Transfer, Vol. 10, No. 4, 1983, pp. 313-321. doi:10.1016/0735-1933(83)90016-7 [6] T. T. Kao, “Local Nonsimilar Solution for Lam Convection Adjacent to a Vinar Free ertical Wall,” Transactions of ASME Journal of Heat Transfer, Vol. 98, No. 2, 1976, pp. 321-322. doi:10.1115/1.3450544 [7] T. Y. Na, “Numerical Solution of Natural Convect Flow Past a Non-Isothermion al Vertical Flat Plate,” Applied ASME Journal of . 1, 1974, pp. 115-117. Scientific R es ea rch, Vol. 33, No. 5-6, 1978, pp. 519-543. [8] S. Roy, “Free Convection from a Vertical Cone at High Prandtl Numbers,” Transactions of Heat Transfer, Vol. 96, No doi:10.1115/1.3450128 [9] R. G. Hering and R. J. Grosh, “Laminar Free Convection Copyright © 2012 SciRes. WJM  S. E. AHMED, A. MAHDY Copyright © 2012 SciRes. WJM 279 from a Non-Isothermal Cone at Low Prandtl Number,” International Journal of Heat and Mass Transfer, Vol. 8, No. 10, 1965, pp. 1333-1337. doi:10.1016/0017-9310(65)90059-1 [10] M. Alamgir, “Over-All Heat Transfer from Vertical Cones in Laminar Free Convection: An Approximate Method,” Transactions of ASME Journal of Heat Trans- fer, Vol. 101, No. 1, 1979, pp. 174-176. doi:10.1115/1.3450912 [11] H. S. Takhar and P. C. Ram, “Magnetohydrodynamics Free Convection Flow of Water at 4˚C, through a Porous Medium,” International Communications in Heat and Mass Transfer, Vol. 21, No. 3, 1994, pp. 371-376. doi:10.1016/0735-1933(94)90005-1 [12] Y. Xuan and O. Li, “Heat Transfer Enhancement of Na no- fluids,” International Journal of Heat and Fluid Flow, Vol. 21, No. 1, 2000, pp. 58-64. doi:10.1016/S0142-727X(99)00067-3 [13] Q. Li and Y. Xuan, “Experimental Investigation of Trans- port Properties of Nanofluids,” In: B. X. Wang, Ed., Heat Transfer Science & Technology, Higher Education Press, Beijing, 2000, pp. 757-784. [14] D. Wen and Y. Ding, “Experimental Investigation 12 into Convective Heat Transfer of Nanofluids at the Entrance Region under Laminar Flow Conditions, International Journal Heat and Mass Transfer, Vol. 47, No. 24, 2004, pp. 5181-5188. doi:10.1016/j.ijheatmasstransfer.2004.07.0 [15] P. Bhattacharya, S. Saha, A. Yadav, P. Phelan and R. Prasher, “Brownian Dynamics Simulation to Determine the Effect Thermal Conductivity of Nanofluids,” Journal of Applied Physics, Vol. 95, No. 11, 2004, pp. 6492-6494. doi:10.1063/1.1736319 [16] A. Mokmeli and M. Saffar-Avval, “Prediction of Nano- fluid Convective Heat Transfer Using the Dispersion Model,” International Journal of Thermal Sciences, Vol. 49, No. 3, 2010, pp. 471-478. doi:10.1016/j.ijthermalsci.2009.09.005 [17] M. Mansour, R. Mohamed, M. Abd-Elaziz and S. Ahmed, “Numerical Simulation of Mixed Convection Flows in a Square Lid-Driven Cavity Partially Heated from Below Using Nanofluid,” International Communications in Heat and Mass Transfer, Vol. 37, No. 10, 2010, pp. 1504-1512. doi:10.1016/j.icheatmasstransfer.2010.09.004 [18] R. Lotfi, Y. Saboohi and A. Rashidi, “Numerical Study of Forced Convective Heat Transfer of Nanofluids: Com- parison of Different Approaches,” International Commu- nications in Heat and Mass Transfer, Vol. 37, No. 1, 2010, pp. 74-78. doi:10.1016/j.icheatmasstransfer.2009.07.013 [19] S. Choi, Z. Zhang, W. Yu, F. Lockwood and E. Grulke, “Anomalously Thermal Conductivity Enhancement in Nanotube Suspensions,” Applied Physics Letter, Vol. 79, No. 14, 2001, pp. 2252-2254. doi:10.1063/1.1408272 [20] A. Mahdy and S. E .Ahmed, “Laminar Free Convection over a Vertical Wavy Surface Embedded in a Porous Me- dium Saturated with a Nanofluid,” Transport in Porous Media, Vol. 91, No. 2, 2012, pp. 423-435. doi:10.1007/s11242-011-9852-4 [21] W. Khan and I. Pop, “Boundary-Layer Flow of a Nan- ofluid Past a Stretching Sheet,” International Journal of Heat and Mass Transfer, Vol. 53, No. 11-12, 2010, pp. 2477-2483. doi:10.1016/j.ijheatmasstransfer.2010.01.032 [22] M. Hojjat, S. Etemad and R. Bagheri, “Laminar Heat Transfer of Non-Newtonian Nanofluids in a Circular Tube,” Korean Journal of Chemical Engineering, Vol. 27, No. 5, 2010, pp. 1391-1396. doi:10.1007/s11814-010-0250-3 [23] H. F. Oztop and E. Abu-Nada, “Numerical Study of Natu- ral Convection in Partially Heated Rectangular Enclo- sures Filled with Nanofluids,” International Journal of Heat Fluid Flow, Vol. 29, No. 5, 2008, pp. 1326-1336. doi:10.1016/j.ijheatfluidflow.2008.04.009 [24] Z. Alloui, P. Vasseur and M. Reggio, “Natural Convec- tion of Nanofluids in a Shallow Cavity Heated from Be- low,” International Journal of Thermal Sciences No. 3, 2011, pp. 385-393. , Vol. 50, doi:10.1016/j.ijthermalsci.2010.04.006 [25] K. A. Yih, “Effect of Radiation on Natural Convection about a Truncated Cone,” International Journal of Heat Mass Transfer, Vol. 42, No. 23, 1999, pp. 4299-4305. doi:10.1016/S0017-9310(99)00092-7 [26] T. Cebeci and P. Bradshaw, “Physical and Computational Aspects of Convective Heat Transfer,” Springer, New York, 1984, p. 270. [27] P. Rana and R. Bhargava, “Numeric Transfer Enhancement in Mixed Convec al Study of Heat tion Flow along a Vertical Plate with Heat Source/Sink Utilizing Nanofluids, Communications in Nonlinear Science and Numerical Simulation, Vol. 16, No. 11, 2011, pp. 4318-4334. doi:10.1016/j.cnsns.2011.03.014
|