 World Journal of Mechanics, 2012, 2, 229-238 doi:10.4236/wjm.2012.25028 Published Online October 2012 (http://www.SciRP.org/journal/wjm) Probabilistic Indicators of Structural Redundancy in Mechanics Branko Blagojević1, Kalman Žiha2 1Department of Mechanical Engineering and Naval Architecture, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture (FESB), University of Split, Split, Croatia 2Department of Ship Structures, Faculty of Mechanical Engineering and Naval Architecture (FSB), University of Zagreb, Zagreb, Croatia Email: bblag@fesb.hr, kziha@fsb.hr Received July 20, 2012; revised August 23, 2012; accepted September 2, 2012 ABSTRACT The paper in the introductory part reviews various definitions and interpretations of structural redundancy in mechanics. The study focuses on the general structural redundancy of systems after sequences of component failures followed by possible load redistributions. The second section briefly summarizes the Event Oriented System Analysis and structural redundancy in terms of the conditional probabilistic entropy. Mechanical responses to adverse loads in this approach are represented by random operational and failure events in the lifetime. The general redundancy measure in the third sec- tion of the paper employs the information entropy and goes beyond existing formulations since it includes all functional modes in service. The paper continues with a summary of traditional redundancy indices. In addition, it proposes an alternative redundancy index that accounts for the transition to secondary functional level in case of failures of primary components. The example of a ship structure illustrates the usage of the conditional entropy of subsystems of opera- tional events and compares it to the traditional and newly proposed redundancy indices. The study at the end investi- gates how to enhance the safety of structures by using the redundancy based design. Keywords: Reliability; Event-Oriented System Analysis; Entropy; Redundancy; Redundancy Index; Structures 1. Introduction Complex load-carrying engineering structures share a number of properties that relate to the overall structural safety. The definitions, applications and mathematical interpretations of important properties such as redun- dancy, robustness and vulnerability are still vague in dif- ferent engineering disciplines [1-5]. Although those prop- erties have been extensively investigated [6-9], the me- chanical and structural redundancy has been one most difficult to quantify. It is usually classified into local and global (overall) redundancy and can be expressed in two forms, as the system reserve strength and the residual strength [10,11]. Reserve strength is the margin between the design load and the ultimate capacity of the overall structure to sustain the applied load. The redundancy of complex engineering systems is commonly related to residual strength that remains in the structure after one or more components have failed [11, 12]. Descriptive redundancy assessment is characterized by a number of functional levels and by a number of al- ternative operational states. Mere deterministic measures, denoted as structural residual resistance factors and re- dundant factors which relate the strength of the intact and damaged structures, are considered as insufficient for problems of system redundancy. The structural engineering for the sake of efficiency often focuses on “fail-safe” or “damage-tolerant” object that remain operational in the case of the first component failure. Redundancy in engineering systems in this paper is assessed as a general probabilistic operational abun- dance rather than deterministic survival ability in the case of first component failure. In complex structures with large number of interacting components possibly in different uncertain states, the redundancy becomes a sig- nificant issue in investigation of general system safety. The study examines the benefits of combining the probabilistic reliability methods and the event oriented system analysis of structural redundancy using the same set of input data. EOSA relates the system redundancy to the conditional entropy of subsystems of failure events. Entropy as a measure of information primarily originates from the information theory [13,14] and lately is gener- alized as an uncertainty measure in probability theory [15,16]. The unconditional information entropy has not been considered as yet as a useful measure of practical importance for structural systems in engineering. However, the concept of conditional entropy in the Copyright © 2012 SciRes. WJM  B. BLAGOJEVIĆ, K. ŽIHA 230 probability theory represents an objective uncertainty measure for systems of events independent of anything else but possible events [17]. The redundancy defined by conditional entropy of failure path is found useful in as- sessment of lifeline systems efficiency in damaged con- ditions [18]. Therefore, the paper compares alternative definitions of the probabilistic redundancy indices to the entropy-based probabilistic redundancy measure in order to add impetus to further investigation of system safety enhancement in mechanical problems. 2. Event Oriented System Analysis (EOSA) The event-oriented approach considers structures and structural components as systems and subsystems of random events in a lifetime. EOSA enumerates all ob- servable, or at least the most important events, and des- ignates their status as intact, operational, transitive, fail- ure or collapsed. To every event status, a probability of occurrence can be assigned. By grouping events of dif- ferent status, and associated probabilities, EOSA forms systems and subsystems of events. Jointly, the event- oriented system analysis combines modes analysis, enu- meration of events, probability and information theory in order to quantify probabilistic systems’ redundancy. Met- hods such as Secon Moment Methods (SM) First Order Reliability Methods (FOSM, FORM), Advanced FORM (AFORM), Second Order Reliability Methods (SORM) or Monte Carlo simulation and Bayesian methods are on disposal for probability calculations [19-23]. Most of these methods have been used in the assessment of safety of ship structures and structural components. EOSA uses these methods and provides additional information about structural behaviour through a calculation of entropies of systems of events. Additionally, methods of operational modes and effects analysis such as minimal cut-sets, minimal tie-sets, event-tree and fault-tree analysis can identify events [24,25] and determine their relationships. EOSA methodology is summarized in the sequel. A system, S, consists of all observable events Ek with probabilities p(Ek), k = 1, 2, ···, N, where N is the total number of events. Events can represent different func- tional states of the structure such as failure or operational state or some other state of the interest. Event realization causes that system has a different functional status “s”. EOSA designates events and sys- tems’ functional statuses with following indexes: i-intact (non-damaged), c-collapse, t-transitive, n-non-transitive, o-operational (with full or reduced capacity), f-failure, d-damage and combinations. Subsystems of events are made of the events of the same type. i.e. So is then a des- ignation of a subsystem of all operational events and Sf is a subsystem of all failure events. Finite schemes are commonly used as mathematical presentation of the sys- tems and subsystems of events [16]: 1 1 N N EE SpE pE (1) The systems of events can be also represented as a summa of subsystems of events: of SSS (2) So ad Sf are subsystems of operational and failure events 1 1 N No oo o oo EE S pE pE 1 1 NN oo NN oo ff f ff EE S pE pE N f N f o N = No + Nf is the total number of events in S. The reliability of a system is equal to the probability of the occurrence of the subsystem of operational events: 1 o N o k k RS pSpE (3) The probability of failure of a system is equal to the probability of a failure subsystem: 1 of o NN f fk kN pS pSpE (4) For complete systems is p(Ek) = 1, otherwise p(Ek) < 1. Redundant structures are operational even if some of the structural components have failed. Thus, the redun- dant systems of events, representing redundant structures, have to be analysed as functional multi-level operational systems. A functional level can be understood as a sys- tem of events comprising all functional states of an ob- ject. The initial intact state of a structure is modelled as a system of events on the first functional level (primary level). After failure of one or more structural components, the system transits from the first level to the second level (secondary level). Further failures cause the system to transit to the third level, and so on. An event is of status “s”, where l = 1, 2, ···, n is a level and , and is the number of events of the same status “s” within a functional level. ls k E 1,2,, ls kNls N EOSA applies the entropy concept from information theory to assess the effects of the number of events, and dispersion of their probabilities, as well as the possible redistribution of loads after failures. The entropy in in- formation theory is a logarithmic function that measures uncertainty originally introduced by [13]. The Rényi en- tropy is a generalization of Shannon entropy, and repre- sents a family of functionals for quantifying the uncer- Copyright © 2012 SciRes. WJM  B. BLAGOJEVIĆ, K. ŽIHA 231 tainty of a system. The entropy of a system of events of order α, for α ≥ 0 is [14]: 2 11 1log 1 nn n ii ii Sp p (5) where log base is commonly 2. For the same probabili- ties of all events, Rényi entropy is log n S n. Higher values of α give a Rényi entropy which is deter- mined by events with the highest probability. Lower values of α give a Rényi entropy that weights events more equally, regardless of their probabilities. The case α = 1 gives the Shannon entropy. Equation (5) represents a measure of uncertainty cor- responding to either incomplete or complete system of events. This is convenient for complex systems with large number of events where probabilities of some events cannot be determined, or even some events remain un- known. System of events can also be considered under the condition that only the operational events are of interest. The conditional entropy of system S can be obtained as follows [26]: 1 log o o oo Nk o No k pE pE HSS pS pS k o (6) The entropy of the operational subsystem does not de- pend on the probability of a system p(S). Nor does it de- pend on whether the system is complete or incomplete. 3. The Probabilistic Redundancy Definition (Redundancy Assessment) The EOSA relates structural redundancy of the system S to the uncertainty of the subsystem of operational modes So [27] by employing the conditional entropy (6), as: o o N RED SHSS (7) The events of a particular interest for redundant struc- tures are the transitive events Et that cause the system lS to transit from a current functional level l to a subsequent level l + 1 denoted . Every transitive event also leads to the emergence of a new functional state j on the next level j, of possibly different status such as opera- tional, failure, collapse, transitive, etc. Functional states represent distinguished independent ways the object per- forms its functions with full or with reduced operational capacity. Newly emerged jth state at level l + 1, after the transition event k occurred at level l, can be defined as a subsystem of compound secondary and primary transitive events 1lS t 1ls 1ls S l E lt k Conditional probability of transition from one level to the next level is defined as: SE . 11lltl lt lt A practical measure of the probability of system’s re- sidual strength 1t pS on the primary level relates on one hand the probability of damage occurrence 1 pS with the probability of system collapse , and on the other, the probability of system operation 1c pS 1o pS in undamaged condition with the probability of the intact system 1i pS. The probability of the primary residual strength 1t pS equals then to the probability of the transitive modes and can be expressed as follows: 11 1 11tfco pSpS pS pSpS i (9) The increase of the probability of residual strength, 1t pS in (9) practically can involve the diminution of the probability of the primary intact mode, rather than of the collapse mode , since 1i pS 1c pS 1i pSc 1 pS for realistic objects. Therefore, the probability of residual strength for realistic objects has to be carefully selected in order to ensure the maximal pro- bability of the primary intact mode, the mi- 1i pS nimal probability of the collapse mode and the 1c pS 1t sufficient probability of transitive modes . More- over, the subsequent functional states also have to satisfy the safety requirements imposed on a redundant system after next component failures. pS The traditional probabilistic redundancy index RI is defined as the system’s primary residual strength condi- tioned by any first component failure 28. Such an index can be calculated in terms of the probabilities of primary structural level l = 1 as shown: 1 11 1 t tf I pS RpSSpS (10) The complement RR of the probabilistic redundancy index is defined as the system’s primary collapse, condi- tioned by any first component failure 29 as shown: 11 11 11 11 ct cf I ff pS pS RpSS R pS pS (11) The traditional redundancy index RI and its comple- ment RR do not account for the intact mode. The probabilistic redundancy factor RF can be defined 30, as the system’s primary residual strength, condi- tioned by the collapse of the system, as follows: 1 11 11 t tc I Fc pS R RpSS R pS (12) Redundancy in engineering problems in this study is viewed rather as an operational abundance than mere survival ability after first component failures. Therefore, an alternative probabilistic redundancy index proposal is introduced in the study that considers the system’s pri- mary residual strength conditioned by operational mode kjk pSEpSEpE k (8) Copyright © 2012 SciRes. WJM  B. BLAGOJEVIĆ, K. ŽIHA 232 as shown [31,32]. 11 11 1 1 ti to Oo pS pS RpSS pS pS 1o (13) The primary redundancy indices (10, 11, 12 and 13) do not account for the redistribution of loads in case of component failures. The probability of the reserve strength in case of load redistribution may be more appropriately expressed by the compound probabilities 21it k pS E 2i pS of the second level intact mode and first level transitive mode, denoted also as secondary reliability cal- culated as: 1 21 1 t N it jj j pS pEpS 2 i i (14) Moreover, the probability of the primary reserve strength may be viewed as the upper bound on the sec- ondary reliability. This reasoning can be extended to a system with any number of functional levels representing redundant structure. The overall reliability of the multi- level system that accounts for probabilities of all intact modes on all levels l = 1, , n is calculated as follows: 12ono i in pSpSpS pSpS (15) 4. Example The example applies EOSA to investigate the probabilis- tic redundancy of a longitudinally stiffened structure lo- cated at the strength deck of a double-hull oil tanker (Figure 1). The ship has following general characteristics: length between perpendiculars 174.8 m; beam 31.4 m; draught at full load 12.2 m; block coefficient Cb = 0.82; depth 17.5 m; height of neutral axis from bottom 7552 m; dis- placement (full load draught) 47,400 tons [33]. Structural analysis, done according to the DNV Rules [34,35], showed that the considered structural configura- tion remained operational when some of the components have failed. All longitudinals and plating between longi- tudinals were involved in redundancy calculation as load carrying elements giving the total number of seven structural elements (Figure 1) on the first functional level (l = 1). After failure of one longitudinal stiffener the system transits into second functional level with six car- rying elements on the second functional level (l = 2). Finally, after failure of two longitudinal stiffeners the system transits into third functional level (l = 3) with five remain carrying elements (3 × plating, T girder and one remaining longitudinal stiffener). First functional level includes the following random events: buckling of plating between longitudinals (3 ba- sic events), torsion buckling of bulb longitudinals (3 ba- sic events), yielding of bulb longitudinals (3 basic events), torsion buckling of T girder (1 basic event) and yielding of T girder (1 basic event). The first functional level has n = 11 events designatedl k , k = 1, 2, ···, 11. Reliability indices are calculated according to [19]: 22 CD ii CD ii ll l i ll (16) where li C represent the mean values of stress random variables. In the cases of yield failure modes the mean values were taken as 60% of the material yield stress. In the cases of buckling failure modes the mean values were taken as calculated from the DNV formulas for critical buckling stress [35] for the corresponding structural ele- ment. i l represent mean values of load stresses de- termined in structural analysis. i l and i l represent corresponding standard deviations of the variables. All the stress random variables are assumed to be in- dependent and uncorrelated, with linear safety margins for all functional levels. All stress variable are taken to be log-normally distributed with coefficient of variation (COV) of 0.7 [36]. Reliabilities, R, and collapse prob- abilities, pf, are calculated respectively: 11i ki RpA and 11 1 ci kk ppA pA where Φ is the standard normal density function. For levels with only one state j index is omitted for simplicity. The mean values of the wave induced bending moments and design pressure on deck are calculated according to the DNV Rules. The mean values of the still-water bending moments were taken as given in the trim and stability book for the full load state of the considered z' y tt bt ht tb b3 tp HP3 HP1HP2 b1b2 2 4 67 5 13 Figure 1. Location and configuration of the investigated panel of the tanker deck. Copyright © 2012 SciRes. WJM  B. BLAGOJEVIĆ, K. ŽIHA 233 ship. Statistical properties of random variables for tank- ers can be found in literature [37-39]. Selected data is presented in Tables 1 and 2. In this investigation the fol- lowing elements of the deck geometry were considered as deterministic variables: thickness of plating tp = 14 mm, span of longitudinals l = 5.08 m, spacing of longitu- dinals s = 0.8 m, web height (T-profile) ht = 450 mm, web thickness (T-profile) tt = 14 mm, flange width (T- profile) bt = 100 mm, flange thickness (T-profile) tb = 14 mm, bulb longitudinals HP 220 × 11.5. Table 3 shows properties of the tanker deck structure for all functional (operational) levels. The number of compound events 1N lon the first functional level is: 1N = 2n = 211 = 2048. There is only one intact functional state represented by the event . Collapse of either one of the longitudinals HP2 or HP3 (Figure 1) causes transition from the first functional level to the second functional level. There is 1Nt = 15 transitive events on the first level, denoted , k = 1, 2, ···, 1Nt. The remaining 1Nc = 2032 events on the first level represent collapse of the structure. E 1 1 1 i E t k E Table 1. Statistical properties of material and loads. Mean DistributionCOV Yield stress (mild shipbuilding steel) 235 N/mm2 Log-normal 0.06 Modulus of elasticity 206,000 N/mm2 Normal 0.01 Stillwater bending moment (sagging) 296,252 kNm Normal 0.4 Stillwater bending moment (hogging) 244,690 kNm Normal 0.4 Wave-induced bending moment (sagging) 1,533,336 kNm Gumbel 0.09 Wave-induced bending moment (hogging) 1,428,791 kNm Gumbel 0.09 Design pressure (deck) 13.6 kN/m2 Normal 0.09 Table 2. Statistical properties of the deck panel. Mean DistributionCOV Width of effective plate flange 800 mm Normal 0.01 Section modulus (longitudinals and plate flange bi) 326 cm3 Log-normal 0.04 Midship section modulus at deck 16.14 m3 Log-normal 0.04 Table 3. Properties of the deck structure (all levels). Level L = 1 Level L = 2 Level L = 3 Panel cross sectional area in cm2 392 360 327 Panel neutral axis in cm 9.3 8.9 8.4 Panel moment of inertia in cm4 74,021 71,021 67,785 Events are appropriately grouped according to their functional state and the structure is modelled by the sys- tem of events with three subsystems: intact, transitive and collapse. The system can be written as 1111itc SSSS. The probability of intact state on the first functional level is calculated as: 11 11 1 1 1 0.9751 ii i k k pE pSpA The probabilities of transitive events at the first level can be calculated likewise: 611 1111 17 18 0.1853 10 tici kk kk pEpA pApA3 711 1111 28 19 0.1853 10 tici kk kk pEpA pApA3 9 1111 31011 1 0.5985 10 tici k k pEpA pApA2 The probabilities of the remaining events are: 1 4 t pE= 0.5985 × 10−2, = 0.3522 × 10−7, 1 5 t pE 1 6 t pE= 0.1137 × 10−5, = 0.1137 × 10−5, 1 7 t pE 1 8 t pE= 0.1137 × 10−5, = 0.1137 × 10−5, 1 9 t pE 1 10 t pE = 0.3673 × 10−4, = 0.2162 × 10−9, 1 11 t pE 1 12 t pE = 0.2162 × 10−9, = 0.6981 × 10−8, 1 13 t pE 1 14 t pE = 0.6981 × 10−8, = 0.1327 × 10−11 1 15 t pE 5 The subsystem of transitive events is modelled as: 11 1 12 15 1 11 1 121 ttt t tt t EE E SpEpEpE Probability of the subsystem of transitive events re- presents the probability of transition from the primary to the secondary level also denoted as the probability of the primary residual strength and can be calculated as: 15 11 1 0.0124 tt k k pS pE The subsystem of collapse events is modelled as: 11 1 2032 1 11 1 2032 cc c cc EE SpE pE The probabilities of individual collapse events are not listed here due to large number of events (Nc = 2032). Probability of the subsystem of collapse events is: Copyright © 2012 SciRes. WJM  B. BLAGOJEVIĆ, K. ŽIHA 234 2032 11 1 0.0125 cc k k pS pE One can easily check that on the first functional level the following relation among probabilities holds: 111 0.9751 0.01240.01251 itc pS pS pS The second functional level emerges when one of the longitudinals, HP2 or HP3, collapses. The remaining part of a structure is still operational, but now with reduced load-carrying capacity. In this case, it is assumed that collapsed longitudinal has no remaining load-carrying capacity. The load is then redistributed to the remaining ele- ments on the deck structure and new values of reliability and probability of failure are calculated. When any of the longitudinals fails the structural con- figuration reduces to 6 load-carrying elements: 3 × deck plating, T longitudinal and remaining two HP longitudi- nals. Hence, the system of events on the second functional level has 9 basic events with probabilities calculated in a same way as for the first functional level: 2 1 i pA0.9955, 0.9955, 2 2 i pA 2 3 i pA 0.9955, 2 4 i pA0.9999, 0.9960, 2 5 i pA 2 6 i pA 0.9999, 2 7 i pA0.9999, 0.9855, 2 8 i pA 2 9 i pA 0.9855. Probability of occurrence of one compound intact event on the second functional level is: 9 22 1 1 0.9541 ii k k pE pA System and subsystems of events, representing deck structure, are presented on Figure 2. The diagram shows levels, subsystems and events as well as transition paths from one functional level to another. This figure illus- trates complexity of modelling of multi-level operational redundant structures. However, a number of random events have extremely low probabilities of occurrence, which gives the oppor- tunity to reduce the number of events in future develop- ment of the EOSA methodology. Failure of the remaining longitudinal, HP2 or HP3, causes emergence of the third functional level. Thus, the second functional level also includes three subsystems: intact, collapse and transitive. The second level is mod- elled by the following system of events: 11 2 12121211 11 ,,,,,, tt it tt jj NN S SSESESES c t 2 89 i 1 This level consist of non-transitive events from the first level (intact, collapse) and new states that emerge (21 ) due to occurrence of some tran- sitive event on the previous level. From 15 transitive events on the first level 15 functional states will emerge on the second level. However, only six of those new states are further transitive (Figure 2). Every transitive state on level 2 has 3 transitive events causing emergence of 18 new states on the third level (Figure 2). The prob- abilities of occurrence of transitive events for the first functional state j = 1 on the second level are calculated: 21 111515 ,, t SE SE 6 2222 17 1 5 0.955510 tici k k pEpApApApA 8 222 29 1 0.1407 10 tic k k pEpAp A 2 9 c 6 2222 378 1 6 0.140810 tici k k pEpApApApA Probabilities of the remaining transitive events and collapse events can be calculated in a same way. Since the total number of compound events on the second level is 2N = 9713 the probabilities of remaining events are not listed here. The reliability and the probability of failure 2i pS 2c S for the second functional level are: 12 1 212 1 11 1 0.0118 ti t NN N itit kk j kk j pSpEpEpEp S 2 i j 2 c j 12 1 212 1 11 1 4 5.610 tc t NN N ctct kk j kk j pSpEp EpEpS The overall reliability of the system with 2 functional levels, 2o pS, is probability that transition from the first level to the second level will result in occurrence of event representing one of undamaged states of second level. It includes all probabilities of intact states on the first level as well as all compound intact states on the second level of transitive states on the first level (1) and one intact event on the second level (): t k E 2 1 i E 212 0.9869 oii pSpS pS Adequately, the overall probability of failure is then: 212 4 0.01255.689 100.0131 fcc pSpS pS Again, 22 1 of pS pS and the second level system (2S) is complete system of events. The third functional level (l = 3) arises when failure of both longitudinals, HP2 and HP3, occurs (not necessarily simultaneously). On the third level there is 5 structural Copyright © 2012 SciRes. WJM 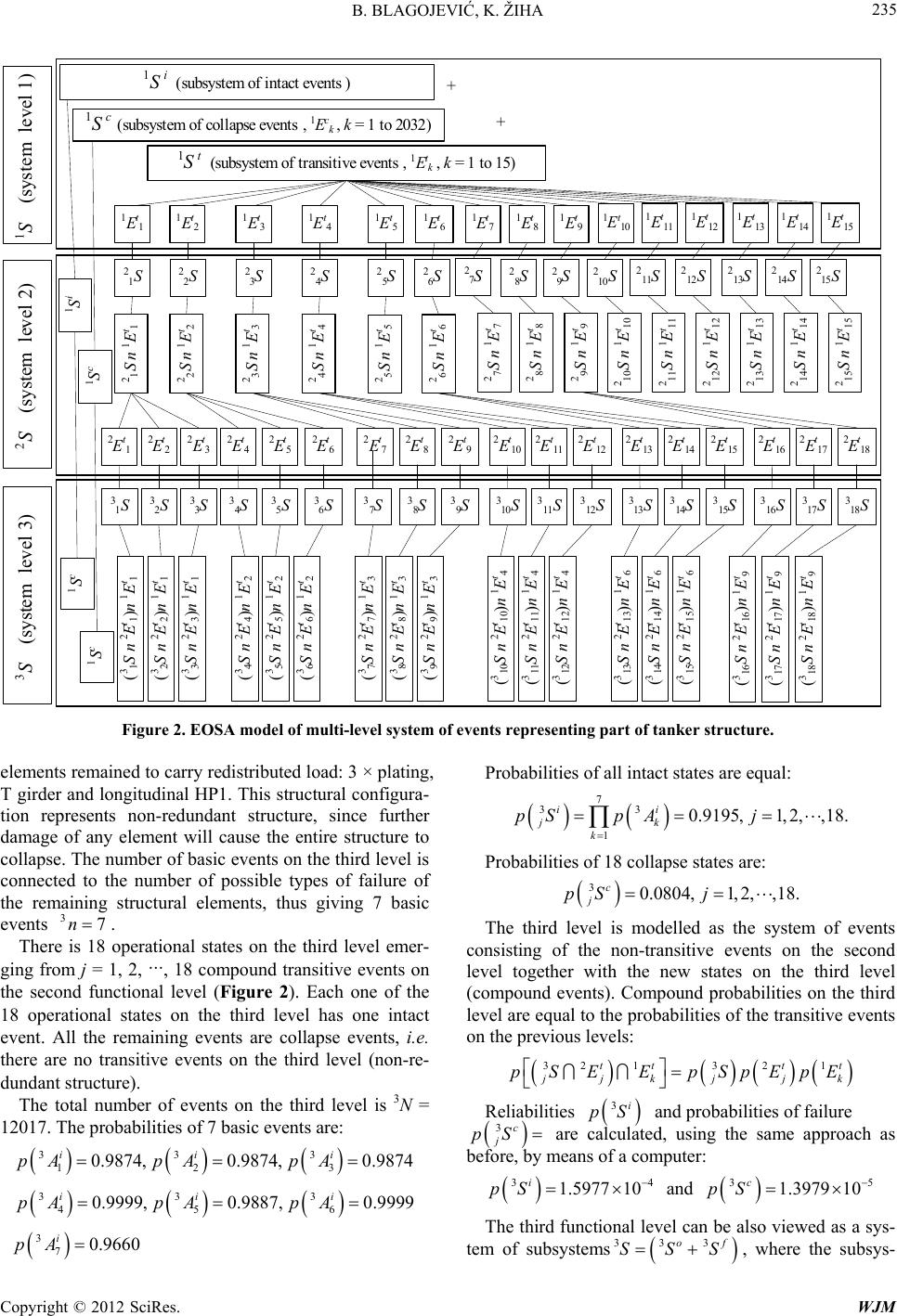 B. BLAGOJEVIĆ, K. ŽIHA Copyright © 2012 SciRes. WJM 235 1S t (subsystem of transitive events, 1Et k, k= 1 to 15) 1Et1 21S 21S n 1Et1 1Et21Et31Et41Et5 22S23S24S25S 22S n 1Et2 23S n 1Et3 24S n 1Et4 25S n 1Et5 1Et6 26S 26S n 1Et6 27S n1Et7 28S n1Et8 29S n1Et9 210S n1Et10 211S n1Et11 212S n1Et12 213S n1Et13 214S n1Et14 215S n1Et15 1Et7 27S 1Et81Et91Et10 1Et11 28S29S210S211S 1Et12 212S 1Et13 1Et14 213S214S 1Et15 215S 2Et12Et22Et32Et42Et5 32S33S 2Et6 31S35S36S 34S 1Sc1Si (31S n2Et1)n1Et1 2Et72Et82Et92Et10 2Et11 2Et12 2Et13 2Et142Et15 2Et16 2Et17 2Et18 38S39S 37S311S312S 310S314S315S 313S317S318S 316S (32S n2Et2)n1Et1 (33S n2Et3)n1Et1 (34S n2Et4)n1Et2 (35S n2Et5)n1Et2 (36S n2Et6)n1Et2 (37S n2Et7)n1Et3 (38S n2Et8)n1Et3 (39S n2Et9)n1Et3 (310S n2Et10)n1Et4 (311S n2Et11)n1Et4 (312S n2Et12)n1Et4 (313S n2Et13)n1Et6 (314S n2Et14)n1Et6 (315S n2Et15)n1Et6 (316S n 2Et16 )n1Et9 (317S n 2Et17 )n1Et9 (318S n 2Et18 )n1Et9 + + 1S i(subsystem of intact events ) 1S c (subsystem of collapse events, 1Ec k, k = 1 to 2032) 1S (system level 1) 2S (system level 2) 3S (system level 3) 1Sc 1Sc Figure 2. EOSA model of multi-level system of events representing part of tanker structure. elements remained to carry redistributed load: 3 × plating, T girder and longitudinal HP1. This structural configura- tion represents non-redundant structure, since further damage of any element will cause the entire structure to collapse. The number of basic events on the third level is connected to the number of possible types of failure of the remaining structural elements, thus giving 7 basic events . 37n Probabilities of all intact states are equal: 7 33 1 0.9195,1,2, ,18. ii jk k pS pAj Probabilities of 18 collapse states are: 30.0804,1,2,,18. c j pS j The third level is modelled as the system of events consisting of the non-transitive events on the second level together with the new states on the third level (compound events). Compound probabilities on the third level are equal to the probabilities of the transitive events on the previous levels: There is 18 operational states on the third level emer- ging from j = 1, 2, ···, 18 compound transitive events on the second functional level (Figure 2). Each one of the 18 operational states on the third level has one intact event. All the remaining events are collapse events, i.e. there are no transitive events on the third level (non-re- dundant structure). 3213 21ttt t jk jj pSEEpSpEpE k The total number of events on the third level is 3N = 12017. The probabilities of 7 basic events are: 333 123 0.9874,0.9874, 0.9874 iii pA pApA Reliabilities 3i pS and probabilities of failure 3c j pS are calculated, using the same approach as before, by means of a computer: 34 1.5977 10 i pS and 35 1.3979 10 c pS 333 456 0.9999, 0.9887, 0.9999 iii pA pA pA The third functional level can be also viewed as a sys- tem of subsystems 333of SSS, where the subsys- 3 70.9660 i pA 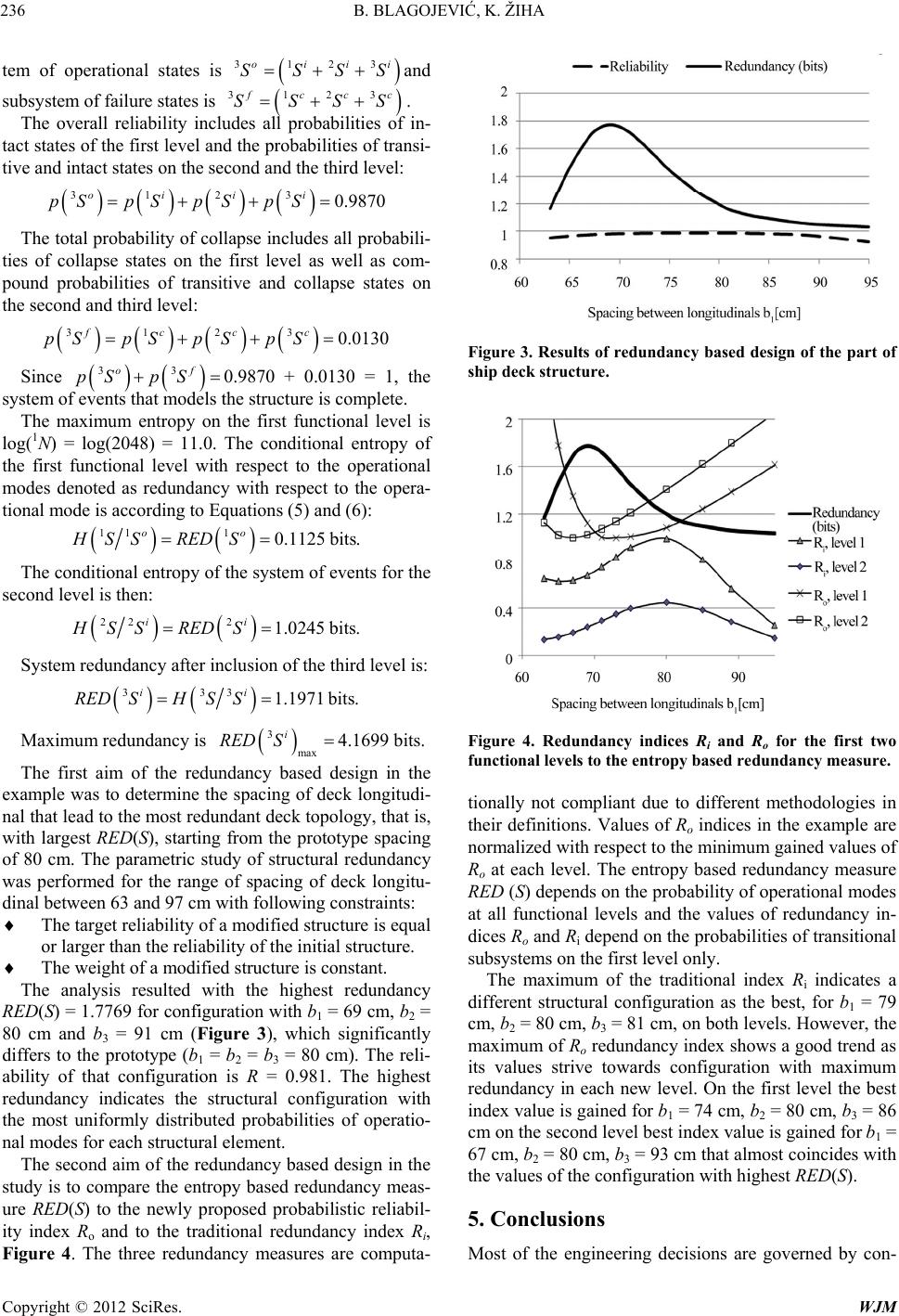 B. BLAGOJEVIĆ, K. ŽIHA 236 tem of operational states is and 3123oii SSSS 3123 i subsystem of failure states is ccc SSSS. The overall reliability includes all probabilities of in- tact states of the first level and the probabilities of transi- tive and intact states on the second and the third level: 3123 0.9870 oiii pSpS pS pS The total probability of collapse includes all probabili- ties of collapse states on the first level as well as com- pound probabilities of transitive and collapse states on the second and third level: 3123 0.0130 fccc pSpS pS pS Since 0.9870 + 0.0130 = 1, the system of events that models the structure is complete. 33of pS pS The maximum entropy on the first functional level is log(1N) = log(2048) = 11.0. The conditional entropy of the first functional level with respect to the operational modes denoted as redundancy with respect to the opera- tional mode is according to Equations (5) and (6): 111 0.1125 bits. oo HSS REDS The conditional entropy of the system of events for the second level is then: 2221.0245 bits. ii HSS REDS System redundancy after inclusion of the third level is: 333 1.1971 bits. ii RED SHS S Maximum redundancy is 4.1699 bits. 3 max i RED S The first aim of the redundancy based design in the example was to determine the spacing of deck longitudi- nal that lead to the most redundant deck topology, that is, with largest RED(S), starting from the prototype spacing of 80 cm. The parametric study of structural redundancy was performed for the range of spacing of deck longitu- dinal between 63 and 97 cm with following constraints: The target reliability of a modified structure is equal or larger than the reliability of the initial structure. The weight of a modified structure is constant. The analysis resulted with the highest redundancy RED(S) = 1.7769 for configuration with b1 = 69 cm, b2 = 80 cm and b3 = 91 cm (Figure 3), which significantly differs to the prototype (b1 = b2 = b3 = 80 cm). The reli- ability of that configuration is R = 0.981. The highest redundancy indicates the structural configuration with the most uniformly distributed probabilities of operatio- nal modes for each structural element. The second aim of the redundancy based design in the study is to compare the entropy based redundancy meas- ure RED (S) to the newly proposed probabilistic reliabil- ity index Ro and to the traditional redundancy index Ri, Figure 4. The three redundancy measures are computa- Figure 3. Results of redundancy based design of the part of ship deck structure. Figure 4. Redundancy indices Ri and Ro for the first two functional levels to the entropy based redundancy measure. tionally not compliant due to different methodologies in their definitions. Values of Ro indices in the example are normalized with respect to the minimum gained values of Ro at each level. The entropy based redundancy measure RED (S) depends on the probability of operational modes at all functional levels and the values of redundancy in- dices Ro and Ri depend on the probabilities of transitional subsystems on the first level only. The maximum of the traditional index Ri indicates a different structural configuration as the best, for b1 = 79 cm, b2 = 80 cm, b3 = 81 cm, on both levels. However, the maximum of Ro redundancy index shows a good trend as its values strive towards configuration with maximum redundancy in each new level. On the first level the best index value is gained for b1 = 74 cm, b2 = 80 cm, b3 = 86 cm on the second level best index value is gained for b1 = 67 cm, b2 = 80 cm, b3 = 93 cm that almost coincides with the values of the configuration with highest RED(S). 5. Conclusions Most of the engineering decisions are governed by con- Copyright © 2012 SciRes. WJM  B. BLAGOJEVIĆ, K. ŽIHA 237 siderations about matter and energy in the physical space. Some of the decisions are additionally supported by the probabilistic and statistical laws governing the probabil- ity space. However, the event-oriented system analysis (EOSA) combines the physical and the probabilistic space to facilitate some of the engineering decisions us- ing the entropy concept valid in the event space. The paper compared the entropy-based redundancy measure and the probabilistic redundancy indices attain- able within the EOSA. The underlying idea of the study is that the entropy-based redundancy measure most ap- propriately captures the intuited meaning of the structural redundancy even in case of cascades of failures and load redistribution. The example reveals at this point of the investigation that the newly proposed redundancy index Ro in the paper, which relates the primary residual strength to the operational modes only for the first com- ponent failure, can be used as an indicator that approxi- mates structural redundancy. It follows at the primary level that the trend of the entropy-based redundancy measure RED(S) that accounts for the multilevel se- quences of component failures more appropriately of the traditional redundancy index. The advantage of the redundancy index, where appli- cable, over the entropy-based redundancy measure, is in simplicity and lower calculation effort. However, for more precise conclusion of redundancy of complex, mul- tilevel operational structures with a large number of indi- vidual components, the calculations of all functional lev- els are necessary. The paper acknowledges that the event- oriented analysis of redundant objects exposed to succes- sive component failures, which change the system con- figuration and provoke a redistribution of demands and capabilities, is a complicated task, but it also proves that it is feasible attainable by appropriate software. Finally, the study confirms that the EOSA has potenti- alities for structural safety enhancement by adopting the entropy concept in the maximal redundancy principle for the redundancy-based design. REFERENCES [1] M. Arvidsson and I. Gremyr, “Principles of Robust De- sign Methodology,” Quality and Reliability Engineering International, Vol. 24, No. 1, 2008, pp. 24-35. [2] G. Taguchi, S. Chowdhury and S. Taguchi, “Robust En- gineering-Learn How to Boost Quality While Reducing Costs and Time to Market,” McGraw-Hill, New York, 2000. [3] J. Agarwal, D. I. Blockley and N. J. Woodman, “Vulner- ability of structural systems,” Structural Safety, Vol. 25, No. 3, 2003, pp. 263-286. doi:10.1016/S0167-4730(02)00068-1 [4] A. Eriksson and A. G. Tibert, “Redundant and Force- Differentiated Systems in Engineering and Nature,” Com- puter Methods in Applied Mechanics and Engineering, Vol. 195, No. 41, 2006, pp. 5437-5453. doi:10.1016/j.cma.2005.11.007 [5] J. W. Baker, M. Schubert and M. H. Faber, “On the As- sessment of Robustness,” Structural Safety, Vol. 30, No. 3, 2008, pp. 253-267. doi:10.1016/j.strusafe.2006.11.004 [6] B. W. Schafer and P. Bajpai, “Stability Degradation and Redundancy in Damaged Structures,” Engineering Struc- tures, Vol. 27, No. 11, 2005, pp. 1642-1651. doi:10.1016/j.engstruct.2005.05.012 [7] L. Dueñas-Osorio and S. M. Vemuru, “Cascading Fail- ures in Complex Infrastructure Systems,” Structural Safety, Vol. 31, No. 2, 2009, pp. 157-167. doi:10.1016/j.strusafe.2008.06.007 [8] Z. Tian and M. J. Zuo, “Redundancy Allocation for Multi-State Systems Using Physical Programming and Genetic Algorithms,” Reliability Engineering and System Safety, Vol. 91, No. 9, 2006, pp. 1049-1056. doi:10.1016/j.ress.2005.11.039 [9] J. England, J. Agarwal and D. Blockley, “The Vulnerabil- ity of Structures to Unforeseen Events,” Computers & Structures, Vol. 86, No. 10, 2008, pp. 1042-1051. doi:10.1016/j.compstruc.2007.05.039 [10] S. G. Stiansen, “Interrelation between Design, Inspection and Redundancy in Marine Structures,” National Acad- emy Press, Washington DC, 1984. [11] Y. Feng, “The Theory of Structural Redundancy and Its Effect on Structural Design,” Computers & Structures, Vol. 28, No. 1, 1988, pp. 15-24. doi:10.1016/0045-7949(88)90087-9 [12] K. Chen and S. Zhang, “Semi-Probabilistic Method for Evaluating Systems Redundancy of Existing Offshore Structures,” Ocean Engineering, Vol. 23, No. 6, 1996, pp. 455-464. doi:10.1016/0029-8018(95)00051-8 [13] C. E. Shannon and W. Weaver, “The Mathematical The- ory of Communication,” Urbana University of Illinois Press, Urbana, 1949. [14] A. Rényi, “Probability Theory,” North-Holland, Amster- dam, 1970. [15] J. Aczel and Z. Daroczy, “On Measures of Information and Their Characterization,” Academic Press, New York, 1975. [16] A. I. Khinchin, “Mathematical Foundations of Informa- tion Theory,” Dover Publications, New York, 1957. [17] K. Žiha, “Event Oriented System Analysis,” Probabilistic Engineering Mechanics, Vol. 15, No. 3, 2000, pp. 261- 275. doi:10.1016/S0266-8920(99)00025-9 [18] M. Hoshiya, K. Yamamoto and H. Ohno, “Redundancy Index of Lifelines for Mitigation Measures against Seis- mic Risk,” Probabilistic Engineering Mechanics, Vol. 19, No. 3, 2004, pp. 205-210. doi:10.1016/j.probengmech.2004.02.003 [19] H. Madsen, S. Krenk and N. C. Lind, “Methods of Struc- tural Safety,” Prentice Hall, Englewood Cliffs, 1986. [20] A. H. S. Ang and W. H. Tang, “Probability Concepts in Engineering,” John Wiley, New York, 2007. [21] S. K. Choi, R. V. Grandhi and R. A. Canfield, “Reliabil- Copyright © 2012 SciRes. WJM  B. BLAGOJEVIĆ, K. ŽIHA Copyright © 2012 SciRes. WJM 238 ity-Based Structural Design,” Springer, New York, 2007. [22] M. Rausand and A. Høyland, “System Reliability Theory: Models, Statistical Methods, and Applications,” Wiley- Interscience, New York, 2003. [23] R. Y. Rubinstein and D. P. Kroese, “Simulation and the Monte Carlo Method,” Wiley-Interscience, New York, 2007. doi:10.1002/9780470230381 [24] M. S. Hamada, A. Wilson, C. S. Reese and H. F. Martz, “Bayesian Reliability,” Springer, New York, 2008. doi:10.1007/978-0-387-77950-8 [25] D. L. Kreher and D. R. Stinson, “Combinatorial Algo- rithms: Generation, Enumeration, and Search,” CRC Press, Boca Raton, 1998. [26] K. Žiha, “Event-Oriented Analysis of Series Structural Systems,” Structural Safety, Vol. 23, No. 1, 2001, pp 1- 29. doi:10.1016/S0167-4730(00)00022-9 [27] K. Žiha, “Redundancy and Robustness of Systems of Events,” Probabilistic Engineering Mechanics, Vol. 15, No. 4, 2000, pp. 347-357. doi:10.1016/S0266-8920(99)00036-3 [28] C. Palion, M. Shinozuka and Y. N. Chen, “Reliability Analysis of Offshore Structures,” Marine Structural Re- liability Symposium, New York, 1987. [29] R. S. De, A. Karamchandani and C. A. Cornell, “Study of Redundancy in Near-Ideal Parallel Structural Systems,” Structural Safety and Reliability, Vol. 2, 1990, pp. 975- 982. [30] S. Hendawi and D. M. Frangopol, “System Reliability and Redundancy in Structural Design and Evaluation,” Structural Safety, Vol. 16, No. 1-2, 1994, pp. 47-71. doi:10.1016/0167-4730(94)00027-N [31] K. Žiha, “Redundancy Based Design by Event Oriented Analysis,” Transactions of FAMENA, Vol. 27, No. 2, 2003, pp. 1-12. [32] K. Žiha, “Event-Oriented Analysis of Fail-Safe Objects,” Transactions of FAMENA, Vol. 27, No. 1, 2003, pp. 11- 22. [33] B. Blagojević and K. Žiha, “On the Assessment of Re- dundancy of Ship Structural Components,” Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering OMAE 2008, Estoril, 15-20 June 2008, pp. 256-262. [34] N. Veritas, “Ship’s Load and Strength Manual,” Det Nor- ske Veritas, Oslo, 1995. [35] N. Veritas, “Rules for Classification of Ships,” Det Nor- ske Veritas, Oslo, 2007. [36] I. A. Assakkaf, “Reliability-Design of Panels and Fatigue Details of Ship Structures,” University of Maryland, Col- lege Park, 1998. [37] C. G. Soares and P. M. Dogliani, “Probabilistic Model- ling of Time-Varying Still-Water Load Effects in Tank- ers,” Marine Structures, Vol. 13, No. 2, 2000, pp. 129- 143. doi:10.1016/S0951-8339(00)00006-X [38] K. Atua, I. A. Assakkaf and M. Ayyub, “Statistical Char- acteristics of Strength and Load Random Variable of Ship Structures,” Proceedings of the 7th Specialty Conference on Probabilistic Mechanisms and Structural Reliability, Worcester, 7-9 August 1996. [39] J. Parunov, I. Senjanović and C. G. Soares, “Hull-Girder Reliability of New Generation Oil Tanker,” Marine Struc- tures, Vol. 20, No. 1-2, 2007, pp. 49-70.
|