Int. J. Communications, Network and System Sciences, 2012, 5, 661-670
http://dx.doi.org/10.4236/ijcns.2012.510068 Published Online October 2012 (http://www.SciRP.org/journal/ijcns)
A Multilevel Tabu Search for the Maximum
Satisfiability Problem
Noureddine Bouhmala1, Sirar Salih2
1Department of Maritime Technology and Innovati on, Vestfold University College, Horten, Norway
2Department of Information and Communication Technology, University of Agder, Grimstad, Norway
Received July 12, 2012; revised August 15, 2012; accepted August 28, 2012
ABSTRACT
The maximum satisfiability problem (MAX-SAT) refers to the task of finding a variable assignment that satisfies the
maximum number of clauses (or the sum of weight of satisfied clauses) in a Boolean Formula. Most local search algo-
rithms including tabu search rely on the 1-flip neighbourhoo d structure. In th is work, we introduce a tabu search algo-
rithm that makes use of the multilevel p aradigm for solving MAX-SAT problems. The multilevel paradigm refers to the
process of dividing large and difficult problems into smaller ones, which are hopefully much easier to solve, and then
work backward towards the solution of the original problem, using a solution from a previous level as a starting solution
at the next level. This process aims at looking at the search as a multilevel process operating in a coarse-to-fine strategy
evolving from k-flip neighbourhood to 1-flip neighbourhood-based structure. Experimental results comparing the mul-
tilevel tabu search against its single level v ariant are presented.
Keywords: Maximum Satisfiability Problem; Tabu Search; Multilevel Techniques
1. Introduction
The satisfiability problem which is known to be NP-
complete [1] plays a central role problem in many appli-
cations in the fields of VLSI Computer-Aided design,
Computing Theory, and Artificial Intelligence. Generally,
a SAT problem is defined as follows. A propositional
formula 1
m
j
jC 
  with m clauses and n Boolean
variable s i s given. Eac h B oo le a n vari able ,


,1,
i
x
in,
takes one of the two values, True or False. A clause, in
turn, is a disjunction of literals and a literal is a variable or
its negation. Each clause
j
C has the form:
jj
j
kl
kI lIx







Cx
 ,
where

,1
I
jIj n, Ij Ij

 and i
x
denotes the
negation of i
x
. The task is to determine whether there
exists an assignment of values to the variables under
which evaluates to True. Such an assignment, if it
exists, is called a satisfying assignment for , and is
called satisfiable. Otherwise, is said to be unsatisfi-
able. Most SAT solvers use a Conjunctive Normal Form
(CNF) representation of the formula . In CNF, the
formula is represented as a conjunction of clauses, with
each clause being a disjunction of literals. The maximum
satisfiability problem which is th e optimizatio n variant of
SAT plays a fundam ental role to many practical problems
in computer science. More formally, letidenote the
weight of clause i. Then expression (1) is the objective
function to be ma ximi zed, with equals to 1 when
is true and 0 otherwise,
Φ
Φ Φ
w
C
i
Ci C

1
m
ii
k
wSC



Φ
Φ
. (1)
There exist two important variations of the MAX-SAT
problem. The weighted MAX-SAT problem is the Max-
SAT problem in which each clause is assigned a positive
weight. The goal of the problem is to maximize the sum of
weights of satisfied clauses. The unweighted MAX-SAT
problem is the MAX-SAT problem in which all the weights
are equal to 1 and the goal is to maximize the number of
satisfied clauses. Efficient methods that can solve large
and hard instances of MAX-SAT are eagerly sought. Due
to their combinatorial explosion nature, large and complex
MAX-SAT problems are hard to solve using systematic
algorithms based on branch and bound techniques [2].
One way to overcome the combinatorial explosion is to
give up completeness. Local search algorithms are tech-
niques which use this strategy and gained popularity due
to their conceptual simplicity and good performance.
However, most local search algorithms including tabu
search algorithm rely on the 1-flip neighbourhood struc-
ture for which t wo t ruth value assignm ents are nei ghbour s
C
opyright © 2012 SciRes. IJCNS

N. BOUHMALA, S. SALIH 662
if they differ in the truth value of exactly one variable. A
typical local search starts with any given assignment, and
then repeatedly changes (flips) the assignment of a vari-
able that leads to the largest decrease in the total number
of unsatisfied clauses. Some attempts have been made to
extend to consider r-flip neighbourhood structure. The
quality of solutions improves if larger neighbourhood is
used; however the computational time to search such
neighbourhood increases exponentially with r [3]. The
work proposed in [4] uses a multi-flip procedure to gen-
erate the next assignment based on simultaneously flip-
ping the value of multiple variables. The approach was
able to provide better results compared to 1-flip neigh-
bourhood on prob lem instances with up to 150 variables.
In this paper, a tabu search combined with the multilevel
paradigm is introduced. The core of the proposed algo-
rithm involves looking at the search as a multilevel proc-
ess operating in a coarse-to-fine strategy evolving from a
k-flip neighbourhood to 1-flip neighbourhood-based stru-
cture enabling tabu search to take long leaps in the search
space. This work is motivated by the recent results pre-
sented in [5] where the multilevel paradigm was capable
of improving the asymptotic convergence of memetic
algorithms dramatically on large industrial instan ces. The
question we intend to answer in this work is whether the
multilevel paradigm improves the asymptotic conver-
gence of TS. To this end, the focus is restricted to for-
mulas in which all the weights are equal to 1 i.e. un-
weighted MA X-SAT) using a of fset of i n dustrial proble m
instances.
The pape r is organiz ed as follows: Sec tion 2 provides a
short survey of algorithms for MAX-SAT. Section 3 de-
scribes the TS algorithm implemented in this work. Sec-
tion 4 introduces TS combined with the multilevel para-
digm. Section 5 presents the experimental results while
finally Section 6 provides a conclusion of the the papers
with future work.
2. Related Work
The simplicity of MAX-SAT combined with its wide ap-
plicability made several researchers eager to develop ef-
ficient algorithms for solving large MAX-SAT problems.
Stochas ti c Loc a l search algo ri thms (SLS) are amongst t h e
many different approaches proposed to deal with MAX-
SAT. They are based on what is perhaps the oldest opti-
mization method trial and erro r. Typically, they start with
an initial assignment of values to variables randomly or
heuristically generated. During each iteration, a new so-
lution is selected from the neighbourhood of the current
one by performing a move. Choosing a good neighbour-
hood and a method for searching it is usually guided by
intuition, because very little theory is available as a guide.
All the methods usually differ from each other on the
criteria used to flip the chosen variable. One of the earliest
local search for solving SAT is GSAT. The GSAT algo-
rithm operates by changing a complete assignment of
variables int o one in whic h the maxim um possible num ber
of clauses are satisfied by changing the value of a single
variable. Another widely used variant of GSAT is the
WalkSAT based on a two stage selection mechanism
originally introduced in [6]. Other algorithms [7,8] have
emerged usi ng hist ory -base d va riabl e sel ectio n st rate gy i n
order to av oid fl ippin g the sam e va riable. Num erous ot her
methods have al so such as Simulate d Annealing [9], Evo -
lutionary Algorit hms [10] a nd Greedy Ra ndomi zed Adap-
tive Search Procedures [11] have also been proposed.
Lacking the theoretical guidelines while being stochastic
in nature, the deployment of several SLS involves exten-
sive experiments to find the optimal noise or walk prob-
ability settings. To avoid manual parameter tuning, new
methods have been designed to automatically adapt pa-
rameter set tings during t he search [12,13] an d results have
shown their effectiveness for a wide range of problems.
The work conducted in [14] introduced Learning Auto-
mata ( LA) as a m ec hani sm for enha nc in g S L S based SAT
solvers, thus laying the foundation for novel LA-based
SAT solvers. Finally, a new recent strategy based on an
automatic procedure for integrating selected components
from various existing solvers have been devised in order
to build new efficient algorithms that draw the strengths of
multiple algorithms [15,16].
3. Tabu Search
Tabu Searc h algorithm (TS) was pr oposed by Glover [17] .
The main feature of the algorithm is the ability to avoid
returning in a previous state by keeping a trace of the
optimization history. In this section, the tabu search al-
gorithm used in this work is described in Algorithm 1.
First, an initial solution of the problem is introduced (lin e
2). Then during each pass of the algorithm, given the
current solution, one examines its corresponding neigh-
bourhood and choose to move to the solution that most
improves the objective function. At the end of each pass,
the literal with the highest gain is selected (line 10) (ran-
domly). To avoid getting stuck in a local minimum, his-
torical information from the last k iterations is used. The
value k may be fixed or a variable that depends on the
search. The set of moves determined by this information
forms a tabu list. Hence, the method has a short term
memory remembering which trajectories have been re-
cently explored. To prevent the method from cycling be-
tween the same solutions, one forbids the reverse of any
move contained in the tabu list. The algorithm proceeds
by choosing a random unsatisfied clause (line 5). There-
after, a non tabu and unvisite d literal is chosen randomly
and flipped (lines 6, 7 and 8). The tabu list is updated be-

N. BOUHMALA, S. SALIH
Copt © 201ciRes IJCNS
663
P
1
P
P
l
fore the start of every new pass (line 11). The selected literal
during each pass is inserted into the tabu list with a value k
that will determine the nu mber of iterations it will remain
tabu. During each pass, the value k assigned to each tabu
literal is decremented by 1. When the value k reaches the
value 0, its corresponding literal becomes non tabu.
constructed from 0 by merging literals. The merging
is computed using a randomized algorithm similar to [20].
The literals are visited in a random order. If a literal i
has not been matched yet, then a randomly unmatched
literal
j
ll
is selected, and a new literal k l (a cluster)
consisting of the two literals i and
j
l is created. Un-
merged literals are simply copied to the next level. The
new formed literals are used to define a new and smaller
problem and recursively iterate the reduction process
until the size of the problem reaches some desired thre-
shold (lines 3,4 and 5 of Algorithm 2). This process is
graphically illu strated in Figure 1 using an example with
12 literals. The coarsening phase uses two levels to
coarsen the problem down to three clusters. 0
corresponds to the original problem. The random coars-
ening procedure is used to merge randomly the literals in
pairs leading to a coarser problem with 5 clusters. This
process is repeated leading to the coarsest problem with 3
clusters. An initial solution is generated where the clus-
ters are assigned randomly th e value of true or false. The
figure shows an initial solution where one cluster is as-
signed the value of true and the remaining two clusters
are assigned the value false. Thereafter, the computed
initial solution is then improved with WalkSAT. As soon
as the convergence criteria is reached at 2, the
ucoarsen- ing phase takes the assignment reached at
2 and then extends it so that it serves as an initial
assignment for the parent level 1 and then proceed
with a new round of TS. This iteration process ends when
TS rea- ches the stop criteria that is met at .
4. Multilevel Tabu Search
Multilevel techn iques have already been introduced for a
limited number of combinatorial optimization problems.
They were first introduced when dealing with the graph
partitioning problem (GCP) [18-23] and have proved to
be effective in producing high quality solutions. The tra-
veling salesman problem (TSP) was the second combi-
natorial optimization problem to which the multilevel
technique was applied [24,25] and has shown a clear im-
provement in the asymptotic convergence of the solution
quality. However, the results obtained when the multi-
level paradigm was applied to the graph coloring prob-
lem [26] did not seem to be in line with the general trend
observed in GCP and TSP as its ability to enhance the
convergence behavior of the local search algorithms.
Graph drawing is another area where multilevel tech-
niques gave a better global quality to the drawing and is
suggested to both accelerate and enhance force drawing
placement algorithms [27]. A recent survey over existing
multilevel techniques is given in [28,29]. The i mplemen-
tation of the multilevel paradigm requires four basic
components: a coarsening algorithm, an initialization al-
gorithm, an extension algorithm (which takes the solu-
tion on one problem and extends it to the parent problem),
and a refinement algorithm. This section describes all
these components which are necessary to derive a tabu
algorithm operating in a multilev el context.
Level
Level
Level Level
0
Level
P
4.2. Initial Solution
The reduction phase ceases when the problem size shrinks
to a desired threshold. Initialization is then trivial and
consists of generating an initial solution for the population
of the prob lem m using a random procedure. The clus-
ters of every individual in the population are assigned the
value of true or false in a random manner (line 7 of Algo-
rithm 2).
4.1. Reduction Phase
Let 0 (the subscript represents the level of problem
scale) be the set of literals. The next coarser level is
Algorithm 1. Tabu search.
yrigh2 S.

N. BOUHMALA, S. SALIH 664
Algorithm 2. Multilevel tabu search.
Level_0
Level_1
Level_2
COARSENING
COARSENING UNCOARSENING
UNCOARSENING
F
F
F
F F
F
F
F
F
F
TS
TS
TS
F
F
T
T
T
TT
TT
T
T
T T
F
INITIAL SOLUTION
Figure 1. The various phases of the multilevel paradigm combined with TS.
4.3. Projection Phase
The Projection phase refers to the inverse process fol-
lowed during the reduction phase. Having improved the
assignment on 1m, the assignment must be extended
on is pare nt m. The extension algorithm is simple; if
a cluster 1im is assigned the value of true then the
merged pair of clusters that it represents,
Level
Level
cS

j
ccS, km

are
also assigned the true value (line 9 of Algorithm 2).
4.4. Improvement Phase
The idea behind the improvement phase is to use the
projected assignment at 1m
Level

as the initial assigment
for m for further refinement using TS described in
Section 3. Even though the assig n ment at the 1m
Level Level

is
at a local minimum, the projected assignment may not be
at a local optimum with respect to m. The projected
assignment is already a good solution leading WalkSAT
to converge quicker to a better assignment (line 10 of
Algorithm 2).
Level
5. Experimental Results
Test Suite & Parameter Settings
The performance of MLV-TS is evaluated against TS
using a set of real industrial problems taken from SAT03

N. BOUHMALA, S. SALIH 665
benchm a rk w ebsite
(http://www.informatik.tu-darmstadt.de/AI/SATLIB). Due
to the randomization nature of both algorithms, each
problem instance was run 100 times with a cut-off para-
meter (max-time) set to 60 minutes. The symbols V and
C denote respectively the number of variables and the
number of clauses.
The tests were carried out on a DELL machine with 800
MHz CPU and 2 GB of memory. The code was written in
C++ and compiled with the GNU C compiler version 4.6.
The follo wi ng pa rameters hav e been fi xe d e x per imentall y
and are listed below:
 Stopping criteria for the reduction phase: The reduc-
tion process stops as soon as the size of the coarsest
problem reaches 100 variables (clusters).
 Convergence during the refinement phase: If there is
no observable improvement of the function value
during 1000 consecutive iterations, TS is assumed to
have reac hed conve rgence and m oves to a higher le vel.
 Tabu length: The length of tabu list is set to be equal to:
0.01875 × n + 2.8125 as proposed in [30] where n is
the number of variable in the problem.
Figures 2-4 show the development of the mean satis-
fied clause for both algorithms. Both algorithm s start from
nearly identical initial so lutions. The plots show immedi-
ately the dramatic improvement obtained using the
Figure 2. MLV-TS vs TS: (above) alu4mul.mi-ter.Shuffled-as.sat03-344.cnf: V = 4736 C = 30,465 (below) c3540mul.
miter.shuffled-as.sat03-345: V = 5248 C = 33191. Evolution of the mean satisfied clause over time.

N. BOUHMALA, S. SALIH 666
Figure 3. MLV-TS vs TS: (above) 6288mul.miter. shuffled-as.sat03-346.cnf: V = 9540 C = 61421 (below) dalumul.miter.
shuffled-as.sat03-349.cnf: V = 9426 C = 59,991. Evolution of the mean satisfied clause over time.
multilevel paradigm. The curves show no crossover im-
plying that MLV- TS dominates TS. The mean number of
unsatisfied clause improves rapidly at first and continues
to improve before it flattens off as we m ount the plateau as
in the Figure 2, marking the start of t he second phase. The
plateau spans a region in the search space where flips
typically leave the best assignment unchanged, and occurs
more specifically once the refinement reaches the finest
level. Comparing the multilevel version with the single
level version, MLV-TS is far better than TS, making it the
clear leading algorithm. The key success behind the effi-
ciency of MLV-TS relies on the multilevel paradigm.
MLV-TS uses the multilevel paradigm and draw its
strength from coupling the refinement process across dif-
ferent levels. This paradigm offers two main advantages
which enables TS to become much more powerful in the
multilevel context. During the refinement phase, TS ap-
plies a local a transformation (i.e. a move) within the
neighbourhood (i.e. the set of solutions that can be rea-
ched from the current one) of the current solution to gen-

N. BOUHMALA, S. SALIH 667
erate a new one. The coarsening process offers a better
mechanism for performing diversification (i.e., the ability
to visit many and different regions of the search space)
and intensification (i.e., the ability to obtain high quality
solutions within those regions). By allowing TS to view a
cluster of variables as a single entity, the search b ecomes
guided and restricted to only those configurations in the
solution space in which the variables grouped within a
cluster are assigned the same value.
As the size of the clusters varies from one level to an-
other, the size of the neighbourhood becomes adaptive
and allows the possibility of exploring different regions in
the search space while intensifying the search by ex-
ploiting the solutions from previous levels in order to reach
better solutions. Tables 1 and 2 show the results of com-
paring MLV-TS against TS). The table shows that MLV-
TS showed a better asymptotic convergence compared to
TS in 32 cases out of 50 with an improvement lying within
9%. The cases whe re TS gave bett er re sult s th an ML V-TS ,
the difference in quality does not exceed 2%. Finally the
plot depicted in Figure 5 shows the variations in quality
between the two algorithms as the size of the problem
increases. For problems with a number of clauses less than
20,000, there seems to be no advantage in using the mul-
tilevel paradigm as the difference in quality is very small
while tending in favour of TS. As the size of the problem
Figure 4. MLV-TS vs TS: (above): i10mul.miter.shuffled-as. sat03-353.cnf V = 12,998 C = 77,941 (below) i8mul.miter.
shuffled-as.sat03-354.cnf V = 14,524 C = 91,139. Evolution of the mean satisfied clause over time.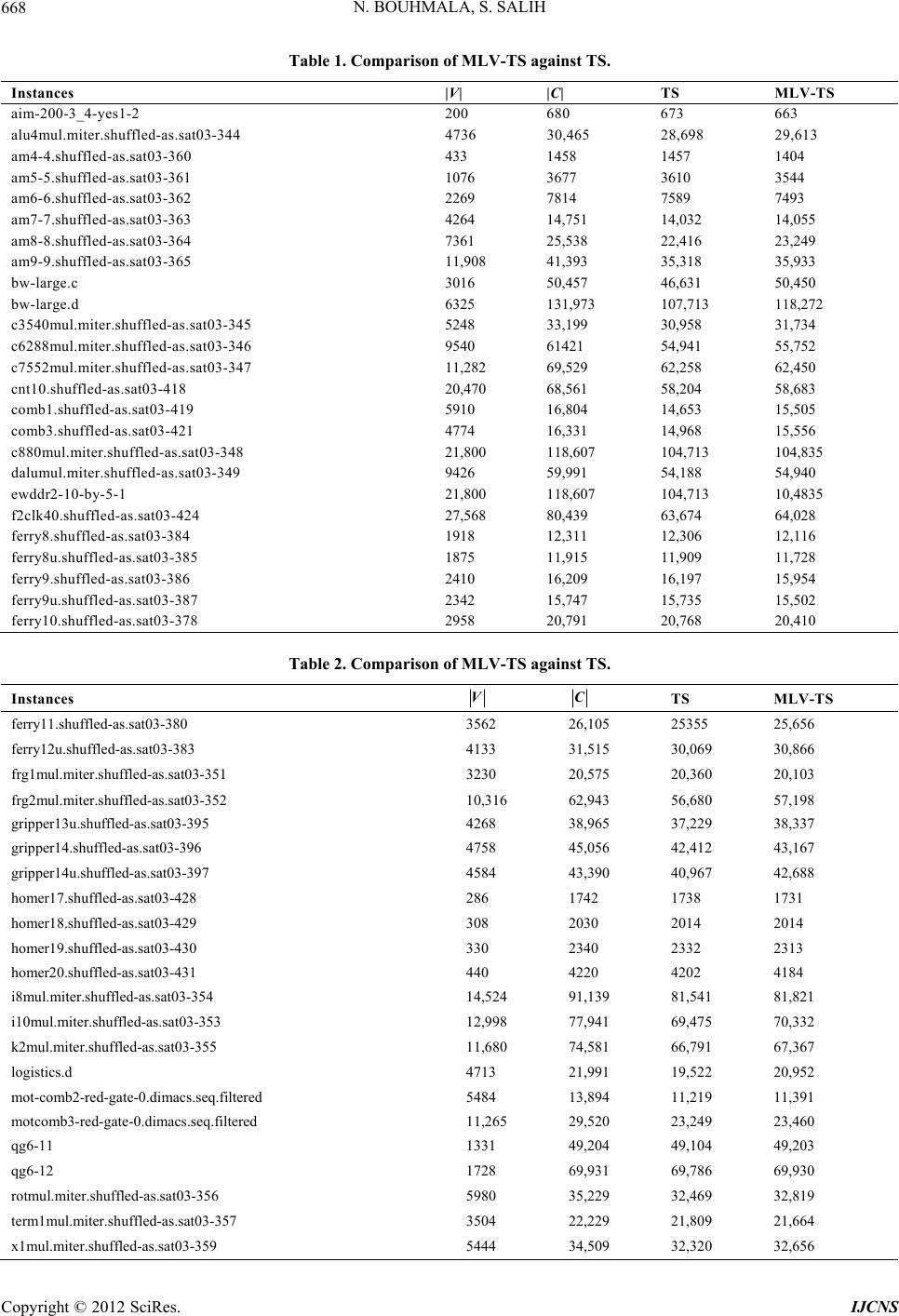

N. BOUHMALA, S. SALIH 668
Table 1. Comparison of MLV-TS against TS.
Instances |V| |C| TS MLV-TS
aim-200-3_4-yes1-2 200 680 673 663
alu4mul.miter.shuffled-as.sat03-344 4736 30,465 28,698 29,613
am4-4.shuffled-as.sat03-360 433 1458 1457 1404
am5-5.shuffled-as.sat03-361 1076 3677 3610 3544
am6-6.shuffled-as.sat03-362 2269 7814 7589 7493
am7-7.shuffled-as.sat03-363 4264 14,751 14,032 14,055
am8-8.shuffled-as.sat03-364 7361 25,538 22,416 23,249
am9-9.shuffled-as.sat03-365 11,908 41,393 35,318 35,933
bw-large.c 3016 50,457 46,631 50,450
bw-large.d 6325 131,973 107,713 118,272
c3540mul.miter.shuffled-as.sat03-345 5248 33,199 30,958 31,734
c6288mul.miter.shuffled-as.sat03-346 9540 61421 54,941 55,752
c7552mul.miter.shuffled-as.sat03-347 11,282 69,529 62,258 62,450
cnt10.shuffled-as.sat03-418 20,470 68,561 58,204 58,683
comb1.shuffled-as.sat03-419 5910 16,804 14,653 15,505
comb3.shuffled-as.sat03-421 4774 16,331 14,968 15,556
c880mul.miter.shuffled-as.sat03-348 21,800 118,607 104,713 104,835
dalumul.miter.shuffled-as.sat03-349 9426 59,991 54,188 54,940
ewddr2-10-by-5-1 21,800 118,607 104,713 10,4835
f2clk40.shuffled-as.sat03-424 27,568 80,439 63,674 64,028
ferry8.shuffled-as.sat03-384 1918 12,311 12,306 12,116
ferry8u.shuffled-as.sat03-385 1875 11,915 11,909 11,728
ferry9.shuffled-as.sat03-386 2410 16,209 16,197 15,954
ferry9u.shuffled-as.sat03-387 2342 15,747 15,735 15,502
ferry10.shuffled-as.sat03-378 2958 20,791 20,768 20,410
Table 2. Comparison of MLV-TS against TS.
Instances V C TS MLV-TS
ferry11.shuffled-as.sat03-380 3562 26,105 25355 25,656
ferry12u.shuffled-as.sat03-383 4133 31,515 30,069 30,866
frg1mul.miter.shuffled-as.sat03-351 3230 20,575 20,360 20,103
frg2mul.miter.shuffled-as.sat03-352 10,316 62,943 56,680 57,198
gripper13u.shuffled-as.sat03-395 4268 38,965 37,229 38,337
gripper14.shuffled-as.sat03-396 4758 45,056 42,412 43,167
gripper14u.shuffled-as.sat03-397 4584 43,390 40,967 42,688
homer17.shuffled-as.sat03-428 286 1742 1738 1731
homer18.shuffled-as.sat03-429 308 2030 2014 2014
homer19.shuffled-as.sat03-430 330 2340 2332 2313
homer20.shuffled-as.sat03-431 440 4220 4202 4184
i8mul.miter.shuffled-as.sat03-354 14,524 91,139 81,541 81,821
i10mul.miter.shuffled-as.sat03-353 12,998 77,941 69,475 70,332
k2mul.miter.shuffled-as.sat03-355 11,680 74,581 66,791 67,367
logistics.d 4713 21,991 19,522 20,952
mot-comb2-red-gate-0.dimacs.seq.filtered 5484 13,894 11,219 11,391
motcomb3-red-gate-0.dimacs.seq.filtered 11,265 29,520 23,249 23,460
qg6-11 1331 49,204 49,104 49,203
qg6-12 1728 69,931 69,786 69,930
rotmul.miter.shuffled-as.sat03-356 5980 35,229 32,469 32,819
term1mul.miter.shuffled-as.sat03-357 3504 22,229 21,809 21,664
x1mul.miter.shuffled-as.sat03-359 5444 34,509 32,320 32,656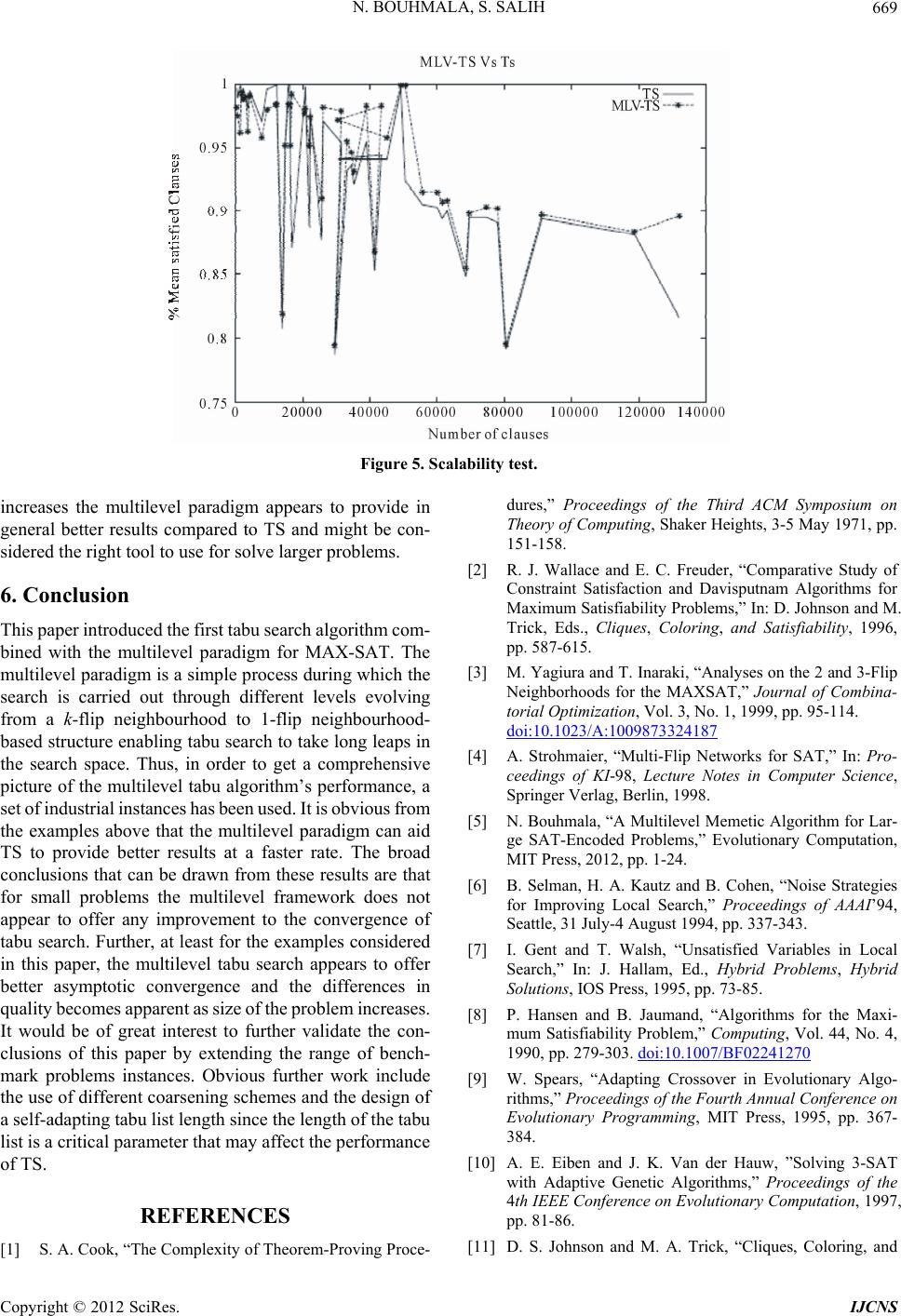

N. BOUHMALA, S. SALIH 669
Figure 5. Scalability test.
increases the multilevel paradigm appears to provide in
general better results compared to TS and might be con-
sidered the right tool to us e for solve larger problems.
6. Conclusion
This paper introduced the first tabu search algorithm com-
bined with the multilevel paradigm for MAX-SAT. The
multilevel paradigm is a simple process during which the
search is carried out through different levels evolving
from a k-flip neighbourhood to 1-flip neighbourhood-
based structure enabling tabu search to take long leaps in
the search space. Thus, in order to get a comprehensive
picture of the multilevel tabu algorithm’s performance, a
set of industrial instances has been use d. It is obvious from
the examples above that the multilevel paradigm can aid
TS to provide better results at a faster rate. The broad
conclusions that can be drawn from these results are that
for small problems the multilevel framework does not
appear to offer any improvement to the convergence of
tabu search. Further, at least for the examples considered
in this paper, the multilevel tabu search appears to offer
better asymptotic convergence and the differences in
quality becomes apparent as size of the problem increases.
It would be of great interest to further validate the con-
clusions of this paper by extending the range of bench-
mark problems instances. Obvious further work include
the use of different coarsening schemes and the design of
a self-adapting tabu list length since the length of the tabu
list is a critical parameter that may affect the performance
of TS.
REFERENCES
[1] S. A. Cook, “The Complexity of Theorem-Proving Proce-
dures,” Proceedings of the Third ACM Symposium on
Theory of Computing, Shaker Heights, 3-5 May 1971, pp.
151-158.
[2] R. J. Wallace and E. C. Freuder, “Comparative Study of
Constraint Satisfaction and Davisputnam Algorithms for
Maximum Satisfiability Problems,” In: D. Johnson and M.
Trick, Eds., Cliques, Coloring, and Satisfiability, 1996,
pp. 587-615.
[3] M. Yagiura and T. Inaraki, “Analyses on the 2 and 3-Flip
Neighborhoods for the MAXSAT,” Journal of Combina-
torial Optimization, Vol. 3, No. 1, 1999, pp. 95-114.
doi:10.1023/A:1009873324187
[4] A. Strohmaier, “Multi-Flip Networks for SAT,” In: Pro-
ceedings of KI-98, Lecture Notes in Computer Science,
Springer Verlag, Berlin, 1998.
[5] N. Bouhmala, “A Multilevel Memetic Algorithm for Lar-
ge SAT-Encoded Problems,” Evolutionary Computation,
MIT Press, 2012, pp. 1-24.
[6] B. Selman, H. A. Kautz and B. Cohen, “Noise Strategies
for Improving Local Search,” Proceedings of AAAI’94,
Seattle, 31 July-4 August 1994, pp. 337-343.
[7] I. Gent and T. Walsh, “Unsatisfied Variables in Local
Search,” In: J. Hallam, Ed., Hybrid Problems, Hybrid
Solutions, IOS Press, 1995, pp. 73-85.
[8] P. Hansen and B. Jaumand, “Algorithms for the Maxi-
mum Satisfiability Problem,” Computing, Vol. 44, No. 4,
1990, pp. 279-303. doi:10.1007/BF02241270
[9] W. Spears, “Adapting Crossover in Evolutionary Algo-
rithms,” Proceedings of the Fourth Annual Conference on
Evolutionary Programming, MIT Press, 1995, pp. 367-
384.
[10] A. E. Eiben and J. K. Van der Hauw, ”Solving 3-SAT
with Adaptive Genetic Algorithms,” Proceedings of the
4th IEEE Conference on Evolutionary Computation, 1997,
pp. 81-86.
[11] D. S. Johnson and M. A. Trick, “Cliques, Coloring, and

N. BOUHMALA, S. SALIH 670
Satisfiability, Volume 26 of DIMACS Series on Discrete
Mathematics and Theoretical Computer Science,” Ameri-
can Mathematical Society, 1996.
[12] C. M. Li, W. Wei and H. Zhang, “Combining Adaptive
Noise and Look-Ahead in Local Search for SAT,” Pro-
ceedings of the Tenth International Conference on Theory
and Applications of Satisfiability Testing(SAT-07), Vol-
ume 4501 of Lecture Notes in Computer Science, 2007,
pp. 121-133.
[13] D. J. Patterson and H. Kautz, “Auto-Walksat: A Self-
Tuning Implementation of Walksat,” Electronic Notes on
Discrete Mathematics, Vol. 9, 2001.
[14] O. C. Granmo and N. Bouhmala, “Solving the Satisfiabil-
ity Problem Using Finite Learning Automata,” Interna-
tional Journal of Computer Science and Applications,
Vol. 4, No. 3, 2007, pp. 15-29.
[15] A. R. KhudaBukhsh, L. Xu, H. H. Hoos and K. Leyton-
Brown, “SATenstein: Automatically Building Local Search
SAT Solvers from Components,” Proceedings of the 25th
International Joint Conference on Artificial Intelligence
(IJCAI-09), 2009.
[16] L. Xu, F. Hutter, H. Hoos and K. Leyton-Brown, “SAT-
zilla: Portfolio-Based Algorithm Selection for SAT,” Jour-
nal of Artificial Intelligence Research, Vol. 32, 2008, pp.
565-606.
[17] F. Glover, “Tabu Search-Part 1. ORSA,” Journal on Com-
puting, Vol. 1, No. 3, 1989, pp. 190-206.
doi:10.1287/ijoc.1.3.190
[18] S. T. Barnard and H. D. Simon, “A Fast Multilevel Im-
plementation of Recursive Spectral Bisection for Parti-
tioning Unstructured Problems,” Concurrency: Practice
and Experience, Vol. 6, No. 2, 1994, pp. 101-117.
doi:10.1002/cpe.4330060203
[19] R. Hadany and D. Harel, “A Multi-Scale Algorithm for
Drawing Graphs Nicely,” Tech.Rep.CS99-01, Weizmann
Institute of Science, Faculty of Mathematics & Computer
Science, 1999.
[20] B. Hendrickson and R. Leland, “A Multilevel Algorithm
for Partitioning Graphs,” Proceedings of Supercomput-
ing’95, San Diego, 1995.
[21] G. Karypis and V. Kumar, “A Fast and High Quality
Multilevel Scheme for Partitioning Irregular Graphs,”
SIAM Journal on Scientific Computing, Vol. 20, No. 1,
1998, pp. 359-392. doi:10.1137/S1064827595287997
[22] G. Karypis and V. Kumar, “Multilevel K-Way Partition-
ing Scheme for Irregular Graphs,” Journal of Parallel
and Distributed Computing, Vol. 48, No. 1, 1998, pp.
96-129. doi:10.1006/jpdc.1997.1404
[23] C. Walshaw and M. Cross, “Mesh Partitioning: A Multi-
level Balancing and Refinement Algorithm,” SIAM Jour-
nal on Scientific Computing, Vol. 22, No. 1, 2000, pp. 63-
80. doi:10.1137/S1064827598337373
[24] C. Walshaw, “A Multilevel Approach to the Traveling
Salesman Problem,” Operations Research, Vol. 50, No. 5,
2002, pp. 862-877. doi:10.1287/opre.50.5.862.373
[25] C. Walshaw, “A Multilevel Lin-Kernighan-Helsgaun Al-
gorithm for the Traveling Salesman Problem,” Tech. Re-
port 01/IM/80, University of Greenwich, Greenwich,
2001.
[26] D. Rodney, A. Soper and C. Walshaw, “The Application
of Multilevel Refinement to the Vehicle Routing Prob-
lem,” In: D. Fogel, et al., Eds., IEEE Symposium on
Computational Intelligence in Scheduling, 2007, pp. 212-
219. doi:10.1109/SCIS.2007.367692
[27] C. Walshaw, “A Multilevel Algorithm for Forced-Di-
rected Graph-Drawing,” Journal of Graph Algorithms
and Applications, Vol. 7, No. 3, 2003, pp. 253-285.
doi:10.7155/jgaa.00070
[28] C. Blum, J. Puchinger, G. R. Raidl and A. Roli, “Hybrid
Metaheuristics in Combinatorial Optimization: A Survey,”
Applied Soft Computing, Vol. 11, 2011, pp. 4135-4151.
doi:10.1016/j.asoc.2011.02.032
[29] C. Walshaw, “Multilevel Refinement for Combinatorial
Optimization: Boosting Metaheuristic Performance,” In:
C. Blum, et al., Eds., Springer, Berlin, 2008, pp. 261-289.
[30] B. Mazure, L. Sas and E. Gregoire, “Tabu Search for
SAT,” AAAI-97 Proceedin g s, 1997, pp. 281-285.