 Journal of Modern Physics, 2012, 3, 1398-1407 http://dx.doi.org/10.4236/jmp.2012.310177 Published Online October 2012 (http://www.SciRP.org/journal/jmp) Multiple Lorentz Groups—A Toy Model for Superluminal Muon Neutrinos Marco Schreck Institute for Theoretical Physics, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany Email: marco.schreck@kit.edu Received July 23, 2012; revised August 31, 2012; accepted September 9, 2012 ABSTRACT In this article an idea is presented, which allows for the explanation of superluminal muon neutrinos. It is based on the introduction of a new superluminal, massless gauge boson coupling to the neutrino only, but not to other standard mod- el particles. The model is discussed with regard to the Supernova 1987 (SN 1987) velocity bound on electron antineu- trinos and the Cohen-Glashow constraint on superluminal neutrino propagation. The latter can be circumvented if— within the framework of the model—a sterile neutrino mixing with the active neutrino mass eigenstates is introduced. The suggestion of a sterile neutrino accounting for superluminal neutrinos has already been proposed in several papers. It is possible to choose mixing angles with the sterile neutrino sector such that the model respects both the SN 1987 bound and the muon neutrino travels superluminally. Keywords: Special Relativity; Dispersion Relations; Neutrino Interactions; Non-Standard-Model Neutrinos 1. Introduction At the end of September 2011, the OPERA collaboration announced the remarkable detection of superluminal muon neutrinos at the 6.2 -level [1]. Their experimen- tal result with statistical and systematical error was given by1: 0.34 5 0.24 10 . 6.1 3.7 1.6 1.1ns. ee 17 GeV 2.37 0.32 E vc c (1) Unfortunately, on February, 2012 two error sources had become evident, which were likely to ruin their re- sult. First, a fiber connection to a computer card had not been attached properly. Second, there had been a prob- lem with the clock at OPERA used between the synchro- nizations with the Global Positioning System. At the 25th International Conference on Neutrino Physics and Astrophysics in Kyoto on June 8th, 2012 a final update on the OPERA time-of-flight measurement was given: t (2) This number states the deviation of the muon neutrino time-of-flight from the time that light needs to travel the distance from CERN to the Gran Sasso underground la- boratory. Hence, the deviation is now consistent with zero. The physics community had considered the result giv- en by Equation (1) with care, since the deviation from the speed of light lay several orders of magnitude above what would be expected, if it was from quantum gravita- tional origin. The authors of [2-7] tried to figure out how the OPERA result could be explained by possible sys- tematical errors. Beyond that, in [8] a cross-check for the result was proposed. It was demonstrated that muon neu- trinos traveling with superluminal velocity can produce signatures for highly-boosted tt-quark pairs at the LHC, where one or both quarks decay semileptonically. Furthermore, on the one hand, Cohen and Glashow showed that a superluminal neutrino would lose its en- ergy quickly by the emission of electron positron pairs [9]. If muon neutrinos moved faster than light, the proc- ess would be energetically possible above a certain neutrino energy threshold resulting in a copi- ous production of electron positron pairs. On the other hand, the authors of [10,11] discussed that the Cohen- Glashow constraint can be avoided. This may be the case when, for example, Lorentz-violating effects de- pend quadratically on the neutrino energy or if Lor- entz-violation is not fixed but covariant with the neu- trino four-momentum. In [12] two models were investigated, where the first gave rise to deformed energy conservation laws and the second resulted in deformed momentum conservation laws. For these models the bounds of [9] are not applica- 1These numbers can be found in the updated version 2.0 of [1]. C opyright © 2012 SciRes. JMP  M. SCHRECK 1399 ble. In the article [13] further constraints on the deviation of the neutrino velocity from the speed of light were given by considering pion decay and TeV-neutrinos de- tected by ICECUBE. These gave severe bounds on Lor- entz symmetry violation in the neutrino sector clashing with the experimental OPERA result. Although the OPERA result has now proven to be wrong, it stimulated theoretical ideas in this field and led to many new models, which can perhaps be applied to other realms of physics. It may also be the case that a certain neutrino species indeed travels superluminally. However, the deviation from the speed of light is then expected to be much smaller than the value measured by OPERA. For this reason some representative examples for models that try to describe superluminal neutrinos will be listed: It is well-known that dispersion relations of particles will be modified, if they propagate through a medium. In [14,15] the superluminal motion of muon neutrinos is interpreted in the framework of deformed disper- sion relations, which are a low-energy manifestation of Lorentz-violating physics at the Planck scale. In these theories the vacuum behaves as an effective medium. Such a medium can result from standard model phys- ics, as well. For example, in [16] superluminal neu- trinos are explained by the assumption that Earth is surrounded by a special kind of matter consisting of separated quarks. If the wave functions of quarks are entangled, they can form colorless objects and, hence, are confined, even when they are spatially separated by a large distance. In [17] a model is proposed which describes a spon- taneous breakdown of Lorentz symmetry by a scalar background field that is added to the action via a La- grange multiplier. This framework leads to a modified neutrino dispersion relation depending on the mo- mentum of the neutrino. The neutrino velocity can be modified by Fermi point splitting (for a recent review see [18]), which re- moves the degeneracy of zeros of the fermionic en- ergy spectrum [19]. The neutrino dispersion relation can change because of environmental effects caused by fields that accu- mulate at the position of the Earth. These may lead to an effective metric, in which the neutrino propagates with superluminal velocity [20,21]2. Furthermore, in the context of general relativity, a particle traveling along a geodesic path in a metric different from the Minkowski metric can be investigated [23]. In the ar- ticle previously mentioned the mean velocity of such a particle is calculated with the assumption that the observer stays at rest. The average velocity can be larger than the speed of light, even if the velocity as a local property defined in a spacetime point is smaller. This is investigated for a Schwarzschild metric. A further alternative is to consider models of modi- fied gravity. In the article [24] particle propagation in a Hořava-Lifshitz modified gravitational background is considered. The authors derive the Dirac equation for a fermion traveling through such a background. The condition for the existence of nontrivial solutions of the Dirac equation leads to a modified neutrino dispersion relation. The neutrino velocity can be lar- ger than the speed of light for a special Hořava-Lif- shitz scenario. In [25] the existence of a sterile neutrino that travels with a superluminal velocity is proposed. Sterile neu- trinos cleverly get around the Cohen-Glashow bound, since they do not couple to the Z boson. An analysis involving sterile superluminal neutrinos is presented e.g. in [26]. Furthermore, assuming superluminal neutrino propa- gation at a certain energy, neutrinos may propagate with a velocity at very high energies leading to a dif- ferent neutrino horizon. In [27] bounds from astrophysi- cal observations are set on vc vc for very high neutrino energies. 2. Extension of the Lorentz Group— Neutrinos and a Hidden Sector Let us, for now, take Equation (1) as it stands, since the idea of superluminal muon neutrinos proposed in the current article is purely theoretical and does not rely on the OPERA result. The goal is to describe a superluminal neutrino species without quantum gravity effects, but by the introduction of new particles coupling to neutrinos. For the analysis presented as follows the OPERA value can be chosen just as an example (independently of its correctness) in order to demonstrate the model proposed. That is why we will often refer to Equation (1) in the rest of the paper. 2.1. Invariant and Maximum Velocity The foundations of special relativity are the relativity principle and the constancy (invariance) of the speed of light. As a result, the Galilei group of classical mechanics is replaced by the Lorentz group, which leads, for exam- ple, to the relativistic law of addition of velocities. The fact that the speed of light is the maximum attainable velocity of all particles does not directly follow from the Lorentz group, since it only delivers an invariant velocity at first. In order to understand this, three Gedankenex- periments will be performed, whose concept was initi- 2Reference [22] gives new experimental bounds on the mass scale M* that is characteristic for the model presented in [20]. Copyright © 2012 SciRes. JMP  M. SCHRECK 1400 ated in [28]. 1) We consider some hypothetical beings living in a fluid. They are assumed to consist of fluid atoms, which are held together solely by phonon-mediated forces. The beings do not feel other forces such as electromagnetism or gravitation. Their dynamics is expected to be governed by an acoustic Lorentz group with the invariant velocity being the velocity of sound c in the fluid [28]. We expect the beings to build a rocket, which can be acceler- ated by phonon emission. From the relativistic addition of velocities it follows that the maximum attainable ve- locity of the rocket is given by c ˆ q ˆ . 2) Einstein found that the dynamics of particles in our universe is governed by the “standard” Lorentz group with the invariant speed of light c. His theory has been heralded or substantiated by various experiments [29-31]. In the second Gedankenexperiment humans build a rock- et which is accelerated by a light engine, namely the emission of photons. In this case, the relativistic addition of velocities leads to c as the upper limit of the rocket velocity. 3) Now we are ready to discuss the central idea of this article. The basic assumption is that the photon is not the gauge boson which moves with the highest velocity. We adopt neutrinos carrying a new charge differing from all charges of the standard model. This charge is to be mediated by a postulated massless gauge boson moving with a speed . Neutrinos couple to these gauge bosons, which form—possibly together with other unknown particles—a hidden sector. The latter does not interact with any other particle of the standard model, cf. Figure 1. This leads to a neutrino dynamics which is based on a “hidden sector Lorentz group” with an in- variant velocity . The third Gedankenexperiment is to build a rocket consisting of neutrinos with an accelera- tion process working by the emission of gauge bosons ˆc ˆ c ˆ c . The limiting velocity of the rocket is then given by , which is larger than the speed of light. ˆ c ˆ The consequences from this deliberation is that differ- ent levels of the Lorentz group each with a distinct in- variant velocity can be realized in nature. The coupling constant is assumed to be small enough such that neu- trino propagation is not affected too much to violate ex- isting bounds on the interaction of neutrinos with matter. The size of the coupling is not important for now—only its existence. The situation described is depicted in Fig- ure 2. Each new coupling of particles to massless gauge bosons3 opens a new sector with a maximum attainable velocity for these particles from left to right. 2.2. Modified Neutrino Kinematics and Lagrangian of the Hidden Sector The gauge boson is assumed to couple to neutrino mass eigenstates. This seems a more natural choice than the coupling to flavor eigenstates, since the hidden sector does not know anything about neutrino flavors. Hence, the neutrino mass eigenstates i obey a kinematics resting upon special relativity, but with the speed of light replaced by the speed of the hidden sector gauge boson 1, 2,3i ˆ c ˆ : 2 22 2 2 2 ˆ 1 ˆˆˆ12 ˆ 1,. 2 i i i i mc Emcpcpc p mc c pc pc E (3) Here i is the relativistic neutrino energy of the i-th mass eigenstate, p the neutrino momentum, and i its mass4. The modified neutrino dispersion relation in Equation (3) is isotropic and gives the deformation. If we suppress the mass eigenstate index i for a moment and interpret neutrinos as matter waves with frequency m and three-momentum k, we have to carry out the re- placements E pk and , which leads to: 2 2 1. 2 mc kc k (4) The front velocity, which corresponds to the velocity of the highest frequency forerunners of a wave, is then given by [32]: fr, lim . k vc k (5) It equals the signal velocity of a -function shaped pulse in configuration space. Hence, any possible distor- tion of a signal does not play a role for the front velocity. The case is related to superluminal, >1 1 < 1 ˆ to luminal, and to subluminal motion. If the gauge boson is assumed to have spin 1 ana- logously to the photon, at the level of Lagrange densities the ordinary minimal coupling procedure can be per- formed with c again replaced by : ˆ c Dirac mass eigenstate hidden sectorMaj,1 Maj,2 ˆ, i i i ii i iD (6) 4We assume that all mass eigenstates propagate with the same momen- tum p. Whenever we refer to kinematics we stick to the notation of m with an index (denoting the mass or flavor eigenstate) for the neutrino mass. 3Remark that the phonon is not a gauge boson, but a Goldstone boson (massless excitation) resulting from the spontaneously broken transla- tion symmetry in a solid. This does not matter for the argument, though. Copyright © 2012 SciRes. JMP 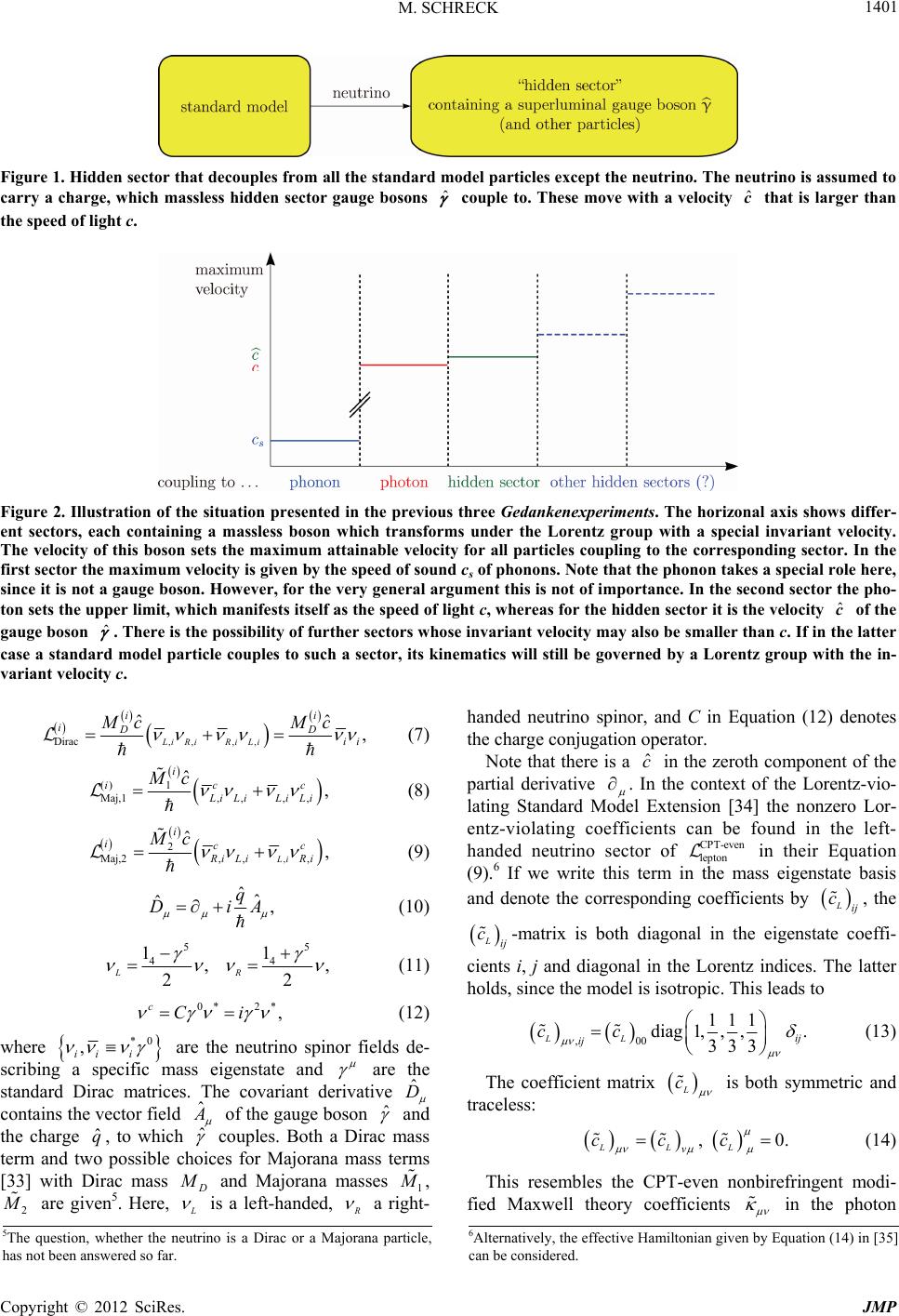 M. SCHRECK 12 SciRes. JMP 1401 Figure 1. Hidden sector that decouples from all the standard model particles except the neutrino. The neutrino is assumed to carry a charge, which massless hidden sector gauge bosons ˆ couple to. These move with a velocity that is larger than the speed of light c. ˆ c Figure 2. Illustration of the situation presented in the previous three Gedankenexperiments. The horizonal axis shows differ- ent sectors, each containing a massless boson which transforms under the Lorentz group with a special invariant velocity. The velocity of this boson sets the maximum attainable velocity for all particles coupling to the corresponding sector. In the first sector the maximum velocity is given by the speed of sound cs of phonons. Note that the phonon takes a special role here, since it is not a gauge boson. However, for the very general argument this is not of importance. In the second sector the pho- ton sets the upper limit, which manifests itself as the speed of light c, whereas for the hidden sector it is the velocity of the gauge boson ˆ c ˆ . There is the possibility of further sectors whose invariant velocity may also be smaller than c. If in the latter case a standard model particle couples to such a sector, its kinematics will still be governed by a Lorentz group with the in- variant velocity c. Copyright © 20 ,, ,,Dirac Li RiRi Li iD ˆˆ , ii D ii Mc Mc (7) ,, , ˆ, ic LiLi Li Mc () 1 Maj,1 , ic Li (8) , 2 , , ˆ, Li i icc Li Ri Mc Maj,2 ,Ri (9) ˆˆ ˆ, q DiA (10) 55 44 11 ,, 22 R L 2* ,i (11) 0*cC (12) where , ii i *0 are the neutrino spinor fields de- scribing a specific mass eigenstate and are the standard Dirac matrices. The covariant derivative ˆ D contains the vector field ˆ of the gauge boson ˆ and the charge , to which ˆ qˆ couples. Both a Dirac mass term and two possible choices for Majorana mass terms [33] with Dirac mass and Majorana masses 1 , 2 are given5. Here, is a left-handed, a right- handed neutrino spinor, and C in Equation (12) denotes the charge conjugation operator. Note that there is a in the zeroth component of the partial derivative ˆ c . In the context of the Lorentz-vio- lating Standard Model Extension [34] the nonzero Lor- entz-violating coefficients can be found in the left- handed neutrino sector of lept on in their Equation (9).6 If we write this term in the mass eigenstate basis CPT-even Lij c , the and denote the corresponding coefficients by Lij c -matrix is both diagonal in the eigenstate coeffi- cients i, j and diagonal in the Lorentz indices. The latter holds, since the model is isotropic. This leads to ,00 111 diag 1,,, 333 LL ij ij cc . (13) L c The coefficient matrix ,0 LLL v ccc is both symmetric and traceless: . (14) This resembles the CPT-even nonbirefringent modi- fied Maxwell theory coefficients in the photon 6Alternatively, the effective Hamiltonian given by Equation (14) in [35] can be considered. 5The question, whether the neutrino is a Dirac or a Majorana particle, has not been answered so far.  M. SCHRECK 1402 sector [36,37], which is clear, since both sectors are re- lated by a coordinate transformation—at least at first order in the Lorentz-violating coefficients [37]. 2.3. Extension of the Toy Model to Three Neutrino Flavors The neutrino masses i are eigenvalues to the mass ei- genstates m i . However, the weak interaction gauge bos- ons couple to flavor eigenstates with ,,e 33 . The transformation from mass to flavor eigenstates and (vice versa) is governed by the unitary -PNMS matrix U: * ,, , , ,. i ie UU 1, 2,3 ii i 131312 12 232312 12 13 1323 13 1323 13 10 000 00100 001 , cscs Ucs sc s s sc s cc (15) When, for simplicity, the CP-violating phases are set to zero7, the matrix U reads 23 23 1313 12 1312 13 12 2312 231312 2312 23 12 2312231312 231223 00sc s c cc sc sc csscc ss ss ccscs sc sin ij ij s (16) where, for brevity, ij c and cos ij have been used [38]. Here, ij for are the neutrino mixing angles. Kinematik measurements of neutrino masses (e.g. for pion decay and beta decay8) lead to “masses of neutrino flavors,” which are the weighted average of the neutrino mass eigenvalues [39]: ,1ij ,2,1,3,2,3 2 22 , 1, 2,3 , eei i i mUm (17) 2 22 , 1, 2,3 , ii i Um m (18) 2 22 , 1, 2,3 ii Um m2 . (19) i m Since in Equation (3) the neutrino mass eigenvalues i are multiplied by , the maximum velocity of each neutrino flavor will be defined in the following way: ˆi c 2 44 , 1, 2,3 ˆˆ, eei i i cUc (20) 2 44 , =1 ,2, 3 ˆ, ii Uc ˆ i c (21) 2 44 , 1, 2,3 ˆ. ii Uc ˆ c i (22) If we assume ˆˆˆˆ 1, , iii i cccc c (23) ˆˆˆˆ 1, ,cccc c (24) it is sufficient to linearize the equations above: 2 43 43 , 1, 2,3 2 43 , 1, 2,3 ˆˆ 44 ˆ 4. ii i ii i cccU ccc ccUc (25) ,,e Here, . From the latter equation follows the simplified result 2 , 1, 2,3 ˆˆ, ii i cUc (26) 2 , 1,2 , 3 ˆˆ. ii i cUc ˆ c ˆ c (27) In the rest of the article the neutrino velocities will be approximated by i for the mass eigenstates and by for the flavor eigenstates, since neutrino masses are assumed to be much smaller than neutrino energies. The Supernova 1987 Bound The point of extending the toy model to all active neu- trino flavors, is to account for the Supernova 1987 (SN 1987) bound on electron antineutrinos9 [40,41]: 7.5,36 MeV9 | 210 ee E vc c . (28) An electron neutrino produced by a weak interaction process is a mixture of neutrino mass eigenstates accord- ing to the relation , 1, 2,3 . eeii i U (29) After the neutrino has traveled through space and reaches a distance L from the origin of its production it holds 2 , 1,2 , 3 2 * ,, ,, 1,2,3 expi 2 exp i, 2 i eei i i i ei i ei m LU L E m ULU E mE (30) where i has been assumed [38]. Hence, the ini- tial electron neutrino state then corresponds to a mixture of all flavor eigenstates. However, the initial composition of mass eigenstates remains the same, because quantum 9An antineutrino is assumed to travel with the same velocity as the corresponding neutrino. This makes sense, since the model presented corresponds to a CPT-even term of the Lorentz-violating Standard Model Extension. See the end of Secition 2.2 for a brief discussion concerning this issue. 7Furthermore, currently no experimental data concerning these phases are on hand [38]. 8Neutrinoless double beta decay that occurs for Majorana neutrinos leads to a different definition of the “flavor eigenstate mass” [39]. C opyright © 2012 SciRes. JMP  M. SCHRECK 1403 mechanically the statement 2 2 2 2 , 2 , iij ej mL E U ˆi 2 , 1, 2 ,3 2 , exp i expi 2 je ei i j ej LU m UL E (31) is valid. As a result of that, also the velocity of the neu- trino does not change during its propagation, since it is determined by the initial composition of mass eigenstates. The antineutrinos coming from the supernova were de- tected as electron antineutrinos on Earth. For this reason the bound of Equation (28) will be considered as a bound on the velocity of electron neutrinos—regardless of whether their flavor was different on their way to Earth. We assume three distinct hidden sectors each with its own gauge boson , where 1 ˆ only couples to the first mass eigenstate, 2 ˆ to the second, and 3 ˆ to the third, via the respective charge for , 2, and 3, respec- tively. If any sector obeys a different invariant velocity 12 3 , the constraint of Equation (28) does not necessarily contradict a deviation from the speed of light of the order of for one single neutrino flavor. This will be shown as follows. ˆi q1i ˆˆ ˆ cc c 5 10 The current experimental values or bounds for the three neutrino mixing angles 12 , 23 , and 13 are [38]: 2 12 sin 2 0.87 0.03, 23 2 0.92, 13 2< 0.15 (32) 2 sin (33) 2 sin. (34) With the lower bound on 23 and the upper bound on 13 we obtain the PNMS matrix 0.81 0 0.55 0.21 U .55 0.20 0.590.59 . 0.58 0.79 (35) Current experimental data imply that neutrinos are al- most massless. Concretely, this means ,, 2 1eV e mc , from neutrino oscillation data [38] and 2 ,, <0.67eV f fe mc (95% CL),10 (36) which is obtained from WMAP observations [42]. There- fore, an approximate value of ˆ c directly follows from Equation (1): 5 ˆ,12.37 10cc 3 ˆ cc and we obtain11: ˆe cc . (37) Assuming 54 12 ˆˆ 5.30 10,1.13 10 cc cc cc . 2 ˆ (38) Hence, Equation (1) for muon neutrinos and the SN 1987 bound for electron neutrinos do not clash, if the velocity of the first mass eigenstate is a little bit lower than c and if the second moves faster than c. Since the first eigenstate propagates slower than c, it need not nec- essarily couple to any hidden sector. In contrast, the sec- ond mass eigenstate has to couple to a traveling faster than light. 2.4. Challenges of the Model and Introduction of Sterile Neutrinos The argument of [9] resulting in the rapid loss of the neutrino energy by electron positron emission relies on fundamental principles: four-momentum conservation and the coupling of the neutrino sector to the Z boson. Models for superluminal neutrino propagation have to compete with the very general result mentioned, and this is also the case for the toy model presented here. 1) We could assume the energy loss of muon neutrinos to be compensated by a Compton scattering type process, where gauge bosons ˆ scatter with muon neutrinos. However, this argument leads to additional problems. First of all, the free parameters of the model (e.g. the charge or the initial energy of a ˆ qˆ boson) have to be chosen such that this compensation is possible, which requires extreme finetuning. If the momentum distribu- tion of ˆ is homogeneous and isotropic, the average energy transfer to the neutrino will be zero. In principle, the distribution may be anisotropic, but then neutrinos might be deflected on their way from CERN to the Gran Sasso underground laboratory. 2) An alternative proposal is that a neutrino itself is part of the hidden sector making it to some kind of su- perluminal, sterile neutrino . Then the neutrino does not couple to the Z boson, rendering the process ss ee forbidden. The sterile neutrino may mix with the active neutrino species leading to superluminal propagation of at least some of the standard model neu- trino flavors. This idea has already been suggested in other publications, see e.g. [25,43] and references therein. Reference [44] states that sterile neutrino models may be in conflict with the atmospheric neutrino data measured at Super-Kamiokande. However, the models considered in the latter article only involve one sterile neutrino and one single mixing angle with this neutrino. Conclusions 10Note that under the assumptions taken, the unit 2 eV cshould be replaced by 2 ˆ eV c, as well. But since the mass values given have een obtained in the context of special relativity, where the speed o light c is the invariant velocity, we keep c. 11The latter choice is reasonable, since 5 exp 8.4 10 e vcvc according to Equations (1) and (28). We keep in mind that the con- straints on e v v and were obtained at different neutrino energies, but this does not play a role in our model, though. Copyright © 2012 SciRes. JMP  M. SCHRECK 1404 for models with more mixing angles have not been ob- tained. According to the second item of the list above, we ex- tend the toy model by N 3 sterile neutrino mass eigen- states. Then the transformation between the N fla- vor and mass eigenstates is governed by a unitary 3 3 s NN -matrix U: 3 , 1 , s Nsii i U (39) Following Equation (2.3) we can write: 32 , 1 ˆˆ . s Nsii i cUc 1 s N (40) For our toy model we consider the simplest case with one single sterile neutrino, hence . In principle, this sterile neutrino mass eigenstate 4 mixes with the active neutrino mass eigenstates i for 1, 2,3i. This mixing can be described by introducing three addi- tional mixing angles 14 , 24 , and 34 . The corre- sponding -mixing matrix 4 4 U can then be con- structed from U as follows12: 14 14 14 14 24 24 24 24 0 0 0 1 0 0 10 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 sT cs U U sc cs sc 0 0 1 0 0 1 0 0 0 0 0, 0, 00 34 34 34 34 0 0 0 0 cs sc (41) where . In what follows, we examine a subspace of the free toy model parameters, which is seven-dimensional. It is spanned by the three sterile neutrino mixing angles 14 , 24 , 34 and by the in- variant velocities of the neutrino mass eigenstates 1, 2, 3, 4. Since this phase space is that large, it will be reduced by the special choice below. We assume that the invariant velocities of the three standard neutrino mass eigenstates correspond to the speed of light, which means 123 . The single sterile neutrino is assumed to travel with superluminal speed: we therefore set . ˆ c ˆ c ˆ ˆ cˆ c ˆ ˆ cc 13 ˆ c 5 10cc c 4 As a result, only the sterile mixing angles remain as free parameters. In Figure 3 three cases are considered, where in each one of these angles is fixed: 14 π3 , 24 π5 , and 34 π5 . We would like to explore, whether in each case the remaining two angles can be chosen such that the electron anti-neutrino velocity re- spects the SN 1987 bound of Equation (28) and that the muon neutrino velocity lies in the error band of Equa- tion (1). In all plots overlapping regions are small, but they exist. At least one of the three mixing angles has to be rather large. A special possibility is 14 5π4 , 24 π5 , and 34 π5 that becomes evident from the third panel. With these values we obtain the following results for the velocities of the three active neutrino fla- vors: 10 ˆ9.0710, e cc c (42) 5 ˆ 2.3310, cc c (43) 7 ˆ2.3110. cc c (44) Whether there exists a choice of angles that does not contradict existing atmospheric neutrino data—as was proposed in [44]—will not be examined here. To summarize, within the toy model presented a su- perluminal sterile neutrino mass eigenstate can be intro- duced, such that the electron neutrino respects the SN 1987 bound and the muon neutrino travels with the su- perluminal velocity that is given by Equation (1). For the parameters chosen above the tau neutrino is then slightly superluminal, as well. 3. Conclusions In this article a concept accounting for superluminal muon neutrinos was presented. It is based on a multiple Lorentz group structure. The dynamics of the neutrino is assumed to obey the Lorentz group with an invariant velocity that is larger than the speed of light. This will be possible, if the neutrino couples to a hidden sector of massless gauge bosons that move faster than photons. Then the neutrino field transforms under the Lorentz group with an invariant velocity which corresponds to the velocity of these gauge bosons. If an experiment measures a deviation of the neutrino velocity that is much larger than the speed of light, this will be very difficult to understand in the context of physics at the Planck scale. The idea presented here leads, in principle, to a modified dispersion relation of the neu- trino, as well. However, the framework is not quantum gravity, but special relativity and field theory with an invariant velocity imposed that differs from the speed of light. First of all, every physical model describing superlu- minal muon neutrinos has to compete with the SN 1987 bound. This is a minor difficulty, since the toy model presented here can be altered such that electron neutrinos behave differently compared to muon neutrinos. More severe is the Cohen-Glashow constraint that is based on fundamental principles of present-day physics, which are 12With all CP-violating phases set to zero. C opyright © 2012 SciRes. JMP  M. SCHRECK Copyright © 2012 SciRes. JMP 1405 (a) (b) (c) Figure 3. Each panel shows the plane of a different pair of sterile neutrino mixing angles, where the remaining angle is set to the special value given below the corresponding panel. Regions of the electron and the muon neutrino velocity are shown, where , and ˆ c ˆˆ 123 ccc ˆ4 5 1310cc is the common choice. The blue areas depict the region ˆe 110cc 8 and the green areas show the region ˆ.. . 55 12.370 320 24101 8110cc . The condition ..0 320 3410 ˆ 1 2.37cc . 55 3 0310 is fulfilled for all possible mixing angles in each panel, so is ˆe 8 110cc . (a) 14π3 ; (b) 24 π5 ; (c) 34 π5 . difficult to circumvent. Honestly, the latter is also a se- vere problem for the current model, unless the superlu- minal neutrino itself is part of a hidden sector, hence ste- rile. Besides that, the toy model makes the following pre- dictions that can be verified or falsified by experiment: If the muon neutrino moves with a superluminal ve- locity, its velocity is isotropic and does not depend on the neutrino energy (besides any mass-related de- pendence). It is not a local effect, i.e. muon neutrinos move with a superluminal velocity in interstellar space, as well. To find a physical theory both explaining superluminal neutrinos without bothering already established data and facts about the neutrino sector is a great challenge for model builders. 4. Acknowledgements It is a pleasure to thank S. Thambyahpillai (KIT) and A. Crivellin (University of Bern) for reading an early draft of the paper and for useful suggestions. Furthermore, the author thanks V. A. Kostelecký (Indiana University, Bloomington) for helpful discussions. The author ac- knowledges support by Deutsche Forschungsgemein- schaft and Open Access Publishing Fund of Karlsruhe Institute of Technology. REFERENCES [1] T. Adam, et al., “Measurement of the Neutrino Velocity with the OPERA Detector in the CNGS Beam,” ar- Xiv:1109.4897. [2] C. R. Contaldi, “The OPERA Neutrino Velocity Result and the Synchronisation of Clocks,” arXiv:1109.6160. [3] O. Besida, “Three Errors in the Article: ‘The OPERA Neutrino Velocity Result and the Synchronisation of Clocks’,” arXiv:1110.2909. [4] R. A. J. van Elburg, “Measuring Time of Flight Using Satellite-Based Clocks,” arXiv:1110.2685. [5] R. Alicki, “A Possible Statistical Mechanism of Anoma- lous Neutrino Velocity in OPERA Experiment?” ar- Xiv:1109.5727. [6] G. Henri, “A Simple Explanation of OPERA Results without Strange Physics,” arXiv:1110.0239. [7] B. Broda, “An OPERA Inspired Classical Model Repro- ducing Superluminal Velocities,” arXiv:1110.0644. [8] H. Davoudiasl and T. G. Rizzo, “Testing the OPERA Superluminal Neutrino Anomaly at the LHC,” Physical Review D, Vol. 84, No. 9, 2011, Article ID: 091903. doi:10.1103/PhysRevD.84.091903 [9] A. G. Cohen and S. L. Glashow, “Pair Creation Con- strains Superluminal Neutrino Propagation,” Physical Review Letters, Vol. 107, No. 18, 2011, Article ID: 181803. doi:10.1103/PhysRevLett.107.181803 [10] S. Mohanty and S. Rao, “Constraint on Super-luminal Neutrinos from Vacuum Cerenkov Processes,” arXiv: 1111.2725. [11] L.-L. Zhou and B.-Q. Ma, “On the Rationality of the OPERA Experiment as a Signal of Lorentz Violation,” arXiv:1111.1574. [12] Y. Huo, T. Li, Y. Liao, D. V. Nanopoulos, Y. Qi and F. Wang, “The OPERA Superluminal Neutrinos from De- formed Lorentz Invariance,” arXiv:1111.4994.  M. SCHRECK 1406 [13] X.-J. Bi, P.-F. Yin, Z.-H. Yu and Q. Yuan, “Constraints and Tests of the OPERA Superluminal Neutrinos,” Phys- ical Review Letters, Vol. 107, No. 24, 2011, Article ID: 241802. doi:10.1103/PhysRevLett.107.241802 [14] G. Cacciapaglia, A. Deandrea and L. Panizzi, “Superlu- minal Neutrinos in Long Baseline Experiments and SN1987a,” Journal of High Energy Physics, Vol. 2011, No. 11, 2011, Article ID: 137. doi:10.1007/JHEP11(2011)137 [15] G. Amelino-Camelia, G. Gubitosi, N. Loret, F. Mercati, G. Rosati and P. Lipari, “OPERA-Reassessing Data on the Energy Dependence of the Speed of Neutrinos,” In- ternational Journal of Modern Physics D, Vol. 20, No. 14, 2011, pp. 2623-2640. [16] N. Nakanishi, “An Interpretation of ‘Superluminal Neu- trino’ Compatible with Relativity in the Framework of Standard Model,” arXiv:1111.1760. [17] S. Nojiri and S. D. Odintsov, “Could the Dynamical Lor- entz Symmetry Breaking Induce the Superluminal Neu- trinos?” The European Physical Journal C, Vol. 71, No. 11, 2011, Article ID: 1801. doi:10.1140/epjc/s10052-011-1801-4 [18] G. E. Volovik, “Topology of Quantum Vacuum,” arXiv: 1111.4627. [19] F. R. Klinkhamer, “Superluminal Muon-Neutrino Veloc- ity from a Fermi-Point-Splitting Model of Lorentz Viola- tion,” arXiv:1109.5671. [20] G. Dvali and A. Vikman, “Price for Environmental Neu- trino-Superluminality,” Journal of High Energy Physics, Vol. 2012, No. 2, 2012, Article ID: 134. doi:10.1007/JHEP02(2012)134 [21] I. Oda and H. Taira, “Superluminal Neutrinos from Gauge Field,” Modern Physics Letters A, Vol. 26, No. 39, 2011, pp. 2917-2921. doi:10.1142/S0217732311037297 [22] L. Iorio, “Constraints from Orbital Motions around the Earth of the Environmental Fifth-Force Hypothesis for the OPERA Superluminal Neutrino Phenomenology,” Journal of High Energy Physics, Vol. 2012, No. 5, 2012, Article ID: 73. doi:10.1007/JHEP05(2012)073 [23] B. Allés, “Relativity Accommodates Superluminal Mean Velocities,” Physical Review D, Vol. 85, No. 4, 2012, Ar- ticle ID: 047501. [24] E. N. Saridakis, “Superluminal Neutrinos in Hořava- Lifshitz Gravity,” arXiv:1110.0697. [25] F. R. Klinkhamer, “Spontaneously Broken Lorentz In- variance from the Dynamics of a Heavy Sterile Neu- trino,” Letters to Journal of Experimental and Theoretical Physics, Vol. 95, No. 10, 2012, pp. 497-500. doi:10.1134/S0021364012100062 [26] W. Winter, “Constraints on the Interpretation of the Su- perluminal Motion of Neutrinos at OPERA,” Physical Review D, Vol. 85, No. 1, 2012, Article ID: 017301. doi:10.1103/PhysRevD.85.017301 [27] B. C. Lacki, “Olber’s Paradox for Superluminal Neutri- nos: Constraining Extreme Neutrino Speeds at TeV-ZeV Energies with the Diffuse Neutrino Background,” Journal of Cosmology and Astroparticle Physics, Vol. 2012, No. 1, 2012, Article ID: 054. doi:10.1088/1475-7516/2012/01/054 [28] S. Liberati, S. Sonego and M. Visser, “Faster-than-c Sig- nals, Special Relativity, and Causality,” Annals of Physics, Vol. 298, No. 1, 2002, pp. 167-184. doi:10.1006/aphy.2002.6233 [29] A. A. Michelson and E. W. Morley, “On the Relative Motion of the Earth and the Luminiferous Ether,” Ameri- can Journal of Science, Vol. 34, No. 203, 1887, pp. 333- 345. [30] R. J. Kennedy and E. M. Thorndike, “Experimental Es- tablishment of the Relativity of Time,” Physical Review, Vol. 42, No. 3, 1932, pp. 400-418. doi:10.1103/PhysRev.42.400 [31] H. E. Ives and G. R. Stilwell, “An Experimental Study of the Rate of a Moving Atomic Clock,” Journal of the Op- tical Society of America, Vol. 28, No. 7, 1938, pp. 215- 219. doi:10.1364/JOSA.28.000215 [32] L. Brillouin, “Wave Propagation and Group Velocity,” Academic, New York, 1960. [33] T. Cheng and L. Li, “Gauge Theory of Elementary Parti- cle Physics,” Clarendon Press, Oxford, 1984. [34] D. Colladay and V. A. Kostelecký, “Lorentz-Violating Extension of the Standard Model,” Physical Review D, Vol. 58, No. 11, 1998, Article ID: 116002. doi:10.1103/PhysRevD.58.116002 [35] V. A. Kostelecký and M. Mewes, “Lorentz and CPT Vi- olation in Neutrinos,” Physical Review D, Vol. 69, No. 1, 2004, Article ID: 016005. [36] Q. G. Bailey and V. A. Kostelecký, “Lorentz-Violating Electrostatics and Magnetostatics,” Physical Review D, Vol. 70, No. 7, 2004, Article ID: 076006. doi:10.1103/PhysRevD.70.076006 [37] B. Altschul, “Vacuum Cerenkov Radiation in Lorentz- Violating Theories without CPT Violation,” Physical Re- view Letters, Vol. 98, No. 4, 2007, Article ID: 041603. doi:10.1103/PhysRevLett.98.041603 [38] K. Nakamura, et al., “The Review of Particle Physics,” Journal of Physics G, Vol. 37, No. 7A, 2010, Article ID: 075021. doi:10.1088/0954-3899/37/7A/075021 [39] E. W. Otten and C. Weinheimer, “Neutrino Mass Limit from Tritium Beta Decay,” Reports on Progress in Phys- ics, Vol. 71, No. 8, 2008, Article ID: 086201. doi:10.1088/0034-4885/71/8/086201 [40] K. Hirata, et al., “Observation of a Neutrino Burst from the Supernova SN 1987a,” Physical Review Letters, Vol. 58, No. 14, 1987, pp. 1490-1493. doi:10.1103/PhysRevLett.58.1490 [41] M. J. Longo, “Tests of Relativity from SN 1987a,” Phys- ical Review D, Vol. 36, No. 10, 1987, pp. 3276-3277. doi:10.1103/PhysRevD.36.3276 [42] E. Komatsu, et al., “Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation,” The Astrophysical Journal Supplement Series, Vol. 180, No. 2, 2009, pp. 330-376. doi:10.1088/0067-0049/180/2/330 [43] F. R. Klinkhamer, “Superluminal Neutrino, Flavor, and Relativity,” Physical Review D, Vol. 85, No. 1, 2012, Ar- C opyright © 2012 SciRes. JMP  M. SCHRECK Copyright © 2012 SciRes. JMP 1407 ticle ID: 016011. [44] D. Marfatia, H. Päs, S. Pakvasa and T. J. Weiler, “A Model of Superluminal Neutrinos,” Physics Letters B, Vol. 707, No. 5, 2012, pp. 553-557. doi:10.1016/j.physletb.2012.01.028
|