Journal of Modern Physics, 2012, 3, 1603-1615
http://dx.doi.org/10.4236/jmp.2012.330198 Published Online October 2012 (http://www.SciRP.org/journal/jmp)
Study of Gas Heating by a Microwave Plasma Torch*
Katell Gadonna1, Oliviez Leroy1, Philippe Leprince1, Luis Lemos Alves2, Canoline Boisse-Laporte1
1Laboratoire de Physique des Gaz et des Plasmas, UMR 8578 CNRS, Université Paris-Sud, Orsay, France
2Instituto de Plasmas e Fusão Nuclear, Instituto Superior Técnico, Universidade Técnica de Lisboa, Lisboa, Portugal
Received August 26, 2012; revised September 24, 2012; accepted October 2, 2012
ABSTRACT
Among the different types of microwave plasma torches, the axial injection torch (TIA) has been used for several years
to create chemically active species, in applications such as gas analysis, surface processing and gaseous waste treat-
ments. The TIA allows the coupling of microwave energy (2.45 GHz) to a gas injected axially at the nozzle’s exit. The
TIA produces non-local thermodynamic equilibrium plasmas with a high luminosity and a maximum density of charged
particles at the nozzle’s exit. The present work is dedicated to study the plasma created by a TIA running at atmos-
pheric pressure. The study involves both experiment and modeling of this torch, in order to maximize the coupling be-
tween the microwave power and the plasma and to define the optimum plasma and flow operating conditions for
plasma-to-gas heat transfer.
Keywords: Microwave Plasma Torch; Non-Equilibrium Plasma; Atmospheric Pressure; Thermal Transfer; Flow
Modeling
1. Introduction
The operation of microwave plasma torches (MPT) en-
sures a strong gas ionization due to an efficient micro-
wave coupling, with potential interest in different appli-
cations [1], generating also a considerable amount of
thermal energy that can be used to heat large volumes of
gas, for example to adjust the altitude of dirigible bal-
loons. These balloons have a renewed interest considering
their possibility to operate vertically during takeoff and
landing procedures, thus without the need for dedicated
infrastructures, and their ability to transport heavy mate-
rials [2].
Unlike resistors, which are commonly used to heat
gases by contact with hot surfaces, heating by MPTs re-
lies on the distribution of the electromagnetic fields exis-
ting within the plasma and leading to its partial ionization.
Therefore, MPT-assisted heating is volumetric and effi-
cient (yielding gas temperatures Tg that can reach 2000 to
4000 K [1]), allowing local rapid Tg variations especially
for working gases like helium, with high thermal conduc-
tivity [3].
Microwave induced plasmas are created and main-
tained by using an electromagnetic energy source, with
frequency in the range of 300 MHz to 10 GHz, in the
absence of electrodes, thus limiting gas contamination.
These sources have a wide range of operating powers
(from a few watts up to ~1 kW), remaining below the
high-power required by thermal torches [4], at pressures
varying from 10−2 Pa to several 105 Pa. Microwave tor-
ches create non-LTE plasmas characterized by a strong
ionization degree (electron densities ne ~ 1012 - 1016 cm−3)
and by different temperatures for the various constitutive
species of the gas/plasma system (higher electron tem-
peratures, Te ~ 12000 - 25000 K, and lower neutral gas
temperatures, Tg ~ 1500 - 10000 K ) [1], thus favoring an
energy flow from the plasma electrons to the gas excited
species.
MPTs can operate in both confined [5,6] and non-con-
fined [7,8] modes, corresponding to semi-metallic
torches and metallic torches, respectively. In the confined
mode the plasma is created within a quartz tube (trans-
parent to microwaves), where the gas flows through an
electromagnetic wave that settles generally in a cylindrical
structure. This wave is a surface-wave, a plasma wave-
mode which creates the plasma medium while it propa-
gates along it. In the non-confined mode the plasma is
created at the outlet of the nozzle that terminates a coax-
ial waveguide (Figure 1). The gas flows inside the inner
metallic tube of the coaxial structure, where a TEM
mode propagates, and the electromagnetic field couples
to the plasma at the nozzle’s exit, where the gas exhausts.
Non-confined plasma systems are more adapted to volu-
metric gas heating. Here we have chosen the well-known
TIA (“Torche à Injection Axiale” or Axial Injection Tor-
ch), which couples the TEM wave through a rectan-
*This work was partially supported by the Portuguese FCT-MCTES
(Project PTDC/FIS/65924/2006).
C
opyright © 2012 SciRes. JMP

K. GADONNA ET AL. 1604
Figure 1. TIA design.
gular waveguide-coaxial line transition (Figure 1) [1].
Note that the non-confined plasma created with this con-
figuration can be launched either in open air or in a con-
trolled atmosphere, for example by adapting some quartz
tube or chamber to the system.
Since the 80s, the TIA has been studied by different
research groups (from the University of Montreal, the
Technical University of Eindhoven and the University of
Cordoba) that focus mainly on the experimental charac-
terization of the plasma it creates [7,9,10], paying also
some attention to its electromagnetic and hydrodynamic
modeling [11,12]. These studies have shown that the TIA
could be efficient in applications such as analytical che-
mistry [13] (in relation also with its ability to create che-
mically active species), surface treatment [14] and gas
treatment [15].
This work focuses on the plasma-to-gas thermal trans-
fer, which is studied using both modeling and experi-
ments. Modeling involves a twofold description of the
TIA (electromagnetic and hydrodynamic), aiming to
maximize the microwave power coupled to the system
and to define the plasma and flow conditions that yield
an optimum transfer of thermal power from the plasma to
the gas. Experiments analyze the MPT efficiency and
stability, as a function of both the input power and the
input gas flow, providing a framework of conditions for
the simulations. Values for the plasma parameters (elec-
tron density and temperature, used as input data to the
model) and for the gas temperature (also at the wall, used
as boundary condition in the model) were obtained
mainly from optical emission spectroscopy (OES) diag-
nostics.
2. Experimental Set-Up
Figure 2 presents a schematic representation of the ex-
perimental set-up adopted here. Helium gas at atmos-
pheric pressure is injected into the inner conductor of the
coaxial waveguide and exits through its end nozzle. We
have used two nozzles, with 0.5 mm and 2 mm diameters,
to extend the range of gas flow from 0.5 to 10 L·min−1 (cf.
Section 4.1).
The microwaves propagate through a circuit of rec-
tangular waveguides after which they are transmitted to
the coaxial line. The system operates at f = 2.45 GHz
excitation frequency, for an incident power ranging from
100 W to 1 kW. The short circuit and the stubs (Figure 2)
enable to optimize the transition between the rectangular
waveguide and the coaxial structure, maximizing the
power coupled to the system. The power delivered by the
generator PG is controlled by a bi-directional coupler
which measures the incident Pinc and the reflected Pref
powers, by redirecting a small part of these powers to a
detector connected to a power meter. The power trans-
mitted to the system Ptrans= Pinc − Pref is then radiated
(Prad) or absorbed (Pabs) by the plasma electrons

22
0
22
2
e
abs
e
ne E
Pm


 (1)
In Equation (1) e and me are the electron charge and
mass, respectively, ν(s−1) ~ 6.8  10−8 N (cm−3) [16] is the
electron-neutral collision frequency (with N the gas den-
sity), ω = 2f, E0 is the amplitude of the wave electric
field and V is the plasma volume.
The plasma is launched into a quartz tube of 5 cm in
diameter and 40 cm in length, with an open-end to pre-
vent gas recirculation (thus favoring flow stability). The
quartz tube limits the contamination of the flowing he-
lium by the surrounding atmospheric air, providing more
definite boundary conditions for the simulations (see Ap-
pendix).
The TIA produces high-luminosity plasmas with a
maximum charged particle density at the nozzle’s exit [8].
For the work conditions considered here, the plasma di-
mensions vary between 0.5 mm and 2 mm in diameter
(nozzle sizes) and between 5 mm and 7 cm in length. The
radiation emitted by the plasma is collected by two lenses
into an optical fiber and then it is transmitted to a spec-
trometer (HR 460 Jobin-Yvon) for OES measurements
(cf. Section 4.2 for a description of the optical diagnos-
tics). The lenses enable to magnify the plasma by a factor
between 2 and 4, allowing focusing a cross section of the
plasma onto the fiber entrane slit, integrating about 3 c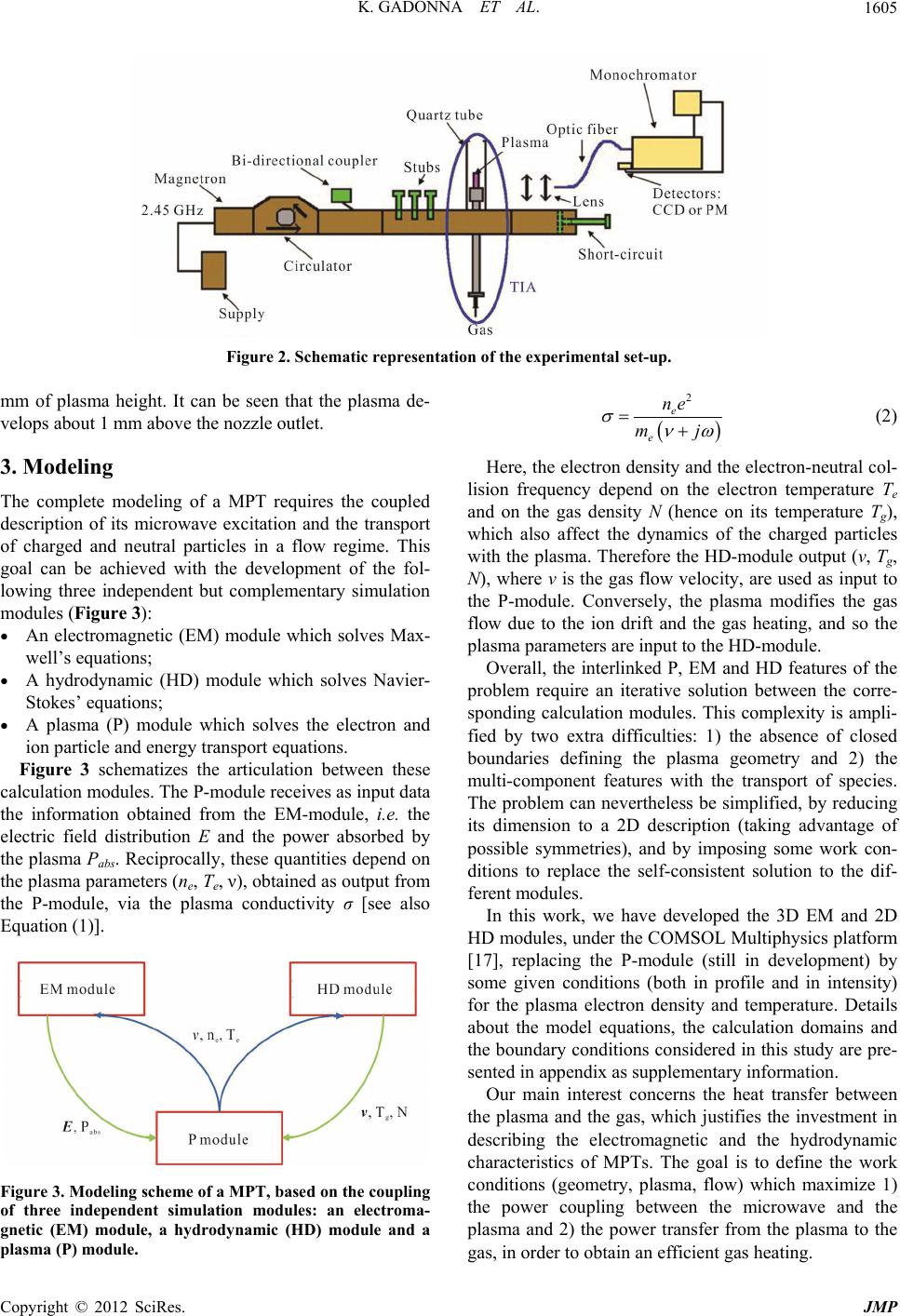

K. GADONNA ET AL. 1605
Figure 2. Schematic representation of the experimental set-up.
mm of plasma height. It can be seen that the plasma de-
velops about 1 mm above the nozzle outlet.

3. Modeling
The complete modeling of a MPT requires the coupled
description of its microwave excitation and the transport
of charged and neutral particles in a flow regime. This
goal can be achieved with the development of the fol-
lowing three independent but complementary simulation
modules (Figure 3):
 An electromagnetic (EM) module which solves Max-
well’s equations;
 A hydrodynamic (HD) module which solves Navier-
Stokes’ equations;
 A plasma (P) module which solves the electron and
ion particle and energy transport equations.
Figure 3 schematizes the articulation between these
calculation modules. The P-module receives as input data
the information obtained from the EM-module, i.e. the
electric field distribution E and the power absorbed by
the plasma Pabs. Reciprocally, these quantities depend on
the plasma parameters (ne, Te, ν), obtained as output from
the P-module, via the plasma conductivity σ [see also
Equation (1)].
Figure 3. Modeling scheme of a MPT, based on the coupling
of three independent simulation modules: an electroma-
gnetic (EM) module, a hydrodynamic (HD) module and a
plasma (P) module.
2
e
e
ne
mj
 (2)



Here, the electron density and the electron-neutral col-
lision frequency depend on the electron temperature Te
and on the gas density N (hence on its temperature Tg),
which also affect the dynamics of the charged particles
with the plasma. Therefore the HD-module output (v, Tg,
N), where v is the gas flow velocity, are used as input to
the P-module. Conversely, the plasma modifies the gas
flow due to the ion drift and the gas heating, and so the
plasma parameters are input to the HD-module.
Overall, the interlinked P, EM and HD features of the
problem require an iterative solution between the corre-
sponding calculation modules. This complexity is ampli-
fied by two extra difficulties: 1) the absence of closed
boundaries defining the plasma geometry and 2) the
multi-component features with the transport of species.
The problem can nevertheless be simplified, by reducing
its dimension to a 2D description (taking advantage of
possible symmetries), and by imposing some work con-
ditions to replace the self-consistent solution to the dif-
ferent modules.
In this work, we have developed the 3D EM and 2D
HD modules, under the COMSOL Multiphysics platform
[17], replacing the P-module (still in development) by
some given conditions (both in profile and in intensity)
for the plasma electron density and temperature. Details
about the model equations, the calculation domains and
the boundary conditions considered in this study are pre-
sented in appendix as supplementary information.
Our main interest concerns the heat transfer between
the plasma and the gas, which justifies the investment in
describing the electromagnetic and the hydrodynamic
characteristics of MPTs. The goal is to define the work
conditions (geometry, plasma, flow) which maximize 1)
the power coupling between the microwave and the
plasma and 2) the power transfer from the plasma to the
gas, in order to obtain an efficient gas heating.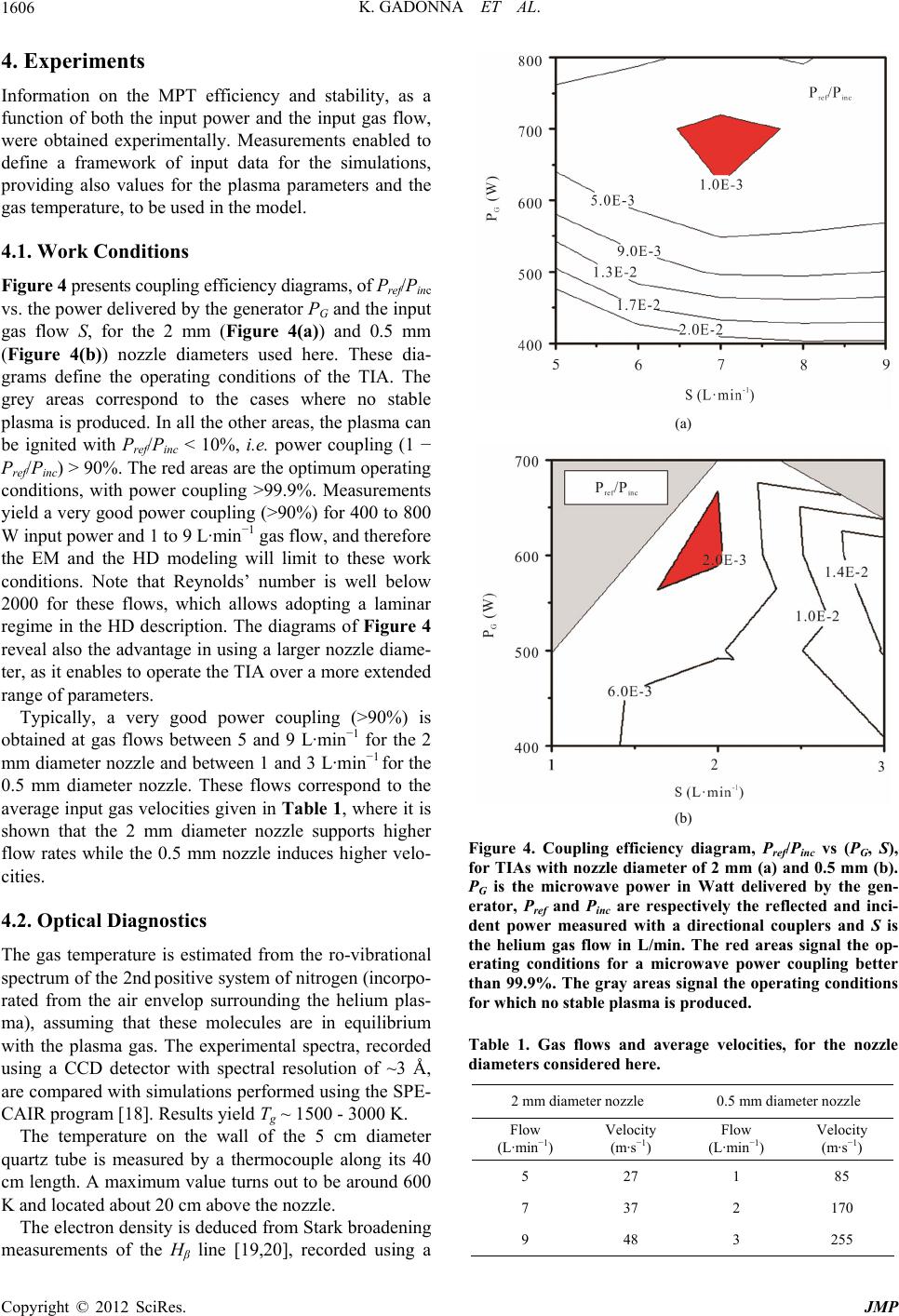

K. GADONNA ET AL. 1606
4. Experiments
Information on the MPT efficiency and stability, as a
function of both the input power and the input gas flow,
were obtained experimentally. Measurements enabled to
define a framework of input data for the simulations,
providing also values for the plasma parameters and the
gas temperature, to be used in the model.
4.1. Work Conditions
Figure 4 presents coupling efficiency diagrams, of Pref/Pinc
vs. the power delivered by the generator PG and the input
gas flow S, for the 2 mm (Figure 4(a)) and 0.5 mm
(Figure 4(b)) nozzle diameters used here. These dia-
grams define the operating conditions of the TIA. The
grey areas correspond to the cases where no stable
plasma is produced. In all the other areas, the plasma can
be ignited with Pref/Pinc < 10%, i.e. power coupling (1 −
Pref/Pinc) > 90%. The red areas are the optimum operating
conditions, with power coupling >99.9%. Measurements
yield a very good power coupling (>90%) for 400 to 800
W input power and 1 to 9 L·min−1 gas flow, and therefore
the EM and the HD modeling will limit to these work
conditions. Note that Reynolds’ number is well below
2000 for these flows, which allows adopting a laminar
regime in the HD description. The diagrams of Figure 4
reveal also the advantage in using a larger nozzle diame-
ter, as it enables to operate the TIA over a more extended
range of parameters.
Typically, a very good power coupling (>90%) is
obtained at gas flows between 5 and 9 L·min−1 for the 2
mm diameter nozzle and between 1 and 3 L·min−1 for the
0.5 mm diameter nozzle. These flows correspond to the
average input gas velocities given in Table 1, where it is
shown that the 2 mm diameter nozzle supports higher
flow rates while the 0.5 mm nozzle induces higher velo-
cities.
4.2. Optical Diagnostics
The gas temperature is estimated from the ro-vibrational
spectrum of the 2nd positive system of nitrogen (incorpo-
rated from the air envelop surrounding the helium plas-
ma), assuming that these molecules are in equilibrium
with the plasma gas. The experimental spectra, recorded
using a CCD detector with spectral resolution of ~3 Å,
are compared with simulations performed using the SPE-
CAIR program [18]. Results yield Tg ~ 1500 - 3000K.
The temperature on the wall of the 5 cm diameter
quartz tube is measured by a thermocouple along its 40
cm length. A maximum value turns out to be around 600
K and located about 20 cm above the nozzle.
The electron density is deduced from Stark broadening
measurements of the Hβ line [19,20], recorded using a
(a)
(b)
Figure 4. Coupling efficiency diagram, Pref/Pinc vs (PG, S),
for TIAs with nozzle diameter of 2 mm (a) and 0.5 mm (b).
PG is the microwave power in Watt delivered by the gen-
erator, Pref and Pinc are respectively the reflected and inci-
dent power measured with a directional couplers and S is
the helium gas flow in L/min. The red areas signal the op-
erating conditions for a microwave power coupling better
than 99.9%. The gray areas signal the operating conditions
for which no stable plasma is produced.
Table 1. Gas flows and average velocities, for the nozzle
diameters considered here.
2 mm diameter nozzle 0.5 mm diameter nozzle
Flow
(L·min−1)
Velocity
(m·s−1)
Flow
(L·min−1)
Velocity
(m·s−1)
5 27 1 85
7 37 2 170
9 48 3 255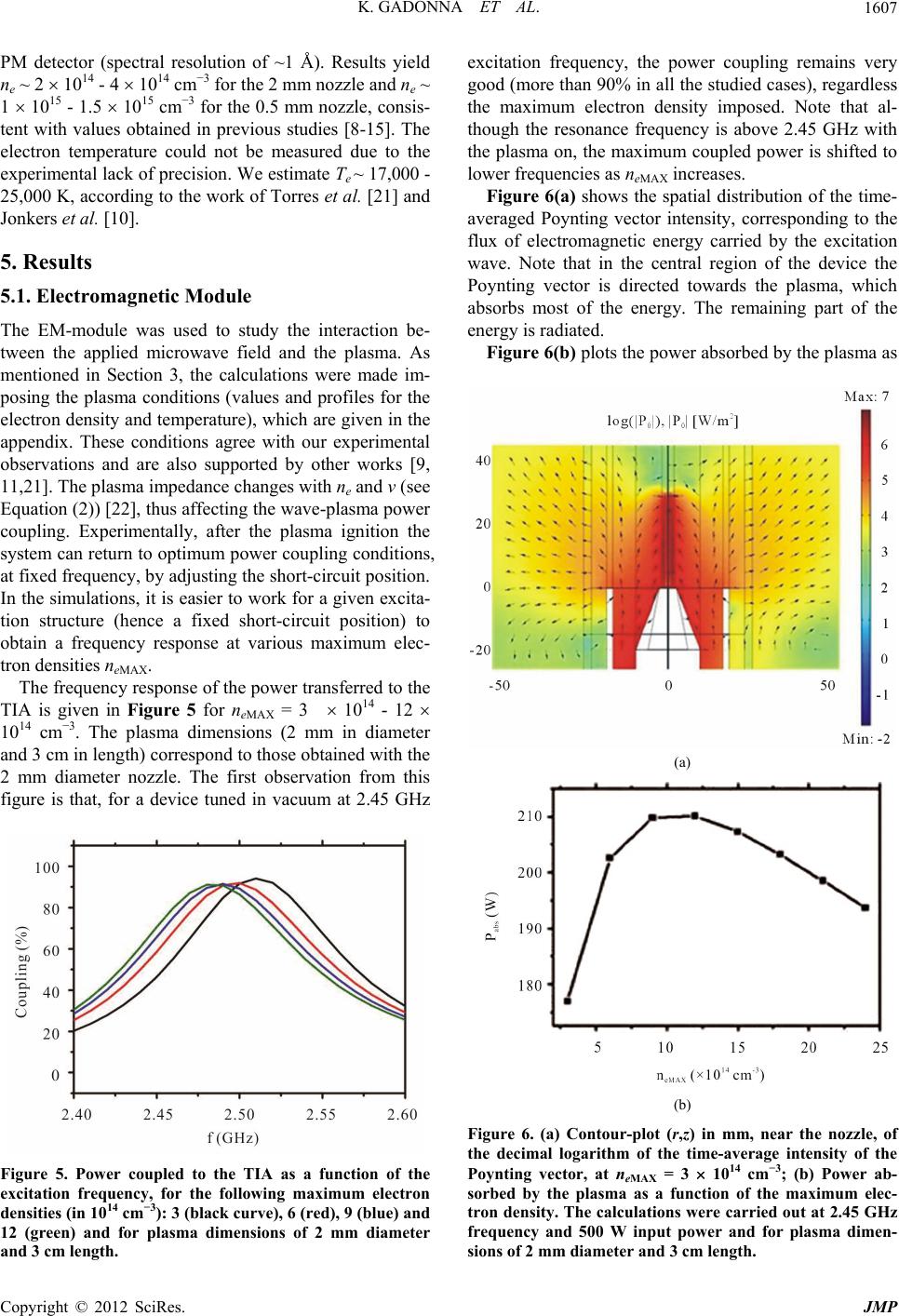

K. GADONNA ET AL. 1607
PM detector (spectral resolution of ~1 Å). Results yield
ne ~ 2  1014 - 4  1014 cm−3 for the 2 mm nozzle and ne ~
1  1015 - 1.5  1015 cm−3 for the 0.5 mm nozzle, consis-
tent with values obtained in previous studies [8-15]. The
electron temperature could not be measured due to the
experimental lack of precision. We estimate Te ~ 17,000 -
25,000 K, according to the work of Torres et al. [21] and
Jonkers et al. [10].
5. Results
5.1. Electromagnetic Module
The EM-module was used to study the interaction be-
tween the applied microwave field and the plasma. As
mentioned in Section 3, the calculations were made im-
posing the plasma conditions (values and profiles for the
electron density and temperature), which are given in the
appendix. These conditions agree with our experimental
observations and are also supported by other works [9,
11,21]. The plasma impedance changes with ne and ν (see
Equation (2)) [22], thus affecting the wave-plasma power
coupling. Experimentally, after the plasma ignition the
system can return to optimum power coupling conditions,
at fixed frequency, by adjusting the short-circuit position.
In the simulations, it is easier to work for a given excita-
tion structure (hence a fixed short-circuit position) to
obtain a frequency response at various maximum elec-
tron densities neMAX.
The frequency response of the power transferred to the
TIA is given in Figure 5 for neMAX = 3  1014 - 12 
1014 cm−3. The plasma dimensions (2 mm in diameter
and 3 cm in length) correspond to those obtained with the
2 mm diameter nozzle. The first observation from this
figure is that, for a device tuned in vacuum at 2.45 GHz
Figure 5. Power coupled to the TIA as a function of the
excitation frequency, for the following maximum electron
densities (in 1014 cm−3): 3 (black curve), 6 (red), 9 (blue) and
12 (green) and for plasma dimensions of 2 mm diameter
and 3 cm length.
excitation frequency, the power coupling remains very
good (more than 90% in all the studied cases), regardless
the maximum electron density imposed. Note that al-
though the resonance frequency is above 2.45 GHz with
the plasma on, the maximum coupled power is shifted to
lower frequencies as neMAX increases.
Figure 6(a) shows the spatial distribution of the time-
averaged Poynting vector intensity, corresponding to the
flux of electromagnetic energy carried by the excitation
wave. Note that in the central region of the device the
Poynting vector is directed towards the plasma, which
absorbs most of the energy. The remaining part of the
energy is radiated.
Figure 6(b) plots the power absorbed by the plasma as
(a)
(b)
Figure 6. (a) Contour-plot (r,z) in mm, near the nozzle, of
the decimal logarithm of the time-average intensity of the
Poynting vector, at neMAX = 3  1014 cm−3; (b) Power ab-
sorbed by the plasma as a function of the maximum elec-
tron density. The calculations were carried out at 2.45 GHz
frequency and 500 W input power and for plasma dimen-
sions of 2 mm diameter and 3 cm length.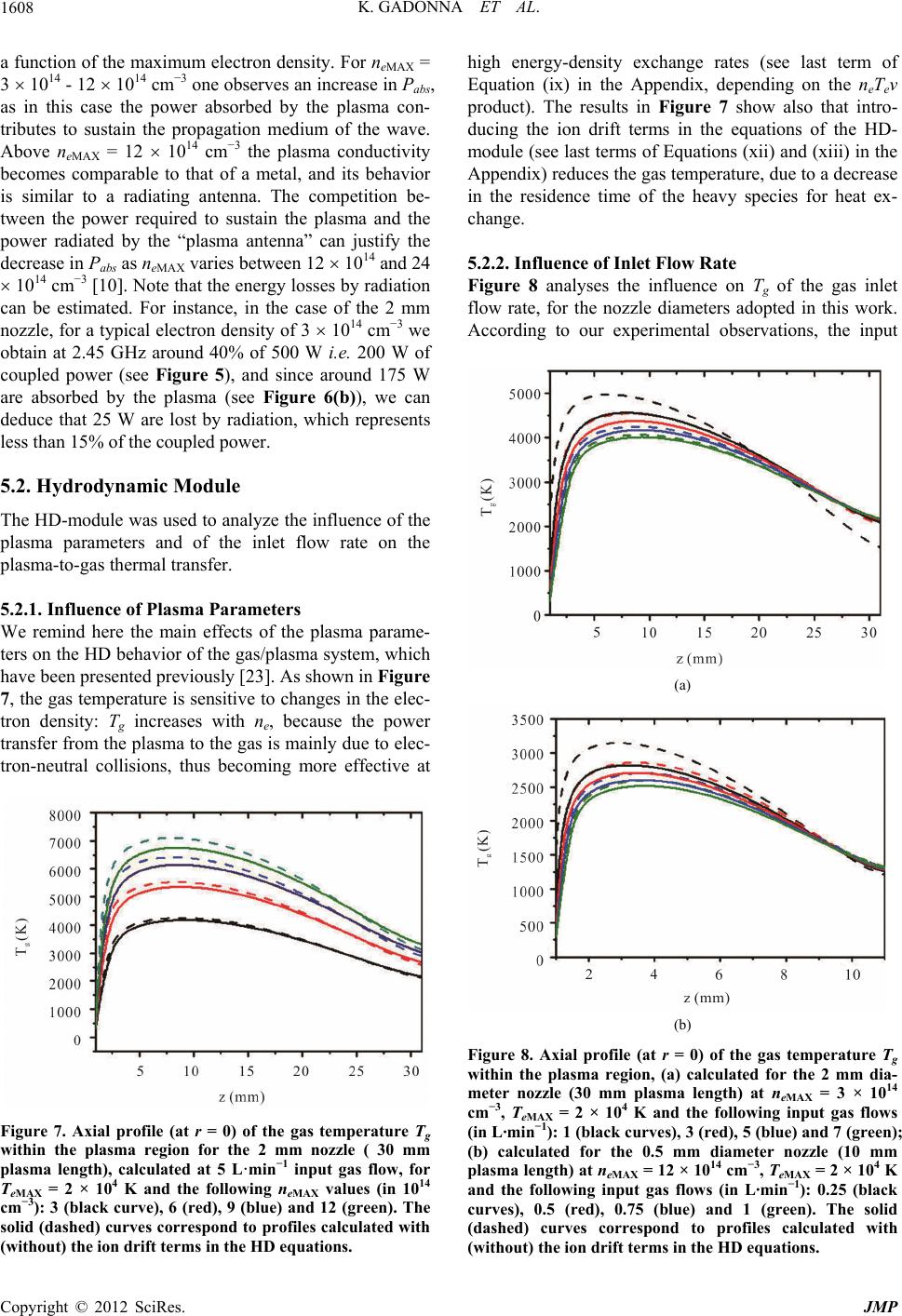

K. GADONNA ET AL. 1608
a function of the maximum electron density. For neMAX =
3  1014 - 12  1014 cm−3 one observes an increase in Pabs,
as in this case the power absorbed by the plasma con-
tributes to sustain the propagation medium of the wave.
Above neMAX = 12  1014 cm−3 the plasma conductivity
becomes comparable to that of a metal, and its behavior
is similar to a radiating antenna. The competition be-
tween the power required to sustain the plasma and the
power radiated by the “plasma antenna” can justify the
decrease in Pabs as neMAX varies between 12  1014 and 24
 1014 cm−3 [10]. Note that the energy losses by radiation
can be estimated. For instance, in the case of the 2 mm
nozzle, for a typical electron density of 3  1014 cm−3 we
obtain at 2.45 GHz around 40% of 500 W i.e. 200 W of
coupled power (see Figure 5), and since around 175 W
are absorbed by the plasma (see Figure 6(b)), we can
deduce that 25 W are lost by radiation, which represents
less than 15% of the coupled power.
5.2. Hydrodynamic Module
The HD-module was used to analyze the influence of the
plasma parameters and of the inlet flow rate on the
plasma-to-gas thermal transfer.
5.2.1. Influence of Plasma Parameters
We remind here the main effects of the plasma parame-
ters on the HD behavior of the gas/plasma system, which
have been presented previously [23]. As shown in Figure
7, the gas temperature is sensitive to changes in the elec-
tron density: Tg increases with ne, because the power
transfer from the plasma to the gas is mainly due to elec-
tron-neutral collisions, thus becoming more effective at
Figure 7. Axial profile (at r = 0) of the gas temperature Tg
within the plasma region for the 2 mm nozzle ( 30 mm
plasma length), calculated at 5 L·min−1 input gas flow, for
TeMAX = 2 × 104 K and the following neMAX values (in 1014
cm−3): 3 (black curve), 6 (red), 9 (blue) and 12 (green). The
solid (dashed) curves correspond to profiles calculated with
(without) the ion drift terms in the HD equations.
high energy-density exchange rates (see last term of
Equation (ix) in the Appendix, depending on the neTeν
product). The results in Figure 7 show also that intro-
ducing the ion drift terms in the equations of the HD-
module (see last terms of Equations (xii) and (xiii) in the
Appendix) reduces the gas temperature, due to a decrease
in the residence time of the heavy species for heat ex-
change.
5.2.2. Influence of Inlet Flow Rate
Figure 8 analyses the influence on Tg of the gas inlet
flow rate, for the nozzle diameters adopted in this work.
According to our experimental observations, the input
(a)
(b)
Figure 8. Axial profile (at r = 0) of the gas temperature Tg
within the plasma region, (a) calculated for the 2 mm dia-
meter nozzle (30 mm plasma length) at neMAX = 3 × 1014
cm−3, TeMAX = 2 × 104 K and the following input gas flows
(in L·min−1): 1 (black curves), 3 (red), 5 (blue) and 7 (green);
(b) calculated for the 0.5 mm diameter nozzle (10 mm
plasma length) at neMAX = 12 × 1014 cm−3, TeMAX = 2 × 104 K
and the following input gas flows (in L·min−1): 0.25 (black
curves), 0.5 (red), 0.75 (blue) and 1 (green). The solid
(dashed) curves correspond to profiles calculated with
(without) the ion drift terms in the HD equations.

K. GADONNA ET AL. 1609
gas flows are lower (see Section 4.1), the maximum elec-
tron density is higher and the plasma length is shorter for
the smaller diameter nozzle.
By analyzing each Figures 8(a) and (b) one concludes
that an increase in the input gas flow reduces the effici-
ency of heat transfer between the gas and the plasma,
leading to longer relaxation lengths in the axial direction
for the gas temperature profile and to a reduction in its
maximum value. For the fixed ne and Te profiles consi-
dered, the maximum gas temperature in the axial direc-
tion is located around 8 - 10 mm for the 2 mm diameter
nozzle and near 3 - 4 mm for the 0.5 mm diameter nozzle,
after the position of neMAX (at z = 1 mm, see Appendix).
By comparing Figures 8(a) and (b) one observes that
the 2 mm diameter nozzle allows obtaining higher gas
temperatures, although the density is lower for this noz-
zle. This low neMAX value is compensated by the lower
relaxation lengths (lower gas velocity, see Table 1) in
this case even if the gas flow is higher, due to larger
nozzle diameter, yielding an overall increase in Tg. This
point will be discussed in the experimental temperature
results (Section 5.3).
These observations show that the HD features of the
gas/plasma system, and particularly the definition of the
gas temperature, are the combined result of local electron
heating (via electron-neutral collisions) and non-local
heat transport (via convection and ion drift effects). Note
that ion drift effects are more important at low input gas
flows, for which the relative influence of these terms is
enhanced.
5.3. Experimental Gas Temperature
Figure 9 presents experimental values of Tg, obtained by
OES of the ro-vibrational band of nitrogen near the noz-
zle (see Section 4.2), as a function of the input gas flow
for various input powers and for the nozzle diameters
considered here. An observation of this figure reveals
that: 1) the gas temperature is higher when the TIA ope-
rates with the larger 2 mm diameter nozzle; 2) Tg de-
creases when the flow increases and/or the input power
decreases. The latter results are obvious for the 0.5 mm
diameter nozzle, and can be drawn also for the 2 mm one
at low input gas flows, in which case there is less com-
petition between the effects of the flow and the input
power (or the electron density) to define the gas tem-
perature value.
The previous observations are in qualitative agreement
with the simulation results presented in Section 5.2.2, the
differences between the calculated and the measured Tg
absolute values being motivated (at least partially) by the
use of imposed plasma profiles in the simulations. This
quantitative disagreement can introduce also a discussion
about the experimental results, beyond the mere obser-
vation that measurements have a significant uncertainty,
confirmed by the error bars depicted in Figure 9. In fact,
measurements use the nitrogen dragged into the plasma
jet from the air envelope which surrounds it, meaning
that probably the experimental gas temperature does not
accurately account for the plasma-to-gas heat transfer
occurring near the discharge axis. Note that our intention
here was to probe the plasma as it is created, thus with
the molecular species coming from O2, N2, …, whose
presence is expected to introduce a significant difference
between the OES-diagnosed ro-vibrational temperature
and the pure helium gas temperature [24].
Figure 10 plots the measured gas temperature as a
function of the average input gas velocity, for the two
nozzle diameters adopted in this work. As mentioned in
Section 5.2.1, the gas temperature values are very sen-
sitive to the residence time of the heavy species for heat
exchange. Therefore, an increase in the gas velocity (due
to an increase in the flow and/or a reduction in the nozzle
(a)
(b)
Figure 9. Measured gas temperature Tg vs. input gas flow S,
for TIAs with nozzle diameters of 2 mm (a) and 0.5 mm (b),
obtained for the following PG values (in W): 400 (green
curves), 500 (blue), 600 (black) and 700 (red).

K. GADONNA ET AL. 1610
Figure 10. Measured gas temperature Tg vs. average input
gas velocity <vi>, for TIAs with nozzle diameters of 0.5 mm
(dashed lines) and 2 mm (solid lines) for microwave powers
of 600 W (black) and 700 W (red).
diameter, see Table 1), is responsible for a decrease in
the residence time (typically of ~1 ms and ~0.1 ms for
the 2 mm and 0.5 mm nozzle diameters, respectively, at 5
and 1 L·min−1 input gas flow), thus for a reduction in Tg
as observed in Figure 10.
6. Conclusions
The work presented in this paper was devoted to the
study of plasmas created by microwave (2.45 GHz fre-
quency) axial injection torches (TIA), running in atmo-
spheric helium in air, in order to study the plasma-to-gas
energy transfer for gas heating. The work adopted two
complementary approaches based on simulations and
experiments.
The TIA is a very complex discharge due to the many
parameters involved in its operation: dimensions, gas
flow, power input. The plasma obtained is not in ther-
modynamic equilibrium and is very inhomogeneous. In
addition, it interacts with the surrounding external me-
dium (air), even if the plasma is launched into some con-
finement chamber, such as a quartz tube. The present stu-
dies were conducted to maximize the coupling between
the microwave power and the plasma and to define the
optimum plasma and flow operating conditions for plas-
ma-to-gas heat transfer.
Modeling involved the development of electromagnetic
(EM) and hydrodynamic (HD) models to analyze the in-
fluence of the plasma parameters on the microwave power
absorbed by the plasma and on the gas temperature.
Experiments analyzed the torch efficiency and stability,
as a function of both the input power and the input gas
flow, providing a framework of conditions for the simu-
lations. Values for the plasma parameters (electron den-
sity and temperature, used as input data to the model) and
for the gas temperature (also at the wall, used as bound-
ary condition in the model) were obtained mainly from
optical emission spectroscopy diagnostics.
Results yielded a good coupling efficiency (>90%) of
the TIA for input powers of 400-800 W (corresponding to
electron densities of 1014 - 1015 cm−3 and estimated elec-
tron temperatures of 17,000 - 25,000 K) and for input gas
flows of 5 - 9 L·min−1 (for a nozzle with 2 mm in dia-
meter) and of 1 - 3 L·min−1 (for another with 0.5 mm).
Under these conditions, simulations showed that the
electron density affects both the power absorbed by the
plasma and the gas temperature, the latter being en-
hanced by higher electron energy densities transferred to
the gas by electron-neutral collisions. It was also found
that by reducing the input gas velocity one increases the
residence time of heavy species for collisional heat ex-
change, thus increasing the gas temperature. The TIA
with the 2 mm diameter nozzle, for which the gas veloci-
ties are lower (and thus the residence time of species is
longer), favors gas heating although the electron density
is lower in this case.
A comparison between calculations and measurements
of the gas temperature provided good qualitative agree-
ment for the influence of the plasma parameters and the
gas flow on results. However, model predictions for the
gas temperature overestimate its measurements probably
due to a combination of different reasons, such as: 1) the
dimensions and parameters characterizing the plasma
(density and temperature) were not self-consistently cal-
culated, and remained fixed for the different work con-
ditions considered (microwave power and gas flow); 2)
the experimental gas temperatures were obtained from
the ro-vibrational spectrum of the second positive system
of N2, dragged into the helium plasma jet from its sur-
rounding air envelop. The model evaluates the gas tem-
perature at the plasma center (assumed hotter) and does
not account for the incorporation of molecular species
(which may decrease the gas temperature value).
Overall, the present work reveals the high potential of
microwave TIAs for gas heating, demonstrating the feasi-
bility of its stable operation, at low input powers and
moderate gas flows, to obtain gas temperatures of 3000 -
4000 K.
REFERENCES
[1] C. Tendero, C. Tixier, P. Tristant, J. Demaison and P.
Leprince, “Atmospheric Pressure Plasmas: A Review,”
Spectrochimica Acta Part B: Atomic Spectroscopy, Vol.
61, No. 1, 2006, pp. 2-30.
doi:10.1016/j.sab.2005.10.003
[2] N. Azouz, S. Chaabani, J. Lerbet and A. Abichou, “Com-
putation of the Added Masses of an Unconventional Air-
ship,” Journal of Applied Mathematics, Vol. 2012, 2012,
Article ID: 714627.
[3] R. B. Bird, W. E. Steward and E. N. Lightfoot, “Trans-
port phenomena,” John Wiley, Hoboken, 1960.
[4] P. Fauchais and A. Vardelle, “Thermal Plasmas,” IEEE

K. GADONNA ET AL. 1611
Transactions on Plasma Science, Vol. 25, No. 6, 1997, pp.
1258-1280. doi:10.1109/27.650901
[5] E. A. H. Timmermans, J. Jonkers, I. A. J. Thomas, A. Ro-
dero, M. C. Quintero, A. Sola, A. Gamero and J. A. M.
van der Mullen, “The Behavior of Molecules in Micro-
wave-Induced Plasmas Studied by Optical Emission Spe-
ctroscopy. 1. Plasmas at Atmospheric Pressure,” Spectro-
chimica Acta Part B: Atomic Spectroscopy, Vol. 53, No.
11, 1998, pp. 1553-1566.
doi:10.1016/S0584-8547(98)00186-4
[6] M. Moisan, Z. Zakrzewski, R. Pantel and P. Leprince, “A
Waveguide-Based Launcher to Sustain Long Plasma Co-
lumns through the Propagation of an Electromagnetic
Surface-Wave,” IEEE Transactions on Plasma Science,
Vol. 12, No. 3, 1984, pp. 203-214.
doi:10.1109/TPS.1984.4316320
[7] M. Moisan, G. Sauve, Z. Zakrzewski and J. Hubert, “An
Atmospheric Pressure Waveguidefed Microwave Plasma
Torch: The Tia Design,” Plasma Sources Science & Te-
chnology, Vol. 3, No. 4, 1994, pp. 584-592.
doi:10.1088/0963-0252/3/4/016
[8] A. Ricard, L. Stonge, H. Malvos, A. Gicquel, J. Hubert
and M. Moisan, “Torche à Plasma Micro-Onde: Deux
Configurations Complémentaires,” Journal de Physique
III, Vol. 5, No. 8, 1995, pp. 1269-1285.
doi:10.1051/jp3:1995185
[9] J. Torres, M. J. van de Sande, J. J. A. M. van der Mullen,
A. Gamero and A. Sola, “Stark Broadening for Simulta-
neous Diagnostics of the Electron Density and Tempera-
ture in Atmospheric Microwave Discharges,” Spectrochi-
mica Acta Part B: Atomic Spectroscopy, Vol. 61, No. 1,
2006, pp. 58-68. doi:10.1016/j.sab.2005.11.002
[10] J. Jonkers, J. M. deRegt, J. A. M. vanderMullen, H. P. C.
Vos, F. P. J. deGroote and E. A. H. Timmermans, “On the
Electron Temperatures and Densities in Plasmas Produced
by the ‘Torche a Injection Axiale’,” Spectrochimica Acta
Part B: Atomic Spectroscopy, Vol. 51, No. 11, 1996, pp.
1385-1392. doi:10.1016/0584-8547(96)01493-0
[11] M. Jimenez-Diaz, J. van Dijk and J. J. A. M. van der
Mullen, “Effect of Remote Field Electromagnetic Bound-
ary Conditions on Microwave-Induced Plasma Torches,”
Journal of Physics D: Applied Physics, Vol. 44, No. 16,
2011, Article ID: 165203.
doi:10.1088/0022-3727/44/16/165203
[12] L. L. Alves, R. Alvarez, L. Marques, S. J. Rubio, A. Ro-
dero and M. C. Quintero, “Modeling of an Axial Injec-
tion Torch,” European Physical Journal: Applied Physics,
Vol. 46, No. 2, 2009, p. 21001.
doi:10.1051/epjap/2009049
[13] E. A. H. Timmermans, F. P. J. de Groote, J. Jonkers, A.
Gamero, A. Sola and J. J. A. M. van der Mullen, “Atomic
Emission Spectroscopy for the On-Line Monitoring of In-
cineration Processes,” Spectrochimica Acta Part B: Ato-
mic Spectroscopy, Vol. 58, No. 5, 2003, pp. 823-836.
doi:10.1016/S0584-8547(03)00017-X
[14] S. S. Asad, C. Tendero, C. Dublanche-Tixier, P. Tristant,
C. Boisse-Laporte, O. Leroy and P. Leprince, “Effect of
Atmospheric Microwave Plasma Treatment on Organic
Lubricant on a Metallic Surface,” Surface & Coatings
Technology, Vol. 203, No. 13, 2009, pp. 1790-1796.
doi:10.1016/j.surfcoat.2008.12.026
[15] S. J. Rubio, A. Rodero and M. C. Quintero, “Application
of a Microwave Helium Plasma Torch Operating at At-
mospheric Pressure to Destroy Trichloroethylene,” Plas-
ma Chemistry and Plasma Processing, Vol. 28, No. 4,
2008, pp. 415-428. doi:10.1007/s11090-008-9133-3
[16] L. L. Alves and C. M. Ferreira, “Electron Kinetics in
Weakly Ionized Helium under DC and HF Applied Elec-
tric-fields,” Journal of Physics D: Applied Physics, Vol.
24, No. 4, 1991, pp. 581-592.
doi:10.1088/0022-3727/24/4/009
[17] http://www.comsol.com
[18] C. O. Laux, T. G. Spence, C. H. Kruger and R. N. Zare,
“Optical Diagnostics of Atmospheric Pressure Air Plas-
mas,” Plasma Sources Science & Technology, Vol. 12,
2003, pp. 125-138.
[19] M. A. Gigosos and V. Cardenoso, “New Plasma Diagno-
sis Tables of Hydrogen Stark Broadening Including Ion
Dynamics,” Journal of Physics B: Atomic Molecular and
Optical Physics, Vol. 29, No. 20, 1996, pp. 4795-4838.
doi:10.1088/0953-4075/29/20/029
[20] M. A. Gigosos, M. A. Gonzalez and V. Cardenoso, “Com-
puter Simulated Balmer-Alpha, -Beta and -Gamma Stark
Line Profiles for Non-Equilibrium Plasmas Diagnostics,”
Spectrochimica Acta Part B: Atomic Spectroscopy, Vol.
58, No. 8, 2003, pp. 1489-1504.
doi:10.1016/S0584-8547(03)00097-1
[21] J. Torres, O. Carabano, M. Fernandez, S. Rubio, R. Alva-
rez, A. Rodero, C. Lao, M. C. Quintero, A. Gamero and
A. Sola, “The Stark-Crossing Method for the Simultane-
ous Determination of the Electron Temperature and Den-
sity in Plasmas,” Journal of Physics Conference Series,
Vol. 44, No. 1, 2006, p. 70.
doi:10.1088/1742-6596/44/1/008
[22] M. A. Heald and C. B. Wharton, “Plasma Dignotics with
Microwave,” Wiley, New York, 1965.
[23] K. Gadonna, O. Leroy, T. Silva, P. Leprince, C. Boisse-
Laporte and L. L. Alves, “Hydrodynamic Study of a Mi-
crowave Plasma Torch,” European Physics Journal of
Applied Physics, Vol. 56, No. 2, 2011, p. 24008.
doi:10.1051/epjap/2011110161
[24] R. P. Cardoso, T. Belmonte, P. Keravec, F. Kosior and G.
Henrion, “Influence of Impurities on the Temperature of
an Atmospheric Helium Plasma in Microwave Resonant
Cavity,” Journal of Physics D: Applied Physics, Vol. 40,
No. 5, 2007, pp. 1394-1400.
doi:10.1088/0022-3727/40/5/012
[25] O. Schenk and K. Gärtner, “Solving Unsymmetric Sparse
Systems of Linear Equations with PARDISO,” Journal of
Future Generation Computer Systems, Vol. 20, No. 3,
2004, pp. 475-487.
[26] J. P. Berenger, “Three-Dimensional Perfectly Matched
Layer for the Absorption of Electromagnetic Waves,”
Journal of Computational Physics, Vol. 127, No. 2, 1996,
pp. 363-379. doi:10.1006/jcph.1996.0181
[27] T. Belmonte, R. P. Cardoso, G. Henrion and F. Kosior,
“Collisional-Radiative Modelling of a Helium Microwave
Plasma in a Resonant Cavity,” Journal of Physics D: Ap-
plied Physics, Vol. 40, No. 23, 2007, pp. 7343-7356.
doi:10.1088/0022-3727/40/23/015

K. GADONNA ET AL. 1612
Appendix
We present here an overview of the plasma description,
the domain of calculation used in the models, and equa-
tions and boundary conditions used in 3D electromag-
netic and 2D hydrodynamic models developed under the
COMSOL Multiphysics platform [17].
A.1. Plasma Description
For both electromagnetic and hydrodynamic models, the
plasma is defined by imposing its dimensions (length and
radius) and the axial and radial profiles of ne (r, z) =
neMAX ner(r)nez(z) and Te(r, z) = TeMAXTer(r)Tez(z), shown
in Figure 11. The axial profile of ne has been chosen in
accordance with measurements of optical emission
spectroscopy (Section 4.2). As it has been experimentally
observed, the beginning of the plasma is located 1 mm
above the nozzle. Te profiles are defined according to
(a)
(b)
Figure 11. Axial (a) and radial (b) profiles of the electron
density ne (black curves) and the electron temperature Te
(red curves). Rp and Lp are respectively the radius and the
length of the plasma.
[9,21]. The studied gas is helium at atmospheric pres-
sure.
Note that Rp, Lp, neMAX and TeMAX are input parameters
of the model. For all the simulations, we chose to fix Rp
equal to the nozzle radius and to take Lp in accordance
with the experiment. Typically Lp = 30 mm for the 2 mm
nozzle and Lp = 10 mm for the 0.5 mm nozzle.
A.2. Domain of Calculation
Figure 12 shows the computational domain on which the
EM and HD modules are solved. All the dimensions
introduced in the model are the same than the ones used
in our experiments.
For the EM module, we chose to build a 3D model of
the system to evaluate the coupling between the rec-
tangular waveguide, the coaxial transition and the plasma.
The tetrahedral meshing uses around 8  104 elements
for the whole computational domain with a refinement at
the nozzle exit, and in the plasma (typically 3  103
elements).
For the HD module, the plasma gas is injected with a
given velocity. We assumed (see Table 1) that the flow
remains laminar, which reduces the computation time by
adopting the axisymmetric 2D geometry in HD module.
The triangular meshing uses around 4  104 elements and
is refined in the plasma.
The solver used is PARDISO [25]. This direct solver
is widely used because of its ease in use and its robust-
ness: it does not need preconditioner. The convergence
criterion imposes relative errors between consecutive
calculations, typically less than 10−6.
A.3. Electromagnetic Module
The distribution of electromagnetic field in the presence
of the plasma is calculated by solving the Maxwell-
Ampere and Faraday-Maxwell equations:

t



 
E
HE (i)
t


 
H
E (ii)
E is the electric field [V/m], H is the magnetic field
[A/m], ε is the permittivity [F/m], μ is the permeability
[H/m] and σ is the conductivity of the medium [S/m].
By writing E(x, y, z, t) = E(x, y, z) exp(jωt) and H(x, y,
z, t) = H(x, y, z) exp(jωt), the two laws can be combined
to obtain the electric field wave equation:
2
0
0
10
r
r
j
k



 

 
 
 
EE (iii)
with μ = μ0μr and ε = ε0εr, where μ0 is the vacuum
permeability and ε0 the vacum permittivity. The relative u

K. GADONNA ET AL.1613
(a) (b)
Figure 12. Transverse section of the 3D (a) and 2D (b) computational domains adopted to solve the EM and HD modules,
showing the waveguides (in brown), the torch (in yellow), the quartz tube (in green), Teflon (in blue) and the plasma (in red).
All dimensions are in millimeters and the diagram is not to scale. The plasma is located 1 mm above the nozzle.
permittivity εr, the relative permeability μr and the
conductivity σ define the different environments. k0 is the
wave number in vacuum.
In these equations, the plasma is considered as a va-
cuum environment, having a conductivity due to free
charges (electrons), i.e.:
1
rp



(iv)
2
e
e
ne
mj
p




0 nE
 (v)
The values of permittivity, permeability and conduc-
tivity of the different media used in the model are given
in Table 2.
The boundary conditions for the waveguide and the
torch (made of brass) are those of a perfect electrical
conductor (), except for the section of the
guide (P.E. on Figure 12) where the microwave exci-
tation is applied. At this point, a condition of port for a
TE10 rectangular mode is imposed. Moreover, this confi-
guration, shown in Figure 12, is surrounded by a region
of PML type (Perfectly Matched Layers) [26], where
boundary conditions of diffusion (non-reflective) are
assumed. This consists in adding an artificial field which
Table 2. Permittivity, permeability and conductivity of air,
brass, teflon, quartz and plasma.
εr μr σ
Air 1 1 0
1.57 × 107 Brass 1 1
10−22 Teflon 2.8 1
10−18 Quartz 3.8 1
σp Plasma 1 1
absorbes the waves.
A.4. Hydrodynamic Module
This section focuses on the transport of heavy species,
neutral or ionized, whose masses are comparable. The
distributions of velocities and temperatures in the pre-
sence of the plasma are calculated by solving the well-
known Navier-Stokes equations:


00


 v (vi)


00 p


 vv τ (vii)

K. GADONNA ET AL. 1614

where ρ is the gas density, v0 is the gas velocity, p is the
gas pressure, is the viscosity tensor given by: τ
00
  τvv 0
2
3

 


vI
I
(viii)
where is the identity tensor.
The viscosity tensor accounts for the dynamic visco-
sity coefficient of the fluid η, which can be obtained by
the Chapman-Enskog theory using Lennard-Jones para-
meters [3].
The combination of the continuity Equation (vi) and
the momentum Equation (vii) provides a description of
the barycentric velocity, in terms of pressure gradient
and viscosity.
The gas flow is then completed by heat transfer using
the equation of energy conservation given by:

 
0
03
vg
e
g
ge
CT
m
Tp
 
 

 
v
vBeg
g
nkTT
M
  (ix)
where kB is the Boltzmann constant, Cv is the specific
heat of gas at constant volume, λg is the thermal conduc-
tivity and ν is the electron-neutral collision frequency. me,
ne and Te are respectively the electron mass, density and
temperature. λg depends on η [3] as following:
15
4
B
g
g
k
M
  (x)
where Mg is the mass of the gas neutrals (here helium).
Each term in Equation (ix) describes the different
means of energy exchange, i.e. from left to right of equa-
tion:
 convective processes (density difference, temperature
difference);
 heat conduction processes (collisions between par-
ticles of the same type);
 work of pressure forces;
 collisions between different particles (here heating of
helium gas by the electrons).
The energy Equation (ix) describes and predicts the
temperature of the flowing gas. It is coupled to the
Navier-Stokes Equations (vi) and(vii), which describe
the velocity fields. This coupling occurs through the con-
vective term and the work of pressure forces that involve
velocities. The Navier-Stokes equations are also coupled
to the energy equation because the gas properties (den-
sity, viscosity) depend on temperature.
All these equations have been established without
taking into account the helium ions whose mass is of the
same order than neutrals. As the ionisation degree is not
negligible in MPTs, we add the influence of ions on the
transport of heavy particles and the heat transfer to gas.
Equations (vi), (vii) and (ix) are then rewritten as fol-
lowing:


00


 v (xi)


00 idc
pen  vv τ
E
 (xii)





00
i
3
vggg
e
eBegdc
g
CT Tp
mnk TTe
M


 


vv
Γ
 
en
(xiii)
E
The ions influence occurs in the momentum equation
(Equation (xii)) with the ionic force term idc
E
and in
the energy equation (Equation (xiii)) with the Joule heat-
ing term idc
e
E
Γ.

dc
E
, ni and i are respectively the space charge
field, the ion density and the ion flow. They are calcu-
lated for ambipolar conditions:
Γ
B
ee
dc
e
kT n
en
E
ie
nn
ie an
D
(xiii)
(xiv)

 Γ (xv)
with


aBei
DkTeu (xvi)
the ambipolar diffusion coefficient and μiN the reduced
ion mobility.
In high temperature gas, both He+ and 2 He

are
present ([2 He

/He+] ~ 0.55 [27]). For simplification and
as a first approach we consider a single type of ion, He2+
(μiN = 4.49 × 1020 V−1·cm−1·s−1 [16]).
Equations (xi)-(xiii) are solved in order to study the
heat transfer from the plasma to the gas taking into ac-
Figure 13. Temperature profile imposed at r = 25 mm. For
0 mm ≤ z ≤ 525 mm: Tg(z) = 0.8 + 1.9z [m] – 4.3z [m]2. For z
≥ 525 mm, Tg = 290 K.

K. GADONNA ET AL. 1615
n
 At the exit (at the exit of the quartz tube z = (570 − 45)
= 525 mm): p = 1 atm and Tg = 290K;
count the influence of ions. We compared these results
with the ones obtained without the ions terms.
The boundary conditions used to solve the HD-module
are the following:
 Temperature of the quartz tube, taken as boundary
value for Tg at r = 25 mm, has been experimentally
measured using a thermocouple (Section 4.2) all
along the tube length (570 − 45) = 525 mm. It has
been found that this profile is quite the same for all
experimental conditions. A unique profile has been
then used as boundary condition for Tg at r = 25 mm.
This profile is shown in Figure 13. The TgMax value is
varying with experimental conditions. But, as it has
been found that it has not a great influence on model
results, it has been fixed to 600 K.
 on the axis (r = 0): axisymmetric conditions;


kT (convective flux) on the metallic parts of
the torch;
 v = 0 (“no-slip” condition) on all the walls;
 At the entrance (z = −45 mm, bottom left of Figure
12.b)), Tg is considered equals to room temperature
(290K) and the gas velocity is given by:

2
0
z
p
r
R









45 21
zi
vr v
  (xvii)