 Open Journal of Statistics, 2012, 2, 460-468 http://dx.doi.org/10.4236/ojs.2012.24058 Published Online October 2012 (http://www.SciRP.org/journal/ojs) An Application of Non-Linear Cobb-Douglas Production Function to Selected Manufacturing Industries in Bangladesh Md. Moyazzem Hossain1, Ajit Kumar Majumder2, Tapati Basak2 1Department of Statistics, Islamic University, Kushtia, Bangladesh 2Department of Statistics, Jahangirnagar University, Dhaka, Bangladesh Email: mmhrs.iustat@gmail.com, ajitm@ewubd.edu, tapati555@yahoo.com Received May 14, 2012; revised June 20, 2012; accepted July 2, 2012 ABSTRACT Recently, businessmen as well as industrialists are very much concerned about the theory of firm in order to make cor- rect decisions regarding what items, how much and how to produce them. All these decisions are directly related with the cost considerations and market situ ations where the firm is to be operated. In this rega rd, this paper should be help- ful in suggesting the most suitable functional form of production process for the major manufacturing industries in Bangladesh. This paper considers Cobb-Douglas (C-D) production func tion with additive error and multiplicative erro r term. The main purpose of this paper is to select the appropriate Cobb-Douglas production model for measuring the production process of some selected manufacturing industries in Bangladesh. We use different model selection criteria to compare the Cobb-Douglas production function with additive error term to Cobb-Douglas production function with multiplicative error term. Finally, we estimate the parameters of the production function by using optimization subroutine. Keywords: Cobb-Douglas Production Function; Newton-Raphson Method; Manufacturing Industry; Bangladesh 1. Introduction A developing country like Bangladesh which is facing enormous problems so far as industrialization policy is concerned does not follow the po licy of Marxian Economy, neither thus it strictly follow the policy of a Capitalist country. The economy of Bangladesh actually turned out to be a mixed economy since a long time. The industry sector was severely damaged during the war of liberation in 1971. After a series of adjustments and temporary changes in state policy, the government finally adopted a new industrial policy in 1982. Every industrialist tries to produce goods with maximum profit but with minimum cost. In order to do this, it has to be decided what to produce, how much to produce and how to produce. The industries need various inputs such as labor, raw material, machines etc. to produces goods. An i ndust ry ’s production cost depends on the quan tities of inputs it buy and on the prices of each input. Thus an industry needs to select the optimal combination of inputs, that is, the combination that enables it to produce th e desired level of output with minimum cost and hen ce with maximum profitab ility. So the main object ive of this pap er is to selec t the a p p r o p r i a t e Cobb-Douglas production function. We use differ en t mod el selection criteria to compare the Cobb-Douglas producti on function with additive error term to Cobb-Douglas pro- duction function with multiplicative error term. Finally, we estimate the parameters of the production function by using optimization subroutine . 2. Cobb-Douglas Production Function The Cobb-Douglas production function is the widely used function in Econometrics. A famous case is the wel l- known Cobb-Douglas production function introduced by Charles W. Cobb and Paul H. Douglas, although antici- pated by Knut Wicksell and, some have argued, J. H. Von Thünen [1]. They have estimated it after studying different industries in the world, for this it is used as a fairly universal law of production. The Cobb-Douglas production function with multipli- cative error term can be represented as, 3 2 1tttt pLKu t pL (2.1) where, is the output at time t; t is the Labor input; t is the Capital input; 1 is a constant; t is the random error term. u 2 and 3 are positive pa- rameters. C opyright © 2012 SciRes. OJS  MD. M. HOSSAIN ET AL. 461 The Cobb-Douglas production function with additive error term can be represented as, 3 2 tttt pLKu t p L 1 (2.2) where, is the output at time t; t is the Labor input; t is the Capital input; 1 is a constant; t is the random error term. u 2 and 3 are positive pa- rameters. 3. Literature Review Production functions for the industrial sector as a whole as well as for seven important industries in India are worked out based on cross-section data relating to indi- vidual firms for the two years 1951 and 1952 (V. N. Murti and V. K. Sastry) [2]. De-Min Wu [3], derives the exact distribution of the indirect least squares estimator of the coefficients of the Cobb-Douglas production func- tion within the context of a stochastic production model of Marschak-Andrews type. The stochastic term in Cobb- Douglas type models is either specified to be additive or multiplicative (Stephen M. Goldfeld and Richard E. Quandt) [4]. They developed a model in which a Cobb- Douglas type function is coupled with simultaneous multiplicative and additive errors. This specification is a natural generalization of the “pure” models in which either additive or multiplicative stochastic terms are intro- duced. A Cobb-Douglas type function with both multi- plicative and additive errors has been proposed by Gold- feld and Quandt [5]. They suggested a maximum likely- hood approach to the estimation of a Cobb-Douglas type model when the model includes both multiplicative and additive disturbance terms. As expected, an analytical expression for the solution to the maximization problem did not exist. Indeed, because of the complexity of the likelihood function, their maximization algorithm had to be used in conjunction with a numerical integration tech- nique. Kelejian [6] generalize and simplify the work by Goldfeld and Quandt [5]. Specifically, an estimation technique is suggested which does not require the speci- fication of the disturbance terms beyond their means and variances, which does not require the compounding of a maximization algorithm with a numerical integration technique, but yet leads to asymptotically efficient esti- mates of the parameters of the regression function. In addition, the procedure readily lends itself to interpreta- tion. For instance, it will become evident that if the dis- tribution of the multiplicative disturbance term is not known, the scale parameter of the model (unlike the other parameters) will not be identified. The origins of the Cobb-Douglas form date back to the seminal work of Cobb and Douglas [1], who used data for the US manu- facturing sector for 1899-1922 (although, as Brown [7]), Sandelin [8], and Samuelson [9], indicate, Wicksell should have taken the credit for its “discovery”, for he had been working with this form in the 19th century). Cheema [10], Kemal [11], and Wizarat [12], showed the performance of large-scale manufacturing sector of Pakistan. Moreover tax holidays also encourage invest- ment in the industrial sector. For example, Azhar and Sharif [13], and Bond [14], empirically proved the posi- tive correlation between tax holidays and industrial out- put. But it is also worth to note that tax rate and output of manufacturing sector are inversely related. The authors used the data of West Virginia State of United States. However, Radhu [15], showed the positive correlation between indirect tax rates an d prices of the commodities. Vijay K. Bhasin and Vijay K. Seth [16], estimate produc- tion functions for Indian manufacturing industries and to find whether plausible and meaningful estimates can be obtained for returns to scale, substitution, distribution, and efficiency parameters. Some studies are based on data collected through surveys specially designed for estimate the levels of technical efficiency (TE) (e.g., Lit- tle et al., [17], Page [18]). Many of the studies are con- cerned with estimating and explaining variations in TE only in Small-Scale Industrial Units by fitting either a deterministic or a stochastic production frontier (e.g., Bhavani [19], Goldar [20], Neogi and Ghosh [21], Ni- kaido [22]). A review of other studies in this area may be found in Goldar [23]. All these studies, however, use data relating to years prior to the economic reforms. For instance, Bhavani [19] uses data collected under the first Census of small scale industrial units in 197 3 to estimate the TE of firms at the 4-digit level indu stries of metal product groups by fitting a deterministic translog production frontier with three inputs-capital, labor and materials- and observes a very level of average efficiency across the four groups. Simi- larly, on the basis of the data made available by the Sec- ond All India Census of Small Scale Industrial Units in 1987-1988, Nikaido [22] fits a single stochastic produc- tion frontier, considering firms under all the 2-digit in- dustry groups and using intercept dummies to distinguish different industry groups. He finds little variation in TEs across industry groups and a high level of average TE in each industry groups. Neogi and Ghosh [21] examine the inetrtemporal movement of TE using panel industry-level summary data for the year s 1974-1975 to 1987-1988 and observe TEs to be falling over time. In recent years, there has been an increasing interest in the examination of productivity from different parts of the economy such as industry, agriculture, and services. Numerous studies have attempted to explain produ ctivity in the economic sector, for example, productivity growth in Swedish manufacturing (Carlsson [24]), the impact of regional investment incentives on employment and pro- Copyright © 2012 SciRes. OJS  MD. M. HOSSAIN ET AL. 462 ductivity in Canada (M. Daly, Gorman, Lenjosek, MacNevin, & Phiriyapreunt [25]), productivity and im- perfect competition in Italian firms (Contini, Revelli, & Cuneo [26]), explaining total factor productivity differ- entials in urban manufacturing of US (Mullen & Wil- liams, [27]). Total factor productivity growth in manu- facturing has been examined by applied parametric and non-parametric approaches. In most of the studies have used non-parametric approach, wherein total factor pro- ductivity growth has decomposed into efficiency change and technological change. Efficiency change measures “catching-up” to the isoquant while technological change measures shifts in the isoquant. For example, see Weber and Domazlicky [28]; Nemoto and Go to [29]; (Maniada- kis and Thanassoulis [30] and Radam [31]. The studies by Golder et al. [32], Lall and Rodrigo [33], and Mukherjee and Ray [34], however, relate to the post-reform era. Using panel data for 63 firms in the engineering industry from 1990-1991 to 1999-2000 drawn from the Prowess database (version 2001) of the Centre for Monitoring Indian Economy, Goldar et al. [32] fit a translog stochastic production frontier to esti- mate firm-level TE scores in each year. They find the mean TE of foreign firms to be higher than that of do- mestically owned firms but do not find any statistically significant variation in mean TE across public and pri- vate sector firms among the latter group. They can at- tempt to explain variation in TEs in terms of economic variables, including export and import intensity and the degree of vertical nitration. Lall and Rodrigo [33] ex- amine TE variation across four industrial sectors in In- dia during 1994 and consider TE in relation to scale, location extent of infrastructure investment and other determinants. Md. Zakir Hossain, M. Ishaq Bhatti, Md. Zulficar Ali, [35], reviews some models recently used in the literature and selects the most suitable one for measuring the pro- duction process of 21 major manufacturing industries in Bangladesh. In particular, they estimates and tests the coefficients of the production inputs for each of the se- lected manufacturing indu stries using Banglad esh Bureau of Statistics annual data over the period 1982-1983 through 1991-1992. Cheng-Ping Lin [36] analyzes the cost function of construction firms with due considera- tion of their available resources by using Cobb-Douglas Production and Cost Func tions. Moosup Jung, et al. [37] made a study on Total Factor Productivity of Korean Firms and Catching up with the Japanese Firms. They measured and compared the TFP of both Korean and Japanese listed firms of 1984 to 2004. They found that the average TFP of Korean firms grew about 44.1% be- tween 1984 and 2005, with 2.1% annual growth rates. Industry was observed to b e outstanding. Danish A. Hashim [38] made research on “Cost and Productivity in Indian Textiles” for Indian Council for Research on International Economic Relations. His ob- servations and findings are: there is an inverse relation- ship between the unit cost and productivity: Industry and States, which witnessed higher productivity (growth) experienced lower unit cost (growth) and vice-versa. Better capacity utilization, reductio ns in Nominal Rate of Protection and increased availability of electricity are found to be favorably affectin g the productivity in all the three industries. M. Z. Hossain and K. S. Al-Amri, [39] find that for most of the selected industries the C-D func- tion fits the data very well in terms of labor and capital elasticity, return to scale measurements, standard errors, economy of the industries, high value of R2 and rea- sonably good Durbin-Watson statistics. The estimated results suggest that the manufacturing industries of Oman generally seem to indicate the case of increasing return to scale. Of the nine industries, seven exhibit increasing return to scale and only the rest two show decreasing return to scale. They also find that no industry with con- stant return to scale. 4. Estimation Procedure Equation (2.1) is nearly always treated as a linear rela- tionship by making a logarithmic transformation, which yields: 12 3 logloglogloglog tttt pLKu logu 1 log (3.1) where, is treated as an additive random error with a zero mean. In this form the function is a single equation which is linear in the unknown parameters: , 2 and 3. In the case of Equation (2.2), the minimization of, 2 u is no longer a simple linear estimation problem. To estimate the production function we need to know different types of non-linear estimation. In non-linear model it is not possible to give a closed form expression for the estimates as a function of the sample values, i.e., the likelihood function or sum of squares cannot be transformed so that the normal equations are linear. The idea of using estimates that minimize the sum squared errors is a data-analytic idea, not a statistical idea; it does not depend on the statistical properties of the observations. Newton-Raphson method is one of the method which are used to estimate the parameters in non-linear system. 4.1. Newton-Raphson Method Newton-Raphson is one of the popular Gradient methods of estimation. In Newton-Raphson method we find the values of that maximize a twice differentiable con- cave function, the objective function g . In this me- Copyright © 2012 SciRes. OJS  MD. M. HOSSAIN ET AL. 463 g t thod we approximate at by Taylor series expansion up to the qu adratic terms 1 2 tt gg t tt t G H where, t i g t G is the gradient vector and 2 t ik g t H g is the Hessian matrix. This Hes- sian matrix is positive definite, the maximum of the ap- proximation occurs when its derivative is zero. tt tt GH 1 0 t t HG 1t (3.11) This gives us a way to compute 1 t t , the next value in iterations is, 1tt HG The iteration procedures continue until convergence is achieved. Near the maximum the rate of convergence is quadratic as define by 2 ˆˆ tt ii c 1 ii 0 for some when ct i is near i ˆ for all . Thus we get estimates i ˆi by Newton-Raphson methods. For the model (2.2), to estimate the parameters we minimize the following error sum squares 1 n t Sp 3 2 2 1ttt LK In case of nonlinear estimation we use the score vector and Hessian matrix. The elements of score vector are given below: 1 1 1 2* n tt t SpLK 33 22 * t tt LK 3 2 2 1 1 2** ln* n ttt t t S pLK L 3 2 1 tt LK 3 2 3 1 1 2** ln* n ttt t t S pLK K 3 2 1 tt LK Also the elements of Hessian matrix are given below: 3 2 2 2 21 1 2* n tt t SLK 33 22 33 22 2 1 1 12 1 2*ln ** *ln* n ttttt t tttt tt SLLKLK pLK LLK 33 22 33 22 2 1 1 13 1 2* ln** *ln * n ttttt t tttt tt SKLKLK pLK KLK 3 2 33 22 22 1 21 2 2 11 2*ln * *ln * n ttt t tttt tt SLLK pLKL LK 33 22 33 22 2 23 11 1 11 2*ln** ln* *ln*ln * n tttttt t ttttt tt S KLK LLK pLKKLLK 3 2 33 22 22 1 21 3 2 11 2* ln* *ln * n ttt t tttt tt SKLK pLKK LK Hence the Score vector is 123 ,, SSS G and Hessian matrix is 222 212 13 1 222 2 12 23 2 222 2 13 233 SSS SSS SSS H model. Some of these criteria are discuss below. 4.2. Model Selection Criteria To find the appropriate production function we use model selection criterion. The model that minimizes the criterion is the best model. The recent years several criteria for choosing among models have proposed. These entire take the form of residual sum of squares (ESS) multiplied by a penalty factor that depend on the complexity of the Copyright © 2012 SciRes. OJS  MD. M. HOSSAIN ET AL. 464 4.2.1. Finite Prediction Error (FPE) Akaike (1970) developed Finite Prediction Error proce- istic of this proce- dure, which is known as FPE. The stat dure can be represente d as, FPE ESS TK TT K whe of observations and re, T is the number is the number of estimated parameter (Ranathan [40]). Akaike (1974) also developed another procedure which The form of am 4.2.2. Akaike Inf orma ti on Cri teria (AI C ) is known as Akaike Information Criteria. this statistic is given below, 2 AIC e T T n me variables are droppe d ( R amanathan [40]). Q) Criterion Hunnan and Quinn (1979) developed a procedure which is procedure ESS The value of AIC deceases wheso 4.2.3. Hunnan and Quinn (H is known as HQ criteria. The statistic of th can be represented as 2 HQ kT ESS lnT T The value of HQ will decrease provided there are at observations (Ramanathan [40]). Craven and Wahba (1978) developed a procedure which C criteria. The form of least 16 4.2.4. SCHWARZ Criterion is known as SCHWARZ BI this procedure is represented as SCHWARZ T E S ST T also decrease provided there are at least 8 observations (Ramanathan [40]). Craven and Wahba (1981) developed a procedure which teria. The form of this pro- The value of SCHWARZ will 4.2.5. SH IBATA Criterion is known as SHIBATA cri cedure is represented as 2 SHIBATA ESS TK TT . When some vari ables dropped SHIBATA will increase (Ramanathan [40] ross Validatio n (GC V ) Generalized Cross Validation (GCV) is another proce- (1979). ). 4.2.6. Generali zed C dure which is developed by Craven and Wahba The form of the statistic is given below 2 GCV 1 ESS K TT If one or more variables are dropped ten GCV will decrease (Ramanathan [40]). The model selection criteria Rice developed by Craven e form of this criterion can be rep- h 4.2.7. Rice Criterion and Wahba (1984). Th resented as 1 2ESSK RICE 1 TT . (Ramanathan [40]). iterion The form of this criterion can be represented as 4.2.8. SGMASQ Cr 1 SGMASQ 1 ESSK . TT If SGMASQ decreases (that is 2 R incses) when one or more variable dropped, then GCV and RICE will also decreas). stries of Bangladesh for This Study ang- ladladesh Census of Leather Products; r; s (Wooden); ; cts; Industries; s; 6. In case of Cobb-Douglas production function with multi- rea es (Ramanathan [40] 5. Selected Manufacturing Indu In recent publications of “Statistical Yearbook of B esh [41]” and “Report on Bang Manufacturing Industries (CMI) [42]” published by BBS, we get the p ublished secondary d ata for the majo r manu- facturing industries of Bangladesh over the period 1978- 2002. We have chosen the following manufacturing in- dustries for the ongoing analysis. 1) Manufacturing of Textile; 2) Manufacturing of Leather & 3) Manufacturing of Leather Footwea 4) Manufacturing of Wood & Cork Products; 5) Manufacturing of Furniture & Fixture 6) Manufacturing of Paper & Paper Products; 7) Manufacturing of Printing & Publications; 8) Manufacturing of Drugs & Pharmaceuticals 9) Manufacturing of Industrial Chemical; 10) Manufacturing of Plastic Products; 11) Manufacturing of Glass & Glass Produ 12) Manufacturing of Iron & Steel Basic 13) Manufacturing of Fabricated Metal Product 14) Manufacturing of Tra ns p ort Eq uipment; 15) Manufacturing of Beverage; 16) Manufacturing of To bacc o. Results and Discussion Copyright © 2012 SciRes. OJS 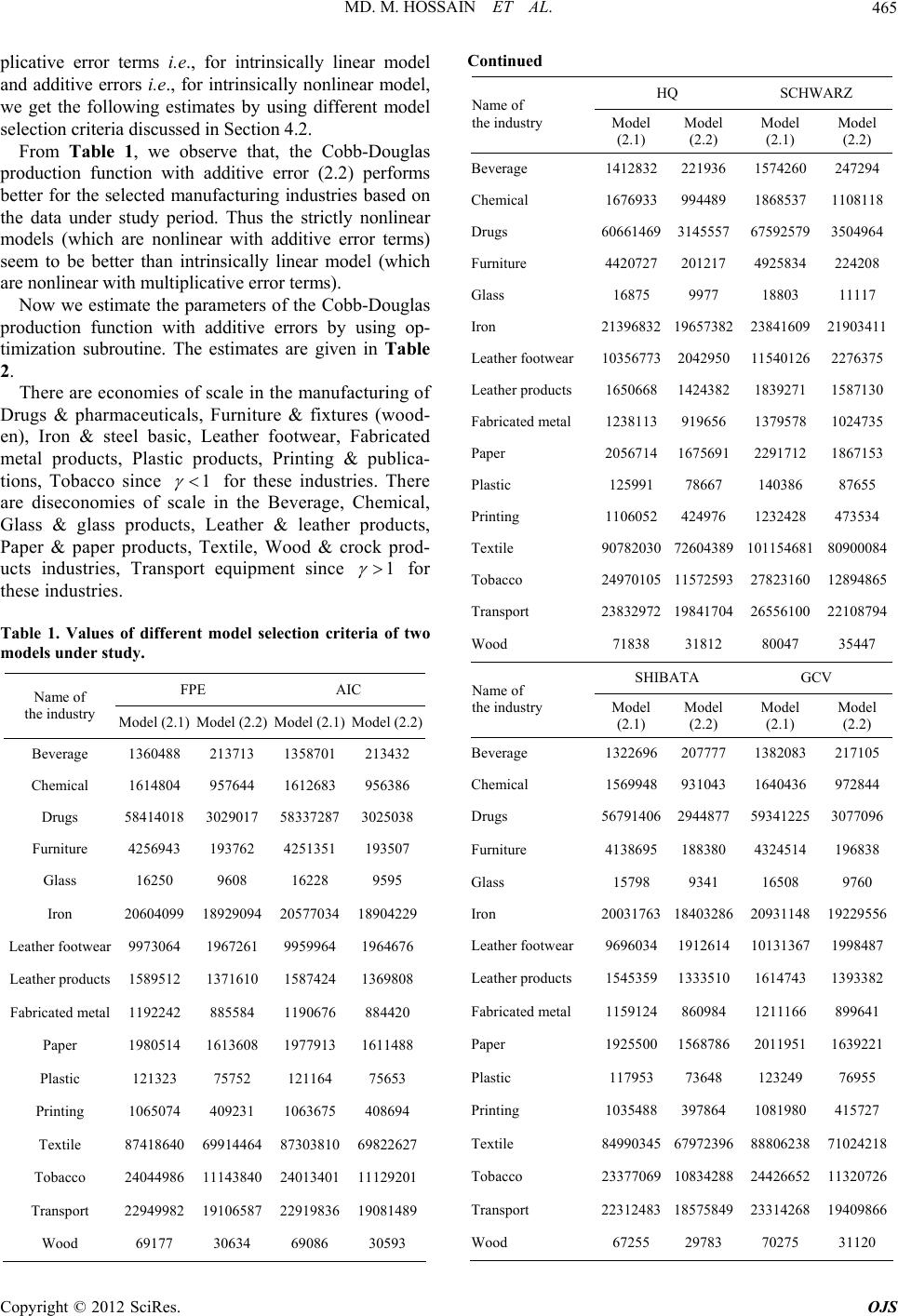 MD. M. HOSSAIN ET AL. 465 Con HQ WA plicative error terms i.e., for intrinsically linear model and additive errors i.e., for intrinsically nonlinear model, we get the following estimates by using different model selection criteria discussed in Section 4.2. From Table 1, we observe that, the Cobb-Douglas production function with additive error (2.2) performs bertter fo the selected manufacturing industries based on the data under study period. Thus the strictly nonlinear models (which are nonlinear with additive error terms) seem to be better than intrinsically linear model (which are nonlinear with multiplicative error terms). Now we estimate the parameters of the Cobb-Douglas production function with additive errors by using op- timization subroutine. The estimates are given in Table 2. There are economies of scale in the manufacturing of Drugs & pharmaceuticals, Furniture & fixtures (wood- en), Iron & steel basic, Leather footwear, Fabricated metal products, Plastic products, Printing & publica- tions, Tobacco since 1 for these industries. There are diseconomies of scale in the Beverage, Chemical, Glass & glass products, Leather & leather products, Paper & paper products, Textile, Wood & crock prod- ucts industries, Transport equipment since 1 for these indus tries. Table 1. Values of different model selection criter two models under studia of y. FPE AIC Name of the industry Model (2.1) Model (2.2) Model (2.1) Model (2.2) Beverage 1360488 13 1358701 32 21372134 Chemical 1 1 Leathear 9 1 1 Leather Pr 8 6 6 1 1 T 1614804 957644 1612683 956386 Drugs 58414018 3029017 58337287 3025038 Furniture 4256943 193762 4251351 193507 Glass 16250 9608 16228 9595 Iron 20604099 892909420577034 8904229 er footw9730649672619959964964676 products1589512 1371610 1587424 1369808 Fabricated metal 1192242 885584 1190676 884420 Paper 1980514 1613608 1977913 1611488 Plastic 121323 75752 121164 75653 inting 1065074 409231 1063675 408694 Textile 7418640991446487303810 9822627 Tobacco 24044986 114384024013401 1129201 ransport 22949982 19106587 22919836 19081489 Wood 69177 30634 69086 30593 tinued SCHRZ Name Model (2.1) Model (2.2) Model (2.1) Model (2.2) of the industry Beverage 141283236 1579422194260 2472 Chemical 11 1 2 r footwear 12 12 er products g 9 718 1 1 t V 6376939 9448987 68531180811 Drugs 606614693145557 675925793504964 Furniture 4420727201217 4925834 224208 Glass 16875 9977 18803 11117 Iron 213968329657382238416091903411 Leathe0356773 0429501540126276375 Leath16506681424382 183 9271 1587130 Fabricated metal 1238113919656 1379578 1024735 Paper 20567141675691 2291712 1867153 Plastic 12599178667 140386 87655 Printin1106052424976 1232428 473534 Textile 07820302604389 011546810900084 Tobacco 249701051572593278231602894865 Transpor2383297219841704 2655610022108794 Wood 71838 31812 80047 35447 SHIBATA GC Name of the industry Model (2.1) Model (2.2) Model (2.1) Model (2.2) Beverage 132277 1382083 0569620772171 Chemical 11 1 1 r footwear 91 11 er products g 8 687 1 1 t 5869949 3104366 4043972844 Drugs 567914062944877 593412253077096 Furniture 4138695188380 4324514 196838 Glass 15798 9341 16508 9760 Iron 200317638403286209311489229556 Leathe696034 912614 0131367998487 Leath15453591333510 161 4743 1393382 Fabricated metal 1159124860984 1211166 899641 Paper 19255001568786 2011951 1639221 Plastic 11795373648 123249 76955 Printin1035488397864 1081980 415727 Textile 49903457972396 88062381024218 Tobacco 233770690834288244266521320726 Transpor2231248318575849 2331426819409866 Wood 67255 29783 70275 31120 Copyright © 2012 SciRes. OJS 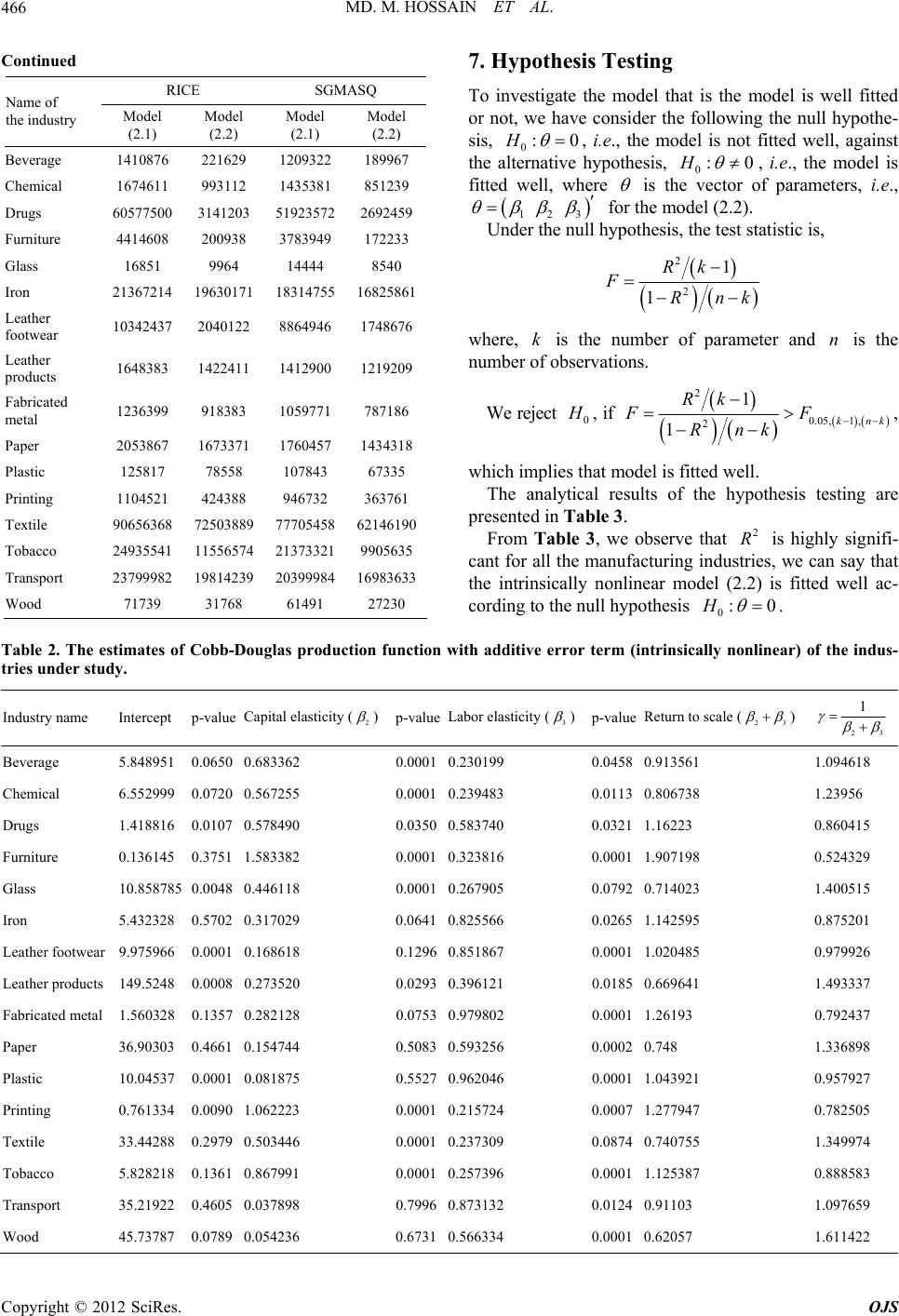 MD. M. HOSSAIN ET AL. Copyright © 2012 SciRes. OJS 466 E ASQ Continued RICSGM Name o 7. Hypothesis Testing To investigate the model that is the model is well fitted or not, we have consider the following the null hypothe- sis, 0 f Model (2.1) Model (2.2) Model (2.1) Model (2.2) the industry :0H Beverage 1410876 29 1209967 2216322 189 Chemical 1 6057 2692 1682 ar 1 2 8 1 er 1236399 918383 1059771 787186 521 424388 946732 363761 9065 6214 2493 9905 t 674611993112 1435381851239 Drugs 7500 3141203 51923572 459 Furniture 4414 Glass 608 16851 9964 1444 200938 3783949 4 172233 8540 Iron Leather 21367214 19630171 18314755 5861 footwe 0342437 040122864946748676 Leath products Fabricated 1648383 1422411 1412900 1219209 metal Paper 2053867 1673371 1760457 1434318 Plastic Printing 1104 125817 78558 107843 67335 Textile 6368 72503889 77705458 6190 Tobacco 5541 11556574 21373321 635 Transpor23799982 19814239 20399984 16983633 Wood 71739 31768 61491 27230 , i.e., the model is not fitted well, against the alternative hypothesis, 0:0H , i.e., the model is fitted well, where is the vector of parameters, i.e., 123 for the model (2.2). Under the null hypothesis, the test statistic is, 2 2 1 1 Rk FRnk kn 0 where, is the number of parameter and is the number of obse rvations. We reject , if 2 0.05,1 , 2 1 1knk Rk FF Rnk 2 R 0:0H , which implies that model is fitted well. The analytical results of the hypothesis testing are presented in Table 3. From Table 3, we observe that is highly signifi- cant for all the manufacturing industries, we can say that the intrinsically nonlinear model (2.2) is fitted well ac- cording to the null hypothesis he ef gtwith additive error term (intrinsically nonlinear) of the indus- der study . Table 2. Tstimates oCobb-Doulas producion function tries un. Industry name Intercept p-valueCapital elasticity (2 ) p-value Labor elasticity (3 ) p-value Return to scale (23 ) 23 1 Beverge 5.51 0.06500.683362 0.00010.230199 0.04580.913561 1.094618 a8489 Chemical 6.552999 0.07200.567255 0.00010.239483 0.01130.806738 1.23956 r footwear e g 47 t Drugs 1.418816 0.01070.578490 0.03500.583740 0.03211.16223 0.860415 Furniture 0.136145 0.37511.583382 0.00010.323816 0.00011.907198 0.524329 Glass 10.8587850.00480.446118 0.00010.267905 0.07920.7140231.400515 Iron 5.432328 0.57020.317029 0.06410.825566 0.02651.142595 0.875201 Leathe9.975966 0.00010.168618 0.12960.851867 0.00011.020485 0.979926 Leathr pr o d uc ts 149.5248 0.00080.273520 0.02930.396121 0.01850.669641 1.4933 37 Fabricated metal 1.560328 0.13570.282128 0.07530.979802 0.00011.26193 0.792437 Paper 36.90303 0.46610.154744 0.50830.593256 0.00020.748 1.336898 Plastic 10.04537 0.00010.081875 0.55270.962046 0.00011.0439210.957927 Printin0.761334 0.00901.062223 0.00010.215724 0.00071.27790.782505 Textile 33.44288 0.29790.503446 0.00010.237309 0.08740.740755 1.349974 Tobacco 5.828218 0.13610.867991 0.00010.257396 0.00011.125387 0.888583 Transpor35.21922 0.46050.037898 0.79960.873132 0.01240.91103 1.097659 Wood 45.73787 0.07890.054236 0.67310.566334 0.00010.62057 1.611422 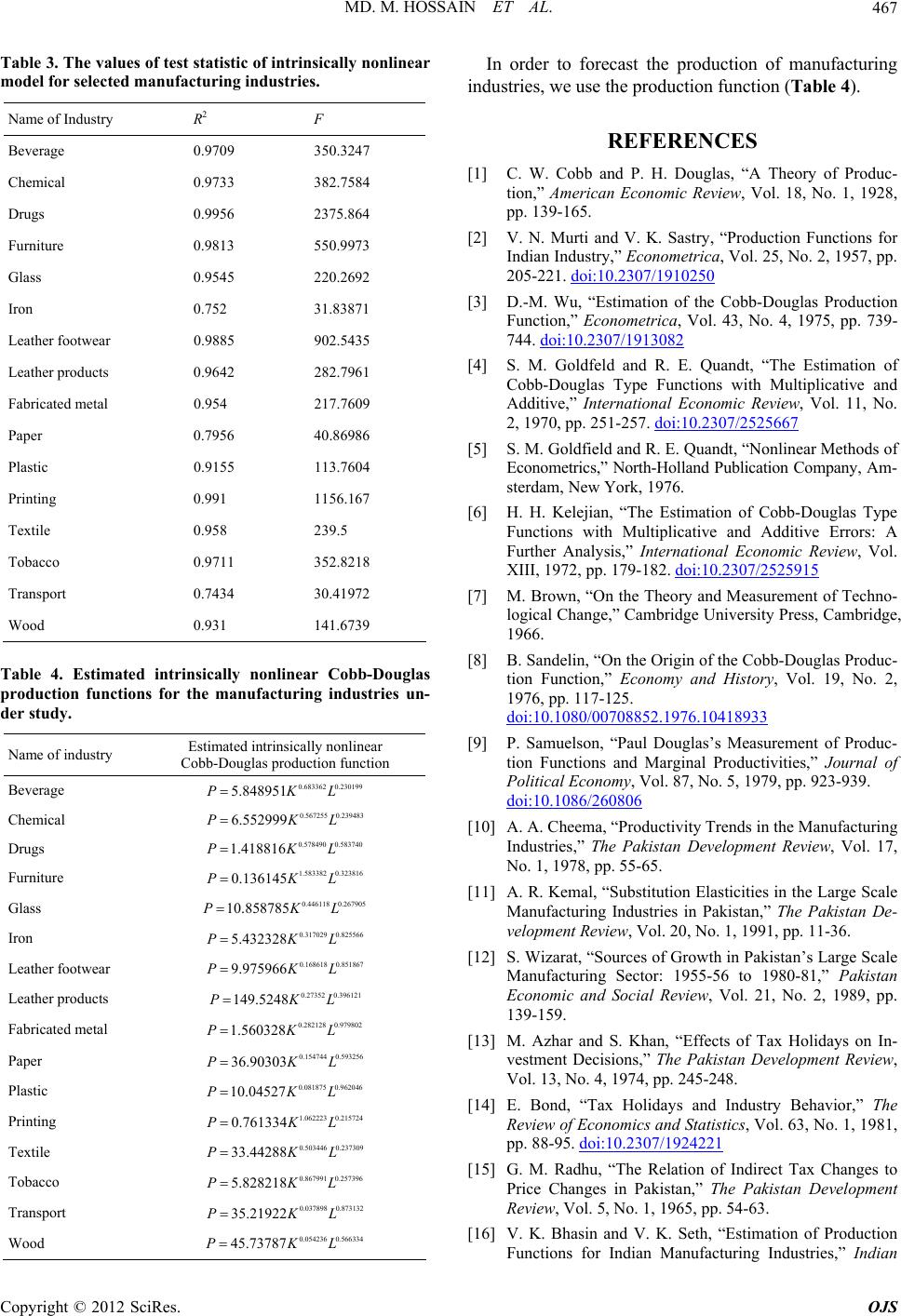 MD. M. HOSSAIN ET AL. 467 Table 3. The values of test statistic of intrinsically nonlinear model for selected manufacturing industries. ndustry F Name of I R2 Beverage 350.3247 0.9709 Chemical 0.9733 382.7584 Drugs 0.9956 2375.864 13 .9973 footwear ted metal o rt Furniture 0.98550 Glass 0.9545 220.2692 Iron 0.752 31.83871 Leather0.9885 902.5435 Leather products0.9642 2 82.7961 Fabrica0.954 217.7609 Paper0.795640.86986 Plastic 0.9155 113.7604 Printing 0.991 1156.167 Textile 0.958 239.5 Tobacc0.9711 352.8218 Transpo0.7434 30.41972 Wood 0.931 141.6739 In order to forecast the production of manufacturing industries, we use the product ion f unctio n (Table 4). NCES [1] C. W. Cobb and P. H. Douglas, “A Theory of Produc- Econ1928, . [. Murti and V. K. Sastry, “Production Functions for Indian Industry,” Econometrica, Vol. 25, No. 2, -221. doi:10.2307/1910250 Table Estimated intrinsic nonlinearuglas pn functions for tufacturinie de f industry ed intrinsically nonlinear Cuglas producn 4.ally Cobb-Do roductiohe mang industrs un- r study. Name oEstimat obb-Dotion functio Beverage 5.848951PKL 0.683362 0.230199 Chemical 0.567255 0.239483 6.552999PKL Drugs 0.578490 0.583740 8816PKL 85 0.317029 0.825566 28PKL footwear0.168618 0.851867 66PKL 0.27352 0.396121 9.5248PKL ted me0.282128 0.979802 0328PKL 0.154744 0.593256 03PKL 0.081875 0.962046 4527PKL 1.062223 0.215724 34KL 0.503446 0.237309 88PKL o 0.867991 0.257396 18PKL rt 0.037898 0.873132 22PKL Wood 0.054236 0.566334 87PKL 1.41 Furniture 1.583382 0.323816 0.136145PKL 0.446118 0.267905 PKL Glass 10.8587 Iron 5.4323 Leather 9.9759 Leather products 14 Fabricatal 1.56 Paper 36.903 Plastic 10.0 Printing 0.7613P Textile 33.442 Tobacc 5.8282 Transpo 35.219 45.737 REFERE tion,” American pp. 139-165omic Review, Vol. 18, No. 1, 2] V. N1957, pp. 205 [. Wu, “Estimation of the Cobb-Douglas Production Econometrica, Vol. 43, No. 4, 1975 doi:10.2307/1913082 3] D.-M Function,” 744. , pp. 739- [ M. Goldfeld and R. E. Quandt, “The Estimation of 4] S. Cobb-Douglas Type Functions with Multiplicative and Additive,” International Economic Review, Vol. 11, No. 2, 1970, pp. 251-257. doi:10.2307/2525667 [5] S. M. Goldfield Methods of Econometrics,ion Company, Am- and R. E. Quandt, “Nonlinear ” North-Holland Publicat sterdam, New York, 1976. [6] H. H. Kelejian, “The Estimation of Cobb-Douglas Type Functions with Multiplicative and Additive Errors: A Further Analysis,” International Economic Review, Vol. XIII, 1972, pp. 179-182. doi:10.2307/2525915 [7] M. Brown, “On the Theory and Measurement of Techno- logical Change,” Cambridge University Press, Cambridge, 1966. [8] B. Sandelin, “On the Origin of the Cobb-Douglas Produc- tion Function,” Economy and History, Vol. 19, No. 2, 1976, pp. 117-125. doi:10.1080/00708852.1976.10418933 [9] P. Samuelson, “Paul Douglas’s Measurement of Produc- tion Functions and Marginal Productivities,” Journal of Political Economy, Vol. 87, No. 5, 1979, pp. 923-939. doi:10.1086/260806 [10] A. A. Cheema, “Productivity Trends in the Manufacturing Industries,” The Pakistan Development Review, Vol. 17, No. 1, 1978, pp. 55-65. [11] A. R. Kemal, “Substitution Elasticities in the Large Scale Manufacturing Industries in Pakistan,” The Pakistan De- velopment Review, Vol. 20, No. 1, 1991, pp. 11-36. [12] S. Wizarat, “Sources of Growth in Pakistan’s Large Scale Manufacturing Sector: 1955-56 to 1980-81,” Pakistan Economic and Social Review, Vol. 21, No. 2, 1989, pp. 139-159. [13] M. Azhar and S. Khan, “Effects of Tax Holidays on In- vestment Decisions,” The Pakistan Development Review, Vol. 13, No. 4, 1974, pp. 245-248. [14] E. Bond, “Tax Holidays and Industry Behavior,” The Review of Economics and Statistics, Vol. 63, No. 1, 1981, pp. 88-95. doi:10.2307/1924221 [15] G. M. Radhu, “The Relation of Indirect Tax Changes to Price Changes in Pakistan,” The Pakistan Development Functions for Indian Manufacturing Industries,” Indian Review, Vol. 5, No. 1, 1965, pp. 54-63. [16] V. K. Bhasin and V. K. Seth, “Estimation of Production Copyright © 2012 SciRes. OJS  MD. M. HOSSAIN ET AL. 468 Journal of Industrial Relations, Vol. 15, No. 3, 1980, pp conomics,” Oxford University Press, Oxford, Survey Data,” . 395-409. [17] I. M. D. Little, D. Mazumdar and J. M. Page Jr., “Small Manufacturing Enterprises: A Comparative Study of India and Other E 1987. [18] J. M. Page Jr., “Firm Size and Technical Efficiency: Ap- plication of Production Frontiers to Indian Journal of Development Economics, Vol. 16, No. 1-2, 1984, pp. 129-152. doi:10.1016/0304-3878(84)90104-4 [19] T. Bhavani, “Technical Efficiency in Indian Modern d B. Ghosh, “Intertemporal Efficiency Var Small Scale Sector: An Application of Frontier Produc- tion Function,” Indian Economic Review, Vol. 26, No. 2, 1991, pp. 149-166. [20] B. Goldar, “Unit Size and Economic Efficiency in Small Scale Washing Soap Industry in India,” Artha Vijnana, Vol. 27, No. 1, 1985, pp. 21-40. [21] C. Neogi ania- tions in Indian Manufacturing Industries,” Journal of Pro- ductivity Analysis, Vol. 5, No. 3, 1994, pp. 301-324. doi:10.1007/BF01073913 [22] Y. Nikaido, “Technical Efficiency of Small-Scale Indus- e tent of Productivity Growth in Sw e d- try: Application of Stochastic Production Frontier Model, ” Economic and Political Weekly, Vol. 39, No. 6, 2004, pp. 592-597. [23] B. Goldar, “Relative Efficiency of Modern Small Scal Industries in India,” In: K. B. Suri, Ed., Small Scale En- terprises in Industrial Development, Sage Publication, New Delhi, 1988. [24] B. Carlsson, “The Con ish Manufacturing,” Research Policy, Vol. 10, No. 4, 1981, pp. 336-355. doi:10.1016/0048-7333(81)90018-4 [25] M. Daly, I. Gorman, G. Lenjosek, A. MacNevin and W. Phiriyapreunt, “The Impact of Regional Investment In- centives on Employment and Productivity: Some Cana- dian Evidence,” Regional Science and Urban Economics, Vol. 23, No. 4, 1993, pp. 559-575. doi:10.1016/0166-0462(93)90047-I [26] B. Contini, R. Revelli and S. Cuneo, “Productivity and Imperfect Competition: Econometric Estimation from Pa nel- Data of Italian Firms,” Journal of Economic Behavior & Organization, Vol. 18, No. 2, 1992, pp. 229-248. doi:10.1016/0167-2681(92)90029-B [27] J. K. Mullen and M. Williams, “Explaining Total Factor Productivity Differentials in Urban Manufacturing,” Jour- nal of Urban Economics, Vol. 28, No. 1, 1990, pp. 103- 123. doi:10.1016/0094-1190(90)90045-O [28] W. L. Weber and B. R. Domazlicky, “Total Factor Pro- ductivity Growth in Manufacturing: A Regional Approach Using Linear Programming,” Regional Science and Ur- ban Economics, Vol. 29, No. 1, 1999, pp. 105-122. doi:10.1016/S0166-0462(98)00013-1 [29] J. Nemoto and M. Goto, “Productivity, Efficiency, Scale Economies and Technical Change: tion Analysis of TFP Applied to the A New Decomposi- Japanese Prefec- tures,” Journal of the Japanese and International Econo- mies, Vol. 19, No. 4, 2005, pp. 617-634. doi:10.1016/j.jjie.2005.10.006 [30] N. Maniadakis and E. Thanassoulis, “A Cost Malmquist Productivity Index,” European Journal of Operational Research, Vol. 154, No. 2, 2004, pp. 396-409. doi:10.1016/S0377-2217(03)00177-2 [31] A. Radam, “Efficiency and Productivity of the Malaysian Food Manufacturing Industry, 1983-2000,” Universiti Pu- tra Malaysia, 2007. [32] B. Goldar, V. S. Renganathan and R. Banga, “Owne and Efficiency in Engineering Firms: 1rship 990-1991 to 1999- 084-5 2000,” Economic and Political Weekly, Vol. 39, No. 5, 2004, pp. 441-447. [33] S. V. Lall and G. C. Rodrigo, “Perspective on the Sources of Heterogeneity in Indian Industry,” World Development, Vol. 29, No. 12, 2001, pp. 2127-2143. doi:10.1016/S0305-750X(01)00 y of Con- udy,” Managerial Auditing Journal, ific Basin Financial Markets and [34] K. Mukherjee and S. C. Ray, “Technical Efficiency and Its Dynamics in Indian Manufacturing: An Inter-State Analysis,” Working Paper, No. 18, Universit necticut, Storrs, 2004. [35] Md. Z. Hossain, M. I. Bhatti and Md. Z. Ali, “An Econometric Analysis of Some Major Manufacturing In- dustries: A Case St Vol. 19, No. 6, 2004, pp. 790-795. [36] C.-P. Lin, “The Application of Cobb-Douglas Production Cost Functions to Construction Firms in Japan and Tai- wan,” Review of Pac Policies (RPBFMP), Vol. 5, No. 1, 2002, pp. 111-128. doi:10.1142/S0219091502000663 [37] M. Jung, K. Lee and K. Fukao, “Total F of Korean Firms and Catching up actor Productivity with the Japanese earch on International Economic ected Manufacturing li- llege Publishers, New gladesh Bureau of Statistics, Statistics Divi- ion, Firms,” Seoul Journal of Economics, Vol. 20, No. 1, 2008, pp. 93-139. [38] D. A. Hashim, “Cost and Productivity in Indian Textiles- Indian Council for Res Relations. Multan District,” Journal of Quality and Tech- nology Management, Vol. 5, No. 2, 2009, pp. 91-100. [39] Md. Z. Hossain and K. S. Al-Amri, “Use of Cobb-Doug- las Production Model on Some Sel Industries in Oman,” Education, Business and Society: Contemporary Middle Eastern Issues, Vol. 3, No. 2, 2010, pp. 78-85. [40] R. Ramanathan, “Introductory Econometrics with App cations,” 3rd Edition, Harcourt Co York, 1995. [41] “Statistical Year Book,” 5th Edition, 7th Edition, 16th Edition, 18th Edition, 21st Edition, 22nd Edition, 24th Edition, Ban sion, Ministry of Planning, Dhaka, 1984, 1986, 1995, 1997, 2000, 2001, 2003. [42] “Reports on Bangladesh Census of Manufacturing Indus- tries,” Bangladesh Bureau of Statistics, Planning Divis Ministry of Planning, Dhaka, 1984, 1987, 1992, 1997, 2000, 2002, 2004. Copyright © 2012 SciRes. OJS
|