 Intelligent Information Management, 2012, 4, 239-250 http://dx.doi.org/10.4236/iim.2012.425035 Published Online October 2012 (http://www.SciRP.org/journal/iim) Finding Optimal Allocation of Constrained Cloud Capacity Using Hyperbolic Voronoi Diagrams on the Sphere Shanthi Shanmugam1, Caroline Shouraboura2 1University of California, Berkeley, USA 2Forest Ridge School, Seattle, USA Email: shanthish@forestridge.org, CarolineSh@forestridge.org Received September 11, 2012; revised October 12, 2012; accepted October 19, 2012 ABSTRACT We consider a network of computer data centers on the earth surface delivering computing as a service to a big number of users. The problem is to assign users to data centers to minimize the total communication distance between comput- ing resources and their users in the face of capacity constrained datacenters. In this paper, we extend the classical planar Voronoi Diagram to a hyperbolic Voronoi Diagram on the sphere. We show that a solution to the distance minimization problem under capacity constraints is given by a hyperbolic spherical Voronoi Diagram of data centers. We also present numerical algorithms, computer implementation and results of simulations illustrating our solution. We note applicabil- ity of our solution to other important assignment problems, including the assignment of population to regional trauma centers, location of airbases, the distribution of the telecommunication centers for mobile telephones in global telephone companies, and others. Keywords: Cloud Computing; Voronoi Diagram; Voronoi Diagram on the Sphere 1. Introduction Cloud Computing could transform the way we use com- puter hardware by eliminating the need to own a com- puter. Instead of placing expensive, fully loaded com- puters in every school, students all over the world could provision computing resources as they need them. A Gartner research report places the total savings of mov- ing away from individually managed desktop computers at 41%. Behind the Public Cloud is a physical network of data centers with millions of servers, hidden from us through virtualization. Virtualization offers Public Cloud providers the flexibility to assign each application to run on any of its available physical servers. The vision of less expensive Tablets powered by the remote computing resources of the Cloud is still in its early days. Combined, the emerging Tablet computers coupled with central Cloud Computing facilities to host applications and data will significantly improve schools ability to increase the use of computers in the classroom, allowing students to expand computing power on de- mand for educational applications anytime anywhere. However, with the transition to the cloud, students’ desk- tops must be moved from local in-classroom computers to large, centralized datacenters. These facilities are typically hundreds, if not thousands, of miles away from the schools and the homes of students. This distance in- troduces network delay between the students and their desktops. The utility of these students’ remote desktops depends on minimizing this network delay. Presently, the approach cloud providers use to allocate users to a datacenter is referred to as Global Server Load Balancing, or GSLB. A user accesses a computer in the cloud using an Internet domain name. The domain name (for example, www.whitehouse.gov) is translated by a Domain Name Service (DNS) into an Internet Protocol (IP) address pointing to a specific computing device. Where there are multiple datacenters that could satisfy the request, the DNS is programmed to return the IP ad- dress of the closest computing device, or the one with the least network delay. The decision of where to put a user is made individually for each connection request. This approach works well for accessing websites where the content is replicated across all cloud locations, such as search engines, social network sites, news, and weather. For student’s desktops, a more static assignment is needed. The CAP Theorem [1] states that a distributed system cannot simultaneously provide Consistency, Availability, and Partition Tolerance. Even if students could afford the cost of replicating their desktops con- tinually between the multiple geographically disperse datacenters selected by a latency-based GSLB, the need for desktop consistency over a WAN would exacerbate the impact of Availability events or Partitioning events. C opyright © 2012 SciRes. IIM  S. SHANMUGAM, C. SHOURABOURA 240 When based in a cloud, students’ desktops require a con- tinual static binding to the network access point of the student. The cloud-based desktop should be highly available (for example, using an Availability Zone [2] architecture such as employed by Amazon Web Services). Latency-based GSLBs are not useful for such constant binding of two locations on the earth’s surface. A form of GSLB is required which can statically assign students to cloud datacenters. One other problem remains. Cloud datacenters, despite their large capacity, are finite in size. They can become constrained in capacity. The solution for balancing stu- dents across cloud facilities must take into account occa- sional capacity constraints and allow weighting of as- signment to potentially more distant facilities to com- pensate. 2. Problem Formulation Combined, the emerging tablet computers coupled with central cloud computing facilities to host applications and data significantly improve schools’ ability to in- crease the use of computing in the classroom. Cloud Computing can provide computing as a service to mil- lions of students world-wide. These students would need tablet computers connected to the cloud via common Wi-fi networks and the Internet. The remaining technol- ogy required to connect these tablets is a placement ser- vice capable of considering proximity and any capacity constraints. Proximity is important due to network delay and the high correlation of this delay to physical distance. Because the relationship between students and their data is continuous, existing GSLB (as described above) will not meet this need. The new placement technology would need to consider occasional capacity constraints as data- centers are physical buildings limited by critical, long- lead-time resources. These include electrical power, cooling capacity and servers, which require many weeks to order, ship, and install. The ideal placement technol- ogy could consider an entire population of students and optimally assign it to either the closest datacenter or an alternate should capacity in that datacenter be unavail- able. We would like to develop an algorithm which could globally optimize for the variables of population, dis- tance, and specific points of capacity on the earth’s sur- face representing datacenters. Our starting point in developing a mathematical framework is to model the network of computer data- centers as a set 1n on the earth’s surface, represented by a sphere ,,SS >0R of a radius . Each datacenter S is described by its geographical coordi- nates, the latitude and the longitude . The popu- lation of students (users) is a set 1 ,, UU . Our task is to create an efficient algorithm to solve the mini- mization problem for the total distance between the data centers and the students. We assume that each stu- dent k is assigned to a data center U k, and the total distance is the sum of the distances between the users and the corresponding data centers, S 1 ,, N k jk k jdSU (1) where jjkU is the function assigning the user k to the data center k S. For any two points x, y on the sphere we denote ,dxy the distance between x and y on the sphere, that is the length of the arc of the great circle connecting x to y. We also must solve the minimi- zation of the total distance under certain constraints. In real life some data centers become capacity constrained, so the solution must take computing capacity into con- sideration. We will assume that each data center S has a capacity C 0 jk which characterizes how many users it can service. For simplicity we assume here that all users are equal in terms of the requested volume of services. It is easy to extend our model to the case when different users request different volume of services. The assumption of the limited capacity for the data centers leads to the minimization problem with con- straints: find an assignment function such that 0 min , jC jj (2) where #: for1, ,. mm Cjjk NkjkmC mn (3) Observe that #:Nkjkm S U m is just the num- ber of users assigned to the data center m. Since the number of users is usually large, it can be useful to con- sider a (nonnegative) measure of users on the sphere. In this case, the total distance functional looks like ,, RjU jdSUdU (4) where jU is the assignment function of the users to the data centers. Respectively, constraint (3) takes the form : for1, ,. m CjjUUjUmC mn (5) To solve the minimization problem we explored the possibility of extending classic Voronoi Diagrams. Vo- ronoi Diagrams are a well-known geometric tool for an- swering distance related queries. Informal use of Voronoi Diagrams can be traced back to Descartes in 1644. In 1854 British physician John Snow used a Voronoi Dia- gram to illustrate how the majority of people who died in Copyright © 2012 SciRes. IIM  S. SHANMUGAM, C. SHOURABOURA 241 the Soho cholera epidemic lived closer to the infected Broad Street pump. There have been numerous applica- tions in science and technology since [3-8]. Voronoi Diagrams have the unique property that any point within a Voronoi cell is closer to the vertex of that cell than any other vertex. As we considered how the edges of a Voronoi cell behave in reaction to vertices constrained in the number of points they could service, we found another well-known geometric construct, the hyperbola, to be especially applicable. Our result is de- scribed below in Theorem 3.1, where we show that the solution to the minimization problem in the face of ca- pacity constraints is given by a new, extended form of Voronoi Diagram, hyperbolic Voronoi Diagrams on the sphere. We believe this form of Voronoi Diagram could prove useful in solving many problems beyond the stu- dent-tablet assignment issue we are tackling here. 3. Solution of the Constrained Minimization Problem Let us begin with the unconstrained minimization prob- lem. In the absence of the capacity constraint, minimiza- tion problem (2) can be solved by assigning each user U to its closest data center S, so that 0 U is the clos- est data center to U. Geometrically, we partition the ere S sph into thls m e cel of the Voronoi Dia- gram V on the sphere with thints e po m S (Figure 1). cell m The is defined as the set of nts on poi which are closer (or at the same distance) to m S than to her l S’s, thot at is :, , mRm forall=. l dxS dxS l m (6) Observe that the cells m are convex spherical poly- gons on the sphere . With the Voronoi Diagram we associate a graph V. The vertices of the graph V are the vertices of the polygons m , and the edges of the graph V are the sides of the polygons m . The De- launay Triangulation, associated with the Voronoi Dia- gram, is the dual graph to V, with vertices Sm and edges connecting vertices m, if and only if the cells Sl S m , l have a common side. Thus, in the absence of the constraint, we assign to each data center all users in the cell m Sm of the Figure 1. Voronoi diagram V on the sphere with the points Voronoi Diagram. To describe the minimizing assign- ment in the presence of the constraint we will introduce hyperbolic Voronoi Diagrams on the sphere. To get an insight into the minimization problem, it’s easiest to start by considering the case of a small number of data centers and then formulate a general result. Begin with two data centers. Two data centers. For two data centers 1, 2, the Voronoi Diagram is described by the spherical bisector of 1, 2. The bisector is the arc of the great circle perpendicular to the arc of the great circle through 1, 2 at the middle point (Figure 2(a)). The bisector parti- tions the sphere into two hemispheres, 1 S S S SS S , 2 , and in the absence of the constraint we assign all users k in U 1 to 1 and all users in 2 S to . Let us denote 2 S m the set of users in m , that is ,1,2 mkm Um . (7) Suppose now that the data center 1 has a limited capacity 1 and the numbers 1 of the users in 1 S C N is bigger than 1. Some users must be redistributed in the cell 1 C from the data center 1 to the one (Figure 2(b)). This will increase the total distance by S2 S m . 12 21 ,,, k kk U jdSUdSU (8) where 12 1 S is the set of users redistributed from S1 to 2 (Figure 3(a)). The goal is to minimize j 12 under the fixed number of the users in , since (a) (b) Figure 2. Two data centers with and without capacity con- straints. (a) Without constraints; (b) With constraints. Copyright © 2012 SciRes. IIM  S. SHANMUGAM, C. SHOURABOURA 242 121 1 NC. (9) This minimization condition implies that if , are any two users such that k Ul U 12k U and U112 \ l , then 21 ,,, ll dSU k U l U2 S j 1 1 , 0 , . kk kk dSU UdSU dd 2 d 21 ,, kk dSU dSUdSU (10) because otherwise we can switch back to S1 and to and in this way decrease in (8). Let ,S 12 112 12 22 \ max and min , k k U U ddU ddS (11) Then (10) means that 21 . Let be any num- ber between and . Then d 1 d 21 21 , , . kk kk SU d dSU 0S 2k 12 112 \ max , min , k k U U dSU d dSU (12) Since 21kk for U ,dSU d ,U , the latter relation can be extended to 12 2 112 \ max , min , k k U U dSU d dSU 21 21 , , . kk kk SU d dSU (13) Consider the spherical hyperbola on the sphere (cyan line on (Figure 3(b))), defined as a locus of points x satisfying the equation, dxS 12 ,,.d dxS (14) It partitions the sphere D S 1 D 2 ,ddxS 2 ,ddxS D DS S into two regions 1 and 2 such that 11 and 22 (Figure 3(b)). The regions and are described as DSD 2 DD 11 :,DxdxS (15) and 21 :,DxdxS (16) The regions 1, 2 are the cells of the hyperbolic Voronoi Diagram of the points 1, 2 with the pa- rameter d. We obtain from (13) that to minimize the total distance j 1 D D1 S S S Sjm we have to find such d that the number of users in the region is equal to the capacity and to assign all users in to the data center . 1 N 1 C1 Now let’s look at the case of three data centers. Three data centers. For three data centers 1, 2, 3 the above considerations prove the following. Sup- pose that 0 is the minimizing assignment, and let (a) (b) Figure 3. Solution for two data centers with capacity con- straints. (a) Illustration for (13); (b) Regions D1, D2. max ,, min,,. km kl mklk ml U mk lk U dS UdSUd dS UdSU d 122331 0.ddd (17) In general, the numbers ml are not unique, because they can be chosen from the intervals (17). I can state that it is possible to choose these numbers in such a way that , be the set of users which assigns to m, . Then there exists numbers such that for , 1,2, 3,mS 1, 2, 3m =ml 0 j ml d 12 (18) Geometrically this equation means that the three spherical hyperbolas, , 23 , and 31 , where :, ,, mlm ml l dS xddSx 12 23 31 ddd (19) intersect in one point. Suppose, for the sake of contradic- tion, that (18) is not possible. The set of all possible val- ues of the sum 1223 31 1223 31 min minmin maxmaxmax . dddx ddd is the interval, ddd (20) If this interval does not contains 0, then the sum 12 23 31 1223 31 min minmin0.dddd is either always positive or always nega- tive. Suppose, for the sake of definiteness, that it is al- ways positive, so that 12 d23 d31 d 1k U (21) Take the minimal values of , , . Then we obtain from (17) that there exists 2l U , , and 3p U such that Copyright © 2012 SciRes. IIM  S. SHANMUGAM, C. SHOURABOURA 243 l dSU d dSU d dSU d 1212 2323 3131 ,,, ,,, ,,. kk l pp SU d SU d SU d U (22) Let us move k from 1 to 2 , l from 2 U to 3 , and U from 3 to 1 . Then the number of us- ers in 1 , 2 , 3 will not change but the total dis- tance will decrease by 3 31 ,, 0, ll dSU d d j 23 d31 d 1 d 2 d3 d 1212 232 3 3131 , , . ddd ddd ddd , lkl dSU d R , mll dSx d d dd m D m1, 2,3md d C 1 C CC 1, 2,3m 0dd d N C 0d d m 1, 3m 12 2 3112 23 ,, ,, kk pp dSUdSUdSU dSUdSUd d (23) (Figure 4(c)). hence 0 is not the minimal total distance assignment. This contradiction proves the possibility of choosing the numbers , and in such a way that (18) holds. 12 d Equation (18) implies that there exist numbers , , such that (24) So, by (17), :, forall,1, 2,3. mk mkm UdSU d lmm (25) This result can be restated as follows. Partition the sphere into the three cells, :, forall,1, 2,3, mm DxdS xd lmm (26) of the hyperbolic Voronoi Diagram with the parameters 1, 2, 3. Then to minimize the total distance func- tion assign the users in the cell to the data center , . S The parameters , 2, 3 are determined by the capacities , 2, 3. We assume that the total capac- ity 123 of the data centers exceeds the number of users, because otherwise it would be impossible to service all users. The following three cases can appear: 1 d 1 C C CCC 1) No constraints are active, which happens when the capacities , 2, 3 are big enough. In this case 123 , so that m, , are the classi- cal Voronoi cells on the sphere (Figure 4(a)). 0dddD 2) One constraint is active, say, 1 C. In this case, 1, 23, and the parameter 1 is deter- mined by the condition that the number 1 of users in the cell is equal to ( Figure 4(b)). 0d 1 1 3) Two constraints are active, say, 1 C, 3. In this case, 1, 2, 3, and the parameters 1, are determined by the conditions that the number of users in the cell is equal to C for D C 0dd 3 d m N 0 m D The subsequent sections present numerical algorithms, computer implementation and results of simulations il- lustrating the solution for 2, 3, and 4 data centers, and also, for a big number of data centers. General case. The general hyperbolic Voronoi Dia- gram of points ,, n SS Sm d 1 is defined as follows. Sup- pose that to each point m a number is assigned. Then the hyperbolic Voronoi Diagram 1 ,,,, n Vd ddd with the parameters d m S m Dm S m and the points , is de- fined as follows. The cell of the point is de- fined as :, , for all. mRmmll DxdxSd dxS d lm ml (27) separating two neighboring cells , m D The curve (a) (b) (c) Figure 4. Three data centers. (a) No constraints; (b) One constraint; (c) Two constraints. Copyright © 2012 SciRes. IIM  S. SHANMUGAM, C. SHOURABOURA rigciRes. IIM 244 l D ,, ll dxS d 4. Numerical Algorithms and Computer Simulations has the equation, , mm dxS d (28) For the computer simulations we wrote a system of pro- grams using the MATLAB 2010 software. Specifically, we wrote programs for constructing the Voronoi Dia- grams and Delaunay Triangulations on the sphere, both classical and hyperbolic, for calculating the total popula- tion in each of the Voronoi cells, and a program with an iterative algorithm for finding a hyperbolic Voronoi Dia- gram which minimizes the total distance functional under given constraints. We have modeled different types of the constraints: so ml is a part of the spherical hyperbola on the sphere . A vertex of the hyperbolic Voronoi Diagram is a point which belongs to three or more cells. The graph V of the hyperbolic Voronoi Diagram v d Vd v e con- sists of the vertices and the edges , which are the curves separating neighboring cells. ml A solution to the constrained minimization problem can be obtained as follows. There is a natural assumption that the total capacity of all data centers is not less than the number of the users, 1) no constraints; 1 n mR m C U jU ,,dj D ly ifm U D S S SS 2) limited number of users in the specific cells; . (29) 3) equal numbers of users in each Voronoi cells. In this section we discuss our algorithm in details and present results of our simulations under the constraints (a) and (b) for 2, 3, and 4 data centers. The case of many data centers will be discussed later. Otherwise, it would be impossible to service all the users. Theorem 3.1 For any measure a minimizer 0 exists, which can be obtained as follows. There exist numbers 1n such that the minimizer 0 is obtained by assigning all users in the cell m of the hyperbolic Voronoi Diagram to the data center , so that d Vd m S Two data centers. 1, 2. As an illustration, start with 1 in Seattle (the magenta diamond in the left up- per corner in Figure 5) and 2 in Atlanta (the red dia- mond in Figure 5), assuming that all users are located in the USA. Let’s also assume that all citizens of the USA are the users. The arc 12 of the great circle con- necting 1 to 2 is shown by the yellow line in Fig- ure 5. Observe that in Figure 5 the background is the 3D projection of the earth from Google Earth. The center of the projection is chosen at some point with the latitude ,SS S S 0 0ifand onjU m. (30) A full proof of this theorem can be obtained by extending the logic described for three data centers to a general case. We omitted it here due to length. Figure 5. The solution to the constrained minimization problem with 2 data centers, in Seattle (the magenta diamond in the left upper corner) and Atlanta (the red diamond). The arc of the great circle connecting Seattle to Atlanta is shown by the yellow line. The cyan line is the spherical bisector between Seattle and Atlanta. The thin magenta lines show spherical hy- perbolas which are the successive approximations to the hyperbolic Voronoi Diagram on the sphere, with the constraint of 80 million users in the Atlanta data center. The thick red line is the final approximation. The region inside the red line contains 79.4 million citizens, which are assigned to the Atlanta data center. C opyht © 2012 S  S. SHANMUGAM, C. SHOURABOURA 245 and the longitude 0 . Notice that the great circle con- necting Seattle to Atlanta (the yellow line) is not a per- fect straight line, and it is slightly curved in the projec- tion. The spherical bisector 0 of , , 1 S2 S 12 , ,SdxS 0 :, R xdx (31) (the cyan line in Figure 5) is a great circle through the midpoint of the arc 12 and perpendicular to ,SS 12 . The bisector divides the sphere ,SS into two hemispheres, Seattle and Atlan ta . Estimating the popu- lation in the two hemispheres suggests that about 73 mil- lion citizens live in Seattle and about 236 million in Atla nta . If the goal were to minimize the total distance without any constraint, then the simple answer would be to assign all the users in Seattle to the data center in Seattle, and all the users in Atla nta , to the data center in Atlanta. But what if the data center in Atlanta has a capacity of only 80 million users? Then we need to redistribute some users from Atlanta to Seattle. Since the goal is to mini- mize the total distance, the answer is to find a hyperbola 1 :, R 2 , , dxS dxS d (32) such that the population in Atl a nta is close to 80 million, but not more. This can be found by successive approxi- mations and by a multiscale analysis of the population distribution. To analyze the population distribution, start with a large scale distribution, in which the states are repre- sented by their geographic centers and the whole state population is put in the state geographic center. By suc- cessive approximations, the hyperbola (32) can be found which gives a large scale solution to the constrained minimization problem. Then, a finer scale is used in which the population of the states near the hyperbola of the large scale solution is represented by smaller units. This results in a solution to the constrained minimization problem at the finer scale. Then, if needed, a second finer scale can be considered, and so on. In the multiscale analysis of the population distribution, we consider big metropolitan areas like New York, Chicago, Houston, etc. as point masses, with all the population of the metropoli- tan area concentrated in one point. For the large scale solution to the constrained minimi- zation problem, use successive approximations of the parameter d in (32). In the first step , where (1) dd 12 1, 2 ddSS (1) 2 ,dxSd (1) (33) The hyperbola 11 :, R xdxS (34) crosses the arc 12 ,SS 1 at the point such that 12 12 1 ,,, 4 dXS dSS (1) (1) (35) see a thin magenta line in Figure 5. An analysis of the population distribution gives that about 127 million citi- zens live in the region Seattle and about 182 million in the one Atlanta , with respect to the hyperbola 1 . It is still more than 80 million. Therefore, the second step is to take the hyperbola 2 through the point 2 on the arc 12 ,SS such that 22 12 1 ,,, 8 dX SdSS (2) (2) (36) the second magenta line in Figure 5, resulting in about 209.6 million citizens living in the hemisphere Seattle and about 99.4 million in the hemisphere Atlanta , with respect to the hyperbola 2 . We continue with this, tak- ing the third, fourth, and subsequent approximations. The first four approximations are shown by thin magenta lines in Figure 5. Observe that the successive hyperbolas are jumping back and forth. We find that the 8-th approximation gives 75.1 million and the 9th one, 83.8 million. After that, all the subse- quent approximations oscillate between these two num- bers. The reason is the large scale representation of the population. The difference of 8.7 million comes from the state of New Jersey. Therefore, we consider a finer scale for the representation of the population distribution in New Jersey and other states near the hyperbola. In the finer scale we find, by successive approximations, a so- lution with 79.2 million population inside hyperbola (32). This solution is shown by a thick red line in Figure 5. In a similar way, if needed, subsequent approximate solu- tions with even better approximation to 80 million can be obtained. Three data centers. The next step is to move on to three data centers 1, 2, and . As an illustration, we will consider 1 in Seattle, in Atlanta, and in New York, see Figure 6. S S3 S S2 S3 S Focus on the three bisectors, :,, , , ijR ij dxSdxSij (37) (the cyan lines in Figure 6), which intersect at some point 0 (the red point in Figure 6). The point 0 is the vertex of the spherical Voronoi Diagram with the three points , 2, and 3. The bisectors ij1 S SS , ema- nating from 0 to the opposite point 0 π on the sphere , are the edges of the Voronoi Diagram. By an analysis of the population distribution, there are about 72.9 million people who live in the cell Seattle , 144.1 million in At lanta , and 92.1 million in NY . To restrict the population in the Atlanta cell by 80 million, there must be a number d such that considering the cells 1 , 2 , 3 of the hyperbolic Voronoi Diagram, Copyright © 2012 SciRes. IIM  S. SHANMUGAM, C. SHOURABOURA 246 Figure 6. The spherical Voronoi Diagram for the 3 data centers, in Seattle, Atlanta, and New York. The arcs of the great cir- cles connecting Seattle to Atlanta, Seattle to New York, and Atlanta to New York are shown by yellow lines. The cyan lines are the spherical bisectors between these cities. The cyan lines intersect at a point which is the vertex of the Voronoi Diagram. , , j :, , ijRi ij dxSddxS 123 ,, 0ddd di j ,,0d (1) dd (38) with the parameters , the popula- tions in the Atlanta cell is close to 80 million but under 80 million. This is done by iterations (successive ap- proximations) and by a multiscale representation of the population distribution. Start with the large scale representation of the popula- tion distribution. At the first step of the successive ap- proximations take , where 23 1, 2 ddSS (2) dd (1) 23 ,dS S (39) and is the distance between Atlanta and New York. This results in a population of 75.4 million in the Seattle cell, 92.4 million in the Atlanta cell, and 141.1 million in the New York cell. Since the population in the Atlanta cell is bigger than 80 million, the second step takes , where 23 3,, 4 ddSS (3) dd (2) (40) and we find the population of 77.4 million in the Seattle cell, 58.3 million in the Atlanta cell, and 173.2 million in the New York cell. The third step takes , where 23 5,, 8 ddSS this point, steps switch to a finer representation of the oximation is shown by a thick red line on w consider four data cen- te 1 Ss iSea 4 S Delaunay Triangulation on the sp i Diagram (t (3) (41) and results in the population of 77.4 million in the Seattle cell, 77.0 million in the Atlanta cell, and 154.5 million in the New York cell. And so on. After several iterations the numbers begin oscillating between two values, and at population distribution near the hyperbolas and continue the iterations. The final appr Figure 7. It gives the population of 77.5 million in the Seattle cell, 79.8 million in the Atlanta cell, and 151.7 million in the New York cell. Four data centers. Let us no rs 1 S, 2 S, 3 S, and 4 S. As an illustration, assume that in ttle, 2 Sin Atlanta, 3 S in New York, and in Phoenix. Figure 8 depicts the here for 1234 ,,,SSSS (the yellow lines) and edges of the Voronohe cyan lines). The edges of the Voronoi Diagram are the arcs of the bisectors between i S, S, ij . There are 4 Voronoi cells , so that j S . Annalysis of the population distron gives 4 million are in the Seattle cell 1 aibuti that 30. , 141.2 million in the Atlanta cell 2 , 92.1 million in tNew York cell 3 he , and 45.3 millioin the Phoenix cell 4 n . Suppose that the Atlanta data center ha as capacity of 80 million, and each of the other centers has a big capac- ity. Then a new number d is required such that consider- ing the cells 1 , 2 , 3 , 4 of the hyperbolic Vo- ronoi Diagram, ,,,, ijRi ijj : d xSddxSdi j (42) with the parameters 12 34 ,,, 0,,0,0dddd d cell 2 , the population in the Atlanta is close to 80 m pa- ra illion but not more. This is done by iterations and by the mul- tiscale representation of the population distribution. After several successive approximations of the meter d, the population in the Atlanta cell begins to Copyright © 2012 SciRes. IIM 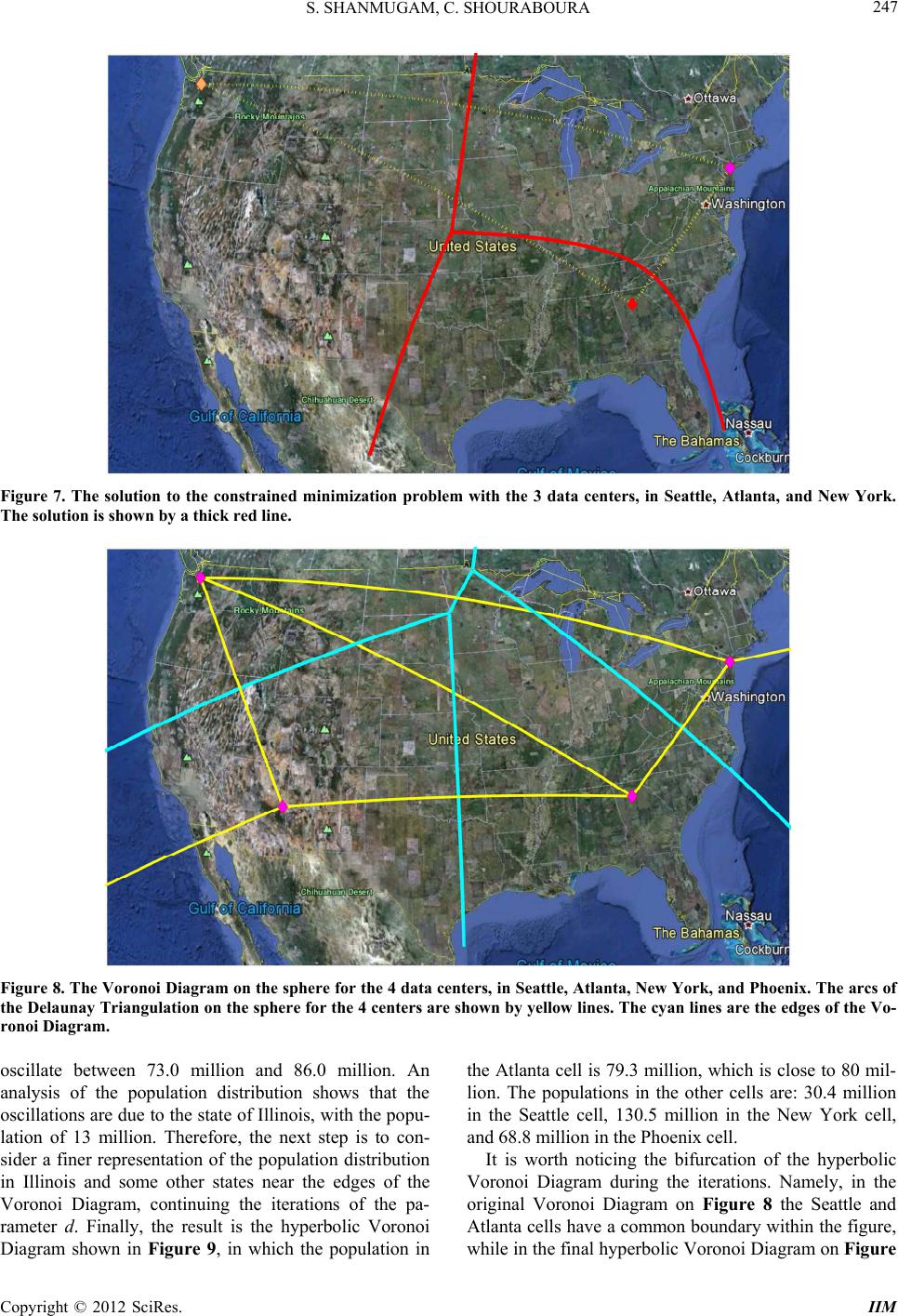 S. SHANMUGAM, C. SHOURABOURA 247 Figure 7. The solution to the constrained minimization problem with the 3 data centers, in Seattle, Atlanta, and New York. The solution is shown by a thick red line. Figure 8. The Voronoi Diagram on the sphere for the 4 data centers, in Seattle, Atlanta, New York, and Phoex. The arcs of scillate between 73.0 million and 86.0 million. An the Atlanta cell is 79.3 million, which is close to 80 mil- s. Namely, in the ori ni the Delaunay Triangulation on the sphere for the 4 centers are shown by yellow lines. The cyan lines are the edges of the Vo- ronoi Diagram. o analysis of the population distribution shows that the oscillations are due to the state of Illinois, with the popu- lation of 13 million. Therefore, the next step is to con- sider a finer representation of the population distribution in Illinois and some other states near the edges of the Voronoi Diagram, continuing the iterations of the pa- rameter d. Finally, the result is the hyperbolic Voronoi Diagram shown in Figure 9, in which the population in lion. The populations in the other cells are: 30.4 million in the Seattle cell, 130.5 million in the New York cell, and 68.8 million in the Phoenix cell. It is worth noticing the bifurcation of the hyperbolic Voronoi Diagram during the iteration ginal Voronoi Diagram on Figure 8 the Seattle and Atlanta cells have a common boundary within the figure, while in the final hyperbolic Voronoi Diagram on Figure Copyright © 2012 SciRes. IIM  S. SHANMUGAM, C. SHOURABOURA 248 Figure 9. The solution to the constrained minimization problem with the 4 data centers, in Seattle, Atlanta, New York, and Gi n on the sphere Phoenix. The solution is shown by a thick red line. Ob serve the bifurcation of th e Voron o i Diagram from Figu re 8. they do not have a common boundary within the figure. 9 5. The Voronoi Diagram on the Sphere and the Convex Hull ven n points 1,,SS , the Vo- ronoi cell o f the point S is defined the set of points whicre closer to as h a S (or at the same distance) than to any other point i S th respect to the spherical metric on wi . The Voronoi cell is a convex spherical polygon ande set of vertices of all Voronoi cells is the set of vertices of the spherical Voronoi Diagram. There is a nice relation between the spherical Voronoi D th iagram and the convex hull H of the points 1,, n SS in the 3D space. This relation was observed by], [10] (see also [11]). Namely, looking at any facet m Brown [9 of the convex hull H and the plane m P through m , the plane m P intersects the sphere by a circ m le . Then th center m v of the circle em on the sphere is a vertex of the Voronoi Diag. More precis, mR v is the center of the spherical cap m , bounded b circle m ram ely y the , which contains no points S inside the cap. The se m v coincides with the set o vertices of the Voronoi Diagram. This gives a powerful method of the construction of the spherical Voronoi Diagram. In particular, since the convex hull of the points 1,, n SS can be constructed in lnnn operations, cal Voronoi Diagram nstructed in tf the spheri- can be co lnnn operations as well. Two neighboring facets m and l of th hu e convex tticll share an edge ml e andwo veres i S and S, the end-points of the edge ml e. The arc of th Delauny Triangulation connecting S and e a i S is thc of th the half-planes through m e are formed by great circle which lies in the dihedral domain and l , which is vertically opposite to the one containig the covex hull H. 6. Numerical Algorithm for Many Centers In the case of many data centers 1,, n SS, th n n e first m. ta ers m N i step is construction of their spherical Voronoi Diagra The next step is to compare the capacity m C of the da center m S with the number of usn the Vo- ronoi cell m containing m S. The following assump- tion is made, which seems plausible for the computer cloud nworks: for most m S’s the capacity m C is big enough so idoes not create any constraint. Mathemati- cally, there is an assumption that for these m S’s we have an unlimited capacity, m C. It is also plausible to assume that the cells with constraints are isolated. Both assumptions stem from the practical obsrvation that capacity constraints resltsuboptimal operational characteristics for computer clouds, and are therefore uncommon. In this case we need to change the Voronoi Diagram only locally. This can be done similarly to the described above procedure for a small number of data centers. As an example, look at a model minimization problem for 10 data centers in Seattle, Atlanta, New York, Phoe- nix, San Francisco, Denver, Houston, Chicago, Boston, an et t e u in d Miami (see Figure 10). The Voronoi Diagram on the sphere for these centers is shown by the cyan line. The distribution of the population in the Voronoi cells looks as follows: Seattle—13.8 million, Atlanta—48.5 million, New York—61.5 million, Phoenix—6.7 million, San Francisco—41.1 million, Denver—18.6 million, Houston Copyright © 2012 SciRes. IIM  S. SHANMUGAM, C. SHOURABOURA 249 Figure 10. The solution to the constrained minimization problem with 10 data centers, Seattle, Atlanta, New York, Phoenix, San Francisco, Denver, Houston, Chicago, Boston, and Miami. The Voronoi Diagram on the sphere with the 10 points is that the data ied the minimization problem for the n distance in a computer cloud under he numbcell es shown by the cyan line. In this case, there are two constraints: in San Francisco the capacity is equal to 15 million users and in Atlanta it is 20 million. The constraints change the Voronoi Diagram locally near Atlanta and San Francisco to the hyper- bolic diagram. The changes are shown in red. —31.5 million, Chicago—57.6 million, Boston—10.9 illion, and Miami—18.7 million. Suppose S. m centers in Atlanta and San Francisco have limited capaci- ties of 20 and 15 million users, respectively. Then their users must be redistributed to the neighboring centers. To solve the minimization problem with these constraints, the hyperbolic Voronoi Diagram is first constructed. Then the iterative method described above is applied together with the multiscale analysis of the population. As a result, the hyperbolic Voronoi Diagram on the sphere depicted in Figure 10 is arrived at. It differs from the initial Voronoi Diagram only locally, near Atlanta and San Francisco. The change from the initial Voronoi Diagram to the new one is shown in red in Figure 10. 7. Conclusions In this work we stud total communicatio the condition of restricted capacity of the data centers. We assumed that the earth is a perfect sphere of radius R, so that the earth distance between two points is the length of the smaller arc of the great circle connecting these points. Our main result is Theorem 3.1, which shows that a solution to the minimization problem is given by a hy- perbolic Voronoi Diagram constructed on the data cen- ters 1,, n SS. The parameters 1,, n dd of the hyper- bolic Voronoi Diagram can be found from the condition that ter of users in each center We discuss numerical algorithms and computer im- the r umerical solution for a small number of da lems. We can mention the problem of lo onsistent, Available, Partition-Tolerant Web Services,” ACM SIGACT News, Vol. 33, No. 2, 2002, pp. 51-564601 plementation for the construction of hyperbolic Vo- ronoi Diagrams satisfying the capacity conditions. We considethe n ta centers, 2, 3, and 4, and for a large number of data centers. In the latter case we make a plausible assump- tion that most of the data centers have sufficient capacity to service the clients, and the data centers of insufficient capacity are isolated. This allows local construction of the hyperbolic Voronoi Diagram from a standard Vo- ronoi Diagram. Although we discuss the application to the computer cloud only, it is interesting to note that our solution and numerical algorithm can be used to solve other important assignment prob cation of air-bases [8], the assignment of population to regional trauma centers, the distribution of facilities in global Internet companies like Amazon.com, the distri- bution of the telecommunication centers for mobile tele- phones in global telephone companies, data collection centers, and others. REFERENCES [1] S. Gilbert and N. Lynch, “Brewer’s Conjecture and the Feasibility of C 9. doi:10.1145/564585.5 D of the diagram does not exceed the capacity of the corresponding data [2] http://docs.amazonwebservices.com/AWSEC2/latest/ Copyright © 2012 SciRes. IIM  S. SHANMUGAM, C. SHOURABOURA 250 UserGuide/using-regions-availability-zones.html [3] F. Aurenhammer, “Voronoi Diagrams—A Survey of a Fundamental Geometric Data Structure,” ACM Comput- ing Surveys, Vol. 23, No. 3, 1991, pp. 345-405. doi:10.1145/116873.116880 [4] P. Bleher and C. Shouraboura, “Placement of Applica- 37-8 tions in Computing Clouds Using Voronoi Diagrams,” Journal of Internet Services and Applications, Vol. 2, No. 3, 2011, pp. 229-241. doi:10.1007/s13174-011-00 lized Voronoi Diagra in [5] M. Gavrilova, Ed., “Generam: A Geometry-Based Approach to Computational Intelligence (Studies in Computational Intelligence 158),” Springer, New York, 2008. [6] W. A. Johnson and R. F. Mehl, “Reaction Kinetics Processes of Nucleation and Growth,” Transactions of the American Institute of Mining, Metallurgical and Petro- leum Engineers, Vol. 135, 1939, pp. 416-458. [7] J. Møller, “Lectures on Random Voronoi Tessellations. Lecture Notes in Statistics,” Springer-Verlag, New York, 1994. doi:10.1007/978-1-4612-2652-9 [8] A. Okabe, B. Boots, K. Sugihara and S. N. Chiu, “Spatial Tessellations—Concepts and Applications of Voronoi Diagrams,” 2nd Edition, John Wiley, Hoboken, 2000. 0190(79)90074-7 [9] K. Q. Brown, “Geometric Transforms for Fast Geometric Algorithms,” Ph.D. Dissertation, Carnegie Mellon Uni- versity, Pittsburgh, 1979. [10] K. Q. Brown, “Voronoi Diagrams from Convex Hulls,” Information Processing Letters, Vol. 9, No. 5, 1979, pp. 223-228. doi:10.1016/0020- . [11] H.-S. Na, C.-N. Lee and O. Cheong, “Voronoi Diagrams on the Sphere,” Computational Geometry: Theory and Applications, Vol. 23, No. 2, 2002, pp. 183-194 doi:10.1016/S0925-7721(02)00077-9 Copyright © 2012 SciRes. IIM
|