Wireless Sensor Network, 2010, 2, 639-644
doi:10.4236/wsn.2010.28075 Published Online August 2010 (http://www.SciRP.org/journal/wsn)
Research on WSN Double-Radius Localization Algorithm
Based on Partition Judgment Mechanism
Jijun Zhao, Hua Li, Zhiyuan Tang, Xiang Sun
Hebei University of Engineering College of Information & Electronic Engineering, Handan, China
Received May 16, 2010; revised May 27, 2010; accepted June 1, 2010
Abstract
Localization technology is an important support technology for WSN(Wireless Sensor Networks). The cen-
troid algorithm is a typical range-free localization algorithm, which possesses the advantages such as simple
localization principle and easy realization. However, susceptible to be influenced by the density of anchor
node and uniformity of deployment, its localization accuracy is not high. We study localization principal and
error source of the centroid algorithm. Meanwhile, aim to resolve the problem of low localization accuracy,
we proposes a new double-radius localization algorithm, which makes WSN node launch periodically two
rounded communications area with different radius to enable localization region to achieve the second parti-
tion, thus there are some small overlapping regions which can narrow effectively localization range of un-
known node. Besides, partition judgment mechanism is proposed to ascertain the area of unknown node, and
then the localization of small regions is realized by the centroid algorithm. Simulation results show that the
algorithm without adding additional hardware and anchor nodes but increases effectively localization accu-
racy and reduces the dependence on anchor node.
Keywords: Wireless Sensor Networks; Localization Technology; Centroid Algorithm; Double-Radius
Localization Algorithm; Partition Judgment Mechanism
1. Introduction
Localization technology, the premise to realize related
applications from determining the localization of the
incident or locking access to the node localization of the
message by wireless sensor network, is a key support
technology in WSN. Node localization information plays
an important part in the target tracking, auxiliary routing,
network management and many other areas [1]. There
are two types of localization algorithms in localization
technology, range-based and range-free localization al-
gorithm. In recent years, with the obvious advantages,
range-free localization algorithm has attracted much at-
tention, meanwhile the centroid algorithm is a typical
range-free localization algorithm which makes full use of
the connectivity of network to locate with the obvious
advantages in simple localization principle, little power
consumption and easy realization. But its localization
error has been prone to influence by the issues such as
laying uniformity of anchor node and density of anchor
nodes [1,2]. In order to solve the problem, the article
studies centroid algorithm principle and error sources of
localization and proposes double-radius algorithm based
on partition judgment mechanism. The algorithm without
adding additional hardware and anchor nodes but in-
creases effectively localization precision and reduces the
dependence on anchor nodes.
2. The Centroid Algorithm and Error
Analysis
2.1. Research on the Centroid Algorithm
In the WSN localization technology, the range-free lo-
calization algorithm with the obvious advantages has
been researched by lots of scholars. Due to its unique
characteristics and advantages, the centroid localization
algorithm is simple in principle with easy realization as
well as little communication expense, so the typical
range-free localization algorithm has get more con-
cerned.
In [3], the enhanced centroid localization algorithm
was proposed. The algorithm, by using more anchor
nodes localization information indirectly from the infor-

J. J. ZHAO ET AL. 640
mation exchange with unknown neighbor nodes, with the
addition of a small amount of traffic circumstances,
made the localization accuracy of anchor node randomly
distributed improved greatly and provided a new option
for node localization in WSN. Furthermore, some re-
searchers proposed decentralized intensity-weighted
multi-hop field centroid localization algorithm improving
localized nodes ratio by multi-hop centroid calculating
and localization accuracy by decentralizing process and
signal strength-weighting process. Compared with the
original centroid algorithm, the average localization error
of the algorithm can be reduced by half or so, and the
localized ratio under the circumstance of low node den-
sity is close to 1 [4].
The paper studies the centroid algorithm from the
view of division judgment in communication district.
Firstly, fundamental questions such as localization prin-
ciple, characteristics and error source of localization are
researched. Then, double-radius localization algorithm
based on partition judgment mechanism is improved to
solve low localization accuracy.
2.2. The Localization Principle and the Pros and
Cons of the Centroid Algorithm
The basic idea of the centroid algorithm is that, using the
geometric centroid to its own estimated localization
which is covered by unknown node and the polygon
which composed of overlay area of beacon node’s com-
munication area in the communication range of the un-
known node. Centroid is the geometric center of a poly-
gon. The average of each vertex coordinates in a polygon
is the coordinate of centroid. The centroid algorithm de-
fines the district containing unknown node firstly,
namely the polygon containing unknown node, then cal-
culates the centroid of the polygon which is the localiza-
tion of the unknown node.
In the centroid algorithm, anchor nodes periodically
broadcast beacon packets which contain anchor node
identification number and localization information to the
neighbor nodes. When the unknown node receives the
amount of beacon group from different anchor nodes
exceeds a certain threshold k or achieves a certain local-
ization accuracy, it will define the centroid of polygon
consisted by these node as its localization.
11
...... ......
,( ),(
iiki
est est)
ik
X
XY Y
XY kk
 

（） ,
(Xi1, Yi1)… (Xik, Yik) is the unknown node can receive the
anchor node coordinates information [5,6].
The centroid localization algorithm is simple in princi-
ple, easy to algorithm realization with small amount of
calculation, without additional hardware, fully Web-based
connectivity, and without coordination between anchor
nodes and unknown nodes [7].
However, centroid is the estimate as the localization of
practical node, the accuracy and anchor node density of
this estimate is related greatly with the evenness of node
distribution, the bigger the density, more uniform of dis-
tribution, and the higher localization accuracy. Besides,
the estimated is also related to the regular level of node’s
wireless signal propagation model, the closer to ball style,
the higher degree.
2.3. Error Analysis [8,9]
Through the above analysis on localization principle of
the centroid algorithm shows that the localization error
of the centroid algorithm has the following four main
sources. Take three anchor nodes to locate an unknown
node as an example.
1) Centroid is the estimate as the localization of prac-
tical node
In the centroid algorithm, according to the connec-
tivity among nodes can determine the region of unknown
node, as shown in Figure 1. It can be defined that node
N1 is inside overlap region A, B, C of three circles, but it
can tell detailed localization of the node. The method
that the algorithm defined the geometric centre N0 of
overlapping region polygon as the actual localization of
unknown node N1 is an estimate.
2) Unreasonable distribution of anchor nodes leading
to big communication overlap region brings about the
error
In the centroid algorithm, the localization accuracy is
impacted by of anchor nodes distribution. When the an-
chor nodes are closer to the communication region of
unknown node and the distribution are more uniform, the
communication overlapping regions are smaller with
more accurate localization. However, sometimes it is
impacted by environmental constraints, so the node can-
not be distributed ideally, but with random laying nodes.
Nevertheless, some nodes have a greater localization
error. As shown in Figure 2, ABC are communication
overlapping regions of three anchor nodes, where N1 is
the actual localization of unknown nodes, N0 is the node
localization to be obtained. When the anchor nodes A, B
and C are laid closely, overlapping regions is too large
Figure 1. Localization diagram of the centroid algorithm.

J. J. ZHAO ET AL.641
Figure 2. Localization diagram of the centroid algorithm.
resulting in large localization errors.
3) The error due to a small amount of anchor node
The localization accuracy is impacted by density of
unknown node’ neighbor nodes, the greater the density,
the smaller the overlap area of each anchor node’ com-
munication region, thus with a higher localization accu-
racy. With the less amount of anchor node, the overlap of
communication region is bigger, thus with higher local-
ization error. As Figure 3 shows that range of overlap
region is larger with just two anchor nodes, so the local-
ization error is higher.
4) Communication regions are not regular spheroid
The centroid algorithm localization accuracy is im-
pacted by the degree of regular level of node’s wireless
signal propagation model. As Figure 4 shows, the com-
munication regions formed by the wireless signal emitted
from node is not a regular spheroid, the more regular the
shape, the smaller the error.
3. Double-Radius Localization Algorithm
3.1. Algorithm Idea
From the above analysis, we can see that the centroid
algorithm is using the overlap part of beacon node’s
communication area to determine the unknown node
areas and calculate the area coordinate of centroid, the
more number of anchor nodes, the more communication
area, when the overlap part is more smaller, the localiza-
tion is more precise, so reducing the scope of overlap
part can improve the localization accuracy. Increasing
the anchor nodes can improve the localization accuracy,
but it will increase input costs, it will be the research
focus that how to achieve multiple communications areas
without increasing anchor node and thus getting as small
as possible overlap of communication area.
We proposes double-radius algorithm based on parti-
tion judgment mechanism, the basic idea is that anchor
node transmits periodically different power signals to
produce two rounded communications area with different
radius, and then realizes a number of overlapping com-
Figure 3. Localization diagram of the centroid algorithm.
Figure 4. Localization diagram of the centroid algorithm.
munication area without increasing the case of anchor
node, it can get a smaller communication overlap part,
just as a secondary partition in the region.
Double-radius localization algorithm uses the two
communication area with different radius which is laun-
ched by node to achieving partition, if the partitions are
uneven and thereby causing occurrence of a larger local-
ization region, but the smaller partition will be good for
localization. The localization results would be influenced
by the ascertainment of the small radiuses and its relation
with big radius which are related to actual application
and layout of anchor nodes. The aim is to achieve uni-
form partition to avoid large overlap.
The centroid algorithm and dual-radius localization
mechanism will be compared from a qualitative point of
view to show advantages of dual-radius localization al-
gorithm. Shown in Figure 5, one solid circle is the node
communication radius under high-power and dashed
circle is the node communication radius under low power.
In Figure 5(a), the centroid algorithm is used to locate
unknown node N1, the result is the centroid N0 of re-
gional BDF, showing a large error. When calculating the
node N2，the centroid of overlap region ABDF, there is
a serious error. In Figure 5(b), using double-radius lo-
calization mechanism to divide the region ABCDEF into
19 small regions, then using partition judgment to ascer-
tain the smallest region, then calculating centroid of the
region, we can obtain that the centroid of region 11 is
coordinate of node N1 and the centroid of region 1 is
coordinate of N2. Obviously, error of double-radius lo-

J. J. ZHAO ET AL. 642
O1、02、O3:Anchor node
O1O2
O3
N1
N0
N2
A
B
CDE
F
1
1
234
567
8910
11
12
13
14
15 16
17
18
19
A
B
C
D
E
F
O1
O1O2
O3
N0Obtained node location
a
：
b (a) (b)
Figure 5. Comparison of the centroid algorithm and double-
radius algorithm.
calization algorithm is smaller than error of centroid.
It will be seen that the double-radius localization algo-
rithm can ascertain unknown node in a small region
without increasing anchor node and additional hardware.
Centroid coordinate, which considered unknown node
coordinate, is obtained using the centroid algorithm in
the region.
3.2. Double-Radius Localization Algorithm
Design
It was shown in Figure 5, nodes transmit signal periodi-
cally with different power, appearing alternately two dif-
ferent radius of communication area, communications
radius under high-power is R(m), the communications
radius under low-power is r(m), the coordinates of O1 is
(X1, Y1), the coordinates of O2 is (X2, Y2), the coordinates
of O3 is (X3, Y3). Communication regions under different
power correspond to the different equation of circle.
Meanwhile, both of the two signals have the ID of node,
the equation message of the two circles and the different
mark, which is easy to receive node to discern it.
The equation of the circle which is corresponded by
node O1, O2, O3 is as follows:
O1 (1)

2
2
1
RXX YY 

2
1

2
1

2
2

2
2

2
3

2
3














2
2
1
rXXYY (2)
O2 (3)

2
2
2
RXX YY

2
2
2
rXX YY (4)
O3 (5)

2
2
3
RXX YY 

2
2
3
rXXYY (6)
4. Partition Judgment Mechanism
Partition judgment mechanism is a method to define the
region of unknown node according to the signal received
by it. As shown in Figure 5, a communication region is
divided into 19 small regions; through partition judgment
mechanism to get the location of node. The followings
are the judgment methods to define the region of the un-
known node according to the different signals it receives.
1) When the node only receives the high-power com-
munication signals from node O1 and node O2, using its
corresponding Equations (1-4) reaches the equation of
intersection regions; the region is shown in Figure 1,
thus using the centroid algorithm to calculate the cen-
troid of the small region.




22
2
11
22
2
11
22
2
22
22
2
22
RXX YY
rXX YY
RXX YY
rXX YY
 

 

 

 


2) When the node only receives the power signal of
the size O1, O2 high-power signals and O3 high-power
signal, using the corresponding Equations (2,4-6) to as-
certain the region in Figure 5.





22
2
11
22
2
22
22
2
22
22
2
33
22
2
33
rXXYY
RXX YY
rXX YY
RXX YY
rXXYY
 

 

 

 

 


3) When the node only receives the low-power signals
O1, O2, and high-power signals O3, using the corre-
sponding Equations (2,4-6) to concludes the region 6.




22
2
11
22
2
22
22
2
33
22
2
33
rXXYY
rXXYY
RXX YY
rXXYY
 

 

 

 


4) When the node only receives the O1 power signal,
O3 power signal and O2 high-power signals, using the
corresponding Equations (2-4,6) to conclude the region
8.




22
2
11
22
2
33
22
2
22
22
2
22
rXXYY
rXXYY
RXX YY
rXX YY
 

 

 

 


5) When the node only receives the O1 low-power sig-
nal, O2 low-power signal and O3 low-power signal, using

J. J. ZHAO ET AL.643












the corresponding Equations (2,4,6) to conclude the re-
gion 9.



22
2
11
22
2
22
22
2
33
rXXYY
rXXYY
rXXYY
 

 

 


6) When the node only receives the O1 high-power
signals, O2 high-power signals, and O3 low-power signal,
using the corresponding Equations (1-4,6) to conclude
the region 11.





22
2
11
22
2
11
22
2
22
22
2
22
22
2
33
r
RXX YY
rXX YY
RXX YY
XX YY
rXXYY
 
 
 
 
 
7) When the node only receives the O1 power signal
and O2 high-power signals, using the corresponding Equa-
tions (1-4) to reach the intersection region 2, 5, 8.



22
2
11
22
2
22
22
2
22
rXXYY
RXX YY
rXX YY
 
 
 

8) When the node only receives the O1 power signal
and O2 power signal, using the corresponding Equations
(2,4) to reach the intersection region 3, 6, 9.


22
2
11
22
2
22
rXXYY
rXXYY
 

The remaining region and the solved region have a
symmetrical relationship, so they can be obtained as
above.
In article, it takes that an unknown node can be located
with three anchor nodes as example. In the case of mul-
tiple anchor nodes, an unknown node can be located.
That is, the unknown node uses the communication re-
gion equation of all the anchor nodes received, it deter-
mines the unknown node’s location according to parti-
tion judgment mechanism, and then uses the existing the
centroid algorithm to get the centroid of this region.
5. Algorithm Simulation
In this simulation we use MATLAB, and the basic idea is:
Firstly, we simulate the location environment and motion
tracks of the node, use dual-radius algorithm and the
centroid algorithm to derive moving nodes’ theoretical
trajectories respectively, and then compare their fitting
degree intuitively. Secondly, using the two algorithms to
calculate the location at every 20m respectively, get the
two theoretical error value of localization, thus derive the
average value, and finally compare the average error
value of the centroid algorithm and dual-radius localiza-
tion error algorithm.
It is shown in Figure 6, we select three anchor nodes
randomly, these are the black point positions at the cen-
ter of these circles, here we assume the coordinates:
(0,0),(-45, 453),(45, 453), and the big circle ra-
dius:90m, the smaller one:60m, then verify our algorithm
in several instances which select quadratic spline curve
to simulate the moving target. In Figure 6, black spots
with crosses are the centroid of overlapping regions; the
compacting curve is the actual trajectory of the node to
be tracked, the dashed line is the virtual trajectory which
is measured by these two algorithms respectively. The
closer the two curves are, the more accurate positioning
we did, we can see that the curve which corresponds to
dual-radius algorithm is closer to the node’s actual tra-
jectory.
As described above, we select 9 positions as the ab-
scissa axis in Figure 6, and the negative sign on the op-
posite direction. We figure out theoretical locations of
these none nodes through the centroid algorithm and the
dual-radius algorithm respectively. Figure 7 is the error
line graph for algorithms, in which thick lines is the error
curve for double-radius algorithm, and the thin one is for
the centroid algorithm, because of their symmetry rela-
tions respectively, we get positioning error values for the
5 position, as shown in Table 1.
Data show that, the average error and accuracy of dou-
ble-radius algorithm are 3.26 m and 3.62% respectively.
However, the parameters of the centroid algorithm are
9.46 m and 10.51%. Obviously, dual-radius algorithm
has a higher positioning accuracy, reducing the depend-
ence on the anchor node, reaching a large extent better
than the centroid algorithm, and is able to meet the needs
of the usual location when there are no additional anchor
nodes and no extra hardware resources. Dual-radius al-
gorithm also has its own inadequacies, it requested the
node periodically launching two different power signals
in order to determine the areas that the unknown node to
be located, and the algorithm power is slightly higher
than the centroid algorithm power.
6. Conclusions
Localization accuracy of the centroid algorithm is low
but related to neighbors’ density of anchor node and dis-
tribution evenness. In the practical application, the algo-
rithm is constrained by the density and distribution of
node without ideal localization accuracy.
To solve the above problems, the paper proposes dou-
ble-radius localization algorithm based on partition judg-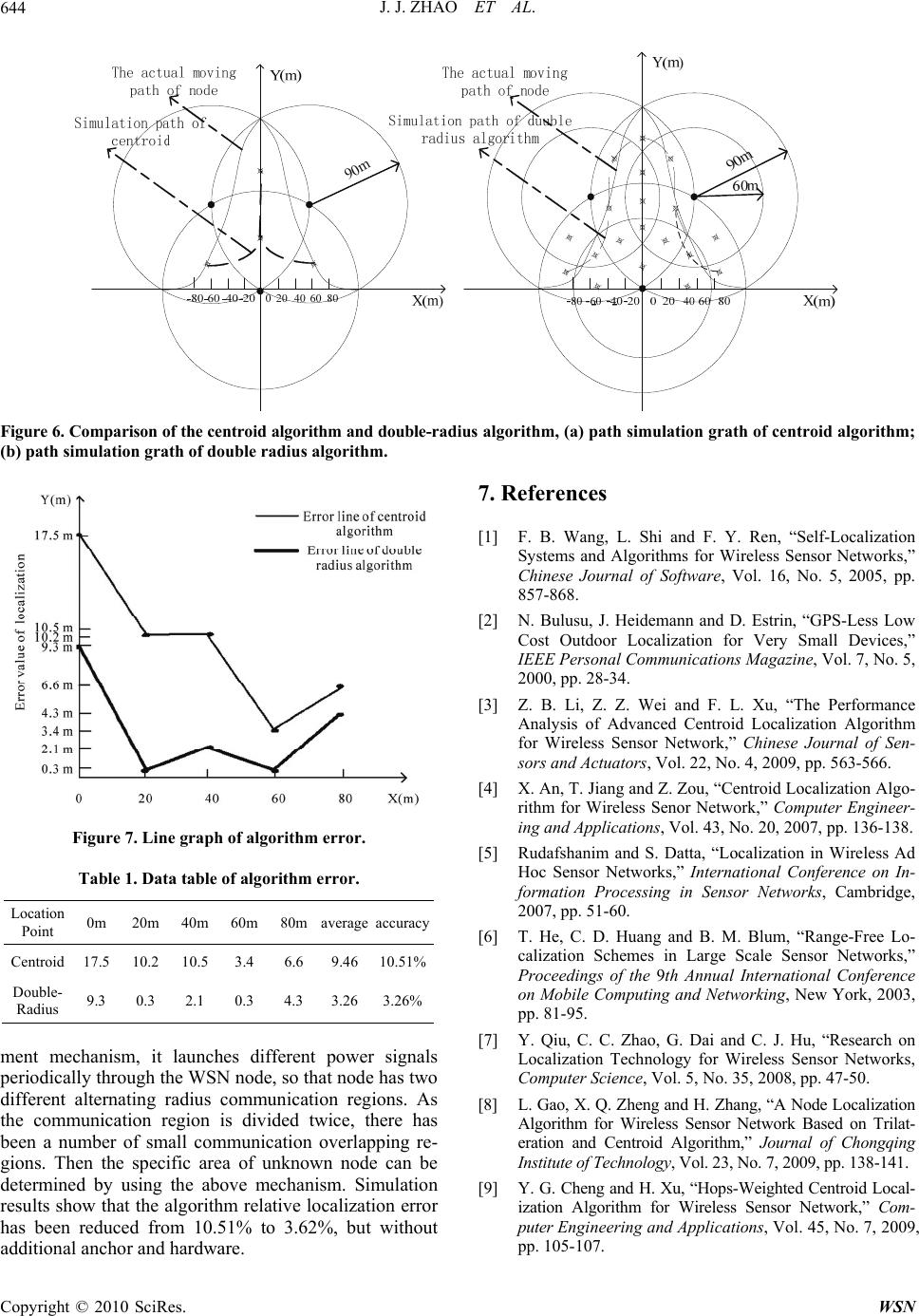

J. J. ZHAO ET AL. 644
Figure 6. Comparison of the centroid algorithm and double-radius algorithm, (a) path simulation grath of centroid algorithm;
(b) path simulation grath of double radius algorithm.
7. References
[1] F. B. Wang, L. Shi and F. Y. Ren, “Self-Localization
Systems and Algorithms for Wireless Sensor Networks,”
Chinese Journal of Software, Vol. 16, No. 5, 2005, pp.
857-868.
[2] N. Bulusu, J. Heidemann and D. Estrin, “GPS-Less Low
Cost Outdoor Localization for Very Small Devices,”
IEEE Personal Communications Magazine, Vol. 7, No. 5,
2000, pp. 28-34.
[3] Z. B. Li, Z. Z. Wei and F. L. Xu, “The Performance
Analysis of Advanced Centroid Localization Algorithm
for Wireless Sensor Network,” Chinese Journal of Sen-
sors and Actuators, Vol. 22, No. 4, 2009, pp. 563-566.
[4] X. An, T. Jiang and Z. Zou, “Centroid Localization Algo-
rithm for Wireless Senor Network,” Computer Engineer-
ing and Applications, Vol. 43, No. 20, 2007, pp. 136-138.
Figure 7. Line graph of algorithm error. [5] Rudafshanim and S. Datta, “Localization in Wireless Ad
Hoc Sensor Networks,” International Conference on In-
formation Processing in Sensor Networks, Cambridge,
2007, pp. 51-60.
Table 1. Data table of algorithm error.
Location
Point 0m 20m 40m 60m 80m averageaccuracy
Centroid 17.5 10.2 10.5 3.4 6.6 9.46 10.51%
Double-
Radius 9.3 0.3 2.1 0.3 4.3 3.26 3.26%
[6] T. He, C. D. Huang and B. M. Blum, “Range-Free Lo-
calization Schemes in Large Scale Sensor Networks,”
Proceedings of the 9th Annual International Conference
on Mobile Computing and Networking, New York, 2003,
pp. 81-95.
[7] Y. Qiu, C. C. Zhao, G. Dai and C. J. Hu, “Research on
Localization Technology for Wireless Sensor Networks,
Computer Science, Vol. 5, No. 35, 2008, pp. 47-50.
ment mechanism, it launches different power signals
periodically through the WSN node, so that node has two
different alternating radius communication regions. As
the communication region is divided twice, there has
been a number of small communication overlapping re-
gions. Then the specific area of unknown node can be
determined by using the above mechanism. Simulation
results show that the algorithm relative localization error
has been reduced from 10.51% to 3.62%, but without
additional anchor and hardware.
[8] L. Gao, X. Q. Zheng and H. Zhang, “A Node Localization
Algorithm for Wireless Sensor Network Based on Trilat-
eration and Centroid Algorithm,” Journal of Chongqing
Institute of Technology, Vol. 23, No. 7, 2009, pp. 138-141.
[9] Y. G. Cheng and H. Xu, “Hops-Weighted Centroid Local-
ization Algorithm for Wireless Sensor Network,” Com-
puter Engineering and Applications, Vol. 45, No. 7, 2009,
pp. 105-107.