 Modern Economy, 2012, 3, 658-670 http://dx.doi.org/10.4236/me.2012.35085 Published Online September 2012 (http://www.SciRP.org/journal/me) Effectiveness of Child Care Policies in an Economy with Child Care Services Masaya Yasuoka1, Atsushi Miyake2 1Faculty of Economics and Business Administration, The University of Kitakyushu, Kitakyushu, Japan 2Faculty of Econo m i c s , Kobe Gakuin University, Kobe, Japan Email: yasuoka@kitakyu-u.ac.jp, miyake@eb.kobegakuin.ac.jp Received June 28, 2012; revised July 25, 2012; accepted August 4, 2012 ABSTRACT This paper describes how fertility is determined in a model that assumes the existence of child-care services. When child-care services exist, two multiple states result: a state that brings about low fertility with low female labor partici- pation, and a state that bring s about high fertility with high female labor participation. This resu lt is consistent with the positive correlation th at is found between the total fertility rate and female labor participation in developed coun tries, as described by Ahn and Mira (2002) [1] and others. Moreover, this paper presents analyses of the effects of child-care policies, for example, a child allowance and a subsidy for child-care services policies. These policies instantaneously raise fertility. However, in a dynamic general equilibrium model, these policies might pull down fertility because capital accumulation decreases in the long run. If income growth continues in the long run, then the child allowance can always pull up fertility. However, if the income level converges to constant level in the long run, then the child allowance mig ht pull down fertility. This result shows that the effect of the child allowance depends on whether income growth ceases or continues in the long run. Keywords: Child-Care Policies; Child-Care Services; Fertility Rate; Labor Participation 1. Introduction We find three positive correlations in developed coun- tries: fertility and female labor participation, fertility and income per capita, and fertility and the magnitude of gov- ernmental family policy. First, the analyses described in this paper demonstrate the positive correlation between fertility and female labor participation. As described by Ahn and Mira (2002) [1], Sleebos (2003) [2], and Yamaguchi (2005) [3], the correlation between fertility and female labor participation in developed cou n- tries was negative in the 1980s (cross-country compare- son). However, that negative correlation has weakened gradually. In recent years, the correlation has changed to a positive one. One explanation for the change in the cor- relation from negative to positive is the enrichment of child- care services. Figure 1 presents the female labor partici- pation rate and total fertility rate in developed countries. As Sleebos (2003) [2] and others poin t out, it is apparent that the higher the female labor participation rate is, the higher the fertility rate is1. By virtue of child-care services, parents need not pay an opportunity cost for children. Even if parents have ch il- dren, they can continue working. Thereby, they gain wa ge income and can yet afford to have more children. Com- patibility between child-care and working is the reason that the negative correlation between fertility and female labor participation is weak ened and chang es to a positive correlation. Galor and Weil (1996) [6] set a theoretical model in- corporating a gender gap in the wage rate and derived a y=0.0201x+0.0647 R²=0.278 1 1.2 1.4 1.6 1.8 2 2.2 60 65 70 75 80 8590 To talFertilityRate FemaleLaborParticipationRate(25‐54YearsOld)(%) 1It is necessary to consider that the difference of female labor p a rt i c i p at i o n is related to labor market factors as well. Kögel (2004) [4]considered country-specific factors and country-heterogeneity and derived the neg- ative correlation between fertility and female labor participation. Enge- lhardt and Prskawetz (2004) [5] identified variables indicating country heterogeneity. Figure1. Positive correlation between total fertility rate and female labor participation. C opyright © 2012 SciRes. ME  M. YASUOKA, A. MIYAKE 659 negative correlation between fertility and the female labor participation rate. An increase in the female labor wage pulls up the labor supply. Therefore, fertility decreases. Apps and Rees (2004) [7] introduced child-care services, which can produce compatibility between child care and working, and derived a positive correlation. Apps and R ee s (2004) [7] assumed a fertility function into which a par- ent’s child care and market child-care services are input- ted; it gives constant returns to scale. Hirazawa and Yakita (2009) [8] specified an elasticity between a parent’s c hi ld - care time and market child-care services and derived fer- tility dynamics for a small open economy. y=0.007x+0.8297 R²=0.4084 1 1.2 1.4 1.6 1.8 2 2.2 406080100 120 140 160 TotalFertilityRate Incomepercapi ta Martínez and Iza (2004) [9] analyzed how fertility is determined under the assumption of complete substitution between a parent’s child care and market child-care ser- vices in a dynamic general equilibrium model and deriv ed a positive correlation between fertility and female labor participation. Yasuoka (2008) [10 ] assumed a constant elas- ticity of substitution (CES) fertility function, which is de- termined by the parent’s child care and market child-care services. Some studies assumed a different fertility func- tion2. Martínez and Iza (2004) [9] insisted that an increase in the skill premium decreases fertility directly; however, market child-care services not only prevent a decrease in fertility but also bring about a positive relation between fertility and the skill premium (capital per capita, labor participation). Galor and Weil (1996) [6] described that an increase in the skill premium decreases fertility because of the ab- sence of market child-care services3. Consequently, with market child-care services considered by Apps and Rees (2004) [7] or Martínez and Iza (2004) [9] in the model economy presented by Galor and W eil (1996 ) [6 ], a posi- tive relation is apparent between fertility and female la- bor participation. Second, this paper considers the positive correlation between fertility and income per capita. The positive cor- relation in developed countries is confirmed to exist be- tween total fertility and income per capita, as shown in Figure 2. Aarssen (2005) [13 ] showed a negative correlation be- tween fertility and income per capita in 223 countries, including both developed and developing countries. This negative correlation is natural because the infant mortal- ity rate is high and parents typically consider children as insurance or investment goods in low-income countries. Figure 2. Positive correlation between total fertility rate and inco me p e r cap it a . Confronting a poor social security system, parents depend on their children in their old age. However, in economi- cally developed countries, which have high income per capita, because of the social security s ystem, parents n eed not depend on children. Other reasons are that child-care costs are high (Educational costs or opportunity costs for child care4) or that parents wan t to in crease the quality of life by decreasing the number of children they plan to have. However, Figure 2 shows the positive correlation between fertility and income per capita in developed c oun - tries. This fact is consistent with theoretical analyses in a market child-care service model (Apps and Rees (2004) [7], Martínez and Iza (2004) [9], Hirazawa and Yakita (2009) [8]). Models that do not consider market ch il d - ca r e services explicitly show a positive correlation (Oshio (2001) [18], van Groezen, Leers and Meijdam (2003) [19], van Groezen and Meijdam (2008 ) [20], Fanti and Gori (2009 ) [21], and others). Third, this paper presents examination of the positive correlation between fertility and the magnitude of gov- ernmental family policy. Although market child-care services play an important role in an increase in the fertility, family policy plays an important role in raising fertility, too. McDonald (2006) [22] surveyed some earlier papers that examined family policy. Some earlier papers showed that financial incen- tives can be effective for increasing fertility (Lutz (1999 ) [23], Milligan (2002) [24], Laroque and Salanie (2005) [25]). In fact, a positive correlation is shown between the fertility and the magnitude of family policy in developed countries, as depicted in Figure 3. This paper describes analyses of the degree to which an d the manner in which fertility is affected by market child - care services and child-care policy, using a model that as- sumes complete substitution between individual child care and child-care services, as in Martínez and Iza (2004) [9]. 2For example, Momota (2000) [11] assumed a fertility function bywhi c h child care by both men and women in addition to governmental service determines fertility. Yasuoka (2007) [12] considered the fertilityf unction, which is determ ined usi ng a par ent’s c hild care an d gover nm ental services. 3Capital accumulation pulls up the wage rate in skilled sector. In Galor and Weil (1996) [6], capital accumulation is described as pulling upthe wage rate of female laborers, which shrinks wage inequality between men and women. An increase in the skill premium corresponds to shrin- king wage inequality between men and women. 4Becker (1960) [14]set the quality and quantity of children model and derived an increase in income raises the quality and decreases quantity because of an opportunity cost. Becker, Murphy, and Tamura (1990) [15], de la Croix and Doepke (2003) [16] and Kimura and Yasui (2009) [17] considered the quality of children as reflected in educational invest- ment for children. Copyright © 2012 SciRes. ME  M. YASUOKA, A. MIYAKE 660 Japan ItalyGermany U.K. France Sweden y=0.2142x+1.0545 R²=0.7959 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 0.00.51.01.52.02.53. TotalFer tilityRate GovernmentExpenditure RelatedF amilyPo 03.54.0 licy/GDP(%) Figure 3. Child-care support policy and the total fertility rate5. This paper presents the following results. Given some parametric conditions, the existence of market child-care services, which rich households consu me, brings about o ne of two states: 1) A state of low-fertility equilibrium with low female labor participation, low income and high in- come growth; or 2) A high-fertility equilibrium with high female labor participation and high income (and low in- come growth). Without market child-care services, one steady state ex - ists with low fertility, low female labor participation and high income growth. Therefore, fertility remains at a low level. However, with market child-care services, the steady state changes to one with high fertility, high female labor participation and low income growth (or high income w i t h no income growth). Therefore, market child-care services raise the fertility an d female labor participation rate, w hi ch indicates a positive correlation between fertility and fe- male labor participation. Zhang (1997) [26] set the model with quality and quan - tity of children. With a small cost for in crease in quantity of children, the equilibrium with high fertility and low income growth rate is derived. Quality and quantity of children show a negative relation between fertility and the income growth rate; our paper derived a negative relation without quality and quantity of children. In the latter part of this paper, we present analysis of whether child-care policies (e.g., a child allowance poli- cy—households receive an allowance in proportion to the number of children they have—or a subsidy for child- care services) can raise the fertility rate. As presented in Figure 3, an active child-care policy brings about a high fertility rate. This paper shows that the effects of child-care po licies differ in the short run a nd in the long run. In the short run, a rise in fertility incre as es the labor supply in th e subsequ ent period, resultin g in the decrease of income in the subsequent period because ac- cumulation of capital per capita is prevented. Therefore, in the long run, fertility doe s not always increase because of the fall in income. This paper shows that the child allowance does not always raise fertility. However, if income growth continues in the long run, then a child al- lowance can always raise fertility. If income converges to a steady state with constant income, the child allowance can not always raise fertility, which conclusions are closely consistent with those reported by Fanti and Gori (2009) [21]; how ever, w ith contin ued inco me grow th, the effects of a child allowance differ from those described by Fanti and Gori (2009) [21]. In summary, child-care support po l ic i e s ca n r a is e f er t ility in the sh ort run, but the long-run effects of the policies are unclear. The dynamic general equilibrium model brings about results that demonstrate that the government must consider effects of child-care policies in the short run as well as in the long run before implementing them. This paper is structured as follows. Section 2 explains our model setting. Section 3 provides a descrip tion of the dynamic equilibrium. Section 4 analyzes the child-care policy. Section 5 presents ex aminatio n of a case in which a child-care service fee depends on the wage rate. The final section presents concluding remarks. 2. The Model The model economy in this paper is constructed in terms of a two-period (young and old) overlapping generations model. The economy comprises agents of three types: households, firms, and the child-care service sector. We explain the agents in the following subsections. 2.1. Households Individua ls in household s live in two periods: young an d old6. Each household supplies labor and gains labor in- come only during t he y oung period, when in d i vi dual s raise their children. The analyses described herein assume that it is necessary for households (parents) to input their ch ild- care time and child-care goods to have children. House- holds have one unit of time, which is assumed to be allo- cated to labor and child care. However, for these analyses, we assume that child-care services exist. If households 5Data: OECD Database (OECD Stat Extracts) (OECD), Demographic Yearbook (UN) and Vital Statistics in Japan (Ministry of Health , Labour and Welfare (in Japan)). The Fertility in Figures 1 and 2an average level for 2000-2007. The female labor participation rate (25 - 52 years old) in Figure 2 is an average level for 2000-2007. The income per capita in Figure 2 is an average level f or 2000-2007. The OECDav e r a g e income per capita is fixed as 100. Figures 1 and 2 show data for Au stral ia , Austria, Denmark, France, Germany, Hungary, Italy, Japan, Net he rl and s, orway, Spain, Sweden, Switzerland, the United Kingdom, and he United States. Government Expenditure Related Family Policy per GDP in Figure 3 is at 2003 and includes a family allowance, maternity and parental leave , other cash be nefits, day-care, home-help and other benefits inkind. Fertility in Figure 3 is at 2003. 6Strictly speaking, individuals in this model live three periods: childhood, young, and old. However, individuals do nothing during childhood. Therefore, we consider this model as substantially a two-period model. Copyright © 2012 SciRes. ME  M. YASUOKA, A. MIYAKE 661 pay a fee to use child-care services, then the child-care time per child will decrease to zero and they can work full time. Each individual distributes labor income across child-care goods and consumption during young and old periods. We obtain the following budget constraint if house- holds do not u se child-care servi ces : 21 11 1t tt t t c zn cn r 1,01, t w (1) where nt represents the number of children; c1t and c2t+1 respectively denote consumption by young and old gen- erations; rt+1 and wt respectively represent the interest rate and wage rate; and t represents the period. It takes units of time to raise one child. Furthermore, the parents must buy some child-care goods z for their child7. There- fore, the child-care cost per child is z + wt. The higher the wage rate wt is, the higher is the marginal cost to have a child. In contrast, households using child-care services must pay a fee p. Therefore, the necessary child-care time per child decreases and changes to zero8. Households with nt children can supply a unit of labor. We can consider 1 – nt as a couple’s or a female’s labor participation rate9. Then, by virtue of child-care services, the female labor participation rate rises from 1 – nt to 1 (by nt). In this case, we obtain the following budget constraint: 21 1 . 1tt t cw r t wp 1tt zp nc (2) Having nt children, the child-care cost is (z + p)nt. If the child-care cost per child in the case in which house- holds use child-care services is less than that in the case in which they do not, then they use child-care services. This condition can be represented as z + wt > z + p, i.e., . 121 lnln1ln , 0, 1,1 ttt t uccn 1tt cw (3) Households use child-care services if this condition is satisfied. The households’ utility function ut is assumed as (4) It is assumed that households gain utility not from the ir children’s lifetime utility but simply by having chil- dren10. Next, we consider the optimization problem in t wo cases: 1) The case in which households use child-care services; and 2) The case in which they do not use these services. 2.1.1. Case in Wh i ch H ouseholds Do No t Use Child-Care Services Each household maximizes its utility (4) under the bud get constraint (1). We therefore obtain the following optimum equation: (5) 21 1 1 ttt crw (6) no 1t tt w nzw ˆt zzwˆ0 (7) where ntno denotes the number of children in the case in which each household uses no child-care services. We assume the child-care cost z as (z is para- meter)11. Then, ntno is deri ve d as 1 ˆ no t nz ˆ z (8) An increase of the child-care cost in or pulls down the fertility ntno. Even if the wage rate wt rises, then the fertility ntno does not increase because an increase in the wage rate raises child-care cost z and the opportunity cost for children wt. 2.1.2. Case in w h i c h Hous eholds Use Chil d -Care Services Each household maximizes its utility (4) under the bud get constraint (2). Although optimal consumption allocation c1t, c2t+1 is the same as the allocation in the case in which households do not use child-care services, nt differs from this case. The number of children (fertility) in this case ntcare is shown as 7van Groezen, Leers and Meijdam (2003) [19] introduced the survey on measurement of the cost of children by Praag and Warnaar (1997) [27]. As in the analysis by van Groezen, Leers and Meijdam [19], this pape considers z as the quality of a child, which reflects the consumption o food, clothing, education, and so on. 8Martínez and Iza (2004) [9] assumed that parents need no time for having children if they us e c hil d-care services, too. 9Apps and Rees (2004) [7] consid ered labor of two types: labor supplied using a working husband and labor supplied using a wife, a female h om- emaker. The y assumed th at a worker supplies a unit of la or inelastically and that a female homemaker supplies labor net of the child-care time. They considered the labor supply offered using a female homemaker as the female labor participation rate. Then, the couple’s labor supply beco- mes 2 – nt because the male supplies a unit of time and the female supplies 1 – nt unit of time. However, we assume the couple’s time as one. Therefore, the couple’s labor time is 1 – nt. This assumption does not affect the following results. If we assume that the labor is supplied inelastically by a male worker, as described in earlier studies, then we can consider 1 nt as the female labor participation rate. care 1 ˆ t tt w nzw p (9) Then, nt = ntcare in wt > p. Other wi se , nt = ntno. 10This assumption is conventional in the endogenous fertility model and is identical to that described in Eckstein and Wolpin (1985) [28], Galor and Weil (1996) [6], van Groezen, Leers, and Meijdam (2003) [19], and others. 11This paper assumes that child-care cost z increases concomitantly with an increase in the wage rate wt. This child-care cost, which is ulled up by an increase in wage income, is assumed in van Groezen and Meijdam (2008) [ 20] and Wigger (1999) [2 9]. Copyright © 2012 SciRes. ME  M. YASUOKA, A. MIYAKE 662 2.2. Firms We assume that the rep resen ta tiv e fir ms th at h ave co nstan t returns to scale production function can be represented as 2 ,, 0, i iii t tttt i t ii tt ii tt t Y YFKBLK YY BL K 2 22 0, 0, 0, i t i tt Y BL (10) where Yti denotes the firm i’s output and Kti and Lti respec- tively signify firm i’s capital stock and labor. In addition, Bt represents labor productivity, which is equal among firms and which is assumed as 1,0 t t K Bb Lb bfbb t (11) Labor productivity Bt is dependent on the capital per labor input, which is also assumed in Romer (1986) [30] and Grossman and Yanagawa (1993) [31]. Therein, Kt and Lt respectively represent aggregate capital stock and agg re- gate labor input. In a perfectly competitive market, consid- ering the symmetry of firms, wage wt and capital rent rt are equal to the marginal product of each factor input. tt wBf (12) t rfb1 (13) We assume that the capital stock fully depreciates wi t h in a period. If we define bfbb , then the w age rate shown by (11) is t tt wbL 1LnN (14) Defining Nt as the population size of young people in t period, ttt unless households use c hi l d- c ar e services, or Lt = Nt if they use it. 2.3. Child-Care Service Sector The child-care service sector supplies child-care services and receives a fee of p per child, which is paid by the parents. It establishes child-care facilities to provide chil d- care services. Originally, in considering the provision of child-care services, we assume that it costs c units of final goods to provide ch ild-care services fo r each child. M a r tí n - ez and Iza (2004) [9] assume that child-care services are produced by unskilled labor input. However, Hirazawa and Yakita (2009) [8] report that child care is produced by inputting market labor as well as market good labor. We assume that child-care services are produced using the latter technology. Then, total rev enue is pntNt and the total expend iture is cntNt. Therefore, assuming profit ma x- imization in a competitive market, we obtain p = c12. Furthermore, c is constant and is measured in terms of market goods. 3. Equilibrium Having considered the agen ts’ behav ior, we proceed to a na- lysis of the equilibrium. The eq uilibrium of this economy depends on the amount of capital-per-capita tt N. Representing the savings per household as st, the capital market clearing condition is given as Kt + 1 = Ntst, i.e., ntkt + 1 = st13. In the followin g subsection s, we derive equ ilib- ria for the case in which child-care services are available and for the case in which these services are not available. 3.1. Equilibrium in No Child-Care Service In the absence of child-care services, labor supply Lt is given as 1t LnN tt . Considering the capital market equilibrium condition 1ttt ksn and the saving per household 1 tt1ttt nw czn ˆ zzw, t, 1LnN ttt , (8) and (14), we obtain the following difference equation for kt: 2 1 ˆ ˆ 1 tt z kk bz (15) Then, wi t h t he de fi n e d in come per ca pit a as yt, the growth rate of income per capita 11ttttt yykk is14 2 1ˆ ˆ 1 t tt z k gkbz (16) We assume that gt>1, i.e., 2 ˆˆ 11zbz . Then, the fertility in this case is given as (8). In this case, both the growth rate of income per capita and fertility are constant over time. 3.2. Equilibrium in Child-Care Service Each household uses child-care services if condition (3) holds. Then, labor supply Lt is given as Lt = Nt. With 1tt ksn t and t he saving per household st = wt – c1t – znt, t ˆ zzw , (9) and (14), we obtain the following difference equation for kt: 1ˆ. 1 tt z kpk b (17) 12Martínez and Iza (2004) [9] assume that child-care service is pr oduced y linear production technology, which has constant marginal cost. As Martínez and Iza (2004) [9] report, the child-care service price is co n s t a n t. However, Yasuoka and Miyake (2010) [32] describe that demand and su pply for child-care services affect child-care service prices in a di ff e re nt model. 13We notify 1ttt nNN . 14With (10) and constant returns to scale, we ob tain tt tt YN KfbN, i.e., tt yfbk. Therefore, 11tttt yykk . We consider 1tt kk as the growth rate of income per capita. Copyright © 2012 SciRes. ME  M. YASUOKA, A. MIYAKE 663 Then, the fertility is shown as care t n1, ˆ t bp zk (18) We consider steady states of two types: one for the steady state defined by the constant growth rate of in- come per capita and the other for that defined by constant capital per capita (income per capita) over time. With (17), 1ttt kk is given as 1ˆ 1 t ttt kpz gkkb (19) If kt , then the growth rate becomes ˆ. z b1 g (20) where g denotes the growth rate in kt. We define ncare, growth as the fertility in con stant growth rate g. Then, ncare, growth is derived as care,growth n1 ˆ z. (21) To obtain this steady state, ˆ zb 11 must hold. If ˆ zb 11 , then the growth of income per capita ceases in the long run, which brings about a steady state of the other type. This steady state is specified by kt +1 = kt = k, where k is the capital per capita at the steady state. Defining ncare, nogrowth as fertility in this case, in this steady state, capital per capita k and the fer- tility ncare, nogrowth are given as , ˆ bp bz 1 k (22) ca nre,nogrowth . b (23) Concluding the dynamics of kt, Figure 4 is depicted as shown below. Figure 4. Dynamics of kt. With condition (3), nno < ncare, nogrowth < ncare, growth15. Therefore, child-care services raise the fertility in the eco- nomy for which no child-care sector exists. In addition, even if gro wth of inco me per capi ta continu es in the s te a d y state with child-care service, then th e growth rate in ch il d- care service (20) is less than that in no child-care service (16)16. Child-care service decreases the growth rate. With a large decrease in th e growth rate, growth ceases and co n- verges to constant capital per capita (22). Without child- care services, the opportunity cost for caring for children (parents must stop working to raise their children) pre- vents parents from choosing to have children. However, with child-care services, the opportunity cost vanishes an d fertility increases. Therefore, it is readily apparent that capital-per-capita kt+1 and the income growth rate gt de- crease. A large decrease in gt halts income growth. The re- fore, the following proposition is established. Propositi on 1 Introduction of child-care services increases fertility. However, it decreases the income-per-capita growth rate in the model economy i n which no child-care sect or exists. Child-care services make child-care and working com- patible: this proposition is an assertion that the countries which suffer from low fertility should carry out family p oli - cies that make child care and working compatible. Beck er and Barro (1988) [33] and Barro and Becker (1989) [34] derived a negative correlation between fertility and the income growth rate. This proposition is consistent with Becker and Barro (1988) [33] and Barro and Becker (1989) [34] even if this model economy setting differs from th os e of Becker and Barro (1988) [33] and Barro and Becker (1989) [34]17. We derived the equilibrium separately for each case. However, based on (3), households use child-care service s. Considering (3) and (14), the condition in which house- holds use child-care services is ˆ ˆ t bp z kz (24) ˆˆˆ kbpzz We define k as ˆ kk . The dynamics of capital per capita (income growth rate) and the fertility in the equilibrium are given respectively as (15) and (8) because households do not use child-care services if t . The dynamics of capital per capita (income growth rate) and the fertility in the steady state are given respectively as (17) and (18) if t. There- fore, we obtain the steady state equilibrium presented in ˆ kk 15We notify ˆ11zb in ncare, nogrowth. 16Subtracting (20) from (16), we obtain . The growth rate (20) is less than (16). ˆ 20z 17Wang, Yip and Scotese (1994) [35] explained that the correlation etween the growth rate of income per capita and population growth is ambiguous in empirical evidence; they examined the determinants o the sign. Copyright © 2012 SciRes. ME  M. YASUOKA, A. MIYAKE 664 Figure 5. Figure 5(a) shows the case of ˆ zb 11 . Considering the steady state characterized by constant in- come per capita growth rate g and constant fertility over time, we obtain two states: one for a state that includes high income growth (or low income per capita), low fer- tility and low female labor p articipation; and the other for a state that has low income growth (or high income per capita), high fertility, and high female labor participation. Figure 5(b) shows the case of ˆ zb 11 . The dynamics of kt converges to constant income growth (20) and the fertility ncare, growth (21) or constant income level (22) and the fertility ncare, nogrowth (23). Then, the fol- lowing proposition is established. Propositi on 2 Two states exist in this model economy: one for a state with low income, high income growth, low fertility, and low female labor participation; and the other for a state with high income (low income growth or no income growth), high fertility and high female labor participation. Finally, the dynamics converges to the steady state, which shows high fertility and high female labor participation even if the fertility and female labor participation are low in an initial period. (a) (b) Figure 5. (a) Steady state with income growth; (b) Steady state with constant income. In tt ˆ kk , fertility, female labor participation and in- come per capita are low. However, capital accumulation raises kt and kt is higher than t. Then, fertility, female labor participation, and income p er capita are higher than the state of tt ˆ k ˆ kk . This result shows a positiv e correla- tion between fertility and female labor participation, and between fertility and income per capita. Although t his result is consistent with the child-care service model (App s and Rees (2004) [7] and Martínez and Iza (2004) [9]), this paper expands Apps and Rees (2004) [7] to a dynamic general equilibrium model and simplifies Martínez and Iza (2004) [9]. 4. Child-Care Policy Analysis This section presents an examination of how child-care policies of two types affect fertility: one for child allow- ance and the other for subsidy for child-care services. Fi r st, we examine the effect of a child allowance. 4.1. Child Allowance We consider a child allowance policy wherein an allow- ance is given to households in direct relation to the num- ber of children they have. The allowance decreases the net child-care cost per child. Assuming that the allowance is financed by a lump-sum tax, then the budget constraint for a no use child-care service is shown as follows18 21 11 ˆ ˆ1 1t tttt tt t c zqwncnwT r ˆ qw ˆ q ˆ ˆ0zq ˆ 01q (25) Therein, t is given for a child, where is the con- stant subsidy rate, assumed as and ˆ tt Tqwn 19. With a balan ced budg et, the lu mp-su m tax Tt i s d etermin ed as t (26) Each household maximizes its utility (4) under the bud- get constraint (25). In addition, con sidering (26), fertility ntno and saving st are given as no 1, ˆ ˆ t nzq (27) no ˆ 1 ttt qn w ˆ q (28) Child allowance always pulls up the fertility ntno, as shown by (27). With (14), (27), and (28) and capital market equilibrium condition 1ttt ksn , we obtain the 18This section assumes a lump-sum tax. For example, we consider t a x a ti o n of another type-a payroll tax. A payroll tax affects the household’s deci - sion to have children through a decrease in the opportunity cost to have children. Then, the policy effect contains not only child allowance effects but also taxation effects. This section uses a lump-sum tax to present a ure policy effect. 19This paper assumes income proportional to the child allowance. The reason is to maintain an appropriate level of child allowance even if an increase in the wage rate wt pulls up child-care cost z. Copyright © 2012 SciRes. ME  M. YASUOKA, A. MIYAKE 665 following difference equation for kt: 1 ˆˆ ˆ 1 zqz bz ˆˆ ˆ tt q kk q (29) ˆ ˆˆ ˆ 1 t zqz gbz ˆ ˆ q q ˆ q ˆ0q (30) By total differentiation with respect to at the ap- proximation of , we obtain 2 20. 1ˆˆ ˆ1ˆ tzz dk dqb z (31) Therefor e, th e ch ild al low an ce d ecr e ases cap ita l p er capi - ta in the subsequent period kt+1, in addition to income growth rate gt. Because of the child allowance, inco me pe r capita continues decreasing to zero if the income growth rate gt is less than one. We consider the effect of a child allowance in the case in which households use child-care serv ices. Then, the b ud- get constraint is shown as follows 21 1 ttt t wT r 1 ˆ ˆ1 tt t t c zqwnpnc (32) Each household maximizes its utility (4) under budget constraint (32). Considering (26), fertility ntcare and sav- ing st are given as care 1 ˆ t n , ˆ t bp zq k care ˆ 1 ttt (33) qn w ˆ q (34) Child allowance increases fertility ntcare for any kt. However, in the steady state, the child allowance does n ot always increase fertility. W ith (14), (33), (34) and capital market equilibrium condition 1t, we obtain the following difference equation for kt: tt ksn 1 ˆ ˆ 1ˆ ˆ t t t k bp zqk bp zqk ˆ ˆ. t zq pk b ˆ q ˆ0q (35) By total differentiation with respect to at the ap- proximation of , we obtain 1 ˆ ˆ 1 1ˆ t t t 0. t dq z pk bk bp b zk ˆ q dk (36) Child allowanc e decreases capital-per-capita kt+1 for any kt. Considering 1tt kk t in kt, 2 ˆ ˆ ˆ ˆ 1 zq gbz q ˆ q ˆ0q (37) By total differentiation with respect to at the ap- proximation of , 20. ˆ1 dg dq b (38) The child allowance decreases the in come growth rate. Income growth ceases and converges to the steady state specified by kt+1 = k t = k if th e income growth rate is less than one in kt because of the child allowance. If in- come growth continues with the child allowance at the steady state, then the fertility is care,growth t1 ˆ ˆ nzq . (39) The child allowance increases the fertility in income growth. However, in the steady state defined as kt+1 = kt = k, the fertility is not always increased by the child allow- ance. In this steady state, k and ncare, no growth are shown as ˆ ˆˆ ˆ, ˆ ˆ bp zqk zq kpk bp b zqk (40) care,nogrowth 1. ˆ ˆ nbp zq k ˆ q ˆ0q (41) The capital per capita in the steady state k is uniquely determined. By total differentiation with respect to at the approximation of , 22 2 ˆ 2 2 . ˆˆ ˆ z pk dk b dq zbp zbk (42) Considering 1tˆ0dk dq for any kt, ˆ0dk dq holds clearly20. Then, we obtain 2 2 1ˆ ˆˆ bp dk dq k dn dq bp zk (43) This sign is ambiguous. The child allowance pulls up the fertility because of ˆ0dndq if 2 ˆ dk dqkbp ˆ k. Finally, the child allowance affects as 20Figure 6(b) depicts ˆ0dk dq . Copyright © 2012 SciRes. ME  M. YASUOKA, A. MIYAKE 666 20. ˆ1 ˆˆ bp dk dq z (44) Figure 6 depicts the effects of a child allowance on the dynamics of kt. Then, the following propo sition is established. Propositi on 3 The child allowance decreases the income growth rate or income level. Given conti nued income growth, t he child allowance pulls up fertility. Otherwise, the child al low an ce does not always pull up fertility. We should consider the effects of child allowance on the fertility in both (39) and (41). If the fertility is given as (41), then the income converges to a steady state in- come. Then, the child allowance pulls up fertility in the short run. However, in the long run, a decrease in capital per capita caused by an increase in fertility diminishes income per capita. This income decrease has negative ef- fects on fertility. Therefore, the child allowance does no t always increase fertility in the long run. This result is fu n- damentally equivalent to that obtained by Fanti and Gori (2009)21. However, the fertility is given by (39) in con- tinued income growth, child allowance can always pull (a) (b) Figure 6. (a) Child allowance in the steady state with in- come growth; (b) Child allowance in the steady state with constant income. up the fertility22. This proposition, which hinges upon w h e- ther a child allowance can always increase the fertility, depends on income growth. van Groezen, Leers, and Mei - jdam (2003) [19] derived positive child allowance effects on the fertility in a small open economy. van Groezen and Meijdam (2008) [20] examined the child allowance in a closed econ omy with the pay-as-you-go pens ion and derived the optimal child allowance. In van Groezen and Meijdam (2008) [20], in troduction of the child allowance pulls up fertility. In contrast, this paper, which contains no externality as a pay-as-you-go pension, reports that introduction of a child allowance decreases fertility. 4.2. Subsidy for Child-Care Service We consider a subsidy for child-care services whereby a subsidy is given to households in proportion to the num- ber of children they have. This subsidy decreases the net child-care service cost per child. Assuming that the sub- sidy is financed by a lump-sum tax, the budg et constraint for using child-care services is shown as follows 21 11 ˆ1t ttttt t t c zw npvncwT r tt Tvn (45) Therein, v is given for a child, where v is constant and assumed v < p. With a balanced budget, the lump-sum tax Tt is determined as (46) Each household maximizes its utility (4) under budget constraint (45). Considering (46), fertility ntcare and sav- ing st are given as no 1, ˆ t t npv zw care ttt swvn (47) (48) With (14), (47), and (48), in addition to capital market equilibrium condition 1ttt ksn , we obtain the follow- ing differe nce equat i on for kt: 1 ˆ 1 t t zk bpv kv b (49) By total differen tiation with respect to v at the app roxi - mation of v = 0, 10. 1 t dk dv (50) 21Fanti and Gori (2009) examined a child tax that implies a negative child allowance and caused an increase in fertility. 22Zhang (1997) sho wed that th e ch ild allo wan ce can in crease th e f e rtil i ty in the quality and quantity of children model. This model considered human capital accu mulation, whic h bri ngs about incom e growth. However, our paper does not consider the quality of children. Copyright © 2012 SciRes. ME 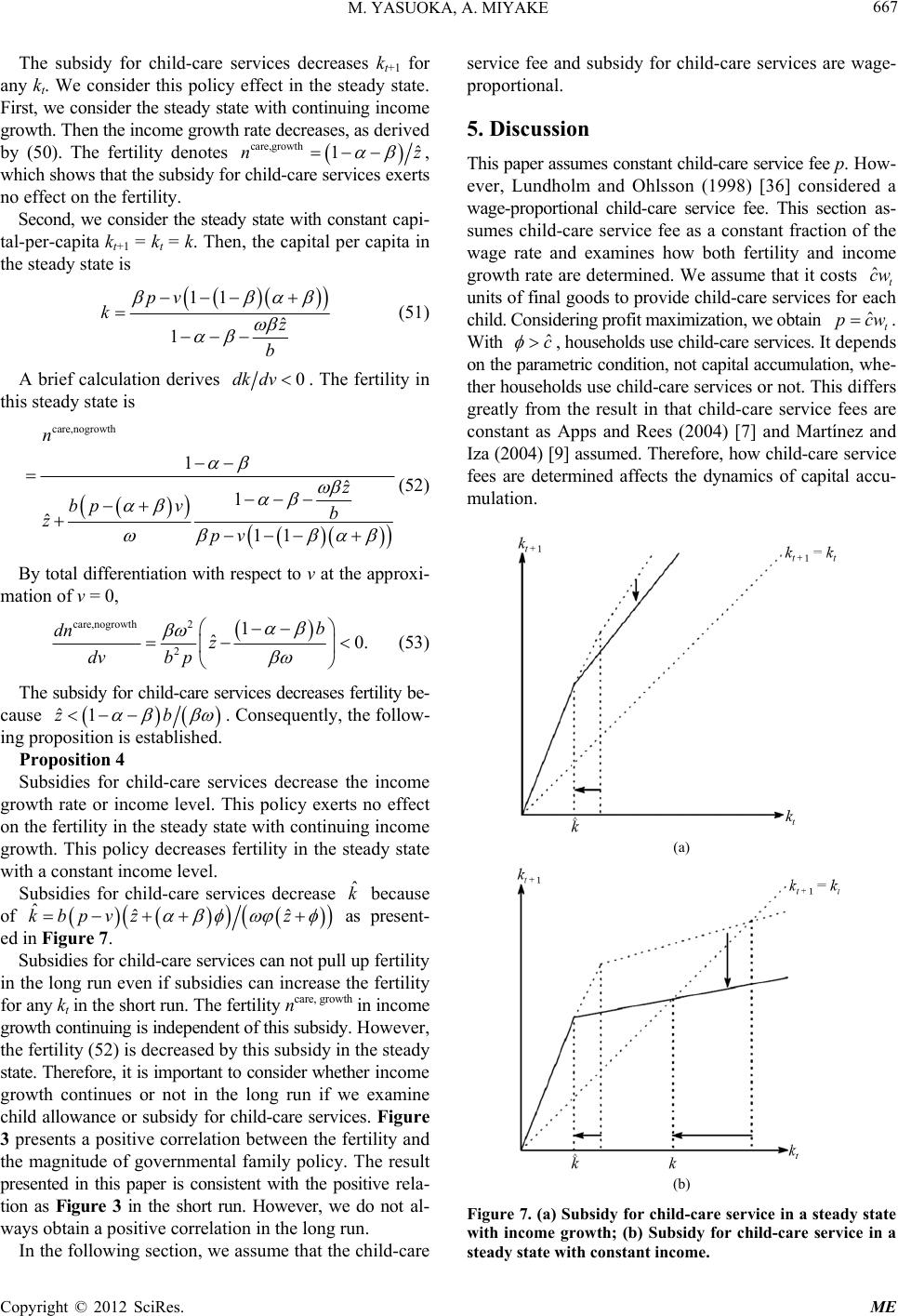 M. YASUOKA, A. MIYAKE 667 The subsidy for child-care services decreases kt+1 for any kt. We consider this policy effect in the steady state. First, we consider the steady state with continuing income growth. Then the income growth rate decreases, as derived by (50). The fertility denotes care,growth ˆ 1nz , which shows that the subsidy for child-care services exerts no effect on the fertility. Second, we consider the steady state with constant cap i- tal-per-capita kt+1 = kt = k. Then, the capital per capita in the steady state is 11 1 pv kˆ z b (51) A brief calculation derives 0dkdv . The fertility in this steady state is care,nogrowth 1 1 ˆ11 n bp v zpv ˆ z b (52) By total differen tiation with respect to v at the app roxi - mation of v = 0, care,nogrowth 2 2 1 ˆ dn z dv bp 0. b (53) The subsidy for child-care services decreases fertility be- cause ˆ1zb ˆ k . Consequently, the follow- ing proposition is established. Propositi on 4 Subsidies for child-care services decrease the income growth rate or income level. This policy exerts no effect on the fertility in th e steady state with continuing inco me growth. This policy decreases fertility in the steady state with a constant income level. Subsidies for child-care services decrease because of ˆˆ kbpvz ˆ z ˆ cw ˆ pcw as present- ed in Figure 7. Subsidies for child-care services can not pull up fertility in the long run even if su bsidies can increase the fertility for any kt in the short run. The fertil ity ncare, growth in income growth continuing is independent of this subsidy. Ho weve r, the fertility (52) is decreased by this su bs idy in th e stead y state. Th erefore, it is importan t to consider whether i nc om e growth continues or not in the long run if we examine child allowance or subsidy for child-care services. Figure 3 presents a positive correlatio n between the fertility and the magnitude of governmental family policy. The result presented in this paper is consistent with the positive rela- tion as Figure 3 in the short run. However, we do not al- ways obtain a positive correlation in th e long run. In the following section, we assume that the child-care service fee and subsidy for child-care services are wage- proportional. 5. Discussion This paper assumes constant child-ca re service fee p. How- ever, Lundholm and Ohlsson (1998) [36] considered a wage-proportional child-care service fee. This section as- sumes child-care service fee as a constant fraction of the wage rate and examines how both fertility and income growth rate are determined. We assume that it costs t units of final goods to provide child-care services for each child. Considering profit maximization, we obtain t . With ˆ c , households use child-care serv ices. It depe nds on the parametric condition, not capital accu mulation, w h e- ther households use child-care services or not. This dif fe r s greatly from the result in that child-care service fees are constant as Apps and Rees (2004) [7] and Martínez and Iza (2004) [9] assumed. Therefore, how child-care ser vic e fees are determined affects the dynamics of capital accu- mulation. (a) (b) Figure 7. (a) Subsidy for child-care ser vice in a steady state with income growth; (b) Subsidy for child-care service in a steady state with constant income . Copyright © 2012 SciRes. ME  M. YASUOKA, A. MIYAKE 668 With t, the fertility and the saving given by (33 ) and (34), respectively, are shown as ˆ pcw 1 ˆˆ q ˆ nzc (54) ˆ1 1ˆ ˆ t q ˆt w q zc (55) Then, considering capital market equilibrium ntkt+1 = st, the income growth rate is derived as shown below: ˆˆ ˆ. 1 zcq b g ˆ q ˆˆ0 t vvwv (56) Comparing (27) with (54), the fertility of (54) is larger than that of (27). In addition, comparing (30) with (56), the income growth rate of (5 6) is lower than that of (30). Therefore, the fertility with child-care services is larger than the cas e of no child-care se rvices, wher eas the in c o me growth rate decreases. An increase in the fertility and a decrease in the income growth rate caused by child-care services do no t depend on whether child-care service fees are fixed or wage-dependent. Con sidering (54) and (56), an increase in the child allow- ance increases the fertility although the income growth rate decreases. If the subsidy for child-care services is , then the fertility of (47) changes to 1 ˆˆ zc v ˆ n (57) Then, the subsidy for child-care services increases the fertility as the child allowance. 6. Conclusions This paper presents analysis of how fertility is d ete rmin ed and affected by child-care services in a dynamic general equilibrium model under the assumption that complete substitution exists b etween ind iv idual ch ild -care ti me and child-care services. Among the results presented herein, the following are most noteworthy. When child-care services exist, one of two multiple states results: one for a state with low fertility, low female labor participation, low inco me level, and high income growth ; and the other for a state with high fertility, high female labor participation, and low income growth or high in co me level w ith no inco me gro wth. Ev en if th e amoun t of c a p i t a l per capita is low in the initial period, income per capita increases; finally, the dynamics converge to the steady state with high fertility and high female labor pa rtic i pat i o n as a result of capital accumulation. The result described in this paper is consistent with the positive correlation in developed countries. This paper sets the dynamic general equilibrium model as simply as possible and derives the positive correlation. In the latter part of this paper, we analyzed whether child-care policies, (e.g., a child allow- ance policy, wherein households receive an allowance in direct relation to the number of children they have, and the subsidy for child-care services policy) can raise the fertility rate. These policies can raise the fertility rate in the short run. However, the effect in the long run might differ. Because of the decrease in income with a decrease in capital per capita, the ch ild allowance does not always increase fertility. If the income level converges to a constant income level in the long run, the child allowance can not always pull up the fertility. However, if income growth continues in the long run, then the child allowance can pull up the fertility in the long run. Therefore, the effect of child allowance on the fertility depends on whether income growth ceases or continues in the long run. Results show that the effect in the short run is consistent with the positive correlation between fertility and the magnitude of governmental family policy. The model in this paper is consistent with the three po sitive correlations described for developed countries: 1) Fertility and female labor participation; 2) Fertility and income per capita; and 3) Fertility and the magnitude of governmental family policy. In addition, this paper pre- sents a proposal that, before implementing child-care po li- cies, the government should consider their short-run and long-run effects. 7. Acknowledgements This paper was presented at the 66th Annual Congress of the International Institute of Public Finance (IIPF 2010) and the Far Eastern and South Asian Meeting of the Ec on- ometric Society 2008 (FEMES 2008). We would like to thank Akiyoshi Furukawa, Egbert Jongen, Shoji Katagiri, Hideaki Murase, Tamotsu Nakamura, Hikaru Ogawa, Ta- kashi Oshio, Keiko Shimono, Ken Tabata, Hideki Toya, Stanley Winer, Akira Yakita and the seminar particip ants at Kobe University, Chuo University, Nagoya City Uni- versity, IIPF 2010, FEMES 2008 and the 2008 Spring Meeting of the Japanese Economic Association. The re- search for this paper was financially supported in part by the Kobe University 21st Century COE program of the Ministry of Education, Culture, Sports, Science and Tech- nology, a grant from the University of Kitakyushu, and Grants-in-Aid for Scientific Research (No. 19530237, No. 21730159, No. 23730283) for the fir st author. REFERENCES [1] N. Ahn and P. Mira, “A Note on the Changing Re- lationship between Fertility and Female Employment Rates in Developed Countries,” Journal of Population Economics, Vol. 15, 2002, pp. 667-682. doi:10.1007/s001480100078 [2] J. E. Sleebos, “Low Fertility Rates in OECD Countries: Copyright © 2012 SciRes. ME  M. YASUOKA, A. MIYAKE 669 Facts and Policy Responses,” OECD Social, Employment and Migration Working Papers, Vol. 15, 2003. http://www.oecd.org/dataoecd/13/38/16587241.pdf [3] K. Yamaguchi, “On the Genuine Relationships between Female Labor Participation and Fertility: Investigations of OECD Countries (in Japanese),” RIETI Discussion Paper Series, 05-J-036, 2005. http://www.rieti.go.jp/jp/publications/dp/05j036.pdf [4] T. Kögel, “Did the Association between Fertility and Fe- male Employment within OECD Countries Really Change in Sign? ” Journal of Populatio n Economics, Vol. 17, 2004, pp. 45-65. doi:10.1007/s00148-003-0180-z [5] H. Engelhardt and A. Prskawetz, “On the Changing Cor- relation between Fertility and Female Employment over Space and Time,” European Journal of Population, Vol. 20, 2004, pp. 35-62. doi:10.1023/B:EUJP.0000014543.95571.3b [6] O. Galor and D. Weil, “The Gender Gap, Fertility, and Growth,” American Economic Review, Vol. 86, No. 3, 1996, pp. 374-387. http://www.jstor.org/stable/2118202 [7] P. Apps and R. Rees, “Fertility, Taxation and Family Policy,” Scandinavian Journal of Economics, Vol. 106, No. 4, 2004, pp. 745-763. doi:10.1111/j.0347-0520.2004.00386 [8] M. Hirazawa and A. Yakita, “Fertility, Child Care outside the Home, and Pay-As-You-Go Social Security,” Journal of Population Economics, Vol. 22, No. 3, 2009, pp. 565- 583. doi:10.1007/s00148-007-0153-8 [9] D. F. Martínez and A. Iza, “Skill Premium Effects on Fertility and Female Labor Force Supply,” Journal of Population Economics, Vol. 17, 2004, pp. 1-16. doi:10.1007/s00148-003-0150-5 [10] M. Yasuoka, “A Relationship between Fertility and In- come (in Japanese),” The Society for Economic Studies, The University of Kitakyushu Working Paper Series, No. 2008-4, 2008. http://www.kitakyu-u.ac.jp/economy_new/research/files/y asuoka2008_2.pdf [11] M. Momota, “The Gender Gap, Fertility, Subsidies and Growth,” Economics Letters, Vol. 69, 2000, pp. 401-405. doi:10.1016/S0165-1765(00)00304-9 [12] M. Yasuoka, “A Study of Childcare Support Policy in the Model Based on Endogenous Introduced the Childcare Goods Provided Publicly (in Japanese),” Quarterly of So- cial Security Research, Vol. 43, No. 3, 2007, pp. 261-274. http://www.ipss.go.jp/syoushika/bunken/data/pdf/186244 08.pdf [13] L. W. Aarssen, “Why Is Fertility Lower in Wealthier Countries? The Role of Relaxed Fertility-Selection,” Po- pulation and Development Review, Vol. 31, No. 1, 2005, pp. 113-126. http://www.jstor.org/stable/i278908 doi:10.1111/j.1728-4457.2005.00054.x [14] G. S. Becker, “An Economic Analysis of Fertility,” In: A. Coale, Ed., Demographic and Economic Change in De- veloped Countries, Princeton University Press, Princeton, 1960. [15] G. S. Becker, K. M. Murphy and R. Tamura, “Human Capital, Fertility, and Economic Growth,” Journal of Po- litical Economy, Vol. 98, No. 5, 1990, pp. S12-S37. http://www.jstor.org/stable/2937630 doi:10.1086/261723 [16] D. de la Croix and M. Doepke, “Inequality and Growth: Why Differential Fertility Matters?” American Economic Review, Vol. 93, No. 4, 2003, pp. 1091-1113. http://www.jstor.org/stable/3132280 doi:10.1257/000282803769206214 [17] M. Kimura and D. Yasui, “Public Provision of Private Child Goods,” Journal of Public Economics, Vol. 93, 2009, pp. 741-751. doi:10.1016/j.jpubeco.2009.02.002 [18] T. Oshio, “Child-Care Reform in Pension System and the Fertility Rate (in Japanese),” Quarterly of Social Security Research, Vol. 36, No. 4, 2001, pp. 535-546. http://www.ipss.go.jp/syoushika/bunken/data/pdf/151581 07.pdf [19] B. van Groezen, T. Leers and L. Meijdam, “Social Secu- rity and Endogenous Fertility: Pensions and Child Allow- ance as Siamese Twins,” Journal of Public Economics, Vol. 87, 2003, pp. 233-251. doi:10.1016/S0047-2727(01)00134-7 [20] B. van Groezen and L. Meijdam, “Growing Old and Stay- ing Young: Population Policy in an Ageing Closed Eco- nomy,” Journal of Population Economics, Vol. 21, No. 3, 2008, pp. 573-588. doi:10.1007/s00148-006-0067-x [21] L. Fanti and L. Gori, “Population and Neoclassical Eco- nomic Growth: A New Child Policy Perspective,” Eco- nomics Letters, Vol. 104, 2009, pp. 27-30. doi:10.1016/j.econlet.2009.03.014 [22] P. McDonald, “Low Fertility and the State: The Efficacy of Policy,” Population and Development Review, Vol. 32, No. 3, 2006, pp. 485-510. http://www.jstor.org/stable/i20058896 doi:10.1111/j.1728-4457.2006.00134.x [23] W. Lutz, “Will Europe Be Short of Children?” Family Observer, European Observatory on Family Matters, European Commission, 1999, pp. 8-16. [24] K. Milligan, “Quebec’s Baby Bonus: Can Public Policy Raise Fertility?” Backgrounder, C.D. Home Institute, Toronto, 2002. [25] G. Laroque and B. Salanie, “Does Fertility Respond to Financial Incentives?” CEPR Discussion Paper Series, No. 5007, Center for Economic Policy Research, London, 2005. [26] J. Zhang, “Fertility, Growth and Public Investments in Children,” Canadian Journal of Economics, Vol. 30, No. 4a, 1997, pp. 835-843. http://www.jstor.org/stable/i301038 doi:10.2307/136272 [27] B. van Praag and M. Warnaar, “The Cost of Children and the Use of Demographic Variables in Consumer De- mand,” In: M. Rosenzweig and O. Stark, Eds., Handbook of Population and Family Economics, Elsevier Science, Amsterdam, 1997. doi:10.1016/S1574-003X(97)80023-2 [28] Z. Eckstein and K. I. Wolpin, “Endogenous Fertility and Optimal Population Size,” Journal of Public Economics, Vol. 27, 1985, pp. 93-106. doi:10.1016/0047-2727(85)90030-1 [29] B. U. Wigger, “Pay-As-You-Go Financed Public Pen- sions in a Model of Endogenous Growth and Fertility,” Copyright © 2012 SciRes. ME  M. YASUOKA, A. MIYAKE Copyright © 2012 SciRes. ME 670 Journal of Population Economics, Vol. 12, No. 4, 1999, pp. 625-640. doi:10.1007/s001480050117 [30] P. M. Romer, “Increasing Return s and Long Run Growth,” Journal of Political Economy, Vol. 94, No. 5, 1986, pp. 1002-1037. http://www.jstor.org/stable/1833190 doi:10.1086/261420 [31] E. Grossman and N. Yanagawa, “Asset Bubbles and En- dogenous Growth,” Journal of Monetary Economics, Vol. 31, No. 1, 1993, pp. 3-19. doi:10.1016/0304-3932(93)90014-7 [32] M. Yasuoka and A. Miyake, “Change in the Transition of the Fertility Rate,” Economics Letters, Vol. 106, No. 2, 2010, pp. 78-80. doi:10.1016/j.econlet.2009.10.005 [33] G. S. Becker and R. J. Barro, “A Reformulation of the Economic Theory of Fertility,” Quarterly Journal of Eco- nomics, Vol. 103, No. 1, 1988, pp. 1-25. doi:10.2307/1882640 [34] R. J. Barro and G. S. Becker, “Fertility Choice in a Model of Economic Growth,” Econometrica, Vol. 57, No. 2, 1989, pp. 481-501. http://www.jstor.org/stable/i332736 doi:10.2307/1912563 [35] P. Wang, C. K. Yip and C. A. Scotese, “Fertility Choice and Economic Growth: Theory and Evidence,” Review of Economics and Statistics, Vol. 76, No. 2, 1994, pp. 255- 266. http://www.jstor.org/stable/i336980 doi:10.2307/2109880 [36] M. Lundholm and H. Ohlsson, “Wages, Taxes and Pub- licly Provided Day Care,” Journal of Population Eco- nomics, Vol. 11, 1998, pp. 185-204. doi:10.1007/s001480050064
|