 Open Journal of Applied Sciences, 2012, 2, 193-197 doi:10.4236/ojapps.2012.23029 Published Online September 2012 (http://www.SciRP.org/journal/ojapps) Approximate Analytical Solutions of Fractional Coupled mKdV Equation by Homotopy Analysis Method Orkun Tasbozan, Alaattin Esen, Nuri Murat Yagmurlu Department of Mathematics, İnonu University, Malatya, Turkey Email: orkun.tasbozan@inonu.edu.tr Received June 1, 2012; revised July 3, 2012; accepted July 15, 2012 ABSTRACT In this paper, the approximate analytical solutions of the fractional coupled mKdV equation are obtained by homotopy analysis method (HAM). The method includes an auxiliary parameter which provides a convenient way of adjusting and controlling the convergence region of the series solution. The suitable value of auxiliary parameter is deter- mined and the obtained results are presented graphically. Keywords: Homotopy Analysis Method; Approximate Analytical Solution; Fractional Coupled mKdV Equation 1. Introduction Fractional derivatives provide an excellent tool for the description of memory and hereditary characteristics of different materials and processes due to their non-locality characteristics. This is the main advantage of fractional derivatives in comparison with integer order model, in which such effects are in fact neglected [1]. Several defi- nitions of fractional integration and derivation such as Riemann-Liouville’s and Caputo’s have been proposed. The Riemann-Liouville integral operator [1] having order 0 , which is a real number, is defined as 1 0 1 d0, x Jfxxtt xft (1) and as for 0 0 fx fx where the real function , x is said to be in the space 0x ,C R , if there exists a real number p such that 1 , p xxfx n C where and it is said to be in the space (0, ),C 1 fx if and only if , n hC Its fractional derivative of order .Nn0 is gen- erally used d ,1 d nn n DfxJ fxnn x where n is an arbitrary integer. The Riemann-Liouville integral operator has an important role for the develop- ment of the theory of both fractional derivatives and in- tegrals. In spite of this fact, it has certain disadvantages when it comes to modelling real-world phenomena with fractional differential equations. This problem has been solved by M. Caputo first in his article [2] and then in his book [3]. Caputo definition, which is a modification of Riemann-Liouville definition, can be given as 1 0 1 =d, Γ 0, 1. nn xnn Dfx JDfx tt nf nn t Note that Caputo derivative has the following two im- portant properties DJf xfx and 1 0 0! 1. k nk k JDfx fxfk nn In recent years, many important phenomena in various scientific and technological areas have been well de- scribed by fractional differential equations. In general, since these type equations are not exactly solved, their numerical solution techniques have become increasingly important. The HAM, a powerful tool for searching the approximate solutions which was first proposed by Liao [4,5], is one of such numerical solution techniques. Un- like perturbation techniques, the HAM is not limited to any small physical parameters in the considered equation. Therefore, the HAM can overcome the foregoing restrict- tions and limitations of perturbation techniques so it pro- vides us with a powerful tool to analyze strongly nonlin- ear problems [6]. The HAM has been proposed and suc- Copyright © 2012 SciRes. OJAppS  O. TASBOZAN ET AL. 194 cessfully applied to solve several fractional differential equations modeling problems arising in science and en- gineering by many authors [6-18] and the references therein. In this paper, we will apply the HAM to frac- tional coupled mKdV equation by using Caputo's defini- tion of fractional differentiation. 2. HAM Solutions of the Time-Fractional Coupled mKdV Equation In this section, we implement the HAM to the fractional coupled mKdV equation defined by 22 22 3330 363 01,0 xx tx txxx xxx x uuu vvuv D Dv vvuuvuuvv t 0 (2) with the initial conditions ,0tanh 2, ,0tanh 2. ux x vx x (3) To investigate the HAM solutions of Equation (2) with the initial conditions given by Equation (3), we can choose the linear operator ,;,; ,1,2 iti xtq Dxtqi having the property 0 i c where are constants. From Equation (2), we can now define nonlinear operators as 1, 2 i csi 1 32 11 1 1 3 2 2 2 12 12 ,; ,;,; 1 3,; 2 ,; ,; 3 ,; , ,, ,, ; 3, , tq xtqxtq xtq x tx xtq xtq x x xtq xt xtq x q x tq 21 2 1 2 3 22 3 1 12 22 2 12 ,;,,; ,; ,; ,; ,; 3 ,; 6,;,; ,; 3,;,;. xtq xtq tq xtq x xtq xtq x tx xtq xtq xtqx xtq xtq xtqx Therefore, we construct the zero-order deformation equation as follows 10 11 12 1,;, ,;, ,;, qxtquxt qxtqxt q (4) 20 221 2 1,;, ,; ,,;. qxtqvxt qxtqxt q (5) If we choose 0q then we get 10 20 ,;0 ,,0, ,;0 ,,0 xtuxtux xtvxtv x and 1q , we obtain 12 ,;1,, ,;1,. tuxt xtvxt Thus, as the embedding parameter q increases from 0 to 1, the solutions ,; 1,2 ixtq i also change from the initial values 0,uxt 0,vx and to the solutions t ,uxt and ,t.i vx If we expand ,; tq for 1, 2i in Taylor series with respect to the embedding parameter q, we obtain 10 1 20 1 ,;,, , ,;,, , m m m m m m tquxtuxtq tqvxtvxtq where 1 0 2 0 ,; 1 ,, ! ,; 1 ,. ! m mm q m mm q xtq uxt mq xtq vxt mq If the auxiliary linear operator, the initial guess and the auxiliary parameter are properly chosen, as pointed out by Liao [5,8], the above series converges at 1q , and one can have 0 1 ,,m m uxtu xtuxt ,, , (6) 0 1 ,,m m vxtvxtvxt (7) which should be one of the solutions of the original equ- ation. Let’s define the following vectors 101 101 ,,,, ,,, ,,,, ,,. mn mn uxtuxtuxt vxtvxt vxt u v By differentiating Equations (4) and (5) m times with respect to the embedding parameter q, we obtain the mth- order deformation equations as follows Copyright © 2012 SciRes. OJAppS  O. TASBOZAN ET AL. 195 111,1 ,, mmm mm uxtuxtR uv1 , m 1m (8) 122,1 ,, , mmm mm vxtv xtR uv (9) subject to the initial conditions ,0tanh 2, ,0tanh2 m m ux x vx x where 1,1 1 3 11 3 1–1 0 11 00 1 –1 00 , ,, 1 2 , 3, , 3,, 3,, mm m mm mmn n n mn mn knk nk mn knk mn nk R uxtuxt tx vxt vxt xx uxt uxtuxtx uxtv xtvxt x uv ,, 2,1 1 3 11 3 1–1 0 1–1 00 1 00 –1 , ,, , 3, , 6,, 3,,, , , mm m mm mmn n n mn mn knk nk mn knknk nk mn R vxtvxt tx uxt vxt xx uxt uxtv xtx uxtu vxtxvx vxt x t uv t and 0, 1, 1, 1. m m m By applying the operator given by Equation (1), which is the inverse of the operator t D , to the both sides of the mth-order deformation Equations (8) and (9) for we obtain 1,m 111,11 ,, , mmm tmmm uxtu xtJR uv , . (10) 122,11 ,, , mmm tmmm vxtvxtJ R uv (11) For the purpose of simplicity, setting 12 and by using Equations (10) and (11) with the initial condi- tions given by Equation (3), we successively obtain 0 12 ,tanh2, 4 ,, Γ1cos 2 uxt x t uxt hx 22 22 2 41 ,Γ1cos 2 32tanh 2 , Γ21cos2 t uxt hx tx hx and 0 12 22 22 2 ,tanh2, 4 ,, Γ1cos 2 41 ,Γ1cos 2 32tanh 2 , Γ21cos2 vxtx t vxt hx t vxt hx tx hx etc. Therefore, the series solutions expressed by the HAM given in Equations (6) and (7) can be written in the fol- lowing forms 012 012 ,,,, ,,,, uxtuxt uxt uxt vxtvxt vxt vxt , . (12) To demonstrate the efficiency of the method, we com- pare the HAM solutions of fractional coupled mKdV equation given by Equation (12) for 0 with its ex- act solutions [19] ,tanh24 ,tanh24 uxtx t vxtx t , . The fact that HAM solution series contains the auxil- iary parameter providing us with a simply way to adjust and control the convergence of the solution series should be noted. To obtain an appropriate range for , we consider the so-called -curve to choose a proper value of which ensures that the solution series is convergent, as pointed by Liao [5], by finding out the valid region of corresponding to the line segments nearly parallel to the horizontal axis. The -curves of 0,0.01u and 0.010v, are given by 3th-order HAM solution given by Equation (12) for various parame- ters in Figure 1. It can be seen from the figure that the valid range of lies in approximately 1.3 0.7. Figure 2 shows the numerical solutions of ,uxt and ,vxt at x = 2 from t = 0 to t = 0.5 for = –0.7, –1 and –1.3 obtained by 3th-order HAM for 1 and analytical solutions, respectively. Between t = 0 and t = 0.5, it can be seen from the figure that the choice of –0.7 is an appropriate value. = Figure 3 shows the numerical solutions of ,uxt and ,vxt at x = 2 during for = –0.7 obtained by 3th-order HAM for 00t 0.9 .5 and 0.8 , Copyright © 2012 SciRes. OJAppS 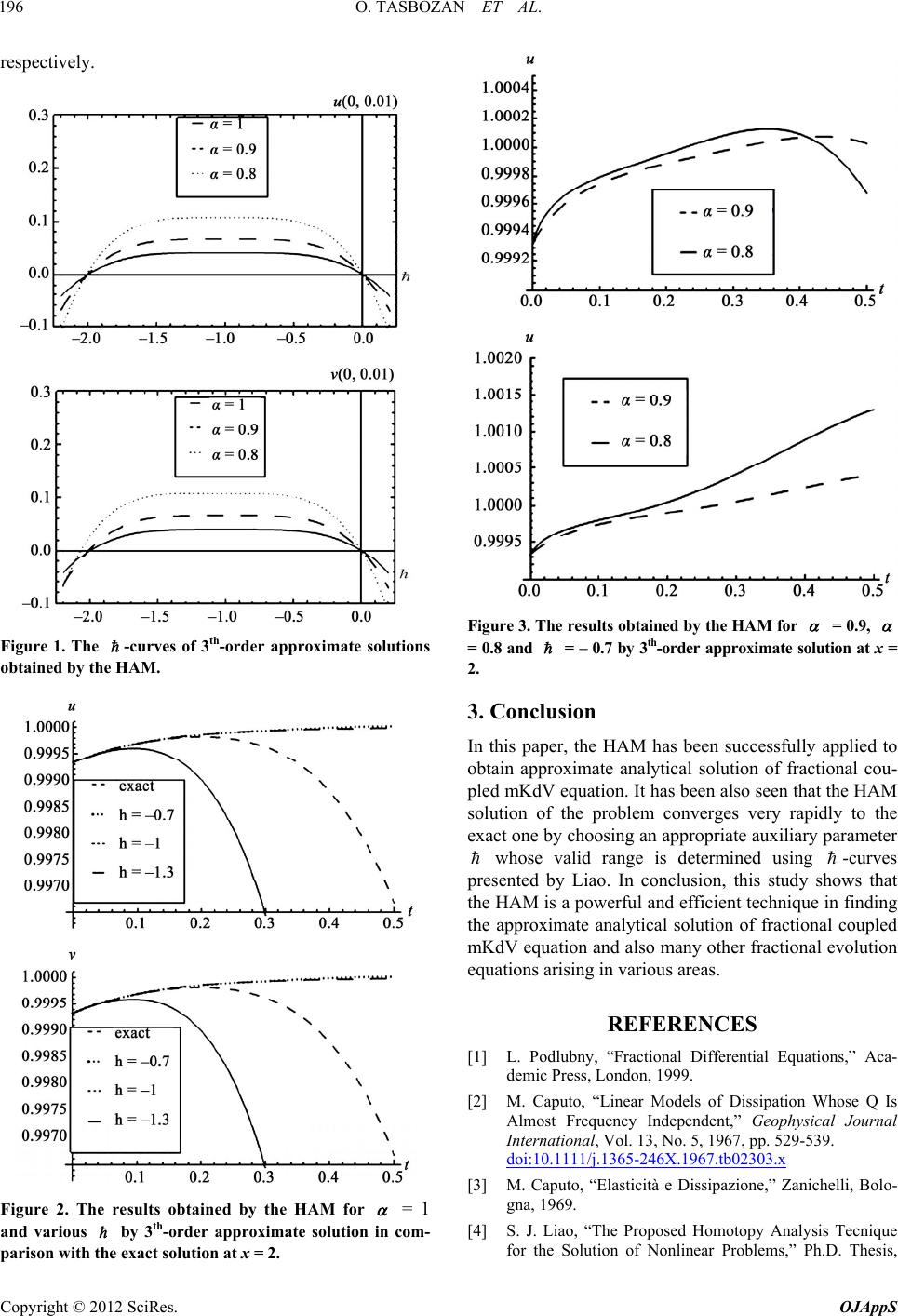 O. TASBOZAN ET AL. 196 respectively. Figure 1. The -curves of 3th-order approximate solutions obtained by the HAM. Figure 2. The results obtained by the HAM for = 1 and various by 3th-order approximate solution in com- parison with the exact solution at x = 2. Figure 3. The results obtained by the HAM for = 0.9, = 0.8 and = – 0.7 by 3th-order approximate solution at x = 2. 3. Conclusion In this paper, the HAM has been successfully applied to obtain approximate analytical solution of fractional cou- pled mKdV equation. It has been also seen that the HAM solution of the problem converges very rapidly to the exact one by choosing an appropriate auxiliary parameter whose valid range is determined using -curves presented by Liao. In conclusion, this study shows that the HAM is a powerful and efficient technique in finding the approximate analytical solution of fractional coupled mKdV equation and also many other fractional evolution equations arising in various areas. REFERENCES [1] L. Podlubny, “Fractional Differential Equations,” Aca- demic Press, London, 1999. [2] M. Caputo, “Linear Models of Dissipation Whose Q Is Almost Frequency Independent,” Geophysical Journal International, Vol. 13, No. 5, 1967, pp. 529-539. doi:10.1111/j.1365-246X.1967.tb02303.x [3] M. Caputo, “Elasticità e Dissipazione,” Zanichelli, Bolo- gna, 1969. [4] S. J. Liao, “The Proposed Homotopy Analysis Tecnique for the Solution of Nonlinear Problems,” Ph.D. Thesis, Copyright © 2012 SciRes. OJAppS  O. TASBOZAN ET AL. Copyright © 2012 SciRes. OJAppS 197 Shanghai Jiao Tong University, Shanghai, 1992. [5] S. J. Liao, “Beyond Perturbation: Introduction to the Homotopy Analysis Method,” Chapman and Hall/CRC Press, Boca Raton, 2003. doi:10.1201/9780203491164 [6] S. J. Liao, “Homotopy Analysis Method: A New Ana- lytical Technique for Nonlinear Problems,” Communica- tions in Nonlinear Science and Numerical. Simulations, Vol. 2, No. 2, 1997, pp. 95-100. doi:10.1016/S1007-5704(97)90047-2 [7] S. J. Liao, “On the Homotopy Analysis Method for Nonlinear Problems,” Applied Mathematics and Compu- tation, Vol. 147, No. 2, 2004, pp. 499-513. doi:10.1016/S0096-3003(02)00790-7 [8] S. J. Liao, “Notes on the Homotopy Analysis Method: Some Definitions and Theorems,” Communications in Nonlinear Science and Numerical Simulations, Vol. 14, No. 4, 2009, pp. 983-997. doi:10.1016/j.cnsns.2008.04.013 [9] S. Abbasbandy, “The Application of Homotopy Analysis Method to Solve a Generalized Hirota-Satsuma Coupled KdV Equation,” Physics Letters A, Vol. 361, No. 6, 2007, pp. 478-483. doi:10.1016/ j.physleta.2006.09.105 [10] E. Babolian and J. Saeidian, “Analytic Approximate So- lutions to Burgers, Fisher, Huxley Equations and Two Combined Forms of These Equations,” Communications in Nonlinear Science and Numerical Simulation, Vol. 14, No. 5, 2009, pp. 1984-1992. doi:10.1116/j.cnsns.2008.07.019 [11] A. Fakhari, G. Domairry and Ebrahimpour, “Approximate Explicit Solutions of Nonlinear BBMB Equations by Homotopy Analysis Method and Comparison with the Exact Solution,” Physics Letters A, Vol. 368, No. 1-2, 2007, pp. 64-68. doi:10.1116/j.physleta.2007.03.062 [12] M. M. Rashidi, G. Domairry, A. Doosthosseini and S. Dinarvand, “Explicit Approximate Solution of the Cou- pled KdV Equations by Using the Homotopy Analysis Method,” International Journal of Mathematical Analysis, Vol. 2, No. 12, 2008, pp. 581-589. [13] Mustafa Inc., “On Numerical Solution of Burgers’ Equa- tion by Homotopy Analysis Method,” Physics Letters A, Vol. 372, No. 4, 2008, pp. 356-360. doi:10.1016/j.physleta.2007.07.057 [14] A. S. Bataineh, M. S. M. Noorani and I. Hashim, “Ap- proximate Analytical Solutions of Systems of PDEs by Homotopy Analysis Method,” Computers and Mathe- matics with Applications, Vol. 55, No. 12, 2008, pp. 2913-2923. doi:10.1016/j.camwa.2007.11.022 [15] S. Abbasbandy, “The Application of Homotopy Analysis Method to Nonlinear Equations Arising in Heat Trans- fer,” Physics Letters A, Vol. 360, No. 1, 2006, pp. 109- 113. doi:10.1016/j.physleta.2006.07.065 [16] T. Hayat and M. Sajid, “On Analytic Solution for Thin Film Flow of a Forth Grade Fluid Down a Vertical Cyl- inder,” Physics Letters A, Vol. 361, No. 4-5, 2007, pp. 316-322. doi:10.1016/j.physleta.2006.09.060 [17] H. Xu and J. Cang, “Analysis of a Time Fractional Wave-Like Equation with the Homotopy Analysis Method,” Physics Letters A, Vol. 372, No. 8, 2008, pp. 1250-1255. doi:10.1016/j.physleta.2007.09.039 [18] L. Song and H. Q. Zhang, “Application of Homotopy Analysis Method to Fractional KdV-Burgers-Kuramoto Equation,” Physics Letters A, Vol. 367, No. 1-2, 2007, pp. 88-94. doi:10.1016/j.physleta.2007.02.083 [19] D. B. Cao, J. R. Yanb and Y. Zhang, “Exact Solutions for a New Coupled MKdV Equations and a Coupled KdV Equations,” Physics Letters A, Vol. 279, No. 1-2, 2002, pp. 68-74. doi:10.1016/S0375-9601(02)00376-6
|