 International Journal of Astronomy and Astrophysics, 2012, 2, 167-173 http://dx.doi.org/10.4236/ijaa.2012.23020 Published Online September 2012 (http://www.SciRP.org/journal/ijaa) Examining the M67 Classification as an Open Cluster Shim’on Naim1, Evgeny Griv2 1Ilan Ramon Physics Center, Ben-Gurion University of the Negev, Beer-Sheva, Israel 2Department of Physics, Ben-Gurion University of the Negev, Beer-Sheva, Israel Email: shimonnaim@yahoo.com, griv@bgu.ac.il Received May 22, 2012; revised June 28, 2012; accepted July 15, 2012 ABSTRACT The cluster M67 (= NGC 2682) in Cancer is a rich stellar cluster, usually classified as an open cluster. Using our own observations with the 0.4 m telescope, we show that M67 is a tight group of about 1200 stars. The actual radius of the cluster is about 3.1 pc and the average mass of a star in the system is about 1.33 . We also show that the ratio of the mean kinetic energy of the cluster to its mean gravitational potential energy clust clust0.3KU , while the value pre- dicted by the virial theorem is equal to . So the system is a gravitationally bound. This value of 0.5clust clust KU is considered as an evidence of quasi-stability of the cluster and allows us to use the Chandrasekhar-Spitzer relaxation time for M67 chand 30 Myr as a characteristic dynamical relaxation time of the system under study. As the cluster is almost twice older its half-life time hal chand tf70 0 , it is argued that M67 was in the past (about 4 Gyr ago, close to its formation) a relatively small ( stars) globular cluster, but got “open cluster” shape due to the dynamical evaporation of the majority of its stars. ~ 10,00 Keywords: Photometers; Techniques; Photometric; Open Clusters and Associations; M67; Galaxies; Star Clusters 1. Introduction Usually classified as an open cluster, the dense stellar cluster M67 in Cancer is one of the oldest known open clusters in our Galaxy with an age clust of Gyr, that is, close to the age of the sun [1-3]. In the present paper we adopt the value clust Gyr [4,5]. It is important to note that open clusters usually get de- structed much faster, over yr timescales. It is some pc distant the Sun. Following Ref. [6], we adopt the distance clust pc. The total number of stars in M67 is estimated at over 700 [7]. M67 is the nearest old open cluster. The cluster is also anomalous with respect to the distance of clust pc to the Galactic equatorial plane, where most open clu- sters are found. This distance clust is even larger than scale height pc of the local thick disk of the Galaxy (see, e.g. Ref. [8]). Other open clusters lie much closer to the Galactic plane. M67 current mass is clust t =4 60 3.5 -4.5 t 8 z ~10 = 770 z 750- 850 = h 1400 r =0 400 0 z -300 M and its initial mass was to be appro- ximately astclust [9]. Mass segregation has been suggested as the cause for the observed structural properties of M67 in Refs. [10,11]. This process has long been suspected for globular star clusters (and has been directly seen in globular cluster 47 Tucanae [12]), but has never been suggested for open clusters. We conclude that M67 has properties of globular clusters. =10MM Here, we study M67 with the use of the Meade LX- 200R robotic 0.4 m telescope of the Ilan Ramon Physics Center Observatory in Israel (http://ilanramon.bgu.ac.il) (Figure 1). The telescope operates from a small dome and is equipped with Meade DSI III pro 1360 1024 CCD camera (Figure 2). In the last four years this telescope was intensively used in a variety of monitoring projects, including the study of stellar clusters, in par- ticular, M67 and M35 (=NGC 2168). 2. Observations The cluster M67 was photographed in two filters, V and B, on 7th April 2010. An (f/6.3) local reducer was used, and therefore the scale is 0.52 arcsec/pixel. Two sets of exposure times were used in the observations, namely, long (10 s in both B and V filters) and short (3 s in both B and V filters). Figure 3 shows a part of M67. This photograph is a combination of 13 frames from each exposure, 10 s and 3 s, summed after a registration. The picture was taken with a blue Johnson filter. First, we estimated the angular size of the cluster = 27.63.6 = 3.1 R 6 arcsec. Then, adopt- ing the revised distance to the cluster pc, its actual radius was found clust pc. In order to cast more light on the structure of M67, in Figure 4 we show a wider field 81 photograph of M67, clust = 770r 0.26 C opyright © 2012 SciRes. IJAA  S. NAIM, E. GRIV 168 Figure 1. The Meade LX200R robotic 16" telescope of the Ilan Ramon Physics Center Observatory in Beer-Sheva (Israel). Figure 2. The dome of the Meade LX200R robotic 16" tele- scope. Figure 3. This photograph shows 173 stars of M67 cluster in our observations. Figure 4. A wider field 8' × 16' photograph of M67, taken from the Atlas Image website. taken from the Atlas Image website. Using these photo- graphs (Figures 3 and 4) and this Rclust, finally we es- timated the total number of stars in the system clust 1200N . Figure 5 shows the observed color-magnitude, vis . -mvsBV, diagram (or the HR diagram) for M67, based on our observations. Each dot denotes a star. The purple color indicates the positions of the main sequence stars. The red color indicates the positions of the hori- zontal branch stars. The yellow color indicates the posi- tions of the giant stars. The positions of blue stragglers are indicated in the diagram by the blue color. As is seen, the color-magnitude diagram for M67 shows a short main sequence extending from , where the turn-off point is located, up to . After -0BV -BV .4 .70 -0.7BV it starts merging in the field region stars and is not seen clearly. The giant branch is also clearly seen. Figure 5 evidently illustrates that M67 is quite old cluster. There are stars that are brighter and bluer than the main sequence stars and giant branch stars. These stars are a part of an exotic class of blue stragglers. A spectroscopic study of the blue stragglers in M67 has been done in Ref. [13]. Notice that the HR diagram shown in Figure 5 is more typical for globular clusters than for open clusters. Figure 6 presents our photometric color-magnitude diagram for the “ordinary” open cluster M35. (The clu- ster age is about 130 Myr [14].) In sharp contrast to M67, the color-magnitude diagram for M35 clearly shows a well-defined long main sequence stretching from -BV 0.1 to -1.BV4, but does not show horizontal branch stars, the giant branch stars, and blue stragglers. Such an HR diagram is typical for open clu- sters. Thus, the following parameters were derived from our observations: =27.63.6 clust = 770r arcsec, Rclust = 3.1 ± 0.26 pc (adopting pc), and . clust 1200N Copyright © 2012 SciRes. IJAA 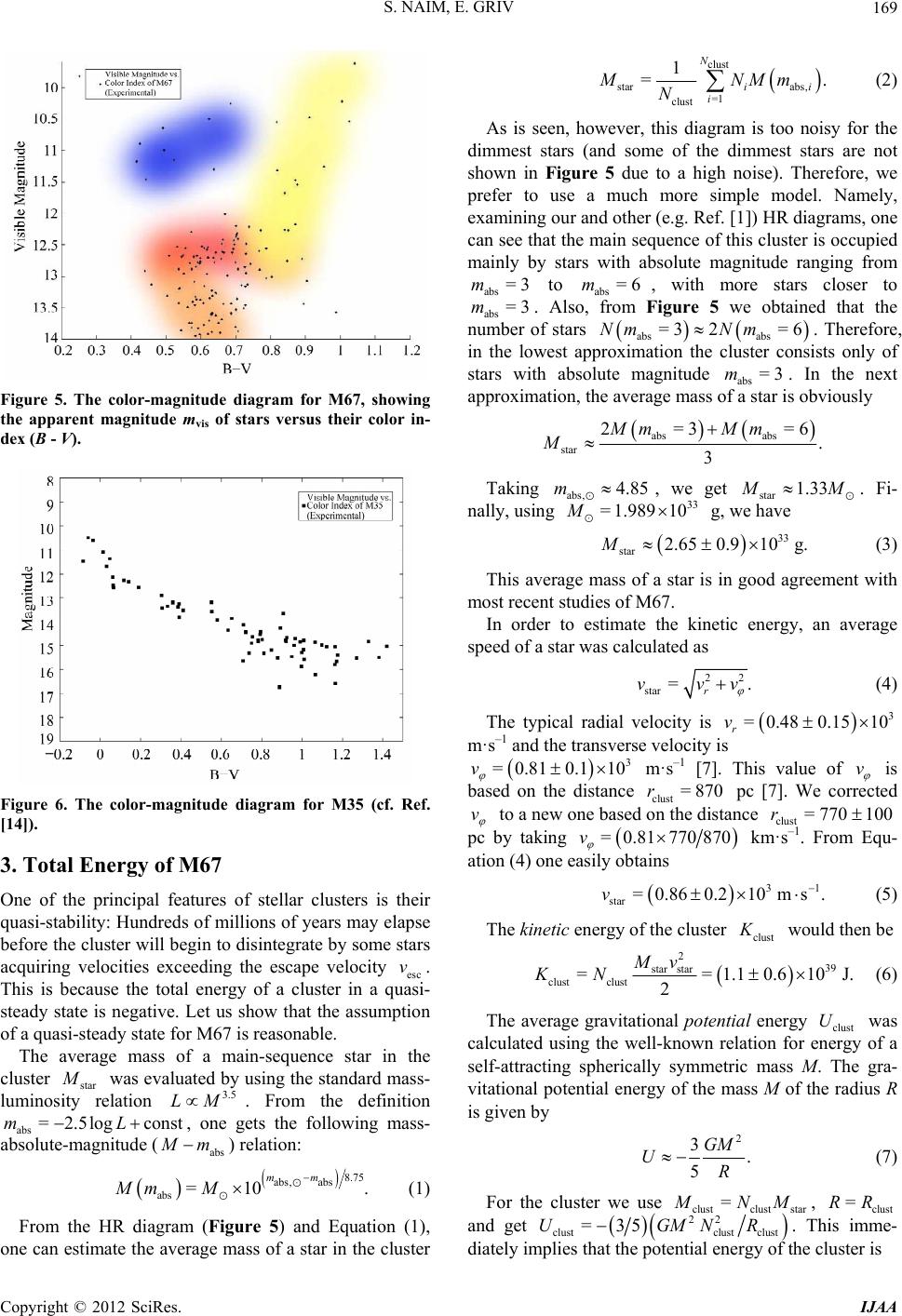 S. NAIM, E. GRIV 169 Figure 5. The color-magnitude diagram for M67, showing the apparent magnitude mvis of stars versus their color in- dex (B - V). Figure 6. The color-magnitude diagram for M35 (cf. Ref. [14]). 3. Total Energy of M67 One of the principal features of stellar clusters is their quasi-stability: Hundreds of millions of years may elapse before the cluster will begin to disintegrate by some stars acquiring velocities exceeding the escape velocity esc . This is because the total energy of a cluster in a quasi- steady state is negative. Let us show that the assumption of a quasi-steady state for M67 is reasonable. v The average mass of a main-sequence star in the cluster star was evaluated by using the standard mass- luminosity relation . From the definition abs , one gets the following mass- absolute-magnitude ( M =2.5l m 3.5 LM onst L abs og c m) relation: 8.75 abs, abs abs =10 . (1) mm Mm M From the HR diagram (Figure 5) and Equation (1), one can estimate the average mass of a star in the cluster clust star abs, =1 clust 1 =. N i i MNM N i m (2) As is seen, however, this diagram is too noisy for the dimmest stars (and some of the dimmest stars are not shown in Figure 5 due to a high noise). Therefore, we prefer to use a much more simple model. Namely, examining our and other (e.g. Ref. [1]) HR diagrams, one can see that the main sequence of this cluster is occupied mainly by stars with absolute magnitude ranging from to abs , with more stars closer to abs . Also, from Figure 5 we obtained that the number of stars abs =3m =3m=6m =3 2=6Nm =3m abs Nm abs . Therefore, in the lowest approximation the cluster consists only of stars with absolute magnitude abs . In the next approximation, the average mass of a star is obviously abs abs star 2=3 = . 3 Mm Mm M 6 Taking abs, 4.85m , we get star 1.33 M. Fi- nally, using g, we have 33 10= 1.989M star 2.650.910 g.M 33 (3) This average mass of a star is in good agreement with most recent studies of M67. In order to estimate the kinetic energy, an average speed of a star was calculated as 22 star = r vvv. (4) The typical radial velocity is m·s –1 and the transverse velocity is 3 =0.48 0.15 10 r v 3 =0.81 0.1 10v m·s–1 [7]. This value of v is based on the distance clust pc [7]. We corrected = 870r v to a new one based on the distance clust = 770100r pc by taking 70= 0.8v 17708 km·s–1. From Equ- ation (4) one easily obtains 3 star=0.860.210 ms.v 1 (5) The kinetic energy of the cluster would then be clust K 2 39 star star clust clust ==1.10.610 J. 2 Mv KN (6) The average gravitational potential energy clust was calculated using the well-known relation for energy of a self-attracting spherically symmetric mass M. The gra- vitational potential energy of the mass M of the radius R is given by U 2 3. 5 GM UR (7) For the cluster we use , clust and get clustclust star =MNM =RR 22 clustclust clust UG . This imme- diately implies that the potential energy of the cluster is =35 MNR Copyright © 2012 SciRes. IJAA  S. NAIM, E. GRIV 170 39 clust =4.3310 JU . (8) Thus, the total energy of M67, 39 clustclust clust =3.2EKU10 J, is negative but small in its absolute value in a sense that the kinetic energy and the potential energy are of the same order of magnitude. Moreover, the value of clust clust0.3KU , while the value predicted by the virial theorem for a stable system consisting of N particles, bound by potential forces, is clust clust KU . From the above, one concludes that the assumption of a quasi-steady state for M67 is indeed reasonable. This is an important fact from the point of view of stellar dynamics. One understands, however, that even though the cluster is dynamically bound, clust, escaping of stars from the system due to the Maxwellian-like velocity spread is possible (see Section 4 below for an explanation). =0.5 <0E 4. Evaporation of Stars from M67 Many factors cause stars to dissipate from dynamically bound clusters. In Ref. [15], it has pointed out that because of the scattering of stars in clusters on the stars in the galactic field the total internal energy of a cluster should rise, ultimately leading to a complete breakup of the cluster. It turned out that the characteristic time for this process of destruction of dense stellar clusters is at most 1010 yr. Spitzer [16,17] has calculated the increase of energy leading to desintegration of a cluster due to encounters with interstellar clouds. Spitzer has argued that the characteristic time for a process of this sort is also 1010 yr. The importance of the galactic tidal force on the evolution and stability of clusters has been also discussed (e.g. Ref. [18]). The characteristic decay time for this process is more than 109 yr. We conclude that the time yr might be regarded as an upper limit on the age of clusters in the Galaxy. 10 age =10t Other investigations have studied the most important mechanism for the destruction of dense stellar clusters, namely, the dissipation which is caused by the interaction of stars as they approach one another [19-22]. See also Refs. [23-25] for a discussion of the problem. Evidently, in this process energy exchange among cluster members will cause individual stars to acquire supercritical velo- cities (escape velocities) of the order of 2 esc 2vv, where 2 v is the rms velocity) in ex- cess of the parabolic velocity and actually to leave the cluster, whose total mass therefore decreases. The escap- ing stars carry away a positive energy and a state of statistical equilibrium is impossible for a cluster contain- ing a finite number of stars if the interactions between stars is strictly taken into account [26,27]. See also Ref. [28] for a discussion. By the time of relaxation of star systems, generally speaking we mean the characteristic time of approach of the distribution function ,, trv of the stars with re- spect to peculiar (random) velocities to a Maxwellian distribution [22]. (The distribution function v ,, trv ddvr ,d is defined by the condition that is the number of stars at time t in volume element ,,ftrv rr M r and in velocity element .) The time of estab- lishment of a Maxwellian distribution of random velo- cities as a result of encounters between test stars test and field stars field (the “collisional” relaxation time) has the order of magnitude [22,23] ,dvvv M 3 chand 22 field =, 10 log v GM n (9) where is the relative velocity, which is approximately the velocity dispersion of the lighter stars, n is the number density of the field stars, and field are the masses of test and field stars, is the so-called Coulomb (Newton) logarithm, by means of which the long- range nature of the gravitational force is taken into ac- count, clust v test M log M 0.4N , and field is the total number of field stars in the system. If we assume that the stellar distribution in the system tends to a Maxwell-Boltzmann distribution as a result of stellar encounters, during re- laxation time the system loses approximately 0.0074 of its members (e.g. Ref. [28]). Thus we can properly regard half chand N 70t as a measure of the half-life time of a cluster. (Although the general conclusions on the relax- ation time reached by Chandrasekhar, Spitzer, and others are correct, the discussions were based on a simplified “molecular-kinetic” theory and not on an explicit solu- tion of the time-dependent problem. In Appendix 8, we follow numerically the relaxation of an isotropic system of like stars through small-angle Coulomb encounters by using the more accurate approach.) In M67, assuming fieldteststar =1.33 MM M =0.86 (Equation (3)), star vv km·s–1 (Equation (5)), and 3 4πR 9 ~4 10 ~10,0 clustclust , one obtains yr for star-star gravitational encounters, So that the half-life time of the cluster is relatively short, of the order of yr only. (We estimate that the dynamical Chandrasekhar-Spitzer relaxation time for M67 is yr, which implies that the cluster age is 133 times its relaxation time. In contrast for the “ordinary” open cluster M35, the cluster age yr is only 1.6 times its relaxation time [14].) We argue therefore that in the past ( yr ago) the cluster M67 was a relatively small ( stars) globular cluster, but got “open cluster” shape due to the dynamical eva- poration of a substantial portion or even the majority of its stars. Interestingly, the direct N-body model with 36,000 stars for M67, evolved from zero age to 4 Gyr, =3nN 7 chand 310 8 1.3 10t 00 9 half =210t 7 310 Copyright © 2012 SciRes. IJAA  S. NAIM, E. GRIV 171 has been presented in Ref. [9]. It has been shown that at 4 Gyr the total mass has reduced to 2000 1200N as a result of mass loss and stellar escapes. 5. Concluding Remark Summarizing, from our own observations, we built the HR diagram for the cluster M67. We showed that this diagram is more typical for relatively old globular clusters than for open clusters. We also estimated the total number of stars in the cluster clust , its actual radius pc, and the average mass of a star star clust 3.1R 1.33 M . We studied the dynamical features of M67 and argued that The total energy of the cluster clust clustust U cl =EK is negative, 39 clust . Moreover 3.210 JE clust clust0.3KU. The latter may be considered as evidence of the quasi-stability of the system under consideration. The cluster is a tight group of about 1200 stars which are gravitationally bound, <0E. clust As the cluster is quasi-stable, its characteristic rela- xation time is the Chandrasekhar-Spitzer time 7 yr and the half-life time is equal to 9 2 10yr, respectively. chand310 70t half chand As the cluster is almost twice older its half-life time, we conclude that many stars have left the cluster since its formation. In the past (9 ~4 10 yr ago) the cluster was a relatively small (~ 10,000 stars) glo- bular cluster, but got “open cluster” shape due to the dynamical evaporation of the majority of its stars. 6. Acknowledgements This work was began while the first author (S.N.) was an undergraduate student at the Ben-Gurion University. S.N. thanks the Head of Astronomical Programs of the Ilan Ramon Physics Center, Netzach Farbiash, and the Scien- tific Director of the Ilan Ramon Physics Center, Moshe Schechter, for making possible observations with Meade LX200R telescope. We thank Amir Bernat, Michael Ge- dalin, and Nimrod Nissim for useful discussions in rela- tion to this work and both anonymous referees for nu- merous comments that improved the presentation of the paper. Atlas Image obtained as part of the Two Micron All Sky Survey, a joint project of the University of Mas- sachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This work was sponsored in part by the Israel Science Foundation, the Israeli Mi- nistry of Immigrant Absorption in the framework of the program “KAMEA,” and the Binational US-Israel Sci- ence Foundation. REFERENCES [1] G. Meynet, J.-C. Mermilliod and A. Maeder, “New Dat- ing of Galactic Open Clusters,” Astronomy and Astrophy- sics Supplement Series, Vol. 98, No. 3, 1993, pp. 477- 504. [2] S. Randich, F. Primas, L. Pasquini, P. Sestito and R. Pal- lavicini, “Tracing Mixing in Stars: New Beryllium Ob- servations of the Open Clusters NGC 2516, Hyades, and M67,” Astronomy & Astrophysics, Vol. 469, No. 1, 2007, pp. 163-172. doi:10.1051/0004-6361:20066218 [3] A. Sarajedini, A. Dotter and A. Kirkpatrick, “Deep 2MASS Photometry of M67,” The Astrophysical Journal, Vol. 698, No. 2, 2009, pp. 1872-1878. doi:10.1088/0004-637X/698/2/1872 [4] X. Fan, D. Burstein, J.-S. Chen, J. Zhu, et al., “Deep Wide- Field Spectrophotometry of the Open Cluster M67,” The Astrophysical Journal, Vol. 112, No. 2, 1996, pp. 628- 648. doi:10.1086/118039 [5] D. A. VandenBerg and P. B. Stetson, “On the Old Open Clusters M67 and NGC 188,” Publications of the Astro- nomical Society of Japan, Vol. 116, No. 825, 2004, pp. 997-1011. doi:10.1086/426340 [6] V. Laugalys, A. Kazlauskas, R. P. Boyle, F. J. Vrba, P. A. Davis and V. Straižys, “CCD Photometry of the M67 Cluster in the Vilnius System. II. New Photometry of High Accuracy,” Baltic Astron., Vol. 13, 2004, pp. 1-33. [7] T. M. Girard, W. M. Grundy, C. E. Lopez and W. F. van Altena, “Relative Proper Motions and the Stellar Velocity Dispersion of the Open Cluster M67,” Astronomical Journal, Vol. 98, No. 1, 1989, pp. 227-243. doi:10.1086/115139 [8] E. K. Kharadze, R. A. Bartaya, O. B. Dluzhnevskaya, A. E. Piskunov and E. D. Pavlovskaya, “Population of the Galactic Disc in the Solar Neighbourhood. I—Parameters of Spatial Distribution for Stellar Groups of A-K Spectral and III-V Luminosity Classes,” Astrophysics and Space Science, Vol. 151, No. 2, 1989, pp. 319-334. doi:10.1007/BF00648388 [9] J. R. Hurley, O. R. Pols, S. J. Aarseth and C. A. Tout, “A Complete N-body Model of the Old Open Cluster M67,” Monthly Notices of the Royal Astronomical Society, Vol. 363, No. 1, 2005, pp. 293-314. doi:10.1111/j.1365-2966.2005.09448.x [10] C. Bonatto and E. Bica, “Mass Segregation in M67 with 2MASS,” Astronomy & Astrophysics, Vol. 405, No. 2, 2003, pp. 525-530. doi:10.1051/0004-6361:20030205 [11] J. R. A. Davenport and E. L. Sandquist, “Death of a Cluster: The Destruction of M67 as Seen by the Sloan Digital Sky Survey,” The Astrophysical Journal, Vol. 711, No. 2, 2010, pp. 559-572. doi:10.1088/0004-637X/711/2/559 [12] D. E. McLaughlin, J. Anderson, G. Meylan, K. Gebhardt, C. Pryor, D. Minniti and S. Phinney, “Hubble Space Telescope Proper Motions and Stellar Dynamics in the Core of the Globular Cluster 47 Tucanae,” The Astro- physical Journal Supplement Series, Vol. 166, No. 1, 2006, pp. 249-297. doi:10.1086/505692 [13] G. Q. Liu, L. Deng, M. Chavez, E. Bertone, A. H. Davo Copyright © 2012 SciRes. IJAA  S. NAIM, E. GRIV Copyright © 2012 SciRes. IJAA 172 and M. D. Mata-Chavez, “A Spectroscopic Study of the Blue Stragglers in M67,” Monthly Notices of the Royal Astronomical Society, Vol. 390, No. 2, 2008, pp. 665- 674. [14] J. S. Kalirai, G. G. Fahlman, H. B. Richer and P. Ventura, “The CFHT Open Star Cluster Survey. IV. Two Rich, Young Open Star Clusters: NGC 2168 (M35) and NGC 2323 (M50),” The Astrophysical Journal, Vol. 126, No. 2, 2003, pp. 1402-1414. doi:10.1086/377320 [15] S. Rosseland, “Scattering of Stars in Clusters,” Zeitschrift fur Astrophysik, Vol. 4, No. 1, 1932, pp. 235-254. [16] L. Spitzer, “Distribution of Galactic Clusters,” The As- trophysical Journal, Vol. 127, No. 1, 1958, pp. 17-27. doi:10.1086/146435 [17] L. Spitzer and R. Harm, “Evaporation of Stars from Iso- lated Clusters,” The Astrophysical Journal, Vol. 127, No. 1, 1958, pp. 544-550. doi:10.1086/146486 [18] E. Terlevich, “Evolution of N-body Open Clusters,” Month- ly Notices of the Royal Astronomical Society, Vol. 224, No. 1, 1987, pp. 193-225. [19] V. A. Ambartsumyan, “Stability of Stellar Clusters,” Uchenye Zapiski LGU, Vol. 22, No. 1, 1938, pp. 19-29. [20] L. Spitzer, “The Stability of Isolated Clusters,” Monthly Notices of the Royal Astronomical Society, Vol. 100, No. 1, 1940, pp. 396-413. [21] T. A. Agekyan, “The Velocity Distribution Function and the Rate of Dissipation in Systems of Gravitating Bod- ies,” Soviet Astronomy, Vol. 3, No. 1, 1959, pp. 280-290. [22] S. Chandrasekhar, “Principles of Stellar Dynamics,” Do- ver, New York, 1960. [23] L. Spitzer and M. H. Hart, “Random Gravitational En- counters and the Evolution of Spherical Systems. I. Me- thod,” The Astrophysical Journal, Vol. 164, No. 1, 1971, pp. 399-409. doi:10.1086/150855 [24] R. de Grijs, “The Long-Term Survival Chances of Young Massive Star Clusters,” Astrophysics and Space Science, Vol. 324, No. 2-4, 2009, pp. 283-291. doi:10.1007/s10509-009-0100-0 [25] J. Schneider, P. Amaro-Seoane and R. Spurzem, “Higher- Order Moment Models of Dense Stellar Systems: Appli- cations to the Modelling of the Stellar Velocity Distribu- tion Function,” Monthly Notices of the Royal Astronomi- cal Society, Vol. 410, No. 1, 2011, pp. 432-454. doi:10.1111/j.1365-2966.2010.17454.x [26] I. King, “The Escape of Stars from Clusters 11. A Simple Theory of the Evolution of an Isolated Cluster,” The As- trophysical Journal, Vol. 63, No. 1258, 1958, pp. 114- 117. doi:10.1086/107702 [27] S. von Hoerner, “Die Auflsungszeit Offener Sternhau- fen,” Zeitschrift fur Astrophysik , Vol. 44, No. 1, 1958, pp. 221-242. [28] L. P. Ossipkov, “On the Jubilee of Academician V. A. Ambartsumyan Statistical Mechanics of Stellar Systems: From Ambartsumyan Onward,” Astrophysics, Vol. 51, No. 4, 2008, pp. 428-442. doi:10.1007/s10511-008-9032-6 [29] A. F. Alexandrov, L. S. Bogdankevich and A. A. Rukhadze, “Principles of Plasma Electrodynamics,” Springer, Berlin, 1984. doi:10.1007/978-3-642-69247-5 [30] G. G. Kuzmin, “The Effect of Star Encounters and the Evolution of Star Clusters,” Publications of Tartu Ob- servatory, Vol. 33, No. 2, 1957, pp. 75-102. [31] M. N. Rosenbluth, W. M. MacDonald and D. L. Judd, “Fokker-Planck Equation for an Inverse-Square Force,” Physical Review, Vol. 107, No. 1, 1957, pp. 1-6. doi:10.1103/PhysRev.107.1 [32] D. C. Montgomery and D. A. Tidman, “Plasma Kinetic Theory,” McGraw-Hill, New York, 1964. [33] B. A. Trubnikov, “Particle Interactions in a Fully Ionized Plasma,” In: M. A. Leontovich, Ed., Reviews of Plasma Physics, Consultants Bureau, New York, 1965, pp. 105- 140. [34] E. Griv, “Numerical Integration of the Landau Kinetic Equation,” In: G. Byrd, Eds., “Order and Chaos in Stellar and Planetary Systems,” ASP, San Francisco, 2004, pp. 352-356. [35] W. M. MacDonald, M. N. Rosenbluth and W. Chuck, “Relaxation of a System of Particles with Coulomb In- teractions,” Physical Review, Vol. 107, No. 2, 1957, pp. 350-353. doi:10.1103/PhysRev.107.350 [36] J. Killeen and A. H. Futch, “Numerical Solution of the Fokker-Planck Equations for a Hydrogen Plasma Formed by Neutral Injection,” Journal of Computational Physics, Vol. 2, No. 3, 1968, pp. 236-254.  S. NAIM, E. GRIV 173 Appendix Relaxation of a System of Stars: Numerical Solution of the Fokker-Planck Equation Let us consider a system of stars interacting through in- verse-square-law Coulombian (Newtonian) forces. As is known, the evolution of an isotropic distribution of like particles (stars) through small-angle Coulomb-like col- lisions is described by the Fokker-Planck equation for an inverse-square force: 2 22 4 23 00 2 00 2 21 =2πlnd d 3 4dd11 3 2 v v ff Gmufu ufu tvv fu ufuufu vvv v f 2 u (10) where , vt is the distribution function of stars, which is defined by the condition that 2 0 =dnvf v is the number density of stars. In this approximation the distribution function depends only on v, the magnitude of the velocity, and t, the time. Equation (10) has been derived by L. D. Landau (e.g. Ref. [29]) and then fully independent in Ref. [30] for gravitational systems and in Refs. [31,32] for an ionized gas. See Refs. [33,34] for a discussion. It can be shown that, in the absence of sources and losses, the number of particles (stars), as well as total momentum and energy, are conserved within the for- malism of the Fokker-Planck equation. The solution of Equation (10), under the same conditions, for a steady state (=0ft ) is the Maxwellian distribution, 2 2 () exp. 2 v fv v Following Refs. [35,36], Equation (10) may be put into dimensionless form 2 2 = fff , BCf x x (11) where 0 = vv , v0 is a constant and is a characteristic velocity, is the dimensionless time, and quantities A, B, and C are defined in Ref. [36]. We integrate this equation directly using the difference equation given in Ref. [36] (see also Ref. [35]). Figure 7. The relaxation of a system of like stars to the equilibrium Maxwellian distribution. The dashed line shows an initial distribution and the dash-dot line shows a Max- wellian of the same density and energy. The time is nor- malized so that τ = 1 corresponds to a Chandrasekhar- Spitzer relaxation time tchand (Equation (9)). We agree with the second referee of this paper that Equation (11) “is neither matching an actual multi-com- ponent system nor a spatially inhomogeneous stellar system.” This equation can serve only as a convenient starting point for more realistic computations. We solve Equation (11) numerically, subject to the initial condition that at time =0 , the initial distri- bution is 2 ,0exp0.3 0.3fx x . The result- ing solution for , x is plotted in Figure 7 for various values of time . The final Maxwellian distri- bution function at is also shown. In fair agree- ment with the simple Chandrasekhar-Spitzer theory [22, 23], at 1 the distribution function of stars becomes Maxwellian-like. As calculations show, near 0.25x and 0.45x the distribution function departs slightly from the equilibrium Maxwellian. However, at =1 the lower energy portion of the spectrum is somewhat underpopulated, while the higher energy part is over- populated. Thus, the higher- and lower-energy parts of the distribution are filled in at a much later time (at times 10 , Figure 7) as one may expect from the Chan- drasekhar-Spitzer theory. We conclude that in quanti- tative terms the collisional relaxation of the high- and low-energy parts of the distribution is only poorly des- cribed by the Chandrasekhar-Spitzer simple “molecular- kinetic” theory. Copyright © 2012 SciRes. IJAA
|