World Journal of Nano Science and Engineering, 2012, 2, 161-169
http://dx.doi.org/10.4236/wjnse.2012.23021 Published Online September 2012 (http://www.SciRP.org/journal/wjnse)
Tunable Bending Stiffness, Buckling Force, and Natural
Frequency of Nanowires and Nanoplates
Hanxing Zhu1*, Zuobin Wang2, Tongxiang Fan3, Di Zhang3
1School of Engineering, Cardiff University, Cardiff, UK
2CNM & IJRCNB Centers, Changchun University of Science and Technology, Changchun, China
3State Key Lab of Metal Matrix Composites, Shanghai Jiao Tong University, Shanghai, China
Received June 10, 2012; revised July 8, 2012; accepted August 20, 2012
ABSTRACT
This paper aims to obtain the simple closed-form results for the combined effects of surface elasticity, initial stress/
strain, and material Poisson ratio on the bending stiffness, natural frequency and buckling force of nanowires and nano-
plates. The results demonstrate that all these properties of nanowires or nanoplates can be designed either very sensitive
or not sensitive at all to the amplitude of an applied electric potential; show how much of those properties can be con-
trolled to vary; and thus provide a reliable guide to the measurement of the Young’s modulus of nanowires/nanoplates
and to the design of nano-devices, such as nano-sensors or the cantilever of an AFM.
Keywords: Nanowires; Nanoplates; Bending Stiffness; Buckling Force; Natural Frequency
1. Introduction
Owing to the large surface area to volume ratio at the
nanoscale, the mechanical properties, such as the bending
stiffness [1-7], yield strength [8], resonant frequency
[9-17] and buckling force [18-21], of nanowires (NWs)
and nanoplates (NPs) are size-dependent. In order to in-
terpret the size-dependent mechanical behaviours of
NWs and NPs, to extract the mechanical properties (e.g.
the Young’s modulus) of the material from experimentally
measured results, and to design nanoelectro-mechanical
systems (NEMS) [22,23], one has to employ a mechanical
model and the associated theoretical formula which re-
lates all the parameters involved such as forces/stresses
and dimensions. Many theoretical models have been
proposed for the purpose for extracting, interpreting, or
predicting the Young’s modulus [2-7], yield strength [8],
resonant frequency [9-17], and buckling force [18-21] of
nanowires. However, if the employed theoretical model
is incorrect (e.g. [21]), it could mislead our under-standing
of the experimentally measured results or result in wrong
predictions for the mechanical behaviour of materi-
als/structures or NEMS designed. It has generally been
recognised that the initial surface stress can greatly affect
the mechanical properties of nanostructures/materials
[10-11,14,24-25]. More important and interesting is that
the initial surface stress can be controlled to vary
by adjusting the amplitude of an applied electric potential
[17,26-31]. For example, the initial surface stress of Au
(111) is 1.13 N/m. Biener et al. [26], however, have ex-
perimentally found that for nanoporous Au material, by
controlling the chemical energy, the adsorbate-induced
initial surface stress 0

can reach 17 - 26 N/m. Weiss-
muller et al. [29, 30] have experimentally demonstrated
the recoverable deformation by adjusting amplitude of
the initial surface stress via controlling an applied
electric potential. There is a linear correlation between
surface stress and surface charge in anion adsorption on
Au(111) [31].
This paper aims to provide the precise theoretical re-
sults of the combined effects of surface elasticity, initial
stress/strain and material Poisson ratio on the bending
stiffness，natural frequency and buckling force of nano-
wires and nanoplates, to give the upper and lower bounds
of those tunable properties, to serve as a guide for the
design and experimental measurement of nanostructures,
and to clarify some existing mistakes in the treatment of
the initial surface stresses.
2. Tunable Bending Stiffness
The combined effects of the surface elasticity and initial
stress/strain on the bending stiffness have been obtained as
44
00
88 ππ
11
6464 1
xx
nn
b
lv lv Ed Ed
DdEd v







(1a)
*Corresponding author.
C
opyright © 2012 SciRes. WJNSE

H. X. ZHU ET AL. 162
for nanowires with a circular cross-section [24], 0.1E

4
4
1
12
1
12
bEd
D
Ed


0
0
83
2
83
2 1
x
n
x
n
lv
dE
lv
dv












(1b)
or
4
4
1
12
1
12
bEd
D
Ed
0
0
42
42
1
x
n
x
n
lv
dE
lv
dv













/lSE


(1c)
for nanowires with a square cross-section [25] when
bending is about a neutral plane parallel to the surface
plane (1b) or about a diagonal plane (1c). Where, d is the
cross-sectional diameter in Equation (1a) or the side
length of the square cross-section in Equations (1b) and
(1c); E is the Young’s modulus of the bulk material;
n is the intrinsic length of the material at the
nano scale; and S is the surface elasticity modulus. In
order to simplify the analysis and results, both the sur-
face and the bulk materials are assumed to be isotropic
and to have the same Poisson ratio v; the initial surface
stresses in both the axial and the circular directions are
assumed to be the same as 0

. The initial residual stress
of the bulk material in the axial direction of the nanowire
with either a circular or a square cross-section is thus
00
because equilibrium in the axial direction
has to be held for a free nanowire such as a cantilever.
For a uniform nanowire with either a circular or a square
cross-section, the initial stresses in the bulk material in
both the radial and the circular directions are half of that
in the axial direction, i.e. 000 0 .
The initial residual elastic strain in the axial direction,
0, of a nanowire is related to the initial surface stresses
by 00 . The von Mises stress of the
bulk material should not exceed the material yield
strength
4/
xd
 
/22 /d  
x


rx 
  
)/()Edv1( 4
x

y

, otherwise, the nanowire would undergo
permanent plastic deformation. Atomistic simulation [32]
has shown that if the diameter of a gold wire is suffi-
ciently small, it can automatically undergo plastic de-
formation solely owing to the presence of the initial sur-
face stresses. It is well known that the yield strength,
y

,
of some conductive polymer materials or nano-sized me-
tallic materials can be (E is the Young’s modulus)
or larger [33]. Biener et al. [26] have experimentally
found that for nanoporous Au material, by controlling the
chemical energy, the adsorbate-induced surface stress
0
E1.0

can reach 17 - 26 N/m. If the diameter of the liga-
ments is 5 nm, 0
x

would be 20 GPa. As the bulk mate-
rial discussed in this paper can be either metallic, or
polymeric or biological, without losing generality, the
von Mises yield strength is assumed to be y


. If
the actual yield strength of the bulk material of a
nanowire/nanoplate is larger or smaller than , its
tunable ranges of the bending stiffness, natural frequency,
and axial compressive buckling force can still be ob-
tained by scaling up or scaling down the results that are
presented in sections that follow.
E1.0
According to the aforementioned assumptions, for
recoverable elastic deformation, the amplitude of the von
Mises stress in the bulk material of a nanowire is limited
by 0ey . The corresponding initial
strain in the axial direction is 00 . The
strain in the radial direction of the nanowire cross-section
is related to the initial surface stresses or the initial re-
sidual elastic strain in the axial direction by
/2 0.1
xE
  

1/
xxvE
 
 

00
00
213
13 13
221
x
rx
v
vv
Ed Ev
  
  (2)

when the effects of both the surface elasticity and the
initial surface stress 0

are absent (i.e. n and
0000
0Sl
xxr


 d
4
00
π/64DdE
4/12DdE
0
0), the diameter or side-length of the
cross-section of a nanowire is assumed to be 0 and the
corresponding conventional bending stiffness to be
for a circular cross-section or
00 for a square cross-section. When the ef-
fect of the initial surface stresses

is present,


000 0
13
11
21
rx
v
dddv









(3)
Substituting Equation (3) into (1a), the combined ef-
fects of the surface elasticity and initial stresses on the
bending stiffness of a nanowire with a circular cross-
section can be obtained as

4
0
0
0
813
11
121
xx
bn
Dlv v
Ddvv




 
 




/0
n
ld
(4)
when the effect of the surface modulus S is absent (i.e.
0

or 0n d), the effect of the initial stress
0
l
x

on the dimensionless bending stiffness 0b of a
nanowire with a circular cross-section is plotted against
the possible value of the Poisson ratio v of the bulk mate-
rial for different amplitudes of the initial stress:
0
/DD
x


0.2E, 0.1E, 0, −0.1E, −0.2E (note that the corre-
sponding von Mises stresses are e


/DD
0.1E, 0.05E, 0,
0.05E and 0.1E, respectively), as shown in Figure 1(a).
As can be seen from Figure 1(a), when the Poisson ratio
of the bulk material v is close to 0, the normalised bend-
ing stiffness, 0b, of a nanowire can be controlled to
vary over a range from 0.65 to 1.4 by adjusting the am-
plitude of the initial stress 0
x

from −0.2E to 0.2E (this,
in turn, can be realised by adjusting the amplitude of an
applied electric potential). The tunable range of
0
/
b
DD

H. X. ZHU ET AL. 163
depends strongly on the Poisson ratio v of the bulk mate-
rial: approximately proportional to the amplitude of the
initial stress 0
x

; narrowing with the increase of v; and
vanishing when . When v is larger than 0.4, the
trend of the effect of 0
0.4v
x

on 0b is reversed. When
the effect of the surface elasticity S is present and when
0 is fixed at 0.1, the combined effects of the ini-
tial stress 0
/DD
/D
b
D
x

and the surface elasticity on the normal-
ised bending stiffness 0b of a nanowire with a
circular cross-section are plotted against the possible
value of the Poisson ratio of the bulk material for differ-
ent amplitudes of the initial stress: 00.2E, 0.1E, 0,
−0.1E, −0.2E, as shown in Figure 1(b). When v is very
small, 0 can be controlled to vary over a range
from 1.25 to 2.45. The larger the amplitude of the initial
stress 0
/DD
x
 
/
b
DD
x

, the larger the tunable range of 0b. The
effect of the initial stress 0
/DD
x

on reduces with
the increase of v and vanishes when . When v is
larger than 0.38, the trend of the effect is reversed. When
the initial stress ,
0
/D
0.38
b
D
v
00
x
 00 18 1.8ld
bn
DD .
(a)
(b)
Figure 1. Effects of the surface elasticity and initial stresses
on the bending stiffness of nanowires with a circular
cross-section: a) 00
n
ld=; b) 00.1
n
ld=
/DD
.
The relationships between 0b and v, shown in
Figures 1(a) and (b), can well be approximated by the
same linear function
 
00
00
142 3925
x
x
bn
Dl vv
DdE E



 


4/
xd
 
/DD
/81 dl
(5)
As the amplitude of the initial stress 000
can be controlled to vary by adjusting the amplitude of
an applied electric potential [26-31], the normalised
bending stiffness of a nanowire 0b could be con-
-trolled to either reduce 30% or to increase 40% form the
amplitude 0n

, depending upon the value of the
Poisson ratio v of the bulk material. It is noted that for
different bulk material, such as a metal, polymer or bio-
logical material, the nano-size scale intrinsic length
may vary between 0.01 to 1 nm. In Figure 1(b), 0n
is fixed at 0.1. If shown in Figure 1(b) is di-
vided by 0n
n
l
/ld
0
/
b
DD
(1 8/)1.8ld


n
l
, the results will be very close
to those given in Figure 1(a). This implies that whether
the effect of the surface elasticity (i.e. S or ) is present
or absent, the relative tunable range,




//18/DD ld
00bn
, of the bending stiffness of a
nanowire depends mainly on the amplitude 0
x

and the
bulk material Poisson ratio v. Likewise, the bending
stiffness of a nanowire with a square cross-section about
a diagonal plane or a plane parallel to the surface plane
can also be controlled to vary over a large range, de-
pending on amplitude of the initial stress/strain and the
material Poisson ratio. The tunable range,




//18/DD ld
00bn
, is close to that of a nanowire
with a circular cross-section. It is noted that in all the
cases, the amplitude of 0
x

(or 0

) is adjustable and
controllable, while the Poisson ratio v remains constant
for a given material.
For a flat, wide and uniform nanoplate of width b and
thickness h, the analytical result for the combined effects
of the surface elasticity and initial stresses on the bending
stiffness is obtained as [25]


3
0
2
1
16 1
12 1
x
n
b
v
l
Ebh
Dhv
v
 



 (6)






bh/lSE where ; E, n

, S and the initial surface
stress 0

are exactly the same as those for nanowires.
Again, both the surface and the bulk material are as-
sumed to be isotropic and to have the same Poisson ratio
v for simplicity in the analysis and results. For recover-
able elastic deformation, the initial von Mises stress
should not exceed the yield strength of the bulk material,
00 0ey
. The amplitude of
the initial in-plane elastic residual strains of a nanoplate
is related to the initial stresses by
2/ 0.1
xy hE
   


00 1/
xy xvE
  
0. When the initial surface stress
0

is absent (i.e. 00 00 0
xyh



0 0
h
), the width and
thickness of the nanoplate are noted as b and .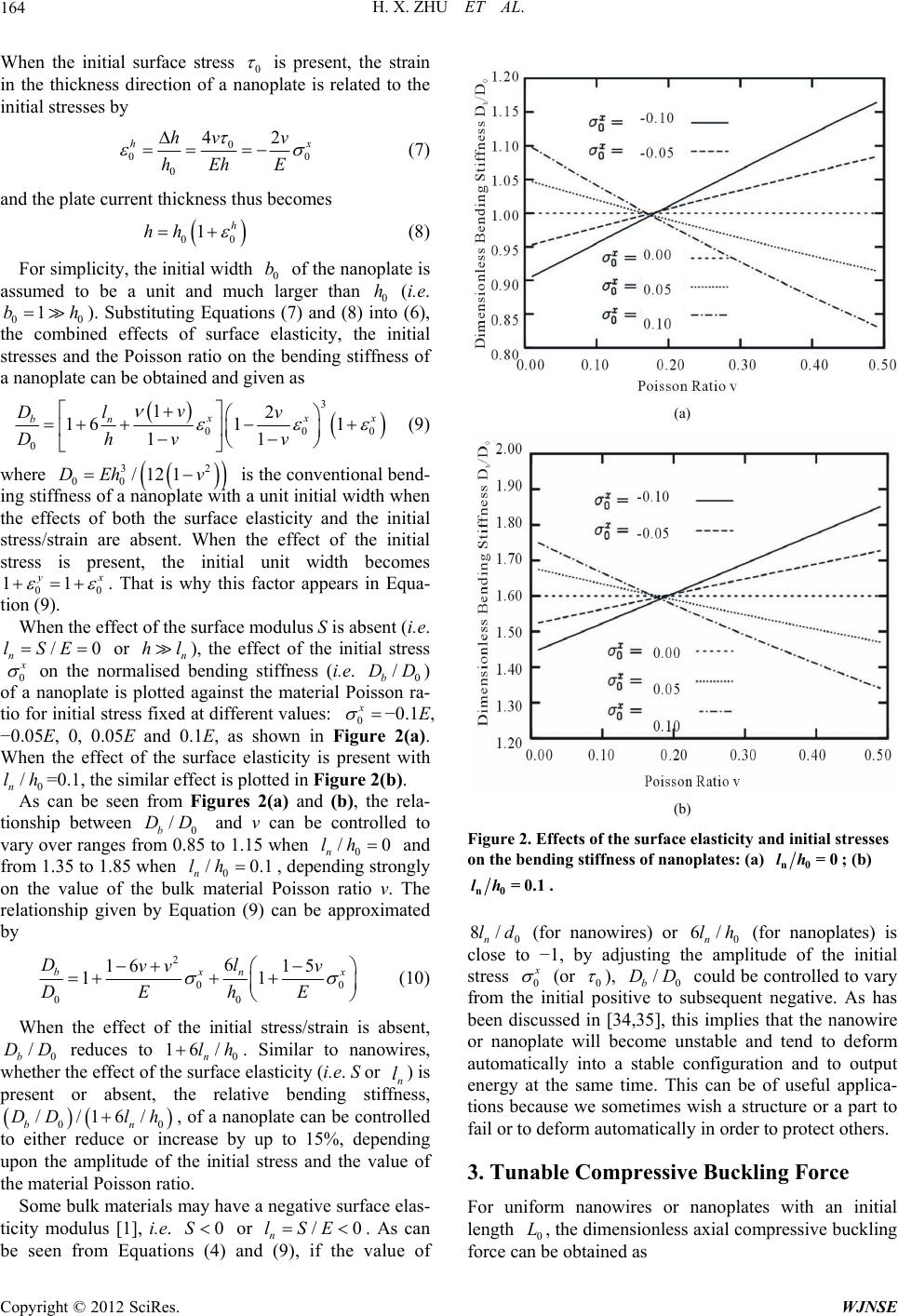

H. X. ZHU ET AL. 164
When the initial surface stress 0

is present, the strain
in the thickness direction of a nanoplate is related to the
initial stresses by
0
00
2
hx
hv
h E

0
4v
hE

  

00
1h hh
 (7)
and the plate current thickness thus becomes


bh
1bh
(8)
For simplicity, the initial width 0 of the nanoplate is
assumed to be a unit and much larger than 0 (i.e.
00
). Substituting Equations (7) and (8) into (6),
the combined effects of surface elasticity, the initial
stresses and the Poisson ratio on the bending stiffness of
a nanoplate can be obtained and given as


3
00
2
16 1 1
11
0
0
1
x
xx
bn
v
Dl v
Dhv v





 





 
2
1v

3
/12
(9)
where 00 is the conventional bend-
ing stiffness of a nanoplate with a unit initial width when
the effects of both the surface elasticity and the initial
stress/strain are absent. When the effect of the initial
stress is present, the initial unit width becomes
0
DEh
0
11
yx

  . That is why this factor appears in Equa-
tion (9).
When the effect of the surface modulus S is absent (i.e.
or n h), the effect of the initial stress
0
/lSE0
nl
x

on the normalised bending stiffness (i.e. 0b)
of a nanoplate is plotted against the material Poisson ra-
tio for initial stress fixed at different values: 0
/DD
x


−0.1E,
−0.05E, 0, 0.05E and 0.1E, as shown in Figure 2(a).
When the effect of the surface elasticity is present with
=0.1, the similar effect is plotted in Figure 2(b).
0
As can be seen from Figures 2(a) and (b), the rela-
tionship between 0b and v can be controlled to
vary over ranges from 0.85 to 1.15 when 0n
/
n
l
/D
/0lh
h
D

and
from 1.35 to 1.85 when 0n/0.1lh

, depending strongly
on the value of the bulk material Poisson ratio v. The
relationship given by Equation (9) can be approximated
by
2
00
6 16
1
00
15
1
x
x n
l v
hE
b
D vv
DE




  


/D16/lh
)

/0lSE

6/lh
(10)
When the effect of the initial stress/strain is absent,
0b reduces to 0n. Similar to nanowires,
whether the effect of the surface elasticity (i.e. S or n
lis
present or absent, the relative bending stiffness,
0bn
, of a nanoplate can be controlled
to either reduce or increase by up to 15%, depending
upon the amplitude of the initial stress and the value of
the material Poisson ratio.
D

0
//1DD
Some bulk materials may have a negative surface elas-
ticity modulus [1], i.e. or n. As can
be seen from Equations (4) and (9), if the value of
0S
(a)
(b)
Figure 2. Effects of the surface elasticity and initial stresses
on the bending stiffness of nanoplates: (a) n0 =0lh ; (b)
n0
=0.1lh
8/ld 6/lh
.
0n (for nanowires) or 0n (for nanoplates) is
close to −1, by adjusting the amplitude of the initial
stress 0
x

(or 0

), 0b could be controlled to vary
from the initial positive to subsequent negative. As has
been discussed in [34,35], this implies that the nanowire
or nanoplate will become unstable and tend to deform
automatically into a stable configuration and to output
energy at the same time. This can be of useful applica-
tions because we sometimes wish a structure or a part to
fail or to deform automatically in order to protect others.
/DD
L
3. Tunable Compressive Buckling Force
For uniform nanowires or nanoplates with an initial
length 0, the dimensionless axial compressive buckling
force can be obtained as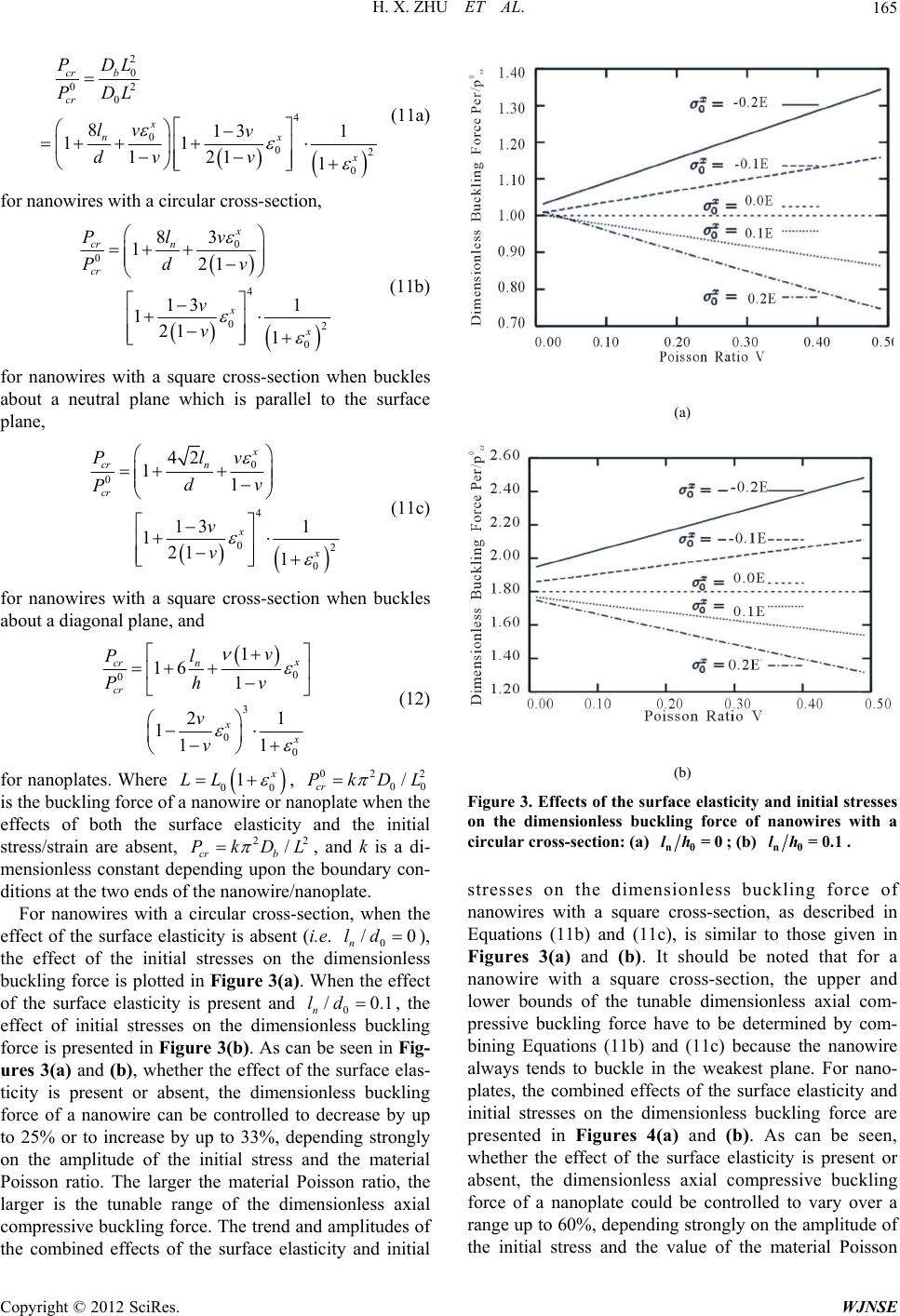

H. X. ZHU ET AL. 165


2
0
02
0
0
0
813
11
121
cr b
cr
xx
n
PDL
PDL
lv v
dv v





 



4
2
0
1
1x 




 
(11a)
for nanowires with a circular cross-section,



0
4
2
0
1
1
x
x
v
dv











0
0
83
121
13
121
cr n
cr
x
Pl
P
v
v


 


(11b)
for nanowires with a square cross-section when buckles
about a neutral plane which is parallel to the surface
plane,


0
4
2
0
1
1
x
x
v
dv













0
0
42
11
13
121
cr n
cr
x
Pl
P
v
v

 


(11c)
for nanowires with a square cross-section when buckles
about a diagonal plane, and


0
3
0
0
1
1
21
1
016
11
x
cr n
cr
x
x
v
hv

Pl
P
v
v



 











(12)
for nanoplates. Where


00
1
x
LL


22
/
cr b
PkDL  
, 00cr
is the buckling force of a nanowire or nanoplate when the
effects of both the surface elasticity and the initial
stress/strain are absent, , and k is a di-
mensionless constant depending upon the boundary con-
ditions at the two ends of the nanowire/nanoplate.
022
/PkDL  
/0ld
For nanowires with a circular cross-section, when the
effect of the surface elasticity is absent (i.e. 0n
(a)
(b)
Figure 3. Effects of the surface elasticity and initial stresses
on the dimensionless buckling force of nanowires with a
circular cross-section : (a)

),
the effect of the initial stresses on the dimensionless
buckling force is plotted in Figure 3(a). When the effect
of the surface elasticity is present and 0n/0.1ld

, the
effect of initial stresses on the dimensionless buckling
force is presented in Figure 3(b). As can be seen in Fig-
ures 3(a) and (b), whether the effect of the surface elas-
ticity is present or absent, the dimensionless buckling
force of a nanowire can be controlled to decrease by up
to 25% or to increase by up to 33%, depending strongly
on the amplitude of the initial stress and the material
Poisson ratio. The larger the material Poisson ratio, the
larger is the tunable range of the dimensionless axial
compressive buckling force. The trend and amplitudes of
the combined effects of the surface elasticity and initial
n0
=0lh ; (b) n0 =0.1lh .
stresses on the dimensionless buckling force of
nanowires with a square cross-section, as described in
Equations (11b) and (11c), is similar to those given in
Figures 3(a) and (b). It should be noted that for a
nanowire with a square cross-section, the upper and
lower bounds of the tunable dimensionless axial com-
pressive buckling force have to be determined by com-
bining Equations (11b) and (11c) because the nanowire
always tends to buckle in the weakest plane. For nano-
plates, the combined effects of the surface elasticity and
initial stresses on the dimensionless buckling force are
presented in Figures 4(a) and (b). As can be seen,
whether the effect of the surface elasticity is present or
absent, the dimensionless axial compressive buckling
force of a nanoplate could be controlled to vary over a
range up to 60%, depending strongly on the amplitude of
the initial stress and the value of the material Poisson

H. X. ZHU ET AL. 166
(a)
(b)
Figure 4. Effects of the surface elasticity and initial stresses
on the dimensionless buckling force of nanoplates: (a)
n0
=0lh ; (b) n0 =0.1lh .
ratio. It should be noted that the results given in Equa-
tions (11) and (12) and shown in Figures 3 and 4 apply
only when the nanowires/nanoplates are relatively thin
and long (e.g. or /Lh /5/
y
Ld E

). Otherwise,
the nanowire/nanoplate may yield before losing stability.
Wang and Feng [21] have studied the combined ef-
fects of the surface elasticity and initial surface stress on
the axial compressive buckling force of nanowires.
However, we do not favour their analysis and results.
The initial surface stresses are actually internal stresses
in a nanowire or nanoplate because the nanowire/nano-
plate contains both the bulk and surface materials. If the
initial surface stresses are treated as external tractions,
their counterparts (i.e. the initial residual stresses in the
bulk material) should also be taken into consideration.
Wang and Feng [21] only treated the initial surface
stresses as external tractions and ignored the effects of
their counterpart, and thus obtained the axial compres-
sive buckling force of nanowires as
2
0
22
cr EI
Pk d
l



2
lEI
22
/2
(13)
For a very thin and long nanowire (i.e. ),
Equation (13) reduces to 0cr
P
kEIlHHd

 
(see the Equation (11) of paper [21]), suggesting that
when the initial surface stress 0

is positive, a very thin
and long nanowire will not buckle if the axial compres-
sive force is no larger than 0 2d

. On the other hand,
when the initial surface stress 0

is negative, the bulk
material of a nanowire is actually stretched in the longi-
tudinal direction by 0

. Equation (13), however, sug-
gests that a free thin and long cantilever nanowire, which
has already stretched in the longitudinal direction by 0

,
would buckle even if a tensile force no larger than
0
2d

is axially applied to stretch it at its two ends. The
implications of their results (i.e. (13)) are entirely against
the common sense. It is noted that the same treatment (i.e.
taking the initial surface stresses as external tractions and
ignoring the effects of the initial residual stresses in the
bulk materials) has appeared in many research papers on
studying the bending stiffness, buckling force and reso-
nant frequency of nanowires, e.g. [6,11,13,21]. We do
not agree with the way of their treatment on the initial
surface stress and thus suspect their obtained results.
4. Tunable Natural Frequency
For a uniform cantilever nanowire or nanoplate, when the
effect of the initial stresses is absent (i.e. 0

or 0
x

is
0), the natural frequency is given by

44
22
nini
i
ii ii
EI
kkD
fmL mL


n
k
3.52k
(14)
where, is a constant for a given vibration mode, e.g.
n

for mode 1; 00in
for nanowires with a circular cross-section, or


4/6418/DEd ld
 




4/1218/DEd ld
00in
for nanowires with a square
cross-section when bending is around a neutral plane
parallel to a surface plane, or




41214 2DEd ld
00in
for nanowires with a
square cross-section when bending is around a diagonal
plane, or




3/121 6/
00in
D
Ehl h
mL
for nanoplates of
an initial unit width; i is the mass of per unit length of
the nanowire or nanoplate; and i is the length of the
cantilever when the initial stress is absent.
When the effect of the initial stresses/strains is present,
the normalised natural frequency becomes
3
22
0
1
1
bi ibx
ii i
Dm LD
f
fDmL D





 
 
b
D
(15)
where is the bending stiffness given by Equation (4)

H. X. ZHU ET AL. 167
for nanowires with a circular cross-section or by Equa-
tion (9) for nanoplates; 0

1
x
i
LL


//
i
LL
/0.1ld
is the length of
the nanowire or nanoplate axially stretched by the initial
surface stresses, and i because of the mass
conservation.
mm
The effects of the surface elasticity and initial stresses
on the normalised natural frequency of a cantilever
nanowire with a circular cross-section and 0n

and a cantilever nanoplate with 0 are plotted
against the Poisson ratio of the bulk material, as shown in
Figures 5(a) and (b). We also found that the effect of the
amplitude 0 on the relationship given by Equation
(15) is so small that it can be neglected. As can be seen
in Figures 5( a) and (b), by adjusting the amplitude of the
initial stresses (this can be realised by adjusting the am-
plitude of an applied electric potential), the normalised
natural frequency could be controlled either to
reduce or to increase by up to around 20% for nanowires
or around 15% for nanoplates from 1, and the tunable
range depends upon the amplitude of the initial
/
n
lh0.1
/
n
ld
/i ff
(a)
(b)
Figure 5. Effects of the surface elasticity and initials tresses
on the normalised natural frequency: (a) For nanowires
with a circular cross-section and n0
=0lh ; (b) For nano-
plates with n0 =0.1lh .
stresses and the value of the bulk material Poisson ratio.
Experiments have demonstrated that micro-or nano-can-
tilever wires or plates can be used as sensors to monitor
the changes in the natural frequency [17,36], and that the
elastic properties, such as the Young’s modulus, of
nanowires can be extracted from the measured natural
frequency [37]. Lagowski et al. [16] experimentally
found that the normal mode of vibration of thin crystals
depends strongly on the surface stress. Wang and Feng
[11] and He and Lilley [13] have also studied the reso-
nant frequency of nanowires. As aforementioned, their
results are suspicious because they simply treated the
initial surface stresses as external tractions and totally
ignored the effects of the initial residual stresses in the
bulk material.
5. Conclusion
The analytic results obtained in this paper demonstrate
that the bending stiffness, resonant frequency, and axial
compressive buckling force of a nanowire or nanoplate
can be designed either very sensitive or not sensitive at
all to the amplitude of the initial stresses (0

or 0
x

);
show how much those properties can be controlled to
vary by adjusting the amplitude of an applied electric
potential; and thus provide a reliable guide to the meas-
urement of the Young’s modulus of nanowires or nano-
plates and to the design of nano-devices, such as
nano-sensor or the cantilever of an AFM.
6. Acknowledgements
This work is supported by the EC project: PIR-SES-
GA-2009-247644.
REFERENCES
[1] R. E. Miller and V. B. Shenoy, “Size-Dependent Elastic
Properties of Nanosized Structural Elements,” Nanotech-
nology, Vol. 11, No. 3, 2000, pp. 139-147.
doi:10.1088/0957-4484/11/3/301
[2] S. Guenot, C. Fretigny, S. Demoustier-Champagne and B.
Nysten, “Surface Tension Effect on the Mechanical Prop-
erties of Nanomaterials Measured by Atomic Force Mi-
croscopy,” Physical Review B, Vol. 69, No. 16, 2004, pp.
165410.1-165410.5. doi:10.1103/PhysRevB.69.165410
[3] J. H. Song, X. D. Wang, E. Riedo and Z. L. Wang, “Elas-
tic Property of Vertically Aligned Nanowires,” Nano Let-
ters, Vol. 5, No. 10, 2005, pp. 1954-1958.
doi:10.1021/nl051334v
[4] G. Y. Jing, H. L. Duan, X. M. Sun, Z. S. Zhang, J. Xu, Y.
D. Li, J. X. Wang and D. B. Yu, “Surface Effects on
Elastic Properties of Silver Nanowires: Contact Atomic-
Force Microscopy,” Physical Review B, Vol. 73, No. 23,
2006, Article ID: 235409.
doi:10.1103/PhysRevB.73.235409

H. X. ZHU ET AL. 168
[5] C. Q. Chen, Y. Shi, Y. S. Zhang and J. Zhu, Y. J. Yan,
“Size Dependent Young’s Modulus in ZnO Nanowires,”
Physical Review Letters, Vol. 96, No. 7, 2006, Article ID:
075505. doi:10.1103/PhysRevLett.96.075505
[6] J. He and C. M. Lilley, “Surface Effect on the Elastic
Behaviour of Static Bending Nanowires,” Nano Letters,
Vol. 8, No. 7, 2008, pp. 1798-1802.
doi:10.1021/nl0733233
[7] A. Heidelberg, L. T. Ngo, B. Wu, M. A. Phillips, S.
Sharma, T. I. Kamins, J. E. Sader and J. J. Boland, “A
Generalized Description of the Elastic Properties of
Nanowires,” Nano Letters, Vol. 6, No. 6, 2006, pp. 1101-
1106. doi:10.1021/nl060028u
[8] B. Wu, A. Heidelberg and J. J. Boland, “Mechanical
Properties of Ultrahigh-Strength Gold Nanowires,” Na-
ture Materials, Vol. 4, No. 7, 2005, pp. 525-529.
doi:10.1038/nmat1403
[9] X. Li, T. Ono, Y. Wang and M. Esashi, “Ultrathin Sin-
gle-Crystalline-Silicon Cantilever Resonators: Fabrication
Technology and Significant Specimen Size Effect on
Young’s Modulus,” Applied Physics Letters, Vol. 83, No.
15, 2003, pp. 3081-3083. doi:10.1063/1.1618369
[10] H. S. Park, “Surface Stress Effects on the Resonant Prop-
erties of Silicon Nanowires,” Journal of Applied Physics,
Vol. 103, No. 12, 2008, Article ID: 123504.
doi:10.1063/1.2939576
[11] G. F. Wang and X. Q. Feng, “Effects of Surface Elasticity
and Residual Surface Stress on the Natural Frequency of
Microbeams,” Applied Physics Letters, Vol. 90, No. 23,
2007, Article ID: 231904. doi:10.1063/1.2746950
[12] D. A. Smith, V. C. Holmberg, D. C. Lee and B. A. Korgel,
“Young’s Modulus and Size-Dependent Mechanical
Quality Factor of Nanoelectromechanical Germanium
Nanowire Resonators,” Journal of Physical Chemistry C,
Vol. 112, No. 29, 2008, pp. 10725-10729.
doi:10.1021/jp8010487
[13] J. He and C. M. Lilley, “Surface Stress Effect on Bending
Resonance of Nanowires with Different Boundary Condi-
tions,” Applied Physics Letters, Vol. 93, No. 26, 2008,
Article ID: 263108. doi:10.1063/1.3050108
[14] H. S. Park, “Quantifying the Size-Dependent Effect of the
Residual Surface Stress on the Resonant Frequencies of
Silicon Nanowires if Finite Deformation Kinematics Are
Considered,” Nanotechnology, Vol. 20, No. 11, 2009, Ar-
ticle ID: 115701. doi:10.1088/0957
[15] M. E. Gurtin and X. Markenscoff, “Effect of Surface
Stress on the Natural Frequency of Thin Crystals,” Ap-
plied Physics Letters, Vol. 29, No. 9, 1976, pp. 529-530.
doi:10.1063/1.89173
[16] J. Lagowski, H. C. Gatos and E. S. Sproles Jr, “Surface
Stress and the Normal Mode of Vibration of Thin Crys-
tals: GaAs,” Applied Physics Letters, Vol. 26, No. 9, 1975,
pp. 493-495. doi:10.1063/1.88231
[17] G. Y. Chen, T. Thundat, E. A. Wachter and R. J. War-
mack, “Dsorption-Induced Surface Stress and Its Effects
on Resonance Frequencey of Microcantilevers,” Journal
of Applied Physics, Vol. 77, No. 8, 1995, pp. 3618-3622.
doi:10.1063/1.359562
[18] V. V. Dobrokhotov, M. M. Yazdanpanah, S. Pabba, A.
Safir and R. W. Cohn, “Visual Force Sensing with Flexi-
ble Nanowires Buckling Springs,” Nanotechnology, Vol.
19, No. 3, 2008, Article ID: 035502.
doi:10.1088/0957-4484/19/03/035502
[19] C. Hsin, W. Wai, Y. Gu, Y. Gao, C. T. Huang, Y. Liu, L.
J. Chen and Z. L. Wang, “Elastic Properties and Buckling
of Silicon Nanowires,” Advanced Materials, Vol. 20, No.
20, 2008, pp. 3919-3923. doi:10.1002/adma.200800485
[20] M. Riaz, O. Nur, M. Willander and P. Klason, “Buckling
of ZnO Nanowires under Uniaxial Compression,” Applied
Physics Letters, Vol. 92, No. 10, 2008, Article ID:
103118. doi:10.1063/1.2894184
[21] G. F. Wang and X. Q. Feng, “Surface Effects on Buckling
of Nanowires under Uniaxial Compression,” Applied
Physics Letters, Vol. 94, No. 14, 2009, Article ID:
141913. doi:10.1063/1.3117505
[22] F. Xu, Q. Qin, A. Mishra, Y. Gu and Y. Zhu, “Mechani-
cal Properties of ZnO Nanowires under Different Loading
Modes,” Nano Research, Vol. 3, No. 4, 2010, pp. 271-
280. doi:10.1007/s12274-010-1030-4
[23] K. L. Ekinci, M. H. Huang and M. L. Roukes, “Ultrasen-
sitive Nanoelectromechanical Mass Detection,” Applied
Physics Letters, Vol. 84, No. 22, 2004, pp. 4469-4471.
doi:10.1063/1.1755417
[24] H. X. Zhu, “The Effects of Surface and Initial Stresses on
the Bending Stiffness of Nanowires,” Nanotechnology,
Vol. 19, No. 40, 2008, Article ID: 405703.
doi:10.1088/0957-4484/19/40/405703
[25] H. X. Zhu, J. Wang and B. L. Karihaloo, “Effects of Sur-
face and Initial Stresses on the Bending Stiffness of Tri-
layer Plates and Nanofilms,” Journal of Mechanics of
Materials and Structures, Vol. 4, No. 3, 2009, pp. 589-
604. doi:10.2140/jomms.2009.4.589
[26] J. Biener, A. Wittstock, L. A. Zepeda-Ruiz, M. M. Biener,
V. Zielasek, D. Kramer, R. N. Viswanath, J. Wessmuller,
M. Baumer and A. V. Hamza, “Surface-Chemistry-Driven
Actuation in Nanoporous Gold,” Nature Materials, Vol. 8,
No. 1, 2009, pp. 47-51. doi:10.1038/nmat2335
[27] R. Raiteri and H. J. Butt, “Measuring Electrochemically
Induced Surface Stress with an Atomic Force Micro-
scope,” Journal of Physical Chemistry, Vol. 99, No. 43,
1995, pp. 15728-15732. doi:10.1021/j100043a008
[28] R. C. Cammarata and K. Sieradzki, “Surface and Inter-
face Stresses,” Annual Review of Materials Research, Vol.
24, 1994, pp. 215-234.
doi:10.1146/annurev.ms.24.080194.001243
[29] J. Weissmuller, R. N. Viswanath, D. Kramer, P. Zimmer,
R. Wurschum and H. Gleiter, “Charge-Induced Reversi-
ble Strain in a Metal,” Science, Vol. 300, No. 5617, 2003,
pp. 312-315. doi:10.1126/science.1081024
[30] D. Kramer, R. N. Viswanath and J. Weissmuller, “Sur-
face-Stress Induced Macroscopic Bending of Nanoporous
Gold Cantilevers,” Nano Letters, Vol. 4, No. 5, 2004, pp.
793-796. doi:10.1021/nl049927d
[31] W. Haiss, R. J. Nichols, J. K. Sass and K. P. Charle,
“Linear Correlation between Surface Stress and Surface
Charge in Anion Adsorption on Au(111),” Journal of
Electroanalytical Chemistry, Vol. 452, No. 2, 1998, pp.

H. X. ZHU ET AL. 169
199-202. doi:10.1016/S0022-0728(98)00137-5
[32] J. Diao, K. Gall, M. L. Duan and J. A. Zimmerman,
“Atomistic Simulations of the Yielding of Gold Nano-
wires,” Acta Materialia, Vol. 54, No. 3, 2006, pp.
643-653. doi:10.1016/j.actamat.2005.10.008
[33] Z. C. Lin and J. C. Huang, “A Study on a Rigid Body
Boundary Layer Interface Force Model for Stress Calcu-
lation and Stress—Strain Behaviour of Nanoscale Uniax-
ial Tension,” Nanotechnology, Vol. 15, No. 11, 2004, pp.
1509-1518. doi:10.1088/0957-4484/15/11/024
[34] H. X. Zhu, “Size-Dependent Elastic Properties of Micro-
and Nano-Honeycombs,” Journal of the Mechanics and
Physics of Solids, Vol. 58, No. 5, 2010, pp. 696-709.
doi:10.1016/j.jmps.2010.02.009
[35] H. X. Zhu, L. B. Yan, R. Zhang and X. M. Qiu,
“Size-Dependent and Tunable Elastic Properties of Hier-
archical Honeycombs with Regular Square and Equilat-
eral Triangular Cells,” Acta Materialia, Vol. 60, No. 12,
2012, pp. 4927-4939. doi:10.1016/j.actamat.2012.05.009
[36] V. Tabard-Cossa, M. Godin, L. Y. Beaulieu and P. Grut-
ter, “A Differential Microcantilever-Based System for
Measuring Surface Stress Changes Inducted by Electro-
chemical Rection,” Sensors and Actuators B: Chemical,
Vol. 107, No. 1, 2005, pp. 233-241.
doi:10.1016/j.snb.2004.10.007
[37] Z. L. Wang, Z. R. Dai, R. P. Gao and J. L. Gole, “Meas-
uring the Young’s Modulus of Solid Nanowires by in Situ
TEM,” Journal of Electron Microscopy, Vol. 51, Suppl. 1,
2002, pp. S79-S85.
doi:10.1093/jmicro/51.Supplement.S79