ABSTRACT

The Global Reaction Model describes a set of chemical reactions that can potentially occur during the process of obtaining silicon rich oxide (SRO) films, regardless of the technique used to grow such films which are an outside stoichiometry material. Particularly, chemical reactions that occur during the process of growing of SRO films by LPCVD technique are highlighted in this model. We suggest and evaluate either some types of molecules or resulting nanostructures and we predict theoretically, by applying the density functional theory, the contribution that they may have to the phenomenon of luminescence which is measured in SRO films. Also, we have calculated the opto- electronic properties of SRO films. The suggested model provides enough information required to identify the molecular structures resulting from the presence of defects in SRO films and also those corresponding to charged structures. It is also possible to detect the molecular structures which are modified due to the effect of heat treatment, and identify the presence of different oxidation states inclusive the formation of siloxanes.

Keywords:

Global Reactions Model, Silicon Rich-Oxide, Defects, LPCVD, Luminescence

1. Background

The motivation of this work is to apply a new model, which we have called the Global Reaction Model (GRM), for the theoretical study of the optical and electronics properties of Silicon Rich Oxides (SRO) structures regardless of the technique used to fabricate such structures. For developing this model, Espinosa et al. [1] have reviewed firstly some important experimental results about measurements of structural and optical properties carried out on SRO samples grown by different techniques and the theoretical models available in order to describe a SRO network. The aim of this review is twofold; on one hand, we have found relevant information in relationship to actual quantification of silicon nano-clusters (Si-nCs) about their size, electromagnetic range of emission, molecular structure and important parameters which are responsible for making variations of optical properties of SRO.

On the other hand, we take experimental information as background in order to focus correctly on our theoretical research based on using the Density Functional Theory (DFT) method corresponding to atomic composition of different silicon isomers suggested simulating the Si-nCs embedded in SRO films, SRO structures with specific defects and charged SRO structures (anions and cations), as possible responsible of luminescence in SRO films.

Silicon Rich Oxide (SRO) thin films have been studied extensively and are very interesting due to their opto- electronic properties, particularly those related with luminescence. In general, luminescent properties can provide significant information regarding the crystalline structure of a material and, in the case of SRO thin films, electro-luminescence properties are particularly important since these films can be used to fabricate luminescent devices [2] .

This paper is outlined as follows: Background, section of Results and Discussion in which we present different UVVis and FTIR spectra of the several molecular structures studied in this work. Finally, in the section of Conclusion we stress the key contributions of this paper.

2. Methods

When SRO is prepared by Low Pressure Chemical Vapor Deposition (LPCVD) technique, a gas mixture of N₂O and SiH₄ is habitually used [3] [4] and the Si excess content can be modified by the gas flow ratio Ro = [N₂O]/[SiH₄] [5] [6] . The silicon excess can be as high as 17 at% for Ro = 3; and experimentally stoichiometric SiO₂ (a non-free silicon film) can be obtained for Ro ≥ 50 [7] . Theoretically, Ro = 40 corresponds to the stoichiometric silica, when a mixture silane-nitrogen at 5 at% is used. Experimentally, there is enough evidence that SRO thin films are constituted by a silicon oxides mixture rather than by only one of them, regardless of the value of Ro.

We apply GRM [1] , which consider the Global and Partial Reaction(s) necessary to generate the oxide matrices (SiO₂, Si₂O₃, SiO and Si₂O), the annealing reactions for explaining the compositional changes after and before the thermal treatment and consequently the changes in luminescence spectra intensity and a set of secondary reactions of the oxide matrixes with the hydrogen produced to obtain the ions that could be associated to the emission in SRO thin films with specific defects.

3. Results and Discussion

3.1. Luminescence in SRO Structures with Specific Oxygen Defects

Besides the point defect in a-SiO₂ (amorphous silica), ab initio cluster approaches have been used to model various phenomena associated directly and/or indirectly with defect centers, for example, oxidation processes of silicon surfaces [8] , H-induced defect formation reactions at Si-SiO₂ interfaces [9] , optical excitations of nano crystalline silicon [10] .

Broadly, it is known that defects strongly affect properties of materials. For example, doping a semiconductor with a small number of impurity atoms leads to a significant change of its conductivity making such materials useful for technological applications. Similarly, optical transitions involving electronic states of defects can induce a coloration of the otherwise transparent solid, a frequently encountered phenomenon in natural crystals. Also, the mechanical properties and the long-term stability of materials are largely controlled by point and line defects.

It is therefore not surprising that the theoretical study of point defects in solid materials has a long history [11] . Many properties of defects are nowadays well understood. These include for instance the nature of hydrogenic impurities in elemental semiconductors and the energy splitting resulting from local crystal fields. However, these kinds of aforementioned defects represent just a small class of all possible defects. A non-exhaustive list of applications includes: solar cells [12] , solid state light-emitting diodes [13] , longer-serving batteries [14] , novel metal-oxide-semiconductor field-effect transistors [15] , and solid fuel cells [16] . The behavior of such devices is generally influenced or governed by an uncountable number of defects which are present in the bulk or at the interfaces between different materials. Such defects are often identified as deep, i.e., they are characterized by localized electronic states which are like the electronic states of the host material and possess ionization energies higher than those of typical thermal energies. The experimental optical characterization of such defects is often very difficult, and thus theoretical studies are necessary and essential in order to understand the nature of such defects and to interpret correctly the experimental data obtained from such characterizations. However, because of their deep nature, the theoretical description of the associated electronic states is beyond the scope of simple models. This justifies the incessant unfolded efforts in the theoretical studies of defects [17] . When one is working with Photoluminescence (PL), it might find thermally stimulated luminescence (TSL) very useful for detection of defects and luminescence centers. The TSL was suggested as a potentially useful research tool for trap- level analyzing by Urbach in 1930 [18] and later by Townsend [19] in 1994, it became one of the main tools for analyzing defect structures in solids. Hall Effect measurement is also useful for investigating defects. It is possible to determine type of carrier (for electron or hole), capture cross section and concentration of defects using deep level transient spectroscopy (DLTS).

Robertson [20] - [23] describes silica as an almost ideal insulating oxide, in that it has a low concentration of defects which give rise to states in the gap. This is fundamentally because it has a low coordination number, so that its bonding can relax and re-bond any broken bonds at possible defect sites. Any remaining defects are passivated by hydrogen. The oxides with a high dielectric constant are not materials with a low intrinsic defect concentration because their bonding cannot relax as easy as one would like. Most of strategies trying to reduce defect densities consist of processing control and annealing procedures.

In Figure 1 we present the molecular structure for a specific type of silica composed of rings with three silicon atoms alternated and joined by oxygen atoms. This structure has already been reported in literature previously [20] . All silicon atoms involved have tetra valences. In every ring, one silicon atom is shared by two rings and the other two silicon atoms, in each ring, are double bonded with one oxygen atom. Graph at the top of Figure 1 corresponds to FTIR spectrum, the peak with the highest intensity corresponds to the stretching mode vibrational frequency of Si-O bond. As we can see in UV Vis spectrum at the bottom of Figure 1, Silica type structure 3MRSiO₂ emits in the violet region.

3.2. Luminescence in SRO Structures with a Low Quantity of Defects

We calculated several structures for Si₉O₁₇ and Si₉O₁₆, assuming most of imagined isomers and never was found emission in visible region in UV Vis one according to calculated spectrum. i.e., when we eliminated only one or

two oxygen atoms of a silica structure type 3MR, modeling as a structure with a defect, the UV VIS spectra are modified but the maximum emission remains in visible region.

Figure 2 and Figure 3 correspond with two isomers from structure Si₉O₁₅. These structures are shunted from original silica type 3MR Si₉O₁₈ from which we have eliminate three oxygen atoms from selected positions. We evaluate eight isomers for Si₉O₁₅, labeled with capital letter from A to H. Selected properties for these structures are calculated and included in Table 1. From this table, we can see that isomer A results the most stable. For obtaining this structure, we have removed three oxygen atoms from the same ring located in one side of the structure. For isomer C shown in Figure 3 we had removed three oxygen atoms from one ring in the middle part of the structure. All the evaluated Si₉O₁₅ isomers exhibit the maximum intensity peak of emission in violet region, as we can make sure in column UVVIS lambda max in Table 1. Consequently, when the structure contains a chain with three silicon atoms least, additional emission peaks in visible region are predicted. Only one exception was found for isomer F which, despite it contains a chain of three silicon atoms, does not display emission in the visible region of electromagnetic spectrum. It is highly probable that this fact is due to the chain includes two rings, instead of only one. The wavelength calculated for emissions in visible region were as follows: Si₉O₁₅A (522.58 nm), Si₉O₁₅G (none), Si₉O₁₅C (541.52 and 742.74 nm), Si₉O₁₅B (none), Si₉O₁₅D (410.26 nm), Si₉O₁₅H (458.78 nm), Si₉O₁₅E (460.94 nm), Si₉O₁₅F (none). Note that structures 3MRSi₉O₁₅ could be related with SRO structures with SiO_x, x = 15/9 = 1.667.

3.3. Luminescence in SRO Structures with a High Quantity of Defects

In Figure 2 and Figure 3, we present the FTIR, UV VIS spectra and molecular structures for two isomers derived from silica type 3MRSiO_x Si₉O₁₂ (SRO or SiO_x, x = 12/9 = 1.334).

For structures 3MRSiO_x Si₉O₁₂ we evaluated eight isomers, labeled like A, B, …, H. Molecular structure forSi₉O₁₂ isomer H, contains a chain constituted by six silicon atoms, along the four rings (see molecular structure in Figure 4). Emission in visible region at 432.24 nm for isomer H corresponds with the second excited state, a singlet with an excitation energy of 2.8684 eV that could be associated to the chain of six silicon atoms.

FTIR spectrum for Si₉O₁₂ isomer H is displayed at the top of Figure 4. Going from left to right, we identified three main peaks. As consequence from this, we can make some commentaries. First, we can identify a peak with a shoulder in the range from 1313.795 to 1213.404 cm⁻¹. In this interval there are six frequencies of vibration which correspond to stretching modes of vibration Si=O (double bonded). Second, we can discriminate the most intense peak, with a shoulder too, in the range from 972.901 to 854.137 cm⁻¹ containing 6 vibrational stretching modes which correspond to Si-O (single bonds). Finally, there is a third peak with a shoulder in the range of frequencies from 767.465 to 686.723 cm⁻¹ due to six frequencies from bending Si-O modes. This nanostructure has a countable number of 57 calculated vibrational modes, where the majority of them (39) have frequencies lesser than 500 cm⁻¹ and with a weak intensity.

On the other hand, the nanostructure labeled as Si₉O₁₂ isomer F, and shown in Figure 5, is most stable that the one discussed previously (isomer H). Despite of the fact that isomer F has the highest dipole moment (8.5 Debye), it is 0.3831 eV less than isomer H in energy. For the lowest energy isomer, our calculations predict emission in three wide bands in visible region. The excited states responsible for these emissions are located at energy levels corresponding to wavelengths of 495.66, 575.69 and 641.03 nm, respectively. Intide this structure there are three small chains Si-Si-Si given by six Si-Si bonds. There is only one ring without Si-Si bonds as indicate by the thick blue arrow in Figure 5. Specifically in this ring we located three Si-O-Si bonds. These bonds are responsible for the most intense vibration peak displayed in FTIR spectrum at the top of Figure 5. This peak contains a shoulder including the vibrational frequencies of 1026.744, 980.647 and 923.72 cm⁻¹ which correspond to three calculated Si-O binding modes.

In FTIR spectrum displayed at the top of Figure 5, we can identify the peak and its shoulder with the highest frequencies (from 1314.175 to 1144.939 cm⁻¹). It corresponds with six vibrational stretching Si=O modes (double bond), in the same manner as noted for isomer H. The only difference respect to isomer H is a wider shoulder.

Complete data for isomers type 3MRSi₉O₁₂ are collected in Table 2. As we can see, the most stable structures correspond to isomer D, E and B, with differences in energy given by the values of 2.48 and 2.61 eV respect to the most stable structure (D).

Structures D, E and B contain one ring formed only with silicon atoms (there are not oxygen atoms forming

Si-O bonds in this ring). It is very likely the “silicon cycle” -Si-Si-Si- to be responsible for luminescence in visible region. In the most favorable energetically structure, the two double Si=O bonds associated to referred silicon cycle, intend to introduce into the cycle forming angles of 18.3˚ with respect to the plane described by the silicon cycle. Normally the oxygen atoms in Si=O (double bonded) forms a dihedral angle of ~180˚ in 3MR cycles.

Our results predicted luminescence with the highest intensity in visible region for isomers D, E, B, F and for isomer A. Isomer A is energetically the least favorable of all evaluated isomers type 3MRSi₉O₁₂, and has a large difference in energy (20.79 eV) respect to the most stable isomer.

3.4. Charged SRO Structures (Anions and Cations)

Pure semiconductor materials include various structural defects such as the intrinsic defects and the residual impurities. Doping of semiconductors allows introducing new impurity defects and modifying their intrinsic defects. In this case the intrinsic defect concentration is changed. At the same time it is possible the formation of complex defects with the participation of the intrinsic defects (for example, cation vacancies) and the impurity atoms. Thus, the distribution of the intrinsic and extrinsic defects may be very complex and that depends on the impurity concentration. Therefore, in this case it is really possible to determine only the relative concentrations of various defects. PL measurements are effective as a method to study the structure of defects of semiconductor materials. However, it is also very useful to use other techniques like photo diffusion current measurements and temperature dependent DLTS measurements to predict the concentration and trap level of the defects. DLTS method is very important to investigate the deep levels. However, the energy levels caused by the vacancies are usually of small energy.

In this section, we report results for the nano structures type 3MRSi₁₂O₁₂ which could be consider as a specific SRO film in which we have SiO_x (x = 1.0). We have evaluated five different cases including: neutral molecule, anion, di-anion, cation and di-cation species.

Figure 6 shows the ion energy levels calculated, including HOMO (+2), HOMO (+1), HOMO, LUMO and LUMO (−1). The order for calculated ions in this figure is as follows: neutro, cation, di-cation, anion and di-anion. Other evaluated energy levels are included in five plots in Figure 11. Only for charged species is possible to represent α and β orbitals.

Neutral defects have sometimes dangling bonds (unsaturated bonding capabilities). These capabilities facilitate the transfer of electronic charge between the defect and the host matrix, and frequently occur to the point that the defect becomes completely ionized. The degree and direction of electron transfer (toward or away from the defect, respectively, for acceptors and donors) of course depend upon the electron abundance in the host, as quantified by the host’s chemical potential in the vicinity of the defect. In semiconductors, the host’s electron richness can be adjusted readily, inter alia, imposing electric fields, by doping and photo stimulation. Thus, the ionization state of the defect can often be controlled.

In Figure 6 we can verify that di-cation has the lowest energy levels, whereas di-anion has the highest ones. On the other hand, the thermodynamic parameters, including band gaps, ionization energies, and energies of defect formation and/or migration, are not the eigenvalues of a Schrodinger equation describing the crystal [21] . The thermodynamic parameters are defined statistically in terms of reactions occurring among ensembles of all possible configurations of the system. Confusion over this distinction sometimes exists particularly with reference to ionization levels. Figure 7 displays calculated band gap in Ions of nanostructures type 3MRSi₁₂O₁₂. In this figure, the numbers in the horizontal axis (1, 2, 3, 4 and 5 going from left to right) are associated to corresponding band gap according to the type of ion, e.g., the calculated band gap for neutral structure (number 5, neutrum) is Eg = 3.012 eV and so on. Bang gap is reduced as far as the structure is charged (positively or negatively), i.e., Eg_cation = 2.577 eV (number 4 in horizontal axis), Eg_anion = 2.254 eV (number 2 in horizontal axis), and is additionally reduced for di-cation (2.508 eV) (number 3) and di-anion (2.129 eV) (number 1). The topics about effect of reduction in the bang gap on the processes of decay, recombination of pair electron-hole and the emission in the visible region are concisely discussed below.

Defects exchange charge with both the conduction and valence bands via either thermal or radiative processes. In the thermal processes, the defect captures or emits a charge carrier directly, with a rate that is generally quite fast for defect eigen-states close to the bands, but sometimes much slower (many seconds) for levels lying deep within the band gap [22] .

If the defect possesses significant capacity to store excess charge within its structure, the range of ionization states can be quite large. For example, a mono-vacancy in silicon nominally incorporates four unsaturated dangling bonds, and permits charge states ranging from (−2) to (+2), (see Fahey et al. [23] ).

Figure 8 contains two plots: the first one represents the energy levels (eV) (left side scale) which corresponds to the highest intensity of emission of neutral and charged nanostructures 3MRSi₁₂O₁₂ and the second one (right side scale) contains the wavelength in nm. Our results predict emission in visible region for neutral and charged structures. A red shift, including a band widening or appearing a second band in NIR is predicted when nanostructure is charged (positively or negatively). It is possible correlate UVVIS_{lambda max} with calculated band gap (Eg) through the next analytical equation:

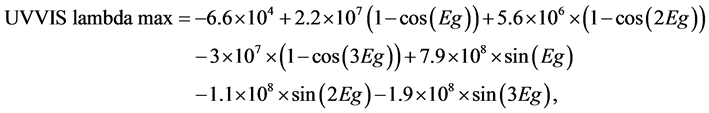
where UVVIS lambda max has units of nm and Eg is expressed in eV. Complete UV Vis spectra are included through five plots in Figure 11.

Table 3 contains details of calculated atomic electrostatic charges for neutral and ions of nanostructure type 3MRSi₁₂O₁₂. In this table, labels Si₅ and O₃ were not employed. Silicon atom labeled as Si₁ (a tetra valence silicon atom) displays an unusual behavior with negative charges for all evaluated species. Other silicon atoms with negative charges are highlighted in yellow in Table 3. One half of all silicon atoms (six), resulted negatively charged in di-anion structure, five of which correspond with silicon atoms with di-valence. Figure 9 shows a slide of potential (KJ/Mol) for Di-cation nanostructure type 3MRSi₁₂O₁₂. Negative values in potential are identified as the most reactive parts of the structure. Complete representation of α HOMO, β HOMO, α LUMO and β LUMO orbitals and calculated electrostatic charges, for Ion’s nanostructures type 3MRSi₁₂O₁₂ are displayed on Figure 10. Note that the graphic has “blue and red” regions. These correspond to positive and negative values of the orbital.

Several distinct phenomena are known which contribute to the emission of electrons, atoms and ions, when a solid is irradiated. For example, near equilibrium evaporation, thermionic emission of electrons not near equilibrium with the lattice, single and multiple photon photoemission of electrons, atoms and ions, electrostatic expulsion of positive ions (cation and dications) all of them either produced by Auger recombination of core holes on anion lattice sites known as Knotek-Feibelman effect [24] , or due to dipole layer at the solid surface that is largely responsible for the work function of the crystal, emission of atoms, ions or molecules by formation of Frenkel excitons.

Figure 11 contains five UV VIS spectra which correspond to all 3MRSi₁₂O₁₂ evaluated species. Likewise, therein there have also been included orbitals energy representation and calculated natural charges. All spectra calculated predict emission in visible region and appear additional emission peaks, mainly in NIR when the structure is ionized. Figure 11(a) corresponds to di-anion nanostructure [3MRSi₁₂O₁₂]⁻². Five excited states are responsible for emission in visible region with wavelengths from 564.47 to 751.72 nm (from green to red) and there is also emission predicted in NIR in 1100.89 nm. Figure 11(b) displays UV Vis spectrum for Anion [3MRSi₁₂O₁₂]⁻¹. In this case, emission in NIR moves towards 998.14 nm and there is a slight change in position, a shift towards blue, and a reduction in overlapped wide bands resulting in an interval from 537.74 to 684.17 nm but equally ranging from green to red again.

When structure is positively charged, there is not a separation of the wide bands. All the emission peaks due to excited states are very close each other and all of them are partially overlapped. Figure 11(c) corresponds to results for di-cation [3MRSi₁₂O₁₂]⁺². For this ion, emission in NIR moves to 868.44 nm. Finally, for anion [3MRSi₁₂O₁₂]⁺¹ Figure 11(d) shows a UV Vis spectrum with emission only in visible region whilst Figure 11(e) predicts emission in UV and visible regions for neutral structure.

4. Conclusion

We have employed the Global Reaction Model in order to predict the theoretical luminescent behavior of nanostructured silicon rich oxide films which are considered as constituted by nanostructures. The proposed model is successfully applied to evaluate: firstly, the contribution to the luminescent phenomenon of the calculated molecular structures. In these structures we have introduced different levels of defects generated by the absence of oxygen atoms. Obtaining luminescent emission in the visible region of the electromagnetic spectrum has been evidenced. The calculated shape of the luminescent spectrum is modified depending on the type of isomer. Secondly, we have evaluated five different charged states to simulate defects in SRO films which include: neutral molecule, anion, di-anion, cation and di-cation species reporting results for the nanostructures type 3MRSi₁₂O₁₂. The ion energy levels calculated, include HOMO (+2), HOMO (+1), HOMO, LUMO and LUMO (−1). We calculated the atomic electrostatic charges for neutral and ions of nanostructures type 3MRSi₁₂O₁₂. Additionally, an analytical expression that correlates the energy of the band gap with the wavelength of most intense emission for charged molecules is presented.

Acknowledgements

This work was supported by a complementary scholarship given by CONACyT, VIEP-BUAP-2015, Cuerpo Académico Semiconductores Nanoestructurados y Orgánicos, BUAP-CA-275, and ELAP grant (Emerging Leaders for America’s Program). Computing calculations were partially performed at the Plasma Processing Laboratory (PPL) of McGill University in Montreal, Canada. Special thanks to Professor Jean-Luc Meunier for allow the use of computing facilities and Spartan Software license at the PPL.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Cite this paper

Néstor David Espinosa-Torres,José Álvaro David Hernández de la Luz,José Francisco Javier Flores-Gracia,José Alberto Luna-López,Javier Martínez-Juárez,Gregorio Flores-Carrasco, (2015) Forecast of the Luminescent Phenomena of Silicon Rich Oxide Films off Stoichiometry by Means of the Global Reaction Model. Journal of Modern Physics,06,1679-1694. doi: 10.4236/jmp.2015.611170

References

NOTES

^*Corresponding author.