Journal of Modern Physics
Vol.05 No.16(2014), Article ID:51088,23 pages
10.4236/jmp.2014.516178
Vibrational Nonequilibrium in the Hydrogen-Oxygen Reaction at Different Temperatures
Oleg V. Skrebkov
Theoretical Department, Institute of Problems of Chemical Physics, Russian Academy of Sciences, Chernogolovka, Russia
Email: skreb@icp.ac.ru
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 September 2014; revised 28 September 2014; accepted 22 October 2014
ABSTRACT
A theoretical model of chemical and vibrational kinetics of hydrogen oxidation is suggested based on the consistent account for the vibrational nonequilibrium of HO2 radical which forms in result of bimolecular recombination H + O2 = HO2 in the vibrationally excited state. The chain branching H + O2 = O + OH and inhibiting H + O2 + M = HO2 + M formal reactions are considered (in the terms of elementary processes) as a general multi-channel process of forming, intramolecular energy redistribution between modes, relaxation, and monomolecular decay of the comparatively long-lived vibrationally excited HO2 radical which is capable to react and exchange of energy with another components of the mixture. The model takes into account the vibrational nonequilibrium for the starting (primary) H2 and O2 molecules, as well as the most important molecular intermediates HO2, OH, O2(1D), and the main reaction product H2O. The calculated results are compared with the shock tube experimental data for strongly diluted H2-O2 mixtures at 1000 < T < 2500 K, 0.5 < p < 4 atm. It is demonstrated that this approach is promising from the standpoint of reconciling the predictions of the theoretical model with experimental data obtained by different authors for various compositions and conditions using different methods. It is shown that the hydrogen-oxygen reaction proceeds in absence of vibrational equilibrium, and the vibrationally excited HO2 radical acts as a key intermediate in the principally important chain branching process. For T < 1500 K, the nature of hydrogen-oxygen reaction is especially nonequilibrium, and the vibrational nonequilibrium of HO2 radical is the essence of this process.
Keywords:
Gas Phase, Hydrogen-Oxygen Reaction, Chemical Kinetics, Vibrational Relaxation, Electronically Excited States

1. Introduction
For over the decades, hydrogen-oxygen reaction, being important for practical implementation, has been in focus of attention as a model system that contains all key kinetic features of gas-phase ignition, combustion, and detonation. After works of N. N. Semenov and C. N. Hinshelwood, this reaction has been investigated for more than seventy years, and presently its mechanism is considered as the most studied one (in contrast with, for example, the mechanism of hydrocarbon oxidation). However, the problem of quantitative description of kinetics in this system remains as before unsolved both from standpoint of an agreement between results of different experiments [1] and from standpoint of an agreement between theoretical models and experiments (see [2] ).
All kinetic calculations performed for the interpretation of experiments based on the assumption of availability of equilibrium in the internal and external degrees of freedom of molecules and radicals. Using this, assumption radically simplifies the task of describing the kinetic mechanism, because it eliminates the need to account for a dependence of the reaction cross sections on the energy of the internal degrees of freedom of molecules. In this case, the kinetic equations are equations only for the concentrations, reaction rate constants only depend on gas temperature, i.e., all the reactions are regarded as elementary (proceeding in one step) processes, the ratio between the rate constants of direct and reverse reactions, k/k¢ = K(T) (K is the equilibrium constant) is used. Here, following [3] , we will call such a kinetics description as the “formal kinetic description”1. Meanwhile, the characteristic relaxation times of internal states, for example, the times of vibrational relaxation is comparable or even greater than the characteristic times of fast chemical reactions, such as, for example, practically barrierless bimolecular recombination reactions. In the terms of formal kinetics, a reaction of recombination (dissociation) is considered as termolecular (bimolecular) process with the participation of the third body M, i.e., A + B + M = AB + M reactions2.
The inconsequence and formal character of this equilibrium kinetic conception, which has become traditional, is illustrated by Figure 1. It shows the k/kmax ratio, where k is the rate constant value for dissociation reactions of the most important species and kmax is their maximally possible value. Here, for the k values used the accepted and recommended (for an interpretation of experiments) dissociation rate constant values, or received, using the relationship k = krec∙K(T), from accepted and recommended recombination rate constant values, krec (which really can be considered equilibrium); see, for example, [1] [5] -[8] and references therein. It will be seen that the rate constant values for these reactions exceed the maximally possible ones (collision frequency multiplied by the Arrhenius factor) in several times (H2, O2) or orders of magnitude (OH, HO2, H2O, H2O2) that takes out theirs beyond bounds of a physical sense ( ) converting into formal fitting parameters. It means that these rate constant values cannot be identified with the rate constants of elementary dissociation reactions because they are effective rate constants of complex overall (detailed mechanism of which is unknown) reactions. (The curve 7 corresponding to the “high pressure limit” for HO2 + M ® H + O2 + M reaction, as was to be expected, located in a region of values z £ 1).
) converting into formal fitting parameters. It means that these rate constant values cannot be identified with the rate constants of elementary dissociation reactions because they are effective rate constants of complex overall (detailed mechanism of which is unknown) reactions. (The curve 7 corresponding to the “high pressure limit” for HO2 + M ® H + O2 + M reaction, as was to be expected, located in a region of values z £ 1).
As a result of accounting, in implicit form, vibrational relaxation time dependencies on conditions, one comes to different formal kinetic schemes (mechanisms), which along with the elementary (proceeding in one step) chemical reactions include formal overall reactions detailed mechanism of which is unknown, and their effective rate constants depend on conditions (composition, pressure, and other). (It is these circumstances that are the
Figure 1. The ratio of the average (on different M) dissociation rate constant values, k, to the corresponding highest possible ones, . (Zcoll is the collision frequency as an estimate from above, p ~ 1 atm; D is the dissociation energy.) (1)―O2 + M ® 2O + M; (2)―H2 + M ® 2H + M; (3)―OH + M ® O + H + M; (4)―HO2 + M ® H + O2 + M; (5)―H2O + M ® H + OH + M; (6)―H2O2 + M ® 2OH + M; (7)―HO2 + M ® H + O2 + M (high pressure limit, see [8] ). Here, k is interpreted (in accordance with obvious canons of gas phase kinetics) as
. (Zcoll is the collision frequency as an estimate from above, p ~ 1 atm; D is the dissociation energy.) (1)―O2 + M ® 2O + M; (2)―H2 + M ® 2H + M; (3)―OH + M ® O + H + M; (4)―HO2 + M ® H + O2 + M; (5)―H2O + M ® H + OH + M; (6)―H2O2 + M ® 2OH + M; (7)―HO2 + M ® H + O2 + M (high pressure limit, see [8] ). Here, k is interpreted (in accordance with obvious canons of gas phase kinetics) as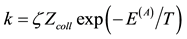 ; ζ is the orientation factor; E(A) is the activation energy equal D as the minimal activation barrier height in the present case. The curves 1-3, 6 correspond to average (for different M, see [1] ) k values. The curves 4 and 5 correspond to average (for different authors, see [1] [5] -[8] ) k values with the following maximal deviations: for the curve 4 that is 3±1 at 1000 K and (2.5)±1 at T = 2500 K; for the curve 5 that is (8.2)±1 at 1000 K and (1.5)±1 at T = 2500 K.
; ζ is the orientation factor; E(A) is the activation energy equal D as the minimal activation barrier height in the present case. The curves 1-3, 6 correspond to average (for different M, see [1] ) k values. The curves 4 and 5 correspond to average (for different authors, see [1] [5] -[8] ) k values with the following maximal deviations: for the curve 4 that is 3±1 at 1000 K and (2.5)±1 at T = 2500 K; for the curve 5 that is (8.2)±1 at 1000 K and (1.5)±1 at T = 2500 K.
main cause of origin of the terms “uncertainty” and “sensitivity” in relation to the reaction rate constants.) Meanwhile, “the problem of the reaction mechanism can be completely solved only on the basis of quantitative information about rate constants of elementary processes” [9] . Currently, the most authoritative source of information on this topic is the Potential Energy Surface (PES) ab initio analysis and the relevant dynamic calculations.
Comparative successes (from the standpoint of use in gas-dynamic and macro-kinetic applications) of formal kinetic schemes in terms of this equilibrium approach have been achieved owing to considerable variations of the rate coefficients for important processes while modeling different conditions (on temperature, pressure, and composition). So, the rate constant of the most important chain branching reaction H + O2 « O + OH obtained by different authors for temperatures over 1000 K [1] considerably differs depending on experimental conditions; about half of obtained values exceed the theoretical estimate from above (see [2] ). To an even greater extent, this is applied to the inhibiting H + O2 + M ® HO2 + M reaction (see [1] [5] ).
Theoretical predictions and experimental data are often reconciled via violation of the relationship between the rate constants of the forward and backward reactions, by introduction of not existing reactions, and/or by use of implausible rate constants. For example, the use of H2 + O2 ® 2OH reaction with activation energy around or less than 24,200 K (underestimated more than by a factor 1.5; see, for example, [10] [11] ) converts this practically non-existing reaction (see [12] -[14] ) into the most important channel of initiation and subsequent formation of OH radical.
Inability to provide physically adequate (in the terms of elementary processes) explanation of the formation (already during the earliest steps of combustion process) of electron-excited radicals OH* º OH(2S+) is another illustrative example of the inconsistency of this (traditional) equilibrium kinetic concept. At the same time, the emission OH* ® OH + hν has long been used in research practice to determine the induction period. The formation of OH* during the most early steps of combustion process, is supposed (see also [2] ) to occur in the following two stages: H + O2 ® HO2(v) and HO2(v) + H2 ® OH* + H2O, i.e., through formation of the vibrationally excited HO2(v) radical. This is in accordance with the only quantitative acceptable overall reaction H + O2 + H2 ® H2O + OH* proposed back in the 60s [15] . (Note that during later stages of combustion, when the OH* concentration attains its maximum, another reactions play an important role also [2] [16] .)
These and other facts3 indicate the need not only to make the kinetic scheme, more precise and detailed but to revise the existing kinetic concept which is based on the assumption of equilibrium in the internal (vibrational) degrees of freedom. In accordance with the conclusions of [2] , the above said refers primarily to the reactions involving the vibrationally excited HO2(v) radical which is formed as a result of bimolecular recombination H + O2 ® HO2(v). These are the following main (in conventional chain branching mechanism of hydrogen oxidation) reactions: the above reaction H + O2 ® O + OH and the inhibiting reaction H + O2 + M ® HO2 + M. (In terms of the existing kinetic concept, these and other overall reactions are interpreted as elementary ones depending only on gas temperature, T.) Meanwhile, in [2] , we suggested “the dependence of the apparent rate constant of the process H + O2 ® O + OH on the concentration of the third body M = H2”, and it was stated the need to consider this reaction as the “H + O2 ® HO2(v) ® O + OH with consideration for intramolecular energy redistribution in the HO2(v) radical and its vibrational relaxation in collisions”. Such a consideration was performed in [16] , where it was shown that “the nonequilibrium character of the process with respect to vibrational degrees of freedom is responsible for the observed dependence of the overall reaction H + O2 ® O + OH effective rate constant on experimental conditions”. In turn, the presence of vibrationally excited HO2(v) radicals leads to the necessity of taking into account the vibrational nonequilibrium of other components in the reacting hydrogen- oxygen mixture.
The subject of this paper is a presentation and approbation of the theoretical model based on a systematic account of vibrational nonequilibrium of HO2 radicals which are assumed to act as a key intermediate in the chain branching process and in the formation of electronically excited species. The paper in a certain sense is the continuation of our previous works [2] [16] . In terms of the proposed model, the chain branching H + O2 ® O + OH and inhibiting H + O2 + M ® HO2 + M formal reactions are considered as the set of elementary processes of forming, intramolecular energy redistribution between modes [16] , relaxation, and monomolecular decay of the comparatively long-lived (see [18] -[21] )4 vibrationally excited HO2(v) radical which moreover is capable to react and to exchange an energy with other components of the mixture. This significantly changes the physical understanding of the chemical mechanism in the reacting hydrogen-oxygen system.
This paper is organized as follows. Section 2 gives a general formulation of the kinetic equations; in the Appendix A, there are the forms of these equations for the particular cases implemented in practice. The kinetic scheme are adduced in the Section 3; in the Appendix B, there is a brief outline of the method of theoretical estimation for unknown characteristic times and/or rate constants of vibrational relaxation channels. Then Section 4 follows where the calculation results are presented and discussed. The final section (Section 5) concludes.
2. Kinetic Equations
Equations of chemical and vibrational kinetics for general case of reacting multi-component gas mixture in frames of macroscopic (or hydrodynamic) description, i.e., in the form of equations for the concentrations of mixture components, ni, and average energies of vibrational degrees of freedom (modes), ek, were first published in [22] (see also [23] ). These equations were used for calculations of chemical and vibrational nonequilibrium multi-component gas flow through a nozzle while studying the combustion-driven CO2-gas-dynamic laser work- ing media. In deriving these equations from the equations of balance of the vibrational level populations (or Master equations) [24] , the following simplifying assumptions were made: 1) chemical reactions do not disturb the Maxwell distribution; 2) rotational degrees of freedom are in equilibrium with the translational ones; 3) each type of molecular vibrations (mode) is modeled by a harmonic oscillator with vibrational temperature Tk as a measure of the average energy of that or another mode (such as the kth). Following [22] [23] in general (see also [16] [24] ), we have the equations for the molar component concentrations per unit mass, ni, and the average numbers of vibrational quanta of kth mode per one molecule, ek, as the time functions at given gas temperature, T, and pressure, p. (In terms of nonequilibrium statistical mechanics, these equations are the corresponding moments of the Master equations.)
For the molar concentrations of the components per unit mass of the gas mixture (ni),
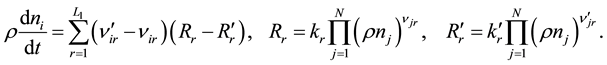 (1)
(1)
Stoichiometric coefficients, njr and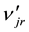 , of the jth chemical component, Yj, in the rth reaction correspond to the following record of the chemical reaction:
, of the jth chemical component, Yj, in the rth reaction correspond to the following record of the chemical reaction:
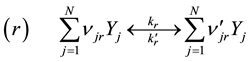 . (2)
. (2)
An influence of the vibrational relaxation processes on kinetics of chemical transformations is expressed via the dependence of reaction rate coefficients on the average energies of reagent vibrational modes, ek, in accordance with the following relationship:
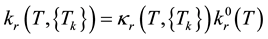 . (3)
. (3)
Here, kr
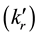 is the rate constant of the rth reaction in the forward (backward) direction.
is the rate constant of the rth reaction in the forward (backward) direction.
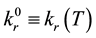 (or equilibrium value) is the rate constant of the rth reaction when all degrees of freedom are at thermodynamic equilibrium. Theoretically,
(or equilibrium value) is the rate constant of the rth reaction when all degrees of freedom are at thermodynamic equilibrium. Theoretically,
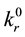 is the value that one obtains from dynamical calculations after averaging corresponding cross sections over equilibrium distributions of reagents and/or as a result of the use of approximate analytical methods as for example different variants of the transition state theory (TST)5. Experimentally, in application to the dissociation-recombination reactions, the rate constant values determined in the high pressure limit (see footnote 2) must coincide with
is the value that one obtains from dynamical calculations after averaging corresponding cross sections over equilibrium distributions of reagents and/or as a result of the use of approximate analytical methods as for example different variants of the transition state theory (TST)5. Experimentally, in application to the dissociation-recombination reactions, the rate constant values determined in the high pressure limit (see footnote 2) must coincide with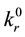 . The
. The




where


parative efficiency

assume here
This rate constant dependency on vibrational temperatures of appropriate modes in the form of Equations (3),
(4) with

deduced [25] [26] for a specific case of the polyatomic molecule dissociation reaction. However, the mentioned specificity is not a matter of principle for its deducing (because of the harmonic oscillator model use) and this dependency has significantly more general character. In the simplest case of the two-atomic molecule dissociation reaction (one mode), Equation (4) gives the known results [27] , obtained for Tk < T, realized in the flow behind the bow shock of reentering hypersonic vehicles at high altitudes.
As an estimate for the portion of activation energy related to the reactant molecular vibrations, we have:

i.e., the activation barrier height,


Simple formula (5) plays the important role in this model of the interaction between vibrational relaxation processes and chemical reactions. According to (5), the height of activation barrier,



For the average numbers of the vibrational quanta of the modes (εk),


The first term in the right parts of the vibrational kinetics Equations (6) describes the change of the average energy (in qk) of the kth vibrational mode (mode k belongs to the molecule of kind j) as a result of its interaction with the other vibrational modes of the gas mixture, (dek/dt)vibr in Appendix A. Here,


of ith component;


Zji is the number of collisions of one jth type molecule with ith type molecules per time unit (the collision frequency),


in which a collision of molecules of the jth and ith kinds causes the decrease in vibrational quantum numbers of modes m, vm, by lmq and the increase in vibrational quantum numbers of modes n, vn, by lnq. In terms of the harmonic oscillator model, the probability of such a process is unambiguously characterized by the probability of

the corresponding transition between the lowest states,

process of vibrational energy exchange between modes which are considered as a whole [24] ; a practical utilization of such values means the replacement of Equation (9) with the following one:

The


The second term in the right side of Equation (6) describes the influence of chemical reactions on the process of vibrational relaxation (mode k belongs to jth type molecule formed in the sth reaction), (dεk/dt)chem in Appendix A. Here, csk is the quantity (in θk) of vibrational quanta obtained by kth mode in average at one act of formation of the j-type molecule in sth reaction. The total set of csk values characterizes the distribution of numbers of vibrational quanta between modes of the products of sth reaction.

where


The vibrational kinetic equations presented in this section are correct as far as harmonic approximation is correct, i.e., when
Appearing in the Equations (4), (5), (11) values

The system of Equations (1), (6) was solved numerically for ni and εk (see [16] ). As the initial condition at t = 0, the ni and εk values corresponding to the gas mixture state before the shock front (at T ≈ 300 K) were taken. The values t* (the maximum OH* concentration moment) and t50 (the moment at which the OH concentration reaches its half-maximum) were determined from the calculated time dependences ni(t) for OH and OH* º OH(2S+) and compared with directly measured in experiments (see below Section 4.2).
3. Kinetic Scheme
Necessary information for solving kinetic Equations (1), (6) is presented in the form of the kinetic scheme for chemical reactions and channels of vibrational relaxation. For description of the initiation and chain reactions in the H2 + O2 + Ar system, we have used the kinetic scheme involving chemical reactions with participation H2, O2, H2O, HO2, H, O, OH, H2O2, O3 in the ground electronic state as well as


The behaviour of the most important intermediate HO2 radicals is defined by the following elementary processes:
1) Formation as a result of the bimolecular recombination and the fast intramolecular redistribution of H-O2 bond energy (or energy randomization), H + O2 ® HO2(v);
2) Dissociation along H-O2 bond, HO2 « H + O2;
3) Dissociation along O-OH bond, HO2 « O + OH;
4) Vibrational-to-vibrational (VV'-) energy transfer, HO2(100) + X(0) « HO2(000) + X(1), X = H2, O2, H2O(ν1), ∙∙∙;
5) VV'-energy transfer, HO2(010) + X(0) « HO2(000) + X(1), X = H2, O2, H2O(ν1), ∙∙∙;
6) Vibrational-to-translational (VT-) energy transfer, HO2(001) + M « HO2(000) + M, M = H2, O2, H2O, Ar;
7) Chemical reactions, HO2 + Yi « Yj + Yk, i, j, k = 1, 2, ∙∙∙.
The process of the HO2(v) radical formation has been presented by the fast bimolecular recombination reaction 1). The fast energy randomization (or, intramolecular energy redistribution) of HO2 bond energy at the modes 2, HO2(ν1), 6, HO2(ν2), and 7, HO2(ν3), in the reaction 1) is simulated by setting up hI,2 = hI,6 = hI,7; see Equation (11). The reactivity of HO2(v) and its subsequent evolution are determined by the processes of decay 2), 3), relaxation 4)-6), and the reactions with its participation 7).
The recent results on dynamics in the HO2 system (see [17] and references therein) showed the existence of significant regularity embedded in the chaotic phase space. I.e., the energy redistribution between HO2 vibrational modes is only partial because of an availability of “a bottleneck in the phase space which inhibits the intramolecular transfer of energy between the H-O and O-O bonds” [17] . In another words, the HO2 system was found to be (in dynamic sense) an intermediate case between regular and chaotic behavior (“the RRKM assumption or the strong-coupling approximation” [30] ). Here, that latter is simulated (on the kinetic level) by the processes 1)-3); see below reactions (c1)-(c3) in the Table 1. To take into account the regular dynamic behavior on the kinetic level, we introduce in the kinetic scheme, in addition to the processes 1)-3), the one-stage process H + O2 ® O + OH (reaction (c4) in the Table 1).
3.1. Chemical Reactions
The reactions determining the mechanism of chemical transformations and their equilibrium rate constants,

The


Chemical reaction (c2)-(c4)7, and (c12) proved to be the most influential on the rate of the process as a whole and on the formation of electronically excited species. Accounting the HO2, H2O, H2, O2 and OH vibrational relaxation processes eliminates the need to include in the kinetic scheme formal reaction of the type A + B + M ® AB + M with an intuitive fit of third bodies, M, efficiencies; see reaction (c2), and (c3'), (c12)-(c16) in Table 1. On the other hand, our ignorance of the vibrational nonequilibrium of O3, H2O2 and OH* (small concentrations, high vibrational relaxation rates) leads to the inclusion in the kinetic scheme of formal reactions of recombination (c17'), (c18'), (c22') and (c23') in the form A + B + M ® AB + M. The effect of these reactions on the final calculation results for the conditions examined is relatively small; the


3.2. Collisional Intermolecular Vibrational Energy Transfer
The channels of vibrational-to-translational (VT) energy transfer and respective characteristic times,




The SSH and SSHM estimations of VT-relaxation times for vibrational modes of polyatomic molecules are based on the assumption about their independence, i.e., on neglecting disturbances caused by interaction during collisions. In the case of H2O molecules (the central atom O is much more massive than the external atoms H) and at relatively low degree of vibrational excitation, this is true [40] [41] . In the case of HO2 radicals (nonlinear molecule with ÐHOO bending), such disturbances are, most probably, not small. Unfortunately, the dynamic problem of intramolecular inter-mode interaction induced by collision is far from solving. As a simplifying assumption, we consider the HO2 molecule during collision as the united set of coupled oscillators which exchange by energy with translational and/or rotational degrees of freedom via the most rapidly relaxing mode; it is one of low frequency modes of HO2; see Note (g) in Table 2.
As a result of our SSH and SSHM estimations (see Appendix B), the relatively most important channels of
Table 1. Essential reactions and their equilibrium rate constants

aThe reaction heat effects in 103 K; here and below, the double arrow means the brief writing for two reactions (forward, r, and reverse, r¢);
aThe reaction heat effects in 103 K; here and below, the double arrow means the brief writing for two reactions (forward, r, and reverse, r¢);
Table 2. The relaxation channels and their characteristic times
aIn terms of Equations (6), (10), for q = 1 - 10, the record (vq) Yj(1) + M « Yi(0) + M correspond to m = n,





vibrational-to-vibrational (VV') relaxation and the values of their rate constants


3.3. Intramolecular Energy Redistribution in HO2 Modes
Since the lifetime of HO2 intermediate is comparable with the time between collisions [18] -[21] , the intramolecular energy exchange between its modes can be significant. It is also natural to assume that the role of this process grows with increasing vibrational excitation. At low energies, the interaction between modes is weak or absent (the “local mode” approximation; see for example [40] [41] and references therein.). At high energies, due to anharmonicity of molecular vibrations and appearance of resonances, as well as due to intensification of VR-transfer, the interaction between modes results in the uniform energy distribution for about 10 vibration periods. With relaxation, the extent of vibrational excitation decreases, and the rate of the energy redistribution process decreases also.
As for the dependence of intramolecular vibrational transfer rate on the excitation energy, this aspect of HO2 dynamics has not been investigated so far. The available dynamical calculations, both classical and quantum, for H2O (see [40] [41] and references therein), and HO2 (see [20] [42] -[46] ) molecules point to the admissibility (on
Table 3. Channels of VV'-relaxation and respective rate constants,


aIn terms of Equation (10); bSee Appendix B; cThis record (vq) X(1) + Y(0) « X(0) + Y(1) correspond to lmq = 1, lnq = 1, wnm = qn/qm (single-quan- tum VV'-energy exchange); dThis record correspond to m = 10, n = 6, 7; l10,33 = 1, l6,33 = 1, l7,33 = 1; wnm = (q6 + q7)/q10 (1 ® 2-quantum VV'-energy exchange); eThis record correspond to m = 8, n = 6, 7; l8,39 = 1, l6,39 = 1, l7,39 = 1; wnm = (q6 + q7)/q8 (1 ® 2-quantum VV'-energy exchange); fOur SSH estimation; gOurSSHM estimation.
the kinetic level) of the following, taken here, assumptions:
1) intramolecular energy redistribution between HO2 vibrational modes (k = 2, 6, 7) tends to equalization of
mode energies, Ek = θk∙εk, i.e.,


2) the rate constant of intramolecular energy exchange decreases with decreasing vibrational excitation (εk, Tk).
On the kinetic level of description (in addition to hr2 = hr6 = hr7, see above), we postulate that the following process of the energy redistribution between HO2 modes takes place:

where the rate constant,

The corresponding term of vibrational kinetics Equation (6), has the form of (7) but with E/θk instead of

where E = E(t).
4. Results and Discussion
The calculated data presented in this section illustrate the efficiency of the above approach and its potential for elucidating the physical essence of high-temperature hydrogen oxidation (as a process essentially nonequilibrium with respect to vibrational degrees of freedom) and for quantitative interpretation of experimental data.
In calculations, the coordinate system associated with the gas flow behind the wave front (gas mixture is at rest, T = const, p = const, and t = 0 is the instant when the shock front passes) was used.
4.1. Kinetics of Chemical Transformations at Various Stages of the Process
Figure 2(a) and Figure 2(b) illustrate {as the result of the numerical solution of the Equations (1), (6)} the typical behavior of component concentrations in the reacting H2 + O2 + Ar mixture behind a shock wave under the conditions examined (see below the Table 4).
As estimated from the behavior of the initial components H2 and O2, the induction period of the reaction lasts up to t ≈ 500 μs in case (a) and up to t ≈ 150 μs in case (b), depending significantly on reaction conditions (composition, temperature, and pressure). However, in any case, the end time of the induction period and the start time of the intensive reaction stage nearly coincide with the maximum concentration of HO2.
A very significant characteristic of a reaction is its rate, which determines its role (contribution) at a particular stage of the complex chemical reaction in the multi-component reacting mixture. Figure 3(a) and Figure 3(b) plot the rates (wr = Rr/ρ, mol・g−1∙s−1) for the most important elementary reactions determining the mechanism and the rate of the chemical process as a whole.
The reactions (c1) and (c33') are the rate determining reactions at the initiation stage of the chain process. At the intensive reaction stage, the most important reactions are the following ones: the vibrationally excited HO2(v) radical formation (c2), which is the main excitation source throughout the process; monomolecular decay of the HO2 radical (c3), which is the key chain branching reaction (together with the reactions (c6) and (c4)); the reaction (c5), which is the main reaction responsible for chain propagation (together with the reaction (c7) as one of the most significant OH formation channels, next in importance for reaction (c3)); the reaction (c12) as a very significant of the recombination-dissociation reactions. Changing roles in dependence on the conditions, the listed reactions were the most important under the conditions examined from the standpoint of the calculation result sensitivity to values of equilibrium rate constants.
4.2. Comparison with Experiment
Direct study of chemical kinetics in real conditions of nature or engineering (for example, in combustion and detonation) is troubled by complicating factors of diffusion, convection, heat release and heat transfer, which are
Table 4. Experimentally measured [14] [35] [36] and calculated (within one kinetic scheme a) values of τ*b and τ50c for different composition at two equivalence ratios Φ = 1 and Φ = 2.
aSee Tables 1-3; bTime interval between the passage of the shock front and the moment of maximum emission at ~306 nm (in calculation, the maximum OH* concentration moment); cTime interval between the passage of the shock front and the moment at which light absorbtion by the OH radical reaches its half-maximum (in calculation, the moment at which the OH concentration reaches its half-maximum).
T = 1178, K T = 1809, K

Figure 2. Time dependences for mole fractions, γi, of (1) H2, (2) O2, (3) H2O, (4) O, (5) OH, (6) H, (7) HO2, (8)
T = 1178, K T = 1809, K

Figure 3. Time dependences of reaction rates (wr = Rr/ρ, mole∙g−1∙s−1) in the cases (a) and (b) (see the caption of Figure 2) for the most important reactions (Table 1): 1―reaction (c1), 2―reaction (c33'), 3― reaction (c2), 4―reaction (c3), 5―reaction (c5), 6―reaction (c6), 7―reaction (c7), 8―reaction (c4), 9― reaction (c12), 10―reaction (c2').
superimposed on the main chemical process and can play determining role. In theoretical models, this causes an appearance of numerous parameters (in addition to kinetic characteristics) which, frequently, either are unknown or have high extent of indeterminacy. It makes difficult the quantitative interpretation of experiments respectively introducing the indeterminacy in simulative kinetic schemes. For this reason, for comparison with calculations, the experimental data [14] [35] [36] obtained by shock tube technique with using H2 + O2 mixtures very strongly diluted (the “stoichiometric part of the combustible mixture” [36] not more than 3%) by Ar were chosen. For the case, direct comparison with our isothermal kinetic calculations is possible since an influence of such a factor as the self-heating of the mixture (when thermal and gas-dynamical phenomena come to foreground) is minimal.
Results of the comparison for compositions I-VII are presented in Table 4. Here, the experimental data [35] [36] for composition III, V-VII are adduced not in full, but only those of them, which were compared with calculations. Generally speaking, an arbitrary choice (for comparison with the calculation) of concrete experimental points is illustrated by the example of experimental series V from [35] ; see Figure 4.
As a general result of this comparison, one can state qualitative and quantitative agreement between calculated and experimental data. The latter concerns all the systems listed in Table 4 except the system IV (experiments [35] on measurements t50 behind reflected shock wave). In this case, there is a considerable systematic quantitative difference between calculated and experimental data which attains 54%. Besides defects of the kinetic scheme used in the calculation, it is possibly the result of some overstating the calculated values gas temperature and pressure behind the front of weak the shock wave, which the authors of [35] give. The latter may be due to difficulties in interpreting a very complex mechanism of a weak shock wave refraction and/or due to an imperfection of the existing standard method for calculation of T and p behind reflected shock waves, based on contradictory assumptions about equilibrium in vibrational degrees of freedom, on the one hand, and the absence of chemical reactions on the other. For this series of experiments (comparatively low temperatures and comparatively considerable amount of the molecular admixture), imperfections of the method used for the shock properties calculation can be found substantial.
It should be noted here (more detailed see [2] ) that the traditional vibrationally equilibrium (and, as a rule, excluding electronically excited components) kinetic models (see for example [2] [6] -[8] [10] [11] [14] and references therein) are unable to provide the quantitative interpretation of these experiments by means of one kinetic scheme without variations of the reaction rate constants.
In fitting the calculated values t* and t50 to the measured ones, a key point was variation and fitting of unknown kinetic constants for collision-induced energy transfers involving vibrational modes of HO2. The performed calculations have shown that the unknown kinetic constants



Figure 4. The measured [35] (circles; black circles mark the values from Table 4) and calculated (open squares mark the values from Table 4) values of τ50 for composition V (see Table 4).
radical in its collisions with H2 molecules was found to be the most important at T < 1500 K (in accordance with conclusions [16] about key role of the HO2 radical vibrational nonequilibrium in the hydrogen oxidation reaction). The value,


which is illustrated by Figure 5.
The relationship (13) should be considered as the quantitative estimation for presently unknown value of



In the future, as the range of compositions and conditions on temperature and pressure will be extended, the kinetic constants


4.3. Vibrational Nonequilibrium at Different Temperatures
The essentially nonequilibrium character of hydrogen oxidation with respect to vibrational degrees of freedom is illustrated by Figure 6 and Figure 7, which plot the typical time dependences of the vibrational temperatures, Tk, and nonequilibrium factors,

The following stages of the process can be distinguished in Figure 6 (see also Figure 2 and Figure 3).
1) At t < 300 μs in case (a) and t < 30 μs in case (b), the H2 and O2 molecules undergo vibrational excitation from initial (near-room) temperature, T0, to the equilibrium gas temperature, T, behind the front of the shock wave (curves 1, 4). Insignificant amounts of H and HO2 radicals and singlet oxygen

Figure 5. Characteristic time (in atm•s) of the V-RT energy transfer of HO2 radical in its collisions with H2 molecules at different temperatures. 1―the superior limit; 2―the mean value (adduced in the Table 2 and used in calculations for all the systems at T > 1500 K); 3―the inferior limit. Different markers correspond to the values of

T = 1178, K T = 1809, K

Figure 6. Time dependences of the vibrational temperatures, Tk, for the cases (a) and (b) (see the caption of Figure 2). The curves 1 - 8 correspond to vibrational temperatures for the following vibrational modes: H2 (1), HO2(ν1) (2), OH (3), O2 (4), HO2(ν3) (5),

T = 1178, K T = 1809, K

Figure 7. Time dependences of the nonequilibrium factor

formed due to endoergic initiation (c1) and collisional electronical excitation (c33') reactions (see Figure 3). Vibrational temperatures of O2 (curve 4) and

2) The time intervals 300 < t < 700 (a) and 60 < t < 300 (b) μs correspond to the intensive reaction stage. At this stage, maximum excitation of vibrational modes is a result of fast exothermal reactions. Here the following reactions are of key importance (see also Figure 3): the monomolecular decay reaction (c3) as the main chain branching one, and reaction (c5) mainly responsible for chain propagation. High rates of reactions (c1'), (c7), and (c32) are conditioned by significant concentrations of HO2 radicals at this stage of the process. Reactions (c1') and (c32) are responsible for forming the vibrationally excited O2 and

2) For t > 700 (a) and t > 300 (b) μs, the vibrational excitation decreases via relaxation of vibrationally excited molecules H2O(v) which is the main reaction product.
Nonequilibrium factors,

Clearly, taking into account the vibrational nonequilibrium reveals the very important effects running throughout all the process. The reaction rate constants depend on the vibrational temperatures of the reactants, and this dependence is characterized by a factor as large as several orders of magnitude. So, the nonequilibrium factor for H2O dissociation reaction (c12'), k12' (curve 7), attains a magnitude of about 1012. This is particularly true for reactions involving the HO2 radical. For example, within the model under consideration, the nonequilibrium factor for reaction (c21), k21 (curve 4), responsible for the formation of the electronically excited radical OH* throughout the induction period, and the nonequilibrium factor for key chain-branching reaction (c3), k3 (curve 3), reach the values of around 2 × 105. Such a deviation of κr from unity means that the reaction between hydrogen and oxygen is an essentially nonequilibrium reaction and the vibrational nonequilibrium of the HO2 radical is an intrinsic feature of hydrogen oxidation.
Referring to Figure 1, we note the following: it is the need when interpreting experiments within the formal kinetics to take into account in implicit form the objectively existing influence of vibrational nonequilibrium that leads to values
A visual characteristic of the degree of deviation from equilibrium for that or another vibrational mode in a complex reacting and relaxing mixture is the ratio of average vibrational energy to its equilibrium value,

One can see (Figure 8 and Table 4) that the vibrational nonequilibrium {and its influence on rate constants (Figure 7)} decreases with increasing the gas temperature T. Thus, the maximum super-equilibrium vibrational excitations,

5. Conclusions
The theoretical model of chemical and vibrational kinetics of hydrogen oxidation based on consistent account for
T = 1178, K T = 1809, K

Figure 8. Time dependences of the ratio of average vibrational energy to its equilibrium value,

Figure 9. Maximum values of the ratio

the vibrational nonequilibrium of HO2 radical formed in bimolecular recombination H + O2 ® HO2 with the super-equilibrium store of vibrational energy has been elaborated and experienced. The chain branching H + O2 = O + OH and inhibiting H + O2 + M = HO2 + M formal reactions are considered (in the terms of elementary processes) as a general multi-channel process of formation and intramolecular energy redistribution between modes, relaxation, and decay of the comparatively long-lived vibrationally excited HO2 radical which is capable to react and exchange of energy with another components of the mixture. For description of reactions in the H2 + O2 + Ar system, the kinetic scheme, which takes into account chemical reactions with participation H2, O2, H2O, HO2, H, O, OH, H2O2, O3 in the ground electronic state as well as O2(1D), O(1D), OH(2S+), and relaxation channels of the vibrational modes H2, HO2(ν1), OH, O2, O2(1D), HO2(ν2), HO2(ν3), H2O(ν1), H2O(ν2), and H2O(ν3), have been used.
The calculated results were compared with the shock tube experimental data for strongly diluted H2-O2 mixtures at 1000 < T < 2500 K, 0.5 < p < 4 atm and two equivalence ratio Φ = 1, 2. As a general result of this comparison, one can state qualitative and quantitative agreement between calculated and experimental data. This approach is promising from the standpoint of reconciling the predictions of the theoretical model with experimental data obtained by different authors for various compositions and conditions using different methods.
According to the calculations, the H2 + O2 reaction is essentially nonequilibrium and the vibrational nonequilibrium of the HO2 radical is an intrinsic feature of hydrogen oxidation. Taking into account the vibrational nonequilibrium reveals the very important effects running throughout all the process. Reaction rate constants depend on the reactant vibrational temperatures, and this dependence is characterized by a factor as large as several orders of magnitude. It is demonstrated that the vibrational nonequilibrium (and consequently its influence on the rate constants and the process on the whole) decreases with increasing the gas temperature T and pressure p remaining determinant up to temperatures T = 1500 K. At T < 1500 K, the nature of hydrogen-oxygen reaction is especially nonequilibrium, and the vibrational nonequilibrium of HO2 radical is the essence of this process.
The suggested model of vibrationally nonequilibrium kinetics is able to provide physically adequate (in the terms of elementary processes) solution of the problem of the H2 + O2 reaction mechanism without using formal overall reactions with their rate constants depending on experimental conditions. As a final result of numerous calculations, we have one (fixed) chemical kinetic scheme (without any “uncertainty” and “sensitivity” of the equilibrium rate constants of elementary reactions).
The characteristic time of the V-RT energy transfer united for all three modes of the HO2 radical in its collisions with H2 molecules,


This relation should be considered as the quantitative estimation for presently unknown value of


In the future, as the range of compositions and conditions on temperature and pressure will be extended, the kinetic constants listed in Tables 1-3 can be corrected. For optimization of the kinetic scheme, the results of ab initio analysis of PESs for HmOn molecular systems as well as the results of corresponding dynamic calculations must become of crucial importance as the independent non-empirical source of kinetic information.
With regard to the currently existing formal kinetic schemes (which along with the elementary chemical reactions include formal overall reactions), the following should be noted. The use of these schemes was and remains to be actual from the standpoint of their use in macro-kinetic applications such as combustion and detonation. Many of the existing kinetic schemes are quite acceptable for these purposes, although in need of substantial reductions and some adjustments in terms of accounting, in implicit form, for the important effect of vibrational nonequilibrium.
Acknowledgements
This work was supported by Russian Foundation for Basic Research (Grant No. 12-03-0052).
Cite this paper
Oleg V.Skrebkov, (2014) Vibrational Nonequilibrium in the Hydrogen-Oxygen Reaction at Different Temperatures. Journal of Modern Physics,05,1806-1829. doi: 10.4236/jmp.2014.516178
References
- 1. Mallard, W.G., Westley, F., Herron, J.T. and Hampson, R.F. (1994) NIST Chemical Kinetics Database, Ver. 6.0. NIST Standard Reference Data, Gaithersburg.
- 2. Skrebkov, O.V. and Karkach, S.P. (2007) Kinetics and Catalysis, 48, 367-375. Original Russian Text in: Kinetika i Kataliz, 48, 388-396.
- 3. Bradley, J.N. (1962) Shock Waves in Chemistry and Physics. Methuen & Co LTD-John Wiley & Sons INC, London-New York.
- 4. Kondratiev, V.N. and Nikitin, E.E. (1981) Gas-Phase Reactions: Kinetics and Mechanisms. Springer, Berlin.
http://dx.doi.org/10.1007/978-3-642-67608-6 - 5. Baulch, D.L., Cobos, C.J., Cox, R.A., Esser, C., Frank, P., Just, Th., Kerr, J.A., Pilling, M.J., Troe, J., Walker, R.W. and Warnatz, J. (1992) Journal of Physical and Chemical Reference Data, 21, 411-429.
http://dx.doi.org/10.1063/1.555908 - 6. Li, Z., Zhao, J., Kazakov, A. and Dryer, F.L. (2004) International Journal of Chemical Kinetics, 36, 566-575.
http://dx.doi.org/10.1002/kin.20026 - 7. Konnov, A.A. (2008) Combustion and Flame, 152, 507-528.
http://dx.doi.org/10.1016/j.combustflame.2007.10.024 - 8. Burke, M.P., Chaos, M., Ju, Y.G., Dryer, F.L. and Klippenstein, S.J. (2012) International Journal of Chemical Kinetics, 44, 444-474.
http://dx.doi.org/10.1002/kin.20603 - 9. Kondratyev, V.N. (1979) Rates of Elementary Chemical Processes in Gases on the Works of the Institute of Chemical Physics Akad. Nauk SSSR. In: Kondratyev, V.N., Ed., Problems of Chemical Kinetics. To the Eightieth Anniversary of Academician N.N. Semenov, Nauka, Moscow, 13-21.
- 10. Dougerty, E.P. and Rabitz, H. (1980) Journal of Chemical Physics, 72, 6571-6586.
http://dx.doi.org/10.1063/1.439114 - 11. Hidaka, Y., Takahashi, S., Kawano, H., Suga, M. and Gardiner Jr., W.C. (1982) Journal of Physical Chemistry, 86, 1429-1433.
http://dx.doi.org/10.1021/j100397a043 - 12. Karkach, S.P. and Osherov, V.I. (1999) Journal of Chemical Physics, 110, 11918-11927.
http://dx.doi.org/10.1063/1.479131 - 13. Michael, J.V., Suhterland, J.W., Harding, L.B. and Wagner, A.F. (2000) Proceedings of the Combustion Institute, 28, 1471-1478.
http://dx.doi.org/10.1016/S0082-0784(00)80543-3 - 14. Skrebkov, O.V., Karkach, S.P., Vasil’ev, V.M. and Smirnov, A.L. (2003) Chemical Physics Letters, 375, 413-418.
http://dx.doi.org/10.1016/S0009-2614(03)00875-3 - 15. Belles, E. and Lauver, M.R. (1964) Journal of Chemical Physics, 40, 415-419.
http://dx.doi.org/10.1063/1.1725129 - 16. Skrebkov, O.V., Karkach, S.P., Ivanova, A.N. and Kostenko, S.S. (2009) Kinetics and Catalysis, 50, 461-473. Original Russian Text in: Kinetika i Kataliz, 50, 483-495.
http://dx.doi.org/10.1134/S0023158409040016 - 17. Jorfi, M., Honvault, P., Bargueno, P., Gonzalez-Lezana, T., Larregaray, P., Bonnet, L. and Halvick, P. (2009) Journal of Chemical Physics, 130, 184301.
http://dx.doi.org/10.1063/1.3128537 - 18. Wadlinger, R.L. and deB. Darwent, B. (1967) Journal of Physical Chemistry, 71, 2057-2061.
http://dx.doi.org/10.1021/j100866a013 - 19. Pack, R.T., Butcher, E.A. and Parker, G.A. (1995) Journal of Chemical Physics, 102, 5998-6012.
http://dx.doi.org/10.1063/1.469334 - 20. Dobbyn, A.J., Stumpf, M., Keller, H.M. and Schinke, R. (1996) Journal of Chemical Physics, 104, 8357-8381.
http://dx.doi.org/10.1063/1.471587 - 21. Harding, L.B., Troe, J. and Ushakov, V.G. (2000) Physical Chemistry Chemical Physics, 2, 631-642.
http://dx.doi.org/10.1039/a908929b - 22. Vasil’ev, V.M., Kulikov, S.V. and Skrebkov, O.V. (1977) Zhurnal Prikladnoy Mekhaniki i Tekhnicheskoy Fiziki, 4, 13-21. English Translation in: Plenum Publishing Corporation, 437-444 (1978).
- 23. Skrebkov, O.V. and Kulikov, S.V. (1998) Chemical Physics, 227, 349-373.
http://dx.doi.org/10.1016/S0301-0104(97)00296-6 - 24. Skrebkov, O.V. (2011) Russian Journal of Physical Chemistry B, 5, 227-234. Original Russian Text in: Khimicheskaya Fizika, 30, 38.
- 25. Kuznetsov, N.M. (1972) Doklady Akademii Nauk SSSR, 202, 1367-1370.
- 26. Kuznetsov, N.M. (1972) Zhurnal Prikladnoy Mekhaniki i Tekhnicheskoy Fiziki, 3, 46-52.
- 27. Marrone, P.V. and Treanor, C.E. (1963) Physics of Fluids, 6, 1215-1221.
http://dx.doi.org/10.1063/1.1706888 - 28. Chapman, S. and Cowling, T.G. (1952) The Mathematical Theory of Non-Uniform Gases. Cambridge University Press, Cambridge.
- 29. Skrebkov, O.V. (1995) Chemical Physics, 191, 87-99.
http://dx.doi.org/10.1016/0301-0104(94)00303-R - 30. Fernandes-Ramos, A., Miller, J.A., Klippenstein, S.J. and Truhlar, D.G. (2006) Chemical Reviews, 106, 4518-4584.
http://dx.doi.org/10.1021/cr050205w - 31. Nikitin, E.E., Osipov, A.I. and Umanskii, S.Ya. (1989) Vibration-Translational Energy Transfer in Collisions of Homonuclear Diatomic Molecules. In: Smirnov, B.M., Ed., Khimiya Plazmy, Vyp. 15, Energoatomizdat, Moscow, 3-43.
- 32. Konovalova, I.A. and Umanskii, S.Ya. (1982) Khimicheskaya Fizika, 1, 901-905.
- 33. Skrebkov, O.V. and Smirnov, A.L. (1992) Soviet Journal of Chemical Physics, 10, 1598-1615. Original Russian Text in: Khimicheskaya Fizika, 10, 1036-1046 (1991).
- 34. Smirnov, A.L. and Skrebkov, O.V. (1992) Soviet Journal of Chemical Physics, 11, 51-63. Original Russian Text in: Khimicheskaya Fizika, 11, 35-42.
- 35. Ryu, S.O., Hwang, S.M. and Rabinovitz, M.J. (1995) Journal of Physical Chemistry, 99, 13984-13991.
http://dx.doi.org/10.1021/j100038a033 - 36. Pavlov, V.A. and Shatalov, O.P. (2011) Kinetics and Catalysis, 52, 157-165. Original Russian Text in: Kinetika i Kataliz, 52, 163-172.
http://dx.doi.org/10.1134/S0023158411020157 - 37. Herzfeld, K.F. and Litovitz, T.A. (1959) Absorbtion and Dispersion of Ultrasonic Waves. Academic Press, New York-London.
- 38. Moore, C.B. (1965) Journal of Chemical Physics, 43, 2979-2986.
http://dx.doi.org/10.1063/1.1697261 - 39. Ormonde, S. (1975) Reviews of Modern Physics, 47, 193-258.
http://dx.doi.org/10.1103/RevModPhys.47.193 - 40. Sibert, E.L., Reinhardt, W.P. and Hynes, J.T. (1982) Journal of Chemical Physics, 77, 3583-3594.
http://dx.doi.org/10.1063/1.444260 - 41. Sibert, E.L., Hynes, J.T. and Reinhardt, W.P. (1982) Journal of Chemical Physics, 77, 3595-3604.
http://dx.doi.org/10.1063/1.444261 - 42. Zhang, D.H. and Zhang, J.Z.H. (1994) Journal of Chemical Physics, 101, 3671-3678.
http://dx.doi.org/10.1063/1.467551 - 43. Mandelshtam, V.A., Taylor, H.S. and Miller, W.H. (1996) Journal of Chemical Physics, 105, 496-503.
http://dx.doi.org/10.1063/1.471903 - 44. Lin, S.Y., Sun, Z., Guo, H., Zhang, D.H., Honvault, P., Xie, D.Q. and Lee, S.Y. (2008) Journal of Physical Chemistry A, 112, 602-611.
http://dx.doi.org/10.1021/jp7098637 - 45. Lin, S.Y., Guo, H., Honvault, P., Xu, C.X. and Xie, D.Q. (2008) Journal of Chemical Physics, 128, 014303.
http://dx.doi.org/10.1063/1.2812559 - 46. Troe, J. and Ushakov, V.G. (2008) Journal of Chemical Physics, 128, 204307.
http://dx.doi.org/10.1063/1.2917201 - 47. Landau, L. and Teller, E. (1936) Physik Zeitschrift der Sowjetunion, 10, 34-38.
- 48. Keck, J. and Carrier, G. (1965) Journal of Chemical Physics, 43, 2284-2298.
http://dx.doi.org/10.1063/1.1697125
Appendix A: Specific Types of Collisional Energy Exchange
The change of the average energy, (dek/dt)vibr, of the kth vibrational mode as a result of qth relaxation channel has the following forms for different implemented types of energy exchange; see Equations (6), (7).
One-quantum VT energy transfer (Table 2, q = 1 - 10):

mode k belongs to a molecule of kind j, the molecule of kind i does not change its vibrational state, i.e.,




One-quantum VV' energy exchange (Table 3, q = 11 - 32, 34 - 38, 40 - 47):

mode k belongs to a molecule of kind j, mode l belongs to a molecule of kind i, i.e.,





1 ® 2 quantum VV' energy exchange (Table 3, q = 33, 39):

mode k belongs to a molecule of kind j, modes l and p belong to a molecule of kind i, i.e.,







Appendix B: To the Calculation of the Vibrational Relaxation Channel Rates
In accordance with the SSH theory, the probability of qth complex vibrational transition from modes m to modes n during one collision of jth and ith molecules, see Equation (10), has the form:

Here,





Although the dependence (B.1), (B.2) has been obtained as a result of the linear dynamic problem solution (the semi-classical calculation in the first order approximation of perturbation theory for the model of an oscillator with an induced force) with using the exponential repulsive potential it can be approximately considered as universal one for a variety of colliding pairs since it is possible to take account of rotation and long-range attraction effects by means of adapting the parameters


The adiabaticity parameter,

and matrix elements,

are defined by the relationships well-known in the theory of vibrational relaxation (see, for example, [29] and references herein). Here, Mji is the reduced mass of the j-i collision, mm is the reduced mass of the mth oscillator, a is the parameter of the intermolecular interaction potential (take here 1/α = 0.2 × 10- 8 cm ), Dm and bm are the parameters of respective intramolecular potential (corresponding Morse potential).
When applying formulae (B.1)-(B.4) to HO2 molecule, the latter was considered as the set of the following oscillators: the stretching along H×××O bond with the reduced mass 1.0693 and the frequency 3698 cm−1; the angle vibration near equilibrium angle value ÐHOO = 104.3˚ with the reduced mass 1.1311 and the frequency 1430 cm−1; the stretching along O∙∙∙O bond with the reduced mass 13.0737 and the frequency 1120 cm−1
For the processes of VT- and non-resonance VV'-energy transfers with participation of oscillators involving light H atom, the relative translational motion is slow as compared to rotation. In the simplest intuitive model of VR-energy transfer [38] , the dynamic parameters of the theory of VT- and VV'-energy transfer (velocity and reduced mass) which characterize the relative translational motion are replaced by the corresponding parameters which characterize the rotational motion; within this approach, the role of translational motion is merely in drawing the molecules together. Consequently, while calculating the rate constants of these processes using relationships (B.1)-(B.4), we have, as SSHM estimation, instead of (B.3), the following relation (see also [39] ):

The main (Table 2 and Table 3) VT- and VV'-relaxation channels in the reacting mixture H2 + O2 + Ar at T ³ 1000 K, p ~ 1 atm were chosen as a result of comparative analysis of the rate constant values calculated for these conditions. This selection was based on the following estimations:

i.e., in the Table 2 and Table 3, it was taken into consideration the processes for which

Of non-single-quanta transitions, only the VV' transfer processes (v33), H2O(001) + HO2(000) « H2O(000) + HO2(011), and (v39), H2O(100) + HO2(000) « H2O(000) + HO2(011), (Table 3) answer the condition (B.7).
NOTES

1The use of the formal kinetic description was and remains relevant in terms of its use in macro-kinetic applications, i.e., when it is enough to quantitatively correctly simulate the density and “heat release function” in the specific conditions of composition, temperature, and pressure.
2According to existing concepts (see, for example, [4] ), if molecules or radicals AB are 2-atomics (O2, H2, OH, ∙∙∙), such a reaction proceeds in two the following elementary steps: forming vibrationally excited AB(v) and its subsequent relaxation to equilibrium distribution on vibrational states (in this case, deactivation in collisions). If the AB are 3(or more)-atomics (HO2, H2O, H2O2, ∙∙∙) such a reaction proceeds in three following elementary steps: forming vibrationally excited AB(v), intramolecular energy redistribution, and relaxation. The vibrational relaxation times, tvib, directly dependent on conditions; so the value of the rate constant of the vibrational-to-translational energy exchange process is proportional to pressure, p, and depends on the buffer gas type, M. If in the course of the reaction is maintained equilibrium distribution in vibrational states (“high pressure limit”), i.e.,
 (tch is the chemical reaction characteristic time), the equilibrium approximation is correct, the reaction rate of recombination (dissociation) is determined by the rate of its first stage, not depends on p and M, the recombination rate constant is defined by the value k¥ (the dissociation rate constant
(tch is the chemical reaction characteristic time), the equilibrium approximation is correct, the reaction rate of recombination (dissociation) is determined by the rate of its first stage, not depends on p and M, the recombination rate constant is defined by the value k¥ (the dissociation rate constant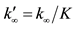 ). In the opposite case, i.e., when
). In the opposite case, i.e., when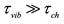 , (“low pressure limit”) the reaction rate is determined by the rate of vibrational relaxation stage, the relationship k/k' = K(T) is invalid. Really in practice, an intermediate case is realized; the reaction rate constant and efficiencies of third-bodies, M, in the framework of the formal kinetics (on the basis of assumed mechanism), is searched empirically as a result of fitting to the experiment. Herewith, the relationship k/k' = K(T) is used that, at least, is inconsistent.
, (“low pressure limit”) the reaction rate is determined by the rate of vibrational relaxation stage, the relationship k/k' = K(T) is invalid. Really in practice, an intermediate case is realized; the reaction rate constant and efficiencies of third-bodies, M, in the framework of the formal kinetics (on the basis of assumed mechanism), is searched empirically as a result of fitting to the experiment. Herewith, the relationship k/k' = K(T) is used that, at least, is inconsistent.
3The inability of the equilibrium kinetics concept to predict efficiencies of different third bodies, M, in recombination-dissociation reactions; the possibility of formation of electronically excited states O2(1D), O(1D), OH(2S+), reactions with their participation, the complex multi- channel character of quenching processes, including the chemical quenching processes (see [2] ).
4i.e., there is an overlap of the HO2(v) lifetime and collision time statistical distributions.
5In this context, non-empirical sources of kinetic information, such as ab initio analysis of PESs and dynamic calculations of equilibrium (as a result of averaging corresponding cross sections over reagent equilibrium distributions) rate constants of elementary reactions, become of particular importance.
6In the simplest case of the single-quanta vibrational-to-translational (VT) transfer, one has the relation
7In accordance with the conclusions of [2] and [16] about “the dependence of the effective rate constant of the overall reaction H + O2 ® O + OH on experimental conditions” and about the “key role of the HO2 radical in the hydrogen oxidation reaction”.
















