Journal of Modern Physics
Vol.4 No.8A(2013), Article ID:41555,5 pages DOI:10.4236/jmp.2013.48A023
Maxwell-Proca Fields in Relativistic Astrophysical Compact Objects
Physical Sciences Department, Eastern Connecticut State University, Willimantic, USA
Email: pazameta@easternct.edu
Copyright © 2013 Zoran Pazameta. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 18, 2013; revised July 16, 2013; accepted September 15, 2013
Keywords: Gravitation; Compact Objects; Einstein Equations; Maxwell-Proca Fields
ABSTRACT
A general-relativistic model is formulated for hypothetical ultra-compact astrophysical objects composed of fluid infused with charges carrying a generalized massless Maxwell-Proca field. The chosen interior metric has the algebraic property that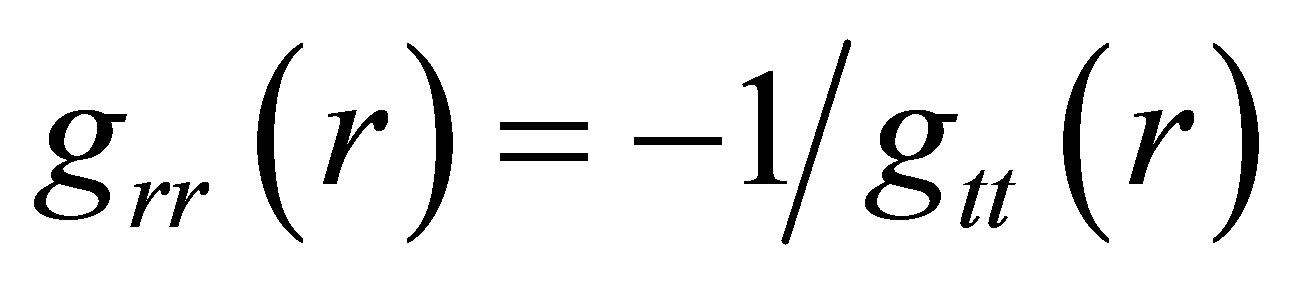 ; the fluid consequently possesses a negative pressure which halts gravitational collapse and establishes hydrostatic equilibrium. For an object containing a global distribution of non-interacting MaxwellProca charges, it is shown that physical considerations define the relationship between the charge density and the metric function uniquely, corroborating an earlier finding (for an electrostatic distribution of charge) that the interior field must increase with radial distance and the exterior field necessarily follows an inverse-square law. For the case of a charged fluid envelope surrounding a core of uncharged fluid, numerous solutions are possible. Assuming the interior field to vary as rn and requiring its strength to increase with radial distance while the charge density decreases, the range of values for n is found to be 0 < n ≤ 1 (where n is not necessarily an integer) with n = 1 denoting the special case of a continuous distribution of charge. For both continuous and stratified charge distributions, the exterior field is found to decrease as
; the fluid consequently possesses a negative pressure which halts gravitational collapse and establishes hydrostatic equilibrium. For an object containing a global distribution of non-interacting MaxwellProca charges, it is shown that physical considerations define the relationship between the charge density and the metric function uniquely, corroborating an earlier finding (for an electrostatic distribution of charge) that the interior field must increase with radial distance and the exterior field necessarily follows an inverse-square law. For the case of a charged fluid envelope surrounding a core of uncharged fluid, numerous solutions are possible. Assuming the interior field to vary as rn and requiring its strength to increase with radial distance while the charge density decreases, the range of values for n is found to be 0 < n ≤ 1 (where n is not necessarily an integer) with n = 1 denoting the special case of a continuous distribution of charge. For both continuous and stratified charge distributions, the exterior field is found to decrease as  regardless of the interior field’s dependence on r.
regardless of the interior field’s dependence on r.
1. Introduction
Until quite recently, it was believed that astrophysical objects more compact than neutron stars could not exist; no physically plausible mechanism had been conceived that could halt the gravitational collapse and establish equilibrium inside such an object, leading inevitably to its collapse to a singularity and the formation of a classical black hole. However, this began to change as research into entities such as vacuum energy and dark energy progressed (and evidence for their existence mounted): These entities all possess the equation of state p = –ρ, meaning that for a positive mass-energy density the pressure must be negative (sometimes called a tension) and therefore act as an “anti-gravity” mechanism to oppose the collapse of a compact object. This has led to models for two classes of such hypothetical compact objects: For those collapsing to an equilibrium radius, R, that is smaller than their Schwarzschild radius rS, the result is a nonsingular black hole (also known as a QBH, or quasi-black hole); and those for which R > rS at equilibrium are referred to as ultra-compact (or, sometimesas hyper-compact) objects.
Any physically acceptable model of a compact object must include a well-behaved transition from the interior metric to an exterior one. As has long been known, the only static, spherically symmetric exterior solutions of the Einstein equations are the (vacuum) Schwarzschild and (charged vacuum) Reissner-Nordstrøm metrics, and they share the algebraic feature that
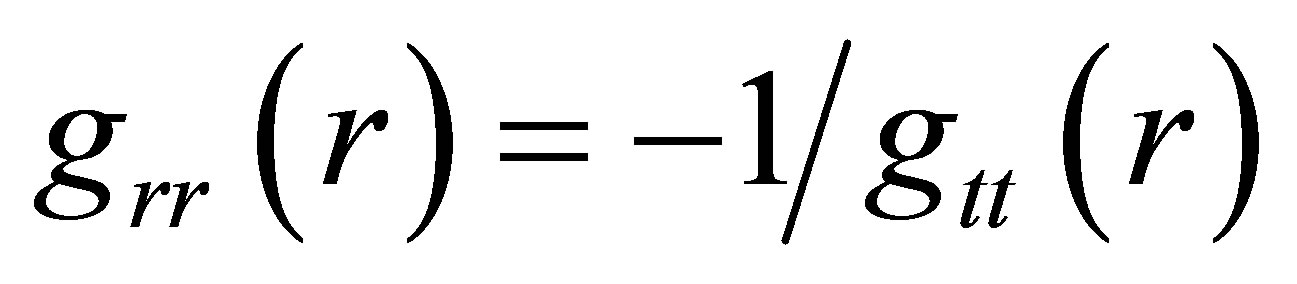 . (1)
. (1)
Not only does an interior metric with the algebraic form of relation (1) reduce the problem of solving the Einstein equations to that of finding just one unknown function, it is also easier to match such a metric to one of the abovementioned exterior metrics across an object’s surface, r = R. Writing the exterior metric as
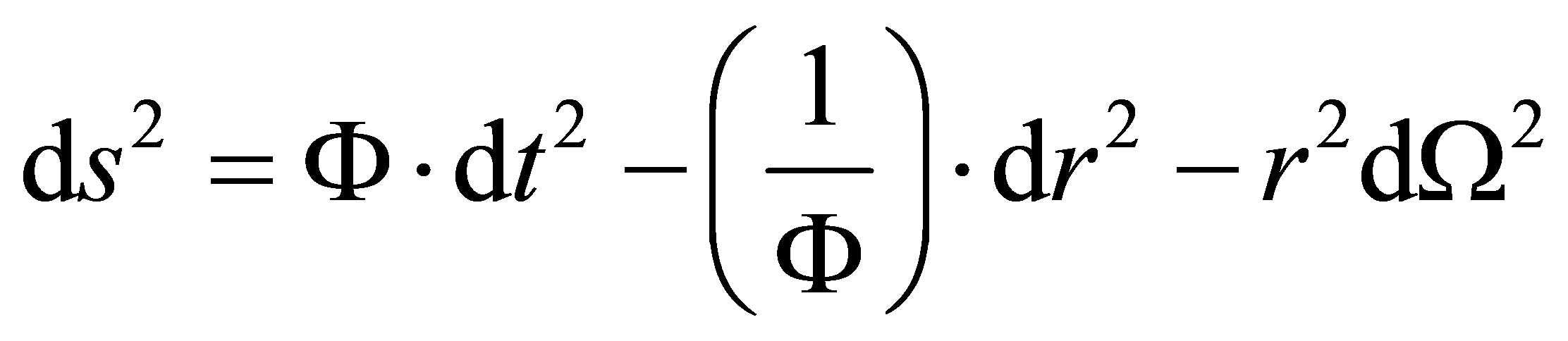 , (2)
, (2)
where 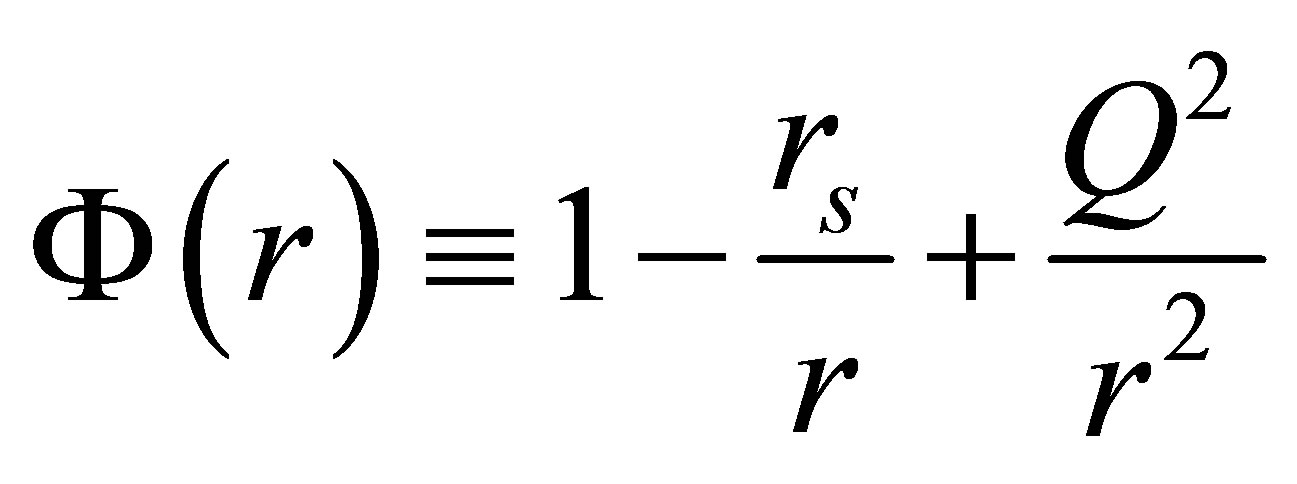 with Q being the object’s global charge—zero for an uncharged (Schwarzschild) object, but not necessarily limited to just electric charge otherwise—and writing the interior metric as
with Q being the object’s global charge—zero for an uncharged (Schwarzschild) object, but not necessarily limited to just electric charge otherwise—and writing the interior metric as
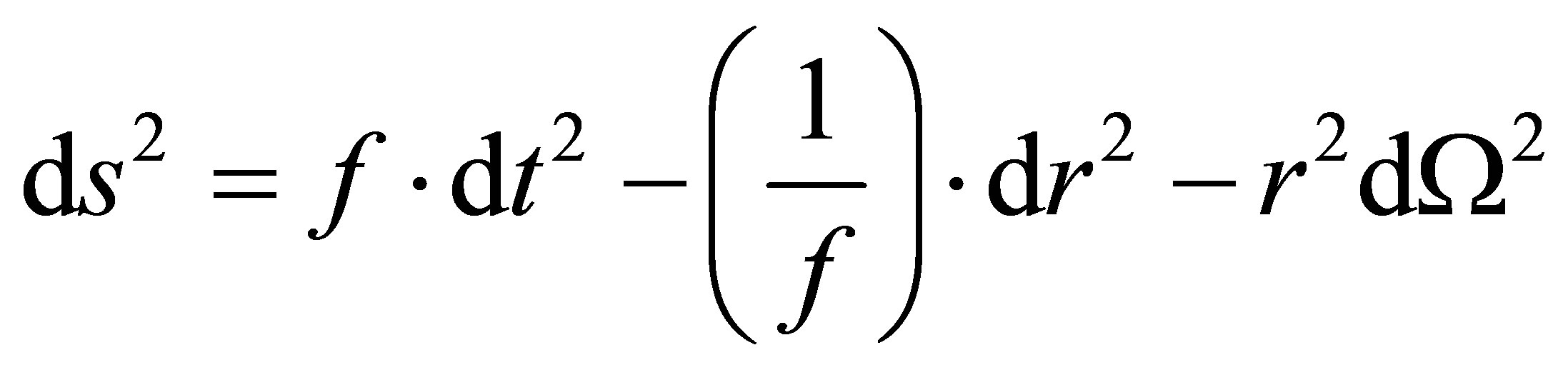 (3)
(3)
where f = f(r) and 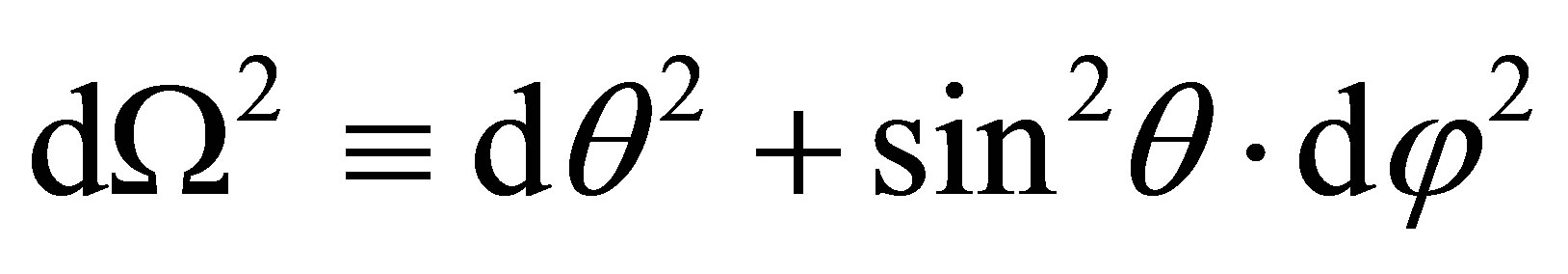 (with θ = π/2 and c = G = 1 throughout), we see that the boundary conditions reduce to the following (where, as usual, ′ ≡ d/dr):
(with θ = π/2 and c = G = 1 throughout), we see that the boundary conditions reduce to the following (where, as usual, ′ ≡ d/dr):
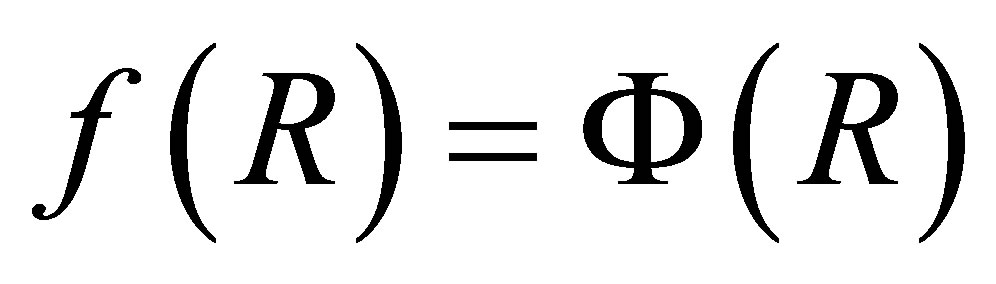 (4)
(4)
with f′(r) and Φ′(r) continuous across r = R. The above applies not just to the transition between an interior metric and an exterior one, but also to the interface between metrics with the algebraic structure of relation (1) that describe different layers inside an object [1].
Another, less well-known, feature of an interior metric of the form of relation (3) is that the Einstein tensor constructed from it has the property that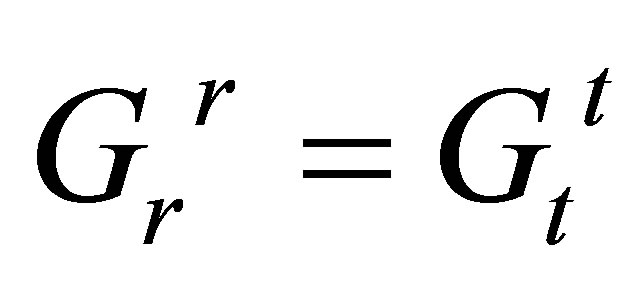 . With the energy-momentum tensor for a perfect fluid, the ensuing Einstein equations will always yield the equation of state p = –ρ; this holds also when other algebraically compatible source fields are added into the total energy-momentum tensor of the system (provided that none of these fields interact with each other or with the perfect fluid). One such family of compatible entities consists of the massless, non-self-interacting Maxwell-Proca (M-P) fields, and these are the subject of our investigation in this paper.
. With the energy-momentum tensor for a perfect fluid, the ensuing Einstein equations will always yield the equation of state p = –ρ; this holds also when other algebraically compatible source fields are added into the total energy-momentum tensor of the system (provided that none of these fields interact with each other or with the perfect fluid). One such family of compatible entities consists of the massless, non-self-interacting Maxwell-Proca (M-P) fields, and these are the subject of our investigation in this paper.
2. The Einstein Equations
In recent years, experiments at the Relativistic Heavy Ion Collider have shown that hot quark-gluon plasma—a state of matter that may well exist inside ultra-compact objects—behaves like a perfect fluid [2]. For the righthand side of Einstein’s equations, we therefore consider as sources a perfect fluid as well as the massless, nonself-interacting M-P field. Assuming the fluid and the field do not interact, the algebraic sum of their energymomentum tensors constitutes the total energy-momentum tensor. This combination is both versatile and physically interesting: In addition to using a perfect fluid to represent the distribution of charged particles that is the source of the M-P field, one (or more) other species of (non-interacting) particles and fields comprising the compact object can be represented merely by adding the appropriate energy-momentum tensor(s) into the total. The total pressure and density would then simply be the sum of the partial pressures and densities of all the fluids and fields involved.
As usual, we write the energy-momentum tensor for a perfect fluid as
 (5)
(5)
where the co-moving 4-velocity uα is defined such that
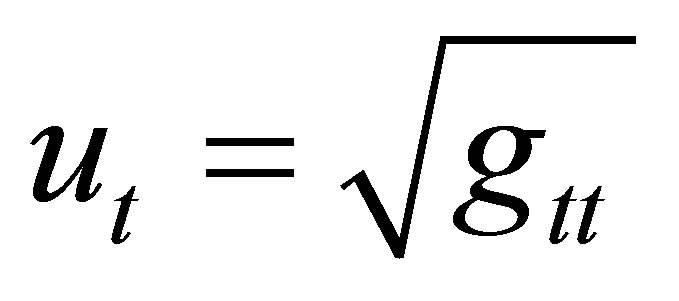 and uαuα = 1. The second source term is that of an arbitrary M-P field,
and uαuα = 1. The second source term is that of an arbitrary M-P field,
 (6)
(6)
built from the M-P tensor
 (7)
(7)
where Aα is the 4-vector potential and a comma symbolizes an ordinary derivative. In the rest-frame of a static, spherically symmetric distribution of charge this potential reduces to Aα = [φ(r), 0, 0, 0], which gives the M-P field strength as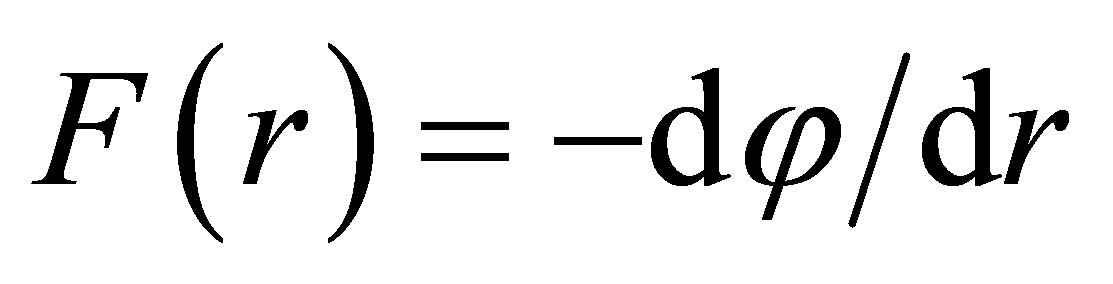 .
.
Substituting relations (5) and (6) into the Einstein equations, written in dimensionless mixed-index form as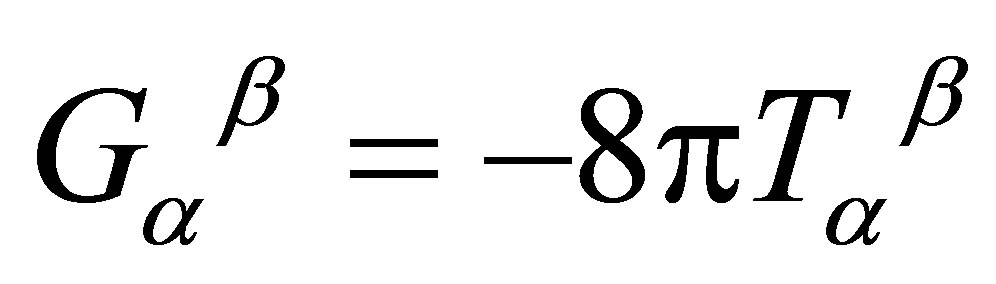 , then gives:
, then gives:
 (8)
(8)
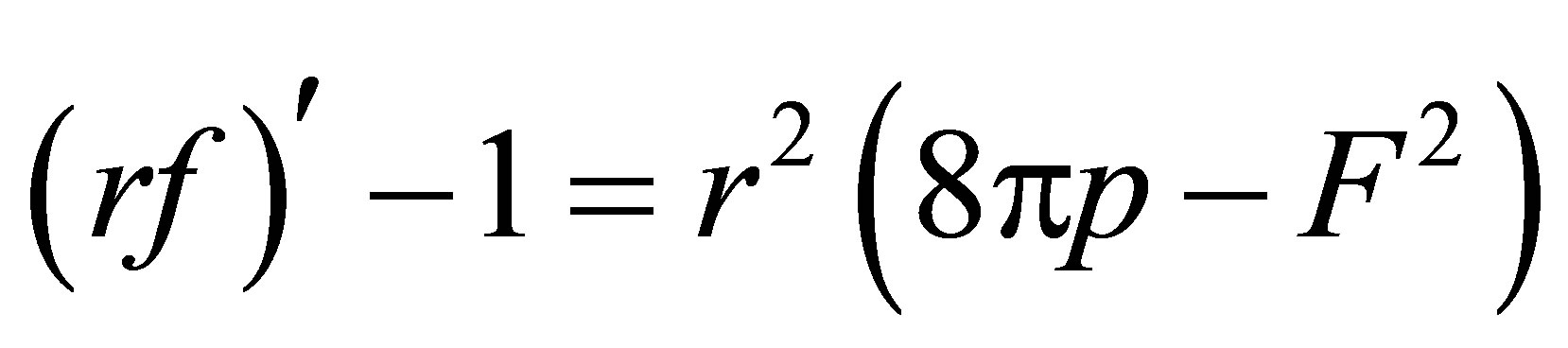 (9)
(9)
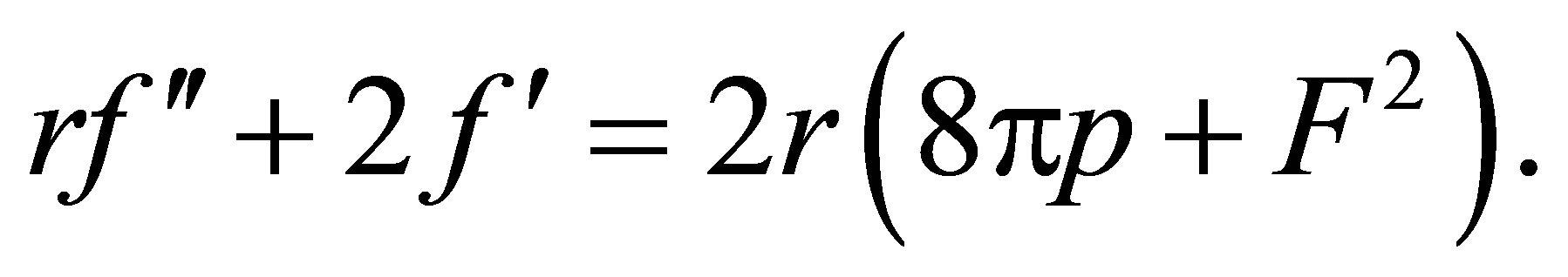 (10)
(10)
As noted above in the Introduction, the Einstein tensor components in Equations (8) and (9) are identical; subtracting one of these equations from the other gives the Oppenheimer relation, from which we immediately obtain the expected relationship between pressure and density (the equation of state): p(r) = –ρ(r). If we require that ρ(r) > 0 for realistic matter, then p(r) < 0; physically, this makes sense because, in order to attain an equilibrium state inside the object, a negative pressure is necessary to counterbalance not just the gravity of the matter comprising the compact object but also that due to the effective gravitational mass of the M-P field [3,4].
We proceed to solve the Einstein equations by considering the conservation equation for the total energy-momentum tensor, 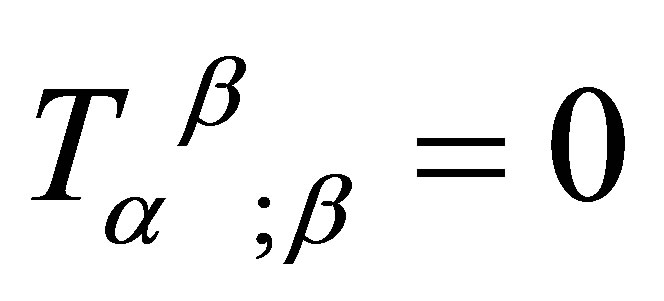 (where the semi-colon denotes a covariant derivative). This reduces to
(where the semi-colon denotes a covariant derivative). This reduces to
 (11)
(11)
after applying the equation of state found above, and is a generalization of the well-known Oppenheimer-Volkoff (O-V) equation for hydrostatic equilibrium. This equation relates the pressure (and, therefore, the density) to the M-P field strength, allowing them to be found once F(r) is known. It also emphasizes the crucial significance of the M-P field: Its absence would make the pressure constant throughout the object’s interior, whereas we expect a function of r that must vanish at the object’s surface. Finally, once p (and, therefore, ρ) is found from relation (11), either of equations (8) or (9) may be solved for the unknown metric function f(r). To complete the model of the compact object, this interior metric must then be matched at the object’s surface, as per the condition (4), to the appropriate metric describing the spacetime exterior to it.
3. Maxwell-Proca Charges and Fields
In order to accomplish all of the above, we first need to determine the field strength F(r) by considering the charge distribution producing it. We begin with the fact that in M-P theory the energy-momentum tensor of each field individually must satisfy the conservation relation
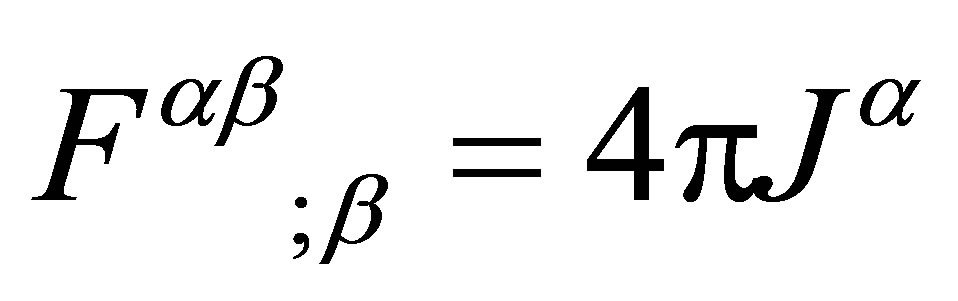 (12)
(12)
where Jα is the current density 4-vector of that field’s charge distribution. In our case, the only nonzero component of Equation (12) is
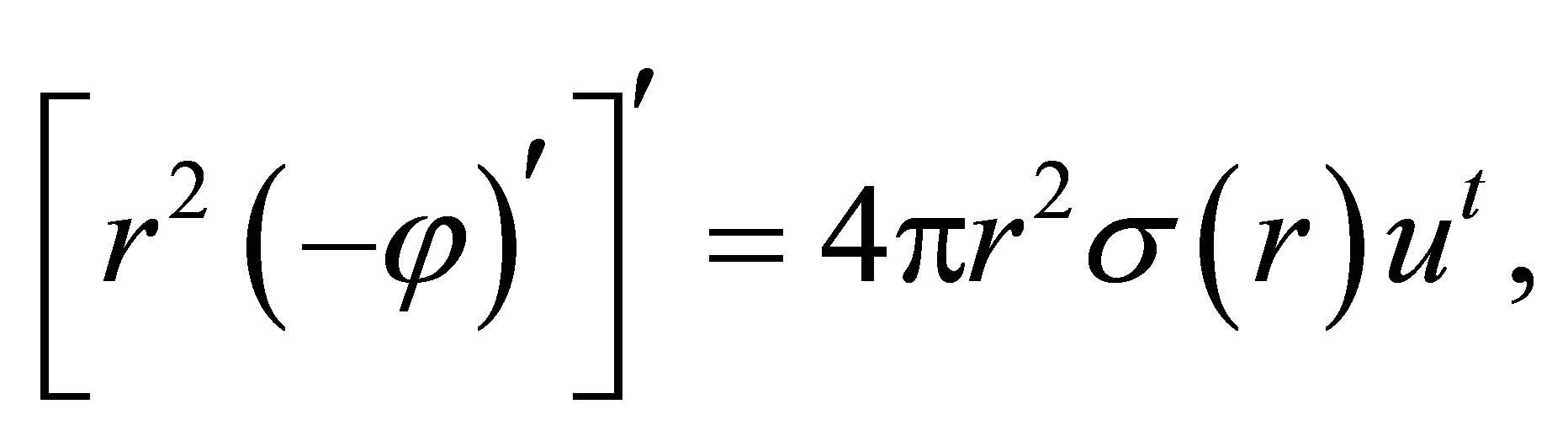 (13)
(13)
where σ(r) is the charge density. Recalling the definitions
 and
and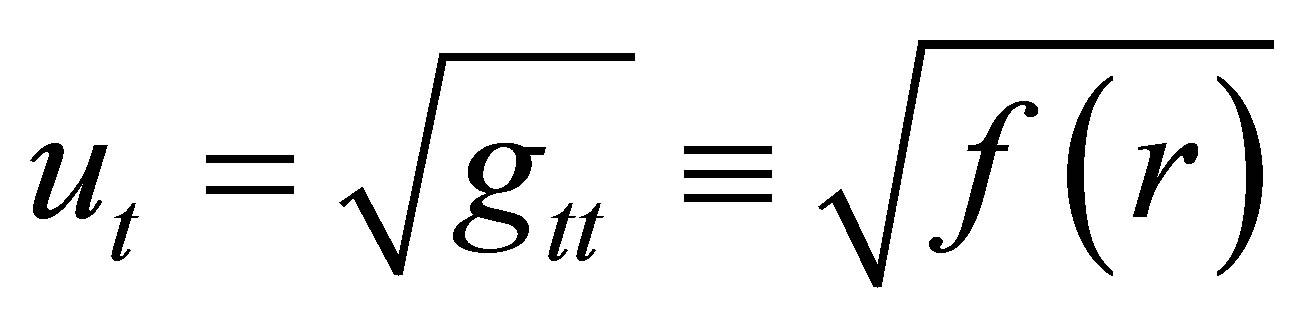 , Equation (13)
, Equation (13)
may immediately be integrated to give
 , (14)
, (14)
in which the constant of integration is set to zero to keep F(r = 0) finite. This equation, though, contains two unknown quantities (σ and f) and is therefore intractable as it stands. However, it has been shown that this equation may immediately be solved by means of the ansatz
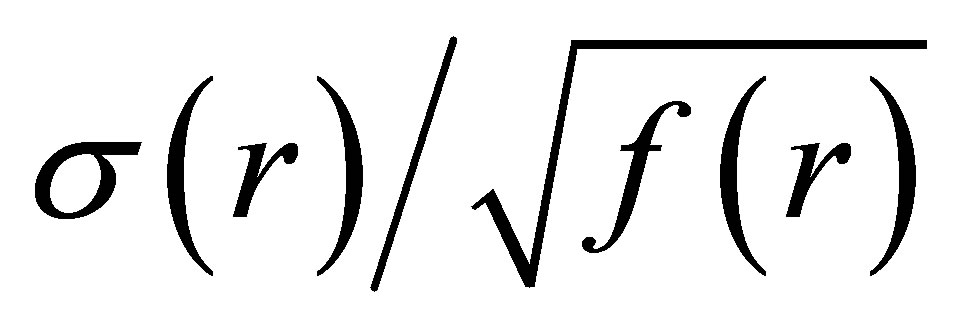 = (constant) [4]. We feel that there is justification for this ansatz: Because f represents the gravitational potential inside the object, surely it is reasonable to assume a functional relationship between it and the charge density—after all, the charged fluid and its inherent field determine the system’s gravitational properties. Then, if we propose a more general form of the abovementioned ansatz and write
= (constant) [4]. We feel that there is justification for this ansatz: Because f represents the gravitational potential inside the object, surely it is reasonable to assume a functional relationship between it and the charge density—after all, the charged fluid and its inherent field determine the system’s gravitational properties. Then, if we propose a more general form of the abovementioned ansatz and write
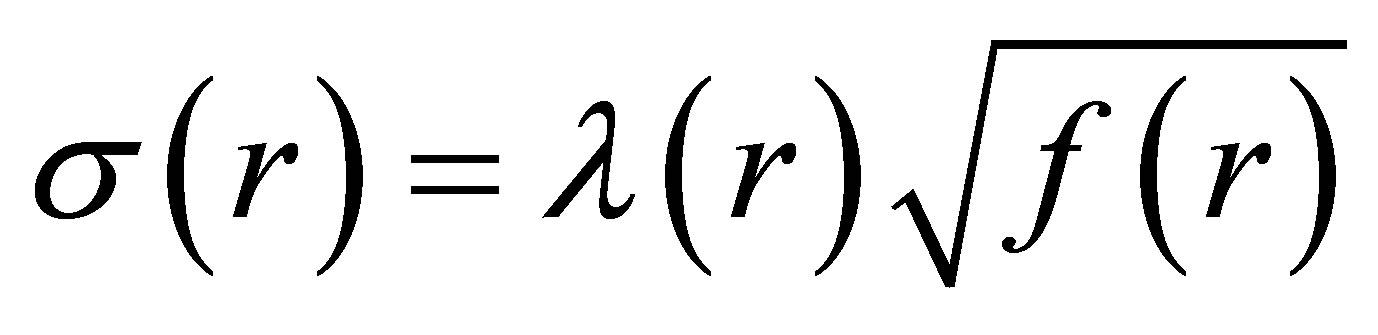 (15)
(15)
where λ is some suitably behaved function of r, equation (14) may readily be solved to give several expressions for F—not all of which, however, may turn out to be physically plausible.
We expect λ to be a simple, closed-form function of r, with the choice of λ limited by physical constraints; for instance, neither σ nor f may diverge at the origin. Moreover, f(r = 0) cannot vanish or grr will become divergent there. And for an object composed of (or infused with) a continuous isotropic distribution of charged particles, the central charge density  must be a constant. Different restrictions, however, apply to a stratified object, in which an uncharged fluid core is surrounded by an arbitrarily thick envelope of charged fluid. We consider both of these cases in detail below.
must be a constant. Different restrictions, however, apply to a stratified object, in which an uncharged fluid core is surrounded by an arbitrarily thick envelope of charged fluid. We consider both of these cases in detail below.
3.1. Continuous Fluid
The right-hand side of Equation (14) becomes just a volume integral of charge density (that is, the total M-P charge q contained within coordinate radius r) upon adopting an ansatz originally employed for a spherical, electrically charged fluid object [4]:
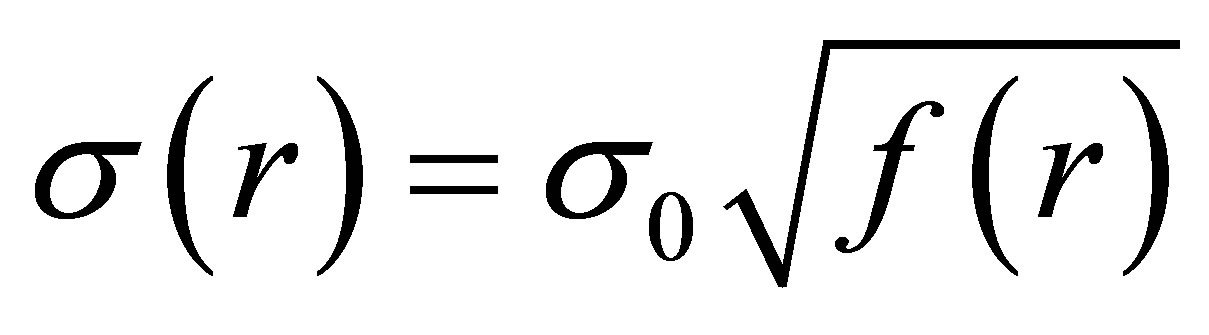 , (16)
, (16)
which is the simplest form of our relation (15). Then,
 (17)
(17)
so that the object’s global charge is just 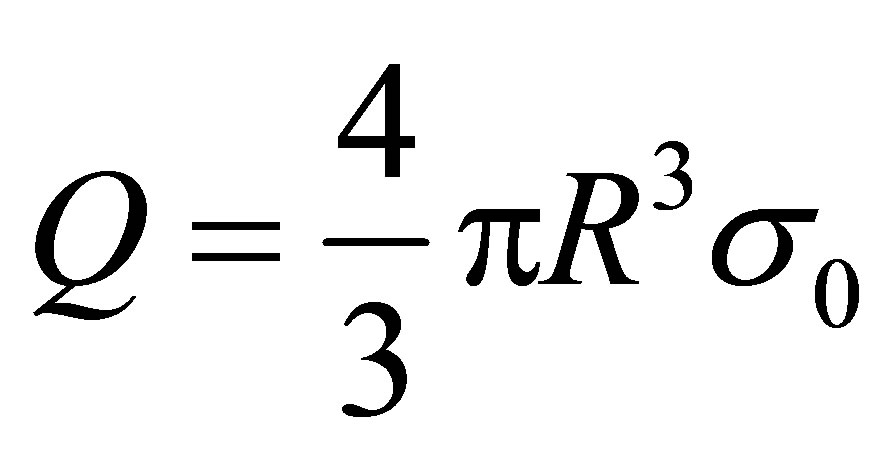
and its exterior field falls off as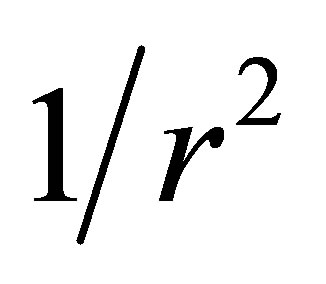 . While it was intended specifically for the case of an isotropic distribution of electric charges, the physical constraint that σ(r = 0) must be a constant evidently makes the solution constructed from the ansatz (16) the only one applicable to any continuous-fluid scenario—for all species of M-P charges.
. While it was intended specifically for the case of an isotropic distribution of electric charges, the physical constraint that σ(r = 0) must be a constant evidently makes the solution constructed from the ansatz (16) the only one applicable to any continuous-fluid scenario—for all species of M-P charges.
To complete the solution, the above expression for F is substituted into the O-V relation (11) to yield the pressure (and, thus, density) functions; inserting either of these into the appropriate Einstein equation then gives the metric function f. It has been shown that all of the interior functions—p, ρ, σ and f—turn out to be wellbehaved, and that p and ρ vanish at the surface as required [4]; also, as intuitively expected, the charge density decreases with increasing r. Finally, the resulting interior metric may be matched across the object’s surface to a Reissner-Nordstrøm metric to complete the model for this type of object; in a study where this was done for an object infused with magnetic monopoles generated by ultra-high-energy particle collisions during the collapse process [5], the effective gravitational mass of the ensuing (monopolar) magnetic field was shown to be three times the mass of the fluid comprising the object—and this may obviously be generalized to an object incorporating any M-P field of the type considered here.
3.2. Stratified Fluid
Suppose that the charged-fluid envelope surrounding the object’s uncharged core extends from some inner radius r1 > 0 to an outer radius r2 ≤ R. Here,  represents the charge density at r1; from relation (15), its value is simply
represents the charge density at r1; from relation (15), its value is simply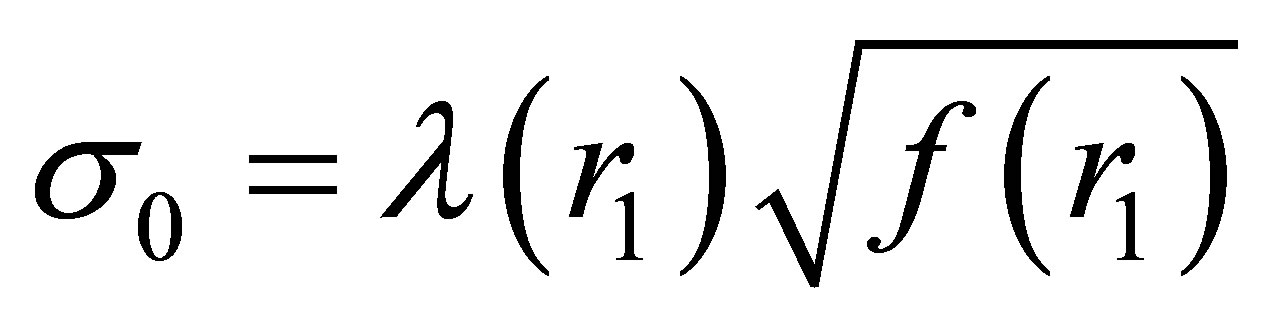 . The first physical restriction affecting the choice of λ(r) arises from the fact that, regardless of the behavior of σ(r), more charge is inevitably enclosed as r increases—therefore, F(r) must be an increasing function of r inside any distribution of charged matter. Secondly, because unusual physical circumstances would be required for charge density to increase with r, σ is expected to be a decreasing function of r inside the envelope. This leads us to consider two scenarios: One in which the charge density is an increasing function of radial distance, and one where it decreases; in both cases, of course, F must increase with r. Let us now assume a simple power-law form for λ:
. The first physical restriction affecting the choice of λ(r) arises from the fact that, regardless of the behavior of σ(r), more charge is inevitably enclosed as r increases—therefore, F(r) must be an increasing function of r inside any distribution of charged matter. Secondly, because unusual physical circumstances would be required for charge density to increase with r, σ is expected to be a decreasing function of r inside the envelope. This leads us to consider two scenarios: One in which the charge density is an increasing function of radial distance, and one where it decreases; in both cases, of course, F must increase with r. Let us now assume a simple power-law form for λ:
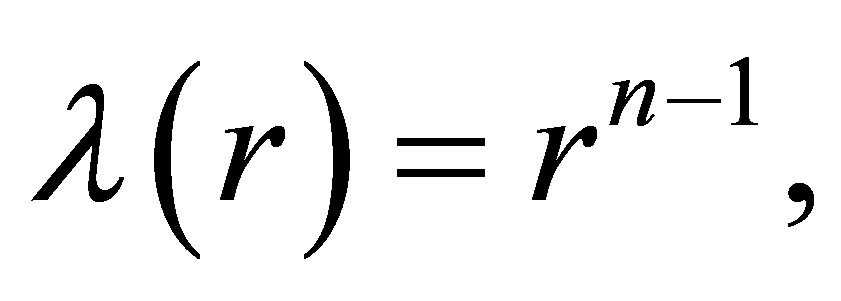 (18)
(18)
where n is any real number; as shown below, the choice of n – 1 rather than n for the exponent gives the power law for the M-P field as F(r) ~ rn. What restrictions on possible values of n will follow from the above physical criteria? We insert relation (18) into Equation (15) in order to perform the integration Equation (14); choosing the constant of integration so that F(r1) = 0 (since the boundary at r1 encloses no charge) then yields
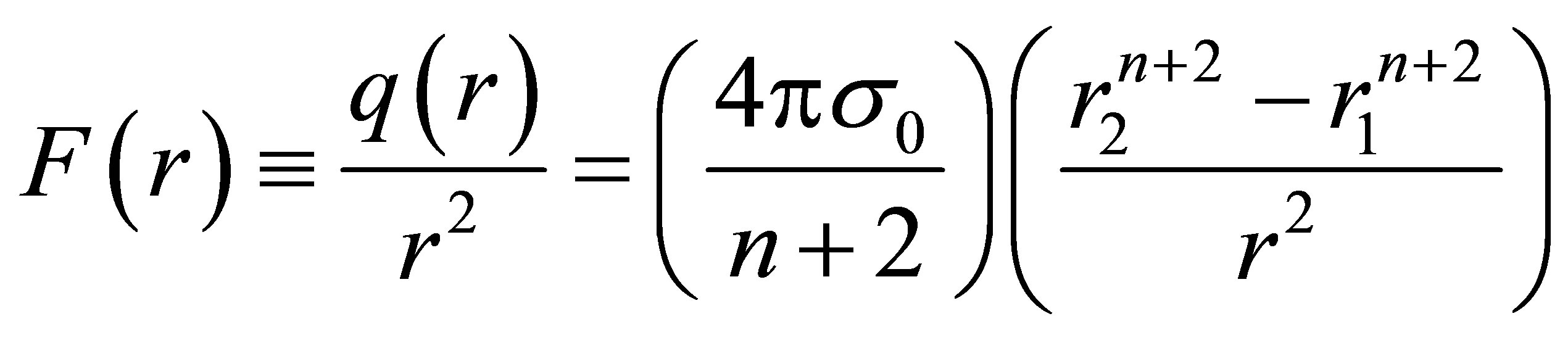 . (19)
. (19)
Examining this, we see that n cannot be –2. Inserting this expression for F into the O-V equation (11) and integrating then gives the pressure—and, from the Oppenheimer relation, the density—as
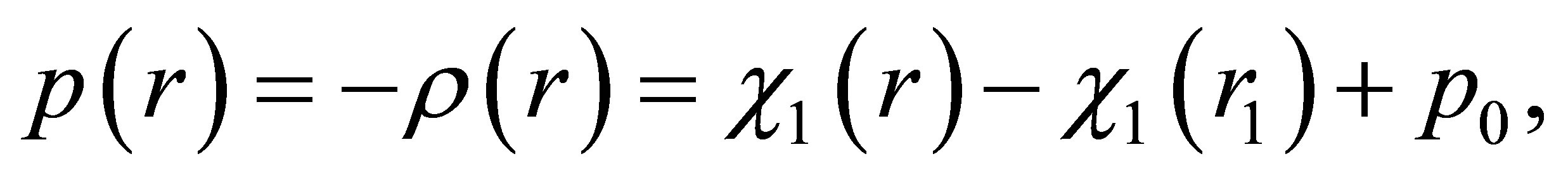 (20)
(20)
where
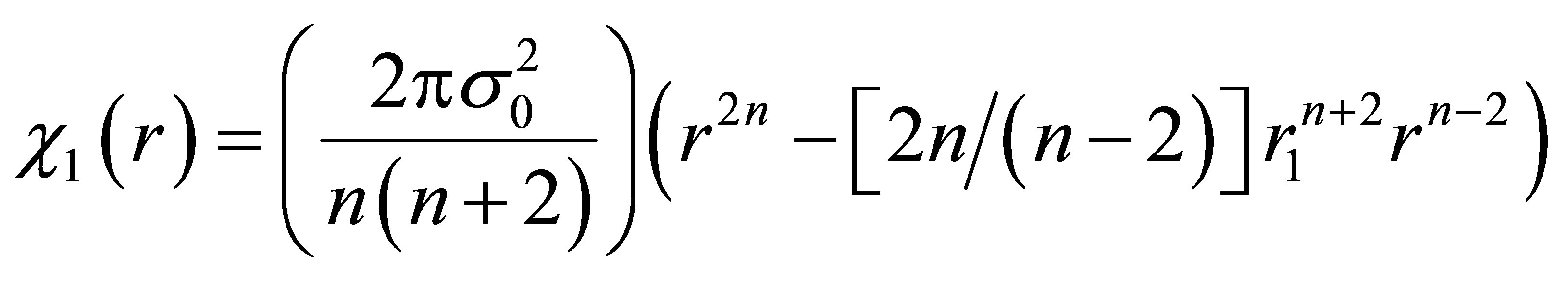 (21)
(21)
and we have defined the pressure at the inner boundary as p(r1) ≡ p0. From this, we see immediately that n cannot take on the values 0 or 2; the interior M-P field strength cannot be constant, or scale as r2.
To complete the solution for the metric function inside the charged envelope, the Einstein equation (9) is integrated with the boundary condition f(r1) ≡ f0, where f0 is obtained by matching f(r) to the core’s metric across this boundary. This gives the formal expression
 , (22)
, (22)
where
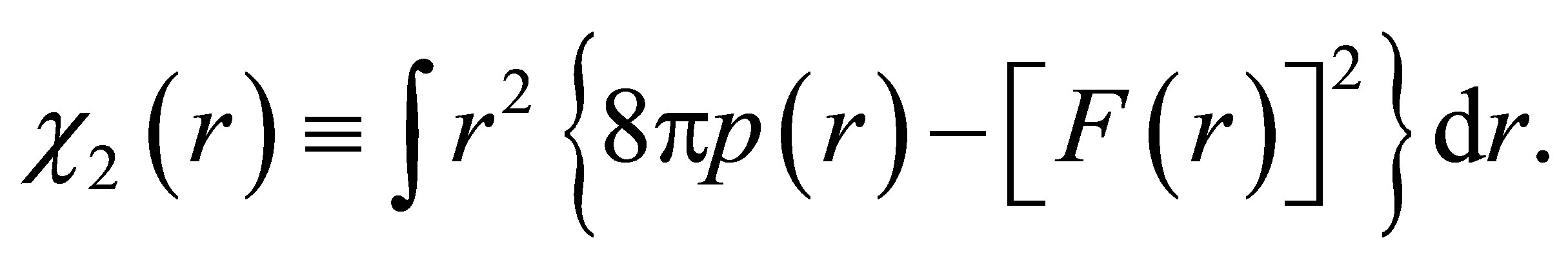 (23)
(23)
For a specific scenario, the metric function (22) may be written out in full as a polynomial in r and its behavior investigated for r1 ≤ r ≤ r2; requiring that f be well-behaved throughout this domain will yield constraints on (or estimates for) some of the object’s fundamental physical parameters such as charge, mass and radius. We note that if we generalize relation (17) to define the object’s global M-P charge as
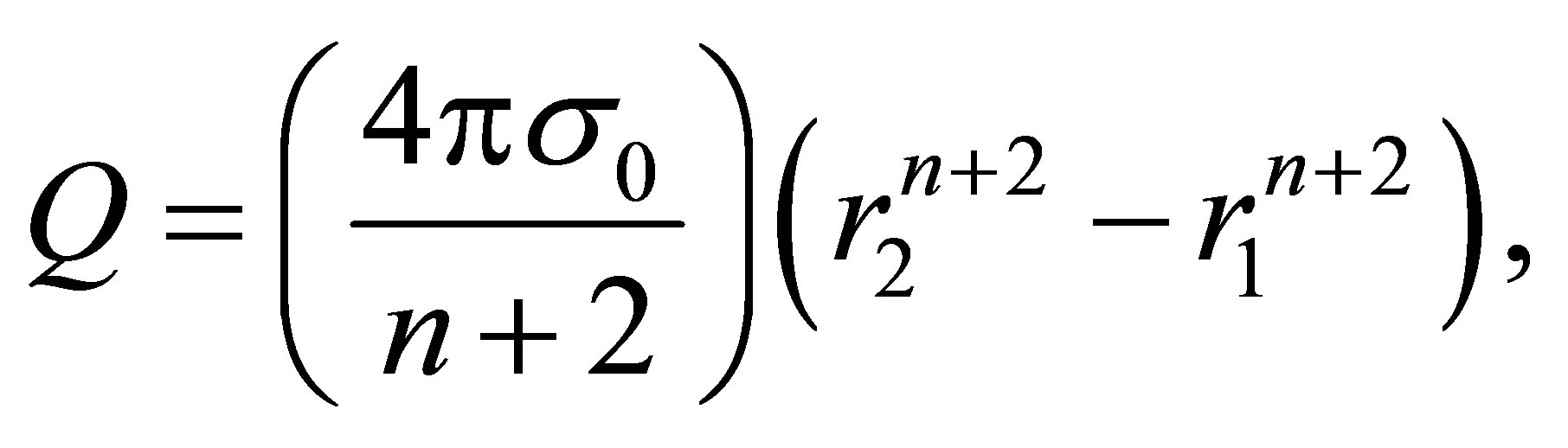 (24)
(24)
then, from relation (19), we obtain the somewhat unexpected result that any field exterior to a M-P charge distribution of the type considered here must fall off as F(r) ~ 1/r2, regardless of the behavior of the interior field; that is, for any and all values of n. Moreover, with the appropriate definition of σ0 and choice of n, this result is valid for both continuous and stratified charged-fluid objects. The interior metric may now be matched across r2 to the metric for another layer of material or, as for the continuous-fluid case, across the object’s surface to a Reissner-Nordstrøm metric; for the latter case, requiring that the object not fall through its Schwarzschild horizon (that is, R > rS) will then give additional constraints on some physical parameters which may be part of the object’s astrophysical signature. (For a detailed application of the techniques in this paragraph, the reader is invited to consult reference [1].)
Finally, examining relations (19)-(22), we conclude that for an unusual situation where the charge density increases with r, F will be an increasing function of r for any value of n > 0. However, n cannot be 2; and from relation (21), we expect that the pressure and density functions will become pathological for n >2. For this scenario, then, we are limited to n < 2. But if we add the requirement that charge density must be a decreasing function of r, this means that n ≤ 1; and since the M-P field will only be an increasing function as long as n is positive, the range of values for n is necessarily limited to 0 < n ≤ 1. We finish by noting that this still allows for a variety of solutions to be constructed; recall that relationships between fundamental quantities in the interiors of compact objects often involve fractional exponents!
4. Conclusions
For the case of a perfect-fluid object composed of (or containing) a global distribution of any non-interacting M-P charged particles, we have shown that physical considerations define the relationship between the charge density and the metric function uniquely, with the intuitively expected general results (originally derived for the specific case of an electrostatic distribution of charge) that the interior M-P field strength increases with r and the only possible behavior of the external field is the familiar inverse-square law.
However, if the charged fluid is confined to an envelope (of arbitrary thickness) surrounding a core of uncharged fluid, a wider range of models is possible. Specifically, for an interior field scaling as F(r) ~ rn, we found that n < 2 regardless of the behavior of the charge density; but if, as is physically most plausible, the charge density is required to be a decreasing function of r, the range of values for n is limited to 0 < n ≤ 1 (with n = 1 denoting the abovementioned special case of a continuous distribution of charge).
For both types of charge distribution, it turns out that the exterior field always decreases as 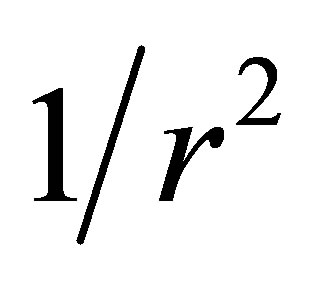 regardless of the interior field’s r-dependence (that is, regardless of the value of n); this of course means that, although it is a fundamental aspect of the object’s astrophysical signature, the exterior field cannot allow us to determine the behavior of the interior M-P charge distribution or of the interior field itself. Even so, by incorporating the detailed algebraic expressions developed here for fundamental quantities pertaining to the M-P fields and charges, the theoretical framework we have outlined may be used to construct complete general-relativistic models of hypothetical compact objects for a variety of interior fluid structures containing such fields.
regardless of the interior field’s r-dependence (that is, regardless of the value of n); this of course means that, although it is a fundamental aspect of the object’s astrophysical signature, the exterior field cannot allow us to determine the behavior of the interior M-P charge distribution or of the interior field itself. Even so, by incorporating the detailed algebraic expressions developed here for fundamental quantities pertaining to the M-P fields and charges, the theoretical framework we have outlined may be used to construct complete general-relativistic models of hypothetical compact objects for a variety of interior fluid structures containing such fields.
REFERENCES
- Z. Pazameta, “A Three-Layer Preon Star Model from Exact Piecewise-Continuous Solutions of Einstein’s Equations,” 2012. arXiv:1209.3355v1
- W. A. Zajc, Nuclear Physics A, Vol. 805, 2008, pp. 283- 294. http://dx.doi.org/10.1016/j.nuclphysa.2008.02.285
- F. I. Cooperstock and V. de la Cruz, General Relativity and Gravitation, Vol. 9, 1978, pp. 835-843. http://dx.doi.org/10.1007/BF00760872
- R. N. Tiwari, J. R. Rao and R. R. Kanakamedala, Physical Review D, Vol. 30, 1984, p. 489.
- Z. Pazameta, Astrophysics and Space Science, Vol. 339, 2012, pp. 317-322. http://dx.doi.org/10.1007/s10509-012-0996-7

