Journal of Modern Physics
Vol.4 No.6(2013), Article ID:33469,7 pages DOI:10.4236/jmp.2013.46119
Numerical Calculation of Normalization Factor for the Analysis of Azimuthal Asymmetry Amplitudes Related to Deeply Virtual Compton Scattering
A.I. Alikhanyan National Science Laboratory (Yerevan Physics Institute), Yerevan, Armenia
Email: maruk@mail.yerphi.am
Copyright © 2013 Hrachya H. Marukyan. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 21, 2013; revised April 1, 2013; accepted May 2, 2013
Keywords: GPDs; DVCS; Transversely Polarized Hydrogen Target
ABSTRACT
Numerical calculation of normalization factor in a maximum likelihood technique providing a bin-free fit in azimuthal angles to the data is presented. It can be used for simultaneous extraction of asymmetry amplitudes with respect to the combined dependence of the cross section of hard exclusive leptoproduction of real photons on transversely polarized protons on beam charge and helicity and target transverse polarization. This method of data processing can reveal previously unseparated contributions from deeply virtual Compton scattering and its interference with the Bethe-Heitler process.
1. Deeply Virtual Compton Scattering
Deeply virtual Compton scattering (DVCS) is one of the cleanest processes that used to constraint Generalized Parton Distributions (GPDs) [1-3] via Compton Form Factors (CFFs). Such CFFs are convolutions of corresponding GPDs with hard scattering coefficient functions.
The five-fold differential cross section for the exclusive leptoproduction of real photons from a transversely polarized hydrogen target reads [4]
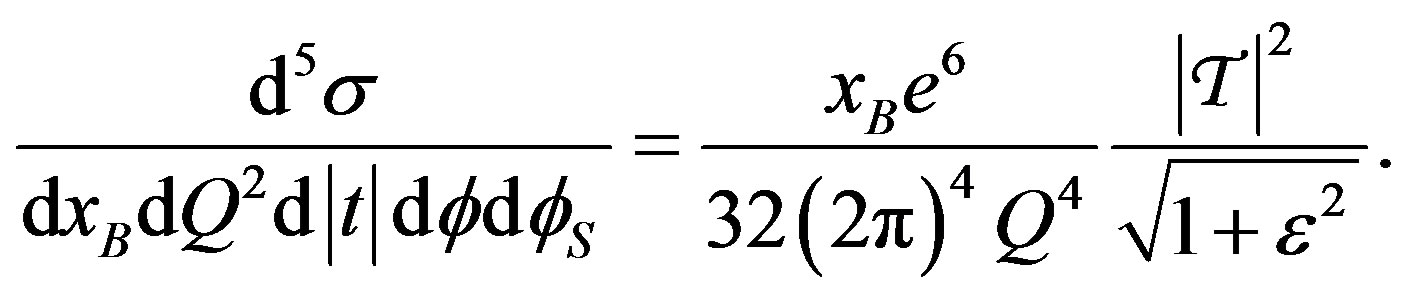 (1.1)
(1.1)
Here, e is the elementary charge, 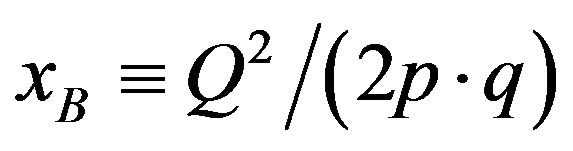 is the Bjorken scaling variable, where p is the proton’s four momentum and Q2 is the negative square of the fourmomentum of the virtual photon q that mediates the lepton-nucleon scattering process, t is the Mandelstam variable, which is the squared momentum transfer to the target nucleon,
is the Bjorken scaling variable, where p is the proton’s four momentum and Q2 is the negative square of the fourmomentum of the virtual photon q that mediates the lepton-nucleon scattering process, t is the Mandelstam variable, which is the squared momentum transfer to the target nucleon, 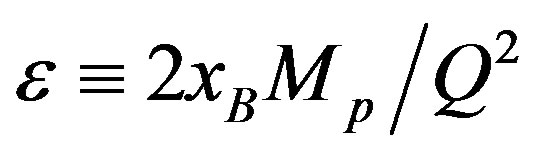 with Mp the proton mass and 𝒯 is the reaction amplitude. Two azimuthal angles 𝜙 and 𝜙S appear in the cross section in the case of transverse polarization of the target. The angle 𝜙 is defined as the angle between the lepton scattering plane and the real photon production plane, while the angle 𝜙S denotes the angle between the lepton scattering plane and the component of the target polarization vector orthogonal to the momentum of the virtual photon The initial and final states of the DVCS process are indistinguishable from those of the Bethe-Heitler (BH) process, which is elastic lepton-nucleon scattering with the emission of a bremsstrahlung photon by the lepton. Hence the cross section contains the coherent superposition of the BH and DVCS amplitudes:
with Mp the proton mass and 𝒯 is the reaction amplitude. Two azimuthal angles 𝜙 and 𝜙S appear in the cross section in the case of transverse polarization of the target. The angle 𝜙 is defined as the angle between the lepton scattering plane and the real photon production plane, while the angle 𝜙S denotes the angle between the lepton scattering plane and the component of the target polarization vector orthogonal to the momentum of the virtual photon The initial and final states of the DVCS process are indistinguishable from those of the Bethe-Heitler (BH) process, which is elastic lepton-nucleon scattering with the emission of a bremsstrahlung photon by the lepton. Hence the cross section contains the coherent superposition of the BH and DVCS amplitudes:
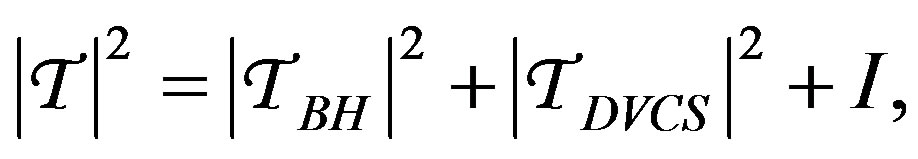 (1.2)
(1.2)
where  denotes the BHDVCS interference term. The BH amplitude is calculable to leading order in QED using the form factors measured in elastic scattering. The interference term I and the squared DVCS amplitude |𝒯DVCS|2 in Equation (1.2) provide experimental access to the (complex) DVCS amplitude through measurements of various cross-section asymmetries [4].
denotes the BHDVCS interference term. The BH amplitude is calculable to leading order in QED using the form factors measured in elastic scattering. The interference term I and the squared DVCS amplitude |𝒯DVCS|2 in Equation (1.2) provide experimental access to the (complex) DVCS amplitude through measurements of various cross-section asymmetries [4].
Each of the three terms of Equation (1.2) can be decomposed as a Fourier series:
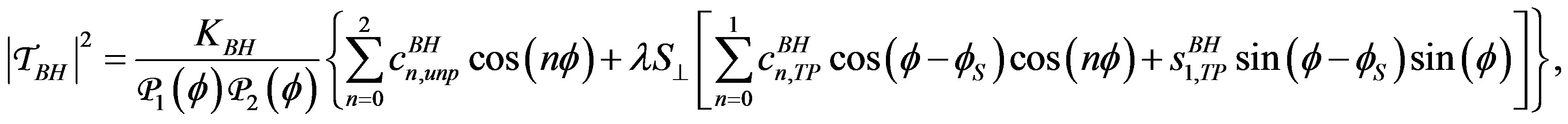 (1.3)
(1.3)
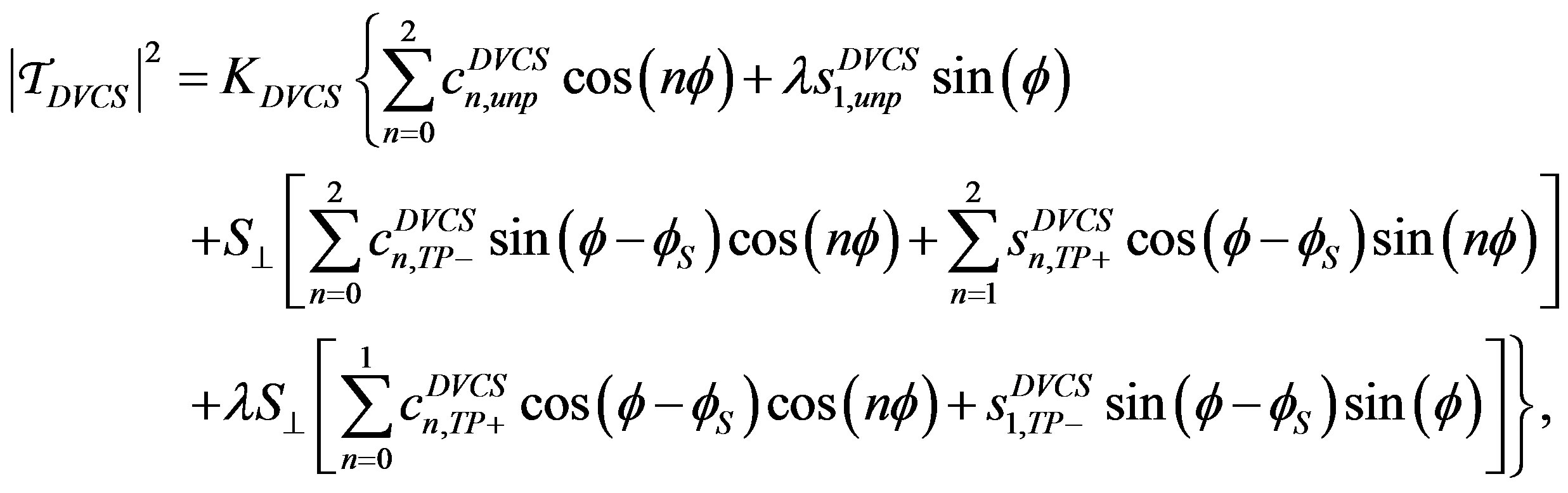 (1.4)
(1.4)
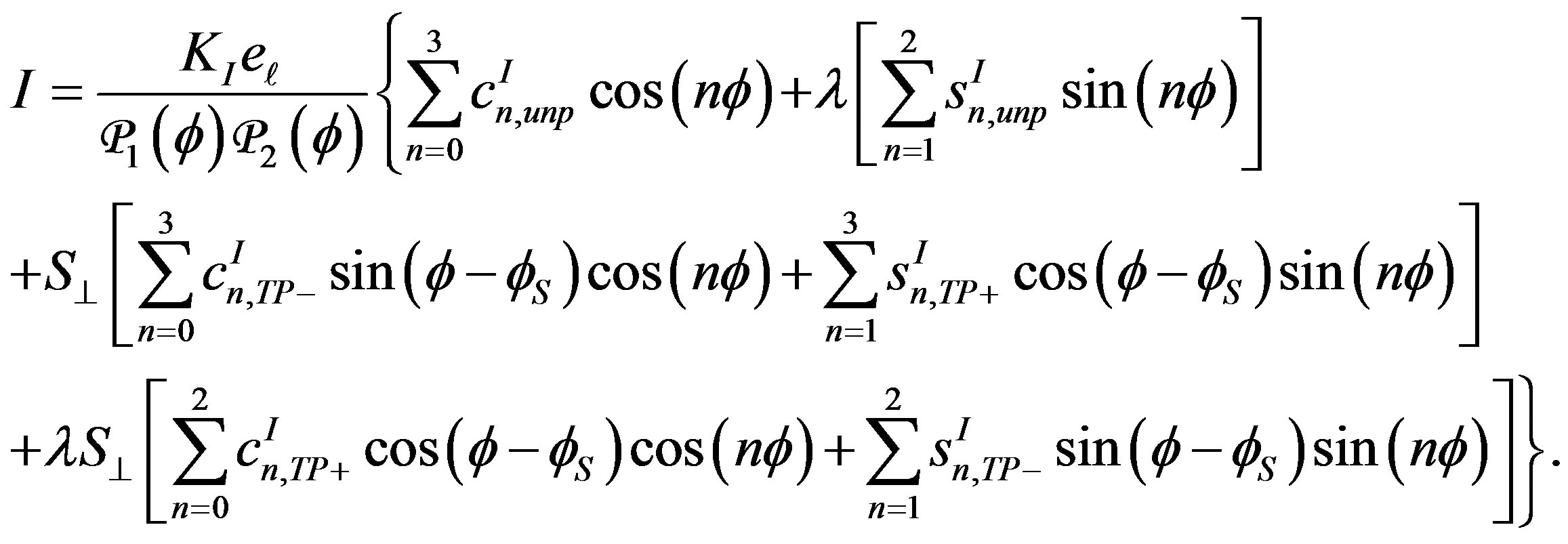 (1.5)
(1.5)
The symbols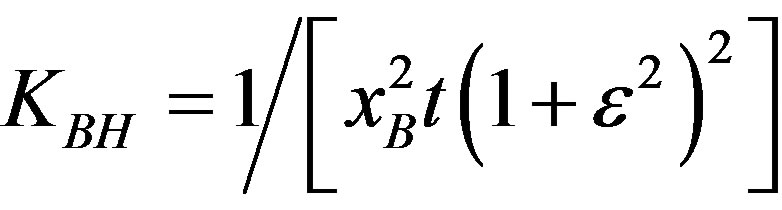 ,
, 
and  denote kinematic factors, where y is the fraction of the beam energy carried by the virtual photon in the target rest frame and eℓ stands for the (signed) lepton charge in units of the elementary charge. Also, λ = ±1 and S⊥ are respectively the helicity of the lepton beam and the magnitude of the component of the target polarization vector that is orthogonal to the direction of the virtual photon. The subscript “TP” is used for BH terms, while the subscript “TP+” (“TP−”) is used for DVCS and interference terms containing cos(𝜙 − 𝜙S) (sin(𝜙−𝜙S)). The BH coefficients
denote kinematic factors, where y is the fraction of the beam energy carried by the virtual photon in the target rest frame and eℓ stands for the (signed) lepton charge in units of the elementary charge. Also, λ = ±1 and S⊥ are respectively the helicity of the lepton beam and the magnitude of the component of the target polarization vector that is orthogonal to the direction of the virtual photon. The subscript “TP” is used for BH terms, while the subscript “TP+” (“TP−”) is used for DVCS and interference terms containing cos(𝜙 − 𝜙S) (sin(𝜙−𝜙S)). The BH coefficients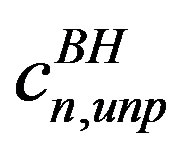 ,
,  and
and  in Equation (1.3) depend on electromagnetic elastic form factors of the target, while the DVCS (interference)
in Equation (1.3) depend on electromagnetic elastic form factors of the target, while the DVCS (interference)
coefficients 
 ,
, 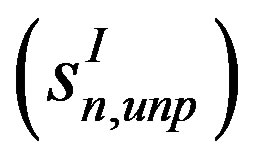
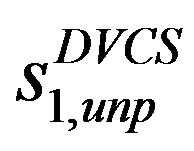 ,
, 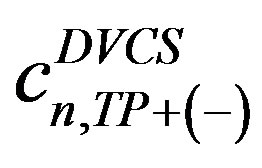
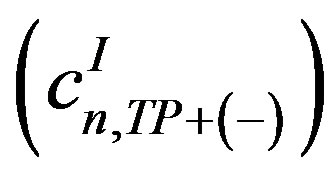 and
and 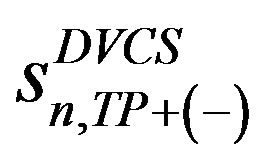
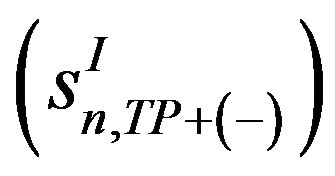 involve various GPDs. The squared BH and interference terms in Equation (1.3) and Equation (1.5) have an additional 𝜙 dependence in the denominator due to the lepton propagators 𝒫1(𝜙) and 𝒫2(𝜙) [4,5]. The Fourier coefficients appearing in the interference term can be expressed as linear combinations of CFFs [4], while the coefficients from the squared DVCS term are bilinear in the CFFs.
involve various GPDs. The squared BH and interference terms in Equation (1.3) and Equation (1.5) have an additional 𝜙 dependence in the denominator due to the lepton propagators 𝒫1(𝜙) and 𝒫2(𝜙) [4,5]. The Fourier coefficients appearing in the interference term can be expressed as linear combinations of CFFs [4], while the coefficients from the squared DVCS term are bilinear in the CFFs.
The coefficients of particular interest in Ref. [6] were ,
,  ,
, 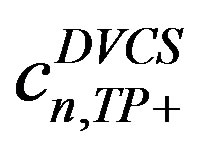 ,
, 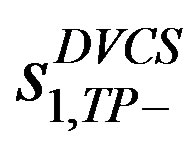 ,
, 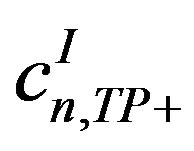 and
and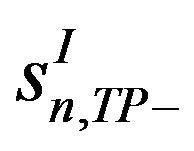 , which relate the double-spin asymmetries involving transverse target polarization. (The dependences of beam-charge and charge-difference or charge-averaged single-spin asymmetry amplitudes on remaining Fourier coefficients in Equations (1.3)-(1.5) were discussed in previously published HERMES papers [7-10]). The leading (twisttwo) coefficients
, which relate the double-spin asymmetries involving transverse target polarization. (The dependences of beam-charge and charge-difference or charge-averaged single-spin asymmetry amplitudes on remaining Fourier coefficients in Equations (1.3)-(1.5) were discussed in previously published HERMES papers [7-10]). The leading (twisttwo) coefficients ,
, 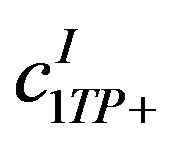 and
and 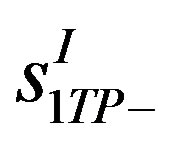 can be approximated as [4]
can be approximated as [4]
 (1.6)
(1.6)
 (1.7)
(1.7)
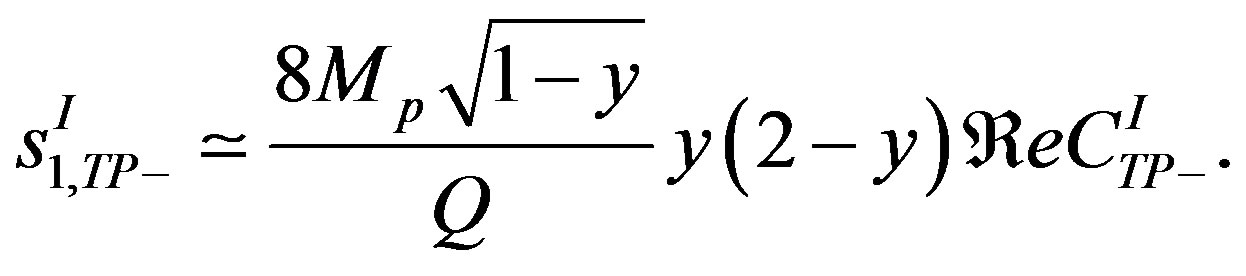 (1.8)
(1.8)
Here, K is a kinematic factor and the C-functions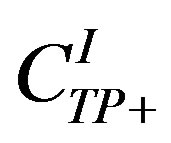 ,
, 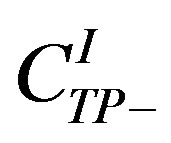 and
and 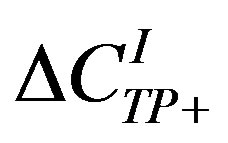 can be expressed as linear combination of four CFFs (H , Ε ,
can be expressed as linear combination of four CFFs (H , Ε ,  and
and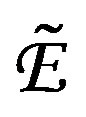 ) and the Dirac and Pauli electromagnetic form factors F1 and F2, respectively:
) and the Dirac and Pauli electromagnetic form factors F1 and F2, respectively:
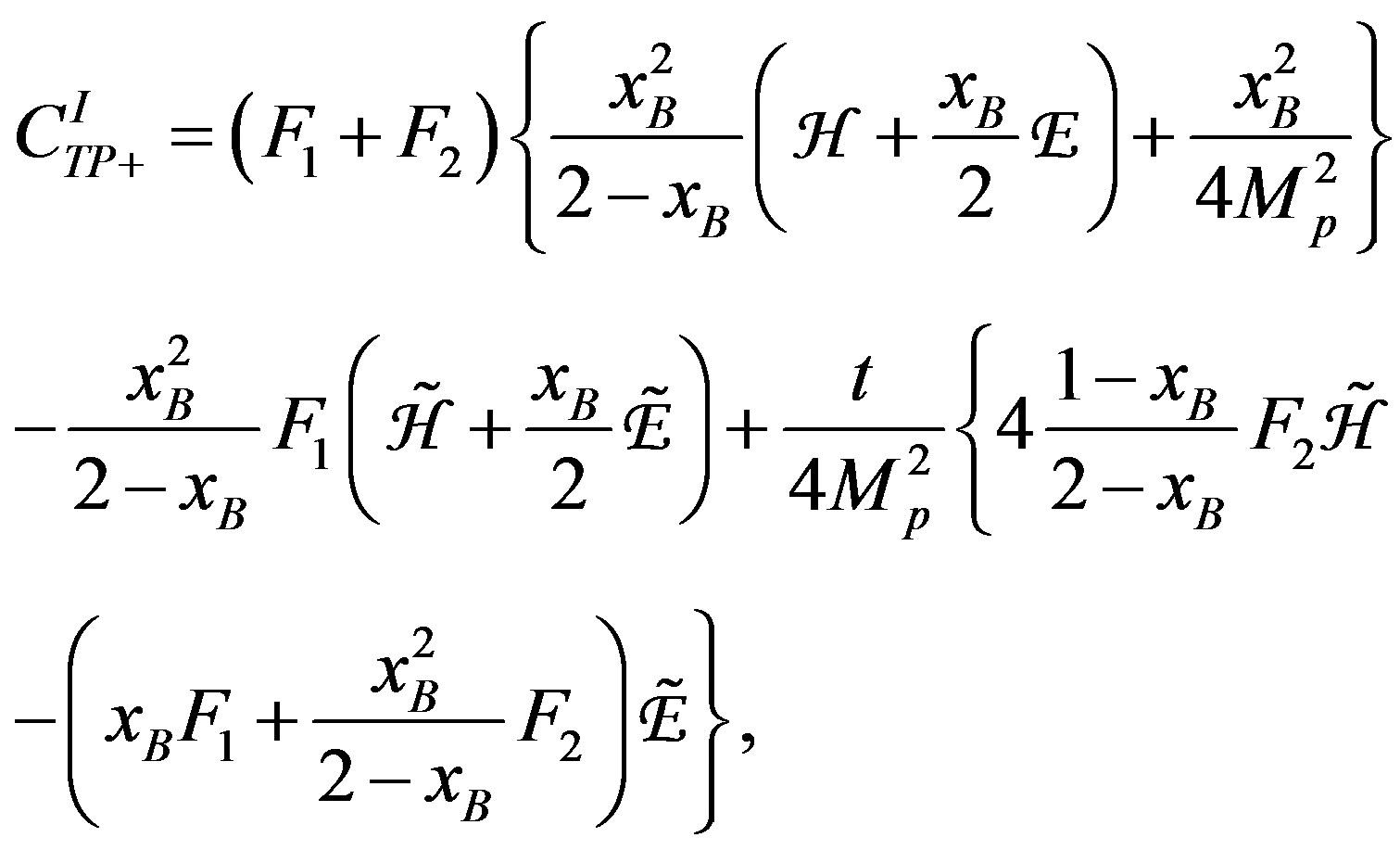 (1.9)
(1.9)
 (1.10)
(1.10)
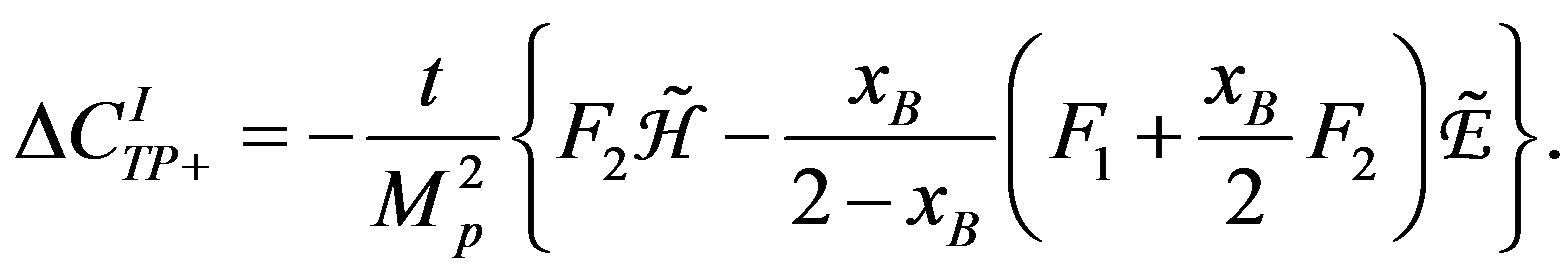 (1.11)
(1.11)
Note that even if the cross sections were measured for all eight possible combinations of beam charge and helicity and target polarization, at fixed Q2 it would still be impossible to separate the coefficients 
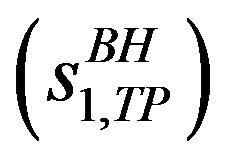 and
and 
 . Nevertheless, the BH coefficients can be calculated from the measured elastic form factors.
. Nevertheless, the BH coefficients can be calculated from the measured elastic form factors.
2. Azimuthal Asymmetries
The asymmetry in the cross section of a longitudinally polarized electron/positron beam off a transversely polarized hydrogen target, which embodies the essential features of the Fourier coefficients in Equations (1.3)- (1.5), can be defined through
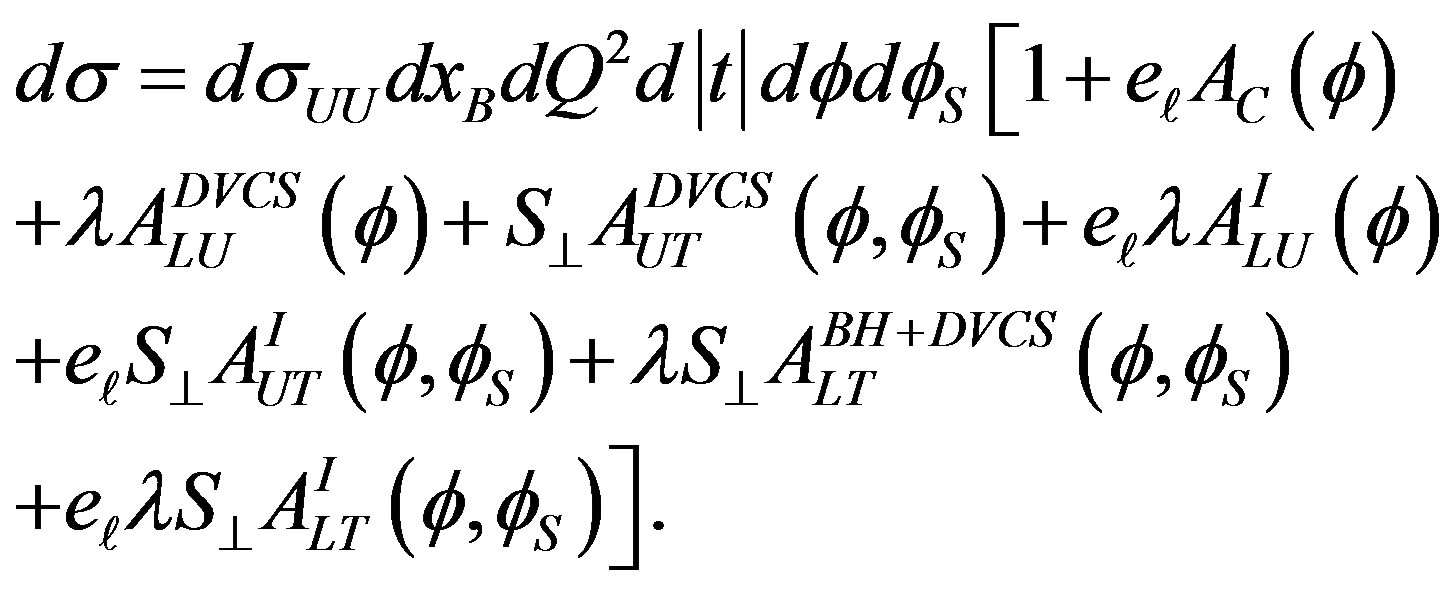 (2.1)
(2.1)
Here, dσUU is the differential cross section of production of real photons from scattering of an unpolarized lepton beam on an unpolarized hydrogen target averaged over both beam charges. The seven asymmetries presented in Equation (2.1) are defined as
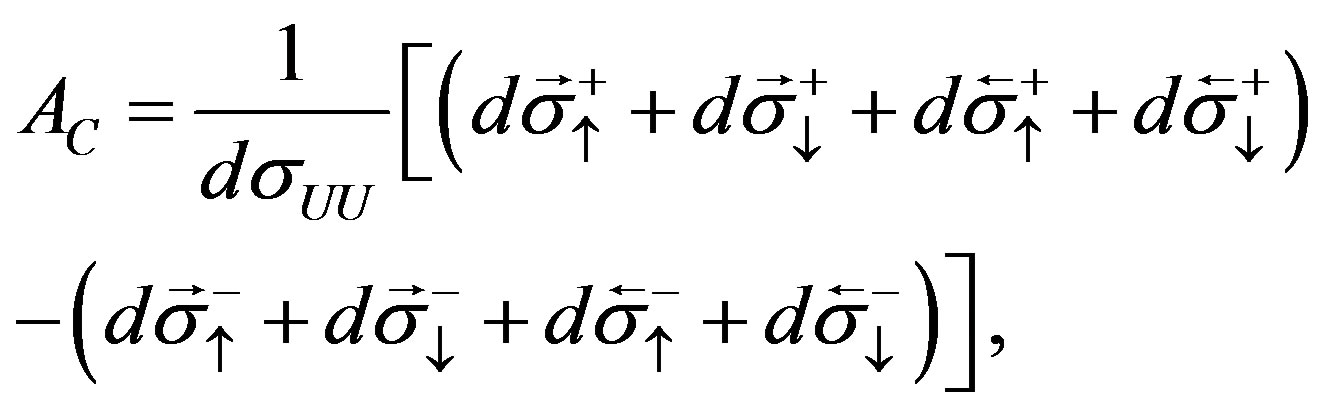 (2.2)
(2.2)

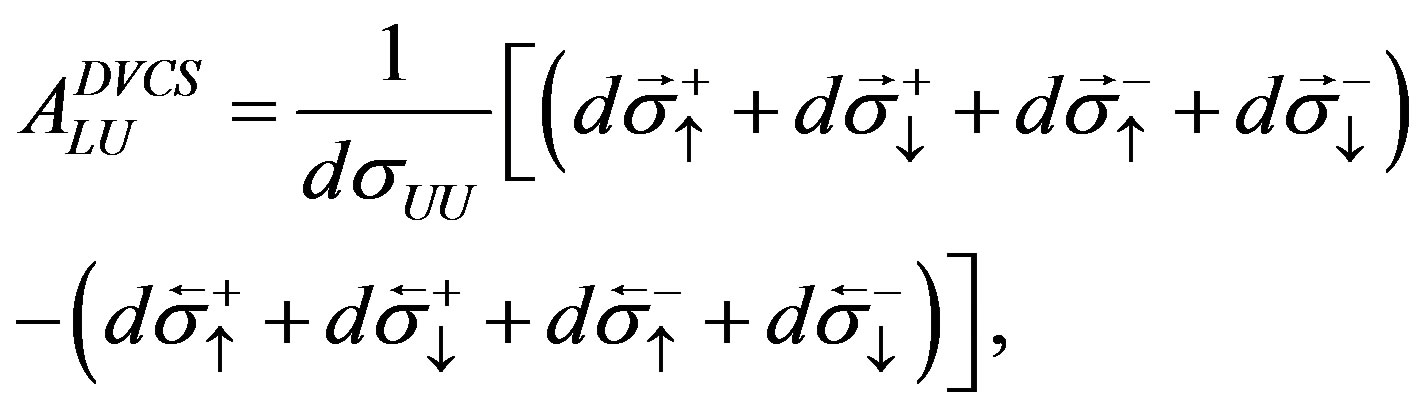 (2.3)
(2.3)

 (2.4)
(2.4)

 (2.5)
(2.5)

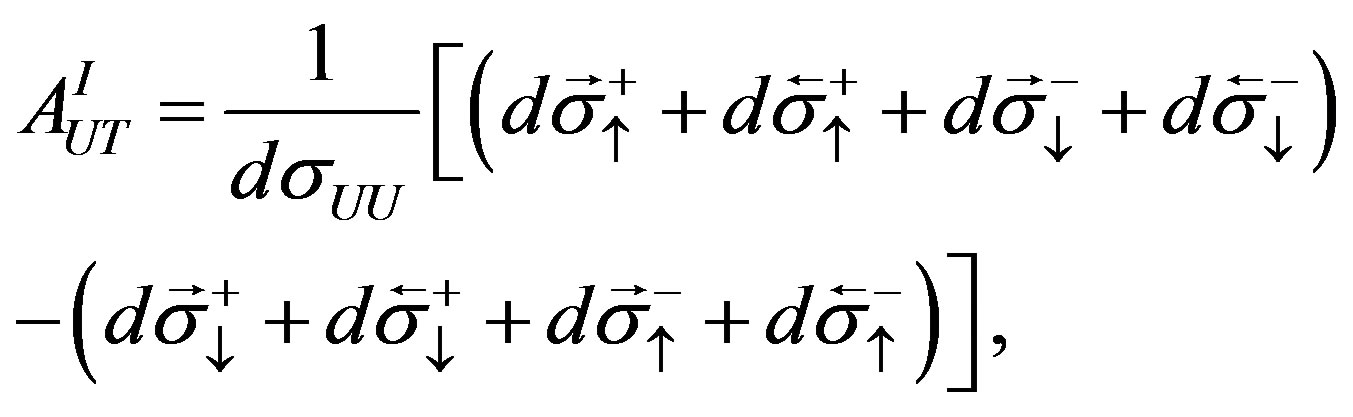 (2.6)
(2.6)
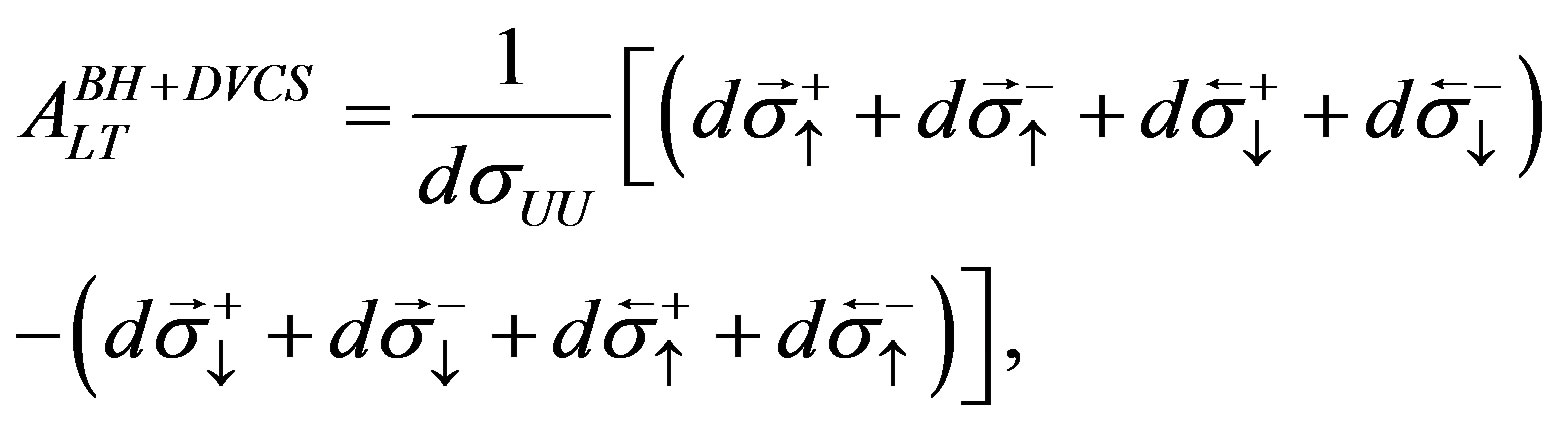 (2.7)
(2.7)
 (2.8)
(2.8)
where the + (−) sign stands for lepton charge and horizontal (vertical) arrows for beam (target) polarization states. The experimentally measured quantities are the trigonometric cos(n𝜙) and sin(n𝜙) moments (amplitudes) of the above defined asymmetries
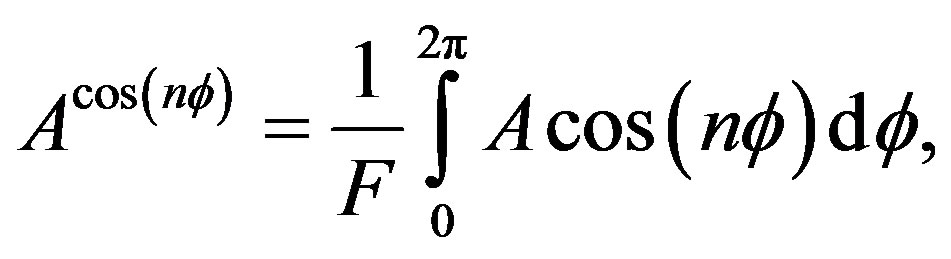 (2.9)
(2.9)
 (2.10)
(2.10)
Here, F is the normalization factor and is equal to 2𝜋 when n = 0, and 𝜋 when n > 1.
When extracting the asymmetry amplitudes from the real experiment, one deals with the measured beam and target polarization values, which are not equal to ±1. Moreover, they can be different for different data sets. In order to account for these imbalances in the luminosityaveraged beam and target polarization values an appropriate normalization needs to be applied. In this case the distribution in the expectation value of the measured yield can be written through the integrated luminosity ℒ and values of the beam and target polarization Pℓ and ST. The number of events dN in a small time period dτ and phase-space interval dx = dQ2dxBd|t|d𝜙d𝜙S can be written as
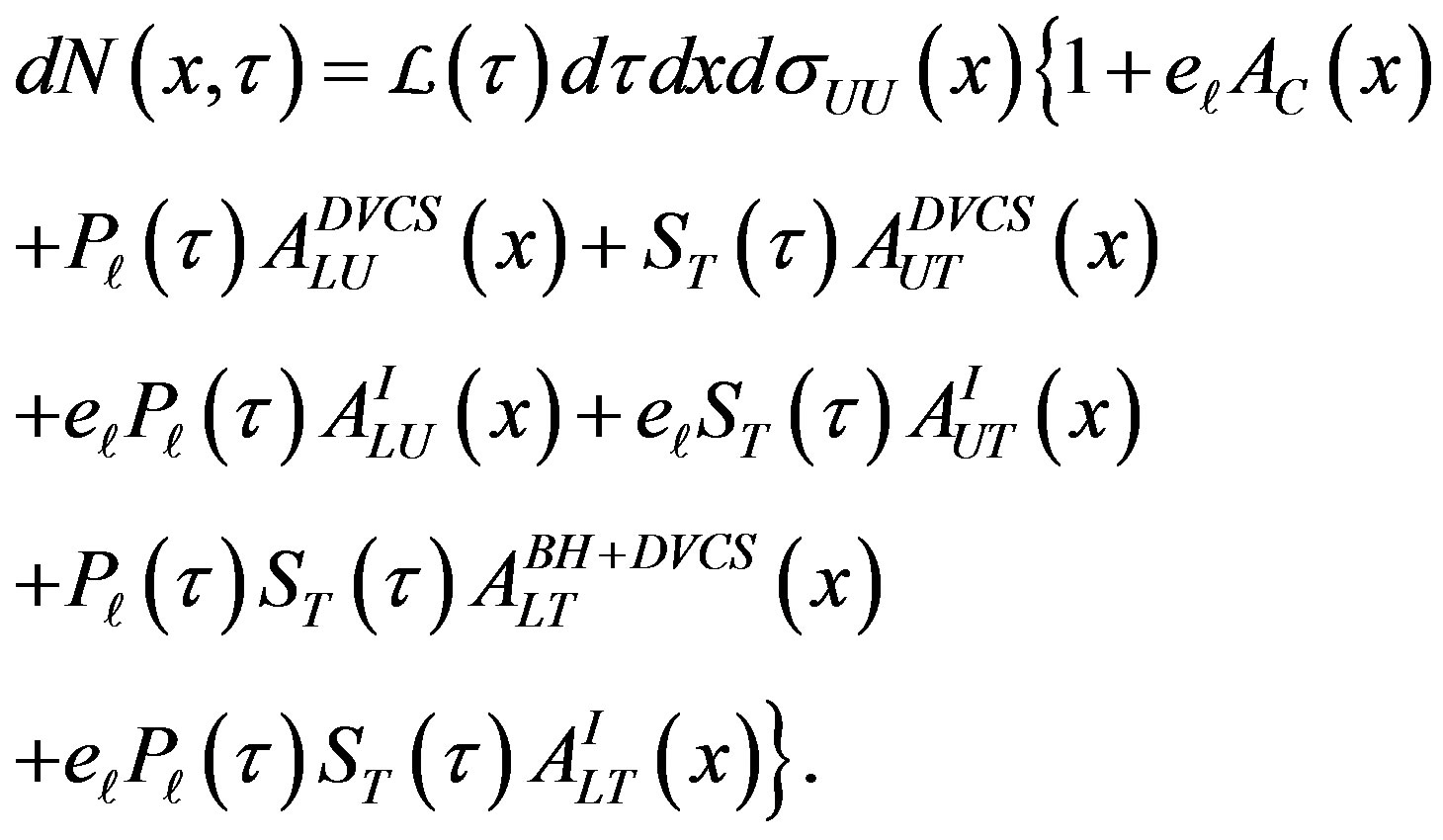 (2.11)
(2.11)
It is convenient to introduce an effective charge Peff as a product of beam charge with beam and target polarization Peff = eℓ Pℓ ST and change an integration variable from time τ to effective charge Peff, then integration of Equation (2.11) over Peff for different states gives
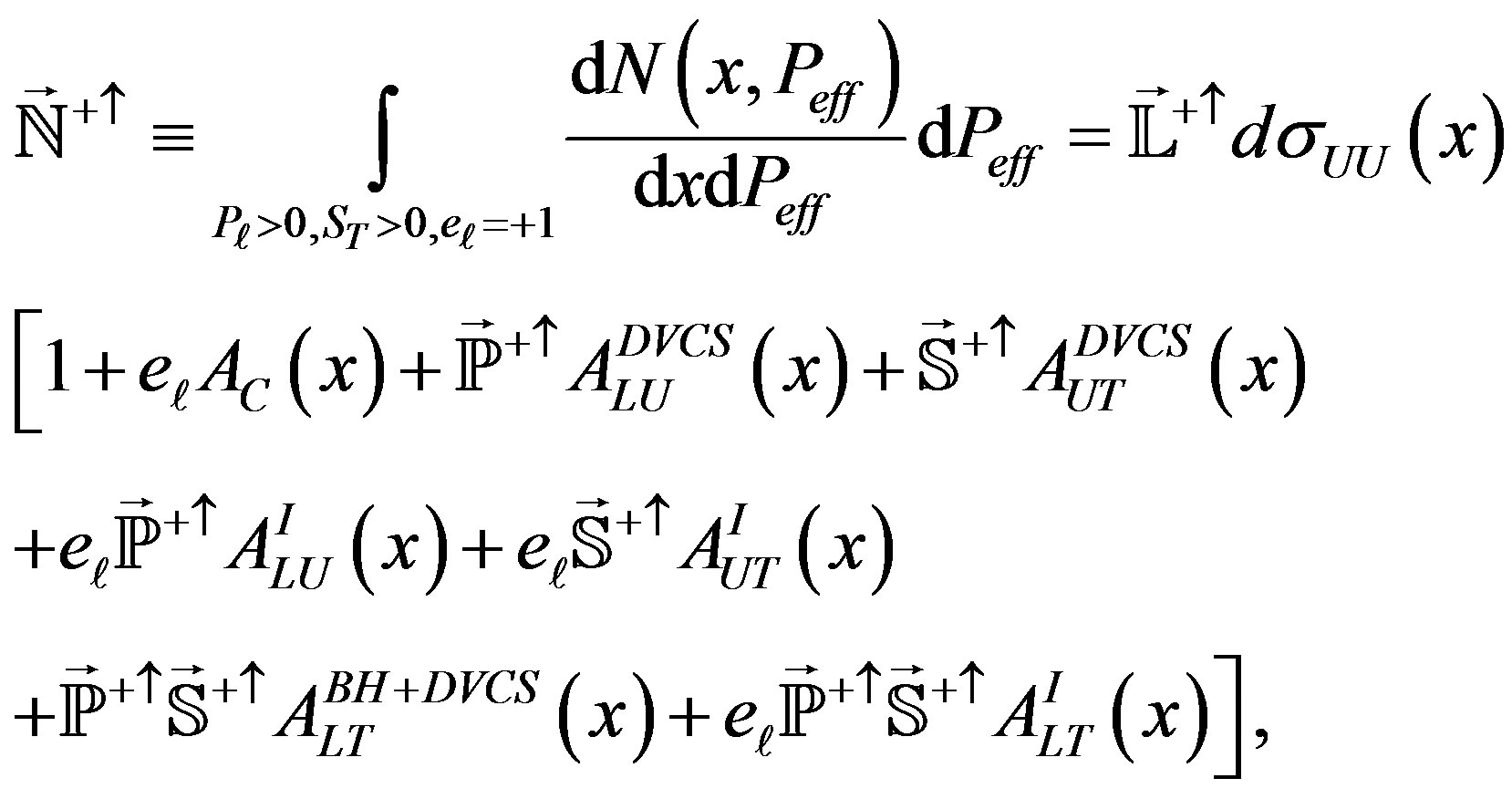 (2.12)
(2.12)
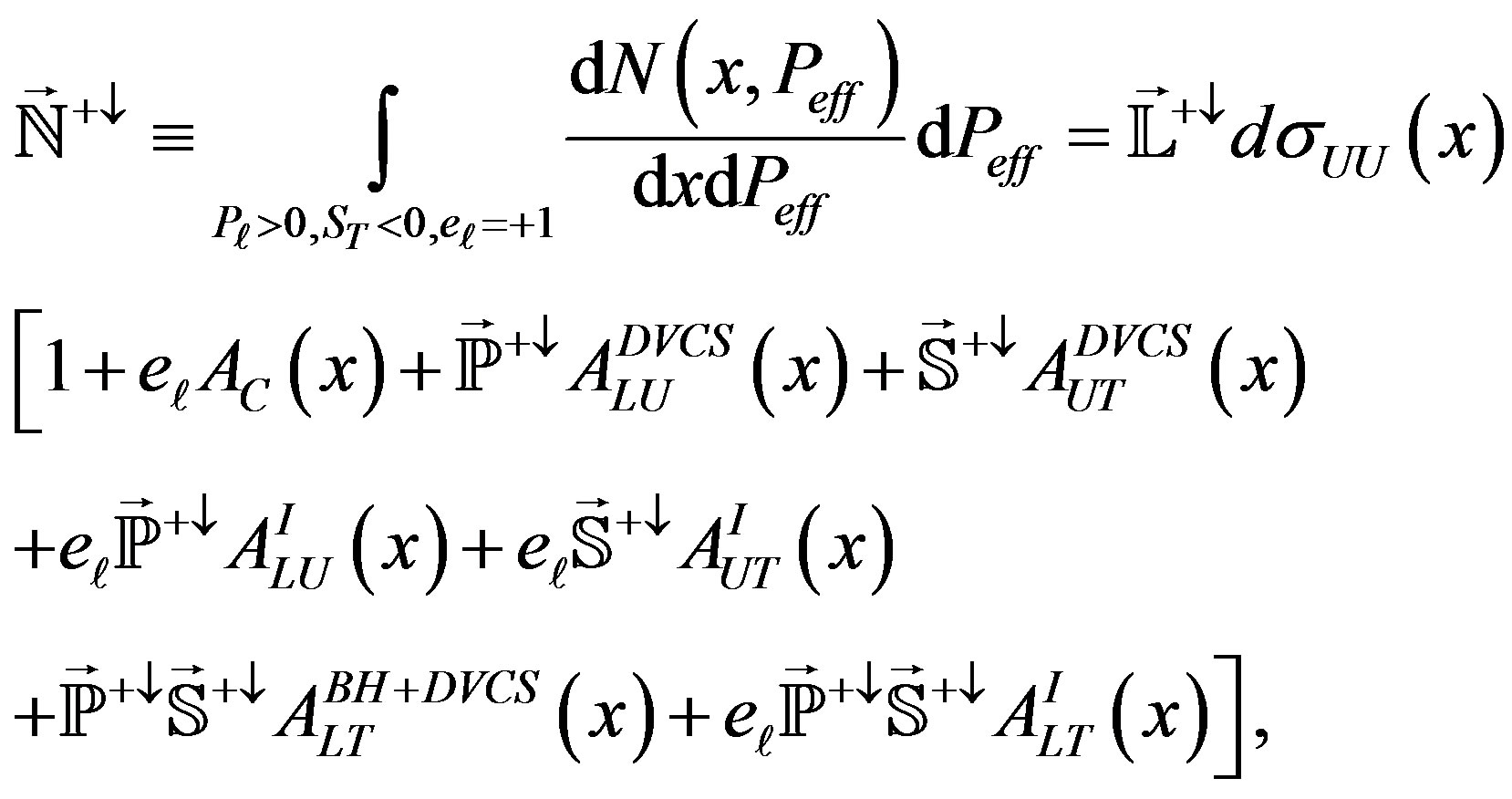 (2.13)
(2.13)
 (2.14)
(2.14)
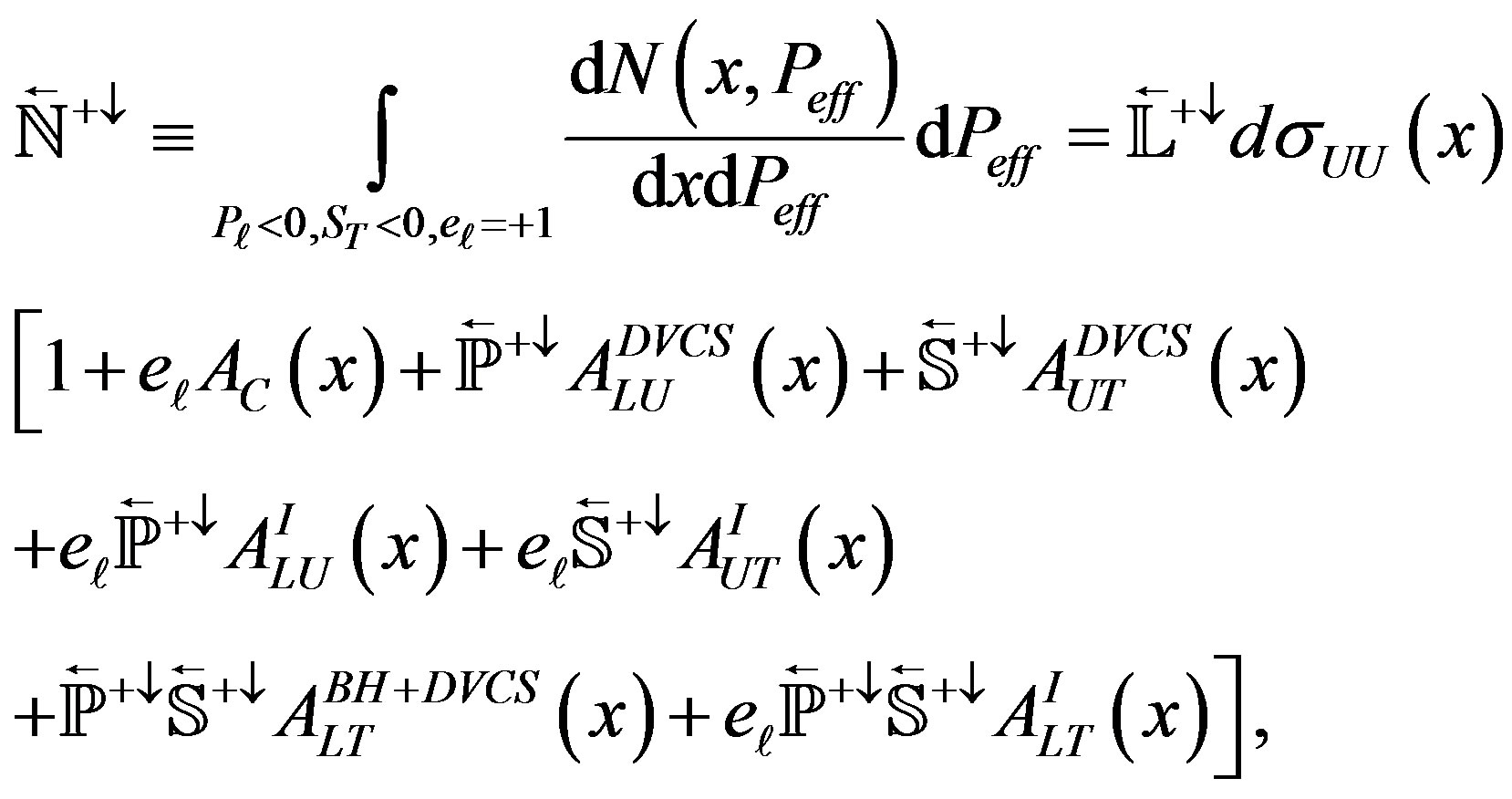 (2.15)
(2.15)
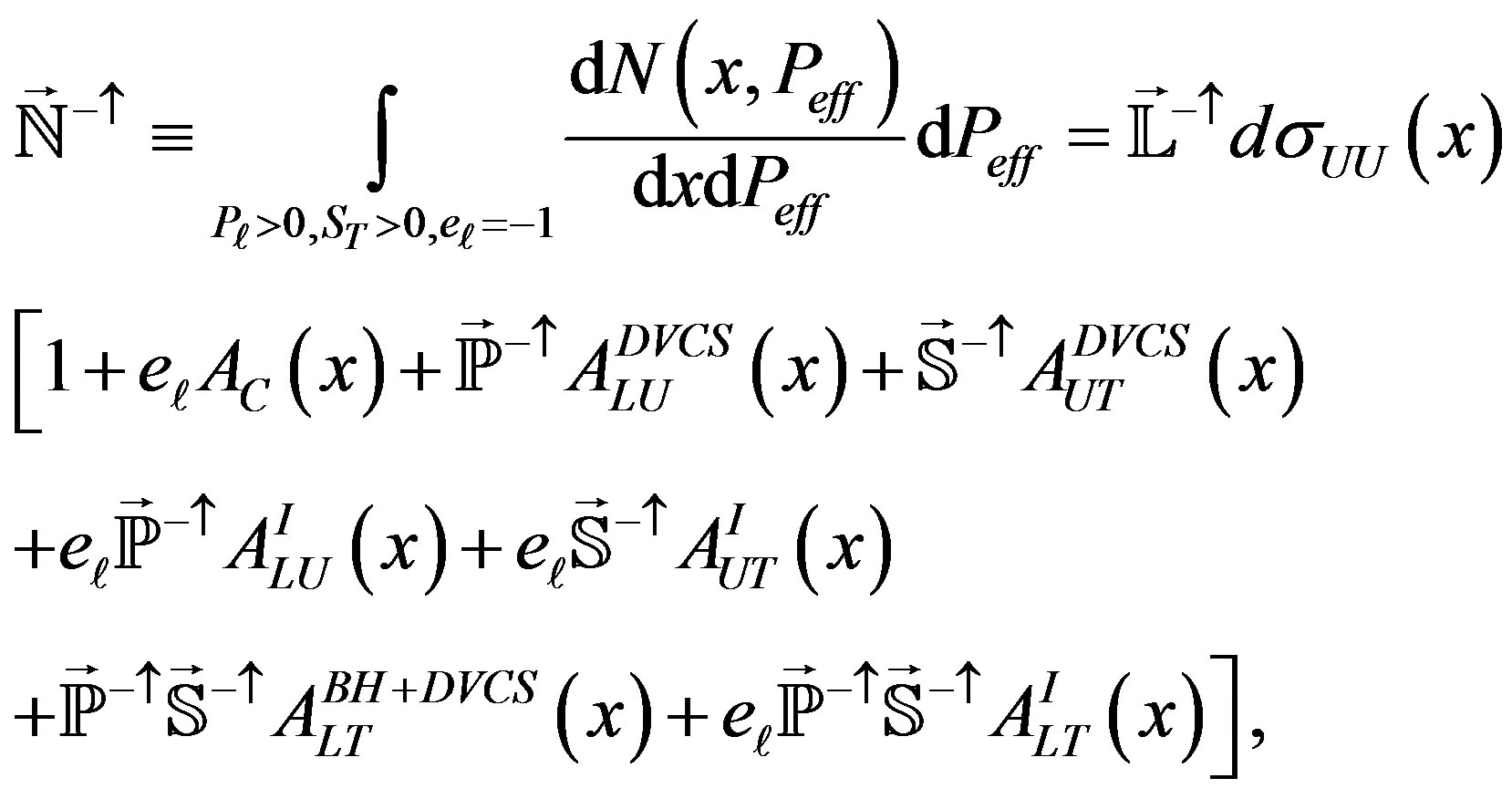 (2.16)
(2.16)
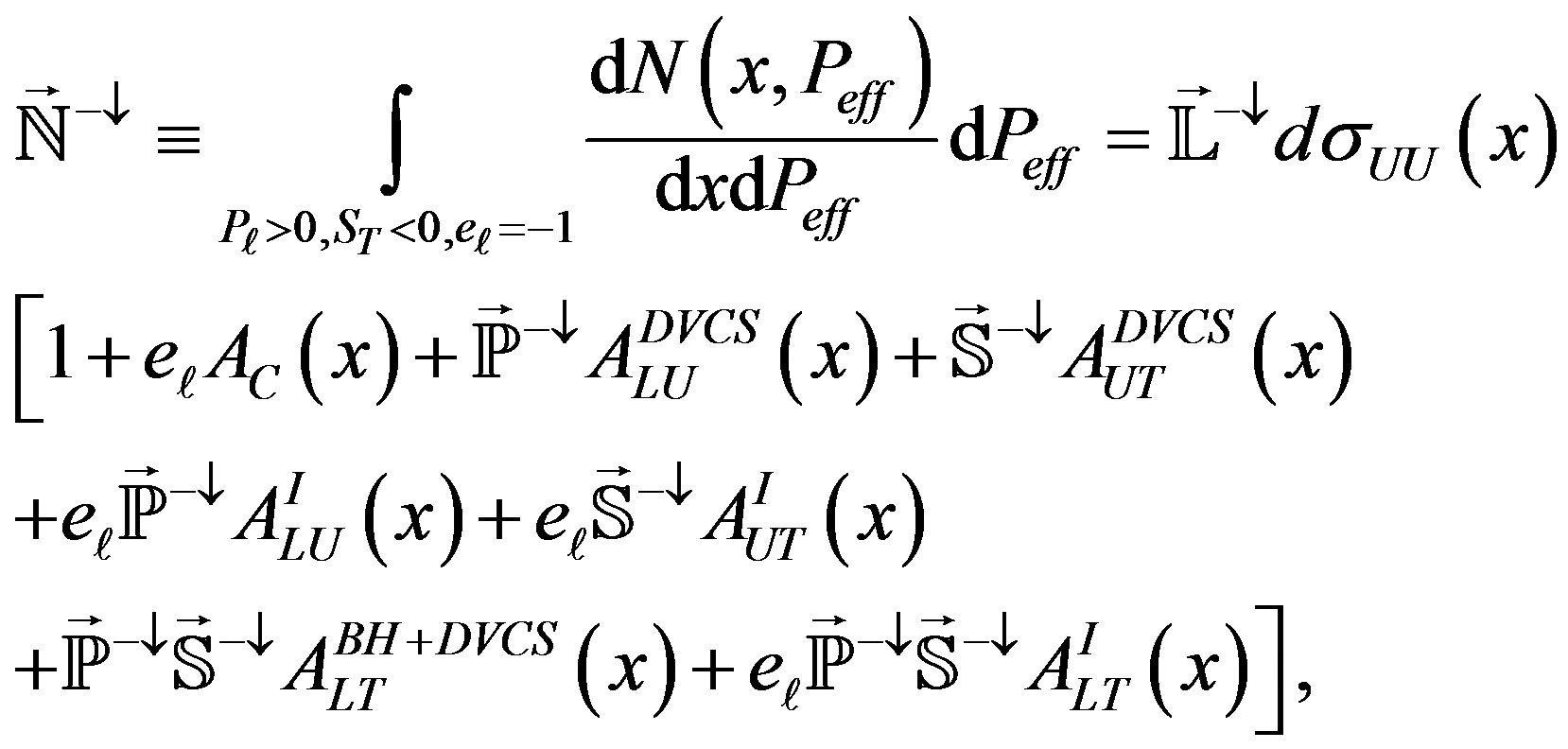 (2.17)
(2.17)
 (2.18)
(2.18)
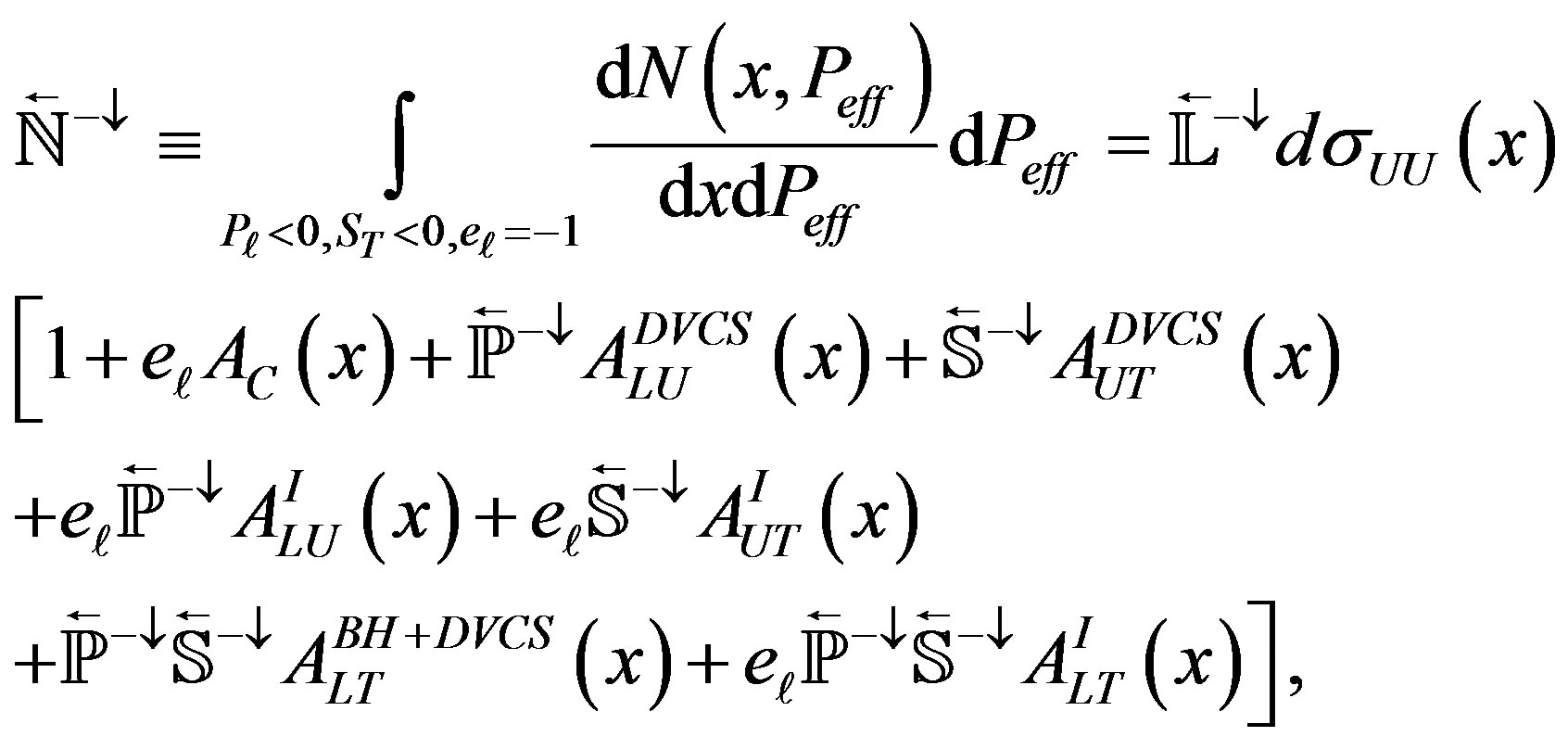 (2.19)
(2.19)
where 𝕃 is the integrated luminosity for the given state (configuration of beam charge and beam (target) polarization), ℕ is the corresponding yield in a small phasespace interval, and ℙ and 𝕊 respectively are luminosityaveraged beam and target polarizations for given states. Since in the analyzed data sample the polarization value was not varying to much the averaged value |𝕊| = 0.721 was used for all states.
Resolving the system of Equations (2.12)-(2.19), one can represent the unpolarized cross section dσUU and seven asymmetries through the luminosity normalized yields n = ℕ/𝕃 for each state and polarization values ℙ and 𝕊. The analytical solution can be approximated by numerical methods using the measured values for the beam/target polarizations for the various helisity states as input. For example, taking into account the measured values of the beam and target polarization for data used in the analysis of DVCS process on transversely polarized hydrogen target at HERMES (see Table 1) one can get
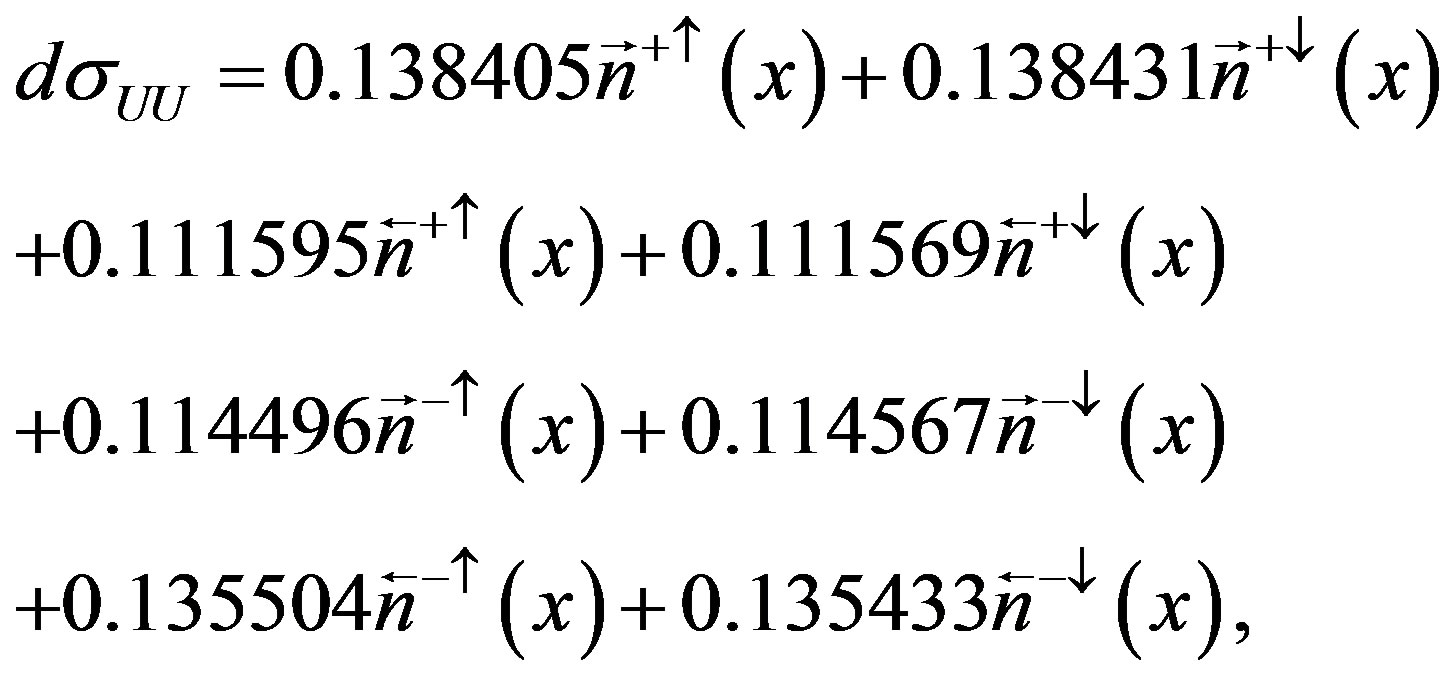 (2.20)
(2.20)
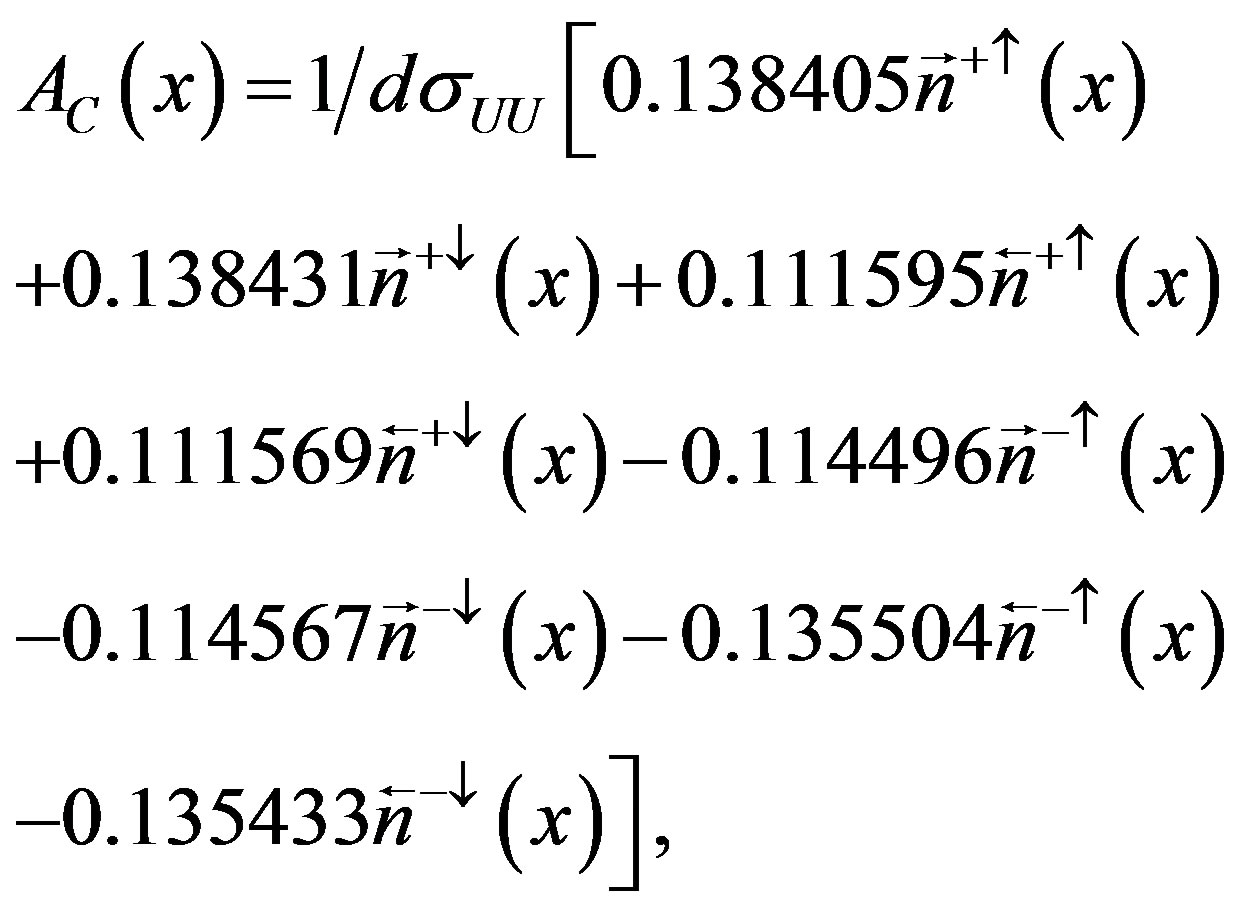 (2.21)
(2.21)
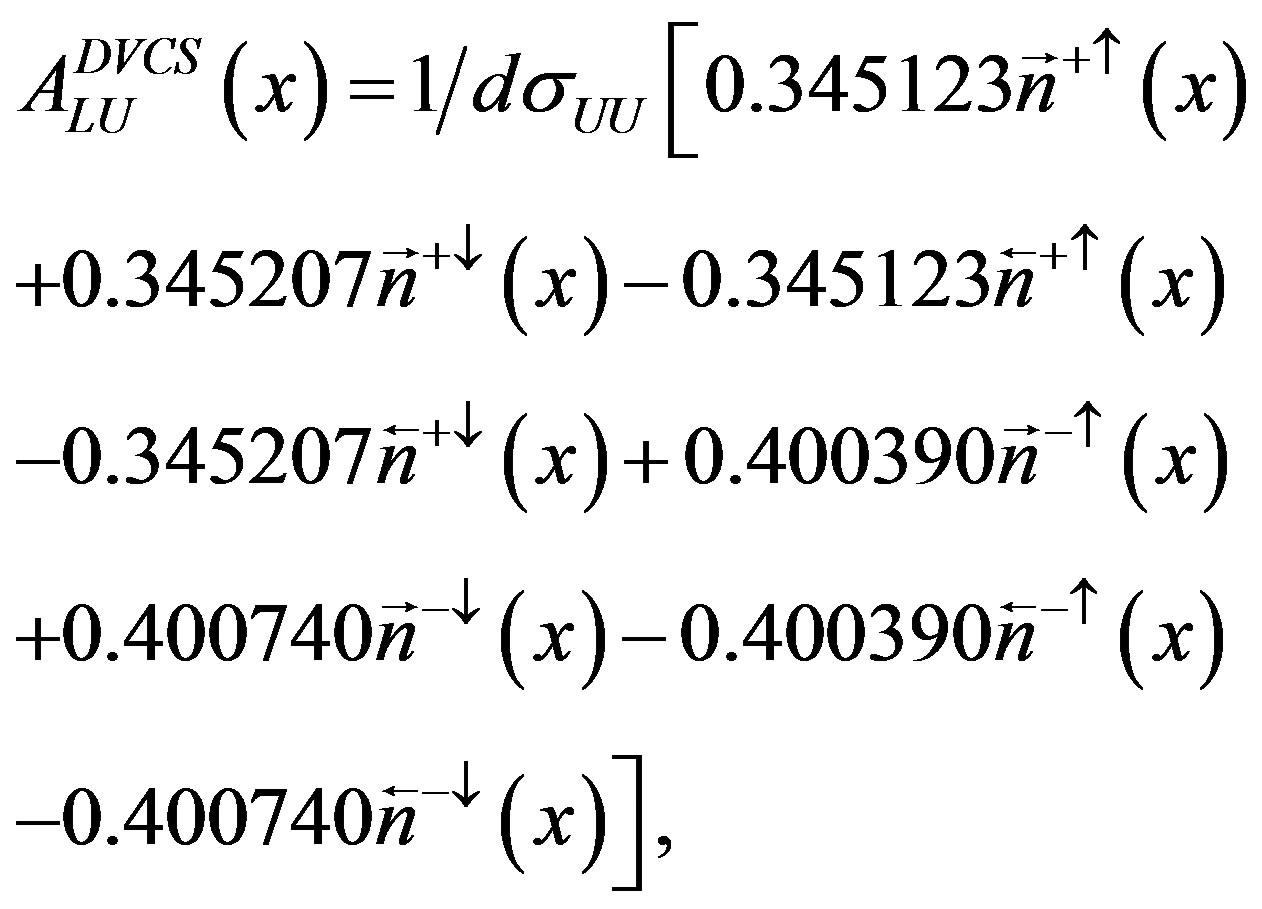 (2.22)
(2.22)
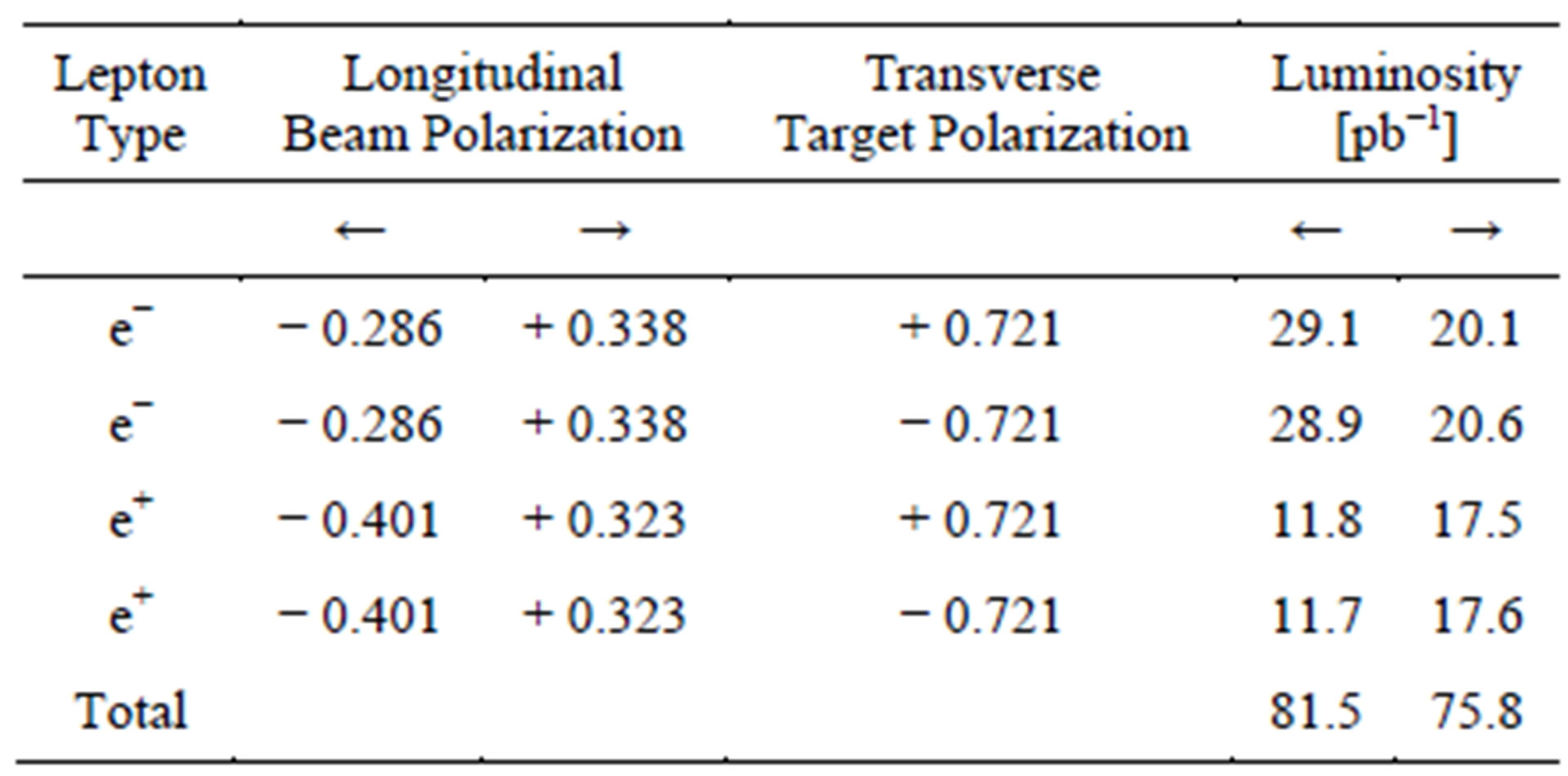
Table 1. The type of the beam particle, the luminosity-averaged beam and target polarizations and the integrated luminosity of the data sets used for the extraction of the various asymmetry amplitudes on a transversely polarized hydrogen target at HERMES experiment [6]. The data were taken with an e+ beam during the years 2003 (6.9 pb−1) and 2004 (51.7 pb−1) and an e− beam during 2005 (98.7 pb−1). The uncertainties for the beam and target polarizations are 2.2% and 8.3%, respectively.
 (2.23)
(2.23)
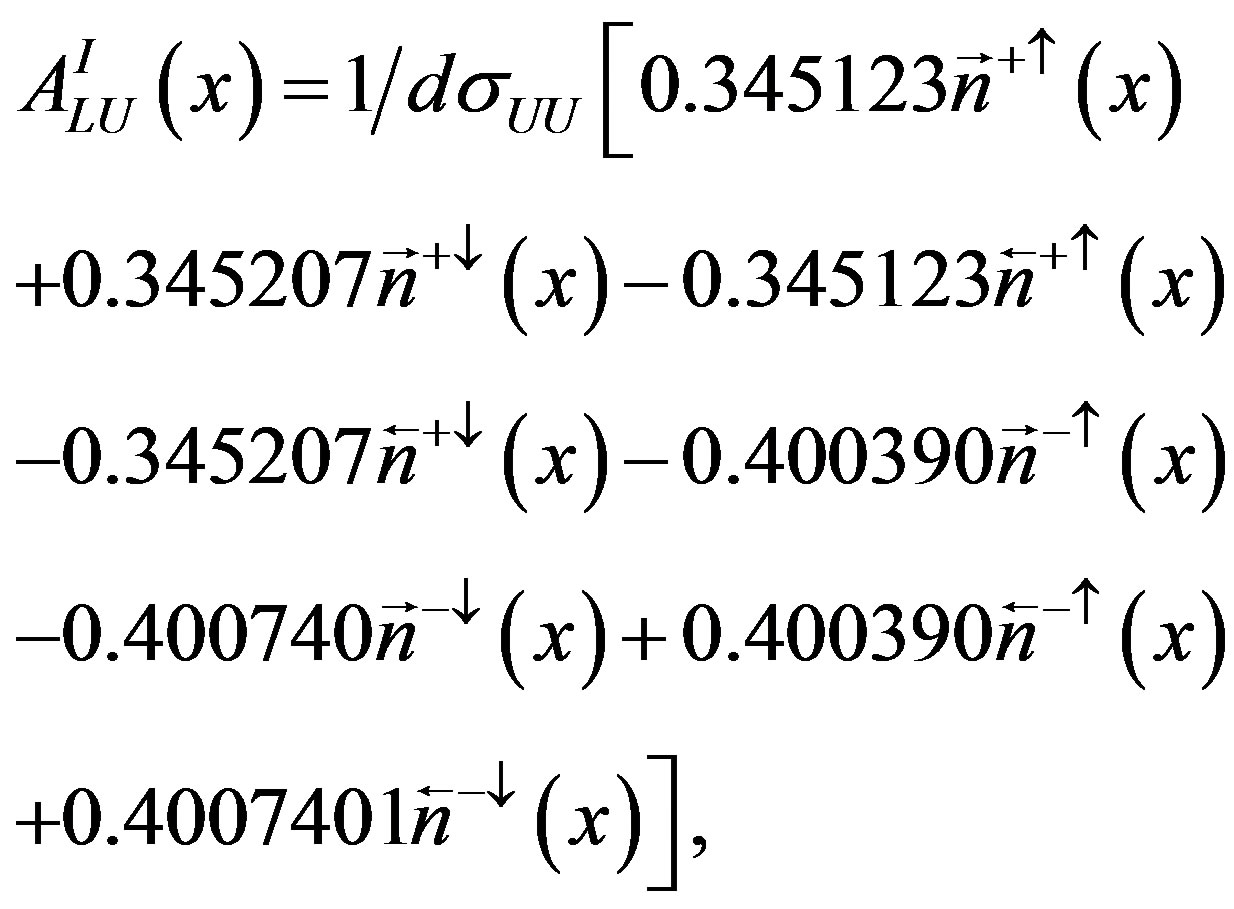 (2.24)
(2.24)
 (2.25)
(2.25)
 (2.26)
(2.26)
 (2.27)
(2.27)
 (2.28)
(2.28)
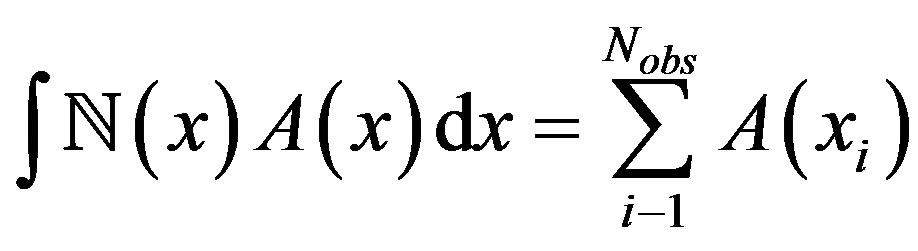 (2.29)
(2.29)
will give the total numbers of events or the normalization
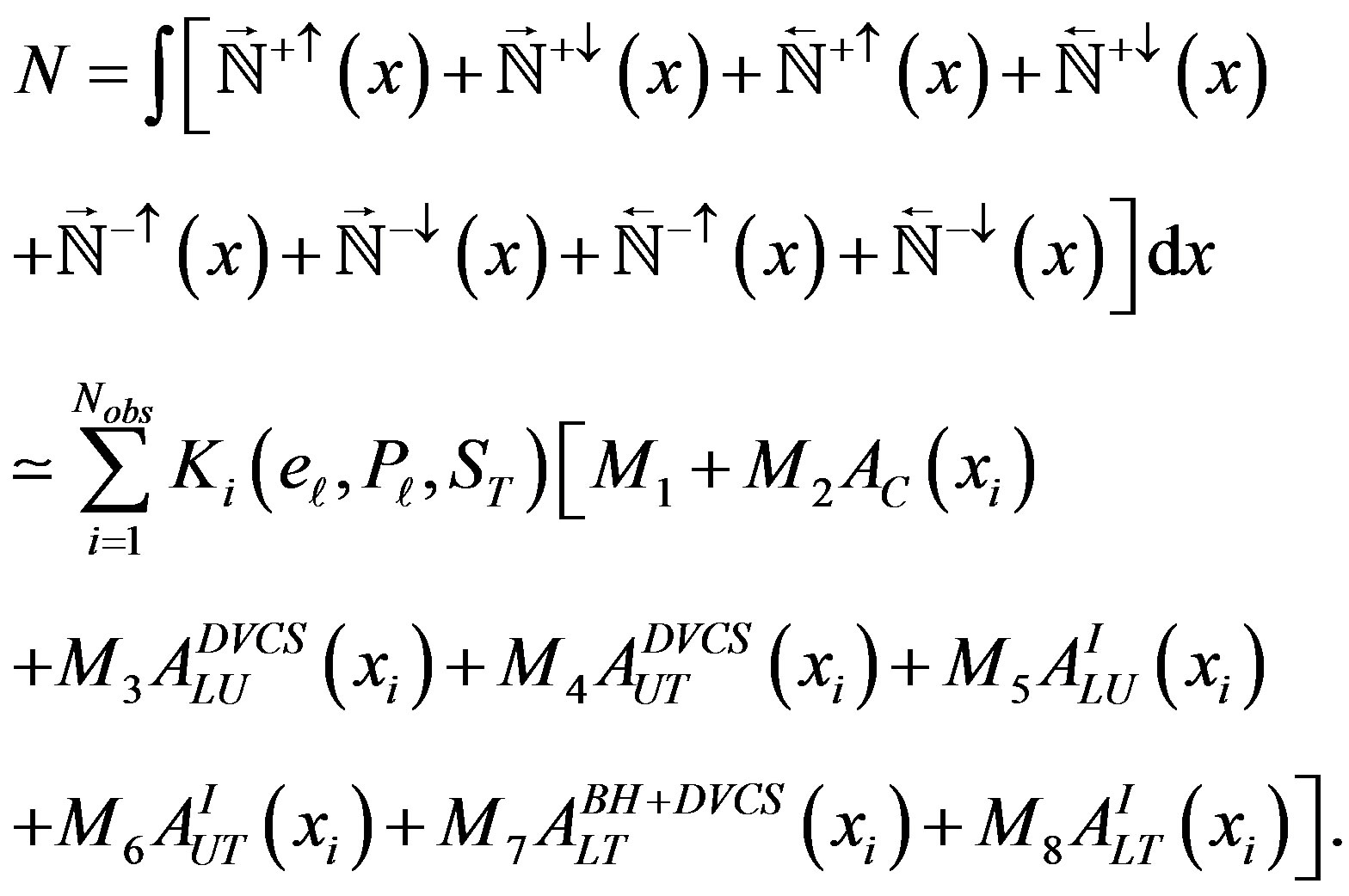 (2.30)
(2.30)
HereThe above given expressions for the asymmetries can be used for a least square fit without applying any helicity balancing cuts, since the coefficients in front of the each normalized yield account for the polarization imbalances in data sets. In order to obtain the normalization of the maximum likelihood function Equation (2.20) can be substituted into the system of Equations (2.12)-(2.19) and an integration over the whole phase-space x according to
 (2.31)
(2.31)
and
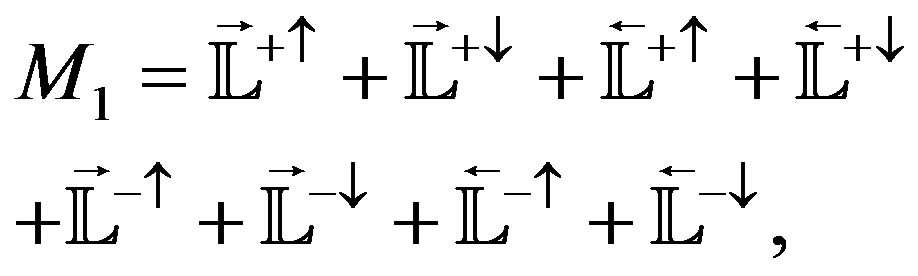 (2.32)
(2.32)
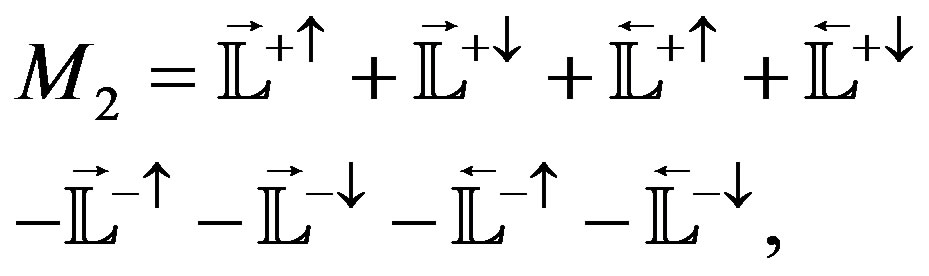 (2.33)
(2.33)
 (2.34)
(2.34)
 (2.35)
(2.35)
 (2.36)
(2.36)
 (2.37)
(2.37)
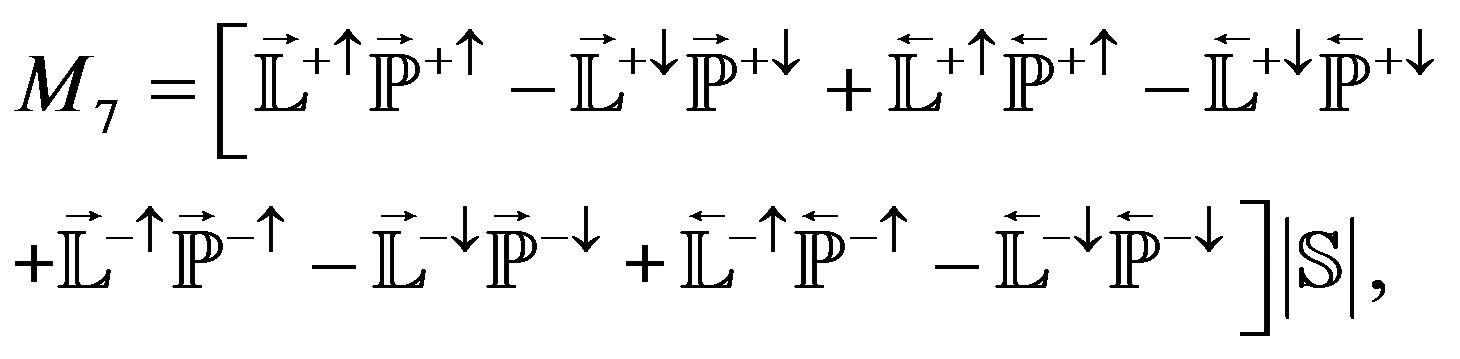 (2.38)
(2.38)
 (2.39)
(2.39)
As an example, in Figure 1 the results of asymmetry amplitudes of particular interest extracted in a single bin over all kinematic variables, obtained from HERMES data on DVCS from transversely polarized hydrogen target [6,9], are shown with their statistical and total uncertainties.
The correlation among all fitted asymmetry amplitudes is presented in Figure 2.
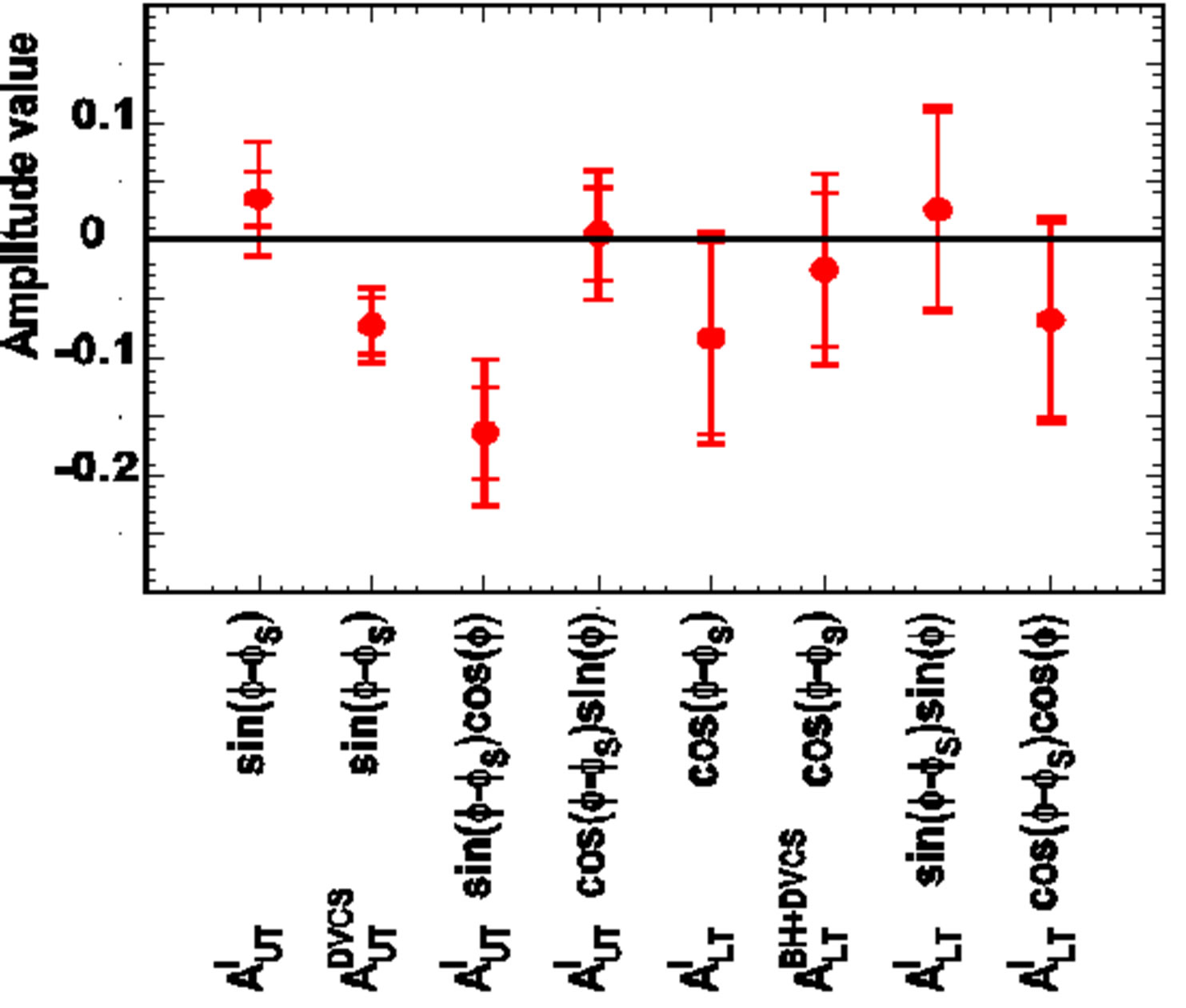
Figure 1. Azimuthal asymmetry amplitudes of particular interest measured at HERMES with transversely polarized proton [6,9], given at the average kinematics.
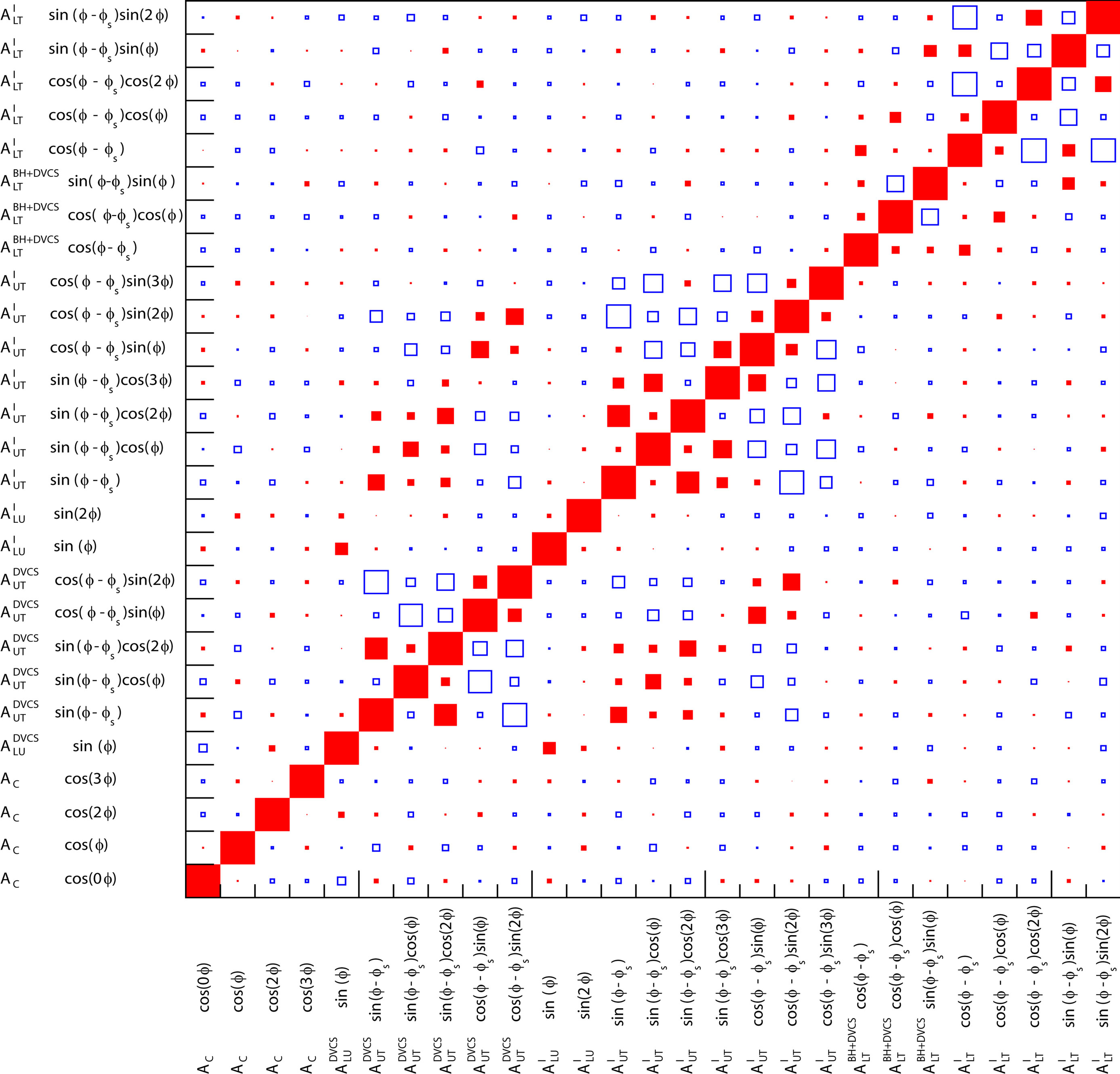
Figure 2. Correlation matrix for all fitted asymmetry amplitudes. The closed symbols represent positive values, while the open ones are for negative values. The area of the symbols represents the size of the correlation [6].
The above described method of simultaneous extraction of the “full set” of asymmetry amplitudes from data obtained from hard exclusive leptoproduction of real photons from transversely polarized protons is applicable for any other experiments (for example the planned COMPASS II program on DVCS at CERN), where measurements with both polarization states of the beam and target can be realized.
3. Acknowledgements
The author would like to thank the HERMES collaboration for support, G. Schell and C. Van Hulse for very useful discussions, comments. The author is also grateful to A. Movsisyan for his significant effort and participation in this work.
REFERENCES
- D. Mueller, D. Robaschik, B. Geyer, F. M. Dittes and J. Horejsi, Fortschritte der Physik, Vol. 42, 1994, pp. 101- 142. doi:10.1002/prop.2190420202
- X. Ji, Physical Review Letters, Vol. 78, 1997, pp. 610- 613. doi:10.1103/PhysRevLett.78.610
- A. V. Radyushkin, Physics Letters B, Vol. 380, 1996, pp. 417-425. doi:10.1016/0370-2693(96)00528-X
- A. V. Belitsky, D. Mueller and A. Kirchner, Nuclear Physics B, Vol. 629, 2002, pp. 323-392. doi:10.1016/S0550-3213(02)00144-X
- M. Diehl, T. Gousset, B. Pire and J. P. Ralston, Physics Letters B, Vol. 411, 1997, pp. 193-202. doi:10.1016/S0370-2693(97)00959-3
- A. Airapetian, et al., Physics Letters B, Vol. 704, 2011, pp. 15-23. doi:10.1016/j.physletb.2011.08.067
- A. Airapetian, et al., Physical Review Letters, Vol. 87, 2001, Article ID: 182001. doi:10.1103/PhysRevLett.87.182001
- A. Airapetian, et al., Physical Review D, Vol. 75, 2007, Article ID: 011103. doi:10.1103/PhysRevD.75.011103
- A. Airapetian, et al., Journal of High Energy Physics, Vol. 2008, 2008. doi:10.1088/1126-6708/2008/06/066
- A. Airapetian, et al., Journal of High Energy Physics, Vol. 2009, 2009. doi:10.1088/1126-6708/2009/11/083

