Journal of Modern Physics
Vol.3 No.8(2012), Article ID:21691,8 pages DOI:10.4236/jmp.2012.38109
On the Nature of the Average Transverse Momenta of the Low-pT Secondaries in Some High Energy Nuclear Collisions
1Department of Microbiology, Surendranath College, Kolkata, India
2Beramara RamChandrapur High School, South 24 Parganas, India
3Department of Physics, Raghunathpur College, Raghunathpur, India
4Physics and Applied Mathematics Unit (PAMU), Indian Statistical Institute, Kolkata, India
Email: dasghosh@yahoo.co.in, sau_goutam@yahoo.com, gpradeepta@rediffmail.com, bsubrata@www.isical.ac.in
Received June 8, 2012; revised July 1, 2012; accepted July 27, 2012
Keywords: Relativistic Heavy Ion Collision; Inclusive Production with Identified Hadrons; Inclusive Cross-Section; Meson Production
ABSTRACT
That the values of average transverse momenta (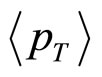 ) of the secondaries produced in high energy collisions rise very slowly with energy is modestly well-known and accepted. We would like to probe into this aspect of the problem for production of the main variety of the “soft” secondaries in two high energy symmetric nuclear collisions with the help of two non-QCD models. Our model-based results are found to be quite consistent with the anticipated behaviours and also with the observations.
) of the secondaries produced in high energy collisions rise very slowly with energy is modestly well-known and accepted. We would like to probe into this aspect of the problem for production of the main variety of the “soft” secondaries in two high energy symmetric nuclear collisions with the help of two non-QCD models. Our model-based results are found to be quite consistent with the anticipated behaviours and also with the observations.
1. Introduction
Amidst the observables measured by the high energy experiments, “average transverse momentum”, denoted normally by , is one of great prominence and importance, so much so, that it is, at times, juxtaposed at par with “average multiplicity” of the secondary particles detected in the high energy accelerators and colliders. Even in Cosmic ray phenomenon and at cosmic ray energies the observable has some special physical significance and bearing. This observable is generally defined as
, is one of great prominence and importance, so much so, that it is, at times, juxtaposed at par with “average multiplicity” of the secondary particles detected in the high energy accelerators and colliders. Even in Cosmic ray phenomenon and at cosmic ray energies the observable has some special physical significance and bearing. This observable is generally defined as
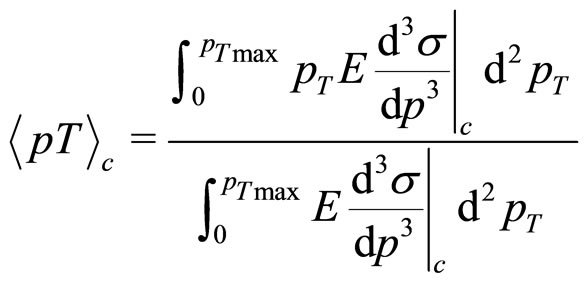 (1)
(1)
where 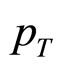 is the transverse momentum of the “c”-type of secondary; where c could any of the pions, kaons, baryon-antibaryons or any other.
is the transverse momentum of the “c”-type of secondary; where c could any of the pions, kaons, baryon-antibaryons or any other.
Quite spectacularly, this observable, by definition, is tied up with the measurements/model-based formulas for inclusive cross-section for any specific variety of the secondary particles. The letter “c” in the expression (1) indicates only the detected particle among the secondaries which comprise of both neutral and charged pions, kaons, baryons etc. Thus, any study on the nature of the average transverse momenta cannot be delinked from the studies on the nature of or expression for inclusive cross-sections, or from the model-based fits to them.
2. Outline of the Theoretical Framework
We will present here the synopsis of the Hagedorn’s Power law model which would lead us to calculate the average transverse momentum values in a somewhat simple manner. This is being delineated here blow.
Hagedorn’s Power Law Model
Our objective here is to study the inclusive 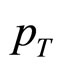 -spectra of the various secondaries of main varieties produced in
-spectra of the various secondaries of main varieties produced in 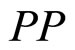 collisions. The kinematics of an inclusive reaction
collisions. The kinematics of an inclusive reaction 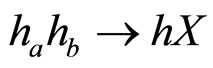 is described by Lorentz invariants. These are e.g. the center-of-mass energy squared s = (
is described by Lorentz invariants. These are e.g. the center-of-mass energy squared s = (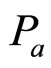 +
+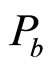 )2, the transverse momentum transverse (squared) t = (
)2, the transverse momentum transverse (squared) t = (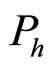 –
–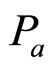 )2 and the missing mass
)2 and the missing mass . It is common to introduce the dimensionless variables (u =
. It is common to introduce the dimensionless variables (u = 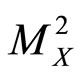 − s − t),
− s − t),
 (2)
(2)
where s, t, u are called Mandelstam variables. These variables are related to the rapidity y and radial scaling factor, 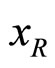 of the observed hadron by
of the observed hadron by
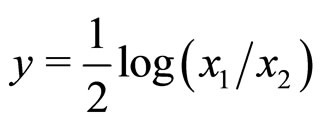 (3)
(3)
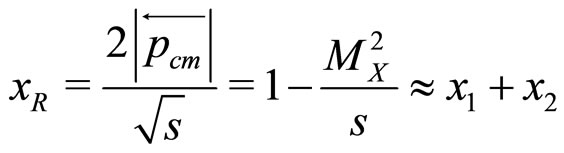 (4)
(4)
Since most of existing data are at y = 0 where 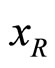 =
= 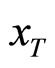 =
=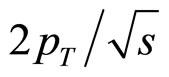 , one often refers to the scaling of the invariant cross section as “
, one often refers to the scaling of the invariant cross section as “ scaling”. For
scaling”. For , we find the variable
, we find the variable 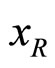 more useful than
more useful than , since
, since 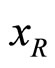 allows a smooth matching of inclusive and exclusive reactions in the limit
allows a smooth matching of inclusive and exclusive reactions in the limit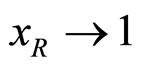 .
.
We will assume that at high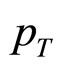 , the inclusive cross section takes a factorized form. And one such a factorized form was given by Back et al. [1].
, the inclusive cross section takes a factorized form. And one such a factorized form was given by Back et al. [1].
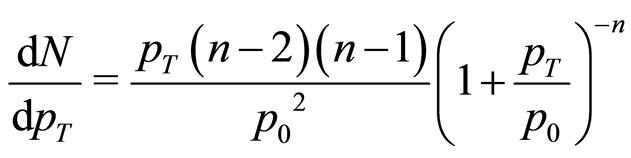 (5)
(5)
where n and  are adjustable parameters. The values of the exponent n are just numbers.
are adjustable parameters. The values of the exponent n are just numbers.  is a critical value of transverse momentum of the secondaries below which no secondary could be detected by the present day detectors set to measure data on hard interactions. So the factor
is a critical value of transverse momentum of the secondaries below which no secondary could be detected by the present day detectors set to measure data on hard interactions. So the factor 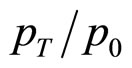 is a dimensionless quantity.
is a dimensionless quantity.
With the simplest recasting of form the above expression (5) and with replacements like 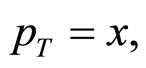
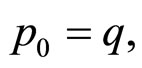
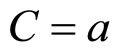 normalisation factor, and in the light of the definitions of the inclusive cross-sections, we get the following form as the final working formula in the applied form of the Power Law.
normalisation factor, and in the light of the definitions of the inclusive cross-sections, we get the following form as the final working formula in the applied form of the Power Law.
 (6)
(6)
Our first task here would be to check up the efficacy of this working expression, for which at the very beginning, we provide some model-based fits to the invariant crosssections for the production of the major varieties of secondaries in Pb + Pb collisions at various respectively low energies (17.3 GeV, 20A GeV, 30A GeV, 40A GeV) and Au + Au reaction at 19.6 GeV. Besides, some important ratio-behaviors based on the same expression have also been studied in the work depicted by several figures. With the fundamental definition of the average transverse momentum given by Equation (1) above and with the acceptance of the 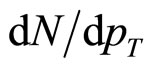 for invariant cross-section, Equation (1) can be transformed in the form
for invariant cross-section, Equation (1) can be transformed in the form
 (7)
(7)
In this power law scaling form it is generally found that q and n are intrinsically related by the average transverse momentum, 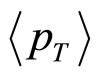 , with the undernoted relationship :
, with the undernoted relationship :
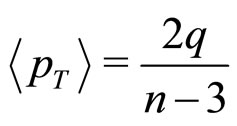 (8)
(8)
Actually ,this work could attain added significance, had we been able to compute the average transverse momentum values based on Equation (1) and compare them with the values obtained by the somewhat empirical formula given by Equation (8). But due to gross uncertainty in the values of q (which would in all cases be entirely arbitrary) we keep ourselves limited to expression (8) alone for the calculational purposes of the average transverse momentum (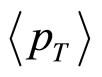 ) values.
) values.
The work presented here is essentially based on some fundamental physical ideas: 1) the idea of large-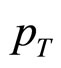 scaling (or
scaling (or 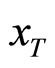 -scaling as was defined earlier), 2) the validity of the factorization hypothesis, 3) the constraint of exclusivity of reactions on inclusivity as was studied and pointed out by Brodsky et al. [2] who set the limit on the value of the exponent n, given by n ≤ 20.
-scaling as was defined earlier), 2) the validity of the factorization hypothesis, 3) the constraint of exclusivity of reactions on inclusivity as was studied and pointed out by Brodsky et al. [2] who set the limit on the value of the exponent n, given by n ≤ 20.
3. Results
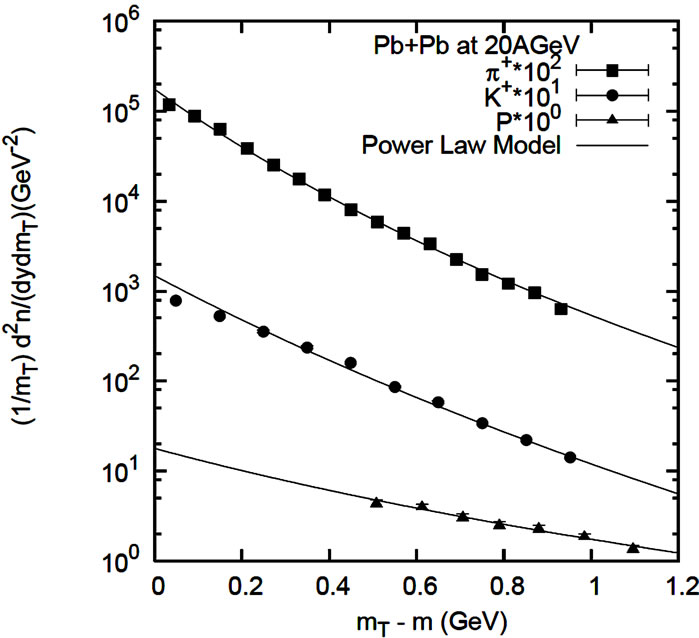
The results are presented here in graphical plots and the accompanying tables for the values of the used parameters. In Figures 1(a) and (b) the differential cross-sections for negative and positive pion, kaon and proton production cases in Pb + Pb collisions at SPS energies (at 20A GeV) are reproduced by the used theoretical framework. The figures in all the cases have been appropriately labeled and the parameters are shown in the table (Table 1). The plots in Figures 2(a) and (b) are for positive and negative pion, positive and negative kaon in Pb + Pb collisions at 30A GeV. The plots presented in Figure 2(c) for proton-antiproton production in Pb + Pb interaction at SPS energies, specifically at 17.3 GeV. The parameter values used to obtain the nature of fits for Figure 2 are shown in Table 2. The graphs in Figures 3 and 4 present the fits to the invariant cross-sections for the secondaries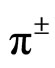 ,
, 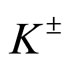 and proton-antiproton produced in the Au + Au collisions at 19.6 GeV and the corresponding parameters are depicted in Table 3. Against the data points, the plots shown in Figure 5 by solid lines depict the fits based on the same model to the invariant cross-sections for various major varieties of secondaries produced in Pb + Pb collisions at 40A GeV, though data on production of
and proton-antiproton produced in the Au + Au collisions at 19.6 GeV and the corresponding parameters are depicted in Table 3. Against the data points, the plots shown in Figure 5 by solid lines depict the fits based on the same model to the invariant cross-sections for various major varieties of secondaries produced in Pb + Pb collisions at 40A GeV, though data on production of 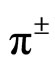 were not available. The parameter values used are given in Table 4. In Figure 6, we demonstrate the fits to the invariant cross-sections for various major varieties of the secondaries produced in central (0% - 10%) Au + Au collisions at 19.6 GeV and the corresponding parameters are depicted in Table 5. The fits to the charge ratio-values of the
were not available. The parameter values used are given in Table 4. In Figure 6, we demonstrate the fits to the invariant cross-sections for various major varieties of the secondaries produced in central (0% - 10%) Au + Au collisions at 19.6 GeV and the corresponding parameters are depicted in Table 5. The fits to the charge ratio-values of the
 (a)
(a)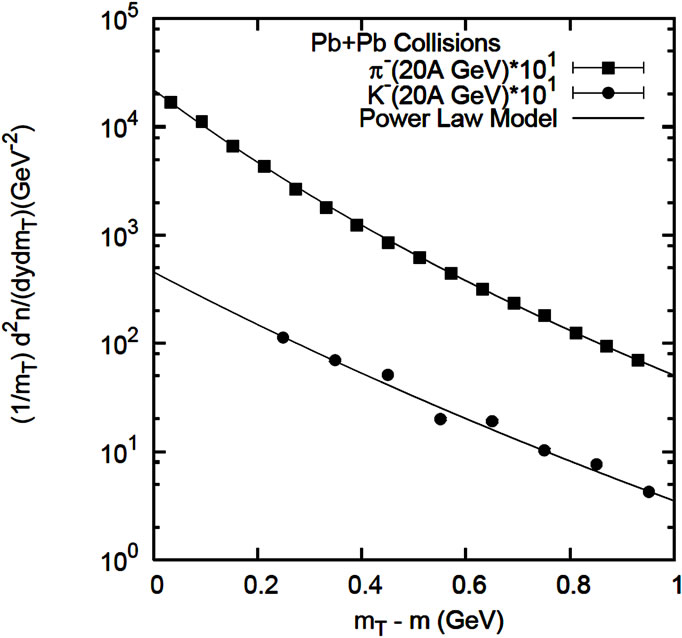 (b)
(b)
Figure 1. Transverse mass spectra of π+, K+, P (left) and π–, K– (right) produced in central Pb + Pb collision at 20A GeV. The lines are fits of equation power law model. The statistical errors are smaller than the symbol size, for which no errors are shown in the figure. Parameter values are taken from Table 1. The experimental data are taken from References [3] and [4].
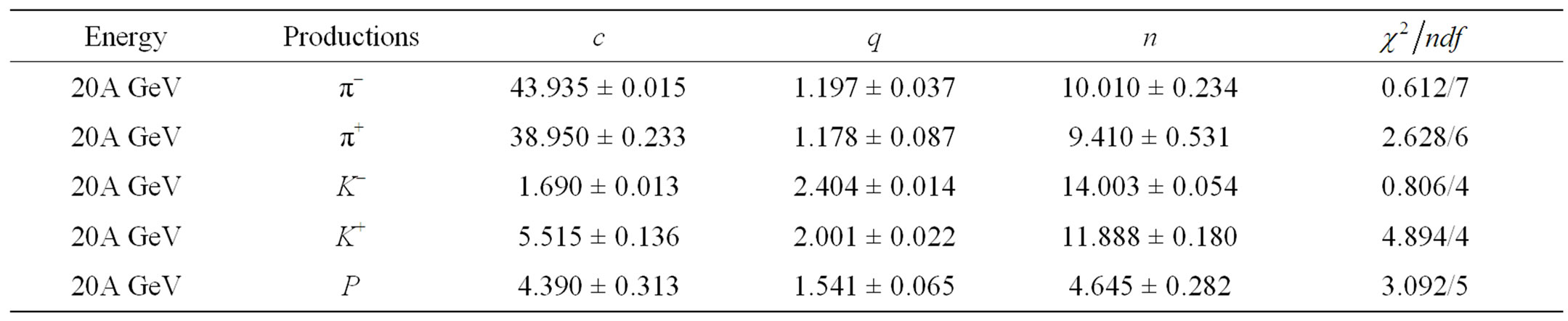
Table 1. Numerical values of the fit parameters of power law equation for Pb + Pb collisions (Reference Figure 1).
 (a)
(a)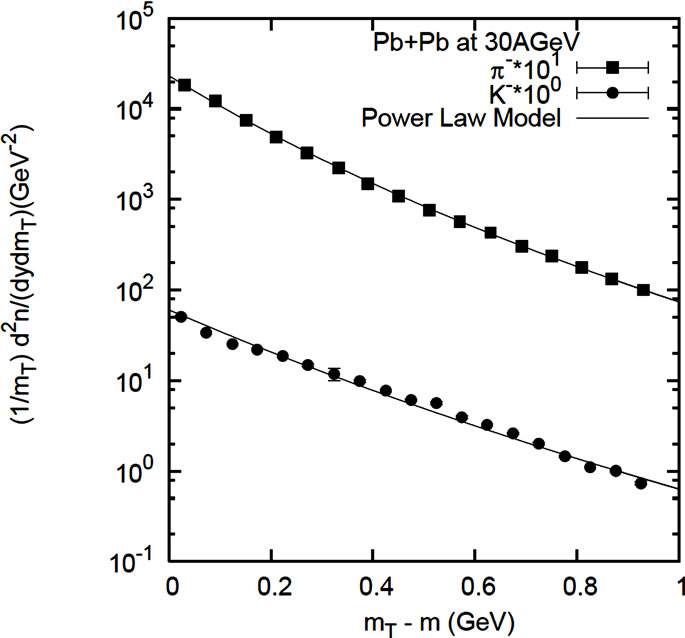 (b)
(b)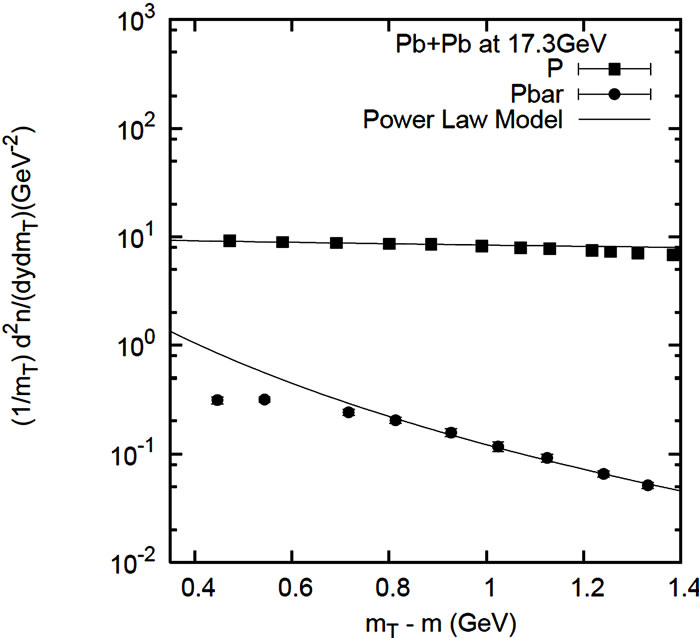 (c)
(c)
Figure 2. Transverse mass spectra of π+, K+ (left) and π–, K– (middle) and P, 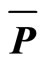 (right) produced in central Pb + Pb collision at 30A GeV and 17.3 GeV. The lines are fits of equation of power law model. The statistical errors are smaller than the symbol size, for which no errors are shown in the figure. Parameter values are taken from Table 2. The experimental data are taken from References [3] and [5].
(right) produced in central Pb + Pb collision at 30A GeV and 17.3 GeV. The lines are fits of equation of power law model. The statistical errors are smaller than the symbol size, for which no errors are shown in the figure. Parameter values are taken from Table 2. The experimental data are taken from References [3] and [5].

Table 2. Numerical values of the fit parameters of power law equation for Pb + Pb collisions (Reference Figure 2).
 (a)
(a)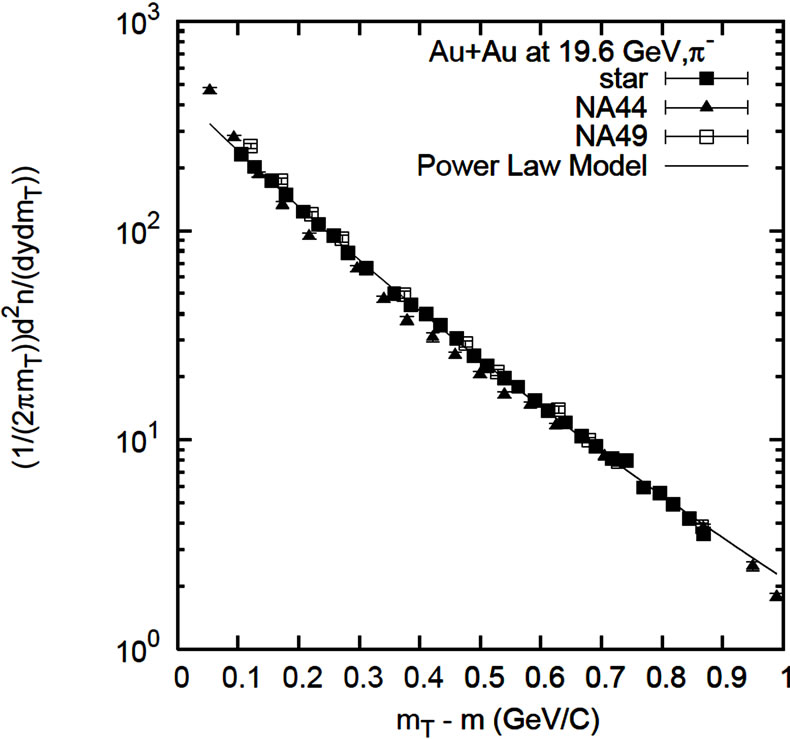 (b)
(b) (c)
(c) (d)
(d)
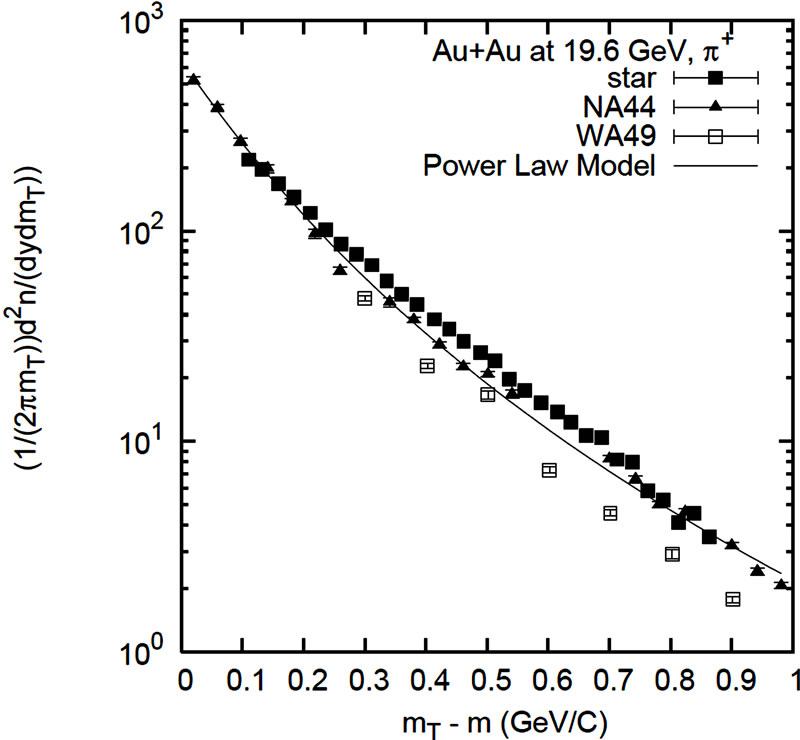
Figure 3. The transverse mass spectra of π+ (upper left), π– (upper right) and K+ (lower left), K– (lower right) from STAR experiment at 19.6 GeV in Au + Au collisions and the results of SPS experiments NA44, NA49, WA98 at 17.3 GeV in Pb + Pb collisions. The line is fit of power law model with all the STAR and SPS experiment. Parameter values are taken from Table 3. The experimental data are taken from Reference [6] and all errors are only of statistical nature.
 (a)
(a)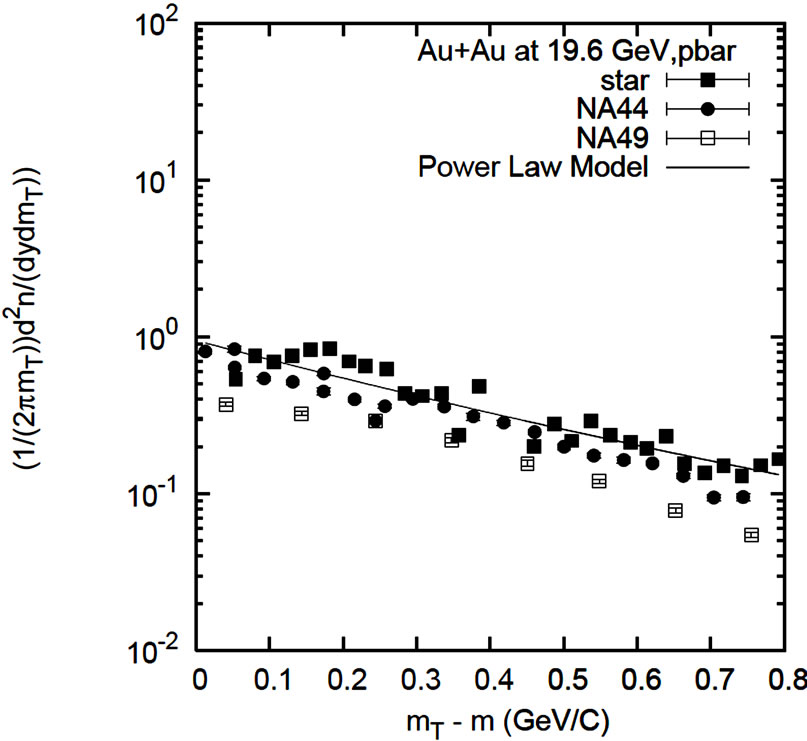 (b)
(b)
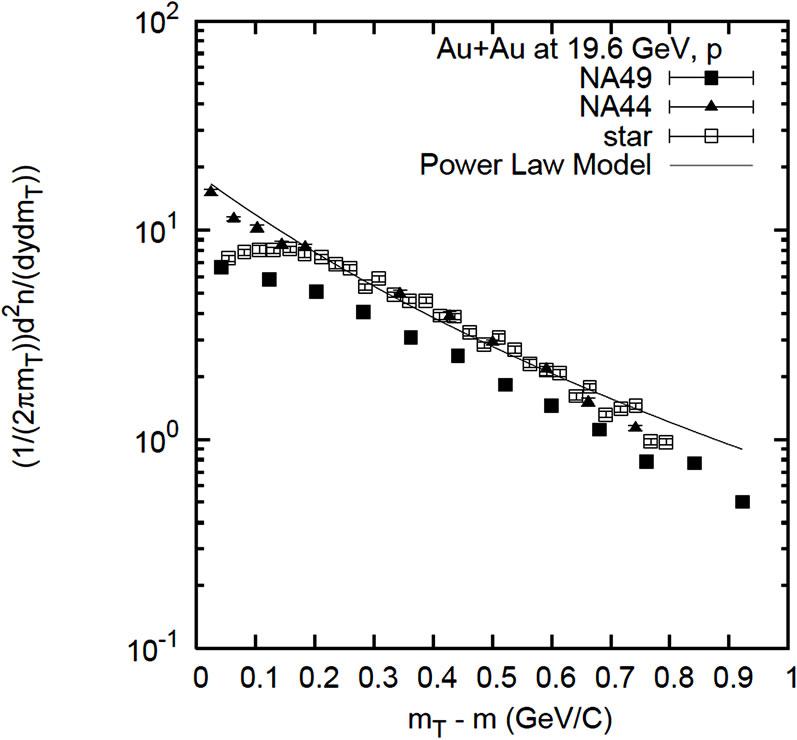
Figure 4. The transverse mass spectra of P (left) and  (right) from STAR experiment at 19.6 GeV in Au + Au collisions and the results of SPS experiments NA44, NA49, WA98 at 17.3 GeV in Pb + Pb collisions. The line is fit of power law model with all the STAR and SPS experiment. Parameter values are taken from Table 3. The experimental data are taken from Reference [6]. The statistical errors are smaller than the symbol size, for which no errors are shown in the figure.
(right) from STAR experiment at 19.6 GeV in Au + Au collisions and the results of SPS experiments NA44, NA49, WA98 at 17.3 GeV in Pb + Pb collisions. The line is fit of power law model with all the STAR and SPS experiment. Parameter values are taken from Table 3. The experimental data are taken from Reference [6]. The statistical errors are smaller than the symbol size, for which no errors are shown in the figure.
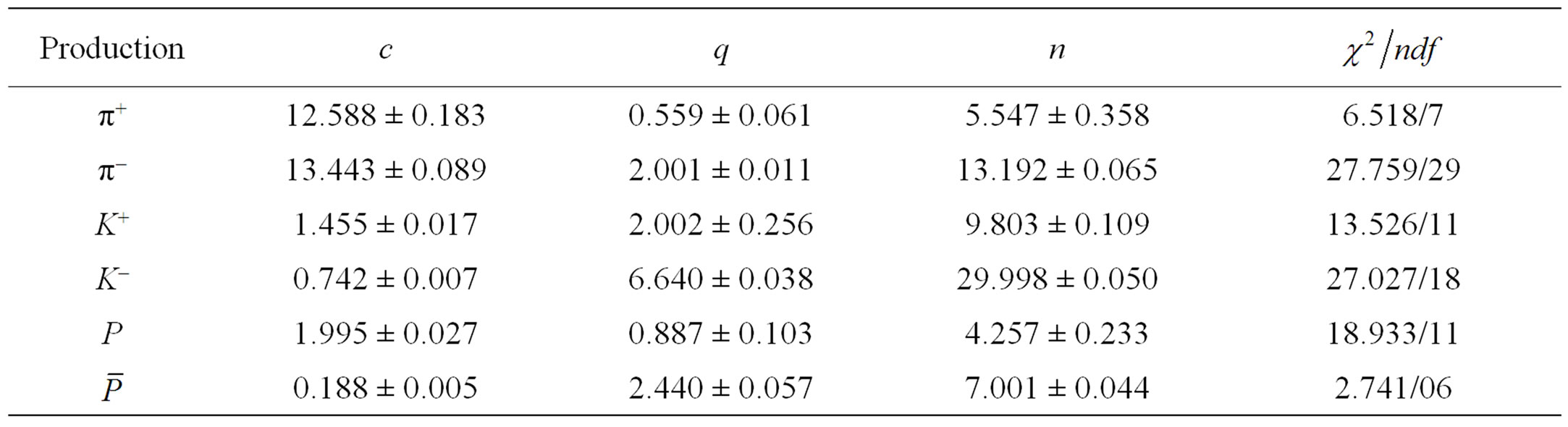
Table 3. Numerical values of the fit parameters for pion, kaon, proton and antiproton using power law model for Au + Au collisions at 19.6 GeV (Reference Figures 3 and 4).
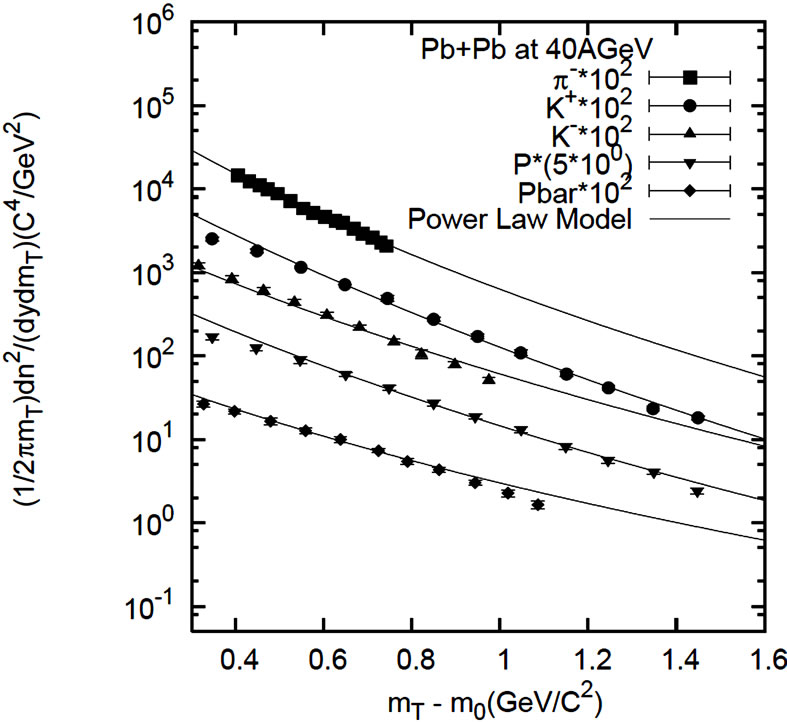
Figure 5. Transverse mass spectra of K+, K–, P, 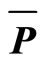 and π– produced in central Pb + Pb collision at 40A GeV. The lines are fits of equation of power law model. The statistical errors are smaller than the symbol size, for which no errors are shown in the figure. Parameter values are taken from Table 4. The experimental data are taken from [4].
and π– produced in central Pb + Pb collision at 40A GeV. The lines are fits of equation of power law model. The statistical errors are smaller than the symbol size, for which no errors are shown in the figure. Parameter values are taken from Table 4. The experimental data are taken from [4].
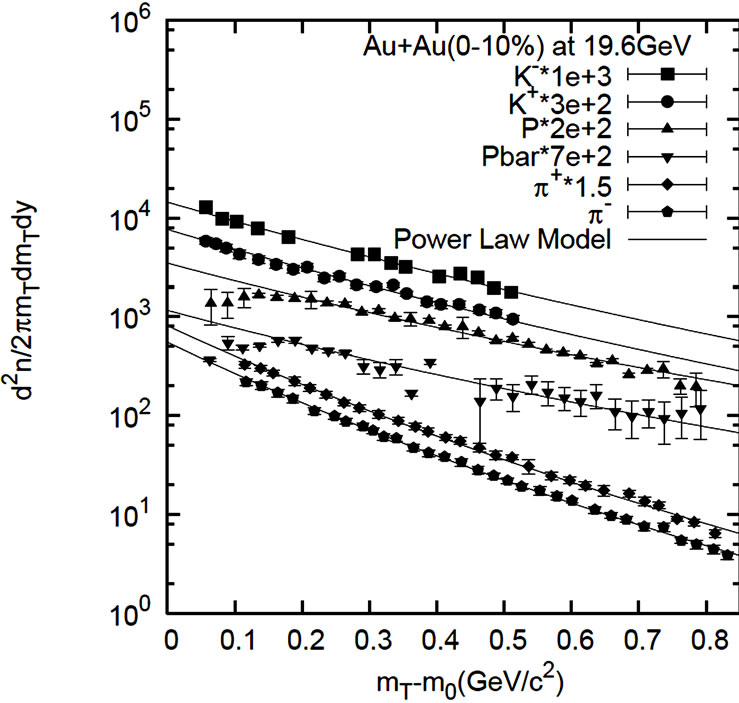
Figure 6. Transverse mass spectra of identified hadrons measured at midrapidity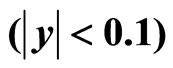 . The results at
. The results at 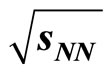 = 19.6 GeV for the production of π+, π–, P,
= 19.6 GeV for the production of π+, π–, P, 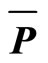 , K+ and K– for 0% - 10% centrality in Au + Au collisions. The solid curves provide the power law model based results. Parameter values are taken from Table 5. The experimental data are taken from Reference [7].
, K+ and K– for 0% - 10% centrality in Au + Au collisions. The solid curves provide the power law model based results. Parameter values are taken from Table 5. The experimental data are taken from Reference [7].

Table 4. Numerical values of the fit parameters for negative pion, positive and negative kaon, proton and antiproton using power law model for Pb + Pb collisions at 40A GeV (Reference Figure 5).
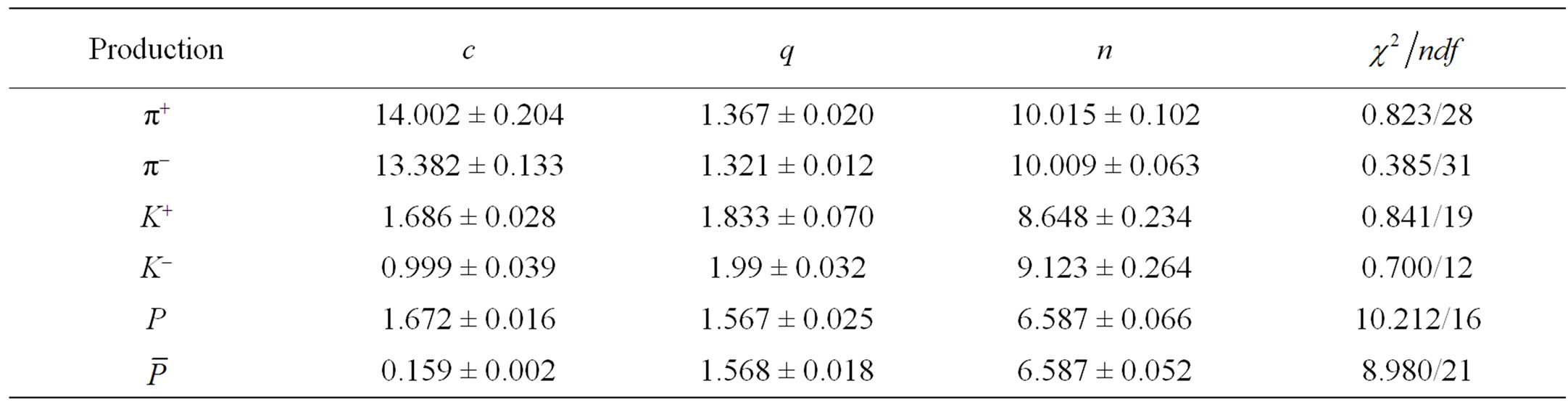
Table 5. Numerical values of the fit parameters for pion, kaon, proton and antiproton using power law model for Au + Au collisions at 19.6 GeV for 0% - 10% centrality (Reference Figure 6).
pionic, kaonic and baryonic particles are drawn in Figure 7. These charge-ratio values offer a cross-check of the results arrived at for the invariant cross-sections. Tables 6 to 10 indicate the calculation of average transverse momentum in Pb + Pb collisions at 20A GeV, 30A GeV, 17.3 GeV, 19.6 GeV, 40A GeV respectively and Table 11 in Au + Au collisions at 19.6 GeV. At last, the plots shown in Figures 8(a) and (b) (Tables 12 and 13) show the nature of the average transverse momentum values, which form the core of this work and its central theme.
 (a)
(a) (b)
(b) (c)
(c)
Figure 7.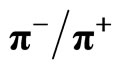 ,
, 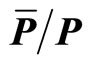 and
and  ratios vs.
ratios vs. 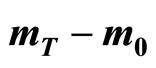 for 0% - 10% centrality in Au + Au collisions at
for 0% - 10% centrality in Au + Au collisions at 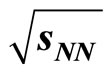 = 19.6 GeV
= 19.6 GeV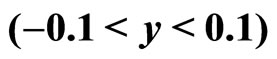 . The solid curves provide the power law model based results. Data are taken from Reference [7]. All errors are only of statistical nature.
. The solid curves provide the power law model based results. Data are taken from Reference [7]. All errors are only of statistical nature.

Table 6. Calculation of average transverse momentum for Pb + Pb collisions at 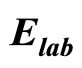 = 20A GeV (Data are taken from Table 1).
= 20A GeV (Data are taken from Table 1).
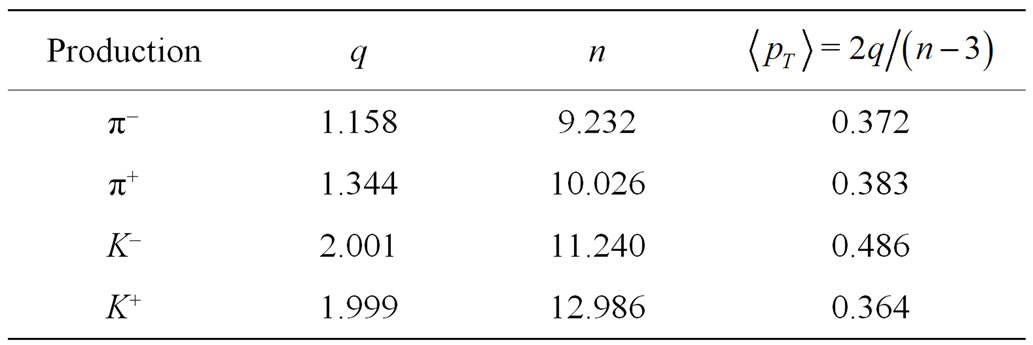
Table 7. Calculation of average transverse momentum for Pb + Pb collisions at 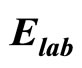 = 30A GeV (Data are taken from Table 2).
= 30A GeV (Data are taken from Table 2).
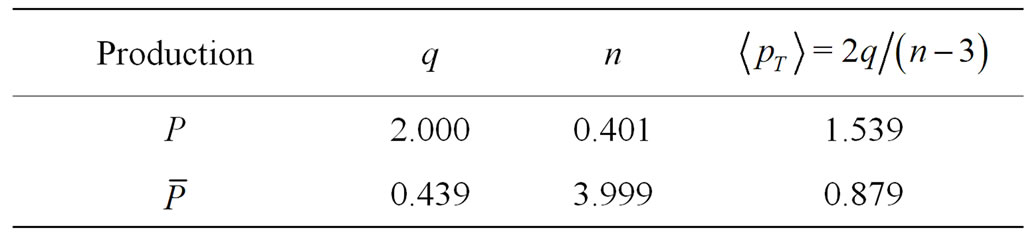
Table 8. Calculation of average transverse momentum for Pb + Pb collisions at  = 17.3 GeV (Data are taken from Table 2).
= 17.3 GeV (Data are taken from Table 2).
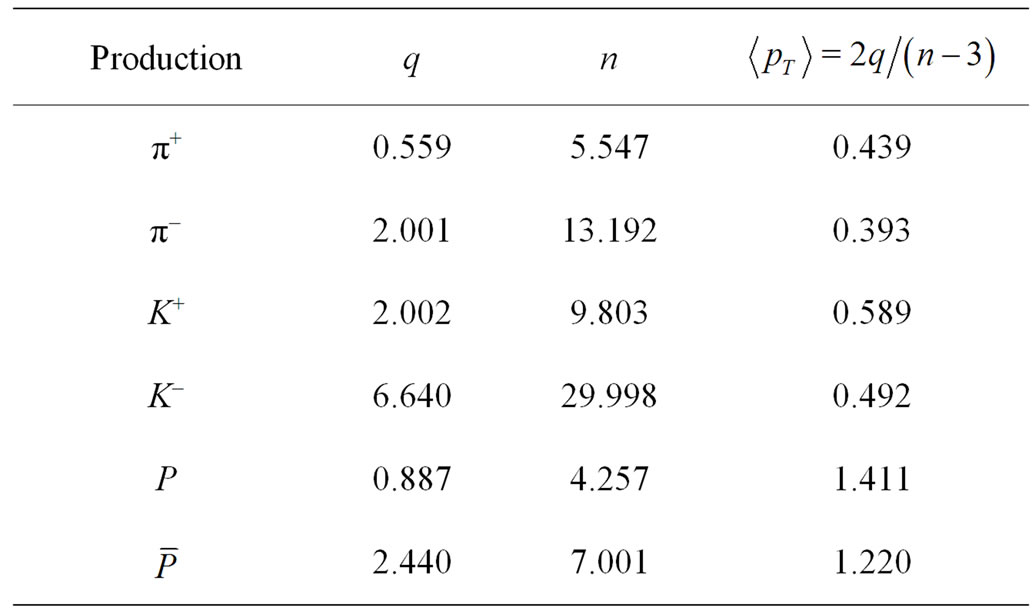
Table 9. Calculation of average transverse momentum for Au + Au collisions at  = 19.6 GeV (Data are taken from Table 3).
= 19.6 GeV (Data are taken from Table 3).
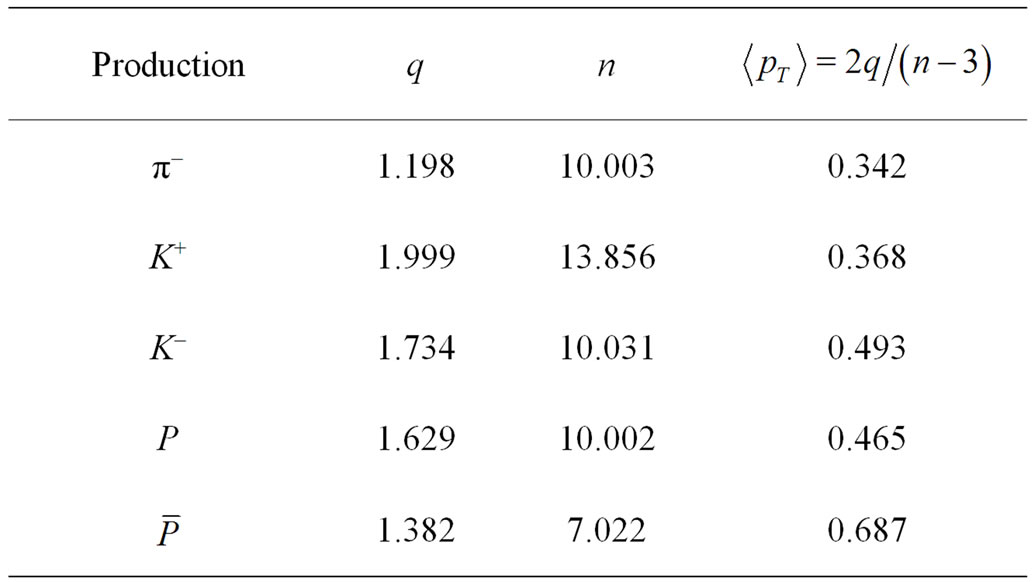
Table 10. Calculation of average transverse momentum for Pb + Pb collisions at 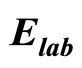 = 40A GeV (Data are taken from Table 4).
= 40A GeV (Data are taken from Table 4).
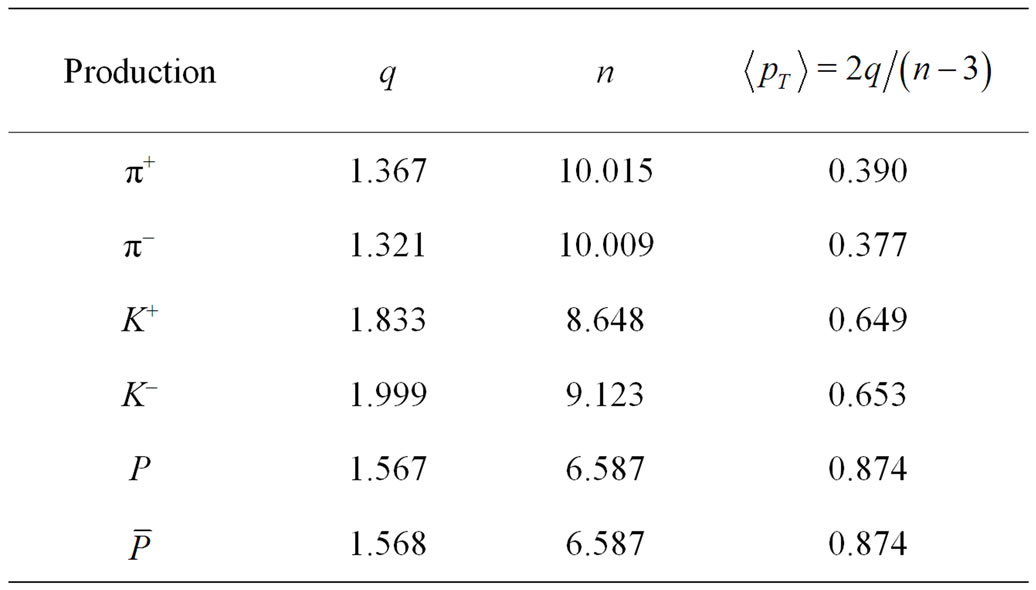
Table 11. Calculation of average transverse momentum for Au + Au collisions at 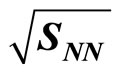 = 19.6 GeV for 0% - 10% centrality (Data are taken from Table 5).
= 19.6 GeV for 0% - 10% centrality (Data are taken from Table 5).
 (a)
(a)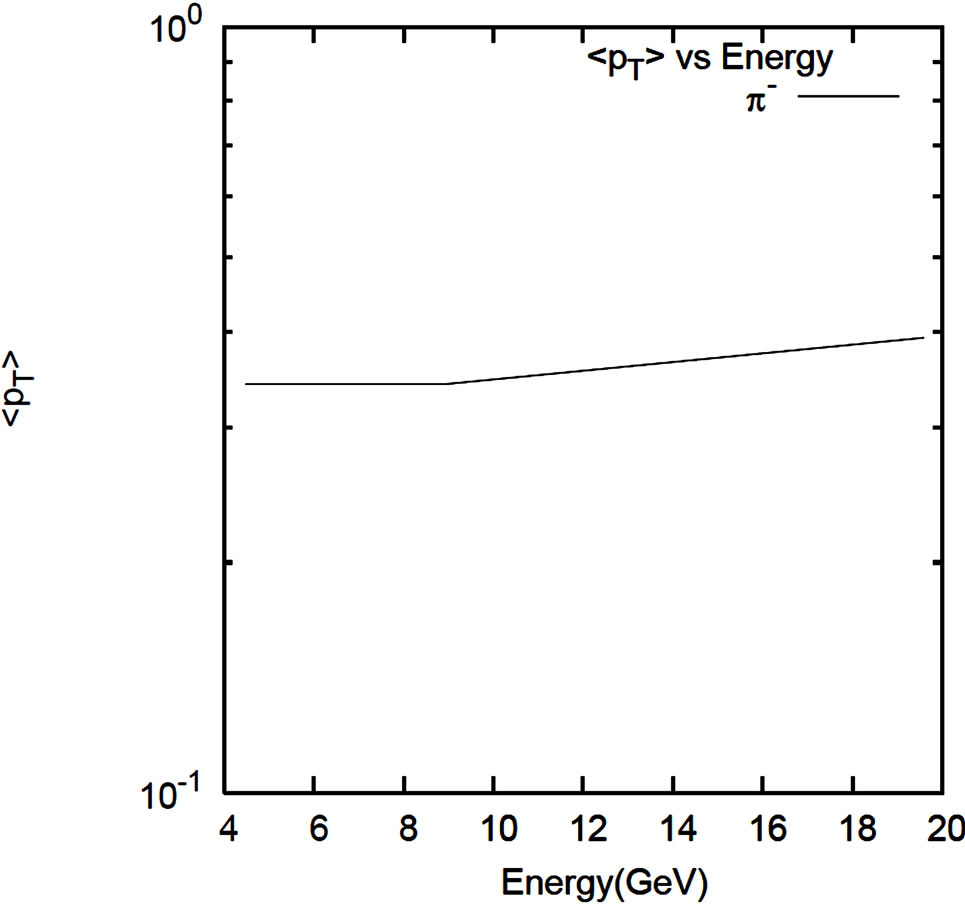 (b)
(b)
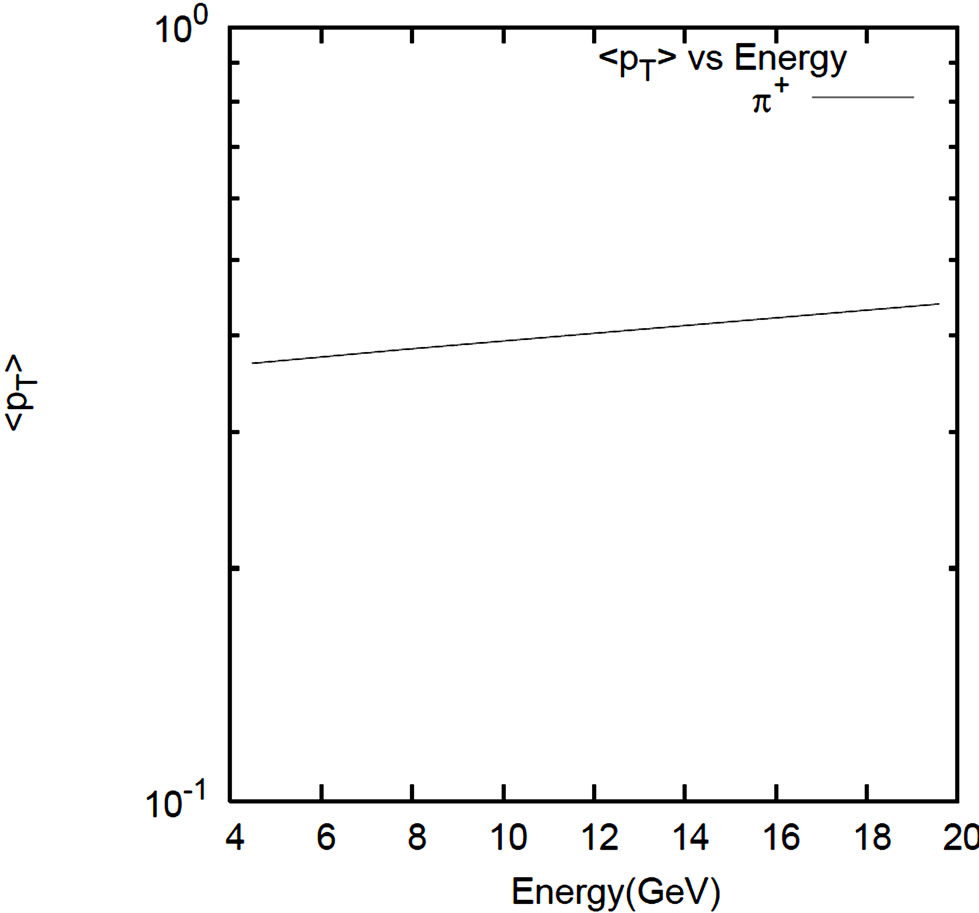
Figure 8. Average transverse momenta vs. c.m. energy plots. Parameter values are taken from Tables 12 and 13.
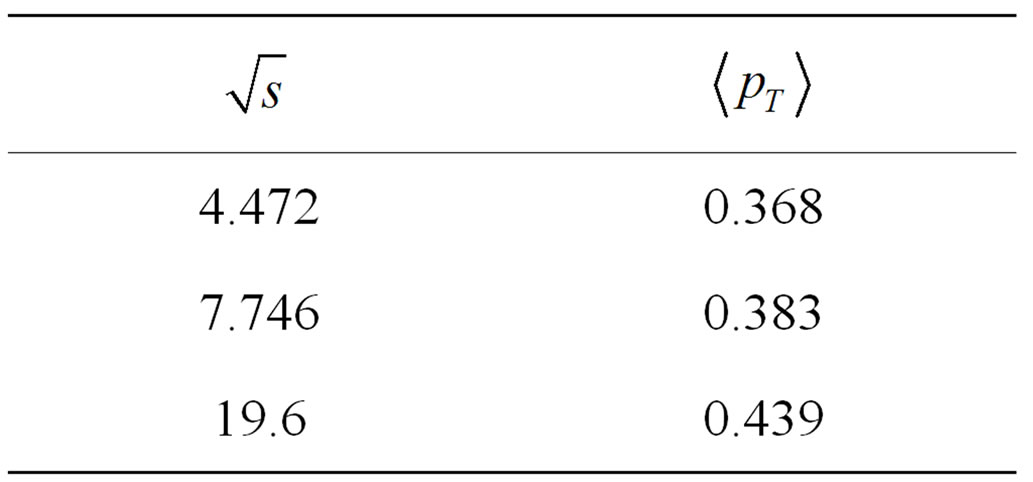
Table 12. Data for drawing graph  vs. average transverse momentum (
vs. average transverse momentum (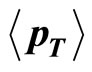 ) (Data are taken from Tables 6, 7 and 9) for
) (Data are taken from Tables 6, 7 and 9) for 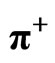 (Reference Figure 8(a)).
(Reference Figure 8(a)).
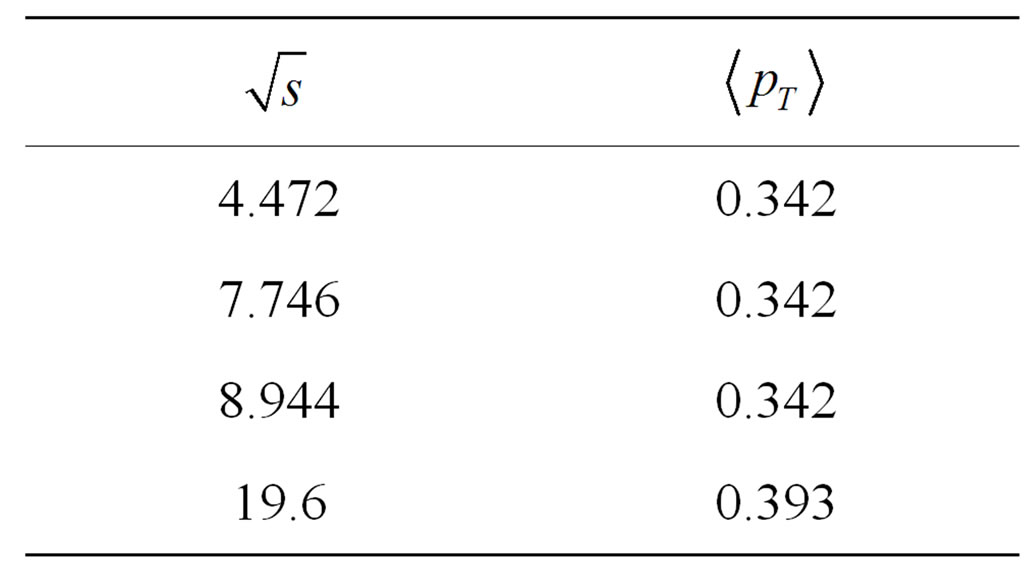
Table 13. Data for drawing graph 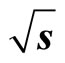 vs. average transverse momentum (
vs. average transverse momentum (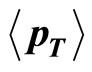 ) (Data are taken from Tables 6, 7 and 9) for
) (Data are taken from Tables 6, 7 and 9) for  (Reference Figure 8(b)).
(Reference Figure 8(b)).
4. Discussion and Conclusions
By all indications, the results manifested in the measured data on the specific observables chosen here are broadly consistent with the power law model put into work here. This is modestly true of even the nature of charge-ratios which provide virtually a cross-check of the model utilised here. Of course, some comments on our modelbased plots, especially the plots on the charge-ratios are in order here. The lack of the predictivity of the used model is caused only by the circumstances, i.e. the lack of measured data at the successive and needed intervals; the problem can be remedied by supplying the necessary and reliable data from the arranged laboratory experiments at high-to-very high energies. However, the problem of constraining the parameters still remains. The other observations are: as is expected for two symmetric collisions of neighbouring values of mass numbers at very close energies do not reveal any significant differences with respect to the observables chosen by the experimental groups. This work demonstrates somewhat convincingly that the power law models can easily take care of data; so the notion of compartmentalisation between the possible applicability of the power law models and of the exponential models is only superficial and also questionable. Thus, the power law models which establish them as more general ones obtain a clear edge over the exponential models. Reliable data on various other related observables are necessary for definitive final conclusions. By all indications, the experimentally observed nature of 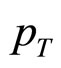 -scaling is found to remain valid in the studied low-
-scaling is found to remain valid in the studied low- range of this paper.
range of this paper.
Now follow a few comments on the nature of the average transverse momenta in nucleus-nucleus collisions: Firstly, the average 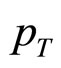 values for the secondaries, especially for the pion secondaries, show very slow rising nature with center of mass energy. Secondly, the ranges of the averages
values for the secondaries, especially for the pion secondaries, show very slow rising nature with center of mass energy. Secondly, the ranges of the averages  -values do not differ any prominently between simple PP reactions and heavy nucleus-nucleus collisions at the similar ranges of energy. Thirdly, differences between the Au + Au reactions at 19.6 GeV and Pb + Pb interaction at 17.3 GeV, 20A GeV, 30A GeV, 40A GeV are quite insignificant. This is, in fact, the main content of the “universality” property of high energy interactions. Fourthly, the nature of average transverse momenta of the secondaries does not show any major difference between “soft” (small-pT) and “hard” (large-
-values do not differ any prominently between simple PP reactions and heavy nucleus-nucleus collisions at the similar ranges of energy. Thirdly, differences between the Au + Au reactions at 19.6 GeV and Pb + Pb interaction at 17.3 GeV, 20A GeV, 30A GeV, 40A GeV are quite insignificant. This is, in fact, the main content of the “universality” property of high energy interactions. Fourthly, the nature of average transverse momenta of the secondaries does not show any major difference between “soft” (small-pT) and “hard” (large-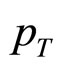 ) reactions. Lastly and finally, that the values of
) reactions. Lastly and finally, that the values of  are insensitive to the collisions-specifies like Au + Au or Pb + Pb at the neighboring energies is only natural. Such minor differences between “A”-values do hardly introduce any significant changes in the magnitudes of the average transverse momenta.
are insensitive to the collisions-specifies like Au + Au or Pb + Pb at the neighboring energies is only natural. Such minor differences between “A”-values do hardly introduce any significant changes in the magnitudes of the average transverse momenta.
REFERENCES
- B. B. Back, “Consequences of Energy Conservation in Relativistic Heavy-Ion Collisions,” Physical Review C, Vol. 72, No. 6, 2005, Article ID: 064906. doi:101103/PhysRevC.72.064906
- S. J. Brodsky, H. J. Pirner and J. Raufeisen, “Scaling Properties of High pT Inclusive Hadron Production,” Physics Letters B, Vol. 637, No. 1-2, 2006, pp. 58-63. doi:10.1016/j.physletb.2006.03.079
- C. Alt, et al., “Pion and Kaon Production in Central Pb + Pb Collisions at A-20 and A-30 GeV: Evidence for the Onset of Deconfinement,” Physical Review C, Vol. 77, No. 2, 2008, Article ID: 024903. doi:10.1103/PhysRevC.77.024903
- C. Alt, et al., “Bose-Einstein Correlations of π-π-Pairs in Central Pb + Pb Collisions at A-20, A-30, A-40, A-80 and A-158 GeV,” Physical Review C, Vol. 77, No. 6, 2008, Article ID: 064908. doi:10.1103/PhysRevC.77.064908
- C. Alt, et al., “High Transverse Momentum Hadron Spectra at
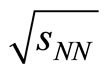 = 17.3 GeV in Pb + Pb and p + p Collisions,” Physical Review C, Vol. 77, No. 3, 2008, Article ID: 034906. doi:10.1103/PhysRevC.77.034906
= 17.3 GeV in Pb + Pb and p + p Collisions,” Physical Review C, Vol. 77, No. 3, 2008, Article ID: 034906. doi:10.1103/PhysRevC.77.034906 - D. Cebra, “Charged Hadron Results from Au + Au at 19.6 GeV,” Invited Talk Presented at Quark Matter, 2008.
- R. Picha, “Charged Hadron Distribution in 19.6 GeV Au + Au Collision,” Ph.D. Thesis, University of California, Davis, 2005.

