Journal of Modern Physics
Vol.2 No.9(2011), Article ID:7153,5 pages DOI:10.4236/jmp.2011.29132
Cation Distribution in Co0.7Me0.3Fe2O4 (Me = Zn, Ni and Mn)
1Department of Physics, GITAM University, Visakhapatnam, India
2Department of Physics, Dadi Institute of Engineering and Technology Engineering College, Anakapalli, India
3Department of Physics, Bhavan’s Vivekananda College, Sainikpuri, Sec’bad, India
4Department of Physics, Andhra University, Visakhapatnam, India
E-mail: *drmaheshnano@gmail.com
Received December 26, 20110; revised May 5, 2011; accepted May 17, 2011
Keywords: Magnetization, Cation Distribution, Lattice Constant
ABSTRACT
Co0.7Me0.3Fe2O4 (Me = Zn, Ni and Mn) were synthesized through co-precipitation method. Cationic distribution for these ferrites was proposed on the basis of magnetization measurements and available occupancy of the substituent ions into the spinel lattice. Theoretical lattice constant calculations confirm the proposed cationic distributions were the correct ones.
1. Introduction
Recently cobalt and cobalt containing ferrites have gained significant impact as they possess high coercivity, modern magnetization, very high positive magnetocrystalline anisotropy and high negative magnetostriction. Partial replacement of Fe by Mn or Co by Mn in CoFe2O4 is shown to affect the magnetostrictive response of the material. Since the structural, electrical and magnetic properties of ferrites depend on magnetic interaction and cation distribution, much attention is needed to understand the distribution of ions in the two sublattices of spinel in various synthesis routes.
Petitt et al. [1] have studied Co1−xZnxFe2O4 ferrite system and found an increase in saturation magnetization with the increase in zinc concentration up to about x = 0.4 and beyond which a decrease in saturation magnetization. Mossbauer study in Co1−xZnxFe2O4 system revealed that Co2+ ions enter A-sites up to 10% for Co-ferrite and the concentration of Co2+ ions at A-site gets reduced with the increasing concentration of Zn2+ ions at A-site. From the Neutron diffraction study, MK Fayek et al. [2] reported that the distribution in Zn0.85Co0.15Fe2O4 as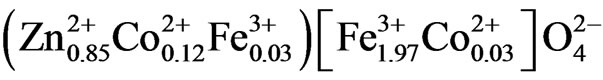 . Partial replacement of Co by Zn in CoFe2O4 helps to understand the exact cation distributions from Mossbauer and Neutron diffraction studies. It is of importance to determine their degree of inversion. The inversion is not complete in cobalt ferrite and the degree of inversion depends on annealing temperature and method of preparation. Krieble et al., have noticed that Mn substitution in Co-ferrite in place of Fe3+ ions, not only replaces Fe3+ ions at B-site, but also has the effect of displacing the Co2+ ions to the A-site [3]. Sonal Singhal et al. observed increase in saturation magnetization with the increase of annealing temperature in nickel substituted cobalt ferrites.
. Partial replacement of Co by Zn in CoFe2O4 helps to understand the exact cation distributions from Mossbauer and Neutron diffraction studies. It is of importance to determine their degree of inversion. The inversion is not complete in cobalt ferrite and the degree of inversion depends on annealing temperature and method of preparation. Krieble et al., have noticed that Mn substitution in Co-ferrite in place of Fe3+ ions, not only replaces Fe3+ ions at B-site, but also has the effect of displacing the Co2+ ions to the A-site [3]. Sonal Singhal et al. observed increase in saturation magnetization with the increase of annealing temperature in nickel substituted cobalt ferrites.
The aim of the present work is 1) processing of fine particles of cobalt containing ferrite samples Co0.7Mn0.3Fe2O4, Co0.7Ni0.3Fe2O4 and Co0.7Zn0.3Fe2O4 by co-precipitation method followed by annealing, 2) study of crystallite size from X-ray diffraction and Curie temperature of the ferrites, 3) determination of cation distribution from saturation magnetization measurements, 4) calculation of the theoretical lattice parameter from the proposed cation distribution and comparison of theoretically estimated and experimental obtained lattice parameters.
2. Experimental Details
For the preparation of Co0.7Me0.3Fe2O4 (Me = Zn, Ni and Mn) through co-precipitation, high pure cobalt, zinc, nickel, manganese and iron chlorides were taken in stioichiometric proportions and made dissolved separately in minimum amount of deionized water according to the chemical formula.
(0.7)CoCl2·6H2O + (0.3)MeCl2·6H2O + 2FeCl3 + 8NaOH → Co0.7Me0.3Fe2O4 + 8NaCl +8H2O Thus prepared cationic solution were mixed intimately so as to obtain the required compositions and stirred intensely for 1 hr to improve homogeneity. The resulting solutions, precursors, subjected to constant heating at 60˚C under continuous stirring. At this stage the co-precipitating base, aqueous NaOH in required proportion was added slowly drop by drop to the precursor solutions till a massy precipitate was formed at the bottom of the reaction vessel. Washing of the precipitate was done several times with deionized water and finally with acetone to remove the traces of water any. Pellets were prepared using 15% polyvinyl alcohol under a uniaxial pressure of 105 psi. X-ray diffraction patterns of all the samples were recorded using Rigaku Miniflex X-ray diffractometer with Cu-Kα radiation (λ = 1.5406 Å). Saturation magnetization was measured using Ponderometer method [4]. Curie temperature was determined with Soohoo method [5].
3. Results and Discussion
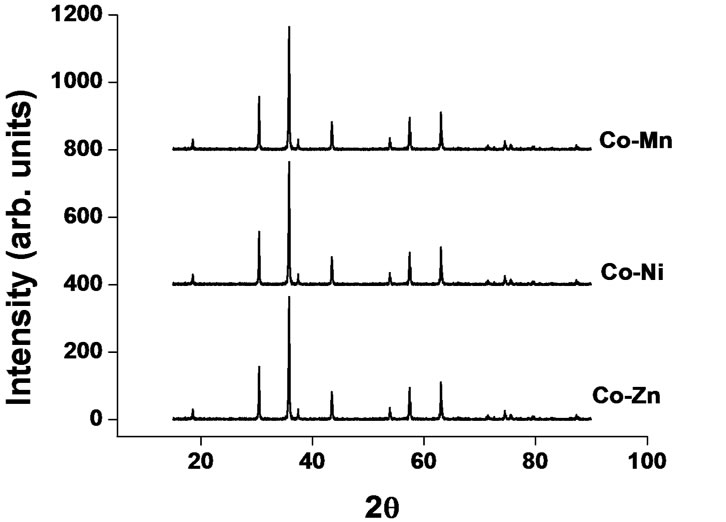
X-ray diffraction patterns of the Co0.7Me0.3Fe2O4 (Me = Zn, Ni and Mn) powders confirmed the single phase spinel structure [Figure 1(a)]. The average crystallite size of all the samples has been estimated using FWHM of each diffraction peak and Debye-Scherrer formula [6,7]. In order to obtain FWHM, a non-linear least square fit has been constructed assuming experimentally obtained diffraction peaks obey Voigt function [Figure 1(b)].
The value of average crystallite size is also estimated by constructing Williamson-Hall plots ( versus
versus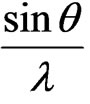 ) using the values of FWHM and incident angle θ corresponding to each diffraction peak. Extrapolation of these graphs provides the value of
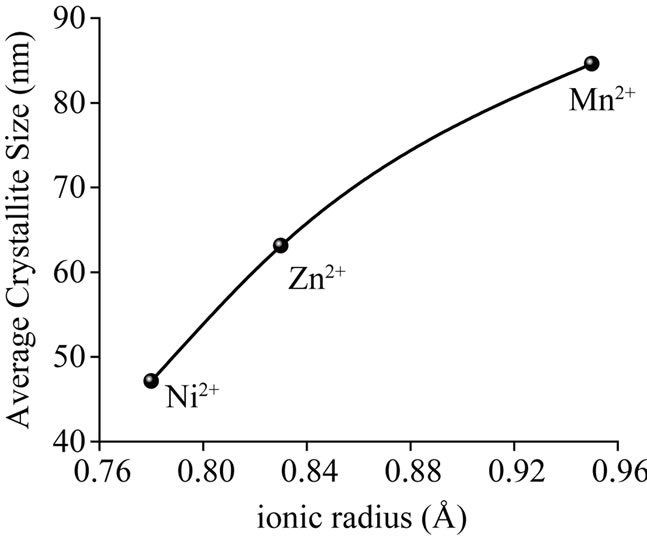
) using the values of FWHM and incident angle θ corresponding to each diffraction peak. Extrapolation of these graphs provides the value of 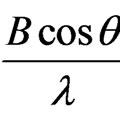 corresponding to zero strain, the reciprocal of which determines the crystallite size [Figure 2(a)]. Average crystallite size calculated from both the methods is found to be in good agreement and increasing with increasing ionic radii of substituted metal cation which might be attributed to entry of each ion into the lattice and variations in the rates of reaction for each specific ion [Figure 2(b)]. Similar tendency has been noticed in lattice constant, obtained from Nelson-Riley function [8].
corresponding to zero strain, the reciprocal of which determines the crystallite size [Figure 2(a)]. Average crystallite size calculated from both the methods is found to be in good agreement and increasing with increasing ionic radii of substituted metal cation which might be attributed to entry of each ion into the lattice and variations in the rates of reaction for each specific ion [Figure 2(b)]. Similar tendency has been noticed in lattice constant, obtained from Nelson-Riley function [8].
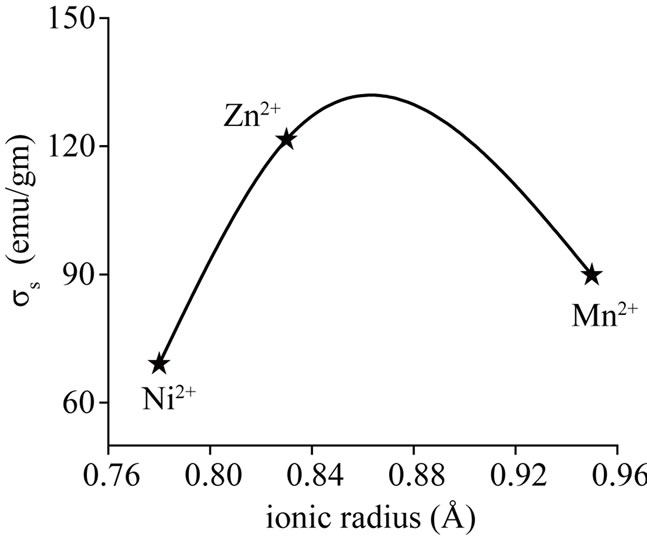
Figure 3(a) shows the variations in saturation magnetization with ionic radius of the dopant. The saturation magnetization of cobalt ferrite decreases with the partial replacement of Co2+ ions by Ni2+ ions because the magnetic moment associated with nickel ion is 2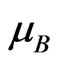 , less than that of Co2+ ion (3
, less than that of Co2+ ion (3 ). Moreover, nickel ions are known to occupy octahedral sites and cause decrease in the B-site magnetic moment. As the net magnetic moment of the sample is equal to the difference in B site and A-site magnetic moments, MB-MA, a decrease in overall magnetic moment of the sample is expected. This kind of explanation is valid provided the strongest A-B interaction persists among various cations existing on A and B sublattices.
). Moreover, nickel ions are known to occupy octahedral sites and cause decrease in the B-site magnetic moment. As the net magnetic moment of the sample is equal to the difference in B site and A-site magnetic moments, MB-MA, a decrease in overall magnetic moment of the sample is expected. This kind of explanation is valid provided the strongest A-B interaction persists among various cations existing on A and B sublattices.
It is well known [9] that Zn2+ ions occupy tetrahedral sites, Ni2+ ions occupy octahedral sites and Mn2+ ions occupy tetrahedral sites. Co2+ ions are reported to occupy A-sites up to a maximum of 10% in cobalt ferrite [10,11] depending on the annealing temperature. From Mossbauer study of cobalt-zinc ferrite [1] it has been observed that the amount of cobalt at A-site decreases from 10% with the increase of zinc content.
In case of Co-Zn ferrite system, non-magnetic Zn2+ ions are known to occupy tetrahedral (A) sites due to their strong preference and decrease the magnetic moment of A-sublattice and hence an increase in the total magnetic moment of the sample is predicted. Similar
 (a)
(a)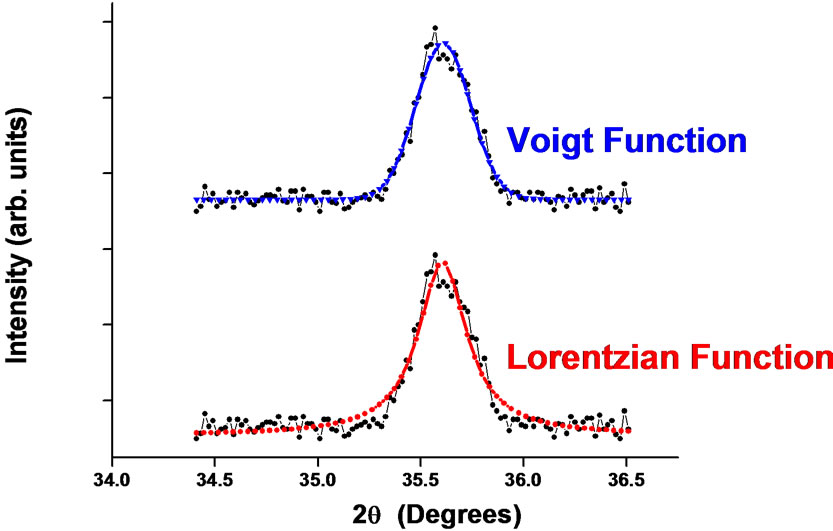 (b)
(b)
Figure 1. (a) X-ray diffraction peaks (b) Least squares fitting for a prominent (311) peak assuming either Lorentzian or Voigt function.
 (a)
(a)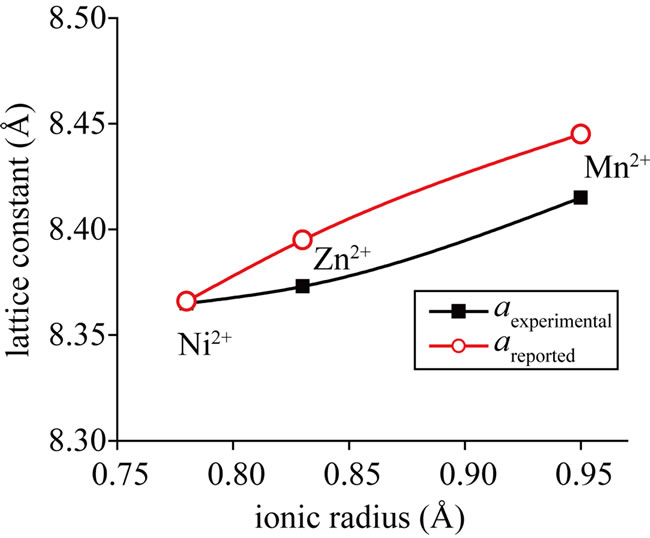 (b)
(b)
Figure 2. (a) Average crystallite size and (b) Lattice constant versus ionic radius.
 (a)
(a)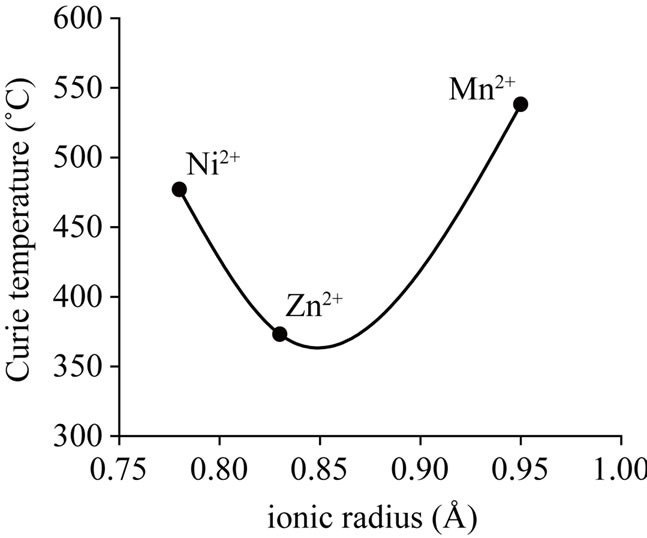 (b)
(b)
Figure 3. (a) Saturation magnetization and (b) Curie temperature versus ionic radius.
behaviour has been reported [12] in Co1−xZnxFe2O4 system up to x = 0.4. The highest value of saturation magnetization for the composition Co0.9Zn0.1Fe2O4 [13] was noticed and explained the result on the basis of cationic distribution and their occupancy in specific sites. The substitution of Mn2+ for Co2+ produces changes in the value of saturation magnetization depending on the heat treatment. Mn3+ ions will have strong preference for the octahedral sites when Fe3+in cobalt ferrite is replaced by Mn3+ [9]. On the other hand, Mn2+ ions will have stronger preference for the tetrahedral sites [10] if Co2+ is replaced by Mn2+. In the present study the experimentally observed value of magnetization in Co-Mn ferrite is in accordance with the replacement of Co2+ ions by Mn2+.
Figure 3(b) shows the variations in Curie temperature. As is clear from the table, except Co-Mn ferrite Table 1 the other two ferrite systems show less value of Curie temperatures than that of the cobalt ferrite. The observed variations in Curie temperature are explained on the basis of the super exchange interactions among the metallic cations distributed between the two sublattices. As described in saturation magnetization, the substitution of Ni2+ in place of Co2+ should decrease the magnetic interactions since the ion having less magnetic moment (Ni2+) is replacing an ion having high magnetic moment (Co2+). In case of Co-Mn ferrite, as Mn2+ ion magnetic moment (5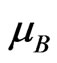 ) more than magnetic moment of Co2+ ion (3
) more than magnetic moment of Co2+ ion (3 ), the rise in magnetic interactions is generally expected which increase the Curie temperature. In case of Co-Zn ferrite system, the substitution of non-magnetic zinc in place of ferromagnetic cobalt leads to a decrease in Curie temperature owing to diminishing A-B super exchange interaction.
), the rise in magnetic interactions is generally expected which increase the Curie temperature. In case of Co-Zn ferrite system, the substitution of non-magnetic zinc in place of ferromagnetic cobalt leads to a decrease in Curie temperature owing to diminishing A-B super exchange interaction.
Cation distribution for these ferrites has been proposed on the basis of saturation magnetization measurements. In the present study, the occupancy amount of cobalt ions at tetrahedral sites has been chosen to be about 5% to provide the following better possible cationic distributions agreeable to experimentally observed number of Bohrmagnetons per molecule.
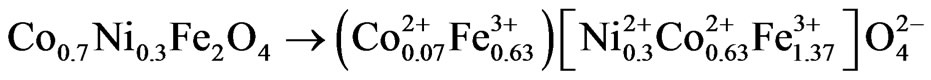

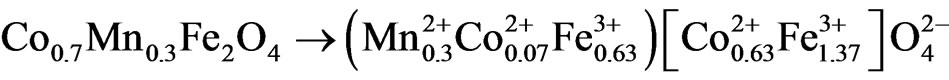
Besides providing the experimentally observed lattice constant, theoretical lattice constants have also been estimated using the following formulae by proposing cati-
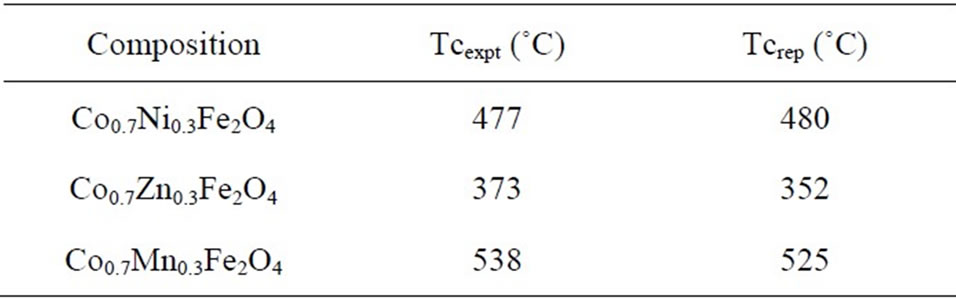
Table 1. Experimental & reported Curie temperatures of Co0.7Me0.3Fe2O4 (Me = Zn, Ni & Mn).
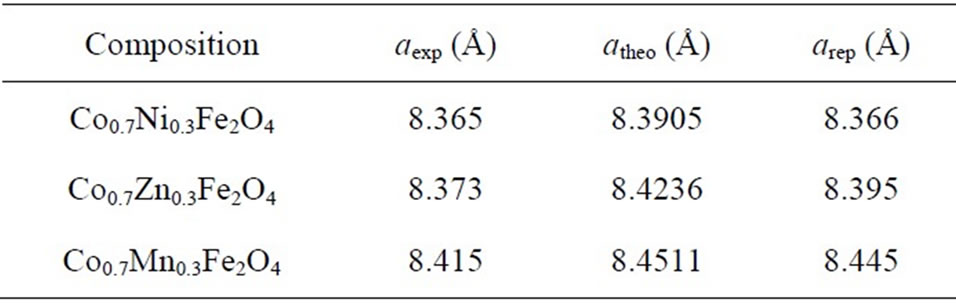
Table 2. Theoretical, experimental and reported values of lattice constants.
onic distribution of metal ions in the spinel lattice.
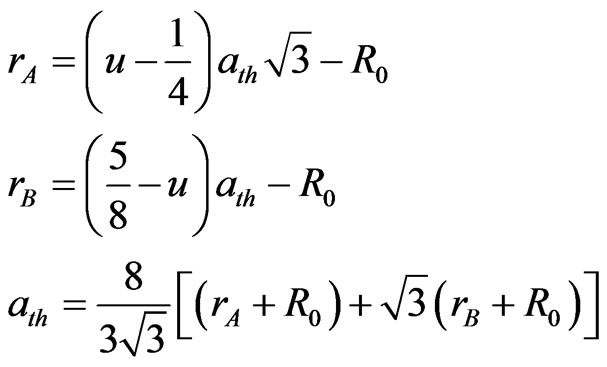
where 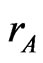 and
and 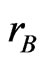 are radii of tetrahedral and octahedral sites respectively.
are radii of tetrahedral and octahedral sites respectively. 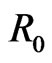 is the radius of oxygen ion. u is oxygen positional parameter. For face centered cubic structure the value of oxygen parameter is 0.375. In the Co-Zn ferrite system the radii of Zn2+ and Co2+ ions are greater than the space occupied by the oxygen ions. This will cause distortion in the cubic lattice and therefore the oxygen parameter may differ from its usual value 3/8 [14].
is the radius of oxygen ion. u is oxygen positional parameter. For face centered cubic structure the value of oxygen parameter is 0.375. In the Co-Zn ferrite system the radii of Zn2+ and Co2+ ions are greater than the space occupied by the oxygen ions. This will cause distortion in the cubic lattice and therefore the oxygen parameter may differ from its usual value 3/8 [14].
Theoretical lattice constants corresponding to these ferrites have been calculated using the proposed cationic distributions. The calculated lattice constants are found to be in agreement with the experimentally observed and reported lattice constant values (Table 2).
4. Conclusions
X-ray diffraction measurements confirmed the single phase spinel structure for all the ferrites and lattice constant has been measured by using Nelson-Riley function. Cation distribution for the compositions has been proposed on the basis of saturation magnetization values and the preferred site occupancy of the ions in the ferrite lattice. Confirmation of cation distribution has been done through theoretical lattice constant calculations. A good agreement between theoretical and experimental lattice constants has been found for all the compositions.
REFERENCES
- G. A. Petitt and D. W. Forester “Mossbauer Study of Cobalt-Zinc Ferrites,” Physical Review B, Vol. 4, No. 11, 1971, pp. 3912-3923. doi:10.1103/PhysRevB.4.3912
- M. K. Fayek, A. A. Bahgat, Y. M. Abbas and L. Moberg, “Neutron Diffraction and Mossbauer Effect Study on a Cobalt Substituted Zinc Ferrite,” Journal of Physics C: Solid State Physics, Vol. 15, No. 11, 1982, p. 2509. doi:10.1088/0022-3719/15/11/027
- K. Krieble, T. Schaeffer, J. A. Paulsen, A. P. Ring, C. C. H. Lo and J. E. Snyder, “Mossbauer Spectroscopy Investigation of Mn-Substituted Co-ferrite (CoMnFeO),” Journal of Applied Physics, Vol. 97, 2005, p. 10F101.
- K. S. Rao, A. M. Kumar, M. C. Varma, G. Choudary and K. H. Rao, “Cation Distribution of Titanium Substituted Cobalt Ferrites,” Journal of Alloys and Compounds, Vol. 488, No. 1, 2010, pp. L6-L9. doi:10.1016/j.jallcom.2009.08.086
- R. F. Soohoo, “Theory and Applications of Ferrites,” Prentice Hall, Englewood Cliffs, 1960.
- A. D. Sheikh and V. L. Mathe, “Anamolous Electrical Properties of Nanocrystalline Ni-Zn Ferrite,” Journal of Materials Science, Vol. 43, 2008, pp. 2018-2025. doi:10.1007/s10853-007-2302-6
- B. Baruwati, R. K. Rana and S. V. Manorama, “Further Insights in the Conductivity Behaviour of Nanocrystalline NiFe2O4,” Journal of Applied Physics, Vol. 101, No. 1, 2007, Article ID: 014302. doi:10.1063/1.2404772
- J. B. Nelson and D. P. Riley, “The Thermal Expansion of Graphite from 15˚C to 800˚C,” Proceedings of the Physical Society, Vol. 57, No. 6, 1945, pp. 477-486. doi:10.1088/0959-5309/57/6/303
- J. M. Hastings and L. M. Corliss, “An Antiferromagnetic Transition in Zinc Ferrite,” Physical Reviews, Vol. 102, No. 6, 1956, pp. 1460-1463. doi:10.1103/PhysRev.102.1460
- G. A. Sawatzky, F. Van Der Woude and A. H. Morrish “Mossbauer Study Several Ferromagnetic Spinel,” Physical Reviews, Vol. 187, No. 2, 1969, pp. 747-757. doi:10.1103/PhysRev.187.747
- E. Prince, “Neutron Diffraction Observation of Heat Treatment in Cobalt Ferrite,” Physical Reviews, Vol. 102, No. 3, 1956, pp. 674-676. doi:10.1103/PhysRev.102.674
- G. V. Duong, N. Hanh, D. V. Linh, R. Groessinger, P .Weinberger, E. Schafler and M. Zehetbauer, “Monodispersed Nanocrystalline Co1−xZnxFe2O4 Particles by Forced Hydrolysis: Synthesis and Characterization,” Journal of Magnetism and Magnetic Materials, Vol. 311, No. 1, 2007, pp. 46-50. doi:10.1016/j.jmmm.2006.11.167
- G. Vaidyanathan, S. Sendhilnathan and R. Arulmurugan, “Structural and Magnetic Properties of Co1−xZnxFe2O4 Nanoparticles By Co-Precipitation Method,” Journal of Magnetism and Magnetic Materials, Vol. 313, No. 2, 2007, pp. 293-299. doi:10.1016/j.jmmm.2007.01.010
- J. B. Goodenouh and A. L. Loeb, “Theory of Ionic Ordering, Crystal Distortion, and Magnetic Exchange Due to Covalent Forces in Spinels,” Physical Review, Vol. 98, No. 2, 1955, pp. 391-408. doi:10.1103/PhysRev.98.391

