Applied Mathematics
Vol.06 No.08(2015), Article ID:58448,8 pages
10.4236/am.2015.68130
Coupled Fixed Point for (α, ψ)-Contractive in Partially Ordered Metric Spaces Using Compatible Mappings
Preeti, Sanjay Kumar
Department of Mathematics, DCRUST, Sonepat, India
Email: preeti1785@gmail.com, sanjaymudgal2004@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 May 2015; accepted 27 July 2015; published 30 July 2015
ABSTRACT
In this paper, first we introduce notions of (α, ψ)-contractive and (α)-admissible for a pair of map and prove a coupled coincidence point theorem for compatible mappings using these notions. Our work extends and generalizes the results of Mursaleen et al. [1] . At the end, we will provide an example in support of our result.
Keywords:
Coupled Coincidence Point, α-ψ-Contractive Mapping, Compatible Mappings

1. Introduction
Fixed point theorems give the conditions under which maps have solutions.
Fixed point theory is a beautiful mixture of Analysis, Topology and Geometry. Fixed points Theory has been playing a vital role in the study of nonlinear phenomena. In particular, fixed point techniques have been applied in diverse fields as Biology, Chemistry, and Economics, Engineering, Game theory and Physics. The usefulness of the concrete applications has increased enormously due to the development of accurate techniques for computing fixed points.
The fixed point theory has many important applications in numerical methods like Newton-Raphson Method and establishing Picard’s Existence Theorem regarding existence and uniqueness of solution of first order differential equation, existence of solution of integral equations and a system of linear equations. The credit of making the concept of fixed point theory useful and popular goes to polish mathematician Stefan Banach. In 1922, Banachproved a fixed point theorem, which ensures the existence and uniqueness of a fixed point under appropriate conditions. This result of Banach is known as Banach fixed point theoremor contraction mapping principle, “Let x be any non empty set and
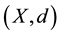 be a completemetric space If T is mapping of X into itself satisfying
be a completemetric space If T is mapping of X into itself satisfying
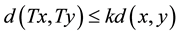 for each
for each
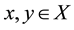 where
where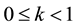 , then T has a unique fixed point in X”. This principle provides a technique for solving a variety of applied problems in Mathematical sciences and Engineering and guarantees the existence and uniqueness of fixed points of certain self maps of metric spaces and provides a constructive method to find out fixed points. Now the question arise what type of problems have the fixed point. The fixed point problems can be elaborated in the following manner:
, then T has a unique fixed point in X”. This principle provides a technique for solving a variety of applied problems in Mathematical sciences and Engineering and guarantees the existence and uniqueness of fixed points of certain self maps of metric spaces and provides a constructive method to find out fixed points. Now the question arise what type of problems have the fixed point. The fixed point problems can be elaborated in the following manner:
1) What functions/maps have a fixed point?
2) How do we determine the fixed point?
3) Is the fixed point unique?
Currently, fixed point theory has been receiving much attention on in partially ordered metric spaces; that is, metric spaces endowed with a partial ordering. Turinici [2] extending the Banach contraction principle in the setting of partially ordered sets and laid the foundation a new trend in fixed point theory. Ran and Reurings [3] developed some applications of Turinici’s theorem to matrix equations and established some results in this direction. The results were further extended by Nieto and Rodŕguez-Ĺpez [4] [5] for non-decreasing mappings. Bhaskar and Lakshmikantham [6] [7] introduced the new notion of coupled fixed points for the mappings satisfying the mixed monotone property in partially ordered spaces and discussed the existence and uniqueness of a solution for a periodic boundary value problem. Later on, Lakshmikantham and Ciríc [8] proved coupled coincidence and coupled common fixed point theorems for nonlinear contractive mappings in partially ordered complete metric spaces.
Choudhury and Kundu [9] , proved the coupled coincidence result for compatible mappings in the settings of partially ordered metric space. Recently, Samet et al. [10] [11] have introduced the notion of α-ψ-contractive and α-admissible mapping and proved fixed point theorems for such mappings in complete metric spaces. For more results regarding coupled fixed points in various metric spaces one can refer to [12] -[23] .
In this paper, we will generalize the results of Mursaleen et al. [1] for α-ψ-contractive and α-admissible mappings using compatible mappings under α-ψ-contractions and α-admissible conditions.
2. Mathematical Preliminaries
In order to obtain our results we need to consider the followings.
Definition 2.1. [6] . Let
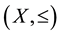 be a partially ordered set and
be a partially ordered set and
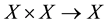 be a mapping. Then a map F is said to have the mixed monotone property if
be a mapping. Then a map F is said to have the mixed monotone property if
 is monotone non-decreasing in x and is monotone non-increasing in y; that is, for any
is monotone non-decreasing in x and is monotone non-increasing in y; that is, for any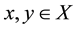 ,
,
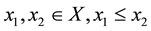 implies
implies
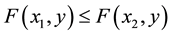 and
and
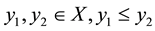 implies.
implies.
Definition 2.2. [6] . An element
 is said to be a coupled fixed point of the mapping
is said to be a coupled fixed point of the mapping
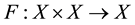 if
if
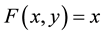 and.
and.
Definition 2.3. [8] . Let
 be a partially ordered set and
be a partially ordered set and
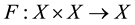 and
and







Definition 2.4. [8] . An element




Choudhury et al. [9] introduced the notion of compatible maps in partially ordered metric spaces as follows:
Definition 2.5. [9] . The mappings F and g where



whenever





In order to obtain our results we need to consider the followings.
Definition 2.6. [1] . Denote by Ψ the family of non-decreasing functions



1)
2)


3)


Lemma 2.7. [1] . If






Definition 2.8. [1] . Let





Definition 2.9. [1] . Let





Now, we will introduce our notions:
Definition 2.10. Let






with


Definition 2.11. Let


Then F and g are said to be (α)-admissible if



3. Main Results
Recently, Mursaleen et al. [1] proved the following coupled fixed point theorem with α-ψ-contractive conditions in partial ordered metric spaces:
Theorem 3.1 [1] Let




Such that for



Suppose also that
1) F is (a)-admissible.
2) There exists


3) F is continuous.
If there exists



Then F has a coupled fixed point, that is, there exist,


Now we are ready to prove our results for compatible mappings.
Theorem 3.2 Let






For all



Suppose also that
1) F and g are (a)-admissible.
2) There exists


3)
4) F is continuous.
If there exists



Then F and g has coupled coincidence point that is there exist,


Proof: Let


and


Let



Continuing this process, we can construct two sequences





Now we will show that



For

and as

We have,


Thus (3.4) holds for
Now suppose that (3.4) holds for some fixed
Then, since


Therefore, by g-mixed monotone property of F, we have


From above, we conclude that

Thus, by mathematical induction, we conclude that (3.4) holds for all
If following holds for some
Then obviously,


Now, we assume that


Since, F and g a-admissible, we have

implies,
Thus by mathematical induction, we have

Similarly, we have


From (3.3) and conditions 1) and 2) of hypothesis, we get

Similarly, we have

On adding (3.7) and (3.8), we get
Repeating the above process, we get
For


Let


that is;
Since,


Hence,



Since,




There exists,


Since, F and g are compatible mappings; therefore, we have


Next we will show that


For all
Taking limit


Similarly, we have
Thus

Hence, we have proved that F and g has coupled coincidence point.
Now, we will replace continuity of F in the theorem 3.2 by a condition on sequences.
Theorem 3.3. Let







1) Inequality (3.3) and conditions 1), 2) and 3) hold.
2) if



for all n and




If there exists



Then F and g has coupled coincidence point, that is, there exist,


Proof. Proceeding along the same lines as in the proof of Theorem 3.2, we know that

are Cauchy sequences in the complete metric space



Similarly,
Using the triangle inequality, (3.11) and the property of

Similarly, on using (3.12), we have
Proceeding limit


Thus,


Remark. On putting
Example 3.4. Let


Then

Let



Let

Let



Let,



Then obviously,

Now, for all



Then it follows that,

Hence, the mappings F and g are compatible in X.
Consider a mapping

Thus (3.3) holds for



mixed monotone property. Let




is a coupled coincidence point of g and F in X.
Cite this paper
Preeti,SanjayKumar, (2015) Coupled Fixed Point for (α, Ψ)-Contractive in Partially Ordered Metric Spaces Using Compatible Mappings. Applied Mathematics,06,1380-1388. doi: 10.4236/am.2015.68130
References
- 1. Mursaleen, M., Mohiuddine, S.A. and Agarwal, R.P. (2012) Coupled Fixed Point Theorems for α-ψ-Contractive Type Mappings in Partially Ordered Metric Spaces. Fixed Point Theory and Applications, 2012, 228.
- 2. Turinici, M. (1986) Abstract Comparison Principles and Multivariable Gronwall-Bellman Inequalities. Journal of Mathematical Analysis and Applications, 117, 100-127.
http://dx.doi.org/10.1016/0022-247X(86)90251-9 - 3. Ran, A.C.M. and Reurings, M.C.B. (2004) A Fixed Point Theorem in Partially Ordered Sets and Some Applications to Matrix Equations. Proceedings of the American Mathematical Society, 132, 1435-1443.
http://dx.doi.org/10.1090/S0002-9939-03-07220-4 - 4. Nieto, J.J. and Rodríguez-López, R. (2005) Contractive Mapping Theorems in Partially Ordered Sets and Applications to Ordinary Differential Equations. Order, 22, 223-239.
http://dx.doi.org/10.1007/s11083-005-9018-5 - 5. Nieto, J.J. and Rodriguez-López, R. (2007) Existence and Uniqueness of Fixed Point in Partially Ordered Sets and Applications to Ordinary Differential Equations. Acta Mathematica Sinica, English Series, 23, 2205.
http://dx.doi.org/10.1007/s10114-005-0769-0 - 6. Bhaskar, T.G. and Lakshmikantham, V. (2006) Fixed Point Theorems in Partially Ordered Metric Spaces and Applications. Nonlinear Analysis, 65, 1379-1393.
http://dx.doi.org/10.1016/j.na.2005.10.017 - 7. Guo, D. and Lakshmikantham, V. (1987) Coupled Fixed Points of Nonlinear Operators with Applications. Nonlinear Analysis, 11, 623-632.
http://dx.doi.org/10.1016/0362-546X(87)90077-0 - 8. Lakshmikantham, V. and Ciric, L. (2009) Coupled Fixed Point Theorems for Nonlinear Contractions in Partially Ordered Metric Spaces. Nonlinear Analysis, 70, 4341-4349.
http://dx.doi.org/10.1016/j.na.2008.09.020 - 9. Choudhury, B.S. and Kundu, A. (2010) A Coupled Coincidence Point Result in Partially Orderedmetric Spaces for Compatible Mappings. Nonlinear Analysis, 73, 2.
http://dx.doi.org/10.1016/j.na.2010.06.025 - 10. Samet, B., Vetro, C. and Vetro, P. (2012) Fixed Point Theorems for α-ψ-Contractive Type Mappings. Nonlinear Analysis, 75, 2154-2165.
http://dx.doi.org/10.1016/j.na.2011.10.014 - 11. Shatanawi, W., Samet, B. and Abbas, M. (2012) Coupled Fixed Point Theorems for Mixed Monotone Mappings in Ordered Partial Metric Spaces. Mathematical and Computer Modelling, 55, 680-687.
- 12. Abdeljawad, T. (2012) Coupled Fixed Point Theorems for Partially Contractive Type Mappings. Fixed Point Theory and Applications, 2012, 148.
- 13. Aydi, H., Samet, B. and Vetro, C. (2011) Coupled Fixed Point Results in Cone Metric Spaces for W-Compatible Mappings. Fixed Point Theory and Applications, 2011, 27.
- 14. Choudhury, B.S., Das, K. and Das, P. (2012) Coupled Coincidence Point Results for Compatible Mappings in Partially Ordered Fuzzy Metric Spaces. Fuzzy Sets and Systems, 222, 84-97.
- 15. Amini-Harandi, A. (2013) Coupled and Tripled Fixed Point Theory in Partially Ordered Metric Spaces with Application to Initial Value Problem. Mathematical and Computer Modelling, 57, 2343-2348.
- 16. Jungck, G. (1996) Compatible Mappings and Common Fixed Points. International Journal of Mathematics and Mathematical Sciences, 9, 771-779.
- 17. Karapinar, E. and Samet, B. (2012) Generalized α-ψ-Contractive Type Mappings and Related Fixed Point Theorems with Applications. Abstract and Applied Analysis, 2012, Article ID: 793486.
- 18. Luong, N.V. and Thuan, N.X. (2011) Coupled Fixed Points in Partially Ordered Metric Spaces and Application. Nonlinear Analysis: Theory, Methods & Applications, 74, 983-992.
http://dx.doi.org/10.1016/j.na.2010.09.055 - 19. Nashine, H.K., Samet, B. and Vetro, C. (2012) Coupled Coincidence Points for Compatible Mappings Satisfying Mixed Monotone Property. The Journal of Nonlinear Science and Applications, 5, 104-114.
- 20. Nashine, H.K., Kadelburg, Z. and Radenović, S. (2012) Coupled Common Fixed Point Theorems for W*-Compatible Mappings in Ordered Cone Metric Spaces. Applied Mathematics and Computation, 218, 5422-5432.
http://dx.doi.org/10.1016/j.amc.2011.11.029 - 21. Samet, B. and Vetro, C. (2010) Coupled Fixed Point, F-Invariant Set and Fixed Point of N-Order. Annals of Functional Analysis, 1, 46-56.
http://dx.doi.org/10.15352/afa/1399900586 - 22. Samet, B. and Vetro, C. (2011) Coupled Fixed Point Theorems for Multi-Valued Nonlinear Contraction Mappings in Partially Ordered Metric Spaces. Nonlinear Analysis, 74, 4260-4268.
http://dx.doi.org/10.1016/j.na.2011.04.007 - 23. Sintunavarat, W., Cho, Y.J. and Kumam, P. (2012) Coupled Fixed Point Theorems for Nonlinear Contractions without Mixed Monotone Property. Fixed Point Theory and Applications, 2012, 170.
























