Applied Mathematics
Vol.05 No.21(2014), Article ID:52590,6 pages
10.4236/am.2014.521329
Loose Waves in Viscoelastic Cylindrical Wave Guide with Radial Crack
Ismail Ibragimovich Safarov, Maqsud Sharipovich Akhmedov, Zafar Ihterovich Boltaev
Bukhara Technological-Institute of Engineering, Bukhara, Republic of Uzbekistan
Email: safarov54@mail.ru, maqsud.axmedov.1985@mail.ru, lazizbek.axmedov.2011@mail.ru
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 October 2014; revised 2 November 2014; accepted 16 November 2014
ABSTRACT
The main features are the length of the waveguide in one direction, as well as limitations and localization of the wave beam in other areas. There is described the technique of the solution of tasks on distribution of waves in an infinite cylindrical waveguide with a radial crack. Also numerical results are given in the article. Viscous properties of the material are taken into account by means of an integral operator Voltaire. Research is conducted in the framework of the spatial theory of visco elastic. The technique is based on the separation of spatial variables and formulates the boundary eigenvalue problem that can be solved by the method of orthogonal sweep Godunov. In the given paper we obtain numeric values of the phase velocity depending on of wave numbers. The obtained numerical results are compared with the known data. This work is continuation of article [1] . Statement of the problem and methodology of partial solutions are described in [1] . In this work, we present a complete statement of the problem, methods of solution and discuss the numerical results.
Keywords:
The Wave Guide, Wave, Cylinder, Crack, Integral Operator, Differential Equations, Relaxation Kernel Orthogonal Sweep, Approximation, Partial Derivatives, The Phase Velocity, Frequency, Damping Factor

1. Introduction
Propagation of waves in a cylinder was the subject in numerous theoretical and experimental investigations. Wave propagation in the cylinder was investigated by Pochhammer L. [2] and Chree Ch. [3] . For an elastic layer (two-dimensional problem) similar results were obtained by Rayleigh [4] . The first numerical results relating to some of the characteristics of normal waves in the layer were given in Lamb H. [5] . The problem of wave propagation in a solid cylinder is investigated in Hrinchenko and Myaleshka V.V. [6] . Many construction and engineering design work in dynamic conditions consist of deformable bodies with viscoelastic (damping) properties. Damping capacity of the material plays an important role in the dynamic behavior of the structure. This leads to a significant weakening of the natural oscillation and reduces the oscillation amplitude. The damping capacity of the material plays a huge role in the dynamic behavior of the structure. The work deals with harmonic waves in a spatial cylinder of the radial cracked considering the damping capacity of the material.
2. Statement of the Problem
This work examined the distribution of free waves in an infinite cylinder with radial cracks with outer and inner radii. Viscoelastic cylinder with a radial crack is a limiting case of a wedge with an angle of 360˚. The problem of propagation of harmonic waves in the infinite elastic cylinder with radial crack is put in cylindrical coordinates of R,
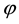 and z [7] :
and z [7] :
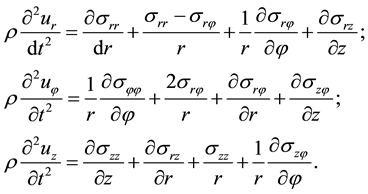 (1)
(1)
Here
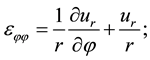 (2)
(2)
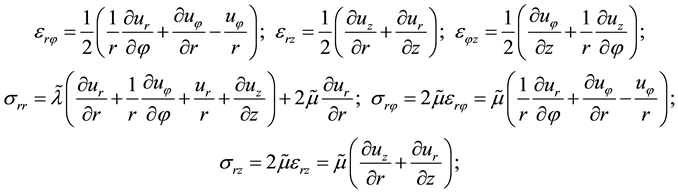 (3)
(3)
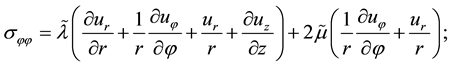
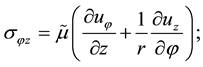
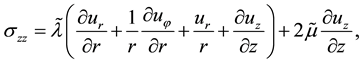
where
 (4)
(4)
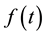 ―a function;
―a function;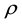 ―density materials,
―density materials,
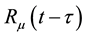 and
and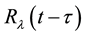 ―the core relaxation,
―the core relaxation,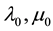 ―the instantaneous modulus of elasticity of a viscoelastic medium,
―the instantaneous modulus of elasticity of a viscoelastic medium,
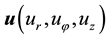 is the vector displacement which depends on
is the vector displacement which depends on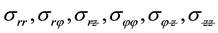 ―the components of the stress tensor;
―the components of the stress tensor;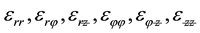 ―the components of the strain tensor. Equation (4) after the application of the method of freezing [8] takes the following form:
―the components of the strain tensor. Equation (4) after the application of the method of freezing [8] takes the following form:
where




complex frequency




where



The boundary conditions are specified as:


Condition (3) at r = 0 in the physical plane can be interpreted as the result of a limiting transition from of a hollow cylinder with a free inner surface to the solid, the inner radius tends to zero.
In the case of harmonic waves traveling along the axis z, the solution of (5), (6) and (7) allows the separation of variables:

where
To clarify the physical meaning of the given case:
1)
2)
In view of (8), the problem (6), (7) are transformed into a spectral boundary value problem for a system of ordinary differential equations with complex the coefficient:

where
On the boundary conditions at



Thus we have obtained the spectral problem (9) and (10) describing the propagation of harmonic waves in infinite elastic cylinder with a radial cracks.
Note, that the choice of boundary conditions on the edges of the slit in the form (4) to determine first of all the possibility of separation of variables r and


Indeed, performing the change of variables so as to satisfy the condition (11)
Obtain the spectral boundary value problem

with boundary conditions:

Not difficult to see that the problem (12), (13) is reduced to the problem (9), (10) by replacing.
Thus, we obtained the spectral problem (10) describing of the propagation of harmonic wave in an infinite cylinder with a radial crack.
A boundary value problem for a system equation in partial derivatives (10) can be kept to boundary value problem for a system of ordinary differential equations using method of lines, which will be used in solving a software unit orthogonal sweep method. According to the method of a rectangular domain of definition of the basic unknowns was covered by lines parallel to the r-axis and evenly spaced. The solution is sought only on these line sand the derivative in the direction of φ, is replaced approximations finite differences. Useful approximate formula of second order for first and the second derivative have the form:


where i varies from 0 to


By central differences (14) and (15) are used for internal lines (1 < i < N), the difference left and right allow taking into account the boundary conditions on φ. In the first case, the derivative with respective to φ in the right sides of Equations (9) can be expressed by the formulas: 1 < i < N

The boundary conditions are


Similarly, the derivatives are presented for the forward with number i = N, taking into account the boundary conditions at

If anti of symmetry the conditions of the transverse oscillations of the cylinder is used, the number of lines possible to reduce by half.
Thus, the initial spectral problem (9) by means of sampling coordinates φ reduced to the problem (14)-(19).
3. The Numerical Results
The solution of (9) is satisfied by orthogonal sweep Marchuk [9] . Solution of the problem on the determination of the velocity of wave propagation and wave form is carried out by method of Muller [10] , without isolation of the complex parameter C (complex phase velocity), or ω―the complex frequency.
On each step the boundary-value problem (9) is solved by method of orthogonal pro-race. Phase velocity (C) and own numbers (ω) are defined from an equality condition to zero determinant of system and are calculated by the Gauss method. Dimensionless parameters in the problem are chosen so that the real and imaginary parts of the complex shear rate Сs the density ρ and outer radius R have the single value, A = 0.0022, α = 0.05, β = 0.05.
Figure 1 shows of the dispersion curves of the first two oscillation modes infinite elastic cylinder with the
Figure 1. Change in the real (СR) and imaginary (СI) parts of the phase velocity from. wave numbers.
Figure 2. Change in the real and imaginary parts mode shapes VR and VI by к.
radial fracture (curve 1 and 2). For comparison, the illustration shows dependence of the wave number of the phase velocity of the flexural vibration modes of the solid cylinder (curve 3) without a gap. Pohgomerom and Cree using special functions already found solution of the problem earlier.
We note the characteristics of the curve 3 in zero phase velocity is zero and infinity approaches the velocity of the Rayleigh wave for a half. In the case of a cylinder with the radial cracked parts first the real fashion has a cutoff frequency, and the phase velocity tends to infinity. At large wave numbers limit the phase velocity of this mode is also equal to the velocity of the Rayleigh wave. At the cutoff frequency of the axial displacement to zero vibration of the cylinder is held in plane strain condition. In this paper, this solution was used for testing tasks.
In the second mode at the cutoff frequency observed only axial movement, circular and radial displacements are zero. The evolution of forms of movement on the first and second modes, depending on the wave number is shown in Figure 2. The curves are numbered in increasing order of k. Note the strong dependence on the wave number of forms. With the growth of the wave, number for the first mode is localized oscillations near the outer surface of the cylinder. It is typical that the second mode, which is on the small wave numbers, is a form of predominantly axial vibration, with growth to gradually turn into a form of predominantly radial oscillations.
Accounting for the viscoelastic properties of the material allows reducing the amplitude of the of wave propagation by 10% - 15%, as well as allows us to estimate damping ability of the system as a whole.
References
- Safarov, I.I., Akhmedov, M.Sh., Nuriddinov, B.Z. and Sharipov, D.Sh. (2014) Waves in Viscoelastic Cylinder with the Radial Crack. Magazine “Young scientist”, 4, 61-66.
- Pochhammer, L. (1876) Über die Fortpflanzung segechwindigkeiten schwingungen in einem unbergrawzten isotropen kreiscylinder. J.reine und angew. Math, 81, 324-336.
- Cri, C. (1886) Longitudinal Vibrations of a Corcablar Bar. Quart. J. Pure and Appl. Math, 21, 287-298.
- Rayleigh, J.W. (1885|1886) On Waves Propagated along the Plane Surface of an Classic Solid. Proceedings of the London Mathematical Society, 17, 4-11.
- Lamb, H. (1917) On Waves in an Elastic Plate. Proceedings of the Royal Society A, 93, 114-128.
- Hrinchenko, V.T. and Meleshko, V.V. (1981) Harmonic Oscillations and Waves in Elastic Bodies. Naukova Dumka, Kiev, 283 p.
- Safarov, I.I., Teshaev, M.K.H. and Boltaev, Z.I. (2012) Wave Processes in a Mechanical Waveguide. LAP LAMBERT Academic Publishing (Germany), 217 p.
- Kravchuk, A.S., Majboroda, V.P. and Urzhumaev, Y.S. (1985) Mechanics of Polymeric and Composite Materials: Experimental and Numerical Methods. Publishing Science, Moscow, 304 p.
- Marchuk, G.I. (1977) Methods of Computational Mathematics. Publishing Science, Moscow, 456 p.
- Bozorov, M.B., Safarov, I.I. and Shokin, Y.I. (1996) Numerical Simulation of Oscillations Dissipative Homogeneous and Inhomogeneous Mechanical Systems. Publisher Siberian Branch of the Academy of Sciences, Novosibirsk, 188 p.












