Applied Mathematics
Vol.05 No.19(2014), Article ID:51329,10 pages
10.4236/am.2014.519299
Habitat Loss, Uneven Distribution of Resources and Fragmented Landscapes― A Resource Based Model of the Patch Size Effect
Paweł Adamski, Adam Marcin Ćmiel
Institute of Nature Conservation, Polish Academy of Sciences, Kraków, Poland
Email: adamski@iop.krakow.pl, cmiel@iop.krakow.pl
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 September 2014; revised 6 October 2014; accepted 18 October 2014
ABSTRACT
The problem of habitat fragmentation is recently an important issue in ecological research as well as in the practical approach of nature conservation. According to the most popular approaches, habitats are considered as the homogenous parts of the landscape. Also the metapopulation concept problem of the inert habitat heterogenity is considered quite seldom. These approaches have some weak points resulting from the assumption that the border between habitat patches and the metapopulation matrix is fairly sharp. This paper presents a resource-based concept of habitats, based on mathematical theory of point processes, which can be easily applied to analysing the problem of uneven distribution of resources. The basic assumption is that the random distribution of resources may be mathematically described as the realisation of a certain point process. According to our method, it is possible to calculate the expected quantities of available resources as well as the minimum area of habitat that includes the expected abundance of the resource. This approach may be very useful to understand some crucial phenomena in landscape ecology, such as the patch size effect and its connection to habitat loss and fragmentation.
Keywords:
Patch Size Effect, Allee Effect, Habitat Loss, Habitat Fragmentation, Poisson Process, Process Intensity, Critical Patch Size

1. Introduction
A number of researchers [1] - [3] regard a far-reaching fragmentation of habitats to be one of the most important challenges faced by theoreticians and practitioners of nature conservation. Most of the natural and―in recent decades―semi natural habitats, have been reduced to fragments of various size separated by roads, compact build-up areas or cultivated fields [4] [5] . The effects of such transformations exceed, markedly, the simple reductions in the size of population areas or changing the structures of existing metapopulations [6] . However quality of the fragmented habitat may be analysed with different assumptions which require a new approach and investigative tools [7] [8] .
In recent two decades, a number of theories have been developed in spatial population dynamics [9] - [11] . Most of these theories have been based on Levin’s [12] model of metapopulation dynamics and assume that the space consists of finite number of homogeneous patches, surrounded by empty matrix. It is a major simplification, as a result of which the models have been judged as largely unrealistic and have received significant criticism. More realistic models, not assuming the homogeneity of the habitat patches, were presented by Day and Possingham [13] , Frank and Wissel [14] , Hanski and Ovaskainen [15] [16] . In some of these models, the matrix has no longer been treated as homogeneous, but showing e.g. dispersible areas and barriers. Equally important is the fact that these models, called stochastic patch occupancy models (SPOM) take into account another feature important for the realism of the model, i.e. stochasticity. Hanski [17] distinguishes two types of stochasticity, which affect population dynamics―demographic stochasticity, including: reproductive parameters, mortality, migrations and environmental stochasticity, including: weather conditions, partial destruction of the habitat, habitat fragmentation. Among all these factors, the broadly defined habitat loss or deteriorating habitat quality. The population dynamics models, that take into account the shifts in habitat quality, are presented by Possingham and Noble [18] and Akceakaya and Ferson [19] , but they are criticized for their excessively many untested assumptions and a large number of parameters that are difficult to estimate [17] .
Anyway, ecologists and conservation biologists have used many measures of landscape structure, to predict the population dynamics consequences of habitat loss and fragmentation [20] . Even though the aforementioned models placed significant emphasis on the functioning of the whole metapopulation system, they also considered, to a lesser or greater extent, the patch size effect (PSE), associated with fragmentation or, simply, reduction of the patch area. The ample empirical data show that the densities of populations living in small patches of habitat are lower than those from large-size habitats [21] . This phenomenon is well known to naturalists, although explaining its mechanisms has sometimes not been easy [22] . There are generally two ways of explanation. According to the first one, the PSE is the result of the set of intrapopulation disorders observed in small populations and empirically described as so-called “Allee effect” [23] - [25] . The second approach is concentrated on the space-related environmental changes. Relatively well recognized within this approach is the issue of “edge effect” [26] , with the main considerations pertaining to aspects of the metapopulation [27] . Another concept assumes that with the progress of fragmentation, a major depletion of available resources can occur, although this has been relatively poorly researched [28] .
Many populations are ultimately limited by resources, and their abundance and distribution will determine the carrying capacity of an environment [29] . If these resources are not distributed evenly in the habitat, the loss of territory may lead to a disproportionately greater loss of the resources [30] . In a way, this assumption concurs with the practice of estimating randomly distributed resources. For several dozen years, the amounts of such resources have been estimated by extrapolating the results of small, representatively distributed study plots, onto the whole area under consideration [31] . Similar techniques also provide a basis for contemporary research, but the extrapolation process now takes into account the “edge effects” [26] and influences of the of neighbourhooding habitats [32] .
The extrapolation models are not particularly good in dealing with the fact that a random distribution of resources is, by definition, uneven [31] . Thus, when we divide a large area into several smaller ones, the required resources will almost certainly not be equally abundant in each part. Therefore, reliable modelling of the fragmentation process needs to solve both problems, namely the amount and distribution of resources. When the resources are not distributed randomly, but are associated with any easily distinguishable element of the habitat, e.g. river as a source of food and water, the situation is obvious. Any fragment without access to this resource (river) is useless to organisms which require permanent access to this resource e.g. amphibians. The situation becomes more complicated when the resources occur more or less randomly, and this situation seems to occur often. For example, the populations of cambiophages depend on the presence of weakened or wounded trees, which are randomly distributed throughout forests [33] . The situation becomes even more complicated, when limiting factors involve several resources that are strictly limited in terms of places of occurrence, such as in the case of Maculinea butterflies, which require food-plants and host-ant’s nests [34] . The aim of this study is to demonstrate that where there is a random distribution of resources, the effects of fragmentation can be successfully predicted by using the point processes theory [35] [36] .
The suggested approach is based on the assumption that the random distribution of resources may be mathematically perceived as a realisation of certain point process, e.g. Poisson process. In estimating therefore the intensity of the process, we can learn about the expected occurrence (number, quantity) of a given resource in the selected area. Consequently, we can also calculate the probability that the resource occurs in the given area. Moreover, we can also calculate the probability of the resource occurring in the given area in sufficient quantity to maintain minimum viable populations of certain species. Consequently, one may try to reliably determine the minimum areas required for viable populations. This mathematical tool may be crucial for the process of the locating and size optimisation of protected areas. The methods of estimating the intensity of the Poisson process were described at length by Ripley [37] . Possible applications of the point processes have been recently presented in landscape planning and nature conservation by Grabarnik and Sarkka [38] , who used those techniques for modelling the spatial structure of the forest, and in the field of random geometric graphs by [39] - [43] .
In this paper we would like to present the possibility of using point process in the more general resource- based analysis of the habitat loss mechanism.
2. Method
2.1. Point Processes
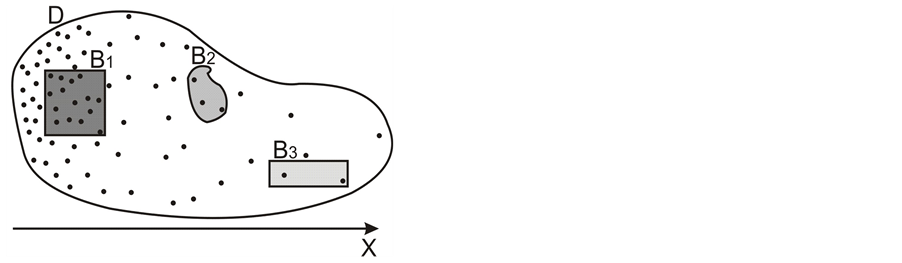
Let us denote a certain stochastic environment called state space by  (Figure 1). This set may represent a certain defined area for example forest or meadow. Let us denote by
(Figure 1). This set may represent a certain defined area for example forest or meadow. Let us denote by  a certain sub area of
a certain sub area of 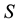 where we conduct our observations called observation space. Let us assume that the area
where we conduct our observations called observation space. Let us assume that the area 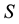 is an open terrain sowing by seeds of anemochorous plants. Other examples are the locations of birds’ nests, rocks, or towns. Of course, none of these is actually a point, but in each case the sizes of the objects are so small compared with the distances between them, that their size may be ignored [37] . Thus, seedlings appear in area
is an open terrain sowing by seeds of anemochorous plants. Other examples are the locations of birds’ nests, rocks, or towns. Of course, none of these is actually a point, but in each case the sizes of the objects are so small compared with the distances between them, that their size may be ignored [37] . Thus, seedlings appear in area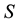 . One may try to describe such a process of sowing by giving the locations of particular seedlings treated as points on a plane. In practice it would be a long and laborious process because of the huge number of seedlings and the time which would be needed to search through the whole study area. Another way may involve the description via the number of points in selected parts of the observation space. We should call this space a sample space
. One may try to describe such a process of sowing by giving the locations of particular seedlings treated as points on a plane. In practice it would be a long and laborious process because of the huge number of seedlings and the time which would be needed to search through the whole study area. Another way may involve the description via the number of points in selected parts of the observation space. We should call this space a sample space . A detailed description of the scenery may be obtained by counting the frequency of points
. A detailed description of the scenery may be obtained by counting the frequency of points 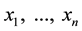 in subsets
in subsets  of
of . The experimental plots established in standard ecological studies are a particular example charged with additional assumptions [37] [44] . Let us assume that we observe
. The experimental plots established in standard ecological studies are a particular example charged with additional assumptions [37] [44] . Let us assume that we observe 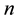 different points within the measurable state space
different points within the measurable state space 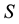 and the order of outcome is of no interest. Therefore, space
and the order of outcome is of no interest. Therefore, space 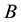 may be represented by the set
may be represented by the set
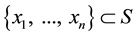 ―also called configuration. If we allow only the countable configurations, then for any con-
―also called configuration. If we allow only the countable configurations, then for any con-
figuration 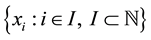 we can rewrite the number of points
we can rewrite the number of points 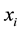 belonging to
belonging to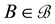 , where
, where 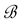

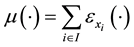
where 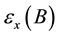
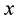
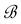
Figure 1. The example of certain two-dimensional point process with state space S, observation area D and sample set B. Black points represent the distribution of seedlings.
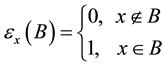
Such a discrete measure 
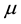

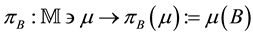
a projection or coordinate function with index B.
Let 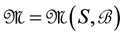

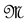
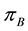
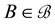
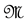

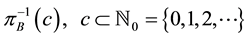
Let us now assume that the number and positions of the points may be random. Let 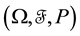
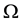

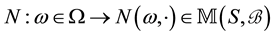
is called a point process on
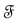
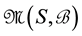

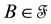
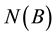
We know that any set 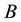
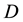

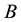


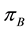
As we mentioned earlier, point process is a random point measure on the state space 
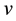
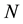
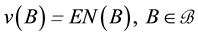
Hence, 
2.2. Poisson Process with a Finite Intensity Measure and Distribution of Resources
The basic point process is a Poisson process. Poisson processes are very convenient building blocks from which to generate other point processes. They can be regarded as the analogue of independent observations and are often called “random” outside mathematics [37] .
Let v be a finite intensity measure on the state space 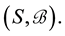





Figure 2. The random variable 
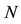
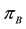
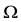
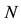
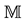
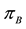
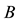
random variables for each natural 

Let us consider a vast open terrain, homogeneous in terms of its characteristics, such as, for example a muddy and dried bed of a shallow lake, and the locations of independently wind propagating seeds of one species selected from those colonising the area. The number of seeds which fall on one square metre of the area is a variable with Poisson distribution, which stems from the fact that there are many such seeds, each with little probability of landing on the marked square [44] . We may therefore, safely assume that the distribution of cells in the bed is a realisation of the Poisson process with intensity
2.3. Distribution of Resources and Patch Size Effect
Let us assume that the distribution of resources is a realisation of a certain Poisson process with the parameter
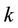
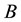

Obviously, the process does not have to have a constant measure of intensity, as the latter may change, for example, with the lapse of time

In such a case, the probability of the resource occurring 
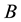
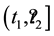
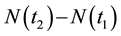
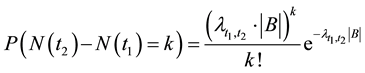
The intensity of a process can also depend on position, which in fact, is commonly seen in biology e.g. we can expect that number of seedlings decrease with distance from the plant producing wind dispersing seeds (Figure 3). In such a case, the probability of hitting exact quantity of recourse is equal to
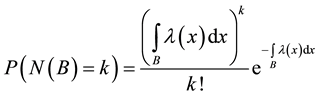
For the sake of simplification, in the following parts of this study, we will consider processes with a constant intensity measure
Figure 3. The intensity of a process can also depend on position 
3. Results
3.1. Habitat Loss and Patch Size Effect
Let us consider a situation where one resource 
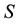

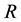
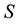
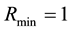


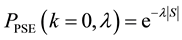
By using (7) we can present the relationship between the size of the area 
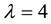

3.2. Number and Quantity of Resources and Patch Size Effect
In biological examples, however, the key is often not the occurrence of the resource alone, but also that it occurs in certain quantities. The example of such a situation could be the presence of shoots of a host plant required to maintain the assumed population abundance of an insect [45] . In the suggested approach, the interpretation of such a case is a situation where a greater number of resource occurrence is required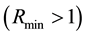
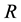
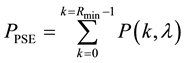
Hence, when the occurrence of the given species is only possible when the given resource occurs in the defined area a minimum of three times, the probability of PSE occurring is equal to
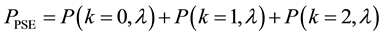
The relationship between the probability of PSE occurrence and the percentage decrease in habitat area size, for three intensity levels: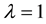



Figure 4. The probability of the PSE occurrence (P) depending on the percentage loss of area

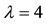
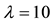
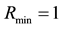
Let us have a closer look at the relationship between the intensity of the process and the minimum amount of the resource and their effects on probability of the PSE occurrence (Figure 5(a)). It can been clearly seen that the less intensive the process, the higher the probability of the PSE occurrence, even for low values of minimum resource quantity. The higher the 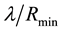
The theory of point processes may be also applied in the analysis of availability of a number of different resources―which is, in biological terms, much closer to the real situation. Let us consider the simplest situation, where we have two resources 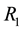
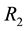
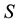
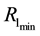
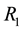
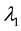
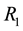
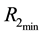

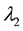
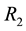
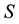

where 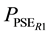

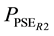

3.3. Critical Patch Size
The crucial question at the patch scale is how much habitat must be conserved to ensure the persistence of populations [46] . The best-known models for critical patch size are KISS models [47] and Skellam [48] . In current usage, a KISS model is generally interpreted as a reaction-diffusion equation for a population density on a bounded region, with the coefficients of the equation being constant in the region and the density falling to zero on the boundary of the region [49] . An example that we shall address in the present article is critical patch size and its connection to the distribution of resources. Using the point processes theory, we can calculate the minimum size of the habitat patch, where the quantity of resources needed to support a population is to occur with a certain level of probability.
Example
Let us assume that the persistence of a certain population in the area 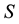
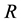

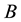
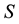
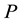
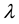


Figure 5. The influence of the Poisson process intensity and minimum quantity of resource (a) and of the ratio 
Let us illustrate this with a simple example (Figure 6). Let us assume that our state space 








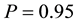
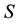
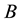
4. Conclusion―Consequences for Practice
One of the most important aspects of practical nature conservation is to establish protected areas whose objective is to preserve naturally a considerable level of biological diversity, as well as the natural characteristics of ecological processes [50] [51] . So far theoretical aspects of the relationship between the patch size and the level of biodiversity it harbours have been discussed in detail [50] [52] - [56] . However, the issue of minimum area necessary to maintain a viable population of a certain species is still a topic of discussion. Because of the widespread occurrence of the phenomenon, a number of studies have focused on the relationships between habitat patches [3] [14] [20] only marginally treating the issue of single patch size. On the other hand, the IUCN guidelines on the planning of protected areas, recommend that they should possibly cover rather large areas. In a number of studies on the planning of protected areas, the area of a habitat is seen as a kind of indirect measure of population abundance [57] [58] . However, in the case of the diversified internal structure of a habitat, this assumption may lead to the occurrence of serious artifacts, which were theoretically and empirically demonstrated by [59] . The use of knowledge rooted in the theory of point processes, as suggested in this study, allows one to determine the probability of a decrease in the availability of resources in tandem with the diminishing habitat patch size. This approach offers an objective way to find the level of threat in different variants of decreasing area size. The question still to be answered is, which level of probability may provide a basis for creating reliable models of the effect of decreasing patch size, upon the availability of resources and hence on the status of the populations depending on them. The approach proposed in this paper offers only answers concerning the decrease in resources. This situation is analogous with the results of population vulnerability analysis (PVA), which determine the probability of extinction of the population within a certain time [60] - [63] . The levels of probability of extinction at which monitoring or protective actions should commence, largely depend on arbitrary decisions depending on the importance of the species, the global status of the threatened species, as well as other detailed factors [64] [65] . The possibility of practical use of the point processes theory, in finding the biological consequences of fragmentation or designing protected areas, increases the widespread application of the GIS systems in these fields [66] -[68] . This can help in the development of tools permitting a more precise determination of the effects of disappearance or fragmentation of habitats, and prevention of the adverse effects of such processes.
Figure 6. Critical patch size. The example shows that the critical patch size falls into the given range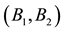
Acknowledgements
We are grateful to Wojciech Solarz from the Institute of Nature Conservation PAS for his valuable suggestions and comments during preparation of the paper. This study was funded by Institute of Nature Conservation PAS and partly by a Polish State Committee for Scientific Research/National Science Centre grant No. N N304 325836.
Cite this paper
PawełAdamski,Adam MarcinĆmiel,Adam MarcinĆmiel, (2014) Habitat Loss, Uneven Distribution of Resources and Fragmented Landscapes—A Resource Based Model of the Patch Size Effect. Applied Mathematics,05,3206-3216. doi: 10.4236/am.2014.519299
References
- 1. Coughley, G. (1994) Directions in Conservation Biology. Journal of Animal Ecology, 63, 215-244.
http://dx.doi.org/10.2307/5542 - 2. Wiens, J.A. (1997) Metapopulation Dynamics and Landscape Ecology. In: Hanski, I. and Gilpin, M.E., Eds., Metapopulation Biology Ecology, Genetics and Evolution, Academic Press, Waltham, 43-68.
- 3. Parker, M. and MacNally, R. (2002) Habitat Loss and the Habitat Fragmentation Threshold: An Experimental Evaluation of Impacts on Richness and Total Abundances Using Grassland Invertebrates. Biological Conservation, 105, 217-229.
http://dx.doi.org/10.1016/S0006-3207(01)00184-7 - 4. Forman, R.T.T. and Collinge, S.K. (1997) Nature Conserved in Changing Landscapes with and without Spatial Planning. Landscape and Urban Planning, 37, 129-135.
http://dx.doi.org/10.1016/S0169-2046(96)00378-7 - 5. Trombulak, S.C. and Frissell, C.A. (2000) Review of the Ecological Effects of Roads on Terrestrial and Aquatic Ecosystems. Conservation Biology, 14, 18-30.
http://dx.doi.org/10.1046/j.1523-1739.2000.99084.x - 6. Nowicki, P., Pepkowska, A., Kudlek, J., Skorka, P., Witek, M., Settele, J. and Woyciechowski, M. (2007) From Metapopulation Theory to Conservation Recommendations: Lessons from Spatial Occurrence and Abundance Patterns of Maculinea Butterflies. Biological Conservation, 140, 119-129.
http://dx.doi.org/10.1016/j.biocon.2007.08.001 - 7. Sih, A., Jonsson, B.G. and Luikart, G. (2000) Habitat Loss: Ecological, Evolutionary and Genetic Consequences. Trends in Ecology and Evolution, 15, 132-134.
http://dx.doi.org/10.1016/S0169-5347(99)01799-1 - 8. Fischer, M. (2000) Species Loss after Habitat Fragmentation. Trends in Ecology and Evolution, 15, 396.
http://dx.doi.org/10.1016/S0169-5347(00)01977-7 - 9. Tilman, D. and Kareiva, P. (1997) Spatial Ecology. Princeton University Press, Princeton.
- 10. Bascompte, J. and Sole, R.V. (1998) Modeling Spatiotemporal Dynamic in Ecology. Springer, New York.
- 11. Hanski, I. (1999) Metapopulation Ecology. Oxford University Press, New York.
- 12. Levins, R. (1969) Some Demographic and Genetic Consequences of Environmental Heterogeneity for Biological Control. Bulletin of the Entomological Society of America, 15, 237-240.
- 13. Day, J.R. and Possingham, H.P. (1995) A Stochastic Metapopulation Model with Variability in Patch Size and Position. Theoretical Population Biology, 48, 333-360.
http://dx.doi.org/10.1006/tpbi.1995.1034 - 14. Frank, K. and Wissel, C. (1998) Spatial Aspects of Metapopulation Survival—From Model Results to Rules of Thumb for Landscape Management. Landscape Ecology, 13, 363-379.
http://dx.doi.org/10.1023/A:1008054906030 - 15. Hanski, I. and Ovaskainen, O. (2003) Metapopulation Theory for Fragmented Landscapes. Theoretical Population Biology, 64, 119-127.
http://dx.doi.org/10.1016/S0040-5809(03)00022-4 - 16. Ovaskainen, O. and Hanski, I. (2004) From Individual Behavior to Metapopulation Dynamics: Unifying the Patchy Population and Classic Metapopulation Models. American Naturalist, 164, 364-377.
http://dx.doi.org/10.1086/423151 - 17. Hanski, I. (1998) Metapopulation Dynamics. Nature, 396, 41-49.
http://dx.doi.org/10.1038/23876 - 18. Possingham, H.P. and Noble, I.R. (1991) An Evaluation of Population Viability Analysis for Assessing the Risk of Extinction: Research Consultancy for the Resource Assessment Commission. In: Forest and Timber Inquiry, Australian Government Printing Office, Canberra.
- 19. AkcËakaya, H.R. and Ferson, S. (1992) RAMAS/Space User Manual: Spatially Structured Population Models for Conservation Biology. Applied Biomathematics, New York.
- 20. Hanski, I. aËnd Ovaskainen, O. (2000) The Metapopulation Capacity of a Fragmented Landscape. Nature, 404, 755-758.
http://dx.doi.org/10.1038/35008063 - 21. Bender, D.J., Contreras, T.A. and Fahrig, L. (1998) Habitat Loss and Population Decline: A Meta-Analysis of the Patch Size Effect. Ecology, 79, 517-533.
http://dx.doi.org/10.1890/0012-9658(1998)079[0517:HLAPDA]2.0.CO;2 - 22. Estades, C.F. (2001) The Effect of Breeding-Habitat Patch Size on Bird Population Density. Landscape Ecology, 16, 161-173.
http://dx.doi.org/10.1023/A:1011197432467 - 23. Berec, L., Angulo, E. and Courchamp, F. (2007) Multiple Allee Effects and Population Management. Trends in Ecology and Evolution, 22, 185-191.
http://dx.doi.org/10.1016/j.tree.2006.12.002 - 24. Greene, C.M. (2003) Habitat Selection Reduces Extinction of Populations Subject to Allee Effects. Theoretical Population Biology, 64, 1-10.
http://dx.doi.org/10.1016/S0040-5809(03)00025-X - 25. Vercken, E., Kramer, A.M., Tobin, P.C. and Drake, J.M. (2011) Critical Patch Size Generated by Allee Effect in Gypsy Moth, Lymantria dispar (L.). Ecological Letters, 14, 179-86.
http://dx.doi.org/10.1111/j.1461-0248.2010.01569.x - 26. Olson, D. and Androw, D. (2008) Patch Edges and Insect Populations. Oecologia, 155, 549-558.
http://dx.doi.org/10.1007/s00442-007-0933-6 - 27. Ries, L. and Sisk, T.D. (2004) A Predictive Model of Edge Effects. Ecology, 85, 2917-2926.
http://dx.doi.org/10.1890/03-8021 - 28. Mortelliti, A. and Boitani, L. (2008) Interaction of Food Resources and Landscape Structure in Determining the Probability of Patch Use by Carnivores in Fragmented Landscapes. Landscape Ecology, 23, 285-298.
http://dx.doi.org/10.1007/s10980-007-9182-7 - 29. Lopez-Sepulcre, A. and Kokko, H. (2005) Territorial Defense, Territory Size and Population Regulation. American Naturalist, 166, 317-329.
http://dx.doi.org/10.1086/432560 - 30. Witkowski, Z. and Adamski, P. (1997) Vanishing Process and Restoration Project of the Apollo Butterfly in the Pieninymts. In: Farina, A., Ed., Perspectives in Ecology, Proceedings of VII international Congress of Ecology, Backhuys Publishers, Leiden, 136-140.
- 31. Brower, J.A. and Zar, J.H. (1977) Field and Laboratory Methods for General Ecology. William C. Brown Company, Dubuque.
- 32. Luoto, M., Kuussaari, M., Rita, H., Salminen, J. and von Bonsdorff, T. (2001) Determinants of Distribution and Abundance in the Clouded Apollo Butterfly: A Landscape Ecological Approach. Ecography, 24, 601-617.
http://dx.doi.org/10.1034/j.1600-0587.2001.d01-215.x - 33. Feurdean, A. and Willis, K.J. (2008) The Usefulness of a Long-Term Perspective in Assessing Current Forest Conservation Management in the Apusseni Natura Park, Romania. Forest Ecology and Management, 226, 421-430.
http://dx.doi.org/10.1016/j.foreco.2008.04.050 - 34. Nowicki, P., Witek, M., Skórka, P., Settele, J. and Wojciechowski, M. (2005) Population Ecology of the Endangered Butterflies Maculinea teleius and M. nausithous and the Implications for Conservation. Population Ecology, 47, 193-202.
http://dx.doi.org/10.1007/s10144-005-0222-3 - 35. Daley, D.J. and Vere-Jones, D. (1988) An Introduction to the Theory of Point Processes. Springer, New York.
- 36. Reiss, R.D. (1993) A Course on Point Processes. Springer, New York.
http://dx.doi.org/10.1007/978-1-4613-9308-5 - 37. Ripley, B.D. (2004) Spatial Statistics. John Wiley & Sons, Inc., Hoboken.
- 38. Grabarnik, P. and Sarkka, A. (2009) Modelling the Spatial Structure of Forest Stands by Multivariate Point Processes with Hierarchical Interactions. Ecological Modelling, 220, 1232-1240.
http://dx.doi.org/10.1016/j.ecolmodel.2009.02.021 - 39. Penrose, M.D. (2003) Random Geometric Graphs. Oxford University Press, Oxford.
http://dx.doi.org/10.1093/acprof:oso/9780198506263.001.0001 - 40. Shang, Y. (2009) Exponential Random Geometric Graph Process Models for Mobile Wireless Networks. Proceedings of the International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery, Zhangjiajie, 10-11 October 2009, 56-61.
http://dx.doi.org/10.1109/CYBERC.2009.5342212 - 41. Shang, Y. (2010) On the Degree Sequence of Random Geometric Digraphs. Applied Mathematical Sciences, 41, 2001-2012.
- 42. Shang, Y. (2010) Laws of Large Numbers of Subgraphs in Directed Random Geometric Networks. International Electronic Journal of Pure and Applied Mathematics, 2, 69-79.
- 43. Ceyhan, E. (2014) Comparison of Relative Density of Two Random Geometric Digraph Families in Testing Spatial Clustering. TEST, 23, 100-134.
http://dx.doi.org/10.1007/s11749-013-0344-4 - 44. Skellam, J.G. (1952) Studies in Statistical Ecology. Biometrika, 39, 346-362.
- 45. Adamski, P. and Witkowski, Z. (2007) Effectiveness of Population Recovery Projects Based on Captive Breeding. Biological Conservation, 140, 1-7.
http://dx.doi.org/10.1016/j.biocon.2007.06.027 - 46. Fahrig, L. (2001) How Much Habitat Is Enough. Biological Conservation, 100, 65-74.
http://dx.doi.org/10.1016/S0006-3207(00)00208-1 - 47. Kierstead, H. and Slobodkin, L.B. (1953) The Size of Water Masses Containing Plankton Bloom. Journal of Marine Research, 12, 141-147.
- 48. Skellam, J.G. (1951) Random Dispersal in Theoretical Populations. Biometrika, 38, 196-218.
http://dx.doi.org/10.1093/biomet/38.1-2.196 - 49. Cantrell, R.S. and Cosner, C. (2001) Spatial Heterogeneity and Critical Patch Size: Area Effects via Diffusion in Closed Environments. Journal of Theoretical Biology, 209, 161-171.
http://dx.doi.org/10.1006/jtbi.2000.2246 - 50. Jackson, S.F., Gaston, K.J. and Kershaw, M. (2004) Size Matters: The Value of Small Populations for Wintering Water-birds. Animal Conservation, 7, 229-239.
http://dx.doi.org/10.1017/S1367943004001337 - 51. Jackson, S.F., Walker, K. and Gaston, K.J. (2009) Relationship between Distributions of Threatened Plants and Protected Areas in Britain. Biological Conservation, 142, 1515-1522.
http://dx.doi.org/10.1016/j.biocon.2009.02.020 - 52. Martinez, I., Carreno, F., Escudero, A. and Rubio, A. (2006) Are Threatened Lichen Species Well-Protected in Spain? Effectiveness of a Protected Areas Network. Biological Conservation, 133, 500-511.
http://dx.doi.org/10.1016/j.biocon.2006.08.003 - 53. Pressey, R.L. and Taffs, K.H. (2001) Scheduling Conservation Action in Production Landscapes: Priority Areas in Western New South Wales Defined by Irreplaceability and Vulnerability to Vegetation Loss. Biological Conservation, 100, 255-376.
http://dx.doi.org/10.1016/S0006-3207(01)00039-8 - 54. Pressey, R.L., Whish, G.L., Barrett, T.W. and Watts, M.E. (2002) Effectiveness of Protected Areas in North-Eastern New South Wales: Recent Trends in Six Measures. Biological Conservation, 106, 57-69.
http://dx.doi.org/10.1016/S0006-3207(01)00229-4 - 55. Rouget, M., Richardson, D.M. and Cowling, R.M. (2003) The Current Configuration of Protected Areas in the Cape Floristic Region, South Africa-Reservation Bias and Representation of Biodiversity Patterns and Processes. Biological Conservation, 112, 129-145.
http://dx.doi.org/10.1016/S0006-3207(02)00396-8 - 56. Canova, L. (2006) Protected Areas and Landscape Conservation in the Lombardy Plain (Northern Italy): An Appraisal. Landscape and Urban Planning, 74, 102-109.
http://dx.doi.org/10.1016/j.landurbplan.2004.10.002 - 57. Noss, R.F. (1996) Ecosystems as Conservation Targets. Trends in Ecology and Evolution, 11, 351-351.
http://dx.doi.org/10.1016/0169-5347(96)20058-8 - 58. Lombard, A.T., Cowling, R.M., Pressey, R.L. and Rebelo, A.G. (2003) Effectiveness of Land Classes as Surrogates for Species in Conservation Planning for the Cape Floristic Region. Biological Conservation, 112, 45-62.
http://dx.doi.org/10.1016/S0006-3207(02)00422-6 - 59. Paulin, M., Bélisle, M. and Cabeza, M. (2006) Within-Site Habitat Configuration in Reserve Design: A Case Study with a Peatland Bird. Biological Conservation, 128, 55-56.
http://dx.doi.org/10.1016/j.biocon.2005.09.016 - 60. Abrams, P.A. (2002) Will Small Population Sizes Warn Us of Impending Extinctions? American Naturalist, 160, 293-305.
http://dx.doi.org/10.1086/341521 - 61. Beissinger, S.R. (1995) Modeling Extinction in Periodic Environments—Everglades Water Levels and Snail Kite Population Viability. Ecological Applications, 5, 618-631.
http://dx.doi.org/10.2307/1941971 - 62. Holmes, E.E. (2004) Beyond Theory to Application and Evaluation: Diffusion Approximations for Population Viability Analysis. Ecological Applications, 14, 1272-1293.
http://dx.doi.org/10.1890/02-5088 - 63. Wagner, G. and Berger, U. (1996) A Population Vulnerability Analysis of the Red-Winged Grasshopper, Oedipoda Germanica (Caelifera: Acrididae). In: Settele, J., Margules, C., Poschlod, P. and Henle, K., Eds., Species Survival in Fragmented Landscapes, Kluwer Academic Publishers, Dordrecht, 312-319.
http://dx.doi.org/10.1007/978-94-009-0343-2_37 - 64. Andelman, S.J. and Fagan, W.F. (2000) Umbrellas and Flagships: Efficient Conservation Surrogates or Expensive Mistakes? Proceedings of the National Academy of Sciences of the United States of America, 97, 5954-5959.
http://dx.doi.org/10.1073/pnas.100126797 - 65. Holmes, E.E. and Fagan, W.E. (2002) Validating Population Viability Analysis for Corrupted Data Sets. Ecology, 83, 2379-2386.
http://dx.doi.org/10.1890/0012-9658(2002)083[2379:VPVAFC]2.0.CO;2 - 66. Baskent, E.Z. and Keles, S. (2005) Spatial Forest Planning: A Review. Ecological Modeling, 188, 145-173.
http://dx.doi.org/10.1016/j.ecolmodel.2005.01.059 - 67. Guo, M., Yu, W.B., Ma, M.G. and Li, X. (2008) Study on the Oasis Landscape Fragmentation in Northwestern China by Using Remote Sensing Data and GIS: A Case Study of Jinta Oasis. Environmental Geology, 54, 629-636.
http://dx.doi.org/10.1007/s00254-007-0830-7 - 68. Eigenbrod, F., Hecnar, S.J. and Fahrig, L. (2008) Accessible Habitat: An Improved Measure of the Effects of Habitat Loss and Roads on Wildlife Populations. Landscape Ecology, 23, 159-168.
http://dx.doi.org/10.1007/s10980-007-9174-7