Applied Mathematics
Vol.3 No.12(2012), Article ID:25599,7 pages DOI:10.4236/am.2012.312273
Homotopy Perturbation Method for the Generalized Hirota-Satsuma Coupled KdV Equation
Department of Mathematics, Faculty of Science, King AbdulAziz University, Jeddah, Saudi Arabia
Email: maturi_dalal@yahoo.com
Received October 2, 2012; revised November 2, 2012; accepted November 11, 2012
Keywords: Homotopy Perturbation Method; Generalized Hirota-Satsuma Coupled KdV Equation
ABSTRACT
In this paper, we consider the homotopy perturbation method (HPM) to obtain the exact solution of Hirota-Satsuma Coupled KdV equation. The results reveal that the proposed method is very effective and simple and can be applied to other nonlinear mathematical problems.
1. Introduction
A number of methods have been proposed in the literature recently for solving different kinds of physical and mathematical problems. Among those methods are: the homotopy perturbation method [1-7], the variational iteration method [8-22] and the domain decomposition method [23]. An elementary introduction to the homotopy perturbation method can be found in [24]. Improved homotopy perturbation method is given in [25-29]. Some applications of He’s homotopy perturbation method [1] are proposed in [30-35]. Homotopy perturbation method is useful for solving many different kinds of linear and nonlinear problems as explored in [36-49] and for numerical solution of 12th order boundary value problems as in [50]. It can be said that He’s homotopy perturbation method is a universal approach and that is able to solve various kinds of nonlinear equations. For example, it was applied to nonlinear Burger’s equation [51-53], to the Fisher’s equation [54-57], and solitary wave solutions for a generalized Hirota-Satsuma coupled KdV equation [58-60]. Solution of the Hirota-Satsuma KdV equation with the aid of homotopy perturbation method, adomian decomposition method, variational iteration method and homotopy analysis method can be found in [61-66].
2. Homotopy Perturbation Method (HPM)
To illustrate the basic idea of this method, we consider the following general non-linear differential equation:
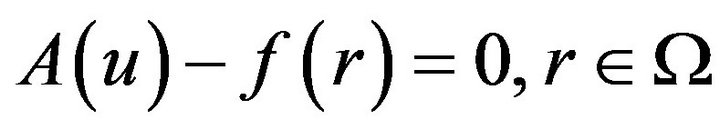 (1)
(1)
with the following boundary conditions:
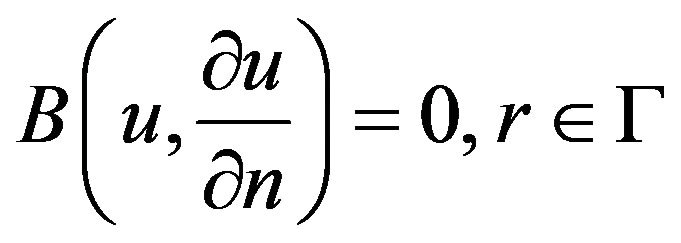
where  is a general differential operator,
is a general differential operator, 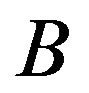 is a boundary operator,
is a boundary operator, 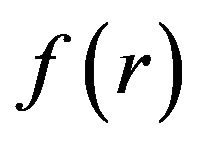 is a known analytical function and
is a known analytical function and ![]() is the boundary of the domain
is the boundary of the domain .
.
The operator  can be decomposed into a linear part and a non-linear one, designated as
can be decomposed into a linear part and a non-linear one, designated as ![]() and
and  respectively. Hence Equation (1) can be written as the following form:
respectively. Hence Equation (1) can be written as the following form:
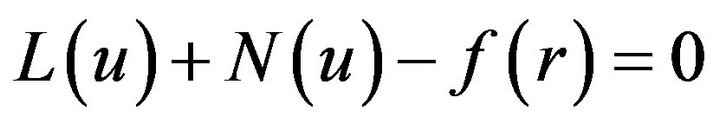
Using homotopy technique, we construct a homotopy 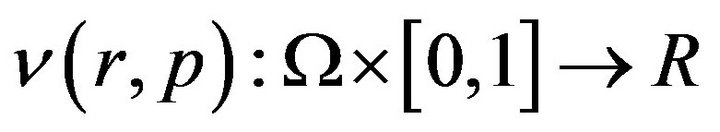 which satisfies:
which satisfies:
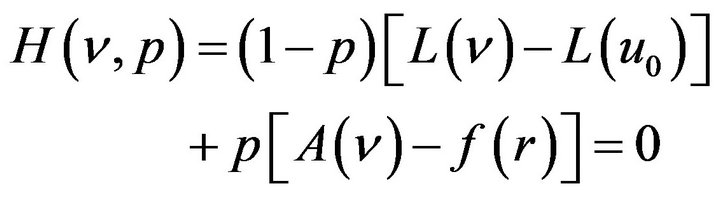 (2)
(2)
where 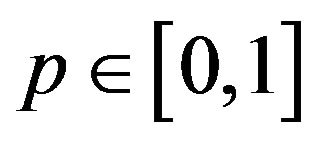 is an embedding parameter and
is an embedding parameter and 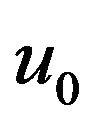 is an initial approximation of Equation (1) which satisfies the boundary conditions. Obviously, from Equation (2) we have
is an initial approximation of Equation (1) which satisfies the boundary conditions. Obviously, from Equation (2) we have
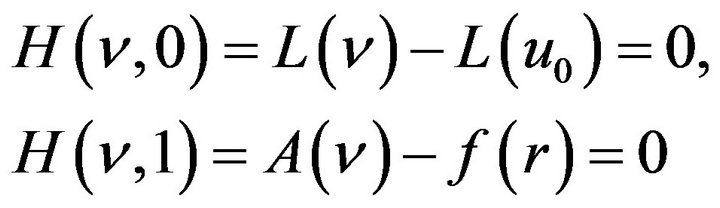
By changing the value of ![]() from zero to unity,
from zero to unity,  changes from
changes from 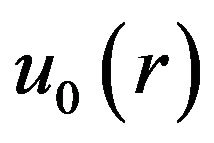 to
to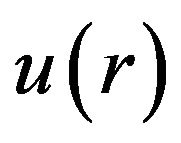 , in topology this is called Deformation and
, in topology this is called Deformation and 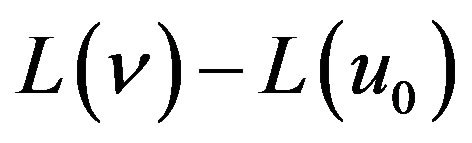 and
and 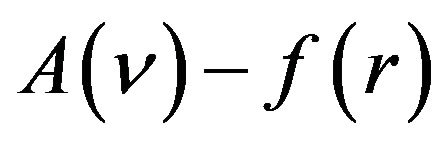 are called Homotopic. Due to the fact that
are called Homotopic. Due to the fact that  can be considered as a small parameter, hence we considered as a small parameter, hence we consider the solution of Equation (2) as a power series in
can be considered as a small parameter, hence we considered as a small parameter, hence we consider the solution of Equation (2) as a power series in ![]() as the following:
as the following:

setting  results in the approximate solution for Equation (1),
results in the approximate solution for Equation (1),
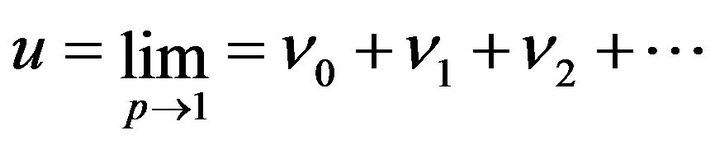
3. Method of Solution
In this section, we consider the generalized Hirota-Satsuma Coupled KdV equation,
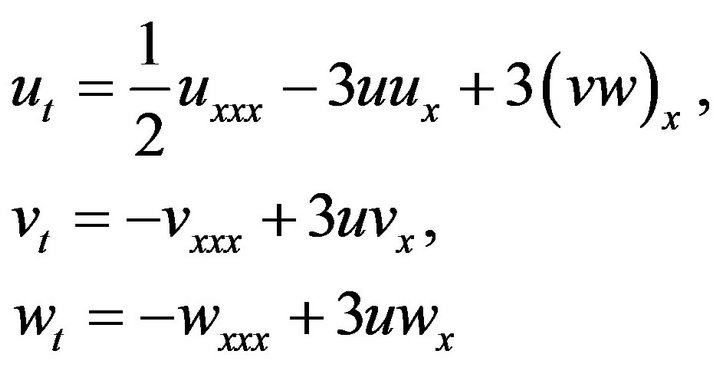 (3)
(3)
with the following initial conditions:
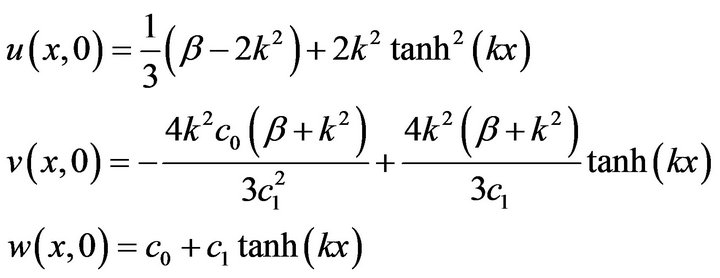
Using homotopy perturbation method, we construct a homotopy in the following from:
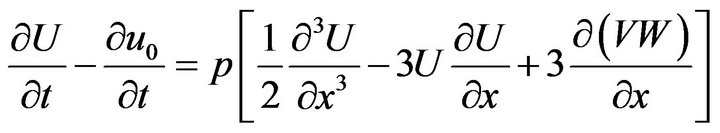 (4)
(4)
 (5)
(5)
 (6)
(6)
Suppose the solution of Equations (4), (5) and (6) has the form
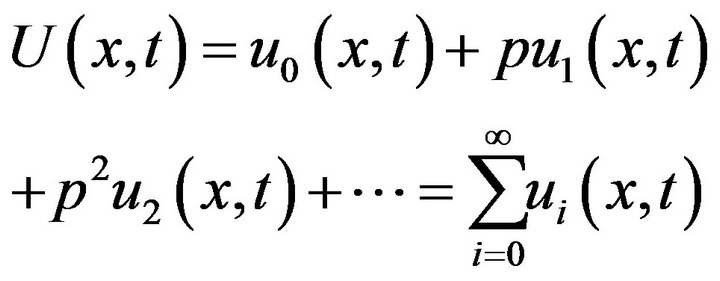 (7)
(7)
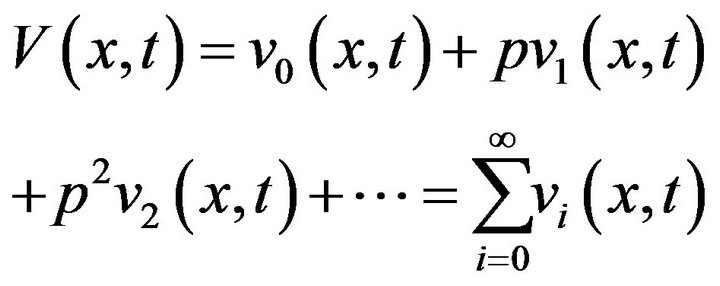 (8)
(8)
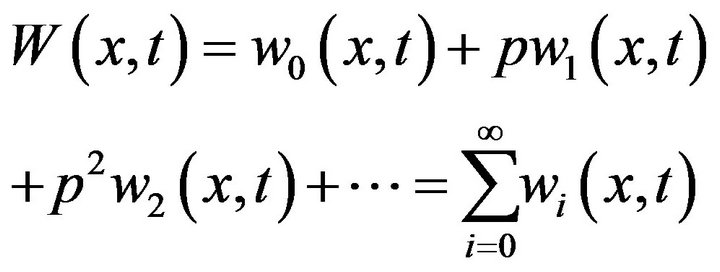 (9)
(9)
where  are functions yet to be determined. Substituting Equations (7), (8) and (9) into Equations (4), (5) and (6), respectively, and equating the terms with identical powers of
are functions yet to be determined. Substituting Equations (7), (8) and (9) into Equations (4), (5) and (6), respectively, and equating the terms with identical powers of![]() , we have
, we have
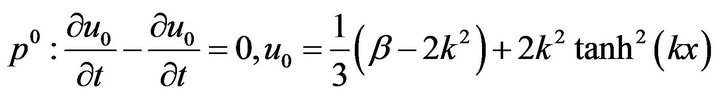

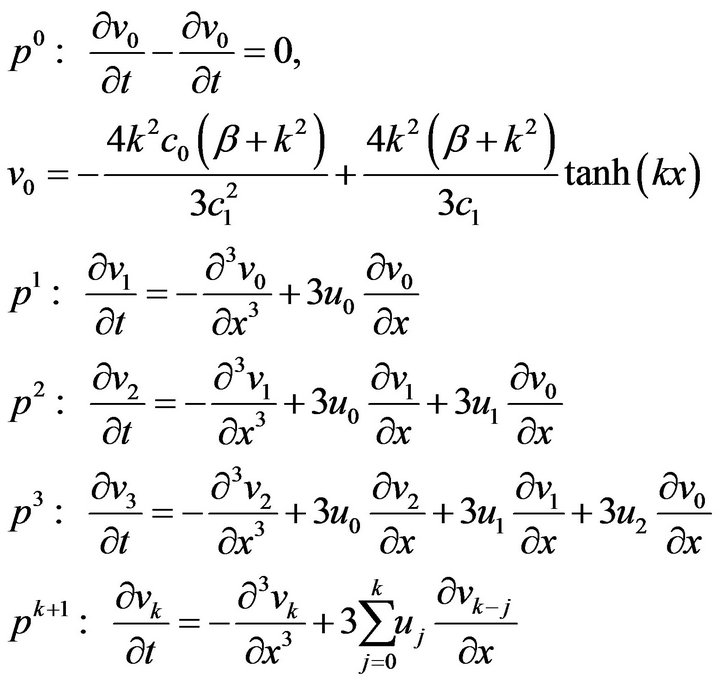
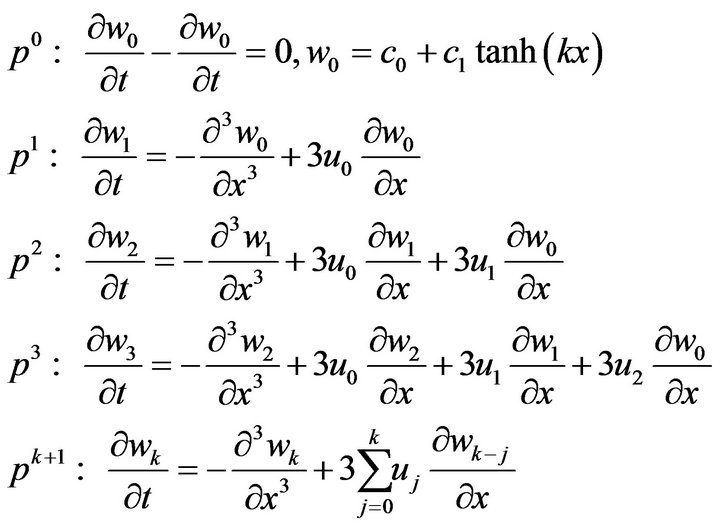
Therefore, the exact solution of Equation (3) can be obtained by setting , i.e.
, i.e.
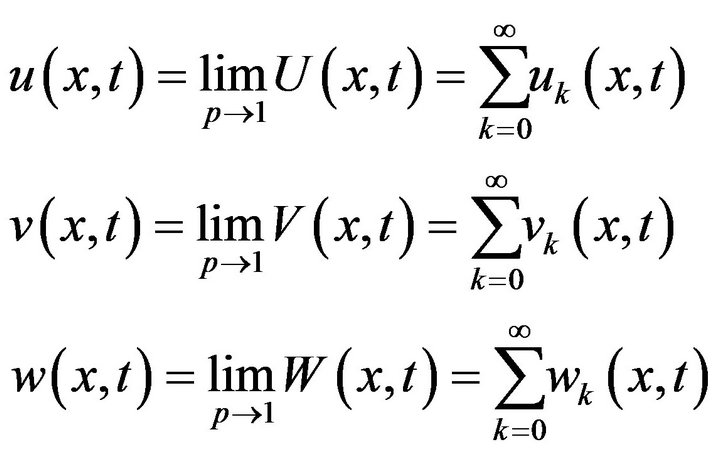
Solving the systems accordingly with using Matlab7.8, thus we obtain,


and so on for other components. The solution in a closedform is given by
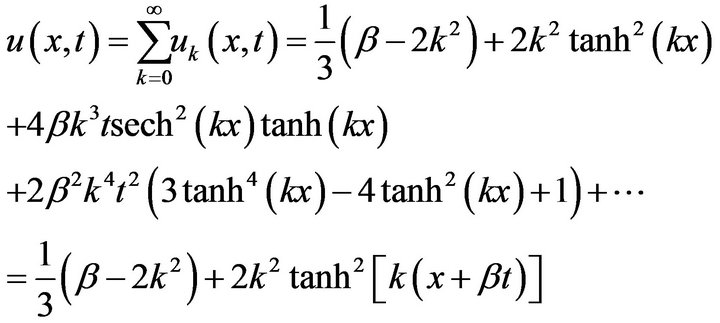
The 3D exact solution of , for
, for , obtained by HPM is given in Figure 1.
, obtained by HPM is given in Figure 1.
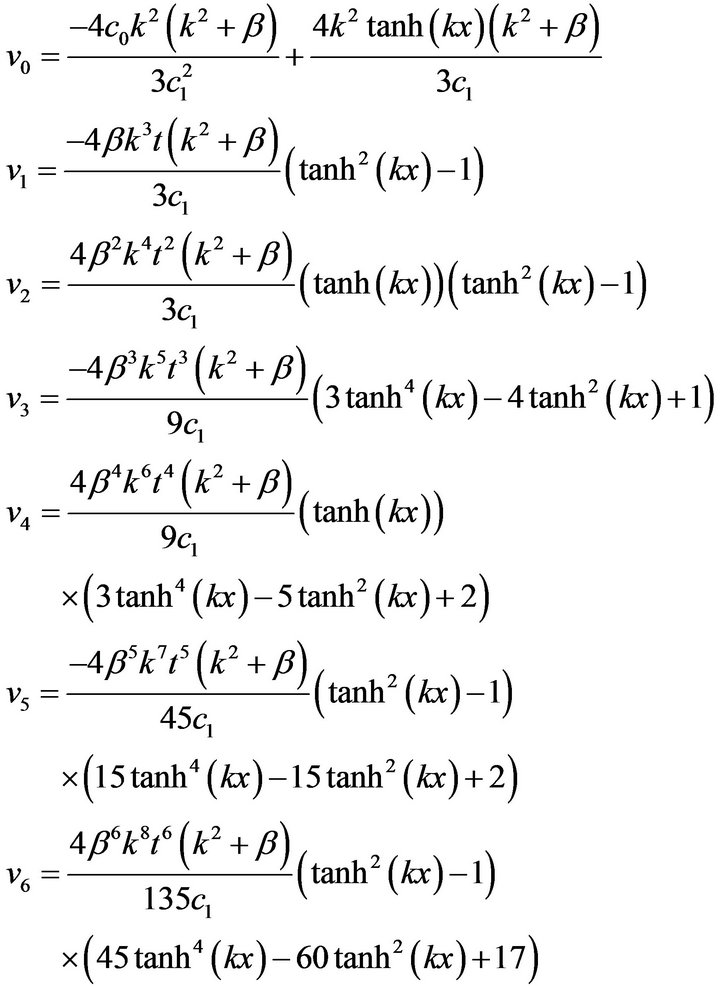
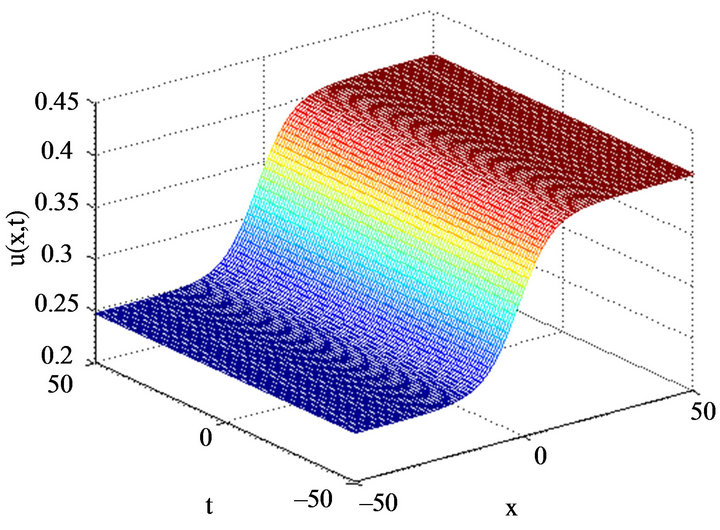
Figure 1. The 3D exact solution of u(x, t), for k = 0.1, β = 1.
and so on for other components. The solution in a closedform is given by
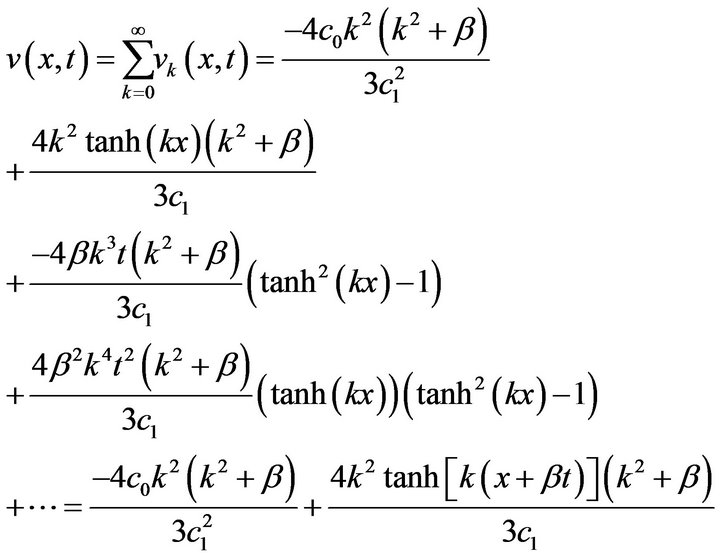
The 3D exact solution of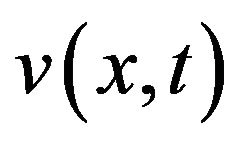 , for
, for 
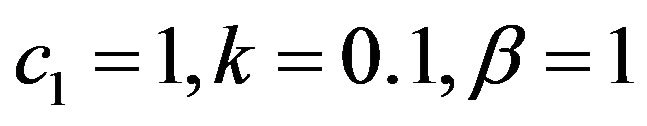 , obtained by HPM is given in Figure 2.
, obtained by HPM is given in Figure 2.
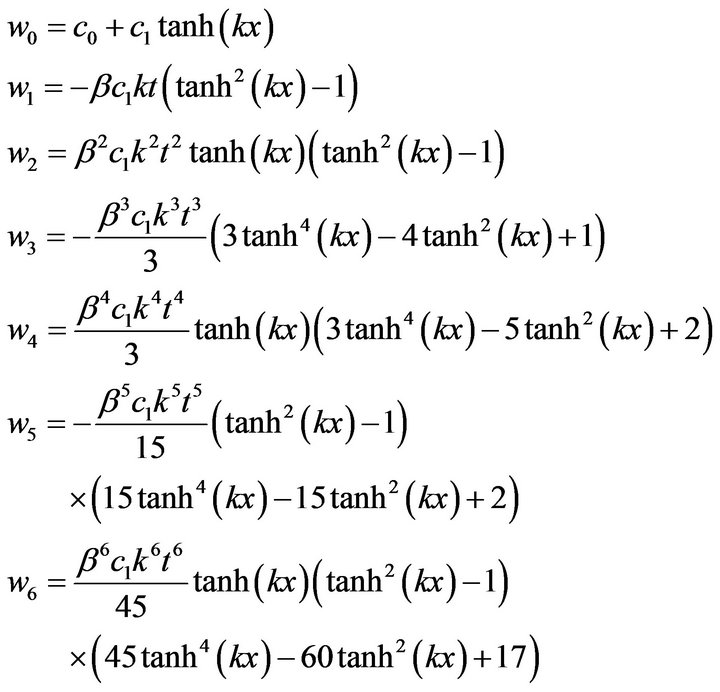

Figure 2. The 3D exact solution of v(x, t), for c0 = 1, c1 = 1, k = 0.1, β = 1.
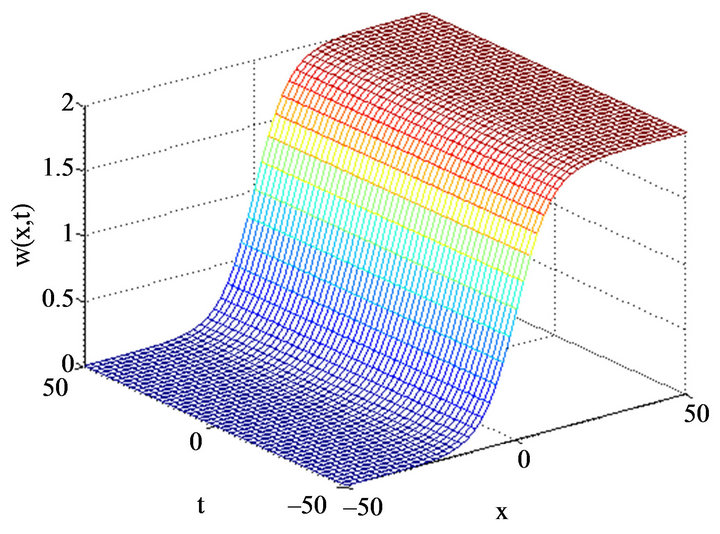
Figure 3. The 3D exact solution of w(x, t), for c0 = 1, c1 = 1, k = 0.1, β = 1.
and so on. The solution in a closed-form is given by
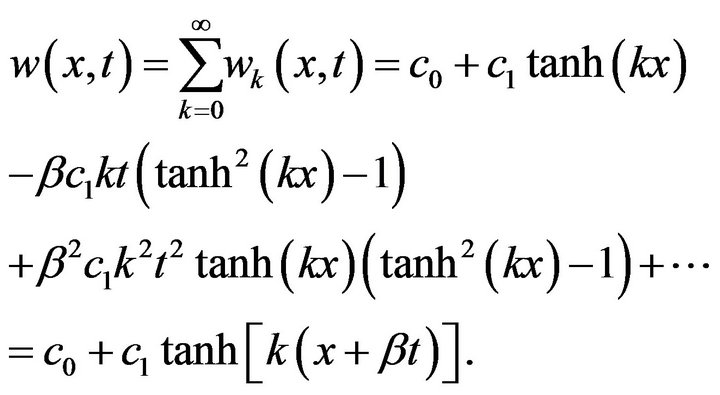
The 3D exact solution of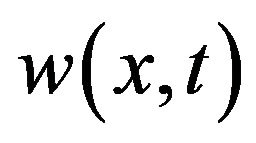 , for
, for 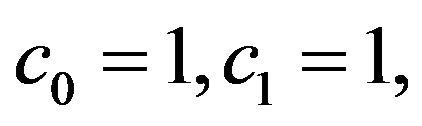
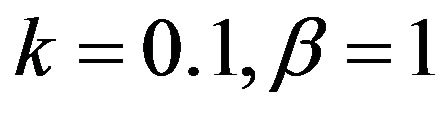 , obtained by HPM is given in Figure 3.
, obtained by HPM is given in Figure 3.
4. Conclusion
In this paper, the homotopy perturbation method was used for finding solutions of a generalized Hirota-Satsuma coupled KdV equation with initial conditions. It can be concluded that the homotopy perturbation method is very powerful and efficient technique in finding exact solutions for wide classes of problems. In our work we use the MATLAB to calculate the series obtained from the homotopy perturbation method.
REFERENCES
- J. H. He, “Homotopy Perturbation Technique,” Computer Methods in Applied Mechanics and Engineering, Vol. 178, No. 3-4, 1999, pp. 257-262. doi:10.1016/S0045-7825(99)00018-3
- J. H. He, “A Coupling Method of a Homotopy Technique and a Perturbation Technique for Non-Linear Problems,” International Journal of Non-Linear Mechanics, Vol. 35, No. 1, 2000, pp. 37-43. doi:10.1016/S0020-7462(98)00085-7
- J. H. He, “Homotopy Perturbation Method: A New NonLinear Analytical Technique,” Applied Mathematics and Computation, Vol. 135, No. 1, 2003, pp. 73-79. doi:10.1016/S0096-3003(01)00312-5
- J. H. He, “Asymptotology by Homotopy Perturbation Method,” Applied Mathematics and Computation, Vol. 156, No. 3, 2004, pp. 591-596. doi:10.1016/j.amc.2003.08.011
- J. H. He, “Application of Homotopy Perturbation Method to Nonlinear Wave Equations,” Chaos, Solitons and Fractals, Vol. 26, No. 3, 2005, pp. 695-700. doi:10.1016/j.chaos.2005.03.006
- J. H. He, “Homotopy Perturbation Method for Solving Boundary Value Problems,” Physics Letters A, Vol. 350, No. 1-2, 2006, pp. 87-88. doi:10.1016/j.physleta.2005.10.005
- J. H. He, “New interpretation of homotopy perturbation method,” International Journal of Modern Physics B, Vol. 20, No. 18, 2006, pp. 2561-2568. doi:10.1142/S0217979206034819
- K. Batiha, “Approximate Analytical Solutions for TimeDependent Emden-Fowler-Type Equations by Variational Iteration Method,” American Journal of Applied Sciences, Vol. 4, No. 7, 2007, pp. 439-443. doi:10.3844/ajassp.2007.439.443
- J. Biazar and H. Ghazvini, “He’s Variational Iteration Metod for Solving Linear and Non-Linear Systems of Ordinary Differential Equations,” Applied Mathematics and Computation, Vol. 191, No. 1, 2007, pp. 287-297. doi:10.1016/j.amc.2007.02.153
- A. Yildirim, “Applying He’s Variational Iteration Method for Solving Differential-Difference Equation,” Mathematical Problems in Engineering, Vol. 2008, 2008, Article ID: 869614. doi:10.1155/2008/869614
- M. T. Atay and S. B. Coskun, “Effects of Nonlinearity on the Variational Iteration Solutions of Nonlinear TwoPoint Boundary Value Problems with Comparison with Respect to Finite Element Analysis,” Mathematical Problems in Engineering, Vol. 2008, 2008, Article ID: 857296. doi:10.1155/2008/857296
- M. A. Noor and S. T. Mohyud-Din, “Modified Variational Iteration Method for Goursat and Laplace Problems,” World Applied Sciences Journal, Vol. 4, No. 4, 2008, pp. 487-498.
- M. Matinfar, H. Hosseinzadeh and M. Ghanbari, “Exact and Numerical Solution of Kawahara Equation by the Variational Iteration Method,” Applied Mathematical Sciences, Vol. 2, No. 43, 2008, pp. 2119-2126.
- A. R. Noiey, D. D. Ganji, M. Naghipour and A. Barari, “Solutions of Nonlinear Oscillator Differential Equations Using the Variational Iteration Method,” Journal of Physics: Conference Series, Vol. 96, 2008, Article ID: 012084. doi:10.1088/1742-6596/96/1/012084
- M. A. Noor, S. T. Mohyud-Din and M. Tahir, “Modified Variational Iteration Method for Thomas-Fermi Equation,” World Applied Sciences Journal, Vol. 4, No. 4, 2008, pp. 479-486.
- M. Kazemnia, S. A. Zahedi, M. Vaezi and N. Tolou, “Assessment of Modified Variational Iteration Method in BVPs of High Order Differential Equations,” Journal of Applied Sciences, Vol. 8, No. 22, 2008, pp. 492-497.
- M. A. Noor and S. T. Mohyud-Din, “Variational Iteration Method for Solving Initial and Boundary Value Problems of Bratu-Type,” Applications and Applied Mathematics: An International Journal, Vol. 3, No. 1, 2008, pp. 89-99.
- M. Matinfar, H. Hosseinzadeh and M. Ghanbari, “A Numerical Implementation of the Variational Iteration Method for the Lienard Equation,” World Journal of Modelling and Simulation, Vol. 4, No. 3, 2008, pp. 205-210.
- M. Jiaqi, W. Hui, L. Wantao and L. Yihua, “Variational Iteration Solving Method for El Nino Phenomenon Atmospheric Physics of Nonlinear Model,” Acta Oceanologica Sinica, Vol. 24, No. 5, 2005, pp. 35-38.
- H. Jafari, A. Golbabai, E. Salehpoor and Kh. Sayehvand, “Application of Variational Iteration Method for Stefan Problems,” Applied Mathematical Sciences, Vol. 2, No. 60, 2008, pp. 3001-3004.
- A. Saadatmandi and M. Dehghan, “Variational Iteration Method for Solving a Generalized Pantograph Equation,” Computers and Mathematics with Applications, Vol. 58, No. 11-12, 2009, pp. 2190-2196. doi:10.1016/j.camwa.2009.03.017
- A. Fereidoom, M. Ghadimi, H. D. Kaliji, M. Efrai and S. Alinia, “Variational Iteration Method for Nonlinear Vibration of Systems with Linear and Nonlinear Stiffness,” International Journal of Research and reviews in Applied Sciences, Vol. 5, No. 3, 2010, pp. 260-263.
- A. M. Wazwaz, “Analytic Treatment for Variable Coefficient Fourth-Order Parabolic Partial Differential Equations,” Applied Mathematics and Computation, Vol. 123, No. 2, 2001, pp. 219-227. doi:10.1016/S0096-3003(00)00070-9
- J. H. He, “An Elementary Introduction to the Homotopy Perturbation Method,” Computers and Mathematics with Applications, Vol. 57, No. 3, 2009, pp. 410-412. doi:10.1016/j.camwa.2008.06.003
- Z. M. Odibat, “A New Modification of the Homotopy Perturbation Method for Linear and Nonlinear Operators,” Applied Mathematics and Computation, Vol. 189, No. 1, 2007, pp. 746-753. doi:10.1016/j.amc.2006.11.188
- E. Yusufoglu, “Improved Homotopy Perturbation Method for Solving Fredholm Type Integro-Differential Equations,” Chaos, Solitons and Fractals, Vol. 41, No. 1, 2009, pp. 28-37. doi:10.1016/j.chaos.2007.11.005
- M. A. Jafari and A. Aminataei, “Improved Homotopy Perturbation Method,” International Mathematical Forum, Vol. 5, No. 32, 2010, pp. 1567-1579.
- D. D. Ganji, A. R. Sahou and M. Famouri, “A New Modification of He’s Homotopy Perturbation Method of Rapid Convergence of Nonlinear Undamped Oscillators,” Journal of Applied Mathematics and Computing, Vol. 30, No. 1-2, 2009, pp. 181-192. doi:10.1007/s12190-008-0165-x
- H. Aminikhah and J. Biazar, “Exact Solution for HighOrder Integro-Differential Equation by NHPM,” International Journal of Nonlinear Science, Vol. 7, No. 4, 2009, pp. 496-500.
- M. Ghasemi, M. T. Kajani and E. Babolian, “Application of He’S Homotopy Perturbation Method to Nonlinear Integro-Differential Equations,” Applied Mathematics and Computation, Vol. 188, No. 1, 2007, pp. 538-548. doi:10.1016/j.amc.2006.10.016
- H. Jafari, M. Zabihi and M. Saidy, “Application of Homotopy Perturbation Method for Solving Gas Dynamics Equation,” Applied Mathematical Sciences, Vol. 2, No. 48, 2008, pp. 2393-2396.
- Y. Yu and H. Li, “Application of the Multistage Homotopy Perturbation Method to Solve a Class of Hyperchaotic Systems,” Ghaos, Solitons and Fratals, Vol. 42, No. 4, 2009, pp. 2330-2337. doi:10.1016/j.chaos.2009.03.154
- P. Roul, “Application of Homotopy Perturbation Method to Biological Population Model,” Applications and Applied Mathematics: An International Journal, Vol. 5, No. 10, 2010, pp. 13969-1378.
- A. Zakeri, A. Aminataei and Q. Jannati, “Application of He’s Homotopy Perturbation Method for Cauchy Problem of III-Posed Nonlinear Diffusion Equation,” Discrete Dynamics in Nature and Society, Vol. 2010, 2010, Article ID: 780207. doi:10.1155/2010/780207
- R. Grzymkowski, E. Hetmaniok and D. Stota, “Application of the Homotopy Perturbation Method for Calculation of the Temperature Distribution in the Cast-Mould Heterogeneous Domain,” Journal of Achievements in Materials and Manufacturing Engineering, Vol. 43, No. 1, 2010, pp. 299-309.
- M. Meran, “Homotopy Perturbation Method for Solving a Model for HIV Infection of CD4+ Cells,” Istanbul Ticaret Universitesi Fen Bilimleri Dergisi, Vol. 12, No. 6, 2007, pp. 39-52.
- Y. X. Wang, H. Y. Si and L. F. Mo, “Homotopy Perturbation Method for Solving Reaction-Diffusion Equations,” Mathematical Problems in Engineering, Vol. 2008, 2008, Article ID: 795838. doi:10.1155/2008/795838
- Y. Chen and H. An, “Homotopy Perturbation Method for a Type of Nonlinear Coupled Equations with Parameters Derivatives,” Applied Mathematics and Computation, Vol. 204, No. 2, 2008, pp. 764-772. doi:10.1016/j.amc.2008.07.018
- J. Biazar and F. Azimi, “He’s Homotopy Perturbation Method for Solving Helmholtz Equation,” International Journal of Contemporary Mathematical Sciences, Vol. 3, No. 15, 2008, pp. 739-744.
- L. Jin, “Homotopy Perturbation Method for Solving Partial Differential Equations with Variable Coefficients,” International Journal of Contemporary Mathematical Sciences, Vol. 3, No. 28, 2008, pp. 1395-1407.
- M. Fazeli, S. A. Zahedi and N. Tolou, “Explicit Solution of Nonlinear Fourth-Order Parabolic Equations via Homotopy Perturbation Method,” Journal of Applied Sciences, Vol. 8, No. 14, 2008, pp. 2619-2624. doi:10.3923/jas.2008.2619.2624
- X. Li, M. Xu and X. Jiang, “Homotopy Perturbation Method to Time-Fractional Diffusion Equation with a Moving Boundary Condition,” Applied Mathematics and Computation, Vol. 208, No. 2, 2009, pp. 434-439. doi:10.1016/j.amc.2008.12.023
- A. Yildirim and H. Kocak, “Homotopy Perturbation Method for Solving the Space-Time Fractional Advection-Dispersion Equation,” Advances in Water Resources, Vol. 32, No. 12, 2009, pp. 1711-1716. doi:10.1016/j.advwatres.2009.09.003
- M. M. Mousa and A. Kaltayev, “Solving Inhomogeneous Wave Equation Cauchy Problems Using Homotopy Perturbation Method,” World Academy of Science, Engineering and Technology, Vol. 55, 2009, pp. 505-508.
- N. B. Desai and M. N. Mehta, “A Solution of Seepage of Ground Water in Soil: Homotopy Perturbation Method,” International Journal of Applied Mathematics and Mechanics, Vol. 6, No. 2, 2010, pp. 85-92.
- M. M. Rashidi and D. D. Ganji, “Homotopy Perturbation Combined with Pade Approximation for Solving Two Dimensional Viscous Flow in the Extrusion Process,” International Journal of Nonlinear Science, Vol. 7, No. 4, 2009, pp. 387-394.
- M. J. Hosseini, M. Gorji and M. Ghanbarpour, “Solution of Temperature Distribution in a Radiating Fin Using Homotopy Perturbation Method,” Mathematical Problems in Engineering, Vol. 2009, 2009, Article ID: 831362. doi:10.1155/2009/831362
- M. S. H. Ghowdhury, I. Hashim and A. F. Ismail, “Analytical Treatment of System of Linear and Nonlinear PDEs by Homotopy-Perturbation Method,” Proceedings of the World Congress on Engineering III, London, 30 June-2 July 2010, pp. 1860-1863.
- J. A. Rad and K. Parand, “Analytical Solution of Gas Flow through a Micro-Nano Porous Media by Homotopy Perturbation Method,” World Academy of Science, Engineering and Technology, Vol. 61, 2010, pp. 546-550.
- M. A. Othman, A. M. S. Mahdy and R. M. Farouk, “Numerical Solution of 12th Order Boundary Value Problems by Using Homotopy Perturbation Method,” Journal of Mathematic and Computer Science, Vol. 1, No. 1, 2010, pp. 14-27.
- N. H. Sweilam and M. M. khader, “Exact Solution of Some Coupled Nonlinear Partial Differential Equations Using the Homotopy Perturbation Method,” Computers and Mathematics with Applications, Vol. 58, No. 11-12, 2009, pp. 2134-2141. doi:10.1016/j.camwa.2009.03.059
- C. Zeng, Q. Yang and B. Zhang, “Homotopy Perturbation Method for Fractional-Order Burgers-Poisson Equation,” Preprint submitted to Elsevier, March, 2010.
- N. Taghizadeh, M. Akbari and A. Ghelichzadeh, “Exact Solution of Burgers Equations by Homotopy Perturbation Method and Reduced Differential Transformation Method,” Australian Journal of Basic and Applied Sciences, Vol. 5, No. 5, 2011, pp. 580-589.
- M. Matinfar and M. Ghanbari, “Homotopy Perturbation Method for the Fisher’s Equation and It’s Generalized,” International Journal of Nonlinear Science, Vol. 8, No. 4, 2009, pp. 448-455.
- D. Agirseven and T. Ozis, “An Analytical Study for Fisher Type Equations by Using Homotopy Perturbation Method,” Computers and Mathematics with Applications, Vol. 60, No. 3, 2010, pp. 602-609. doi:10.1016/j.camwa.2010.05.006
- M. Matinfar, M. Mahdavi and Z. Reisy, “The Implementation of Variational Homotopy Perturbation Method for Fisher’s Equation,” International Journal of Nonlinear Science, Vol. 9, No. 2, 2010, pp. 188-194.
- M. Matinfar and M. Ghanbari, “Homotopy Perturbation Method for the Generalized Fisher’s Equation,” Journal of Applied Mathematics, Islamic Azad university of Lahijan, Vol. 7, No. 4, 2011, pp. 39-44.
- D. Kaya, “Solitary Wave Solutions for a Generalized Hirota-Satsuma Coupled KdV Equation,” Applied Mathematics and Computation, Vol. 147, No. 1, 2004, pp. 69- 78. doi:10.1016/S0096-3003(02)00651-3
- D. D. Ganji and M. Rafei, “Solitary Wave Solutions for a Generalized Hirota-Satsuma Coupled KdV Equation by Homotopy Perturbation Method,” Physics Letters A, Vol. 356, No. 2, 2006, pp. 131-137. doi:10.1016/j.physleta.2006.03.039
- [61] F. Kangalgil and F. Ayaz, “Solitary Wave Solutions for Hirota-Satsuma Coupled KdV Equation and Coupled mKdV Equation by Differential Transform Method,” The Arabian Journal for Science and Engineering, Vol. 35, No. 2D, 2010, pp. 203-213.
- [62] J. Biazar, K. Hosseini and P. Gholamin, “Homotopy Perturbation Method for Solving KdV and Sawada-Kotera Equations,” Journal of Applied Mathematics, Islamic Azad University of Lahijan, Vol. 6, No. 21, 2009, pp. 11- 16.
- [63] E. M. E. Zayed, T. A. Nofal and K. A. Gepreel, “On Using the Homotopy Perturbation Method for Finding the Travelling Wave Solutions of Generalized Nonlinear Hirota-Satsuma Coupled KdV Equations,” International Journal of Nonlinear, Science, Vol. 7, No. 2, 2009, pp. 159-166.
- [64] H. Zareamoghaddam, “Analytic Study for Solving Coupled KdV Equations,” Middle-East Journal of Scientific Research, Vol. 7, No. 6, 2011, pp. 1061-1064.
- [65] D. D. Ganji, G. A. Afrouzi and R. A. Talarposhti, “Explicit Solution of Homotopy-Perturbation Method for Some Fifth-Order KdV Equations and Comparing It with Other Methods,” Journal of Information and Computing Science, Vol. 3, No. 4, 2008, pp. 258-268.
- [66] S. T. Mohyud-din, M. A. Noor, “Variational Iteration Method for Solving Discete KdV Equation,” Bulletin of the Institute of Mathematics, Vol. 5, No. 1, 2010, pp. 69-73.
- [67] X. Li, “The Application of Homotopy Analysis Method to Solve the Coupled KdV Equations,” International Journal of Nonlinear Science, Vol. 11, No. 1, 2011, pp. 80-85.

