International Journal of Astronomy and Astrophysics
Vol.4 No.1(2014), Article ID:43985,30 pages DOI:10.4236/ijaa.2014.41023
A Cosmological Model without Singularity Based on RW Metric (1)
Shihao Chen1,2
1Yue-Hong Institute for Advanced Study, Yunnan University, Kunming, China
2Institute of Theoretical Physics, Northeast Normal University, Changchun, China
Email: shchen@nenu.edu.cn
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 25 December 2013; revised 23 January 2014; accepted 30 January 2014
ABSTRACT
A new conjecture is proposed that there are two sorts of matter called s-matter and v-matter which are symmetric, whose masses are positive, but whose gravitational masses are opposite to each other. Based on the conjecture and the SUS(5) × SUV(5) gauge group, a cosmological model has been constructed and the following inferences have been derived. There are two sorts of symmetry breaking called V-breaking and S-breaking. In the V-breaking, SUV(5) breaks finally to SUV(3) × UV(1) so that v-particles get their masses and form v-atoms and v-galaxies etc., while SUS(5) still holds so that s-fermions and s-gauge bosons are massless and form SUS(5) color-singlets. There is no interaction among the SUS(5) color-singlets except gravitation so that they distribute loosely in space, cannot be observed, and cause space to expand with an acceleration. Evolution of the universe is explained. There is no space-time singularity. There are the highest temperature and the least scale in the universe. It is impossible that the Plank temperature and length are arrived. A formula is obtained which describes the relation between a luminous distance and its redshift. A huge void is not empty, and is equivalent to a huge concave lens. The densities of hydrogen in the huge voids must be much less than that predicted by the conventional theory. The gravitation between two galaxies whose distance is long enough will be less than that predicted by the conventional theory. A black hole with its big enough mass will transform into a white hole.
Keywords:Cosmology: Theories; (Cosmology:) Early Universe; (Cosmology:) Inflation; (Cosmology:) Cosmological Parameters; Galaxies: Distances and Reshifts

1. Introduction
In view of the fact that the space-time singularity and the cosmological constant issues are not solved in the frame of the conventional theory up to now. We suggest two conjectures to solve the issues. Based on the conjectures, we construct a cosmological model. Based on this model, we solve the two issues, explain the evolution of the universe, primordial nucleosynthesis, cosmic microwave background radiation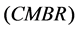 , and give three new predictions.
, and give three new predictions.
As is now well known, there is space-time singularity under certain conditions [1] . “These conditions fall into three categories. First, there is the requirement that gravity shall be attractive. Secondly, there is the requirement that there is enough matter present in some region to prevent anything escaping from that region. The third requirement is that there should be no causality violations” [1] . There must be space-time singularity in the conventional theory, because the conditions can be satisfied.
There should be no space-time singularity in physics, hence this problem must be solved. But it is not solved satisfactorily up to now.
In order to solve the space-time singularity problem, Ref. [2] [3] had assumed that there exists a fundamental length, i.e., the Planck length,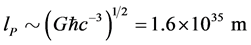 . There is no curvature corresponding to scale l < lp.
. There is no curvature corresponding to scale l < lp.
Based on this, they proposed the limiting curvature hypothesis. Thereby they had proved that all isotropic cosmological solutions are nonsingular. We find that its conclusion is included in the hypothesis. On the other hand, the model does not explain the expansion of the universe with an acceleration and cannot solve the cosmological constant problem.
The Planck length lp, time  and temperature
and temperature 
reveal that the quantum theory and the general relativity are not self-consistent. Relativity is a theory of continuous space-time geometry. But the presence of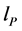 ,
,  and
and 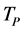 makes it virtually to come to a not continuous space-time structure. According to the conventional theory, only the quantum theory of gravity can solve the problem of not self-consistency. This is not true. According to the present model, there is no singularity of space-time, and there are the highest temperature
makes it virtually to come to a not continuous space-time structure. According to the conventional theory, only the quantum theory of gravity can solve the problem of not self-consistency. This is not true. According to the present model, there is no singularity of space-time, and there are the highest temperature  and the least scale
and the least scale  (see later). Consequently, it is impossible that
(see later). Consequently, it is impossible that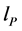 ,
, 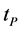 and
and  are arrived, because the transformation of the S-breaking and V-breaking from one to another at the highest temperature
are arrived, because the transformation of the S-breaking and V-breaking from one to another at the highest temperature . Thus, the quantum theory and the general relativity can be self-consistent, although the gravitational field is not quantized.
. Thus, the quantum theory and the general relativity can be self-consistent, although the gravitational field is not quantized.
Recent astronomical observations show that the universe expanded with a deceleration earlier, while it is expanding with an acceleration now [4] -[6] . This implies that there is dark energy. Among the total energy density of the universe, 73 percent is dark energy [4] -[6] . What is dark energy? Many possibilities have been suggested. One interpretation adopts the effective cosmological constant  where
where  and
and 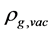 are the Einstein cosmological constant and the gravitational mass density of the vacuum state, respectively. The subscript “g” denotes the physical quantities relating to gravity in the following. According to the equivalence principle,
are the Einstein cosmological constant and the gravitational mass density of the vacuum state, respectively. The subscript “g” denotes the physical quantities relating to gravity in the following. According to the equivalence principle,  ,
, 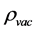 is the energy density of the vacuum state. Hence
is the energy density of the vacuum state. Hence  may be written as
may be written as 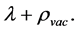
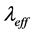 cannot be derived from basic theories [7] [8] , and
cannot be derived from basic theories [7] [8] , and . Hence the interpretation is unsatisfactory. Alternatively, dark energy is associated with the dynamics of scalar field
. Hence the interpretation is unsatisfactory. Alternatively, dark energy is associated with the dynamics of scalar field 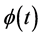 which is uniform in space [9] -[11] . This is a seesaw cosmology [12] . Thus, problem about the universe expansion with an acceleration is still open to the public.
which is uniform in space [9] -[11] . This is a seesaw cosmology [12] . Thus, problem about the universe expansion with an acceleration is still open to the public.
That  originates from the conventional quantum field theory and the equivalent principle. Both
originates from the conventional quantum field theory and the equivalent principle. Both  and the singularity issues imply that the conventional theory is incomplete. In some supersymmetric models,
and the singularity issues imply that the conventional theory is incomplete. In some supersymmetric models,  can be obtained. But this is not a necessary result of the supersymmetric quantum field theory. On the other hand, supersymmetric theory lacks of experiment bases. In contrast with the supersymmetric quantum field theory,
can be obtained. But this is not a necessary result of the supersymmetric quantum field theory. On the other hand, supersymmetric theory lacks of experiment bases. In contrast with the supersymmetric quantum field theory,  is a necessary result of our quantum field theory without divergence [13] -[15] . In this theory, there is no divergence of loop corrections as well, and dark matter which can form dark galaxies is predicted [16] [17] .
is a necessary result of our quantum field theory without divergence [13] -[15] . In this theory, there is no divergence of loop corrections as well, and dark matter which can form dark galaxies is predicted [16] [17] .
In fact, 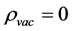 is not a necessary condition of
is not a necessary condition of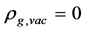 . We will see that although
. We will see that although 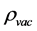 is divergent according to the conventional quantum field theory, we have still
is divergent according to the conventional quantum field theory, we have still  based on the present model.
based on the present model.
Huge voids in the cosmos have been observed [18] . Such a model in which hot dark matter (e.g. neutrinos) is dominant can explain the phenomenon. However, it cannot explain the structure with middle and small scales. Hence this is an open problem as well.
We consider that all important existing forms of matter (including dark matter and dark energy) have appeared. Hence these basic problems should be solved. As mentioned above, we have constructed a quantum field theory without divergence which predicts that there must be dark matter. We can construct a cosmological model which can solve the space-time singularity and cosmological constant issues and explain the evolution of the universe in the present paper.
The bases of the present model are the general relativity, the conventional quantum field theory for finite temperature and grand unified theory (GUT).
The basic idea of the present model is conjecture 1 in Section 2.
We consider the following condition to be necessary in order to solve the space-time singularity and the cosmological constant problems on the basis of the classical cosmology and the conventional quantum field theory.
Condition: There are two sorts of matter which are symmetric, whose gravitational masses are opposite to each other, although whose masses are all positive.
The two sorts of matter are called solid matter (s-matter) and void matter (v-matter), respectively. The condition implies that if  then
then  here
here 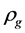 denotes a gravitational mass density. The conditions cannot be realized in the conventional theory, but can be realized in the present model. In order to uniformly solve the above four problems, we present a new conjecture equivalent to the condition and construct two cosmological model, i.e. [19] [20] and this model in the present paper.
denotes a gravitational mass density. The conditions cannot be realized in the conventional theory, but can be realized in the present model. In order to uniformly solve the above four problems, we present a new conjecture equivalent to the condition and construct two cosmological model, i.e. [19] [20] and this model in the present paper.
The present model has the following results:
 There is no space-time singularity in this model.
There is no space-time singularity in this model.
 It is derived from this model that there are the critical temperature
It is derived from this model that there are the critical temperature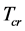 , the highest temperature
, the highest temperature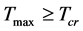 , the least scale
, the least scale 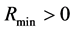 and the largest energy density
and the largest energy density 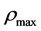 in the universe. Both
in the universe. Both 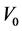 and
and 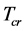 are new important constants. Both
are new important constants. Both  and
and 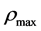 are finite. It is impossible that the Plank temperature
are finite. It is impossible that the Plank temperature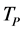 , length
, length 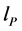 and time
and time 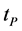 are arrived, because
are arrived, because , and
, and 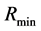 is not small. In general, the radius of a local inertial system is so large,
is not small. In general, the radius of a local inertial system is so large, 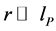 , that the quantum effects corresponding to
, that the quantum effects corresponding to  may be neglected.
may be neglected.
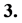 The evolution of the universe which is derived from this model are consistent with the observations up to now.
The evolution of the universe which is derived from this model are consistent with the observations up to now.
There are two sorts of spontaneous symmetry breaking in the present model because of conjecture 1, and they are called S-breaking and V-breaking.
According to the present model, the evolving process of space is as follows.
In the S-breaking, space can contract so that temperature ![]() rises. When
rises. When ![]() arrives the critical temperature
arrives the critical temperature , the universe is in the most symmetric state with
, the universe is in the most symmetric state with 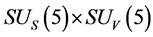 symmetry. When space continues to contract so that
symmetry. When space continues to contract so that ![]() arrives the highest temperature
arrives the highest temperature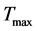 , space expands and then inflates. After inflation, the most symmetric state transits to the state with the V-breaking. After reheating, the evolving process is as follows: Space expands with a deceleration, expands with an acceleration, then expands with a deceleration, finally comes to static and begin to contract, in turn.
, space expands and then inflates. After inflation, the most symmetric state transits to the state with the V-breaking. After reheating, the evolving process is as follows: Space expands with a deceleration, expands with an acceleration, then expands with a deceleration, finally comes to static and begin to contract, in turn.
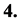 The relation between the optical distance and the redshift is derived from the present model. It is consistent with the observations up to now.
The relation between the optical distance and the redshift is derived from the present model. It is consistent with the observations up to now.
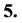 Equations governing nonrelativistic fluid motion are generalized to the present model. Galaxies can form earlier according to this model than that according to the conventional theory.
Equations governing nonrelativistic fluid motion are generalized to the present model. Galaxies can form earlier according to this model than that according to the conventional theory.
 Three predictions are given.
Three predictions are given.
 Primordial nucleosynthesis and cosmic microwave background radiation are explained.
Primordial nucleosynthesis and cosmic microwave background radiation are explained.
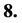 Dark energy is explained as s-matter when the universe is in the V-breaking. In contrast with the dark energy,
Dark energy is explained as s-matter when the universe is in the V-breaking. In contrast with the dark energy, 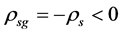 in the V-breaking.
in the V-breaking.

 is proved, although
is proved, although  is still very large. Consequently,
is still very large. Consequently, 
Problems 5 and 7 will be discussed in the following paper.
Section 2 is “Conjectures, action, energy-momentum tensor and field equations”; Section 3 is “Spontaneous symmetry breaking”; Section 4 is “Evolution equations”; Section 5 is “Temperature effect”; Section 6 is “Space can contract, but there is no singularity”; Section 7 is “Space inflation”; Section 8 is “Evolving process of space after inflation”; Section 9 is “After expansion with an acceleration, space expands with a deceleration, then comes to static and finally begin to contract”. Section 10 is “Existing and distribution forms of 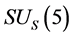 color singlets”. Section 11 is “New predictions, an inference, and there is no restriction for
color singlets”. Section 11 is “New predictions, an inference, and there is no restriction for ”; Section 12 is “Conclusions”.
”; Section 12 is “Conclusions”.
2. Conjectures, Action, Energy-Momentum Tensor and Field Equations
2.1. Conjectures
In order to solve the problems mentioned before, we propose the following conjectures:
Conjecture 1 There are two sorts of matter which are called solid-matter (s-matter) and void-matter (v-matter), respectively. Both are symmetric and the symmetric gauge group is 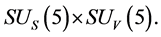 Both contributions to the Einstein tensor are opposite each other. There is no other interaction between both except interaction (2.10) of s-Higgs fields and v-Higgs fields.
Both contributions to the Einstein tensor are opposite each other. There is no other interaction between both except interaction (2.10) of s-Higgs fields and v-Higgs fields.
Conjecture 2 When 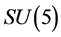 symmetry holds, there is the critical temperature
symmetry holds, there is the critical temperature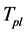 , all particles exist in
, all particles exist in  color singlets when
color singlets when .
.
Because of conjecture 1, there are two sorts of symmetry breaking which are called S-breaking in which 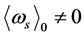 and
and 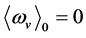 and V-breaking in which
and V-breaking in which  and
and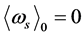 , here
, here 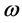 denotes an arbitrary Higgs field. The meanings of conjecture 1 are as follows. The model and its all inferences are invariant when
denotes an arbitrary Higgs field. The meanings of conjecture 1 are as follows. The model and its all inferences are invariant when ![]() and
and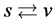 . The multiplet of
. The multiplet of  is the same as that of
is the same as that of  When temperature
When temperature , s-particles and v-particles are completely symmetric, here
, s-particles and v-particles are completely symmetric, here  is the critical temperature (see section 5. B); When temperature
is the critical temperature (see section 5. B); When temperature 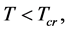
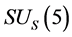 or
or 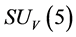 is broken. Let
is broken. Let  be broken, then
be broken, then 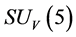 still holds.
still holds.
Conjecture 2 holds obviously. In fact, this conjecture is a direct generalization of SU(3) color singlets.
Another premise of the present model is the conventional SU(5) grand unified theory (GUT). But it is easily seen that the present model does not rely on the special GUT. Provided conjecture 1 and such a coupling as (2.10) are kept, the GUT can be applicable.
The gravitational properties of matter and the mode of symmetry breaking determine the features of spacetime. We consider that there are only two possibilities.
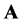 . The first possibility can be described by the conventional theory. There is only one sort of matter so that the equivalence principle strictly holds. This theory is simple, but there must be essential difficulties. For example, there must be the singularity and cosmological constant issues which cannot be solved in the frame of this theory because of the Hawking theorems etc.
. The first possibility can be described by the conventional theory. There is only one sort of matter so that the equivalence principle strictly holds. This theory is simple, but there must be essential difficulties. For example, there must be the singularity and cosmological constant issues which cannot be solved in the frame of this theory because of the Hawking theorems etc.
 The basis of the second possibility is conjecture 1.
The basis of the second possibility is conjecture 1.
We explain it in detail as follows:
 It must be emphasized that there is no negative mass or negative probability in the present model at all. Conjecture 1 implies that
It must be emphasized that there is no negative mass or negative probability in the present model at all. Conjecture 1 implies that  when
when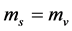 . In the S-breaking,
. In the S-breaking, 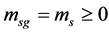 and
and 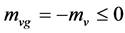 because of the reasons 6 - 7 below. Here
because of the reasons 6 - 7 below. Here 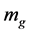 denotes a gravitational mass. Consequently, both s-energy and v-energy must be positive (see (2.20)-(2.21)).
denotes a gravitational mass. Consequently, both s-energy and v-energy must be positive (see (2.20)-(2.21)).
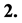 The observation basis of conjecture 1 is that space expands with an acceleration now. One of the two sorts of matter must exist in
The observation basis of conjecture 1 is that space expands with an acceleration now. One of the two sorts of matter must exist in 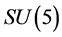 color singlets. The color singlets must loosely distribute in whole space, and can cause space to expand with an acceleration, but cannot be observed as so-called dark energy (see 4 - 6 below).
color singlets. The color singlets must loosely distribute in whole space, and can cause space to expand with an acceleration, but cannot be observed as so-called dark energy (see 4 - 6 below).
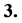 Because of conjecture 1, there must be two sorts of symmetry breaking.
Because of conjecture 1, there must be two sorts of symmetry breaking.
Because of conjecture 1, s-Higgs fields and v-Higgs fields must be symmetric as well. If the symmetry of s-matter and v-matter was not broken, both s-matter and v-matter will exist in the same form at arbitrary time and place. This implies that the nature is simply duplicate. This is impossible because the nature does like duplicate. Of course, this contradicts experiments and observations as well. Consequently the symmetry must be broken when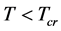 . Thus the coupling constant
. Thus the coupling constant  etc. in (2.10) must be positive so that there must be the two sorts of breaking.
etc. in (2.10) must be positive so that there must be the two sorts of breaking.
The existing probability of the S-breaking and the V-breaking must be equal because of conjecture 1. This equality can be realized by two sorts of modes.
 The universe is composed of infinite s-cosmic islands with the S-breaking and v-cosmic islands with the V-breaking; This possibility has been discussed [19] [20] .
The universe is composed of infinite s-cosmic islands with the S-breaking and v-cosmic islands with the V-breaking; This possibility has been discussed [19] [20] .
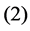 The whole universe is in the same breaking (e.g. the S-breaking). But one sort of breaking can transform to another as space contracts to the least scale
The whole universe is in the same breaking (e.g. the S-breaking). But one sort of breaking can transform to another as space contracts to the least scale  (see later)
(see later)![]() We discuss the case in the present paper. The RW metric is applicable to the case.
We discuss the case in the present paper. The RW metric is applicable to the case.
 . There is only the repulsion between s-matter and v-matter. Consequently, any bound state is composed of only the s-particles or only the v-particles, i.e. there is no bound state which is composed of the s-particles and the v-particles.
. There is only the repulsion between s-matter and v-matter. Consequently, any bound state is composed of only the s-particles or only the v-particles, i.e. there is no bound state which is composed of the s-particles and the v-particles.
Because of conjecture 1, there is the repulsion between s-matter and v-matter and the repulsion constant is the same as the gravitation constant so that the repulsion is weak as the gravitation. The interaction (2.10) is repulsive as well. After reheating, Higgs particles can get very large masses, hence the interaction (2.10) is weak and may be ignored.
 s-matter and v-matter are no longer symmetric after the symmetry breaking.
s-matter and v-matter are no longer symmetric after the symmetry breaking.
In the S-breaking,  is finally broken to
is finally broken to 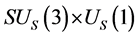 and
and 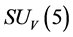 holds all the time. Consequently, s-particles get their masses and form s-atoms, s-observers and s-galaxies etc.; while all v-fermions and v-gauge bosons are still massless and must form
holds all the time. Consequently, s-particles get their masses and form s-atoms, s-observers and s-galaxies etc.; while all v-fermions and v-gauge bosons are still massless and must form 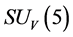 color-singlets after reheating.
color-singlets after reheating.
There is no interaction (e.g. the electroweak interaction) except the gravitation among the  colorsinglets, because
colorsinglets, because 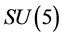 is a simple group. Hence the
is a simple group. Hence the  color-singlets cannot form v-atoms and vgalaxies etc., and must distribute loosely in space as the so-called dark energy.
color-singlets cannot form v-atoms and vgalaxies etc., and must distribute loosely in space as the so-called dark energy.
Thus, in the S-breaking, s-matter is identified with the conventional matter, while v-matter is similar to dark energy. In contrast with the dark energy, the gravitational masses of v-matter is negative.
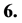 The
The 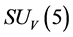 color-single states cannot be observed by an s-observer.
color-single states cannot be observed by an s-observer.
As mentioned above, there is only the repulsion between s-matter and v-matter The repulsions originating from conjecture 1 and (2.10) are very weak after reheating. The v-particles can only form the  color singlets with their very small masses. The
color singlets with their very small masses. The 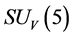 color singlets cannot form atoms and galaxies etc., and can only distribute loosely in space. On the other hand,
color singlets cannot form atoms and galaxies etc., and can only distribute loosely in space. On the other hand, 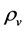 must be very small when
must be very small when 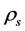 is very large because of the repulsion. Consequently, in fact, it is impossible to observe the
is very large because of the repulsion. Consequently, in fact, it is impossible to observe the 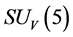 color-singlets even by the repulsion as well.
color-singlets even by the repulsion as well.
In the S-breaking, only the cosmological effects of v-matter are important and are consistent with the observation up to now.
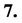 The equivalence principle still strictly holds for the s-particles
The equivalence principle still strictly holds for the s-particles , but is violated by the v-particles
, but is violated by the v-particles 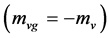 in the S-breaking. But the motion equations of all s-particles and all v-particles are still independent of their masses.
in the S-breaking. But the motion equations of all s-particles and all v-particles are still independent of their masses.
In the S-breaking, there are only s-observers and s-galaxies, and there is no v-observer and v-galaxy. Hence the gravitational masses of s-particles must be positive, i.e. 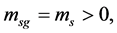 while the gravitational masses of v-matter must be negative relatively to s-matter, i.e.
while the gravitational masses of v-matter must be negative relatively to s-matter, i.e. 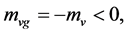 because of conjecture 1. Thus, a s-photon falling in a gravitational field must have ‘purple shift’, but a v-particle (there is no v-photon and there are only the
because of conjecture 1. Thus, a s-photon falling in a gravitational field must have ‘purple shift’, but a v-particle (there is no v-photon and there are only the 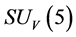 color singlets) falling in the same gravitational field will have ‘redshift’.
color singlets) falling in the same gravitational field will have ‘redshift’.
Although the equivalence principle is violated by v-particles in the S-breaking, there is no contradiction with any observation and experiment, because the  color singlets cannot be observed by a s-observer (see 6).
color singlets cannot be observed by a s-observer (see 6).
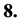 When temperature is high enough, the expectation values of Higgs fields are small so that all masses of Higgs particles are small. Thus,
When temperature is high enough, the expectation values of Higgs fields are small so that all masses of Higgs particles are small. Thus, 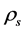 and
and  can transform from one into another by (2.10). Consequently, space cannot contract to infinite small and inflation must occur.
can transform from one into another by (2.10). Consequently, space cannot contract to infinite small and inflation must occur.
The interaction (2.10) can be neglected after reheating, because the masses of the Higgs particles are very large in low temperatures. Thus, the transformation of s-particles and v-particles from one into another may be neglected.
In summary, in the S-breaking, the 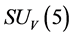 color singlets cannot be observed and have only the cosmological effects. Conjecture 1 does not contradict any experiment and observation up to now.
color singlets cannot be observed and have only the cosmological effects. Conjecture 1 does not contradict any experiment and observation up to now.
We will see in the following that the evolution of the universe can be well explained, and the singularity and cosmological constant issues can be solved.
2.2. Action
The breaking mode of the symmetry is only one of the S-breaking and the V-breaking due to . In the S-breaking, there are only s-observators. Analogously, in the V-breaking, there are only v-observators. Hence the actions should be written as two sorts of form,
. In the S-breaking, there are only s-observators. Analogously, in the V-breaking, there are only v-observators. Hence the actions should be written as two sorts of form, 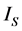 in the S-breaking and
in the S-breaking and  in the V-breaking. Of course, only one of both
in the V-breaking. Of course, only one of both 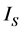 and
and  can describe the evolution of the universe. Hence, in any case, the action is unique. But the S-breaking can transform to the V-breaking when temperature is high enough, hence both
can describe the evolution of the universe. Hence, in any case, the action is unique. But the S-breaking can transform to the V-breaking when temperature is high enough, hence both  and
and 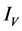 are necessary. Because of conjecture 1, the structures of
are necessary. Because of conjecture 1, the structures of 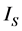 and
and 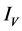 are the same, i.e.
are the same, i.e. 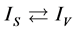 when
when 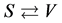 and
and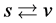 . Thus, at the zero-temperature, we have
. Thus, at the zero-temperature, we have
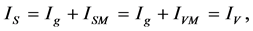 (2.1)
(2.1)
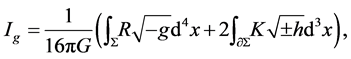 (2.2)
(2.2)
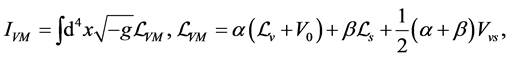 (2.3)
(2.3)
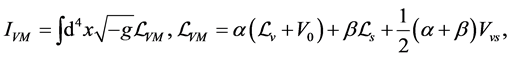 (2.4)
(2.4)
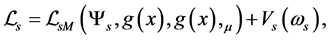 (2.5)
(2.5)
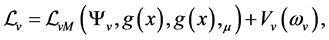 (2.6)
(2.6)
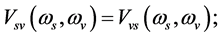 (2.7)
(2.7)
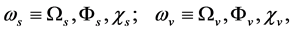
where the meanings of the symbols are as follows: , and
, and 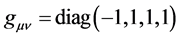 in flat space.
in flat space. 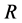 is the scalar curvature. Here
is the scalar curvature. Here 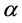 and
and 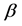 are two parameters, may be called “gravitation charges”, and are finally taken as
are two parameters, may be called “gravitation charges”, and are finally taken as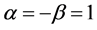 .
.  in
in 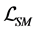
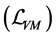 is a parameter in order to determine the zero-point of the potential
is a parameter in order to determine the zero-point of the potential 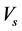
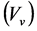 .
. 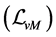
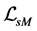 is the Lagrangian density of all s-fields (v-fields) and their couplings of the
is the Lagrangian density of all s-fields (v-fields) and their couplings of the 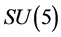 GUT except the Higgs potentials
GUT except the Higgs potentials 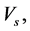
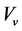 and
and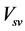 .
. 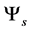 and
and  represents all s-fields and all v-fields, respectively. For a boson field,
represents all s-fields and all v-fields, respectively. For a boson field, 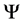 denotes its covariant derivative as well. Both
denotes its covariant derivative as well. Both 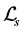 and
and 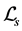 do not contain the contribution of the gravitation energy and the repulsion energy. It may be seen that the set of equation (2.1)-(2.7) is unchanged when the subscripts
do not contain the contribution of the gravitation energy and the repulsion energy. It may be seen that the set of equation (2.1)-(2.7) is unchanged when the subscripts 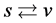 and
and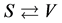 . This shows the symmetry of s-matter and v-matter. The physics quantities with the subscript ‘S’ (‘V’) denotes that they have meaning only when the universe is in the S (‘V’)-breaking. It is the same for the subscript ‘V’ as for ‘S’. For simplicity, the subscripts ‘S’ and ‘V’' may be elided in the following when there is no confusion.
. This shows the symmetry of s-matter and v-matter. The physics quantities with the subscript ‘S’ (‘V’) denotes that they have meaning only when the universe is in the S (‘V’)-breaking. It is the same for the subscript ‘V’ as for ‘S’. For simplicity, the subscripts ‘S’ and ‘V’' may be elided in the following when there is no confusion.
Gibbons and Hawking pointed out that in order to get the Einstein field equations [21] , it is necessary that
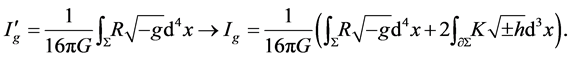
This is because it is not necessary that 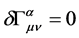 on the boundary
on the boundary 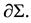 Hence
Hence 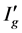 is replaced by
is replaced by 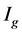 in (2.2).
in (2.2).  is a manifold with four dimensions.
is a manifold with four dimensions.  is the boundary of
is the boundary of 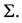
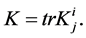
 is the outer curvature on
is the outer curvature on 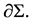
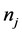 is the vertical vector on
is the vertical vector on 
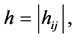 and
and  is the induced outer metric on
is the induced outer metric on . When
. When  is space-like,
is space-like,  takes positive sign. When
takes positive sign. When 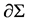 is time-like,
is time-like, 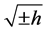 takes negative sign.
takes negative sign.
The Higgs potentials in (2.5)-(2.7) is the following:
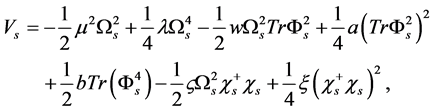 (2.8)
(2.8)
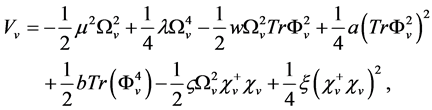 (2.9)
(2.9)
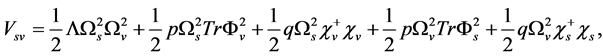 (2.10)
(2.10)
where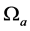 ,
,  and
and 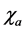 are respectively
are respectively ,
,  and
and 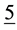 dimensional representations of the
dimensional representations of the 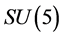 group,
group, 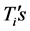 are the
are the 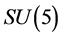 generators, a = s, v. Here the couplings of
generators, a = s, v. Here the couplings of 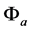 and
and 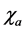 are ignored for short [22] [23] . (2.8) is the same as that in [22] [23] . The coupling constants in (2.8)-(2.10) are all positive, especially, as mentioned before,
are ignored for short [22] [23] . (2.8) is the same as that in [22] [23] . The coupling constants in (2.8)-(2.10) are all positive, especially, as mentioned before,  p and q in (2.10) must be positive.
p and q in (2.10) must be positive.
We do not consider the terms coupling to curvature scalar, e.g.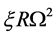 , for a time. In fact,
, for a time. In fact,  when temperature
when temperature 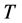 is high enough due to the symmetry between s-matter and v-matter.
is high enough due to the symmetry between s-matter and v-matter.
2.3. Energy-Momentum Tensors and Field Equations
By the conventional method, from 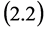 we can get
we can get
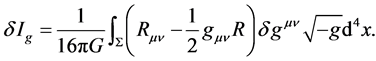 (2.11)
(2.11)
Considering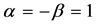 , from (2.3)-(2.4) we have
, from (2.3)-(2.4) we have
 (2.12)
(2.12)
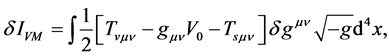 (2.13)
(2.13)
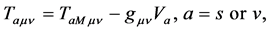 (2.14)
(2.14)
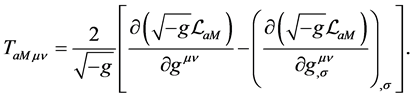 (2.15)
(2.15)
From (2.11)-(2.13) we obtain
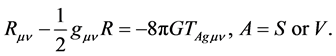 (2.16)
(2.16)
In the S-breaking,
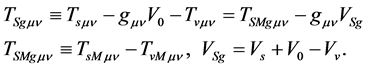 (2.17)
(2.17)
In the V-breaking,
 (2.18)
(2.18)
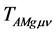
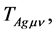 and
and 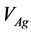 are the gravitational energy-momentum tensor density, the gravitational energymomentum tensor density without the Higgs potential and the gravitational potential density of the Higgs fields in the A-breaking, respectively.
are the gravitational energy-momentum tensor density, the gravitational energymomentum tensor density without the Higgs potential and the gravitational potential density of the Higgs fields in the A-breaking, respectively.
It is seen from (2.17)-(2.18) that 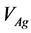 is independent of
is independent of 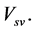 This implies that the potential energy
This implies that the potential energy  is different from other energies in essence. There is no contribution of
is different from other energies in essence. There is no contribution of 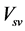 to
to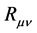 , i.e., there is no gravitation and repulsion of the potential energy
, i.e., there is no gravitation and repulsion of the potential energy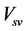 . This does not satisfy the equivalence principle. But this does not cause any contradiction with all given experiments and astronomical observations, because
. This does not satisfy the equivalence principle. But this does not cause any contradiction with all given experiments and astronomical observations, because 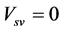 in either of breaking modes.
in either of breaking modes.
We will see that, in fact, 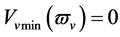 because
because 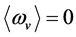 in the S-breaking, and
in the S-breaking, and 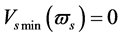 because
because  in the V-breaking. Hence
in the V-breaking. Hence
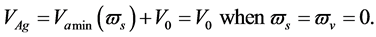 (2.19)
(2.19)
From (2.1) the energy-momentum tensor density which does not contain the energy-momentum tensor of gravitational and repulsive interactions can be defined as
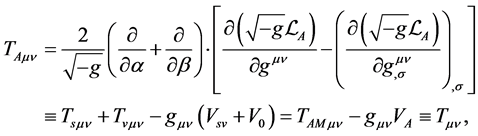 (2.20)
(2.20)
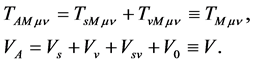 (2.21)
(2.21)
As mentioned before, 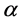 and
and  in (2.3)-(2.4) may be regarded as the gravitation charges. The the gravitation charges of
in (2.3)-(2.4) may be regarded as the gravitation charges. The the gravitation charges of 
 and
and 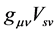 are regarded as 1, ‒1 and 0 in the S-breaking, respectively. The energy-momentum tensor should be independent of the gravitation charges, because the energy-momentum tensor of the gravitation fields is not considered. Hence it is necessary to eliminate
are regarded as 1, ‒1 and 0 in the S-breaking, respectively. The energy-momentum tensor should be independent of the gravitation charges, because the energy-momentum tensor of the gravitation fields is not considered. Hence it is necessary to eliminate  and
and 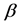 from the definition of
from the definition of 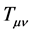 by the operator
by the operator 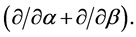 The operator is the only difference between the definition of
The operator is the only difference between the definition of 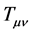 in this model and that in the conventional theory. This definition does not contradict any basic principle and it is completely consistent with the conventional theory. In fact, there is one sort of matter in the conventional theory (i.e.
in this model and that in the conventional theory. This definition does not contradict any basic principle and it is completely consistent with the conventional theory. In fact, there is one sort of matter in the conventional theory (i.e.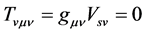 ) so that
) so that  can be reduced to
can be reduced to 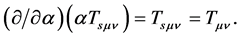
It is seen from (2.20)-(2.21) that both s-energy and v-energy must be positive.
It should be pointed out that only (2.16) and (2.17) is applicable in the S-breaking, and only (2.16) and (2.18) applicable in the V-breaking.
Considering 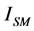
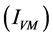 to be a scalar [24] or considering
to be a scalar [24] or considering
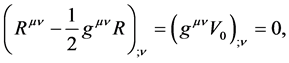
and (2.16) and (2.14) we obtain
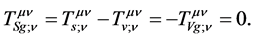 (2.22)
(2.22)
2.4. The Difference of Motion Equations of a v-Particle and a s-Particle in the Same Gravitational Field
From (2.16) we have
 (2.23)
(2.23)
In the S-breaking,  ,
, 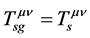 and
and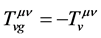 .
.
Consider a point-particle with its gravitational mass 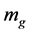 to move in a gravitational field with its strength
to move in a gravitational field with its strength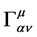 . From (2.23) we can get
. From (2.23) we can get
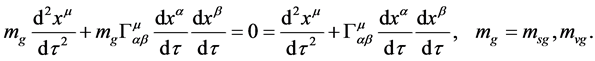 (2.24)
(2.24)
It is seen from (2.24) that the motion equation of the gravitation mass  is the same as that of the gravitation mass
is the same as that of the gravitation mass 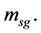 This is the same as the conventional theory.
This is the same as the conventional theory.
It must be given one's attention to that (2.24) is only the equation of a gravitation mass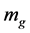 , but is not the equation of an inertial mass
, but is not the equation of an inertial mass . According to the equvalence principle in the conventional theory,
. According to the equvalence principle in the conventional theory, 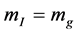 , here
, here 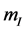 is the inertial mass. Consequently, (2.24) is the equation of an inertial mass
is the inertial mass. Consequently, (2.24) is the equation of an inertial mass 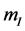 as well.
as well.
According to the present model, because of conjecture 1, the gravitational field equation can determine only the motion equation of a gravitation mass (2.24), but cannot determine the motion equation of an inertial mass . The motion equation of an inertial mass
. The motion equation of an inertial mass  must be determined on the bases of conjecture 1 and the gravitational field equation.
must be determined on the bases of conjecture 1 and the gravitational field equation.
In the S-breaking, according to conjecture 1,  and
and . Hence the equation of
. Hence the equation of  is the same as that of
is the same as that of 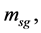 i.e. (2.24), but the equation of
i.e. (2.24), but the equation of  must be different from that of
must be different from that of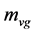 . According to conjecture 1, both
. According to conjecture 1, both  and
and  are positive, and
are positive, and  when
when .
.  in (2.24) is the coupling of the gravitational charge
in (2.24) is the coupling of the gravitational charge  and the gravitational field with its strength
and the gravitational field with its strength 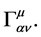 The second term in (2.24) determines the force acting on
The second term in (2.24) determines the force acting on . Considering
. Considering  in the S-breaking so that the acceleration of
in the S-breaking so that the acceleration of  is opposite to that of
is opposite to that of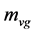 , we get the motion equation of
, we get the motion equation of 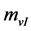 in the gravitational field with its strength
in the gravitational field with its strength 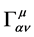 to be
to be
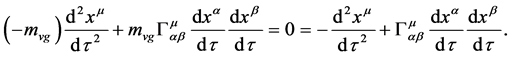 (2.25)
(2.25)
Comparing (2.24) and (2.25), we see that in the same gravitational field, the motion equation of a s-particle is different from that of a v-particle.
Analogous to the case in the S-breaking, in the V-breaking, because of the symmetry of s-matter and v-matter, we have
 (2.26)
(2.26)
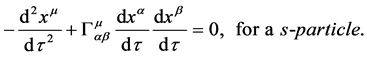 (2.27)
(2.27)
Considering the Newtonian approximation, i.e. the velocity of a particle is low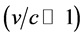 , a gravitational field is weak (
, a gravitational field is weak (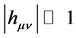
 ) and static
) and static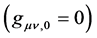 , and
, and 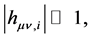 from
from  we have
we have
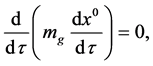 (2.28)
(2.28)
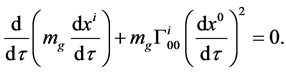 (2.29)
(2.29)
From (2.28), 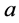
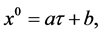 and
and 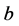 are two constants. Considering
are two constants. Considering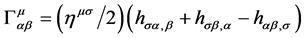 , and let
, and let  be Newtonian gravitational potential, we can reduce (2.29) to
be Newtonian gravitational potential, we can reduce (2.29) to
 (2.30)
(2.30)
Let 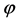 is caused by a static and spheral-symmetric s-object with its mass M. In the S-breaking,
is caused by a static and spheral-symmetric s-object with its mass M. In the S-breaking, 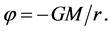 Thus, from (2.24)-(2.25) and (2.30) we get
Thus, from (2.24)-(2.25) and (2.30) we get
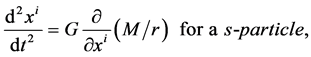 (2.31)
(2.31)
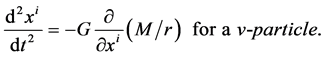 (2.32)
(2.32)
Let 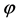 is caused by a static and spheral-symmetric v-object with its mass M. In the S-breaking,
is caused by a static and spheral-symmetric v-object with its mass M. In the S-breaking,  because conjecture 1. Thus, from (2.24)-(2.25) and (2.30) we get
because conjecture 1. Thus, from (2.24)-(2.25) and (2.30) we get
 (2.33)
(2.33)
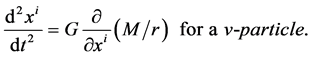 (2.34)
(2.34)
It is seen that the motion equation of a v-particle in such a gravitational field caused by v-matter is the same as that of a s-particle in the gravitational field caused by s-matter in the Newtonian approximation, when the distributing mode of v-matter is the same as that of s-matter.
In the V-breaking, we can get the same results as above, provided 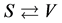 and
and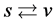 .
.
3. Spontaneous Symmetry Breaking
Ignoring the couplings of 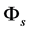 and
and 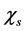 and suitably choosing the parameters of the Higgs potential, analogously to Ref. [22] [23] , we can prove from (2.8)-(2.10) that there are the following vacuum expectation values (the S-breaking) at the zero-temperature and under the tree-level approximation
and suitably choosing the parameters of the Higgs potential, analogously to Ref. [22] [23] , we can prove from (2.8)-(2.10) that there are the following vacuum expectation values (the S-breaking) at the zero-temperature and under the tree-level approximation
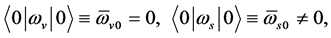 (3.1)
(3.1)
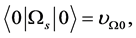 (3.2)
(3.2)
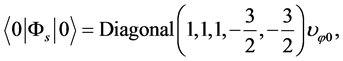 (3.3)
(3.3)
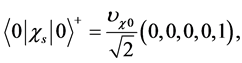 (3.4)
(3.4)
Ignoring the contributions of 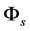 and
and 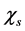 to
to 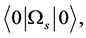 at the zero-temperature we get
at the zero-temperature we get
 (3.5)
(3.5)
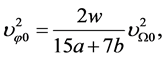 (3.6)
(3.6)
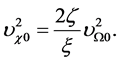 (3.7)
(3.7)
We take  From (2.9)-(2.10) and (3.1)-(3.7) it can be proved that all v-Higgs bosons can get their big enough masses. The masses of the Higgs particles exclusive of the
From (2.9)-(2.10) and (3.1)-(3.7) it can be proved that all v-Higgs bosons can get their big enough masses. The masses of the Higgs particles exclusive of the  -particles and the
-particles and the  -particles in the S-breaking are respectively
-particles in the S-breaking are respectively
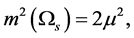 (3.8)
(3.8)
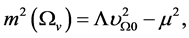 (3.9)
(3.9)
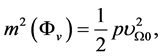 (3.10)
(3.10)
 (3.11)
(3.11)
We can choose such parameters that
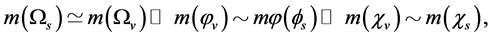 (3.12)
(3.12)
e.g., 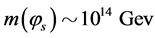
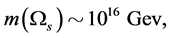 and
and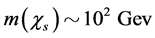 . It is easily seen from (3.8)-(3.11) that all real components of
. It is easily seen from (3.8)-(3.11) that all real components of 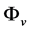 have the same mass
have the same mass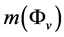 , and all real components of
, and all real components of  have the same mass
have the same mass 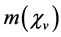 in the S-breaking.
in the S-breaking.
The S-breaking and the V-breaking are symmetric because s-matter and v-matter are symmetric. Hence when 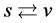 and
and 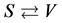 in (3.1)-(3.12), the formulas are still kept.
in (3.1)-(3.12), the formulas are still kept.
Let
 (3.13)
(3.13)
we have
 (3.14)
(3.14)
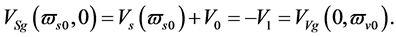 (3.15)
(3.15)
It is easily seen that 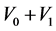 is strictly determined by
is strictly determined by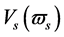 , but
, but  or
or 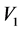 is a undetermined parameter.
is a undetermined parameter.  is the zero point of
is the zero point of 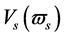 and
and 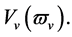 We take
We take 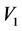 to be so small that it may be neglected when
to be so small that it may be neglected when 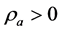 in the A-breaking,
in the A-breaking, 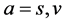 and
and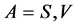 .
.
4. Evolution Equations
4.1. Evolution Equations of R in RW Metric
As is well known, based on the RW metric metric,
 (4.1)
(4.1)
In the present model, we take  Taking
Taking 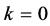 or 1, we can get the results similar to those when
or 1, we can get the results similar to those when . We will discuss the two cases in the following paper. In fact, it is possible that
. We will discuss the two cases in the following paper. In fact, it is possible that 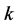 is changeable with the gravitational mass density
is changeable with the gravitational mass density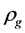 . In this case, the results of the present model are more easily obtained [19] [20] .
. In this case, the results of the present model are more easily obtained [19] [20] .
Matter in the universe may approximately be regarded as ideal gas distributed evenly in space. Considering the potential energy densities in (2.14), we can write  as
as
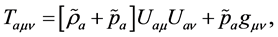 (4.2)
(4.2)
 (4.3)
(4.3)
where 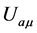 is a 4-velocity and
is a 4-velocity and 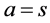 or v. In comoving coordinates
or v. In comoving coordinates 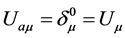 in a comoving coordinates.
in a comoving coordinates. 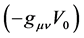 can be written as
can be written as
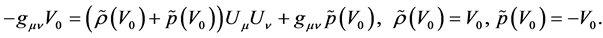 (4.4)
(4.4)
Considering  substituting (4.2)-(4.4) and the RW metric in (4.1) into (2.16), we get the evolution equations
substituting (4.2)-(4.4) and the RW metric in (4.1) into (2.16), we get the evolution equations
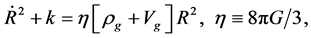 (4.5)
(4.5)
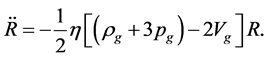 (4.6)
(4.6)
In the S-breaking,
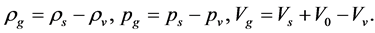 (4.7)
(4.7)
In the V-breaking,
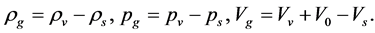 (4.8)
(4.8)
Comparing (4.5)-(4.6) with the Friedmann equations, we see that provided ,
, 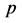 and V in the Friedmann equations are replaced by
and V in the Friedmann equations are replaced by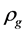 ,
, 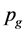 and
and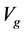 , (4.5)-(4.6) are obtained.
, (4.5)-(4.6) are obtained.
4.2. Evolution Equation of ρg
In contrast with the conventional theory, it is possible that 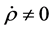 although
although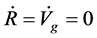 . This is because
. This is because 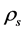 and
and  can transform from one to another by (2.10), especially when temperature is high enough (see section 6B).
can transform from one to another by (2.10), especially when temperature is high enough (see section 6B).
Let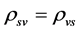 , e.g.
, e.g. , it is obvious that in the S-breaking,
, it is obvious that in the S-breaking,
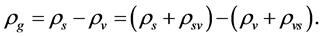 (4.9)
(4.9)
When 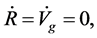
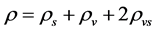 is the total energy density and is conservational, i.e.
is the total energy density and is conservational, i.e.
 (4.10)
(4.10)
It is possible that 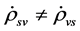 although
although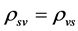 . This is because in general,
. This is because in general, 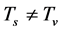 and
and  here
here 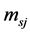
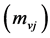 is the mass of a sort of s-particles (v-particles). If
is the mass of a sort of s-particles (v-particles). If  transforms into the energy density of v-particles and
transforms into the energy density of v-particles and 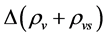 transforms into the energy density of s-particles in an interval of time
transforms into the energy density of s-particles in an interval of time , there must be
, there must be
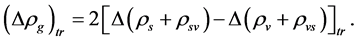 (4.11)
(4.11)
Consequently, we have
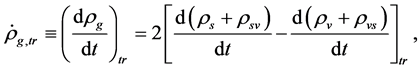 (4.12)
(4.12)
where 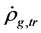 denotes the change of
denotes the change of 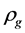 because of the transformation of
because of the transformation of 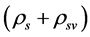 and
and 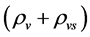 to each other.
to each other.
According to this model, 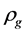 is a function of R Vg,
is a function of R Vg, 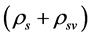 and
and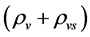 , i.e.
, i.e.
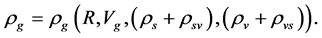 Thus,
Thus,
 (4.13)
(4.13)
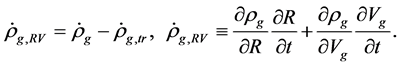 (4.14)
(4.14)
From (4.5)-(4.6) we have
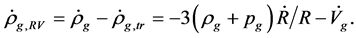 (4.15)
(4.15)
This is because  and
and 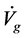 determine only
determine only , but do not determine
, but do not determine . It is obvious that (4.6) can be derived from (4.5) and (4.15). Considering the two equations (4.5)-(4.6), the equation determining
. It is obvious that (4.6) can be derived from (4.5) and (4.15). Considering the two equations (4.5)-(4.6), the equation determining 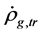 (see section 6B),
(see section 6B), 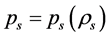 and
and 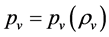 or
or  we can determine the five variables
we can determine the five variables 
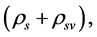
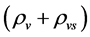 ,
, 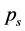 and
and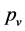 , and further can determine
, and further can determine 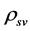 by (4.10).
by (4.10).
When 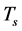 and
and 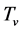 are low or
are low or 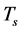 and
and  are high enough so that
are high enough so that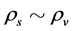 , the transformation of
, the transformation of  and
and 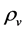 may be neglected. Thus,
may be neglected. Thus, 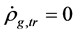 and
and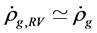 , i.e.
, i.e.
 (4.16)
(4.16)
Pressure density is a function of masses of particles and temperature, i.e.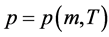 . Let
. Let 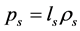 and
and 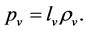 In the S-breaking, from
In the S-breaking, from 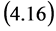 we have
we have
 (4.17)
(4.17)
It is obvious that when , the solution of (4.14) is
, the solution of (4.14) is
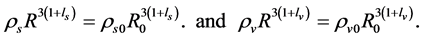 (4.18)
(4.18)
In general, 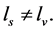
In order to determine the pressure at a given temperature, we divide the particles into three sorts according to their masses. The first sort is composed of such particles whose masses 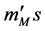 satisfy
satisfy 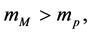 here mp is the mass of a proton. The second sort of particles is composed of such particles whose masses
here mp is the mass of a proton. The second sort of particles is composed of such particles whose masses 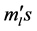 satisfy
satisfy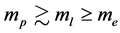 , here
, here  is the mass of an electron. The third sort is composed of photon-like particles whose masses
is the mass of an electron. The third sort is composed of photon-like particles whose masses 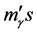 satisfy
satisfy 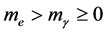 and
and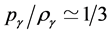 . When
. When 
 When mp > T > me,
When mp > T > me, 
 and
and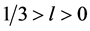 . When
. When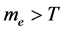 ,
, . Thus, we have
. Thus, we have
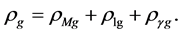 (4.19)
(4.19)
In the S-breaking,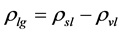
 . Considering all v-particles must be in v-SU(5) color singlets whose masses are not zero so that
. Considering all v-particles must be in v-SU(5) color singlets whose masses are not zero so that 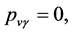 we have
we have 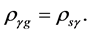
When 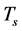 and
and 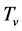 are so large that all masses may be neglected (
are so large that all masses may be neglected (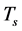 and
and ), from (4.16) we have
), from (4.16) we have
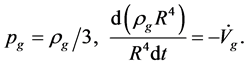 (4.20)
(4.20)
When 
 . Letting
. Letting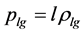 , we have
, we have
 (4.21)
(4.21)
When 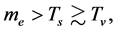
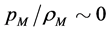 and
and 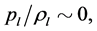 we have
we have
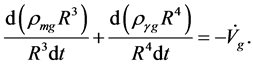 (4.22)
(4.22)
where .
.
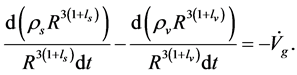 (4.23)
(4.23)
It is obvious that when 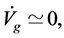 (4.21) has such solutions in the following form,
(4.21) has such solutions in the following form,
 (4.24)
(4.24)
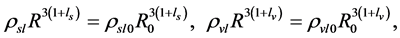 (4.25)
(4.25)
 (4.26)
(4.26)
In contrast with the conventional theory, 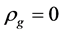
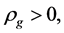 and
and 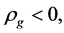 and
and 
 and
and  are all possible in the present model, here
are all possible in the present model, here . For example, when temperature is so low that
. For example, when temperature is so low that 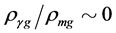 and
and  we have
we have 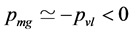 and
and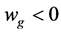 .
.
5. Temperature Effect
The thermal equilibrium between the v-particles and the s-particles can be realized by only (2.10). The Higgs bosons  and
and 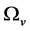 are hardly produced because their masses are all very big in low temperatures. Consequently, the interaction between the v-particles and the s-particles may be ignored so that there is no thermal equilibrium between the v-particles and the s-particles. Thus, when temperature is low, we should use two sorts of temperature
are hardly produced because their masses are all very big in low temperatures. Consequently, the interaction between the v-particles and the s-particles may be ignored so that there is no thermal equilibrium between the v-particles and the s-particles. Thus, when temperature is low, we should use two sorts of temperature 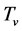 and
and 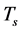 to describe the thermal equilibrium of v-matter and the thermal equilibrium of s-matter, respectively. Generally speaking,
to describe the thermal equilibrium of v-matter and the thermal equilibrium of s-matter, respectively. Generally speaking,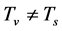 . When temperature is high enough, e.g.
. When temperature is high enough, e.g.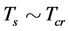 , the masses of the Higgs particles originating from (2.10) are small so that
, the masses of the Higgs particles originating from (2.10) are small so that 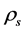 and
and 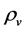 can transform from one to another by (2.10). In the case,
can transform from one to another by (2.10). In the case, 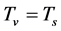 is possible.
is possible.
5.1. Effective Potentials
Influence of finite temperature on the Higgs potential in the present model are consistent with the conventional theory. When the finite temperature effect is considered, the Higgs potential at zero-temperature becomes effective potential.
For short, we consider only 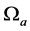 and
and 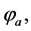
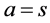 or
or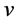 . When
. When 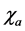 is considered as well, the following inferences are still qualitatively valid. From (2.8) we take
is considered as well, the following inferences are still qualitatively valid. From (2.8) we take
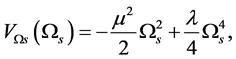 (5.1)
(5.1)
to ignore the terms proportional to 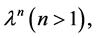 to consider the temperature effect, the effective potential approximate to 1-loop in flat space is [25] -[27]
to consider the temperature effect, the effective potential approximate to 1-loop in flat space is [25] -[27]
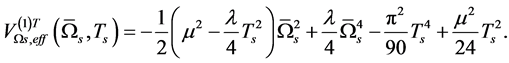 (5.2)
(5.2)
Considering the contributions of the expectation values 
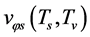 and
and 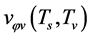 to
to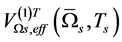 , and ignoring the terms irrelevant to
, and ignoring the terms irrelevant to 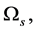 we have
we have
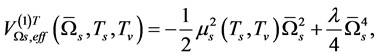 (5.3)
(5.3)
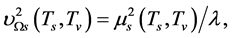 (5.4)
(5.4)
 (5.5)
(5.5)
Similarly (5.1)-(5.5), from (2.9) we have
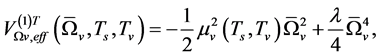 (5.6)
(5.6)
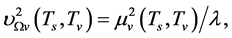
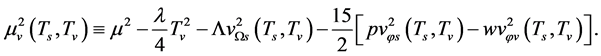 (5.7)
(5.7)
From (2.8) we take
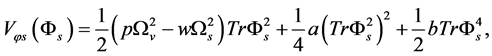 (5.8)
(5.8)
ignoring the contributions of the Higgs fields and the fermion fields to one loop correction, and only considering the contribution of the gauge fields, when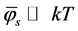 , here
, here 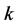 is the Boltzmann constant (here
is the Boltzmann constant (here ), we get the effective potential approximate to 1-loop in flat space at finite-temperature [25] -[27]
), we get the effective potential approximate to 1-loop in flat space at finite-temperature [25] -[27]
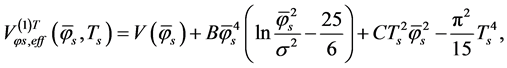 (5.9)
(5.9)
where 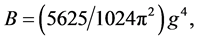 and
and  In general,
In general,
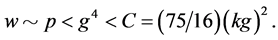 We take
We take ![]() for simplicity. Here
for simplicity. Here ![]() is a parameter at which the renormalization coupling-constant is defined.
is a parameter at which the renormalization coupling-constant is defined.
Only considering the contribution of the expectation values of  and
and 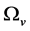 to
to , taking
, taking 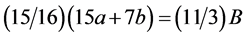 and ignoring the terms irrelevant with
and ignoring the terms irrelevant with 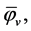 from (2.8) and (5.8)-(5.9), we have
from (2.8) and (5.8)-(5.9), we have
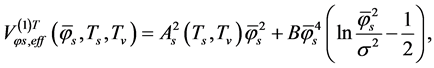 (5.10)
(5.10)
 (5.11)
(5.11)
It is easily seen from (5.10) that 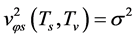 when
when 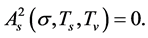
Similarly, from (2.9) we have
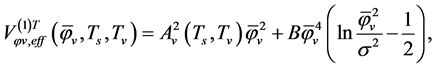 (5.12)
(5.12)
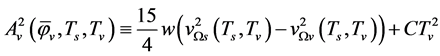 (5.13)
(5.13)
When the masses of all particles may be neglected, pg = ρg/3 and 
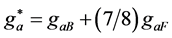 .
. 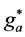 is the total number of spin states, and
is the total number of spin states, and 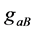 and
and  are the total number of spin states of
are the total number of spin states of 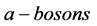 and the total number of spin states of a-femions, respectively.
and the total number of spin states of a-femions, respectively.  because s-particles and v-particles are symmetric. Considering (4.5)-(4.7), (4.9), (5.2) and (5.9) in the S-breaking, we have
because s-particles and v-particles are symmetric. Considering (4.5)-(4.7), (4.9), (5.2) and (5.9) in the S-breaking, we have
 (5.14)
(5.14)
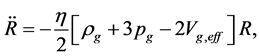 (5.15)
(5.15)
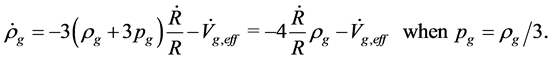 (5.16)
(5.16)
 (5.17)
(5.17)
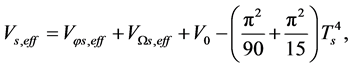 (5.18)
(5.18)
 (5.19)
(5.19)
5.2. The Critical Temperature Tφcr and Substable States in the S-Breaking
For short, we take 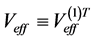 in the following. We consider such a space-contracting stage in which
in the following. We consider such a space-contracting stage in which 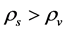 and
and 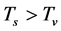 in the S-breaking. We will see that there are the critical temperatures
in the S-breaking. We will see that there are the critical temperatures 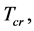
 and
and 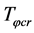 and
and . For the effective potential, there still is the S-breaking, i.e.
. For the effective potential, there still is the S-breaking, i.e. 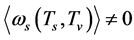 and
and
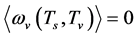 when
when 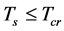 and
and  when
when 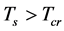 by suitably choosing the parameters in the Higgs potential.
by suitably choosing the parameters in the Higgs potential.
As mentioned before, there is the S-breaking in low temperatures. Talking  for short, we have
for short, we have
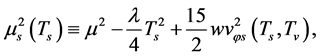 (5.20)
(5.20)
 (5.21)
(5.21)
 (5.22)
(5.22)
 (5.23)
(5.23)
Both 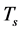 and
and 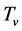 will rise as space contracts. We will see that
will rise as space contracts. We will see that 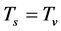 is possible when
is possible when .
.
From (5.10) and (5.22) we can determine the minimum . Let
. Let  It is obviously that
It is obviously that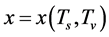 . It is seen from (5.10) and (5.22) that there are absolute minimums when
. It is seen from (5.10) and (5.22) that there are absolute minimums when  is low, i.e.
is low, i.e.
 (5.24)
(5.24)
 will decrease monotonously as
will decrease monotonously as 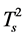 increases and its lower limit is
increases and its lower limit is 
There is the critical temperature  at which the minimum is degenerate, i.e.
at which the minimum is degenerate, i.e.
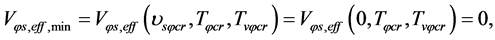 (5.25)
(5.25)
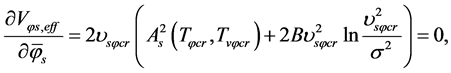 (5.26)
(5.26)
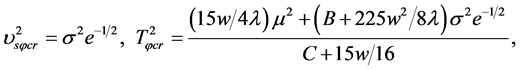 (5.27)
(5.27)
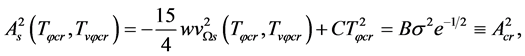 (5.28)
(5.28)
 (5.29)
(5.29)
where 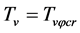 when
when 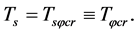
There is the critical temperature  at which
at which
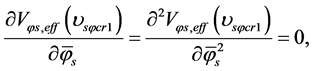 (5.30)
(5.30)
 (5.31)
(5.31)
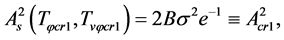 (5.32)
(5.32)
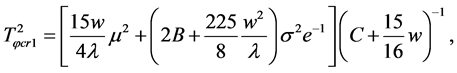 (5.33)
(5.33)
where 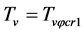 when
when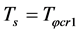 .
.
Sum up, when 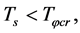

 and
and  is the absolute minimum, i.e.
is the absolute minimum, i.e.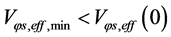 . There is such a
. There is such a 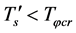 that
that 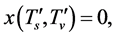
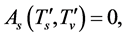
 and
and
 When
When 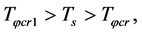

 and
and  is a relative minimum and larger than
is a relative minimum and larger than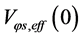 , i.e. there are substable states when
, i.e. there are substable states when . When
. When  i.e.
i.e. 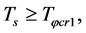
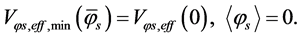 (5.34)
(5.34)
In the case, there is no relative minimum, as shown in Figure 1.
Analogously to that  when
when , it is seen from (5.12) that
, it is seen from (5.12) that  when
when .
.
When 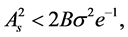 i.e.
i.e. 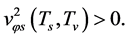
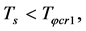 We can get the masses of
We can get the masses of ,
, 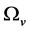 ,
, 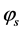 and
and  from (5.3), (5.6), (5.10), (5.12) and (5.20)-(5.23)
from (5.3), (5.6), (5.10), (5.12) and (5.20)-(5.23)
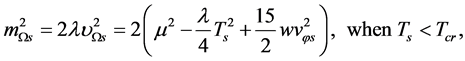 (5.35)
(5.35)
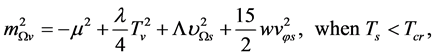 (5.36)
(5.36)
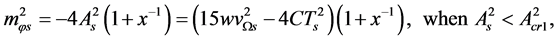 (5.37)
(5.37)
 (5.38)
(5.38)
 (5.39)
(5.39)
5.3. The Critical Temperature Tcr
It is easily seen from (5.3)-(5.7) that 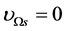 when
when  and
and 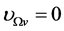 when
when  In the S-breaking,
In the S-breaking, 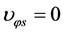 when
when 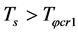 and
and 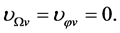 Thus, from (5.3) we can determine the critical temperature
Thus, from (5.3) we can determine the critical temperature  of
of 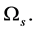
 (5.40)
(5.40)
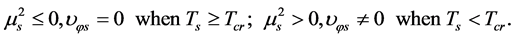 (5.41)
(5.41)
Both  and
and 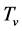 will rise as space contracts. Let
will rise as space contracts. Let 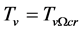 when
when 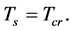 We will see
We will see 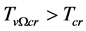 in the following. It is easily seen from (5.5) and (5.41) when
in the following. It is easily seen from (5.5) and (5.41) when  increases from
increases from  to
to 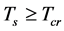 that
that 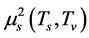 will decrease from
will decrease from 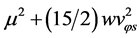 to
to 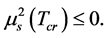
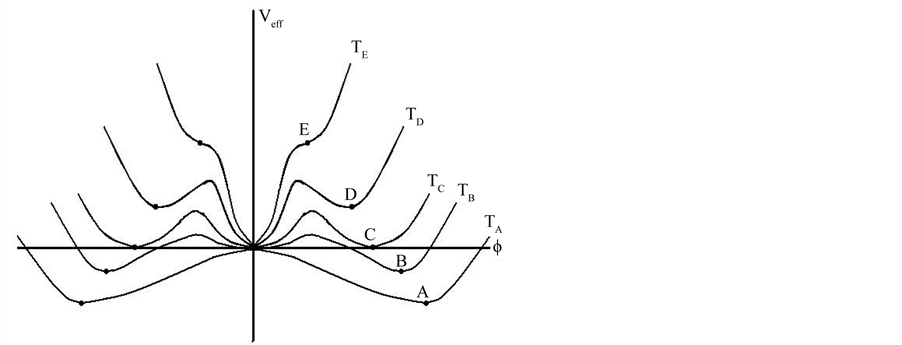
Figure 1. The states changes from A to E when Ts rises from T < Tφcr to Tφcr1.
6. Space Can Contract, But There Is No Singularity
On the basis of the cosmological principle, if there is the space-time singularity, it may be a result of space contraction. Thus, we discuss the contracting process. From the contracting process we will see that there is no space-time singularity in present model.
6.1. The Initial Condition and the Boundary Condition
We consider the contracting process of the universe after expansion in the S-breaking. It is seen from (3.15) that in the case,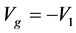 . The initial condition is that at
. The initial condition is that at 
 (6.1)
(6.1)
 (6.2)
(6.2)
 (6.3)
(6.3)
It is obvious that 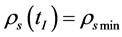 and
and . Space will contract when t > tT = 0, because
. Space will contract when t > tT = 0, because  and
and 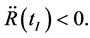 We consider that the physical boundary condition of the Equations (5.14)-(5.15) should be
We consider that the physical boundary condition of the Equations (5.14)-(5.15) should be
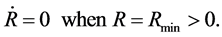 (6.4)
(6.4)
In contrast with the conventional theory, there are such solutions which satisfy the boundary condition. This implies that there is no singularity in the model.
There is no singularity in the model [19] [20] as well. This is because 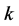 is changeable in the model [19] [20] . It is possible that the model [19] [20] is better.
is changeable in the model [19] [20] . It is possible that the model [19] [20] is better.
6.2. Transformation of ρs and ρv from One to Another
When both 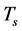 and
and  are low, the transformation of
are low, the transformation of  and
and  may be neglected because the masses of the Higgs particles are all very large. Consequently,
may be neglected because the masses of the Higgs particles are all very large. Consequently, 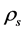 and
and  are independent of each other. When both
are independent of each other. When both  and
and  rise because space contracts, as mentioned before, the masses of the Higgs particles originating from the couplings (2.8)-(2.10) will reduce. Thus, the transformation of the s-Higgs particles and the v-Higgs particles by (2.10) is striking.
rise because space contracts, as mentioned before, the masses of the Higgs particles originating from the couplings (2.8)-(2.10) will reduce. Thus, the transformation of the s-Higgs particles and the v-Higgs particles by (2.10) is striking.
We discuss the transformation of 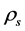 and
and 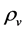 follows.
follows.
Let 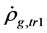 originate from decay the Higgs particles as
originate from decay the Higgs particles as  and
and 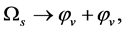
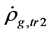 originate from scattering of the Higgs particles as
originate from scattering of the Higgs particles as 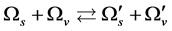 and
and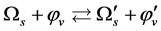 , and
, and  originate from scattering of the Higgs particles as
originate from scattering of the Higgs particles as 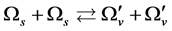 and
and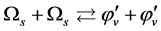 ,
, 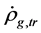 may be written as
may be written as
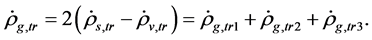 (6.5)
(6.5)
6.2.1. ρg(tφcr) < 0 Is Possible When Tv ≤ Ts < Tφcr
In the initial stage, temperature is low, i.e. 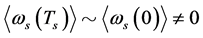
 and
and . Thus,
. Thus, 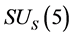 breaks to
breaks to  when
when 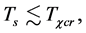 then to
then to 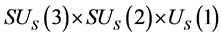 (
(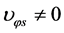
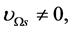 and
and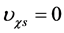 ) when
) when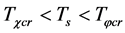 . When
. When 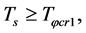
 symmetry holds (
symmetry holds (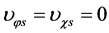
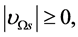 ).
).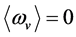 and
and 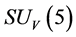 hold all the time. Here
hold all the time. Here 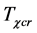 is such a temperature that
is such a temperature that 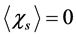 when
when 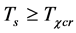 and
and  when
when 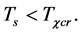
When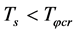 , the masses of the Higgs particles are large and the number of the Higgs particles is little. In the case,
, the masses of the Higgs particles are large and the number of the Higgs particles is little. In the case, . Thus, (4.18) holds so that the transformation of
. Thus, (4.18) holds so that the transformation of  and
and 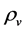 may be neglected. When
may be neglected. When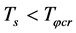 , the s-particles must form celestial bodies with their large masses so that
, the s-particles must form celestial bodies with their large masses so that 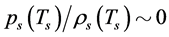 and
and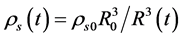 . However, the v-particles must be in
. However, the v-particles must be in 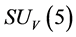 color singlets so that
color singlets so that
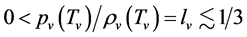 and
and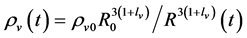 . It is obvious that the less the masses of the color singlets are, the larger
. It is obvious that the less the masses of the color singlets are, the larger 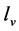 is. Consequently,
is. Consequently,
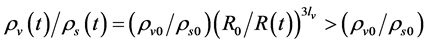 (6.6)
(6.6)
and it is possible that  when
when , here
, here 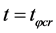 when
when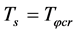 . In the case, there are such solutions satisfying (6.4) (see the discussion below,
. In the case, there are such solutions satisfying (6.4) (see the discussion below, 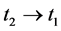 in (6.13)-(6.15).
in (6.13)-(6.15).
6.2.2. A Super-Heating Process
As mentioned in the preceding section, there are the substable states. Consequently, the universe will be in the substable states when 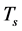 rises from
rises from  to
to . The states changes from
. The states changes from  to
to  when
when 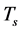 rises from
rises from 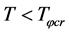 to
to 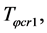 as shown by Figure 1. Thus, there still are
as shown by Figure 1. Thus, there still are 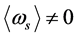 and
and 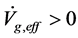 although
although  . It is seen that the contracting process is a super-heating process when
. It is seen that the contracting process is a super-heating process when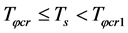 . The substable states are not stable. A substable state can transit to the stable state with
. The substable states are not stable. A substable state can transit to the stable state with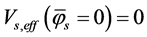 .
.
 when
when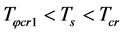 , even if
, even if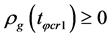 .
.
(1) The effective masses of the Higgs particles and the transformation of 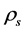 and
and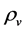 .
.
If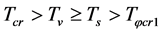 , there must be
, there must be 
 and
and 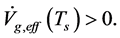 Thus, it is easily proved that there must be such a solution satisfying (6.4) in this case. Hence we consider such a contracting process when
Thus, it is easily proved that there must be such a solution satisfying (6.4) in this case. Hence we consider such a contracting process when 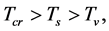
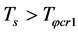 and
and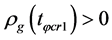 .
.
The masses containing the temperature effect are called effective masses.
The effective masses of  and
and  are important for
are important for 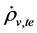 and
and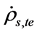 . As mentioned before,
. As mentioned before, 
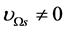 and
and , and both
, and both  and
and  hold when
hold when  and
and 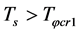 . From (5.35)-(5.36) we have
. From (5.35)-(5.36) we have
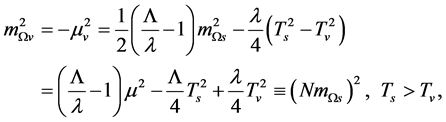 (6.7)
(6.7)
It is seen from (6.7) that there must be such a 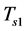 that
that 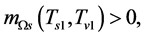
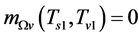 because
because 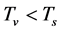 in this case. Here
in this case. Here  when
when 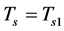 and
and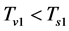 .
.  and
and 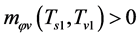 because
because  Thus, there must be such a
Thus, there must be such a  that
that  and
and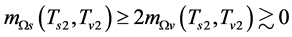 , here
, here 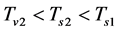 and
and  when
when . Consequently, there are such decays
. Consequently, there are such decays 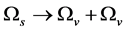 and
and 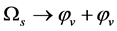 so that
so that 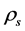 can transform to
can transform to  and
and 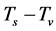 decreases, even if
decreases, even if 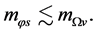 Consequently, there must is
Consequently, there must is
 (6.8)
(6.8)
where 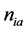 is the number density of the i-th sort of a-Higgs particles,
is the number density of the i-th sort of a-Higgs particles, 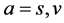 , and
, and 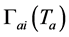 is the decay rate of the i-th sort of a-Higgs particles to the b-Higgs particles at the temperature
is the decay rate of the i-th sort of a-Higgs particles to the b-Higgs particles at the temperature ,
, 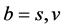 and
and . Here (6.5) is considered so that the factor
. Here (6.5) is considered so that the factor 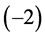 emerges in (6.8).
emerges in (6.8).
(2) 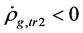 and
and 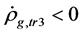 when
when 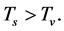
When both 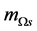 and
and 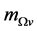 are small (i.e. when
are small (i.e. when  and
and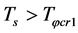 ), it is striking that such reactions as
), it is striking that such reactions as 
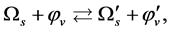
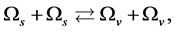 and
and 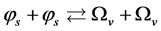 etc. due to (2.10). Considering
etc. due to (2.10). Considering 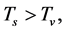 we have
we have
 (6.9)
(6.9)
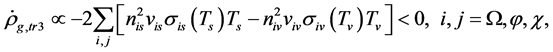 (6.10)
(6.10)
where 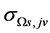
 is a scattering cross section of a
is a scattering cross section of a 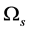
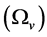 particle and a
particle and a 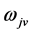
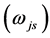 particle,
particle, 
 is a relative velocities of a
is a relative velocities of a 
 particle to a
particle to a 
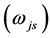 particle, and
particle, and 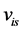
 is a relative velocities of two
is a relative velocities of two 
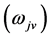 particles. (6.5) is considered so that the factor
particles. (6.5) is considered so that the factor 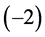 emerges in (6.9)-(6.10).
emerges in (6.9)-(6.10). 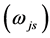
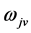 is the j-th sort of v-Higgs (s-Higgs) particles.
is the j-th sort of v-Higgs (s-Higgs) particles.
(3) 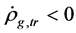 when
when 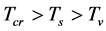 and
and 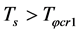
It is obvious that the larger 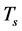 is, the less
is, the less 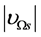 is and
is and 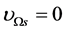 when
when . The larger
. The larger 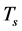 is, the less the masses of all Higgs particles originating from the couplings (2.8)-(2.10) are. Thus, the masses of all Higgs particles originating from the couplings (2.8)-(2.10) are very small when
is, the less the masses of all Higgs particles originating from the couplings (2.8)-(2.10) are. Thus, the masses of all Higgs particles originating from the couplings (2.8)-(2.10) are very small when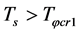 .
.
The masses of all gauge bosons and fermions are zero when 
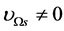 and
and . Thus, the a-Higgs particles and the a-gauge bosons or the a-ferminos can transform from one to another by the
. Thus, the a-Higgs particles and the a-gauge bosons or the a-ferminos can transform from one to another by the  couplings, here
couplings, here  and
and . Thus, the number density of the a-Higgs particles is large. The transformation of s-Higgs particles and the v-Higgs particles from one to another is striking when
. Thus, the number density of the a-Higgs particles is large. The transformation of s-Higgs particles and the v-Higgs particles from one to another is striking when 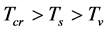 and
and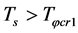 .
.
It is seen from the above mentioned and (6.8)-(6.10) that there must be
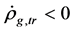 (6.11)
(6.11)
when 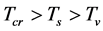 and
and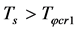 . In the case,
. In the case, 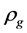 and
and  must decrease so that
must decrease so that 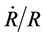 decreases.
decreases.
(4)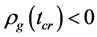 .
.
Because of the symmetry of the s-particles and the v-particles,  here
here 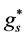
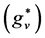 is the spinfreedom of the s-particles (the v-particles). When
is the spinfreedom of the s-particles (the v-particles). When 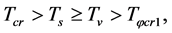
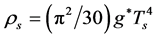 and
and
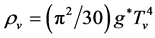 . In contrast with the contracting process
. In contrast with the contracting process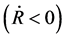 ,
,  causes
causes  and
and 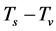 to decrease and the thermal equilibrium of s-matter and v-matter.
to decrease and the thermal equilibrium of s-matter and v-matter.
When 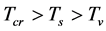 and
and 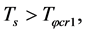
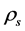 is very large and the masses of all particles are so small that they may be neglected. Consequently,
is very large and the masses of all particles are so small that they may be neglected. Consequently, 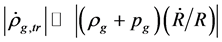 so that
so that
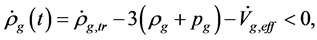 (6.12)
(6.12)
and there is such a moment  at which
at which
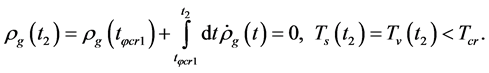 (6.13)
(6.13)
When 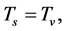
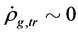 and
and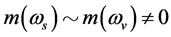 , but
, but 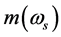 and
and 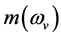 are very small so that they may be neglected. In this case, (4.5)-(4.6) and (4.12) reduce to
are very small so that they may be neglected. In this case, (4.5)-(4.6) and (4.12) reduce to

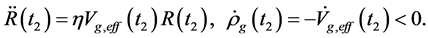 (16)
(16)
Thus, space will contract with a deceleration. Let  when
when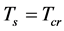 , considering
, considering  because
because 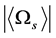 decreases due to space contraction, we have
decreases due to space contraction, we have
 (6.15)
(6.15)
6.2.3. 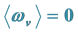 and
and 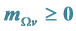 in the S-Breaking for All Time
in the S-Breaking for All Time
We see from the discussion above that  can hold when
can hold when 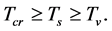 This is because
This is because
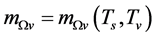 is a continuous function of
is a continuous function of 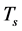 and
and 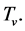 If
If 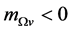 was arrived at some a time
was arrived at some a time  there must be such a time
there must be such a time 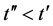 so that
so that . When
. When , the transformation of
, the transformation of 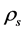 to
to 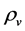 must be striking so that
must be striking so that  decreases to 0 and
decreases to 0 and 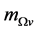 will increase from
will increase from  to
to 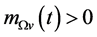 when
when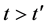 . Hence
. Hence 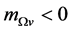 cannot occur so that the S-breaking can hold all the time for the effective potential
cannot occur so that the S-breaking can hold all the time for the effective potential 
6.3. There Is No Singularity of Space-Time in the Present Model
From (6.15) we see when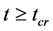 ,
,
 (6.16)
(6.16)
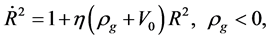 (6.17)
(6.17)
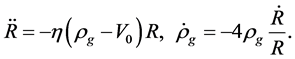 (6.18)
(6.18)
Here 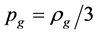 is considered. In the case, space can continue to contract, but there must be such a moment
is considered. In the case, space can continue to contract, but there must be such a moment 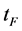 at which
at which
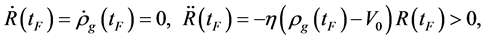 (6.19)
(6.19)
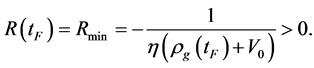 (6.20)
(6.20)
This is because 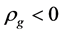 and
and 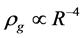 when
when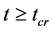 . It is easily seen that
. It is easily seen that
 (6.21)
(6.21)
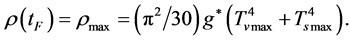 (6.22)
(6.22)
 and
and 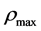 are the highest temperature and the largest energy density in the universe, respectively. According to the present model,
are the highest temperature and the largest energy density in the universe, respectively. According to the present model, 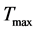 and
and 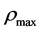 must exist. We will see that
must exist. We will see that 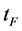 is just the final moment
is just the final moment  of the S-world and the initial moment
of the S-world and the initial moment 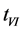 of the V-world as well, i.e.
of the V-world as well, i.e. 
In summary, there are 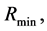
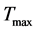 and
and 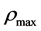 which are finite for the contracting process
which are finite for the contracting process![]() Because of the cosmological principle, all
Because of the cosmological principle, all 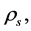
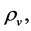
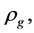
 ,
, 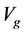
 and
and 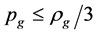 are finite. Consequently
are finite. Consequently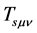 ,
, 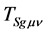
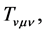 and
and  must be finite. On the other hand, because of the cosmological principle, it is obvious that if there is no space contraction, the physical quantities must be finite as well. Substituting the finite
must be finite. On the other hand, because of the cosmological principle, it is obvious that if there is no space contraction, the physical quantities must be finite as well. Substituting the finite 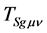 or
or 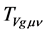 into the Einstein field equation
into the Einstein field equation![]() we see that
we see that 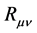 and
and  must be finite. Consequently, there is no singularity of space-time in the present model.
must be finite. Consequently, there is no singularity of space-time in the present model.
6.4. The Result above Is Not Contradictory to the Singularity Theorems
We first intuitively explain the reasons that there is no space-time singularity. It has been proved that there is space-time singularity under certain conditions [1] . These conditions fall into three categories. First, there is the requirement that gravity shall be attractive. Secondly, there is the requirement that there is enough matter present in some region to prevent anything escaping from that region. The third requirement is that there should be no causality violations.
Hawking considers it is a reasonable the first condition that 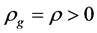 and
and 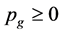 [1] . But this conjecture is not valid in the present model, because all
[1] . But this conjecture is not valid in the present model, because all 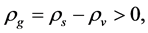
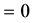 or
or 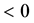 are possible.
are possible.  in general relativity is equivalent with
in general relativity is equivalent with 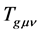 in the present model. In contrast with
in the present model. In contrast with 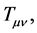
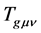 is not the energymomintum tensor so that it does not satisfy the energy condition due to the conjecture 1. On the other hand,
is not the energymomintum tensor so that it does not satisfy the energy condition due to the conjecture 1. On the other hand, 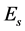 and
and 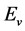 can transform from one to other, especially when temperature
can transform from one to other, especially when temperature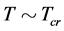 . Hence the premise of the singularity theorems does not hold so that the the singularity theorems are invalid in the present model.
. Hence the premise of the singularity theorems does not hold so that the the singularity theorems are invalid in the present model.
As mentioned above, there must be  when
when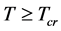 . It is seen that
. It is seen that  does not only stop increasing, but also decreases from
does not only stop increasing, but also decreases from 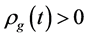
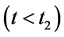 to
to 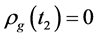 and finally to
and finally to 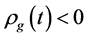 when
when 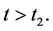 Hence the second condition of the singularity theorem is violated.
Hence the second condition of the singularity theorem is violated.
The key of non-singularity is conjecture 1, i.e. 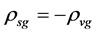 when
when 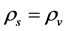 and
and  and
and 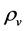 can transform from one to another.
can transform from one to another.
We explain the reasons that there is no space-time singularity from the Hawking theorem as follows. S.W. Hawking has proven the following theorem [1] .
The following three conditions cannot all hold:
(a) every inextendible non-spacelike geodesic contains a pair of conjugate point;
(b) the chronology condition holds on 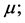
(c) there is an achronal set 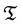 such that
such that 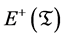 or
or  is compact.
is compact.
The alternative version of the theorem can obtained by the following two propositions.
Proposition 1 [1] :
If  and if at some point
and if at some point 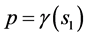 the tidal force
the tidal force  is non-zero, there will be values
is non-zero, there will be values 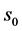 and
and 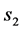 such that
such that 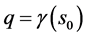 and
and 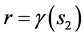 will be conjugate along
will be conjugate along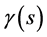 , providing that
, providing that 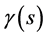 can be extended to these values.
can be extended to these values.
Proposition 2 [1] :
If 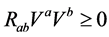 everywhere and if at
everywhere and if at 
 is non-zero, there will be
is non-zero, there will be 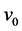 and
and 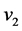 such that
such that 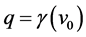 and
and 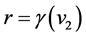 will be conjugate along
will be conjugate along  provided that
provided that 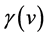 can be extended to these values.
can be extended to these values.
An alternative version of the above theorem is as following.
Space-time  is not timelike and null geodesically complete if:
is not timelike and null geodesically complete if:
(1)  for every non-spacelike vector
for every non-spacelike vector ![]()
(2) The generic condition is satisfied, i.e. every non-spacelike geodesic contains a point at which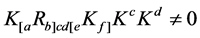 , where
, where ![]() is the tangent vector to the geodesic.
is the tangent vector to the geodesic.
(3) The chronology condition holds on  (i.e. there are no closed timelike curves).
(i.e. there are no closed timelike curves).
(4) There exists at least one of the following:
(A) a compact achronal set without edge(B) a closed trapped surface(C) a point  such that on every past (or every future) null geodesic from
such that on every past (or every future) null geodesic from  the divergence
the divergence  of the null geodesics from
of the null geodesics from 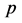 becomes negative (i.e. the null geodesics from
becomes negative (i.e. the null geodesics from ![]() are focussed by the matter or curvature and start to reconverge).
are focussed by the matter or curvature and start to reconverge).
In fact, 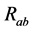 is determined by the gravitational energy-momentum tensor
is determined by the gravitational energy-momentum tensor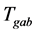 . According to the conventional theory,
. According to the conventional theory, 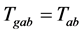 so that the above theorem holds.
so that the above theorem holds.
In contrast with the conventional theory, according to conjecture 1,
 (6.23)
(6.23)
 ,
, ![]() and
and ![]() are all possible. Thus, although the strong energy condition still holds, i.e.
are all possible. Thus, although the strong energy condition still holds, i.e.
 (6.24)
(6.24)
the conditions of propositions 1 and 2 and condition (1) no longer hold, because the gravitational mass density 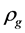 determines
determines  and
and 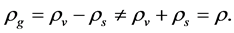 Hence (a) and (c) do not hold, but (b) still holds, and
Hence (a) and (c) do not hold, but (b) still holds, and  is timelike and null geodesically complete.
is timelike and null geodesically complete.
7. Space Inflation
7.1. Space Inflation
When 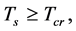
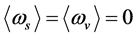 and
and 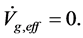 We call such a state in which
We call such a state in which  the most symmetric state. In this state the
the most symmetric state. In this state the 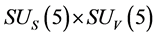 symmetry holds strictly and the s-particles and the v-particles are symmetric.
symmetry holds strictly and the s-particles and the v-particles are symmetric.
When 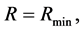
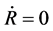 and
and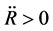 . Hence space will expand when
. Hence space will expand when .
.
Consider the initial stage of expansion in which 
 and
and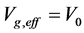 .
. 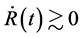 is small due to
is small due to . On the other hand,
. On the other hand, 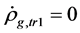 because
because  and the s-particles and the v-particles are symmetric.
and the s-particles and the v-particles are symmetric.  and
and 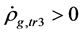 because (6.5)-(6.6),
because (6.5)-(6.6),  and
and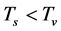 . Hence
. Hence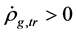 . In the case, (4.5)-(4.6) and (4.15) become
. In the case, (4.5)-(4.6) and (4.15) become
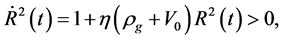 (7.1)
(7.1)
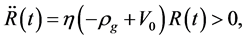 (7.2)
(7.2)
 (7.3)
(7.3)
because 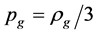 and
and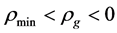 . It is seen from (7.1)-(7.3) that there is such a time
. It is seen from (7.1)-(7.3) that there is such a time  at which
at which 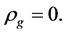 Furthermore,
Furthermore, 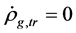 because
because 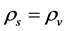 and
and . Thus, when
. Thus, when 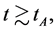 (7.1)-(7.3) reduce to
(7.1)-(7.3) reduce to
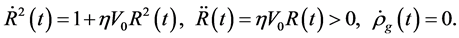 (7.4)
(7.4)
Consequently, space inflation must occur
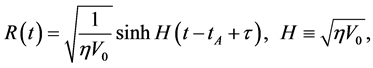 (7.5)
(7.5)
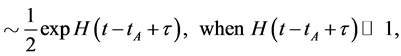 (7.6)
(7.6)
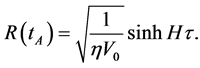 (7.7)
(7.7)
7.2. The Process of Space Inflation
Supposing 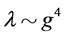 and
and 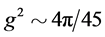 for
for  and considering
and considering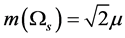 , from (5.40) we can estimate
, from (5.40) we can estimate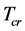 ,
,
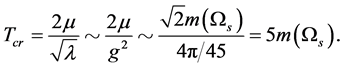 (7.8)
(7.8)
We may take , because
, because  when
when 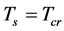 and
and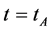 .
.
The temperature will strikingly decrease in the process of inflation, but the potential energy
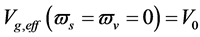 cannot decrease to
cannot decrease to 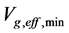 at once. This is a super-cooling process. We can get the expecting results by suitably choosing the parameters in (2.8)-(2.10). In order to estimate
at once. This is a super-cooling process. We can get the expecting results by suitably choosing the parameters in (2.8)-(2.10). In order to estimate 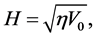 taking
taking  from (7.8) we have
from (7.8) we have
 (7.9)
(7.9)
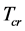 is larger than the temperature corresponding to GUT. Taking
is larger than the temperature corresponding to GUT. Taking  and
and
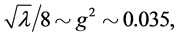 we have
we have  If the duration of the super-cooling state is
If the duration of the super-cooling state is 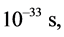 Rcr will increase
Rcr will increase  times. The result is consistent with the Guth’s inflation model [28] .
times. The result is consistent with the Guth’s inflation model [28] .
If there is no v-matter, because of contraction by gravitation, the world would become a thermal-equilibrating singular point, i.e., the world would be in the hot death state. As seen, it is necessary that there are both s-matter and v-matter and both the S-breaking and the V-breaking.
8. Evolving Process of Space after Inflation
8.1. The Reheating Process
After inflation, the temperature must sharply descend. In this case, it is easily seen that the most symmetric state with 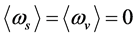 is no longer stable and must decay into such a state with
is no longer stable and must decay into such a state with 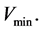 This is the reheating process. Either of the S-breaking and the V-breaking can come into being, because s-matter and v-matter are completely symmetric at
This is the reheating process. Either of the S-breaking and the V-breaking can come into being, because s-matter and v-matter are completely symmetric at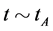 . Letting the V-breaking comes into being
. Letting the V-breaking comes into being![]() then the symmetry breaking is
then the symmetry breaking is 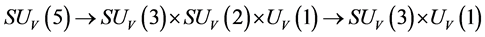 and
and  symmetry is still kept all time. After the reheating process, when temperature is low, considering (3.15) we have
symmetry is still kept all time. After the reheating process, when temperature is low, considering (3.15) we have
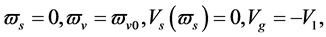 (8.1)
(8.1)
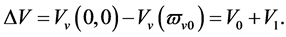 (8.2)
(8.2)
After reheating,  must first transform into v-energy by (2.9) and the SUV(5) couplings and into s-energy by (2.10). Letting
must first transform into v-energy by (2.9) and the SUV(5) couplings and into s-energy by (2.10). Letting  transform the v-energy, then
transform the v-energy, then  transforms the s-energy. It is necessary
transforms the s-energy. It is necessary . There is
. There is 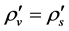 before the reheating. Thus, after reheating, we have
before the reheating. Thus, after reheating, we have
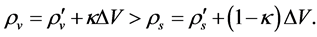 (8.3)
(8.3)
8.2. The Change of Mass Densities
Let 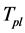 be such a temperature that particles exist in the
be such a temperature that particles exist in the  plasma form when
plasma form when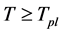 , and particles exist in the form of
, and particles exist in the form of  color singlets when
color singlets when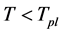 . After reheating process, in the initial stage, both
. After reheating process, in the initial stage, both 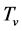 and
and 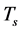 are high and all particles must exist in the plasma form when
are high and all particles must exist in the plasma form when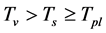 . Thus, the masses of particles may be neglected so that
. Thus, the masses of particles may be neglected so that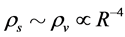 . After temperature descends further so that
. After temperature descends further so that , s-particles will form
, s-particles will form  color singlets whose masses are all non-zero. Thus, there is no s-photon, i.e.
color singlets whose masses are all non-zero. Thus, there is no s-photon, i.e.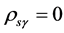 . The
. The 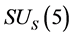 color singlets cannot form any clustering and their masses are all small. Let
color singlets cannot form any clustering and their masses are all small. Let  is the largest mass of the stable
is the largest mass of the stable 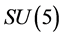 color singlets, then we may suppose
color singlets, then we may suppose 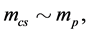 here
here 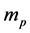 is the mass of a proton. However v-particles will exist in the forms of nucleons, leptons and photons, and can form galaxies in low temperatures. Consequently, in the V-breaking,
is the mass of a proton. However v-particles will exist in the forms of nucleons, leptons and photons, and can form galaxies in low temperatures. Consequently, in the V-breaking,
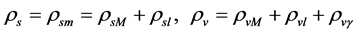 (8.4)
(8.4)
Let the reheating process ends at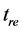 . Considering
. Considering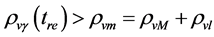 , we suppose
, we suppose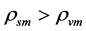 . From (8.3) we have
. From (8.3) we have
 (8.5)
(8.5)
After reheating process ends, temperature is low, 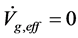 and all masses of the Higgs particles are large enough so that the transformation
and all masses of the Higgs particles are large enough so that the transformation 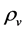 and
and 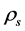 may be neglected. Thus,
may be neglected. Thus, .
.
As mentioned in section 4 (see (4.21)-(4.26)), the evolving laws of 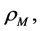
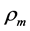 and
and 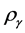 as space contraction are different from each other. For simplicity, we do not differentiate
as space contraction are different from each other. For simplicity, we do not differentiate 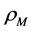 and
and 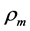 for a time. Thus, neglecting
for a time. Thus, neglecting 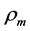 and
and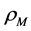 , considering
, considering  and
and 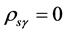 in the V-breaking, from (4.24)-(4.26) (
in the V-breaking, from (4.24)-(4.26) ( in (4.26)) and (8.5) we have
in (4.26)) and (8.5) we have
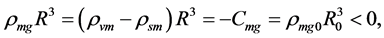 (8.6)
(8.6)
 (8.7)
(8.7)
where both 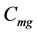 and
and 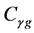 are constants. From (4.8), (8.3) and (8.6)-(8.7), (4.5)-(4.6) is reduced to
are constants. From (4.8), (8.3) and (8.6)-(8.7), (4.5)-(4.6) is reduced to
 (8.8)
(8.8)
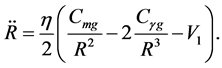 (8.9)
(8.9)
As mentioned in section 3,  may be neglected when
may be neglected when  in the V-breaking. Thus we neglects
in the V-breaking. Thus we neglects  for a time in the following.
for a time in the following.
We discuss (8.8)-(8.9) as follows.
 If
If  when
when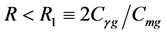 ,
,  and
and , i.e. space expands with a deceleration; when
, i.e. space expands with a deceleration; when ,
,  and
and ; when
; when 
 and
and  i.e.
i.e.
space expands with an acceleration. In the process, 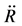 increases from
increases from 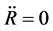 to
to 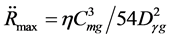 when
when  then
then  decreases from
decreases from  to
to 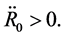
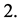 If
If 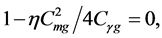 when
when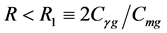 ,
, 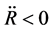 and
and ; when
; when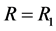 ,
,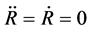 ; In the case, space can be static.
; In the case, space can be static.
 If
If  when
when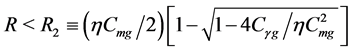 ,
, 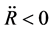 and
and ; when R =
; when R =
R2,  and
and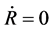 . In the case, space will begin to contract.
. In the case, space will begin to contract.
The first case is consistent with observations. A computation in detail is the same as that of Ref. .
.
Even 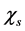 and
and  are considered
are considered![]() the above conclusions still hold qualitatively.
the above conclusions still hold qualitatively.
8.3. To Determine a(t)
Letting 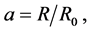

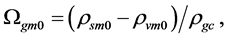
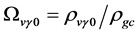 and
and  and considering
and considering
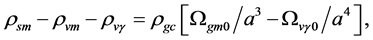 (8.10)
(8.10)
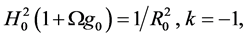 (8.11)
(8.11)
we rewrite (8.6) as
 (8.12)
(8.12)
From (8.12) we have
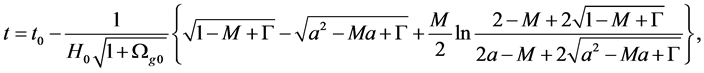 (8.13)
(8.13)
If 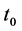 is taken as
is taken as
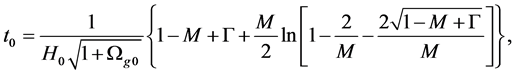 (8.14)
(8.14)
 (8.15)
(8.15)
where  and
and 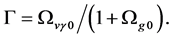
Taking 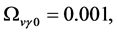

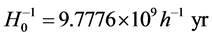 [18] . and h = 0.8, we get
[18] . and h = 0.8, we get 
 is shown by the curve
is shown by the curve  in the Figure 2 and describes evolution of the universe from
in the Figure 2 and describes evolution of the universe from 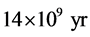 ago to now. Taking
ago to now. Taking 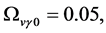
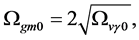 we get the
we get the  which is shown by the curve B in the Figure 2 and describes evolution of the cosmos from
which is shown by the curve B in the Figure 2 and describes evolution of the cosmos from 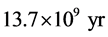 ago to now. Provided
ago to now. Provided 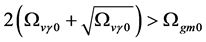 which is equivalent to
which is equivalent to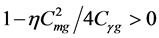 , we can get a curve of
, we can get a curve of  which describes evolution of the cosmological scale. The curves A and B show that when the parameters alter in a definte scope, the qualitative features of the evolving curves are changeless, but their concrete-changing forms are differnt from each other. Thus, the parameters in the model should be determined based on astronomical observations.
which describes evolution of the cosmological scale. The curves A and B show that when the parameters alter in a definte scope, the qualitative features of the evolving curves are changeless, but their concrete-changing forms are differnt from each other. Thus, the parameters in the model should be determined based on astronomical observations.
From the two curves we see that the cosmos must undergo a period in which space expands with a deceleration in the past, and undergo the present period in which space expands with an acceleration.
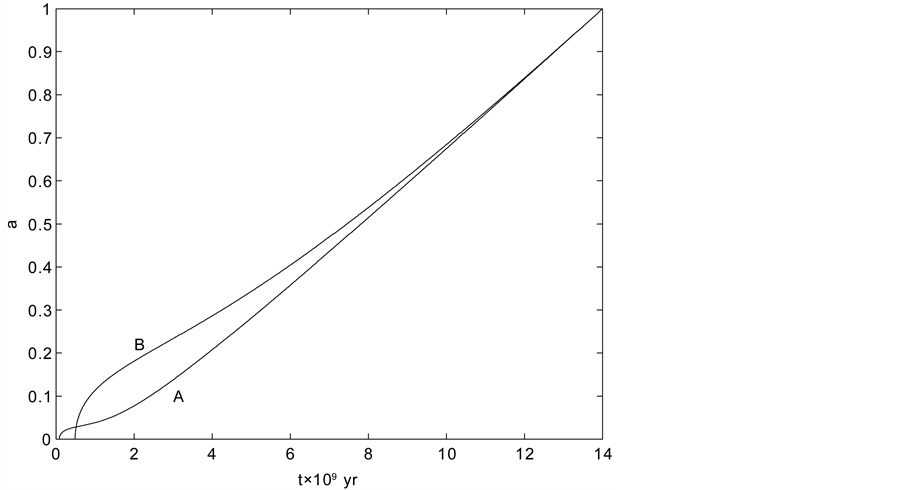
Figure 2. The curve A describes evolution of a(t) from 14 × 109 yr ago to now; The curve B describes evolution of a(t) from 13.7 × 109 yr ago to now. The starting point of curve A is different from that of curve B.
It should be noted that 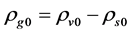 in the V-breaking, but here
in the V-breaking, but here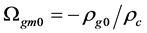 . Neglected
. Neglected 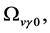 noting
noting  and taking
and taking
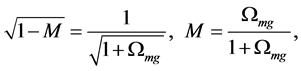 (8.16)
(8.16)
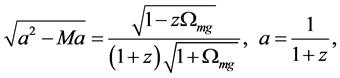 (8.17)
(8.17)
 (8.18)
(8.18)
we can reduce (8.15) to
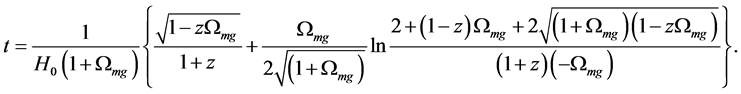 (8.19)
(8.19)
Replacing 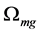 by
by 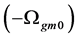 because
because 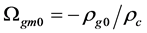 and and ignoring
and and ignoring 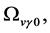 we see (8.19) to be the same as the corresponding formula (3.44) in Ref. [18] .
we see (8.19) to be the same as the corresponding formula (3.44) in Ref. [18] .
8.4. The Relation between Redshift and Luminosity Distance
From (8.12) and the RW metric we have
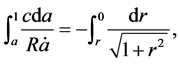 (8.20)
(8.20)
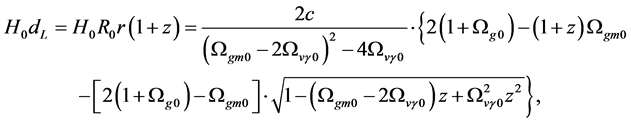 (8.21)
(8.21)
where  is the redshift caused by
is the redshift caused by 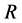 increasing.
increasing.
Considering 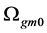 in (8.21) corresponds to
in (8.21) corresponds to 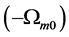 in (3.81) in Ref. [18] and
in (3.81) in Ref. [18] and 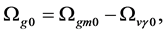 we see that (8.21) is consistent with (3.81) in Ref. [18] .
we see that (8.21) is consistent with (3.81) in Ref. [18] .
Ignoring 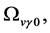 taking
taking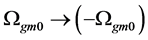 , we reduce (8.21) to
, we reduce (8.21) to
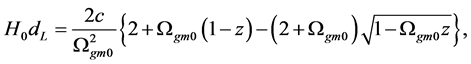 (8.22)
(8.22)
which is consistent with (3.78) in Ref. [18] . Approximating to 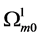 and
and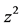 , we obtain
, we obtain
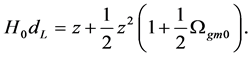 (8.23)
(8.23)
Taking 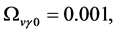
 and
and 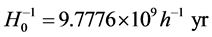 [18] and h = 0.8, from (8.22) we get the
[18] and h = 0.8, from (8.22) we get the 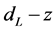 relation which is shown by the curve
relation which is shown by the curve  in the Figure 3. Taking
in the Figure 3. Taking  and
and
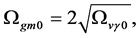 we get the
we get the 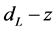 relation which is shown by the curve
relation which is shown by the curve  in the Figure 3.
in the Figure 3.
9. After Expansion with an Acceleration, Space Expands with a Deceleration, Then Comes to Static and Finally Begin to Contract.
As mentioned before, the evolving laws of  and
and 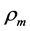 as space contracts or expands are different from each other. After space expands with an acceleration, we should consider the difference between
as space contracts or expands are different from each other. After space expands with an acceleration, we should consider the difference between 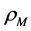 and
and .
.
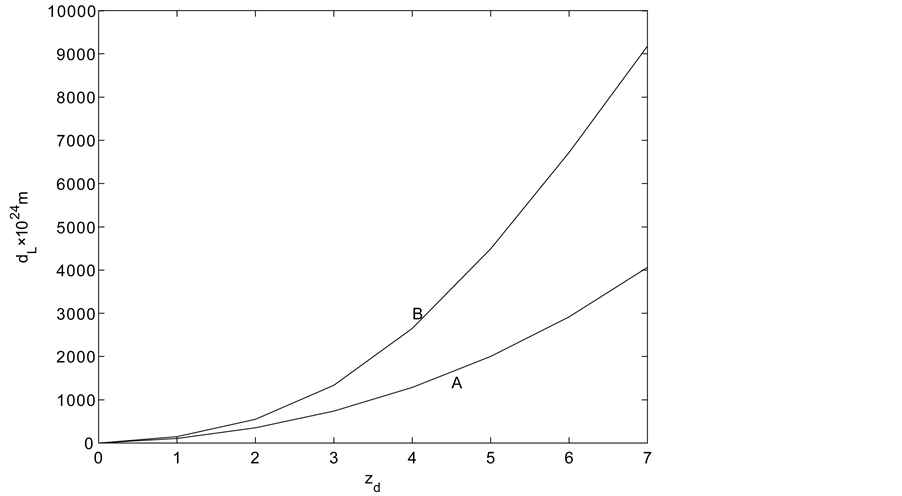
Figure 3. The curve A describes the 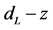 relation when
relation when 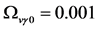 and
and 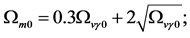 The curve B describes the
The curve B describes the 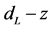 relation when
relation when 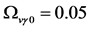 and
and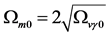 .
.
When R is large enough, 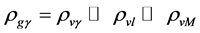 so that
so that  and
and  may be neglected. Thus, considering
may be neglected. Thus, considering  in low temperatures, neglecting
in low temperatures, neglecting 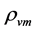 and
and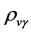 , we can reduce (4.5)-(4.6) to
, we can reduce (4.5)-(4.6) to
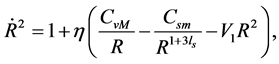 (9.1)
(9.1)
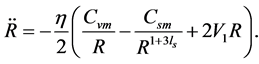 (9.2)
(9.2)
where 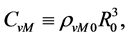
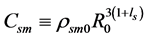 and
and . As mentioned in section 3,
. As mentioned in section 3,  is so small that it may be neglected when
is so small that it may be neglected when 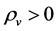 in the V-breaking. It is seen from (9.2) that
in the V-breaking. It is seen from (9.2) that 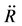 changes from
changes from  to
to  and finally
and finally 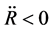 as space expands. It is seen from (9.1) that there must be
as space expands. It is seen from (9.1) that there must be 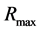 so that
so that  when
when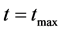 . Space will begin to contract when
. Space will begin to contract when  because
because 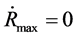 and
and 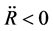 at
at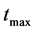 . It is seen that after space expands with an acceleration, it will expands with a deceleration, then comes to static, and final begin contracts. This is different from the conventional theory and the model [19] [20] .
. It is seen that after space expands with an acceleration, it will expands with a deceleration, then comes to static, and final begin contracts. This is different from the conventional theory and the model [19] [20] .
When 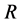 is large enough,
is large enough,  and
and 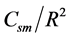 may be neglected. Thus, from (9.1) we have
may be neglected. Thus, from (9.1) we have
 (9.3)
(9.3)
To sum up, according to the present model, the universe can expand from  to
to , and then contract to
, and then contract to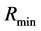 ; Both
; Both 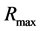 and
and 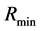 are finite. The universe can be in the S-breaking, and can be in the V-breaking as well; The S-breaking can transform to the V-breaking after space contracts to
are finite. The universe can be in the S-breaking, and can be in the V-breaking as well; The S-breaking can transform to the V-breaking after space contracts to 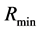 and vice versa.
and vice versa.
10. Existing and Distribution Forms of SUS(5) Color Singlets
In the V-breaking, all s-gauge particles and s-fermions are massless. When the temperature , all s-particles must exist in plasma form. When
, all s-particles must exist in plasma form. When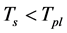 , all s-particles will exist in s-SU(5) color-singlets (conjecture 2). Let
, all s-particles will exist in s-SU(5) color-singlets (conjecture 2). Let ,
,  ,
,  ,
, 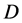 ,
,  denote the 5 sorts of colors. A component of
denote the 5 sorts of colors. A component of 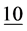 representation carries color
representation carries color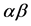 ,
,  ,
, 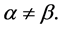 A component of
A component of 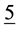 representation carries color
representation carries color ![]() A gauge boson carries colors
A gauge boson carries colors 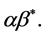 There are the following sorts of the s-SU(5) color-singlets.
There are the following sorts of the s-SU(5) color-singlets.
2-fermion states: 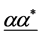 or
or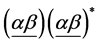 ,
, 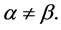 3-fermion states:
3-fermion states: 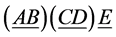 or
or 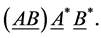 4-fermion states:
4-fermion states: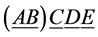 . 5-fermion states:
. 5-fermion states:  or
or  Gauge boson single-states:
Gauge boson single-states: 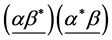 or
or 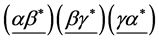 etc.
etc.![]()
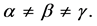 Fermion-gauge boson singlets:
Fermion-gauge boson singlets: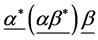 ,
,
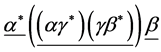 etc.
etc.
The masses of all color singlets are non-zero, hence . The fermions with the spin
. The fermions with the spin  and the least mass are stable, and the bosons with the spin
and the least mass are stable, and the bosons with the spin  and the least mass are stable as well. This is because there is no the electroweak interaction among
and the least mass are stable as well. This is because there is no the electroweak interaction among  color single states so that they cannot decay. Of course, there are the s-antiparticles corresponding to the s-colour singlets above as well.
color single states so that they cannot decay. Of course, there are the s-antiparticles corresponding to the s-colour singlets above as well.
There is no interaction among the  color singlets, because
color singlets, because 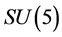 is a simple group. There are interaction among the
is a simple group. There are interaction among the 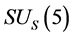 color singlets by exchanging the
color singlets by exchanging the  color single states. The interaction radius must be very small because the masses of all
color single states. The interaction radius must be very small because the masses of all 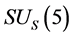 color singlets are non-zero. Thus, the interaction may be neglected so that we can approximately regard the
color singlets are non-zero. Thus, the interaction may be neglected so that we can approximately regard the 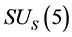 color singlets as ideal gas without collision. The ideal gas has the effect of free flux damping for clustering. Consequently, the
color singlets as ideal gas without collision. The ideal gas has the effect of free flux damping for clustering. Consequently, the  color single states cannot form clustering and must distribute loosely in space, and their decoupling temperature must be very high so that their relative velocities are large and invariant. But they can form s-superclusterings, because there is the gravitation among them and there is repulsion between s-matter and v-matter. The superclusterings are similar to neutrino superclusterings and are huge voids for v-observers.
color single states cannot form clustering and must distribute loosely in space, and their decoupling temperature must be very high so that their relative velocities are large and invariant. But they can form s-superclusterings, because there is the gravitation among them and there is repulsion between s-matter and v-matter. The superclusterings are similar to neutrino superclusterings and are huge voids for v-observers.
11. New Predictions, an Inference, and There Is No Restriction for 
11.1. New Predictions
11.1.1. The Essence and Characters of Huge Voids
It is possible that Huge voids are not empty and are equivalent to huge concave lenses. The density of hydrogen inside the huge voids is more less than that predicted by the conventional theory.
Based on above mentioned, we consider, the huge voids for the v-observers are, in fact, superclusters of the  color singlets. The huge v-voids are not empty. There must be the
color singlets. The huge v-voids are not empty. There must be the 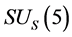 color singlets inside them, and
color singlets inside them, and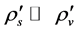 ,
, 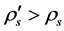 , and
, and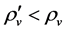 . Here
. Here 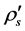 and
and 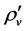 denote the densities inside the huge v-voids, and
denote the densities inside the huge v-voids, and 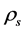 and
and  denote the densities outside the huge v-voids. The characters of such a huge v-void are as follows:
denote the densities outside the huge v-voids. The characters of such a huge v-void are as follows:
A. A v-void must be huge, because there is no other interaction among the s-SU(5) color singlets except the gravitation and the masses of the s-SU(5) color singlets are very small.
B. When v-photons pass through such a huge v-void, the v-photons must suffer repulsion coming from s-matter inside the huge void and are scattered by the v-void as they pass through a huge concave lens. Consequently, the galaxies behind the huge v-void seem to be darker and more remote. Hence the huge voids are equivalent to huge concave lenses.
C. Both density of matter and density of dark matter in the huge voids must be more lower than those predicted by the conventional theory. Consequently, the densities of hydrogen and helium inside the huge voids must be more less than that predicted by the conventional theory.
The predict can be confirmed or negated by the observation of hydrogen distribution.
This is a decisive prediction which distinguishes the present model from other models.
11.1.2. The Gravity between Two Galaxies Whose Distance Is Long Enough
There must be s-superclusterings between two v-galaxies when both distance is long enough, hence the gravity between the two v-galaxies must be less than that predicted by the conventional theory due to the repulsion between s-matter and v-matter. When the distance between two v-galaxies is small, the gravitation is not influenced by s-matter, because 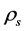 must be small when
must be small when 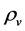 is big.
is big.
11.1.3. A Black Hole with Its Mass and Density Big Enough Will Transform into a White Hole
Letting there be a v-black hole with its mass and density to be so big that its temperature can arrive at  because the black hole contracts by its self-gravitation, then the expectation values of the Higgs fields inside the v-black hole will change from
because the black hole contracts by its self-gravitation, then the expectation values of the Higgs fields inside the v-black hole will change from 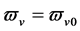 and
and 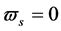 into
into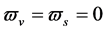 . Consequently, inflation must occur. After inflation, the most symmetric state
. Consequently, inflation must occur. After inflation, the most symmetric state  will transit into the V-breaking. Thus, the energy of the black hole must transform into both the v-energy and the s-energy. Thus, a v-observer will find that the black hole disappears and a white hole appears.
will transit into the V-breaking. Thus, the energy of the black hole must transform into both the v-energy and the s-energy. Thus, a v-observer will find that the black hole disappears and a white hole appears.
In the process, a part of v-energy transforms into v-energy and the other part transforms into s-energy. A v-observer will consider the energy not to be conservational because he cannot detect s-matter except by repulsion. The transformation of black holes is different from the Hawking radiation. This is the transformation of the vacuum expectation values of the Higgs fields. There is no contradiction between the transformation and the Hawking radiation or another quantum effect, because both describe different processes and based on different conditions. According to the present model, there still are the Hawking radiation or other quantum effects of black holes. In fact, the universe is just a huge black hold. The universe can transform from the S-breaking into the V-breaking because of its contraction. This transformation is not quantum effects.
11.2. An inference:  Although
Although 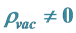
The effective cosmological constant 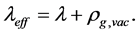 The conventional theory can explain evolution with a small
The conventional theory can explain evolution with a small  but
but 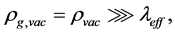 Consequently, the issue of the cosmological constant appears.
Consequently, the issue of the cosmological constant appears.
 can be obtained by some supersymmetric model, but it is not a necessary result. On the other hand, the particles predicted by the supersymmetric theory have not been found, although their masses are not large.
can be obtained by some supersymmetric model, but it is not a necessary result. On the other hand, the particles predicted by the supersymmetric theory have not been found, although their masses are not large.
 is a necessary result of our quantum field theory without divergence [13] -[15] . In this theory,
is a necessary result of our quantum field theory without divergence [13] -[15] . In this theory, 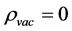 is naturally obtained without normal order of operators, there is no divergence of loop corrections, and dark matter which can form dark galaxies is predicted [16] [17] . But the model does not explain the evolution of the universe.
is naturally obtained without normal order of operators, there is no divergence of loop corrections, and dark matter which can form dark galaxies is predicted [16] [17] . But the model does not explain the evolution of the universe.
As mention above, the present model can explain evolution of the universe without  hence
hence
 (11.1)
(11.1)
Applying the conventional quantum field theory to the present model, we have 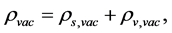 here
here  is the energy density of the vacuum state. According to the conjecture 1, s-particles and v-particles are symmetric. Hence both ground states must be symmetric as well. Hence
is the energy density of the vacuum state. According to the conjecture 1, s-particles and v-particles are symmetric. Hence both ground states must be symmetric as well. Hence
 (11.2)
(11.2)
According to conjecture 1,  when
when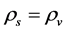 . Consequently, although
. Consequently, although
 (11.3)
(11.3)
we have still
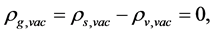 (11.4)
(11.4)
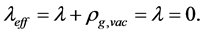 (11.5)
(11.5)
Here 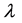 is the Einstein cosmological constant. This is a direct inference of the present model, and independent of a quantum field theory.
is the Einstein cosmological constant. This is a direct inference of the present model, and independent of a quantum field theory.
Because of (11.4), for the vacuum state in the S-breaking or the V-breaking, the Einstein field equation is reduced to
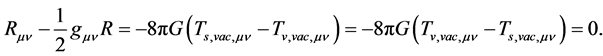 (11.6)
(11.6)
This is a reasonable result.
11.3. There Is No Restriction for 
The problem of total energy conservation in the general relativity is unsolved up to now. This is because tensors at different points cannot be summed up. On the other hand, according to the Einstein equation, . In contrast with this result, according to the present model, we have (2.22). This result (2.22) implies that there is no restriction for
. In contrast with this result, according to the present model, we have (2.22). This result (2.22) implies that there is no restriction for  or
or . The dominant energy condition and the positive energy theorem are not applicable to
. The dominant energy condition and the positive energy theorem are not applicable to 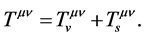
Whether does 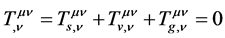 holds? We will discuss the problem in another paper.
holds? We will discuss the problem in another paper.
12. Conclusions
A new conjecture is proposed that there are s-matter and v-matter which are symmetric, whose gravitational masses are opposite to each other, although whose masses are all positive. Both can transform from one to another when temperature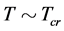 . Consequently there is no singularity in the model. The cosmological constant
. Consequently there is no singularity in the model. The cosmological constant 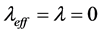 is determined although the energy density of the vacuum state is still very large. A formula is derived which well describes the relation between a luminosity distance and the redshift corresponding to it.
is determined although the energy density of the vacuum state is still very large. A formula is derived which well describes the relation between a luminosity distance and the redshift corresponding to it.
The conjecture are not in contradiction with given experiments and astronomical observations up to now, although the conjecture violates the equivalence principle.
There are two sorts of breaking modes, i.e. the S-breaking and the V-breaking. In the V-breaking, 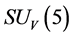 is broken to
is broken to 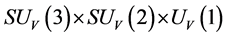 and finally
and finally 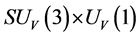 and
and 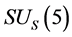 is kept all time
is kept all time![]() Consequently, v-particles get their masses and form v-atoms, v-observers and v-galaxies etc., while s-gauge bosons and s-fermions are still massless and must form
Consequently, v-particles get their masses and form v-atoms, v-observers and v-galaxies etc., while s-gauge bosons and s-fermions are still massless and must form 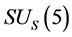 color-single states when
color-single states when 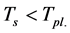 There is no interaction among the
There is no interaction among the 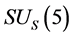 color-single states except the gravitation, because
color-single states except the gravitation, because  group is a simple group. Hence they must distribute loosely in space, cannot be observed and can cause space to expand with an acceleration. Thus, v-matter is identified with conventional matter (include dark matter) and s-matter is similar to the dark energy. But in contrast with the dark energy, the gravitational mass of s-matter is negative in the V-breaking.
group is a simple group. Hence they must distribute loosely in space, cannot be observed and can cause space to expand with an acceleration. Thus, v-matter is identified with conventional matter (include dark matter) and s-matter is similar to the dark energy. But in contrast with the dark energy, the gravitational mass of s-matter is negative in the V-breaking.
There are the critical temperature 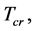 the highest temperatures
the highest temperatures 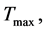 and the least scale
and the least scale  in this model. Hence it is impossible that the Plank temperature, length and time are arrived.
in this model. Hence it is impossible that the Plank temperature, length and time are arrived.
Based on the present model![]() the space evolving process is as follows. Firstly, in the S-breaking,
the space evolving process is as follows. Firstly, in the S-breaking, 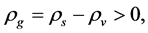 hence space contracts and
hence space contracts and 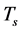 and
and 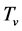 rises
rises![]() When
When 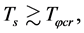 the transformation of
the transformation of  and
and  from one to another is striking so that
from one to another is striking so that 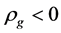 is possible. Hence there are such solutions of the evolution equations which satisfy the physical boundary condition, i.e.
is possible. Hence there are such solutions of the evolution equations which satisfy the physical boundary condition, i.e. 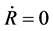 when
when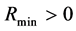 . When
. When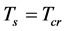 ,
,  the
the 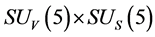 symmetry (the highest symmetry) is kept, and
symmetry (the highest symmetry) is kept, and . When space contracts further,
. When space contracts further, 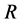 arrives the least scale
arrives the least scale 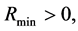
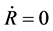 and
and  arrives the highest temperature
arrives the highest temperature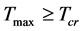 . Then space expands and
. Then space expands and 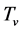 descends to
descends to 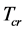 so that
so that 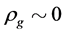 and inflation must occur. After the inflation, the phase transition of the vacuum (the reheating process) occurs. After the reheating process, this state with the highest symmetry transits to the state with the V-breaking. In the V-breaking, the evolving process of space is as follows. Space firstly expands with a deceleration because
and inflation must occur. After the inflation, the phase transition of the vacuum (the reheating process) occurs. After the reheating process, this state with the highest symmetry transits to the state with the V-breaking. In the V-breaking, the evolving process of space is as follows. Space firstly expands with a deceleration because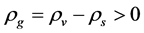 ; Secondly, space expands with an acceleration because
; Secondly, space expands with an acceleration because  and
and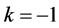 ; Thirdly, space expands with a deceleration, and then comes to static; Finally, space begin contract.
; Thirdly, space expands with a deceleration, and then comes to static; Finally, space begin contract.
It is seen that according to the present model, the universe can expand from  to
to , and then contract from
, and then contract from  to
to ; Both
; Both  and
and 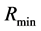 are finite. The universe can be in the S-breaking, and can be in the V-breaking as well; The S-breaking can transform to the V-breaking after space contracts to
are finite. The universe can be in the S-breaking, and can be in the V-breaking as well; The S-breaking can transform to the V-breaking after space contracts to 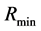 and vice versa.
and vice versa.
Three new predicts have been given.
Huge v-voids in the V-breaking are not empty, but are superclusterings of s-particles. The huge voids are equivalent to huge concave lens. The densities of hydrogen helium in the huge voids predicted by the present model must be much less than that predicted by the conventional theory.
The gravitation between two galaxies whose distance is long enough will be less than that predicted by the conventional theory.
It is possible that a v-black hole with its big enough mass and density can transform into a huge white hole by its self-gravitation.
I am very grateful to professor Zhao Zhan-yue, professor Wu Zhao-yan, professor Zheng Zhi-peng and professor Zhao Zheng-guo for their helpful discussions and best support. I am very grateful to professor Liu Yun-zuo, professor Lu Jingbin, doctor Yang Dong and doctor Ma Keyan for their helpful discussions and help in the manuscript.
References
- Hawking, S.W. and Ellis, G.F.R. (1999) The Large Scale Structure of Space-Time, Cambridge University Press, 7, 98, 101, 137, 256-298.
- Brandenberger, R., Mukhanov, V. and Sornborger, A. (1993) Cosmological Theory without Singularities. Physical Review D, 48, 1629-1642. http://dx.doi.org/10.1103/PhysRevD.48.1629
- Frolov, V.P, Markov M.A. and Mukhanov V.F. (1990) Black Holes as Possible Sources of Closed and Semiclosed Worlds. Physical Review D, 41, 383-394. http://dx.doi.org/10.1103/PhysRevD.41.383
- Caldwell, R.R. (2004) Dark Energy. Physics World, 17, 37-42.
- Padmanabhan, T. (2003) Cosmological Constant—The Weight of the Vacuum. Physics Reports, 380, 235-320. http://dx.doi.org/10.1016/S0370-1573(03)00120-0
- Peebles P.J.E. and Ratra, B. (2003) The Cosmological Constant and Dark Energy. Reviews of Modern Physics, 75, 559. http://dx.doi.org/10.1103/RevModPhys.75.559
- Weinberg, S. (1987) Anthropic Bound on the Cosmological Constant. Physical Review Letters, 59, 2607-2610. http://dx.doi.org/10.1103/PhysRevLett.59.2607
- Martel, H., Shapiro, P.R. and Weinberg, S. (1998) Likely Values of the Cosmological Constant. The Astrophysical Journal, 492, 29-40. http://dx.doi.org/10.1086/305016
- Peebles, P.J.E. and Ratra, B. (1988) Cosmology with a Time-Variable Cosmological “Constant”. The Astrophysical Journal, 325, L17-L20. http://dx.doi.org/10.1086/185100
- Ratra, B. and Peebles, P.J.E. (1988) Cosmological Consequences of a Rolling Homogeneous Scalar Field. Physical Review D, 37, 3406; http://dx.doi.org/10.1103/PhysRevD.37.3406
- Peebles, P.J.E. and Ratra, B. (2003) The Cosmological Constant and Dark Energy. Reviews of Modern Physics, 75, 559. http://dx.doi.org/10.1103/RevModPhys.75.559
- Hall, L.J. Nomura Y. and Oliver, S.J., (2005) Evolving Dark Energy with w≠-1. Physical Review Letters, 95, 14. http://dx.doi.org/10.1103/PhysRevLett.95.141302
- Chen, S.H. (2002) Quantum Field Theory without Divergence A. arXiv: hep-th/0203220.
- Chen, S.H. (2002) Significance of Negative Energy State in Quantum Field Theory A. arXiv: hep-th/0203230.
- Chen, S.H. (2005) Quantum Field Theory without Divergence. In: Kovras, O., Ed., Quantum Field Theory: New Research, Nova Science Publishers, Hauppauge, 103-170.
- Chen, S.H. (2001) A Possible Candidate for Dark Matter. arXiv: hep-th/0103234.
- Chen, S.H. (2005) A Possible Candidate for Dark Matter. In: Val Blain, J., Progress in Dark Matter Research, Nova Science Publishers, Hauppauge, 65-72.
- Peacock, J.A. (1999) Cosmological Physics. Cambridge University Press, 78, 89, 90, 296, 458, 460-464, 579, 664.
- Chen, S.-H. (2009) Discussion of a Possible Universal Model without Singularity. arXiv: 0908.1495v2.
- Chen, S.-H. (2006) A Possible Universal Model without Singularity and its Explanation for Evolution of the Universe. High Energy Physics—Phenomenology, arXiv:hep-ph/0611283.
- Gibbons, G.W. and Hawking, S.W. (1977) Action Integrals and Partition Functions in Quantum Gravity. Physical Review D, 15, 2752. http://dx.doi.org/10.1103/PhysRevD.15.2752
- Chaichian, M. and Nelipa, N.F. (1984) Introduction to Gauge Field Theories. Springer-Verlag, Berlin, Heidelberg, 269.
- Ross, G.G. (1984) Grand Unified Theories. Benjamin/Cummings Publishing Company, Inc., 177-183.
- Weinberg, S. (1972) Gravitation and Cosmology. Wiley, New York, Chapter 12, Section 3.
- Coleman, S. and Weiberg, E.J. (1973) Radiative Corrections as the Origin of Spontaneous Symmetry Breaking. Physical Review D, 7, 1888-1910. http://dx.doi.org/10.1103/PhysRevD.7.1888
- Brandenberg, R.H. (1985) Quantum Field Theory Methods and Inflationary Universe Models. Reviews of Modern Physics, 57, 1-60. http://dx.doi.org/10.1103/RevModPhys.57.1
- Liu, L., Jiang, Y. and Qian, Z. (1989) The Inflationary Universe Scenario in 10−35 Sec after Big-Bang. Progress in Physics, 9, 121-187. (in Chinese)
- Guth, A.H. (1981) Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Physical Review D, 23, 347-356. http://dx.doi.org/10.1103/PhysRevD.23.347.53

