American Journal of Plant Sciences
Vol.07 No.01(2016), Article ID:63279,8 pages
10.4236/ajps.2016.71023
Validation of a Technique for Estimating Alfalfa (Medicago sativa) Biomass from Canopy Volume
Christopher G. Misar1, Lan Xu2*, Arvid Boe3, Roger N. Gates4, Patricia S. Johnson4, Andrew E. Olson2
1Northern Crop Science Laboratory, USDA-ARS, Fargo, ND, USA
2Department of Natural Resource Management, South Dakota State University, Brookings, SD, USA
3Department of Plant Science, South Dakota State University, Brookings, SD, USA
4Department of Natural Resource Management, WRAC, South Dakota State University, Rapid City, SD, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 December 2015; accepted 26 January 2016; published 29 January 2016
ABSTRACT
Determining biomass production of individual alfalfa (Medicago sativa L.) plants in space planted evaluation studies is generally not feasible. Clipping plants is time consuming, expensive, and often not possible if the plants are subjected to grazing. A regression function (Bʹ = 0.72558 + 0.11638 × Vʹ) was developed from spaced plants growing on rangeland in northwestern South Dakota near Buffalo to nondestructively estimate individual plant biomass (B) from canopy volume (V). However, external validation is necessary to effectively apply the model to other environments. In the summer of 2015, new data to validate the model were collected from spaced plants near Brookings, South Dakota. Canopy volume and clipped plant biomass were obtained from ten alfalfa populations varying in genetic background, growth habit, and growth stage. Fitted models for the model-building and validation data sets had similar estimated regression coefficients and attributes. Mean squared prediction errors (MSPR) were similar to or smaller than error mean square (MSE) of the model-building regression model, indicating reasonable predictive ability. Validation results indicated that the model reliably estimated biomass of plants in another environment. However, the technique should not be utilized where individual plants are not easily distinguished, such as alfalfa monocultures. Estimating biomass from canopy volume values that are extrapolations (>2.077 × 106 cm3) of the model-building data set is not recommended.
Keywords:
Forage Production, Forage Yield, Lucerne, Phytomass, Predictive Ability

1. Introduction
Numerous studies have evaluated survival and performance of various alfalfa (Medicago sativa L.) populations in semiarid environments [1] -[4] . Populations are established by interseeding [2] [5] or space planting transplants [1] [3] [4] into rangeland. Grazing or cutting the alfalfa is often conducted to increase selection pressure for survival. However, directly quantifying biomass production (i.e., yield) of populations in these studies is difficult, particularly under grazing because the biomass is consumed. Mechanically harvesting or clipping many alfalfa plants to determine biomass production is also time consuming and expensive.
Nondestructive measurements of alfalfa vigor are more feasible than obtaining biomass data in population evaluation studies. Vigor score [1] , plant cover index [2] , stem numbers and total basal area [3] , and canopy volume [6] have been used to measure alfalfa vigor. Variables that evaluate vigor are informative but are less easily interpreted than directly quantifying biomass production. However, high correlations between some of these variables and biomass production have been determined. Plant cover index was correlated with dry matter yield [2] and canopy volume was correlated with individual plant biomass [4] . Previous researchers [7] [8] obtained dimension measurements and biomass data from shrub plants and then established regression functions (i.e., equations) for estimating aerial biomass from plant volume.
A technique utilizing a regression function to nondestructively estimate individual plant biomass from canopy volume was developed and utilized in Misar et al. [4] . However, validation is necessary to ensure that the model can be applied to new and independent data on which the model is not based [9] . The preferred method of validation is collecting new data [10] , which are used to check the regression model and its ability to predict [9] . The objective of this study was to externally validate this model using new data to determine the applicability of the regression function for future studies.
2. Materials and Methods
2.1. Overview of the Model-Building Regression Model
The model-building data set (Table 1) consisted of canopy volume (V) and estimated biomass (B) for individual plants of 11 alfalfa populations evaluated for stand persistence and yield [4] . Plants had been space transplanted as seedlings on 1-m centers into semiarid rangeland in northwestern South Dakota near Buffalo [4] . Biomass was not directly harvested but was estimated using a double sampling reference unit method [4] . Fitting a simple linear regression model to the data after remedial measures resulted in the estimated regression function [4] :
Bʹ = 0.72558 + 0.11638 × Vʹ (1)
where Vʹ is the double square root of canopy volume. The coefficient of determination (r2) for the model indicated that canopy volume accounted for 75% of the variation in biomass.
Diagnosis of a plot of residuals against canopy volume during regression analysis revealed that the residuals were small for plants with small canopy volumes. However, error variance increased as canopy volume increased, indicating nonconstant error variance and the need for a simultaneous transformation on B and V. The double square root transformation (M. H. Kutner, personal communication, March 2014) stabilized nonconstant error variance and corrected nonnormality of error terms. Estimated biomass (Bʹ) can be back transformed to the original units (B) by raising values to the fourth power (i.e., B = Bʹ4).
2.2. Validation Location and Description
The model was validated using space planted alfalfa plants at the South Dakota State University Felt Family Farm near Brookings, South Dakota (lat 44˚18ʹ41ʹʹN, long 96˚47ʹ53ʹʹW). The environment at Brookings is more mesic and humid than Buffalo. Climate is continental and average annual precipitation (1971-2000) is 579 mm, with 78% occurring from April through September [11] . A monthly mean maximum temperature of 28.2˚C occurs in July and a monthly mean minimum temperature of −17.6˚C occurs in January [11] . Tallgrass prairie is the native vegetation. Soils at the validation site are a Vienna-Brookings complex [12] . Vienna soils are fine-loamy, mixed Udic Haploborolls while Brookings soils are fine-silty, mixed Pachic Udic Haploborolls [13] .
2.3. Materials
Validation data were collected from ten alfalfa populations that were selected to provide variation in genetic
Table 1. Data sets used to build and validate a regression model that estimated alfalfa biomass from canopy volume.
a. South Dakota State University Antelope Range and Livestock Research Station. b. South Dakota State University Felt Family Farm. c. Nondestructive biomass estimation method [4] . d. Biomass clipped at ground level and oven-dried at 60˚C for 4 days. e. CV, coefficient of variation = [standard error × (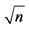 /mean)] × 100.
/mean)] × 100.
background, origin, and growth habit (Table 2). One-year-old greenhouse-grown plants were transplanted on 0.9-m centers in September 2012 and November 2013. Populations included six pure falcata [Medicago sativa L. subsp. falcata (L.) Arcang.] populations, three predominantly falcata populations, and one hay-type sativa (Medicago sativa L. subsp. sativa) population. Five of the pure falcata populations were Plant Introductions (PIs) from the National Plant Germplasm System [14] . The three predominantly falcata populations and SD 201 (pure falcata) had been used previously in building the model.
2.4. Data Collection
Data collection occurred at three sampling periods during 2015, which had a growing season with favorable moisture conditions for alfalfa biomass production. The first sampling occurred on 19 June when plants were at pre-bloom growth stages. The second sampling occurred on 18 July when plants were in full bloom. A third sample on 2 August obtained data for vegetative regrowth of plants that had been sampled in June.
A total of ten plants of each population were sampled (if possible) during each sampling period. Plants from only seven populations were sampled in August. Plant height (based on several stems) and canopy diameter measurements were obtained for each plant. In addition, a growth habit score (1 = prostrate, 2 = semisprawling, 3 = bowl-shaped, 4 = upright) based on illustrations in Sinskaya [15] was determined for each plant. Individual plants were then clipped at ground level and oven-dried (60˚C) for 4 days. Biomass (g) was determined using a laboratory balance.
Table 2. Functional group/descriptions and mean growth habit scores with standard errors (SE) for ten alfalfa populations sampled to validate a regression model that estimated alfalfa biomass from canopy volume. Populations were located at the South Dakota State University Felt Family Farm near Brookings, South Dakota.
a. 1 = Prostrate, 2 = Semisprawling, 3 = Bowl-shaped, 4 = Upright [15] . b. PI, Plant Introduction from National Plant Germplasm System [14] .
Canopy volume was calculated using the following formula of Thorne et al. [16] :
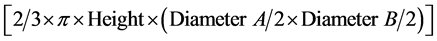 (2)
(2)
where A is the longest canopy diameter (major axis) and B is the perpendicular (minor axis) dimension. Biomass was then estimated from the double square root of canopy volume using Equation (1).
2.5. Statistical Analysis
Descriptive statistics for individual plant biomass in the model-building and validation data sets were computed using PROC MEANS in SAS [17] . For the validation data set, statistics were computed for each sampling period followed by a combined analysis. The combined analysis was conducted by merging data from all three sampling periods and computing descriptive statistics. Combining the data provided a robust data set that had a larger sample size and more variation in plant biomass (i.e., small plants to large plants). A validation data set should be large enough and variable enough to be representative of the “typical” quantities to be estimated [18] . The validation data did not contain any values that were outside the range of values in the model-building data set (Table 1).
Actual biomass values in the validation data set were double square root transformed prior to validation. Validation of the model was conducted using two methods in Kutner et al. [19] . The first method was fitting a simple linear regression model to the combined validation data using PROC REG in SAS. The estimated regression coefficients, estimated standard errors, error mean square (MSE), and r2 of this fitted model were compared for consistency to the coefficients and attributes of the model-building regression model. For illustrative purposes, the model-building and validation regression functions were used to estimate biomass from 2,000 randomly generated canopy volume values. Regression lines were plotted to assess their similarity.
The second method assessed the predictive ability of the model using the following equation from Kutner et al. [19] to calculate mean squared prediction error (MSPR):
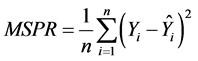 (3)
(3)
where:
Yi is the value of the response variable in the ith validation case
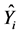 is the predicted value for the ith validation case based on the model-building data set
is the predicted value for the ith validation case based on the model-building data set
n is the number of cases in the validation data set
MSPR is compared with MSE of the regression model fitted to the model-building data. MSPR should be similar to MSE, indicating that the predictive ability of the model is valid [19] . MSPR values were calculated for the combined validation data set in addition to subsets of this data. Subsets were based on growth stage, growth habit, and functional group. Computing MSPR values for these subsets evaluated predictive ability under conditions that were less variable than the combined validation set.
Reliability of estimated MSPR is questionable if n is small, and large variances relative to MSPR are evidence of poor reliability [20] . To assess reliability and assure that sample size was adequate, variance was calculated for each MSPR value. Variance of MSPR was determined using the following expression in Wallach and Goffinet [20] :
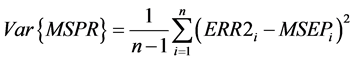 (4)
(4)
where:
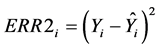
MSEPi is the acronym for mean squared error of prediction and is equivalent to MSPR
n is the number of cases in the validation data set
Summing the actual harvest data and the corresponding estimated data will also assess the predictive ability of the model. This simple approach should be used in addition to computing MSPR. Estimates of biomass were back transformed to original units before summing the values to obtain total estimated biomass. If Equation (1) effectively estimated individual plant biomass, then total estimated biomass and actual harvested biomass will be reasonably close.
3. Results and Discussion
3.1. Comparison of Model-Building and Validation Regression Coefficients and Attributes
Conditions between the two data sets differed in terms of time (i.e., year), geographic area, alfalfa populations, people collecting the data, and biomass determination methods. The validation set generally had larger plants than the model-building set (Table 1). However, results revealed that the estimated regression coefficients, standard errors, MSE values, and r2 values were reasonably consistent between these two data sets (Table 3). The slopes (b1) of the regression lines for the two functions were similar (Table 3, Figure 1).
Thus, the level of consistency was reasonable for the purpose of estimating alfalfa biomass from canopy volume.
3.2. Comparison of MSPR Values with MSE
MSPR computed from the combined validation data was similar to MSE (i.e., 0.1265) of the model fitted to the
Table 3. Estimated regression coefficients and attributes of a simple linear regression model fitted to model-building and validation data. Alfalfa biomass (B) was the dependent variable and canopy volume (V) was the independent variable. Double square root transformations on B and V were conducted prior to fitting the regression model to the data.
Figure 1. Regression lines for model-building and validation regression functions resulting from estimates of biomass for 2000 randomly generated canopy volume values.
model-building data (Table 4). This result indicates that the predictive ability of the model based on MSE was valid. MSPR is usually larger than MSE [19] but in Table 4 MSPR was often smaller than MSE. Recall that the model-building data were estimated biomass values whereas the validation data were actual biomass values. MSPR was smaller than MSE because direct harvesting is inherently more accurate than estimation using reference units for obtaining biomass data. Prediction errors (ERR2i) will generally be smaller if Yi are actual values obtained by direct harvesting, resulting in a smaller MSPR. A small MSPR relative to MSE is preferred to a large MSPR. Large MSPR values relative to MSE indicate that the predictive ability of the model is biased [19] . In these situations, the model has less predictive accuracy under the conditions that produced the validation data.
A majority of the MSPR values for validation data subsets (Table 4) were fairly close to MSE. MSPR values for regrowth and hay-type sativa subsets differed more from MSE, however, the values were smaller than MSE. These two subsets generally had smaller prediction errors than the other subsets, indicating more accurate estimation of biomass. Plants in the regrowth subset had small canopy volumes and the hay-type sativa subset consisted of only one population (Persist II). Variances of the MSPR values were small relative to MSPR (Table 4), indicating that estimates of MSPR were reliable and sample sizes were adequate.
Total harvested and estimated biomass for the combined data set and subsets supported the corresponding MSPR values in validating predictive ability (Table 4).
3.3. Applicability of the Model for Future Use
External validation indicated that Equation (1) was effective for estimating biomass of plants that differed in genetic background, growth habit, and growth stage. The model is suitable for situations where dimension measurements of a large number of individual plants can be obtained and distinguishing individual plants is feasible. Applicable situations include space planted evaluation studies, semiarid hayfields and grazing lands, and road ditches. The model has been utilized to estimate biomass of regrowth following grazing [4] .
Validation results revealed that the model was applicable to conditions that differ from the environment in which the model was developed. However, the model is not applicable to situations where individual plants are not distinguishable. Examples are alfalfa monocultures and certain interseeded stands, depending on stand condition. In addition, the model should not be used to estimate biomass of plants that have been defoliated by insects or plants that are dry and have shed leaves because of dormancy. Estimating biomass of large plants that are extrapolations of the model-building data set is not recommended. Individual plants that exceed 700 g in dry matter yield or 2.077 × 106 cm3 in canopy volume would exceed the limits of this model. Plants this large are not common but may be present if biomass is stockpiled (i.e., not harvested) until late summer, competition is low, and good growing conditions exist. Boe et al. [21] found that mean individual plant biomass of certain falcata- based entries space planted in central South Dakota exceeded 1000 g・plant−1. The model was not validated for plants that are prostrate because plants with this growth habit were not present in the validation data set. However, the model could be validated by obtaining biomass and canopy volume data from prostrate plants, computing MSPR, and comparing it to MSE (i.e., 0.1265).
Table 4. Mean squared prediction errors (MSPR) and variances for data used to validate a regression model that estimated alfalfa biomass from canopy volume. Total plant biomass (kg dry matter) harvested and estimated is provided.
a. Computed using double square root transformed data. b. MSPR is compared with error mean square (MSE) of the regression model (MSE = 0.1265) to assess predictive ability. c. Computed using back transformed data (biomass values raised to the fourth power).
Acknowledgements
The authors thank Roger Assmus, Tian Shengni, Jordan Purintun, and Diane Narem for their assistance in collecting validation data.
Cite this paper
ChristopherG. Misar,LanXu,ArvidBoe,RogerN. Gates,Patricia S.Johnson,AndrewE. Olson, (2016) Validation of a Technique for Estimating Alfalfa (Medicago sativa) Biomass from Canopy Volume. American Journal of Plant Sciences,07,238-245. doi: 10.4236/ajps.2016.71023
References
- 1. Berdahl, J.D., Wilton, A.C., Lorenz, R.J. and Frank, A.B. (1986) Alfalfa Survival and Vigor in Rangeland Grazed by Sheep. Journal of Range Management, 39, 59-62.
http://dx.doi.org/10.2307/3899688 - 2. Berdahl, J.D., Wilton, A.C. and Frank, A.B. (1989) Survival and Agronomic Performance of 25 Alfalfa Cultivars and Strains Interseeded into Rangeland. Journal of Range Management, 42, 312-316.
http://dx.doi.org/10.2307/3899501 - 3. Hendrickson, J.R. and Berdahl, J.D. (2003) Survival of 16 Alfalfa Populations Space Planted into a Grassland. Journal of Range Management, 56, 260-265.
http://dx.doi.org/10.2307/4003816 - 4. Misar, C.G., Xu, L., Gates, R.N., Boe, A. and Johnson, P.S. (2015) Stand Persistence and Forage Yield of 11 Alfalfa (Medicago sativa) Populations in Semiarid Rangeland. Rangeland Ecology & Management, 68, 79-85.
http://dx.doi.org/10.1016/j.rama.2014.12.012 - 5. Manske, L.L. (2005) Evaluation of Alfalfa Varieties Interseeded into Grassland. In: Evaluation of Alfalfa Interseeding Techniques, North Dakota State University, Dickinson Research Extension Center, Dickinson, 40-47.
- 6. Misar, C.G. (2011) Evaluation of Yellow-Flowered Alfalfa [Medicago sativa L. subsp. falcata (L.) Arcang.] for Grazing in the Northern Great Plains. M.S. Thesis, South Dakota State University, Brookings.
- 7. Uresk, D.W., Gilbert, R.O. and Rickard, W.H. (1977) Sampling Big Sagebrush for Phytomass. Journal of Range Management, 30, 311-314.
http://dx.doi.org/10.2307/3897313 - 8. Thomson, E.F., Mirza, S.N. and Afzal, J. (1998) Predicting the Components of Aerial Biomass of Fourwing Saltbush from Shrub Height and Volume. Journal of Range Management, 51, 323-325.
http://dx.doi.org/10.2307/4003418 - 9. Neter, J., Wasserman, W. and Kutner, M.H. (1989) Applied Linear Regression Models. 2nd Edition, Richard D. Irwin, Inc., Homewood.
- 10. Snee, R.D. (1977) Validation of Regression Models: Methods and Examples. Technometrics, 19, 415-428.
http://dx.doi.org/10.1080/00401706.1977.10489581 - 11. High Plains Regional Climate Center (2015) Historical Climate Data Summaries.
http://www.hprcc.unl.edu/ - 12. United States Department of Agriculture-Natural Resources Conservation Service (2015) Web Soil Survey.
http://websoilsurvey.sc.egov.usda.gov/App/HomePage.htm - 13. United States Department of Agriculture-Natural Resources Conservation Service (2004) Soil Survey of Brookings County, South Dakota.
http://www.nrcs.usda.gov/wps/portal/nrcs/surveylist/soils/survey/state/?stateId=SD - 14. United States Department of Agriculture-Agricultural Research Service (2015) National Plant Germplasm System. Germplasm Resources Information Network.
http://www.ars-grin.gov/npgs/aboutgrin.html - 15. Sinskaya, E.N. (1961) Flora of Cultivated Plants of the USSR. XIII Perennial Leguminous Plants. Part I Medic, Sweetclover, Fenugreek. Israel Program for Scientific Translations, Jerusalem.
- 16. Thorne, M.S., Skinner, Q.D., Smith, M.A., Rodgers, J.D., Laycock, W.A. and Cerekci, S.A. (2002) Evaluation of a Technique for Measuring Canopy Volume of Shrubs. Journal of Range Management, 55, 235-241.
http://dx.doi.org/10.2307/4003129 - 17. SAS Institute (2012) The SAS System for Windows. Release 9.4, SAS Institute, Inc., Cary.
- 18. Sheiner, L.B. and Beal, S.L. (1981) Some Suggestions for Measuring Predictive Performance. Journal of Pharmacokinetics and Biopharmaceutics, 9, 503-512.
http://dx.doi.org/10.1007/BF01060893 - 19. Kutner, M.H., Nachtsheim, C.J. and Neter, J. (2004) Applied Linear Regression Models. 4th Edition, McGraw-Hill/Irwin, New York.
- 20. Wallach, D. and Goffinet, B. (1989) Mean Squared Error of Prediction as a Criterion for Evaluating and Comparing System Models. Ecological Modelling, 44, 299-306.
http://dx.doi.org/10.1016/0304-3800(89)90035-5 - 21. Boe, A., Bortnem, R., Higgins, K.F., Kruse, A.D., Kephart, K.D. and Selman, S. (1998) Breeding Yellow-Flowered Alfalfa for Combined Wildlife Habitat and Forage Purposes. South Dakota Agricultural Experiment Station B 727, South Dakota State University, Brookings.
NOTES

*Corresponding author.



