Received 6 April 2016; accepted 25 April 2016; published 28 April 2016

ABSTRACT

In Japan, there exist many sustainable companies. Their distinctive feature is mutualism; they often take altruistic behaviors. To explain such behaviors, we carry out iterated prisoner’s dilemma games by lattice gas model. Each lattice point is regarded as a company which contains m + 1 pla- yers with an identical strategy. Simulations reveal that All Cooperation wins, when m takes a value larger than a threshold. We obtain a power law depending on error level. This law implies altruism may prevail in a company which has many employees or high error level.

Keywords:

Long-Lived Companies, Repeated Prisoner’s Dilemma, Intra-Cellular Interaction, Error Level, Altruism, Happiness of Employees

1. Introduction

Sustainability is an important issue for company management. In Japan, there are approximately 4,000 long- lived companies which have survived for more than two centuries (Goto, 2011) [1] . This number is overwhelmingly high relative to that in other countries. A distinct feature of long-lived companies is the presence of cooperation (Tateoka and Morishita, 2013 [2] , Morishita, 2014 [3] ). They often take altruistic behaviours (Tateoka, 2006) [4] . A famous example of altruism has been reported by newspaper (Asahi Newspaper, 2011) [5] . On March 2011, a powerful earthquake occurred and a large “Tsunami” attacked the Japanese shore. In the northern area of Japan, one long-lived company (Suisen Shuzo Co.), which make “sake” (a kind of alcohol), received devastating damages by Tsunami (Morishita et al., 2015) [6] . However, another sake-maker (Iwate Meijo Co.) saved the company by financial aid. The owner of Iwate Meijo explained the reason for support as follows: “a good rival is necessary for fair competition; monopoly of market share is a tragedy for consumers”. The purpose of the present article is to explain the emergence of altruism by iterated prisoner’s dilemma (IPD) game.

Altruistic behaviors have been studied by many researchers, such as biologists and social psychologists (Fehr & Fischbacher, 2003 [7] , Bowles, 2006 [8] , Wenseleers & Francis, 2006 [9] ). On the other hand, literatures on the importance of altruism for company managements are not so many (Tateoka, 2006) [4] . In the context of the IPD game, altruism implies that you should always cooperate. Hence, the most widely accepted altruism is the strategies close to AC (Tainaka and Itoh, 2002) [10] . We never say altruism for the strategies of “revanchism”: players of these strategies immediately betray, if they are betrayed. Typical examples of revanchism are tit-for-tat (TFT) and Pavlov (PAV) (Axelrod, 1997 [11] , Nowak and Sigmund, 1993 [12] , Kraines and Kraines, 1993 [13] ).

Recently, Yokoi et al. (2014) [14] have developed prisoner’s dilemma game on one-dimensional (1-d) lattice. They have introduced “intra-cellular” interactions. Each lattice point (cell) contains 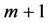players with an identical strategy; a player plays with all other players in the same cell. Yokoi et al. explored the optimal strategy among four strategies: tit-for-tat TFT, PAV, AC and All Defection (AD). These strategies have been reported to be optimal under certain conditions (Nowak, 2006 [15] ). In Yokoi’s model, each cell was regarded as animal family (or colony), and simulation was carried out by “local interaction”. Namely, inter-cellular interaction occurred between adjacent cells. In the present paper, however, we regard the cell as a company, and apply “global interaction” (lattice gas model): cellular interaction occurs between any pair of cells.

2. The Model

We use a typical IPD game (Axelrod 1997) [12] . Each player takes one of two options: either to cooperate or to defect. If both players cooperate, both get the pay-off R. If one cooperates and the other defects, then the former (latter) gets pay-off S (T). If both defect, both get pay-off P. In the present paper, the values of payoffs are given by:

(1)

The game (move) is infinitely repeated between the same pair of players. We use average payoff per one move. For instance, when AC and AD play with no error, then the average payoffs of AC and AD are 0 and 5, respectively.

Simulations of lattice model are carried out by either local or global interaction (Tainaka 1988) [16] . In most lattice models, the local interaction is applied. For this reason, we first explain the simulation procedure of local interaction [see Figure 1(a)]. Initial condition is set to be random, where four strategies AC, TFT, PAV and AD occupy with equal probability (1/4). We randomly choose two “neighboring cells” α and β. A player in cell α plays with intra- and inter-cellular opponents. In the former case, the opponents are m other players in the same cell. In the latter case, there are two opponents in “adjacent cells (β and γ)”. Hence each player plays 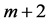games. The fitness of cell α (or β) is defined by the total payoff over games. When the fitness of α is larger than that of β, then both cells become the strategy of α (and vice versa). If both have the same fitness, both become either strategy of α or β with the probability 1/2.

Next we explain the simulation procedure of global interaction (lattice gas model) [see Figure 1(b)]. Almost all procedures are the same as for local interaction, but two terms are changed as follows: 1) the term “neighboring cells” is replaced by “a pair of cells which are randomly chosen”. 2) the term “adjacent cells (β and γ)” is changed to “cell β and a new cell γ which is randomly chosen”. In the case of lattice gas model, spatial structure has no meaning (Iwata et al., 2011) [17] .

3. Results

The population dynamics for global interaction become much simpler than those for local interaction. We carry out simulations up to; the total cell number is 1000. In Figure 2, typical examples of dynamics are shown, where the time dependences of densities are displayed. In most cases, only one strategy survives; we call it winner. However, in several cases three strategies survive during a long period; their relation has a cyclic

balance which is similar to paper-scissors-rock game. For example, Figure 2(a) illustrates the cyclic balance among three strategies (TFT, PAV and AD); TFT beats AD, but beaten by PAV. In this case, the winner is not uniquely determined; according to the simulations for longer period (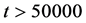), only one strategy survives by chance.

Table 1 shows the winners for lattice gas model. All strategies can win depending on both parameters company size (m) and error level (x). In human communities, the error level x may be small. For this reason, we pay attention in the region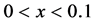. When the size of company is small (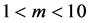), the optimal strategy is Pavlov which is known as a win-stay, lose-shift strategy (Nowak and Sigmund 1993). On the other hand, if m is sufficiently large, then AC becomes a winner. This comes from the property of intra-cellular interaction. Namely, AC has the maximum payoff, when both players have the same strategy. Yokoi et al. (2014) [14] have obtained the condition that AC wins as follows:

(2)

where the threshold was estimated by

(3)

This equation has been derived for local interaction on 1-d lattice. By global simulations, we explore whether Equation (3) holds or not. In Figure 3, the threshold () is depicted against the error level (x), where the curve

Winners are represented by the colors: AC (green), PAV (red), TFT (blue), and AD (yellow). The white regions are the cyclic cases that the winner is determined by chance.

and plots denote theoretical prediction and simulation result, respectively. It is found from Figure 3 that 1) Equation (3) also holds for global interaction, and that 2) the threshold roughly satisfies the following power law:

(4)

Hence, the altruistic strategy AC becomes optimal with the increase of m or x.

4. Conclusion and Discussion

We have developed an iterated prisoner’s dilemma game to explain altruistic behaviors in long-lived companies. Our model is a lattice gas version of Yokoi’s model (see Figure 1). Yokoi et al. (2014) [14] have explained altruistic behaviors in animal societies, such as ants and wasps. On the other hand, in our model, each cell is regarded as a company; players mean employees. The winners of IPD game are summarized in Table 1. This table is much simpler than that reported by Yokoi et al. If no error occurs (), only TFT wins. When each cell is occupied by a single player (), the non-cooperative strategy AD wins. This is because non-cooperative strategies are profitable for non-spatial IPD game (Nowak and May 1992 [18] , Fort and Viola 2005 [19] ). Hereafter we consider the case of. The winner strongly depends on the error level (x). When the error level takes, then the winner is PAV for but AC for; for, the winner is one of three strategies AD, TFT and PAV. In the case of, the relation among three strategies is similar to rock- paper-scissors rule [see Figure 2(a)]. When the error level increases, the winning region of PAV is reduced.

If the company size m is sufficiently large, then AC becomes a winner. In both local and global simulations, the altruistic strategy AC is found to be optimal for, where. This power law indicates that altruism should prevail in a company which has many employees or high error level. If errors hardly occur in mutual communications, the altruism can emerge hardly. If m is not so large, then PAV wins. Pavlov is known as a win-stay, lose-shift strategy. Namely, when business condition of a company is good (bad), the company should maintains (shifts) its management.

We assume that strategies of employees are identical in each company. This assumption may be oversimple (Luft, 2016) [20] , but companies usually have their specific culture; a close relation exist between the management policy of owners and the cooperative mind of employees (Schein 2010) [21] . Morishita (2014) [22] has conducted questionnaire survey to employees in some companies, and reported that the degrees of cooperative minds in long-lived companies have been commonly high compared to the other companies. Cooperative minds of employees are correlated in the identical company.

World economy faces some serious problems, such as excess bankruptcy, monopoly and inequality (Porter and Kramer 2011 [23] , Piketty 2014 [24] ). Tateoka (2006) [4] has reported that cooperation and altruism can avoid these problems in some extent. As described in the present article, cooperation (altruism) rises the happiness (fitness) of employees, especially in a large company.

Cite this paper

Hiroki Yokoi,Ayako Morishita,Yasuo Tateoka,Keiichi Tainaka, (2016) Lattice Gas Model for Iterated Prisoner’s Dilemma Games: Emergency of Altruism in a Company. Theoretical Economics Letters,06,324-329. doi: 10.4236/tel.2016.62036

References

NOTES

^*Corresponding author.