Circuits and Systems, 2010, 1, 18-29
doi:10.4236/cs.2010.11004 Published Online July 2010 (http://www.SciRP.org/journal/cs)
FPGA Design of an Intra 16 × 16 Module for H.264/AVC
Video Encod er
Hassen Loukil1, Imen Werda1, Nouri Masmoudi1, Ahmed Ben Atitallah2, Patrice Kadionik3
1University o f S f a x, National School of Engineering, Sfax, Tunisia
2University o f S f a x, High Institute of Electronics and Communication, Sfax, Tunisia
3IMS laboratory-ENSEIRB-MATMECA-University Bordeaux 1-CNRS UMR 5218, 351 Cours de la Libération, Talence
Cedex, France
Received May 16, 2010; revised June 18, 2010; accepted June 23, 2010
Abstract
In this paper, we propose novel hardware architecture for intra 16 × 16 module for the macroblock engine of
a new video coding standard H.264. To reduce the cycle of intra prediction 16 × 16, transform/quantization,
and inverse quantization/inverse transform of H.264, an advanced method for different operation is proposed.
This architecture can process one macroblock in 208 cycles for all cases of macroblock type by processing 4
× 4 Hadamard transform and quantization during 16 × 16 prediction. This module was designed using VHDL
Hardware Description Language (HDL) and works with a 160 MHz frequency using ALTERA NIOS-II de-
velopment board with Stratix II EP2S60F1020C3 FPGA. The system also includes software running on an
NIOS-II processor in order to implementing the pre-processing and the post-processing functions. Finally,
the execution time of our HW solution is decreased by 26% when compared with the previous work.
Keywords: Nios H.264, FPGA, Intra 16 × 16, NIOS-II, SOPC Design
1. Introduction
Currently, video system development is generally based
on embedded systems. Such systems need to find a com-
promise between computational complexity and timing
execution constraints. On the other hand, the H.264/AVC
standard for video compression [1-5], due to its high
complexity, needed powerful processors and hardware
acceleration in order to respect application requirements.
In order to take advantages of hardware acceleration,
each functional module of the H.264 video encoder has
been carefully studied in order to determine its computa-
tional complexity. Furthermore, the intra process pre-
sents one of the highest computational complexities in
H.264/AVC encoder [6]. This process is based on the
hybrid encoding scheme shown in Figure 1 which uses
the intra prediction, integer cosine transform and quanti-
zation. The intra process is used to remove spatial redun-
dancy. There are two types of intra modes: intra 4 × 4
Current
Frame
(Fn)
Reconstructed
Frame
F(n)
Intra
Prediction
+
-
+
+
Transform Quantization CAVLC
Inverse
Transform Inverse Quantization
Deblocking
Filter
Figure 1. Hybrid encoder for video compression.

H. LOUKIL ET AL.
19
and intra 16 × 16 modes. The intra 16 × 16 is composed
of intra 16 × 16 prediction (IP 16 × 16), integer cosine
transform (ICT), quantization AC (QAC), inverse integer
cosine transform (IICT), inverse quantization AC (IQ-
AC), quantization DC (QDC), Hadamard transform (HT),
inverse quantization DC (IQDC) and inverse Hadamard
transform (IHT). Special hardware implementations of
intra 16 × 16 for H.264 have been proposed [7,8]. They
were shown that some of these parts can be optimized
with parallel hardware structures implemented into the
hardware system. These previous works have implement-
ed the intra 16 × 16 algorithm with serial [7] and parallel
[8] architectures directly into hardware device. But, our
architecture uses both a parallel and pipelined structures
in order to reduce the number of operations and the abil-
ity to achieve fast execution. Our design is described
with VHDL (VHSIC Hardware Description Language)
language and has been synthetized with the Altera NIOS
II softcore processor for experimental validation into a
single Altera Stratix II EP2S60 FPGA (Field Program-
mable Gate Array) device.
This paper is organized as follows: Section 2 presents
an overview of intra 16 × 16 algorithm. In the next Sec-
tion, we present the intra 16 × 16 architecture. The exp-
eriment results are shown in Section 4. Finally, Section 5
concludes the paper.
2. Overview of the Intra 16 × 16 Algorithm
The intra 16 × 16 algorithm is a critical component used
in the H.264/AVC. There are eleven functional opera-
tions in this module: intra 16 × 16 prediction, residual
calculation, integer transform, AC coefficient quantiza-
tion, DC coefficient quantization, inverse AC coefficient
quantization, inverse DC coefficient quantization, Hada-
mard transform, inverse Hadamard transform, inverse
integer transform and pixel reconstruction. The 16 × 16
intra prediction mode is designed according to directions:
vertical, horizontal, DC and plane modes are specified in
the H.264 standard based on the reconstituted pixels
from the previous macroblock (MB). Figure 2 shows the
intra 16 × 16 prediction mode.
For each MB, we compute the difference between the
predicted pixel and the original pixel. After this step, we
calculate the integer transform coefficients. In the H.264/
AVC standard, the equation of the 4 × 4 integer trans-
form is defined by [3,4].























1221
1111
2112
1111
I×



































1121
2111
2111
1121
XXXX
XXXX
XXXX
XXXX
15141312
111098
7654
3210
(1)
“Xi” is the residual 4 × 4 block.
After this operation, we obtain two coefficients types:
AC and DC coefficients. For the AC coefficients, we
compute the quantization operation. In general the AC
quantization operation is defined by [3,4].
)
QStep
PF
I
round(
Zijij (2)
We can write (5) as follows:
)
2qbits
MF
I
round(
Zij
ij  (3)
where:
Qstep
PF
qbits
2
MF  (4)
qbits = 15 + floor(QP/6) (5)
Iij is the uncalled coefficients after ICT for QAC. PF
represents the scaling factor of the integer transform and
QStep is the quantization step size. A total of 52 values
of QStep are supported by the standard as shown in Tab-
le 1 where QStep doubles in size for every 6 values of
the step of quantization QP.
V…………… .
Mode 0 (vertical)
V
…
…
…
…
.
.
Mode 1 (horizontal)
VMean (H+V)
Mode 2 (DC)
V
Mode 3( plane)
H
H
H H
Figure 2. 16 × 16 intra prediction mode.

H. LOUKIL ET AL.
20
Table 1. Quantization step size in H.264/AVC.
QP 0 1 2 3 4 5
QStep 0.625 0.6875 0.8125 0.875 1 1.125
QP 6 7 8 9 10 11
QStep 1.25 1.375 1.6251.75 2 2.25
QP … … … … … …
QStep … … … … … …
QP 48 49 50 51
QStep 160 … … 224
Hence, the shift operation can be greatly used in the qu-
antization and rescaling stages. To simplify the arithmetic,
the quantization stated in (6) can be rewritten as (9, 10)
for the AC coefficients [3,4].
qbitsf).MFI(Zijij  (6)
)
I
sign()
Z
sign( ijij

(7)
Zij is the uncalled coefficients after QAC operation.
The first 6 values of MF used in the H.264 references are
listed in Table 2.
The 2nd and 3rd columns are the different positions in
the scaling matrix. QP%6 represents the QP division rest
by 6.
After the calculation of QAC, we must compute the
inverse AC quantization. This operation is defined as
[3,4].
.QstepZY ijij  (8)
A constant equal to 64 is integrated in order to avoid
rounding errors. The inverse quantization AC equation
becomes therefore:
.64 .PF .QstepZYijij  (9)
Yij is the result of inverse AC quantization. It must be
divided by 64 for recovering the exact value without
factor of scaling. The H.264 draft standard doesn’t pre-
cise Qstep or PF directly. It uses a parameter given by:
64)(Qstep.PF.V  (10)
The final equation for the inverse quantization is:
)floor(QP/6
.2.VZY ijijij  (11)
The first 6 values of V used in the H.264 standard are
listed in Table 3. The 2nd and 3rd columns are the diff-
erent positions in the scaling matrix.
For the DC coefficients, Hadamard transform is ap-
plied. The equation of 4 × 4 hadamard transform is de-
fined by [3,4].























1111
1111
1111
1111
H×



































1111
1111
1111
1111
DDDD
DDDD
DDDD
DDDD
15141312
111098
7654
3210
(12)
“Di” is the DC coefficients.
In next step, we calculate the quantization operation
for the DC coefficients. This operation is defined by [3,
4].
1)(qbits2f)0)(Hij.MF(0,
K
ij 

(13)
Kij is the uncalled coefficients after QDC operation.
MF (0, 0) is the multiplication factor for position (0, 0) in
Table 2. After the calculation of QDC, we must compute
the 4 × 4 inverse hadamard transform. This operation is
defined by [3,4].



































15141312
111098
7654
3210
D'D'D'D'
D'D'D'D'
D'D'D'D'
D'D'D'D'
1111
1111
1111
1111
H'






















1111
1111
1111
1111
(14)
Table 2. Multiplication factor MF in H.264/AVC.
QP%6 Positions
(0,0),(2,0),
(0,2),(2,2)
Positions
(1,1),(1,3),
(3,1),(3,3) Others positions
0 13107 5243 8066
1 11916 4660 7490
2 10082 4194 6554
3 9362 3647 5825
4 8192 3355 5243
5 7282 2893 4559
Table 3. Values of V used in the H.264 standard.
QP%6
Positions
(0,0),(2,0),
(0,2),(2,2)
Positions
(1,1),(1,3),
(3,1),(3,3)
Others positions
0 10 16 13
1 11 18 14
2 13 20 16
3 14 23 18
4 16 25 20
5 18 29 23

H. LOUKIL ET AL.
21
“D’i” is the block 4 × 4 quantified DC.
The final step for the DC coefficient is the inverse DC
quantization. This operation is defined by [3,4].
ij ij
for(QP 12)
floor(QP / 6)2
WH' .V(0,0).2


 (15)
ij ij
for(QP 12)
1floor(QP/6 )
W[H'.V(0,0)2](2floor(QP/6 ))



where V(0,0) is the multiplication factor for position (0,0)
in Table 3.
After all operations, we can combine the AC and the
DC coefficients for compute the inverse integer trans-
form. Equation (19) gives the equation of 4 × 4 inverse
integer defined as [3,4].

























































1/2111
111/21
111/21
1/2111
X'X'X'X'
X'X'X'X'
X'X'X'X'
X'X'X'X'
1/2111/2
1111
11/21/21
1111
I'
15141312
111098
7654
3210
(16)
“X’i” is the block 4 × 4 after all operations (AC and
DC coefficients).
3. Intra 16 × 16 Architecture
The intra 16 × 16 architecture partitions the MB into six-
teen 4 × 4 blocks. The scanning order for one MB is
shown in Figure 3. This order is scanned in the x direc-
tion first and then performs the scanning in the y direc-
tion. The scanning order is the label order from top to
bottom, from left to right which is the actual processing
order for one MB. The MB is partitioned into sixteen 4 ×
4 small sub-blocks. The partitions between the 16 × 16
scanning order labels and the 4 × 4 scanning order labels
are shown in Figure 4.
The 4 × 4 scanning order labels are shown in Figure 5.
0123
16 17 18 19
32
48
4 5 6 7
20 21 22 23
89 10 11
24 25 26 27
12 13 14 15
28 29 30 31
64
80
96
112
128
144
160
176
192
208
224
240 241 242 243 244245 246 247 248 249250 251 252 253 254255
33 34 35 3637 38 39 40 4142 43 44 45 46 47
49 50 51 5253 54 55 56 5758 59 60 61 62 63
65 66 67 6869 70 71 72 7374 75 76 77 78 79
81 82 83 8485 86 87 88 8990 91 92 93 94 95
979899100 101 102 103 104 105 106 107 108 109 110 111
113 114115116 117 118 119 120 121 122 123124 125 126 127
129 130131132 133 134 135 136 137 138 139140 141 412 143
145 146147148 149 150 151 152 153 154 155156 157 158 159
161 162163164 165 166 167 168 169 170 171172 173 174 175
177 178179180 181 182 183 184 185 186 187188 189 190 191
193 194195196 197 198 199 200 201 202 203204 205 206 207
209 210211212 213 214 215 216 217 218 219220 221 222 223
225 226227228 229 230 231 232 233 234 235236 237 238 239
x
y
Figure 3. 16 × 16 scanning order labels.
Figure 4. Relationship between 16 × 16 and 4 × 4 scanning order labels.

H. LOUKIL ET AL.
22
0 1 2 3
4 5 6 7
89 10 11
12 13 1415
Figure 5. 4 × 4 scanning order labels.
Figure 6 shows the functional flow diagram of the in-
tra 16 × 16 process.
In the first step, we compute the intra prediction 16 ×
16 for all 4 × 4 blocks. After this, we calculate the resi-
dual, the integer transform, the AC quantization and the
inverse AC quantization for each 4 × 4 block. During the
calculation of integer transform, we extract the DC coeff-
icient for each 4 × 4 block. After obtain the 16 DC coeff-
icients, we calculate the hadamard transform, the DC
quantization, the inverse hadamard transform and the
inverse DC quantization. Finally, we combine AC and
DC coefficient for each 4 × 4 block to perform the in-
verse integer transform and the reconstruction pixels.
The intra 16 × 16 hardware architecture is composed
by two modules. The first component contains the intra
16 × 16 prediction module and the residual module. The
second component contains the coding chain module and
the reconstruct module. The block diagram of the pro-
posed hardware architecture for H.264 video coding is
shown in Figure 7.
intra 16x16 p rediction
Combine reconstructed
coefficients
Inverse Integer
transform
Reconst ruct pixels
For 4x4block from 0 to 15
Wait until all 4x4 blocks
were Integer transformed
Extract DC coefficients
( 16 coeff = one 4x4
block)
Hadamard
DC Quantization
Inverse Hadamard
Inverse DC
Quantization
Calculate residual
Integer transform
AC Q u antization and
inverse AC
Quantization
For 4x4block from 0 to 15
Stor e and reorder quantized
coefficients
and output them when
needed
AC pathDC path
4x4block = 15
Yes
No
4x4block = 15
Yes
No
Start
End
Figure 6. Intra 16 × 16 functional flow diagram.

H. LOUKIL ET AL.
23
3.1. Intra 16 × 16 Prediction
Different works have been proposed [9-13]. For our arc-
hitecture, the MB pixels are loaded into a dual RAM
(Random Access Memory) for reordering and then give
(to the residual or reconstruction blocks) by sets of 16
pixels (4 × 4 block).
This block calculates the predicted pixels of MB for
all 3 intra 16 × 16 prediction modes specified in the
H.264 standard (horizontal, vertical and DC) in parallel
based on the reconstituted pixels from the previous MB
(planar mode is not used [14]). Figure 8 presents the
intra prediction hardware architecture. These predicted
pixels are stored into RAM for all modes. We also use a
SAD_ 4 × 4 block for calculating the SAD value for each
mode. We accumulate this value 16 times in order to ob-
tain the SAD_16 × 16 for each mode. Those absolute va-
lues permit to give the sum of absolute differences (SAD)
for each prediction mode. The comparator compares the
SAD values for all prediction modes and picks the lowest
value for determining which prediction mode will be
used. After obtaining the best SAD (MIN_SAD), the best
MB is given. The difference between the predicted pixels
and the source pixels is then calculated for the best pre-
diction mode for obtain the residual MB.
Control Unit
START
Done
Intra 16x16
Pre diction
SRC_0
SRC_15
.
.
.
8
RECON_IN0
RECON_IN31
.
.
.
16
Residual_0
Residual_15
.
.
.Coding chain
Residual _out0
Residual_out15
.
.
.
16
16
Reconstruction
RECON_OUT0
RECON_OUT15
.
.
.
8
8
Start_PRED Start_CHAIN Start_RECON
8
8
8
16
16
Pred_pixel_0
Pred_pixel_15
.
.
.Residual
Star t _RES
8
8
Figure 7. Intra 16 × 16 hardware architecture.
Horizontal
mode
Vertical
mode
DC m o de
RAM
Horizontal
RAM
Vertical
RAM D C
Pixels_h
128 bits
Pixels_dc
128 bits
Pixels_v
128 bits
Pixels_h
12 8 bits
Pixels_v
12 8 bits
Pixels_dc
12 8 bits
Horizontal
SA D4x4
Vertical
SA D4x4
DC
SA D4x4
+
+
+
Comparator
12 bits
SAD4x4_h Hor_SAD_16x16
Ver_SAD_16x16
DC_SAD_16x16
16 bits
16 b i ts
16 bits
MIN_SAD
RECON_IN0
RECON_IN31
8 bits
8 bits
SRC_0
SRC_15
12 bits
SAD4x4_v
12 bits
SAD4x4_dc
Start_pred
Start_pred
Start_pred
Wren Rden
WrenRden
Wren Rden
Start_sad
Start_sad
Start_sad Start_comp
Control Unit
CLK
Reset
Start
Start_pred
Wren
rden
Start_sad
Start_comp
Figure 8. Intra 16 × 16 prediction hardware architecture.

H. LOUKIL ET AL.
24
3.2. ICT and HT Architectures
Different works have been published on the integer trans-
form [15-19]. It is obvious that “I” shown in (1) or “H”
shown in (12) can be implemented by a 1-D transform.
Figure 9 shows the fast implementation for the integer
transform. The matrix contains only four coefficients: 1,
–1, 2, and –2. It also can be implemented by using addi-
tion, subtraction and shift operations.
The Hadamard transform matrix is very similar to the
integer transform matrices. The difference is that the co-
efficients of Hadamard transform are only 1 or –1. There-
fore, the fast implementation for the Hadamard trans-
form is shown in Figure 10.
The hardware implementation of 1-D ICT or HT is
given in Figure 11. The input for this module is a 4 × 4
block. For full transform operation, we use two 1-D
transforms in order to obtain the 2-D transform. Figure
12 presents the architecture for the 2-D transform.
x0-x3x0+x3 x1+x2 x1-x2
<<
<<
y1 y3
y2
y0
Figure 9. Fast implementations of H.264 integer transform.
x0 -x3x0+x3 x1+x2 x1-x2
y1 y3
y2
y0
Figure 10. Fast implementations of H.264 Hadamard trans-
form.
ICT_0
y0
y3
y1
y2
x0
x3
x1
x2 ICT_1
y0
y3
y1
y2
x0
x3
x1
x2
ICT_2
y0
y3
y1
y2
x0
x3
x1
x2 ICT_3
y0
y3
y1
y2
x0
x3
x1
x2














3,32,31,30,3
3,22,21,20,2
3,12,11,10,1
3,02,01,00,0
xxxx
xxxx
xxxx
xxxx














3,32,31,30,
3
3,22,21,20,2
3,12,11,10,1
3,02,01,00,0
yyyy
yyyy
yyyy
yyyy














3,0
2,0
1,0
0,0
x
x
x
x














3,1
2,1
1,1
0,1
x
x
x
x














3,2
2,2
1,2
0,2
x
x
x
x














3,3
2,3
1,3
0,3
x
x
x
x














0,3
0,2
0,1
0,0
y
y
y
y














1,3
1,2
1,1
1,0
y
y
y
y














2,3
2,2
2,1
2,0
y
y
y
y














3,3
3,2
3,1
3,0
y
y
y
y
1-D transform block
reset
CLK
Done
start
Figure 11. Fast implementations of H.264 1-D transform.
1-D
transform1-D transform
CONTROL
CLK
reset
st a rt
Input_0..15
9
output_0..15
9
Done
Figure 12. Fast implementations of H.264 2-D transform.
3.3. QAC & QDC Architectures
The Quantization hardware architectures have been pro-
posed in [8,20]. The architecture of DC quantization is
similar to the AC quantization presented in Figure 13.
The multiplication factors stated in Table 1 are stored
into ROM (Read Only Memory) and selected according
to the QP%6 values. The correct factor is multiplied by
the uncalled coefficient in the corresponding position.
The shifter will shift the product to right with qbits.
The QAC or QDC modules will quantify at the same
time 16 pixels according to QP factor. These modules are
composed by a quantization block (noted 0…15), a me-
mory for storing the input pixels (noted input_0..15) and
two read-only memories for storing QE (equal to QP%6)
and F values noted respectively ROM_QE and ROM_F.
The AC and DC quantization blocks are constituted by
three basic components presented in Figure 14.
0 123
4 567
89 10 11
12 1314 15
ROM_F
ROM_QE
F
QE
Input_0..15
Input_0..15
CLK
reset
st art
6qp
16 16
Input_0..15 Output_0..15
Figure 13. Quantization architecture.

>> out
MF(i,j)
F
QE
input
SIGN
30
15
16
416
Figure 14. AC or DC quantification.

H. LOUKIL ET AL.
25
A multiplier deals perform the multiplication opera-
tion of AC coefficients with the corresponding MF (i, j)
factor and gives the absolute value. An adder will per-
form the sum operation of values given by the multiplier
with the F parameter given by the ROM memory. A
shifter allows performing the shift operation the result
from the adder by “qbits” (varies 15 to 23 according to
the value of QP).
3.4. IQAC & IQDC Architectures
The IQAC or IQDC modules will quantify 16 pixels acc-
ording to the QP factor. The architecture of these modu-
les is similar to the QAC or QDC modules respectively
presented by the Figure 13. The difference between quan-
tization (AC or DC) and inverse quantization (AC or DC)
is presented in the quantization block. For having the
inverse AC quantization values, we use a multiplier to
perform the multiplication operation between the QAC
coefficients and the V (i, j) values. We also use a shifter
for shifting the result from the multiplier floor (QP/6).
The architecture for this module is presented by the Fig-
ure 15.
For the DC coefficients, we use a multiplier to per-
form the multiplication operation between the QDC co-
efficients and the V (0, 0) value. An adder will perform
the sum of values given by the multiplier with {0, 1, 2}
(0 for QP > = 12, 1 for QP < 12, 2 others parts). A shifter
will perform the shift of result from the adder by floor
(QP/6) – 2) for QP >= 12 and by (2 – floor (QP/6)) for
QP < 12. The architecture for this module is presented in
Figure 16.
3.5. IICT and IHT Architectures
The IICT or IHT architectures are similar to the ICT or
HT architectures respectively presented by the Figures
12 and 13. The inverse integer transform matrix con-
tains only four coefficients: 1, –1, 1/2, and –1/2. Figure
17 shows the fast implementation for the inverse integer
transform. The inverse Hadamard transform matrix con-
tains only two coefficients, 1 and –1. Figure 18 shows
the fast implementation for the inverse Hadamard trans-
form.
>> out
V(i,j)
input
SIGN
qp
6
23
16
6
Figure 15. AC inverse quantification.

>> out
V(0,0)
{ 0 ,1 ,2}
QE
inp ut
SIGN
6
6
6
23
Figure 16. DC inverse quantification.
y0-y2y0+y2 y1+(y3>>1) (y1>>1)-y3
x3 x1 x2x0
Figure 17. Fast implementations of H.264 inverse integer
transform.
y0 -y2y0+y2 y1+y3 y1-y3
x3x0 x1 x2
Figure 18. Fast implementation of H.264 inverse Hadamard
transform.
3.6. Intra 16 × 16 Execution Time
The intra 16 × 16 execution time is presented in Figure
19. This figure is divided into two parts. The first part
concerns the intra 16 × 16 prediction. This part takes 115
clock cycles for the best predicted MB [21]. The second
part concerns the coding chain block that needs 77 clock
cycles. In this part, we use a pipeline as shown in Figure
19. To get the reconstructed MB, we need 16 clock cy-
cles. Finally, 208 clock cycles are necessary to achieve
the intra 16 × 16 operations. Comparing with [7] and [8],
the proposed architecture takes less clock cycles. Simu-
lation of our proposed RTL design shows major im-
provements by reducing clock cycles for the intra 16 ×
16 operation as shown in Table 4. Thus, our hardware
implementation is optimized to achieve higher perform-
ances for the H.264 video encoder than the hardware
architecture presented in [7-8].
4. Experimental Results
The whole design has been designed by using VHDL

H. LOUKIL ET AL.
26
(RTL level). The VHDL code of all modules was synth-
esized for an EP2S60F1020C3 Altera Stratix II FPGA
circuit by using the Altera Quartus tool. Table 5 shows
the implementation results of the intra 16 × 16 module
for the Stratix II EP2S60 FPGA circuit.
For experimental verification, we have developed a C
language reference model of H.264 software. We have
compared the output results of our C reference model
with the JM 10.1 model [22] and we have confirmed the
correctness of our model. We have also used the NIOS II
softcore processor for sending data to the intra frame hard-
ware coprocessor. The block diagram of the implement-
ed H.264 intra frame encoder is shown in Figure 20. The
design is composed by three parts: the NIOS II processor,
the intra 16 × 16 frame module and the other peripherals
connected to the Altera Avalon Bus. The Avalon bus has
control, data and address signals and has its bus arbitra-
tion logic.
Our embedded system has been tested by using the Al-
tera NIOS II development board. The heart of the target
board is the Altera Stratix II EP2S60F1020C3 FPGA
circuit. For all experiments, CIF test sequences are coded
at 30 Hz. We have focussed on the following video test
sequences: “Foreman”, “Paris”, “Mobile”, “Tb420” and
“Akiyo”. These test sequences have different movement
and camera particularities.
We have determined the processing time of intra 16 ×
16 for the SW (software) solution. From the Table 6, we
can conclude that a 35 time improvement for the proce-
ssing speed compared to the software solution can be
obtained by using our HW implementation.
Table 4. Comparison between different intra 16 × 16 archi-
tectures.
architectures [7] [8]
Proposed
architecture
Number cycles/MB 3307 269 208
Frequency (Mhz) 71 54 160
Execution time/MB(ns) 46.57 4.98 1.3
Table 5. Implementation results for Stratix II FPGA.
Used Resources
ALUTs 22,685/48,352 (47%)
Memory (KB) 27/2484 (1%)
Pins 526/719 (73%)
DSP block 124/288 (43%)
Table 6. Time comparison betwee n SW and HW implemen-
tations.
Total time (ms)Sequence SW HW
Time Foreman 684.74 18.73
(ms) Paris 688.21 18.88
Mobile [phone]
Tb420 685.78 19.08
Akiyo 687.95 18.70
ICT 0
ICT 1ICT 15
QAC 0 QAC 1
QAC 15
IQAC
0
IQAC 1
IQAC 15
HT QDC IHT IQDC
IICT 0IICT 1
IICT 15
2
4 3
24242
77 cycles
2
4
3
9
+( 15
x
2
) = 39 cycles
2
x
16 = 32 cycles
5 cycles1 cycle
F
I
F
O
Intra prediction 16 x16 Coding chaineRec o ns t ructio n
115 cycles
77 cycles 16 cycles
Figure 19. Intra 16 × 16 execution time.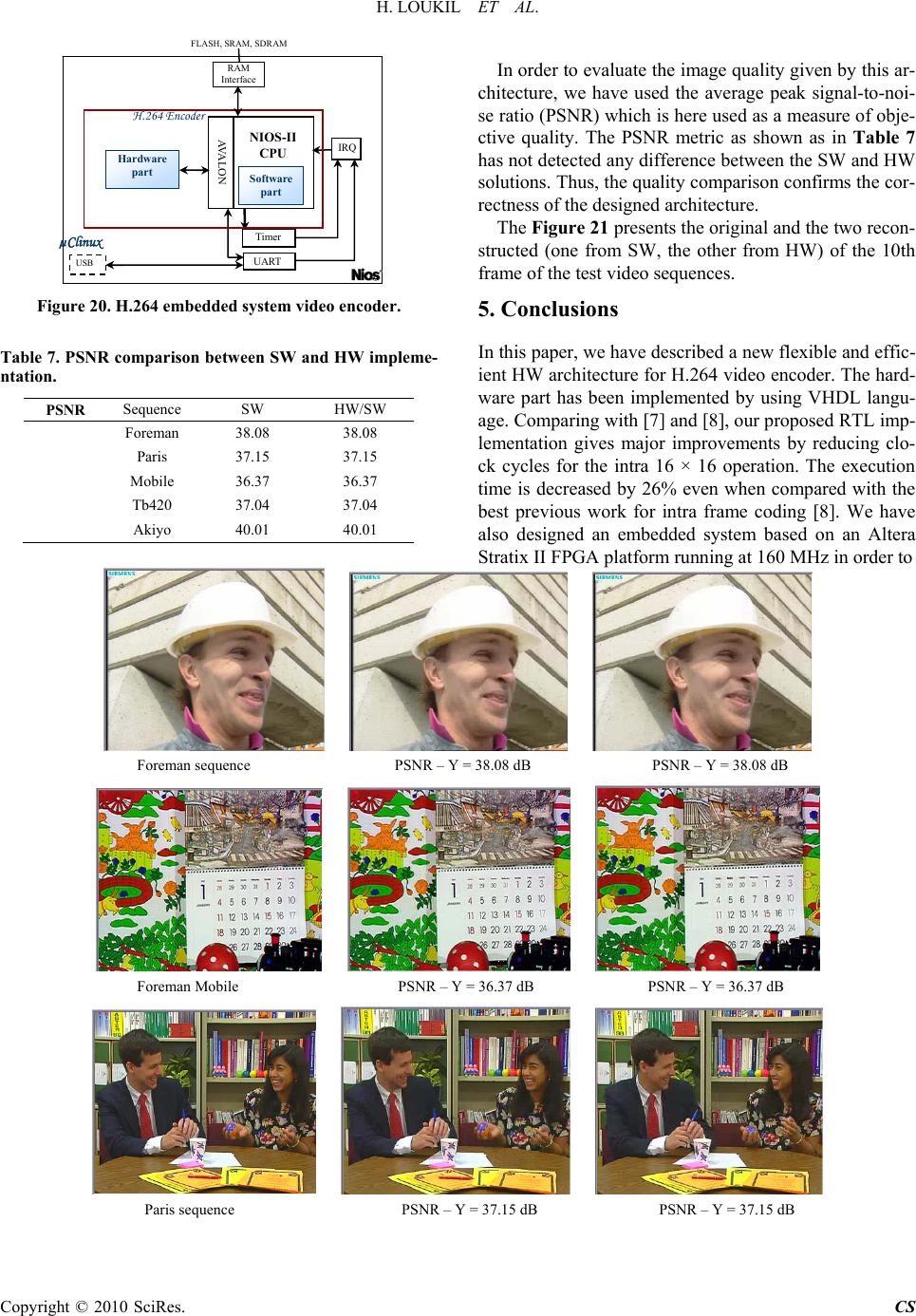

H. LOUKIL ET AL.
NIOS-II
CPU
AVALON
IRQ
Ti m er
UART
USB
RAM
Interface
H.26
4
Encoder
FLASH, SRAM, SDRAM
Hardware
part
µClinux
Software
part
Figure 20. H.264 embedded system video encoder.
Table 7. PSNR comparison betwee n SW and HW impleme-
ntation.
PSNR Sequence SW HW/SW
Foreman 38.08 38.08
Paris 37.15 37.15
Mobile [phone]
Tb420 37.04 37.04
Akiyo 40.01 40.01
In order to evaluate the image quality given by this ar-
chitecture, we have used the average peak signal-to-noi-
se ratio (PSNR) which is here used as a measure of obje-
ctive quality. The PSNR metric as shown as in Table 7
has not detected any difference between the SW and HW
solutions. Thus, the quality comparison confirms the cor-
rectness of the designed architecture.
The Figure 21 presents the original and the two recon-
structed (one from SW, the other from HW) of the 10th
frame of the test video sequences.
5. Conclusions
In this paper, we have described a new flexible and effic-
ient HW architecture for H.264 video encoder. The hard-
ware part has been implemented by using VHDL langu-
age. Comparing with [7] and [8], our proposed RTL imp-
lementation gives major improvements by reducing clo-
ck cycles for the intra 16 × 16 operation. The execution
time is decreased by 26% even when compared with the
best previous work for intra frame coding [8]. We have
also designed an embedded system based on an Altera
Stratix II FPGA platform running at 160 MHz in order to
Foreman sequence PSNR – Y = 38.08 dB PSNR – Y = 38.08 dB
Foreman Mobile PSNR – Y = 36.37 dB PSNR – Y = 36.37 dB
Paris sequence PSNR – Y = 37.15 dB PSNR – Y = 37.15 dB

H. LOUKIL ET AL.
28
Tb420 sequence PSNR – Y = 37.04 dB PSNR – Y = 37.04 dB
Akiyo sequence PSNR – Y = 40.01 dB PSNR – Y = 40.01 dB
(a) (b) (c)
Figure 21. (a) Original, (b) Reconstructed from SW and (c) Reconstructed from HW/SW of the 10th frame of the test video
sequences.
evaluate the performance of our design in HW/SW code-
sign context. We have shown that our HW solution impr-
oves considerably the intra 16 × 16 process (35 times fa-
ster) compared to an all software solution with the same
image quality.
6. References
[1] T. Wiegand, G. J. Sullivan, G. Bjøntegaard and A. Luthra,
“Overview of the H.264/AVC Video Coding Standard,”
IEEE Transactions on Circuits and Systems for Video
Technology, Vol. 13, No. 7, 2003, pp. 560-576.
[2] A. Luthra, G. J. Sullivan and T. Wiegand, “Introduction
to the Special Issue on the H.264/AVC Video Coding
Standard,” IEEE Transactions on Circuits and Systems
for Video Technology, Vol. 13, No. 7, 2003, pp. 557-559.
[3] I. Richardson, “H.264 and MPEG-4 Video Compression,”
John Wiley and Sons Ltd., Chichester, 2003.
[4] Joint Video Team (JVT) of ITU-T VCEG and ISO/IEC
MPEG, “Draft ITU-T Recommendation and Final Draft
International Standard of Joint Video Specification (ITU-T
Rec. H.264 and ISO/IEC 14496-10 AVC),” May 2003.
[5] G. J. Sullivan and T. Wiegand, “Video Compression―
from Concepts to the H.264/AVC Standard,” Proceed-
ings of the IEEE, Vol. 93, No. 1, 2005, pp. 18-31.
[6] Y.-W. Huang, B.-Y. Hsieh, T.-C. Chen and L. G. Chen,
“Analysis, Fast Algorithm, and VLSI Architecture De-
sign for H.264/AVC Intra Frame Coder,” IEEE Transac-
tions Circuit and Systems for Video Technology, Vol. 15,
No. 3, 2005, pp. 378-401.
[7] İ. Hamzaoğlu, Ö. Taşdizen and E. Şahin, “An Efficient
H.264 Intra Frame Coder System Design,” IEEE Trans-
actions on Consumer Electronics, Vol. 54, No. 4, 2008,
pp. 1903-1911.
[8] K. Suh, S. Park and H. Cho, “An Efficient Hardware Ar-
chitecture of Intra Prediction and TQ/IQIT Module for
H.264 Encoder,” ETRI Journal, Vol. 27, No. 5, 2005, pp.
511-524.
[9] B. Meng, O. C. Au, C.-W. Wong and H.-K. Lam, “Effi-
cient Intra-Prediction Mode Selection for 4 × 4 Blocks in
H.264,” Proceedings of International Conference on
Multimedia and Expo, Baltimore, 2003, pp. 521-524.
[10] F. Pan, X. Lin, S. Rahardja, K. P. Lim, Z. G. Li, D. Wu
and S. Wu, “Fast Mode Decision Algorithm for Intra pre-
diction in H.264/AVC Video Coding,” IEEE Transac-
tions on Circuits and Systems for Video Technology, Vol.
15, No. 7, 2005, pp. 813-822.
[11] B. Meng, O. C. Au, C. W. Wong and H. K. Lam, “Effi-
cient Intra-Prediction Algorithm in H.264,” Proceedings
of International Conference on Image Processing, Bar-
celona, 2003, pp. 837-840.
[12] S. S. Chun, J.-C. Yoon and S. Sull, “Efficient Intra Pre-
diction Mode Decision for H.264 Video,” Lecture Notes
in Computer Science, Vol. 3767, 2005, pp. 168-178.
[13] H. Loukil, A. Ben Atitallah and N. Masmoudi, “An Effi-
cient FPGA Parallel Architecture for H.264/AVC Intra
Prediction Algorithm,” Proceeding of International Con-
ference on Embedded Systems and Critical Applications,
Gammarth, Tunisia, 2008, pp. 191-196.
[14] A. Kessentini, B. Kaanich, I. Werda, A. Samet and N.
Masmoudi, “Low Complexity Intra 16 × 16 Prediction for

H. LOUKIL ET AL.
29
H.264/AVC,” Proceedings of International Conference
on Embedded Systems & Critical Applications, Tunis,
Tunisia, 2008, pp. 197-201.
[15] T.-C. Wang, Y.-W. Huang, H.-C. Fang and L.-G. Chen,
“Parallel 4 × 4 2D Transform and Inverse Transform Ar-
chitecture for MPEG-4 AVC/H.264,” Proceedings of the
2003 IEEE International Symposium on Circuits and
Systems, Bangkok, 2003, pp. 800-803.
[16] L. Liu, Q. Lin, M. Rong and J. Li, “A 2-D Forward/In-
verse Integer Transform Processor of H.264 Based on
Highly-Parallel Architecture,” Proceedings of the 4th
IEEE International Workshop on System-on-Chip for
Real-Time Applications, Banff, July 19-21, 2004, pp.
158-161.
[17] K.-H. Chen, J.-I. Guo and J.-S. Wang, “An Efficient Di-
rect 2-D Transform Coding IP Design for MPEG-4
AVC/H.264,” IEEE International Symposium on Circuits
and Systems, Kobe, May 23-26, 2005, pp. 4517-4520.
[18] G. Raja, S. Khan and M. J. Mirza, “VLSI Architecture &
Implementation of H.264 Integer Transform,” The 17th
International Conference on Microelectronics, Islamabad,
December 13-15, 2005, pp. 218-223.
[19] C.-P. Fan, “Fast 2-Dimensional 4 × 4 Forward Integer
Transform Implementation for H.264/AVC,” IEEE Trans-
actions on Circuits and Systems—II: Express Briefs, Vol.
53, No. 3, 2006, pp. 174-177.
[20] R. Kordasiewicz and S. Shirani, “Hardware Implemen-
tation of the Optimized Transform and Quantization
Blocks of H.264,” IEEE Canadian Conference on Elec-
trical and Computer Engineering, Canada, May 2-5,
2004, pp. 943-946.
[21] H. Loukil, S. Arous, I. Werda, A. Ben Atitallah, P. Kadi-
onik and N. Masmoudi, “Hardware Architecture for H.264/
AVC INTRA 16 × 16 Frame Processing,” IEEE Interna-
tional Multi-Conference on Systems, Signals and Devices,
Djerba, March 23-26, 2009, pp. 1-5
[22] “JVT H.264 Reference Software Version JM10.1,” http://
iphome.hhi.de/suehring/tml/download/old_jm/