Open Journal of Soil Science, 2012, 2, 203-212
http://dx.doi.org/10.4236/ojss.2012.23025 Published Online September 2012 (http://www.SciRP.org/journal/ojss)
203
Test of the Rosetta Pedotransfer Function for Saturated
Hydraulic Conductivity
Carlos Alvarez-Acosta1, Robert J. Lascano1, Leo Stroosnijder2
1USDA-ARS* Cropping System Research Laboratory, Wind Erosion and Water Conservation Research Unit, Lubbock, USA; 2Land
Degradation and Development Group, Soil Science Centre, Wageningen University, Wageningen, Netherlands.
Received April 28th, 2012; revised May 30th, 2012; accepted June 10th, 2012
ABSTRACT
Simulation models are tools that can be used to explore, for example, effects of cultural practices on soil erosion and
irrigation on crop yield. However, often these models require many soil related input data of which the saturated hy-
draulic conductivity (Ks) is one of the most important ones. These data are usually not available and experimental de-
termination is both expensive and time consuming. Therefore, pedotransfer functions are often used, which make use of
simple and often readily available soil information to calculate required input values for models, such as soil hydraulic
values. Our objective was to test the Rosetta pedotransfer function to calculate Ks. Research was conducted in a 64-ha
field near Lamesa, Texas, USA. Field measurements of soil texture and bulk density, and laboratory measurements of
soil water retention at field capacity (–33 kPa) and permanent wilting point (–1500 kPa), were taken to implement
Rosetta. Calculated values of Ks were then compared to measured Ks on undisturbed soil samples. Results showed that
Rosetta could be used to obtain values of Ks for a field with different textures. The Root Mean Square Difference
(RMSD) of Ks at 0.15 m soil depth was 7.81  10–7 m·s–1. Further, for a given soil texture the variability, from 2.30 
10–7 to 2.66  10–6 m·s−1, of measured Ks was larger than the corresponding RMSD. We conclude that Rosetta is a tool
that can be used to calculate Ks in the absence of measured values, for this particular soil. Level H5 of Rosetta yielded
the best results when using the measured input data and thus calculated values of Ks can be used as input in simulation
models.
Keywords: Rosetta; Saturated Hydraulic Conductivity; Ks; Pedotransfer Function
1. Introduction
In order to model soil physical processes related to soil-
water content, it is important to know the hydraulic
properties of the soil [1]. Vigiak et al. [2] also remarked
the importance of characterizing soil hydraulic parame-
ters in order to understand the occurrence and movement
of overland flow at field, hill-slope, and catchment scale.
These soil hydraulic properties include the saturated (Ks)
and unsaturated hydraulic conductivity, and the water
retention curve. Furthermore, in any modeling study on
water flow and solute transport in soils, the water reten-
tion and hydraulic conductivity functions for soil hori-
zons in the profile are crucial input parameters [3]. Ex-
amples of two simulation models that require soil hy-
draulic properties as inputs are the Energy Water Balance
Model [4,5] and HYDRUS [6,7]. In addition, soil hy-
draulic properties are a required input in models used to
calculate water runoff and soil erosion, e.g. Precision
Agricultural Landscape Modeling System [8-10] and ex-
amples of other models are given by Aksoy and Kavvas
[11].
Although the soil hydraulic properties can be measured
directly, this practice is both costly and time-consuming,
and sometimes results obtained are unreliable because of
the associated soil heterogeneity and experimental errors
[12,13]. When large areas of land are under study, it is
virtually impossible to perform enough measurements to
be meaningful, indicating the need for an inexpensive
and rapid way to determine soil hydraulic properties [14].
For example, some research results indicated that in a
10-ha field, 1300 measurements would have to be made
in order to accurately measure saturated hydraulic con-
ductivity to within 10% of the mean value [13]. Further-
more, Stroosnijder [15] indicated that measurements
*The US Department of Agriculture (USDA) prohibits discrimination in
all its programs and activities on the basis of race, color, national origin,
age, disability, and where applicable, sex, marital status, familial status,
p
arental status, religion, sexual orientation, genetic information, poli
t
i-
cal beliefs, reprisal, or because all or part of an individual’s income is
derived from any public assistance program.
alone would provide data difficult to extrapolate in time
and space, meaning that erosion in large fields would not

Test of the Rosetta Pedotransfer Function for Saturated Hydraulic Conductivity 204
be known without prediction technologies, but also that
predictions need measurements to work. Therefore, many
indirect methods such as pedotransfer functions (PTFs)
have been developed to reduce the effort and cost [16].
These PTFs are predictive functions of certain soil pro-
perties estimated from other simpler measured soil
proper-ties [17]. They can be used as inputs to models in
order to reduce costs and accelerate the investigations. A
detailed review of PTFs is given by Wösten et al. [3] and
scaling of soil physical properties in relation to models is
given by Pachepsky et al. [18]. In summary, many efforts
have been made to develop PTFs at large scale, but little
has been done to evaluate the performance of Artificial
Neural Networks (ANNs) in estimating saturated Ks at a
landscape scale [19].
A soil hydraulic property that is often a required input
to simulation models is the saturated hydraulic conduc-
tivity, Ks. It is one of the most important soil physical
properties for determining infiltration rate and other hy-
drological processes [20]. In general, the Ks refers to the
capacity of the soil to drain water and gives information
about the presence of disruptive soil strata, and the cor-
relation between the permeability and other soil charac-
teristics. The geometry of the complex pores that depend
on texture, structure, viscosity and density, determine the
Ks. In hydrologic models, this is a sensitive input pa-
rameter and is one of the most problematic measure-
ments at field-scale in regard to variability and uncer-
tainty [21]. The Ks is known to be one of the most vari-
able of all soil physical properties, varying up to 10 or-
ders of magnitude for different geo-materials [22]. Thus,
the objective of this study was to determine the applica-
bility of the Rosetta pedotransfer function [14] to calcu-
late Ks for different soil textures of a large field in the
Texas Southern High Plains. The calculated values of Ks
were evaluated by comparing them to laboratory-mea-
sured values. Furthermore, the differences between mea-
sured and calculated values of Ks were evaluated using
two statistical parameters, the mean square deviation [23]
and the Nash Sutcliffe Efficiency parameter [25]. A use
of the Rosetta PTF is to assist researchers in studying the
hydrological processes that could lead to better water
management practices in the region of study. This is im-
portant because in the Texas Southern High Plains the
combination of common droughts and a declining water
table from the Ogallala Aquifer are a challenge to man-
age the irrigation of crops and establish crops under dry-
land conditions [5,25].
2. Materials and Methods
2.1. Study Area
The study area is located in the region known as Llano
Estacado, near Lamesa, which is a small town, popula-
tion of close to 10,000, located in Dawson County, Texas,
USA (Figure 1). The coordinates are 32˚327.4N;
101˚468.24W; and, an elevation of 833 m above sea
level with a semi-arid climate. The field is 63.8 ha and
has an average slope of 0.33%, although parts of the field
have slopes in excess of 5%. In this region, about half the
cultivated land is irrigated from an underground aquifer,
called the Ogallala, which is classified, as non-recharge-
able [25]. The predominant soil series at this site is an
Amarillo fine sandy loam, a fine-loamy, mixed, superac-
tive, thermic, Aridic Paleustalf [26]. These soils are
characterized by a high content of Ca and Mg carbonates
(pH > 7), low organic matter (<2 g·kg–1), and are classi-
fied as moderately permeable.
2.2. Soil Sampling
To determine the Ks as well as the water retention curve,
18 undisturbed soil samples were collected using a gouge
auger, from 0.10 - 0.15 m depth from the surface at the
locations shown in Figure 2. Sampling was done on 15
July 2009. The sampler rings were 0.05 m in diameter by
0.051 m long. For the purpose of this study, only one
sample was taken at each of the 18 locations; therefore,
they can be considered as replicates.
To determine the textural classes, 36 soil cores were
sampled over the field on the 15 July 2009 at the loca-
tions shown in Figure 3, which were geo-referenced us-
ing a Global Positioning System (Model 4700 Dual
Channel RTK system, Trimble, Sunnyvale, CA). These
samples were taken with a commercial tractor-mounted
hydraulic core sampler system (Giddings Machine Com-
pany, Model HDGSRTS, Windsor, CO). This system
pushed into the soil a tube-sampler with a plastic sleeve
inside, i.e., 1.2 m long and 0.05 m in diameter. Once the
sampler was removed from the soil the sleeve inside the
core was extracted and the undisturbed soil sample ob-
tained. Thereafter, the soil cores were stored in a cold-
room at a temperature of 5˚C. These sampling locations
were selected using the NRCS (2008) soil map [26] as a
guide to ensure that all the different soil types within the
field were included in the sampling scheme. The soil
cores were used to identify the lower and upper depth of
soil horizons (Table 1). This soil was then oven-dried at
105 for 24 hrs and the dry samples were ground with a
mill˚C and sieved to 2 mm.
2.3. Rosetta Description
Rosetta is an algorithm that calculates soil water reten-
tion parameters, Ks and unsaturated hydraulic conducti-
1Mention of this or other proprietary products is for the convenience o
f
the readers only, and does not constitute endorsement or preferential
treatment of those products by USDA-ARS.

Test of the Rosetta Pedotransfer Function for Saturated Hydraulic Conductivity 205
United States of America
Figure 1. Location of the field-study, Lamesa, Dawson
county, Texas, USA. (Source: Self composition on a Google-
USDA farm service agency image).
Figure 2. Sampling locations in the field where 18 soil cores
were obtained and saturated hydraulic conductivity (Ks),
and water retention were measured. (Source: Self composi-
tion on a Google-USDA farm service agency image).
0 100 200 400 600 800
met er s
Figure 3. Spatial distribution of the textural classes in
Lamesa, Texas.
Table 1. Upper and lower depth limits of the soil horizons
for the 18 soil cores taken at the field in Lamesa, Texas.
Soil horizon Upper limit (m) Lower limit (m)
vity using hierarchical PTFs based on five levels of input
data [14]. It is of great practical use, allowing flexibility
for the user towards the required input data [27]. The first
level (H1) consists of a lookup table that provides aver-
age parameters for each of the USDA textural classes.
The second level (H2) uses values from H1 plus sand, silt,
and clay fractions as inputs, and provides a hydraulic
parameter that varies continuously with texture. The third
level (H3) includes the predictors used in level H2 and
the soil dry-bulk density (

d). The fourth level (H4) uses
H3 and soil volumetric water content (
 ) at a water suc-
tion of −33 kPa. The last level (H5) consists of all the
other parameters, H4, plus the
 at a water suction of
–1500 kPa. While H1 is a simple table with average hy-
draulic parameters for each textural class, all other mo-
dels involve a combination of neural networks and the
bootstrap method [14].
In Rosetta, the relation between
 and water suction
(h), i.e. water retention [
 (h)], as well as the saturated
and unsaturated hydraulic conductivity, are described
with the well known Mualem-Van Genuchten equation
[28,29] and is given by:



1
sr
rm
n
h
h








(1)
where
 (h) is the soil volumetric water content (m3·m−3)
at suction h (cm);

s and

r are the saturated and the re-
sidual water content (m3·m−3) at h = 0 cm and −15,000
cm, respectively;
 (> 0 in cm−1) is related to the inverse
of the air entry suction; and n (> 1) is a measure of the
pore-size distribution and m = 1 – 1/n. The unsaturated
hydraulic conductivity, K(Se), is described with the
Mualem-Van Genuchten model as:

2
1
011
m
n
Ln
ee e
KS KSS









 






(2)
where K0 is a fitted value of K at saturation (cm·d−1),
which is similar but not considered equal to Ks, and L is a
pore connectivity factor (negative in most cases). The
effective saturation (Se) is given by:
 


1
1
m
r
en
sr
h
S
h

 







 (3)
Ap1 0.0 0.3
Ap2 0.1 0.3
Therefore, the relative hydraulic conductivity Kr(h) is
given by:
  

2
1
2
11
1
m
nn
rm
n
hh
Kh
h






 









(4)
Bt1 0.2 0.5
Bt2 0.3 1.2
Bt3 0.4 1.2
Btk 0.5 1.2
Btkk 0.5 1.2
which is a function given the quotient of hydraulic con-

Test of the Rosetta Pedotransfer Function for Saturated Hydraulic Conductivity 206
ductivity function, K(h) to saturated hydraulic conductiv-
ity, Ks [27]. In summary, the seven parameters calculated
with the Rosetta PTF (Equations (1)-(4)) are: 
r,

s,
 , n,
Ks, K0, and L.
2.4. Model Performance Evaluation
Calculated values of Ks obtained with Rosetta were
compared to corresponding measured values and evalu-
ated using two statistical parameters. First, by using the
Root Mean Squared Difference (RMSD) and second, by
using the Nash Sutcliffe Efficiency (NSE). The RMSD,
gives the mean difference between measured and calcu-
lated values of Ks and is calculated as [23]:

2
1
1
RMSD n
ii
i
x
y
n

 (5)
where xi is the measured value of Ks and yi is the corre-
sponding calculated value of Ks obtained with Rosetta.
The NSE compares measured and calculated values of
Ks and is given by [24]:


2
1
2
mean
1
NSE 1
nmc
ii
i
nm
ii
i
YY
YY





 






(6)
where is measured value of Ks and is the cor-
responding calculated value of Ks, is the average
of measured values of Ks, and n is number of measure-
ments. Values of NSE may range from − to 1. A value
of NSE = 1, corresponds to a perfect match of calculated
compared to the measured values of Ks. Conversely, an
efficiency of 0 (NSE = 0) indicates that the Rosetta cal-
culations of Ks are as accurate as the mean of the mea-
sured data; whereas, an efficiency <0 (NSE < 0) occurs
when the measured mean is a better predictor than the
model or, in other words, when the residual variance,
described by the nominator in Equation (6), is larger than
the data variance, described by the denominator [24].
m
i
Yc
i
Y
mean
i
Y
2.5. Measurements
Textural Analysis. Clay, silt and sand fraction of all
36-soil samples were determined using the hydrometer
method [30]. This method uses the Navier-Stokes equa-
tion to calculate soil particles in suspension in an infinite
soil column and is adequate for textural class identifica-
tion, but cannot be used to accurately define the particle
size [31]. Nevertheless, it provides a reasonable input to
Rosetta [14].
Saturated Hydraulic Conductivity (Ks). The Ks was
measured under laboratory conditions using the constant
and falling head methods [31] on undisturbed soil sam-
ples. For both methods, Ks were measured using a labo-
ratory permeameter [32]. In some soil samples, water
flowed in the range of operation for the falling head
method, while in other samples the water flowed in the
range of the constant-head method. For this reason, both
methods were used and thereafter matched to the Ks of
each soil sample. Our first approach was to use the con-
stant head method and if Ks was < 1.16  10–7 m·s–1, the
falling head method was selected. As previously de-
scribed, the undisturbed soil samples used for the mea-
surement of Ks were collected using a gouge auger at the
locations shown in Figure 2. To avoid the possible dis-
integration of soil particles in each sample, which would
cause silting of the pores and a reduction of the flow and
Ks, we used ultrahigh-pure water that was autoclaved at
120˚C for 30 minutes. The solution was saturated with
calcium sulphate (CaSO4·2H2O) and toluene was added
to eliminate microorganisms.
Water Retention Determination. The relation between
soil volumetric water content (  ) and water suction (h) at
saturation (h = 0) and field capacity (h = −33 kPa) was
measured using a sand/kaolin box (pF-Determination,
Eijkelkamp, Giesbeek, The Netherlands), that operates in
the 0 - 50 kPa range [33]. For these two measurements
we used the undisturbed soil samples that were also used
to measure Ks. Weights of the soil samples, before and
after drying, and ring volumes were used to calculate the
soil gravimetric water content (

g, kg·kg–1) and the cor-
responding value of the soil dry-bulk density (ρd, kg·m–3)
was used to convert

g to
 , assuming a density of water
equal to 1000 kg·m–3.
For the soil water content at wilting point, pF = 4.18 (h
= −1500 kPa  −15 bar), the water in the soil is retained
in small pores, and thus the retention of water is domi-
nantly influenced by texture. For this reason, disturbed
soil samples can be used for this determination, which
were saturated with water for 2 - 3 days and placed on a
plate (Pressure-Membrane Apparatus, Eijkelkamp, Gies-
beek, The Netherlands) and a pressure of 1500 kPa was
applied for 3 days to the three replicates [34]. Afterwards
soil samples were weighed (wet mass), oven-dried at
105˚C and weighed again (dry mass). With these values
the 
g water content, was calculated for a pF = 4.18, and
converted to  using the 
d of the undisturbed samples
used in the sand/kaolin box.
3. Results and Discussion
3.1. Measurements
There were three textural classes corresponding to the 18
spots where undisturbed soil samples were taken (Figure
2) and these were: clay loam, sandy clay loam, and sandy
clay. Of the total number of soil samples, there were thir-
teen samples of sandy clay loam, four of clay loam and
one sandy clay. The ESRI software (version 9.2) of Ar-
cGIS (2006) was used as the Geographic Information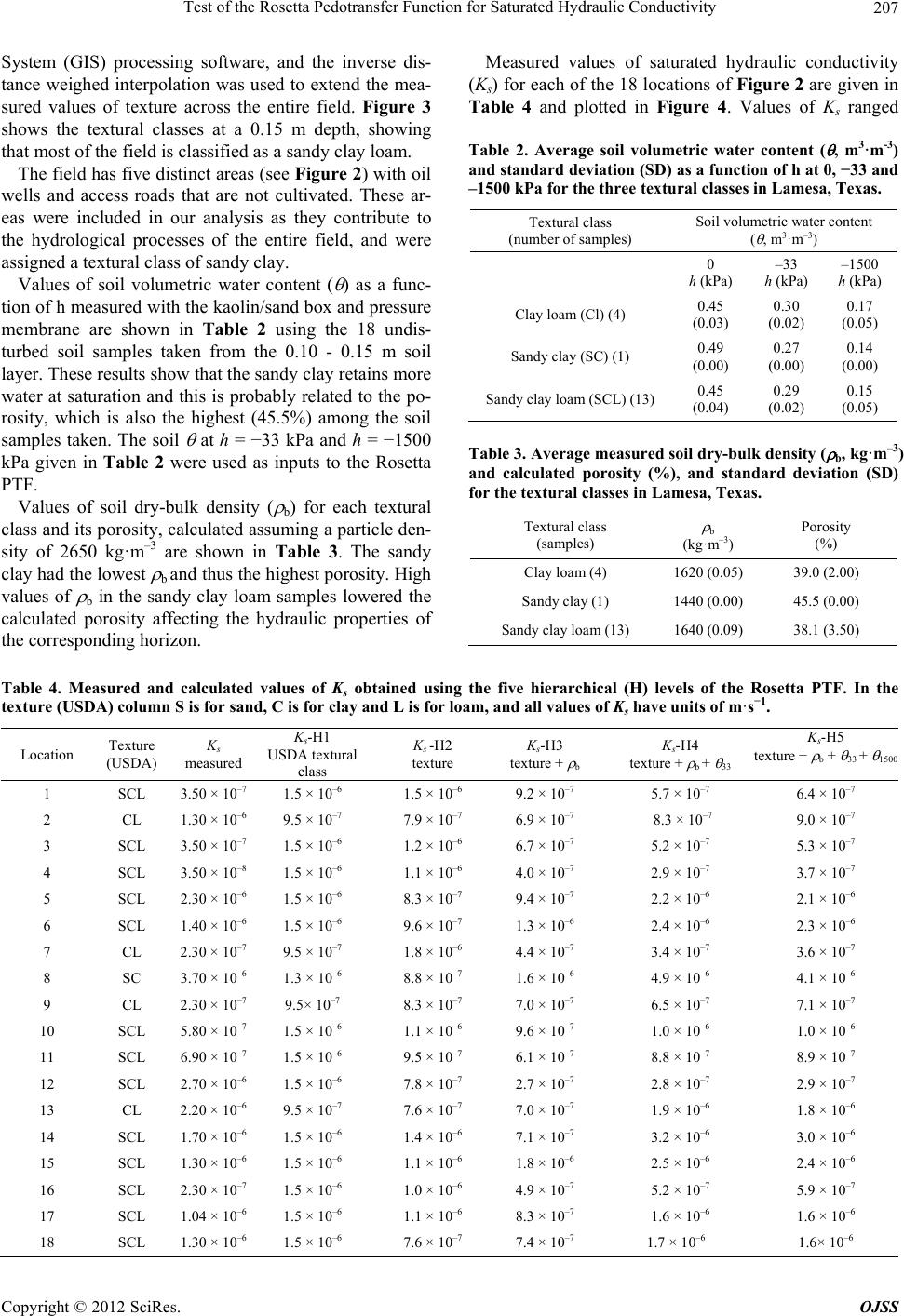

Test of the Rosetta Pedotransfer Function for Saturated Hydraulic Conductivity 207
System (GIS) processing software, and the inverse dis-
tance weighed interpolation was used to extend the mea-
sured values of texture across the entire field. Figure 3
shows the textural classes at a 0.15 m depth, showing
that most of the field is classified as a sandy clay loam.
The field has five distinct areas (see Figure 2) with oil
wells and access roads that are not cultivated. These ar-
eas were included in our analysis as they contribute to
the hydrological processes of the entire field, and were
assigned a textural class of sandy clay.
Values of soil volumetric water content (
 ) as a func-
tion of h measured with the kaolin/sand box and pressure
membrane are shown in Table 2 using the 18 undis-
turbed soil samples taken from the 0.10 - 0.15 m soil
layer. These results show that the sandy clay retains more
water at saturation and this is probably related to the po-
rosity, which is also the highest (45.5%) among the soil
samples taken. The soil
 at h = −33 kPa and h = −1500
kPa given in Table 2 were used as inputs to the Rosetta
PTF.
Values of soil dry-bulk density (

b) for each textural
class and its porosity, calculated assuming a particle den-
sity of 2650 kg·m–3 are shown in Table 3. The sandy
clay had the lowest 
b and thus the highest porosity. High
values of 
b in the sandy clay loam samples lowered the
calculated porosity affecting the hydraulic properties of
the corresponding horizon.
Measured values of saturated hydraulic conductivity
(Ks) for each of the 18 locations of Figure 2 are given in
Table 4 and plotted in Figure 4. Values of Ks ranged
Table 2. Average soil volumetric water content (  , m3·m-3)
and standard deviation (SD) as a function of h at 0, −33 and
–1500 kPa for the three textural classes in Lamesa, Texas.
Textural class
(number of samples)
Soil volumetric water content
(  , m3·m–3)
0
h (kPa)
–33
h (kPa)
–1500
h (kPa)
Clay loam (Cl) (4) 0.45
)0.03(
0.30
)0.02(
0.17
)0.05(
Sandy clay (SC) (1) 0.49
)0.00(
0.27
)0.00(
0.14
)0.00(
Sandy clay loam (SCL) (13) 0.45
)0.04(
0.29
)0.02(
0.15
)0.05(
Table 3. Average measured soil dry-bulk density ( 
b, kg·m–3)
and calculated porosity (%), and standard deviation (SD)
for the textural classes in Lamesa, Texas.
Textural class
(samples)

b
(kg·m–3)
Porosity
(%)
Clay loam (4) 1620 (0.05) 39.0 (2.00)
Sandy clay (1) 1440 (0.00) 45.5 (0.00)
Sandy clay loam (13) 1640 (0.09) 38.1 (3.50)
Table 4. Measured and calculated values of Ks obtained using the five hierarchical (H) levels of the Rosetta PTF. In the
texture (USDA) column S is for sand, C is for clay and L is for loam, and all values of Ks have units of m·s−1.
Location Texture
(USDA)
Ks
measured
Ks-H1
USDA textural
class
Ks -H2
texture
Ks-H3
texture + 
b
Ks-H4
texture + 
b +

33
Ks-H5
texture + 
b +

33 +

1500
1 SCL 3.50 × 10–7 1.5 × 10–6 1.5 × 10–6 9.2 × 10–7 5.7 × 10–7 6.4 × 10–7
2 CL 1.30 × 10–6 9.5 × 10–7 7.9 × 10–7 6.9 × 10–7 8.3 × 10–7 9.0 × 10–7
3 SCL 3.50 × 10–7 1.5 × 10–6 1.2 × 10–6 6.7 × 10–7 5.2 × 10–7 5.3 × 10–7
4 SCL 3.50 × 10–8 1.5 × 10–6 1.1 × 10–6 4.0 × 10–7 2.9 × 10–7 3.7 × 10–7
5 SCL 2.30 × 10–6 1.5 × 10–6 8.3 × 10–7 9.4 × 10–7 2.2 × 10–6 2.1 × 10–6
6 SCL 1.40 × 10–6 1.5 × 10–6 9.6 × 10–7 1.3 × 10–6 2.4 × 10–6 2.3 × 10–6
7 CL 2.30 × 10–7 9.5 × 10–7 1.8 × 10–6 4.4 × 10–7 3.4 × 10–7 3.6 × 10–7
8 SC 3.70 × 10–6 1.3 × 10–6 8.8 × 10–7 1.6 × 10–6 4.9 × 10–6 4.1 × 10–6
9 CL 2.30 × 10–7 9.5× 10–7 8.3 × 10–7 7.0 × 10–7 6.5 × 10–7 7.1 × 10–7
10 SCL 5.80 × 10–7 1.5 × 10–6 1.1 × 10–6 9.6 × 10–7 1.0 × 10–6 1.0 × 10–6
11 SCL 6.90 × 10–7 1.5 × 10–6 9.5 × 10–7 6.1 × 10–7 8.8 × 10–7 8.9 × 10–7
12 SCL 2.70 × 10–6 1.5 × 10–6 7.8 × 10–7 2.7 × 10–7 2.8 × 10–7 2.9 × 10–7
13 CL 2.20 × 10–6 9.5 × 10–7 7.6 × 10–7 7.0 × 10–7 1.9 × 10–6 1.8 × 10–6
14 SCL 1.70 × 10–6 1.5 × 10–6 1.4 × 10–6 7.1 × 10–7 3.2 × 10–6 3.0 × 10–6
15 SCL 1.30 × 10–6 1.5 × 10–6 1.1 × 10–6 1.8 × 10–6 2.5 × 10–6 2.4 × 10–6
16 SCL 2.30 × 10–7 1.5 × 10–6 1.0 × 10–6 4.9 × 10–7 5.2 × 10–7 5.9 × 10–7
17 SCL 1.04 × 10–6 1.5 × 10–6 1.1 × 10–6 8.3 × 10–7 1.6 × 10–6 1.6 × 10–6
18 SCL 1.30 × 10–6 1.5 × 10–6 7.6 × 10–7 7.4 × 10–7 1.7 × 10–6 1.6× 10–6

Test of the Rosetta Pedotransfer Function for Saturated Hydraulic Conductivity 208
(m·s
-1
)
Figure 4. Measured values of saturated hydraulic conducti-
vity (Ks, m·s–1) for the 18 soil samples of the field in Lamesa,
Texas.
from a low of 3.5  10–8 m·s–1 at location 4, a sandy clay
loam texture, to a high of 3.7  10–6 m·s−1 at location 8, a
sandy clay texture. Soil sample number 8 corresponds to
a sandy clay; whereas, samples 2, 7, 9 and 13 are a clay
loam. The rest of the soil samples (1, 3, 4, 5, 6, 10, 11, 12,
14, 15, 16, 17 and 18) were sandy clay loam. From Fig-
ure 4, it is clear that the sandy clay sample 8 has the
higher Ks; whereas, the clay loam (samples 2, 7, 9, 13) is
as random as the sandy clay loam. The average Ks was
1.20  10–6 m·s–1 with a standard deviation of 9.95  10–7
m·s –1. The high variation could be the result that these
soil samples were from a plowed layer and invariably
some compression occurred during sampling confirming
that Ks is problematic to measure due to its associated
variability and uncertainty [21].
3.2. Rosetta Simulations
Results from comparing measured values of Ks with
those obtained with the five levels of Rosetta are given in
Table 4 and plotted in Figure 5. As previously, des-
Figure 5. Comparison of measured and calculated values of saturated hydraulic conductivity (Ks, m·s-1) for 18 locations of a
field in Lamesa, Texas. Calculated values of Ks were obtained with the Rosetta PTF [14]. (a) Textural class, level H1; (b) H1
plus sand, silt and clay, level H2; (c) H2 plus soil dry-bulk density, level H3; (d) H3 plus soil water content at −33 kPa, level
H4; and (e) H4 plus soil water content at −1500 kPa, level H5.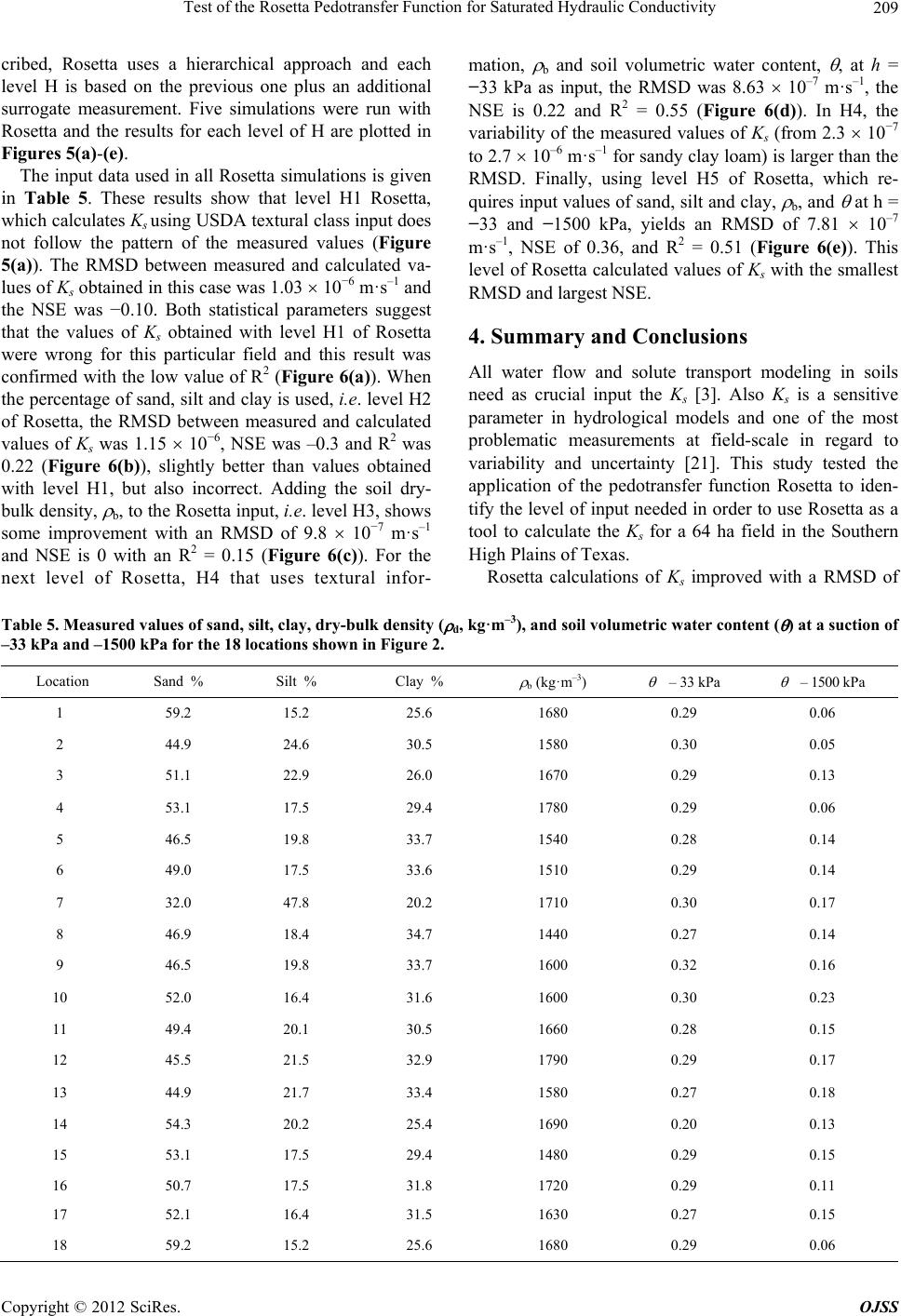

Test of the Rosetta Pedotransfer Function for Saturated Hydraulic Conductivity 209
cribed, Rosetta uses a hierarchical approach and each
level H is based on the previous one plus an additional
surrogate measurement. Five simulations were run with
Rosetta and the results for each level of H are plotted in
Figures 5(a)-(e).
The input data used in all Rosetta simulations is given
in Table 5. These results show that level H1 Rosetta,
which calculates Ks using USDA textural class input does
not follow the pattern of the measured values (Figure
5(a)). The RMSD between measured and calculated va-
lues of Ks obtained in this case was 1.03  10−6 m·s–1 and
the NSE was −0.10. Both statistical parameters suggest
that the values of Ks obtained with level H1 of Rosetta
were wrong for this particular field and this result was
confirmed with the low value of R2 (Figure 6(a)). When
the percentage of sand, silt and clay is used, i.e. level H2
of Rosetta, the RMSD between measured and calculated
values of Ks was 1.15  10−6, NSE was –0.3 and R2 was
0.22 (Figure 6(b)), slightly better than values obtained
with level H1, but also incorrect. Adding the soil dry-
bulk density, 
b, to the Rosetta input, i.e. level H3, shows
some improvement with an RMSD of 9.8  10−7 m·s–1
and NSE is 0 with an R2 = 0.15 (Figure 6(c)). For the
next level of Rosetta, H4 that uses textural infor-
mation, 
b and soil volumetric water content,
 , at h =
−33 kPa as input, the RMSD was 8.63  10–7 m·s–1, the
NSE is 0.22 and R2 = 0.55 (Figure 6(d)). In H4, the
variability of the measured values of Ks (from 2.3  10−7
to 2.7  10–6 m·s–1 for sandy clay loam) is larger than the
RMSD. Finally, using level H5 of Rosetta, which re-
quires input values of sand, silt and clay,

b, and
 at h =
−33 and −1500 kPa, yields an RMSD of 7.81  10–7
m·s –1, NSE of 0.36, and R2 = 0.51 (Figure 6(e)). This
level of Rosetta calculated values of Ks with the smallest
RMSD and largest NSE.
4. Summary and Conclusions
All water flow and solute transport modeling in soils
need as crucial input the Ks [3]. Also Ks is a sensitive
parameter in hydrological models and one of the most
problematic measurements at field-scale in regard to
variability and uncertainty [21]. This study tested the
application of the pedotransfer function Rosetta to iden-
tify the level of input needed in order to use Rosetta as a
tool to calculate the Ks for a 64 ha field in the Southern
High Plains of Texas.
Rosetta calculations of Ks improved with a RMSD of
Table 5. Measured values of sand, silt, clay, dry-bulk density ( 
d, kg·m–3), and soil volumetric water content (
 ) at a suction of
–33 kPa and –1500 kPa for the 18 locations shown in Figure 2.
Location Sand % Silt % Clay % 
b (kg·m–3)
 – 33 kPa  – 1500 kPa
1 59.2 15.2 25.6 1680 0.29 0.06
2 44.9 24.6 30.5 1580 0.30 0.05
3 51.1 22.9 26.0 1670 0.29 0.13
4 53.1 17.5 29.4 1780 0.29 0.06
5 46.5 19.8 33.7 1540 0.28 0.14
6 49.0 17.5 33.6 1510 0.29 0.14
7 32.0 47.8 20.2 1710 0.30 0.17
8 46.9 18.4 34.7 1440 0.27 0.14
9 46.5 19.8 33.7 1600 0.32 0.16
10 52.0 16.4 31.6 1600 0.30 0.23
11 49.4 20.1 30.5 1660 0.28 0.15
12 45.5 21.5 32.9 1790 0.29 0.17
13 44.9 21.7 33.4 1580 0.27 0.18
14 54.3 20.2 25.4 1690 0.20 0.13
15 53.1 17.5 29.4 1480 0.29 0.15
16 50.7 17.5 31.8 1720 0.29 0.11
17 52.1 16.4 31.5 1630 0.27 0.15
18 59.2 15.2 25.6 1680 0.29 0.06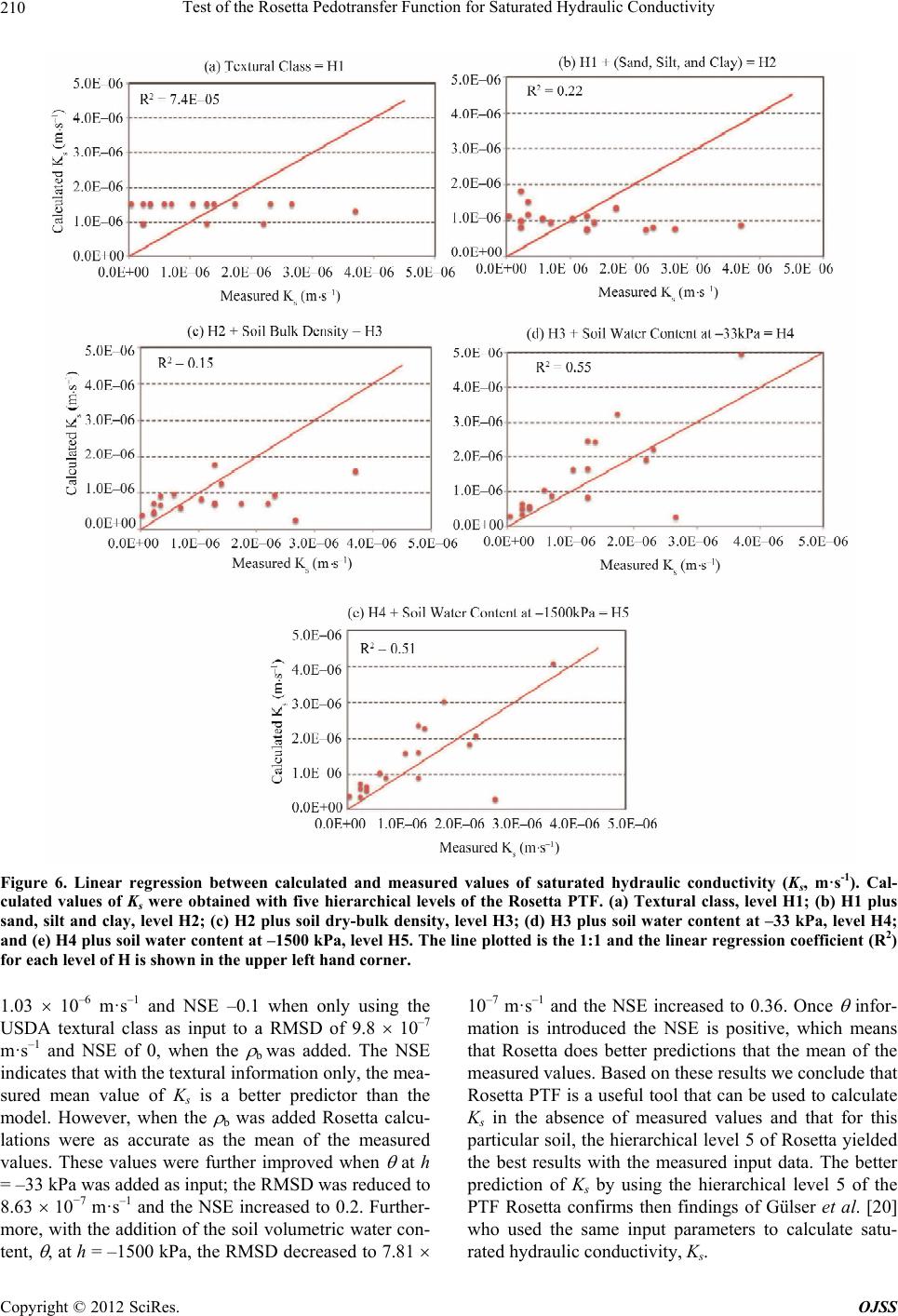

Test of the Rosetta Pedotransfer Function for Saturated Hydraulic Conductivity 210
Figure 6. Linear regression between calculated and measured values of saturated hydraulic conductivity (Ks, m·s-1). Cal-
culated values of Ks were obtained with five hierarchical levels of the Rosetta PTF. (a) Textural class, level H1; (b) H1 plus
sand, silt and clay, level H2; (c) H2 plus soil dry-bulk density, level H3; (d) H3 plus soil water content at –33 kPa, level H4;
and (e) H4 plus soil water content at –1500 kPa, level H5. The line plotted is the 1:1 and the linear regression coefficient (R2)
for each level of H is shown in the upper left hand corner.
1.03  10–6 m·s–1 and NSE –0.1 when only using the
USDA textural class as input to a RMSD of 9.8  10–7
m·s –1 and NSE of 0, when the 
b was added. The NSE
indicates that with the textural information only, the mea-
sured mean value of Ks is a better predictor than the
model. However, when the

b was added Rosetta calcu-
lations were as accurate as the mean of the measured
values. These values were further improved when  at h
= –33 kPa was added as input; the RMSD was reduced to
8.63  10−7 m·s–1 and the NSE increased to 0.2. Further-
more, with the addition of the soil volumetric water con-
tent,  , at h = –1500 kPa, the RMSD decreased to 7.81 
10–7 m·s–1 and the NSE increased to 0.36. Once  infor-
mation is introduced the NSE is positive, which means
that Rosetta does better predictions that the mean of the
measured values. Based on these results we conclude that
Rosetta PTF is a useful tool that can be used to calculate
Ks in the absence of measured values and that for this
particular soil, the hierarchical level 5 of Rosetta yielded
the best results with the measured input data. The better
prediction of Ks by using the hierarchical level 5 of the
PTF Rosetta confirms then findings of Gülser et al. [20]
who used the same input parameters to calculate satu-
rated hydraulic conductivity, Ks.

Test of the Rosetta Pedotransfer Function for Saturated Hydraulic Conductivity 211
5. Acknowledgements
The authors would like to thank Jill and J. D. Booker
aswell as John Randall Nelson and Vinicius Bufon from
the USDA-ARS Cropping Systems Research Laboratory,
Lubbock, Texas, for their assistance in the field and
laboratory work.
REFERENCES
[1] C. M. Rubio, P. Llorens and F. Gallart, “Uncertainty and
Efficiency of Pedotransfer Functions for Estimating Wa-
ter Retention Characteristics of Soils,” European Journal
of Soil Science, Vol. 59, No. 2, 2008, pp. 339-347.
doi:10.1111/j.1365-2389.2007.01002.x
[2] O. Vigiak, S. J. E. van Dijck, E. E. van Loon and L.
Stroosnijder, “Matching Hydrologic Response to Meas-
ured Effective Hydraulic Conductivity,” Hydrological Pro-
cesses, Vol. 20, No. 3, 2006, pp. 487-504.
doi:10.1002/hyp.5916
[3] J. H. M. Wösten, Y. A. Pachepsky and W. J. Rawles,
“Pedotransfer Functions: Bridging the Gap between Avail-
able Basic Soil Data and Missing Soil Hydraulic Charac-
teristics,” Journal of Hydrology, Vol. 251, No. 3-4, 2001,
pp. 123-150. doi:10.1016/S0022-1694(01)00464-4
[4] S. R. Evett and R. J. Lascano, “ENWATBAL.BAS: A
Mechanistic Evapotranspiration Model Written in Com-
piled Basic,” Agronomy Journal, Vol. 85, No. 3, 1993, pp.
763-772.
doi:10.2134/agronj1993.00021962008500030044x
[5] R. J. Lascano, “A General System to Measure and Calcu-
late Daily Crop Water Use,” Agronomy Journal, Vol. 92,
No. 5, 2000, pp. 821-832.
doi:10.2134/agronj2000.925821x
[6] J. Šimünek, M. Šejna and M. T. van Genuchten, “The
Hydrus-2D Software Package for Simulating the Two-
Dimensional Movement of Water, Heat, and Multiple
Solutes in Variably-Saturated Media. IGWMC-TPS 53-
251 v. 2.0,” Colorado School of Mines International,
Ground Water Modeling Center Golden, Colorado, 1999.
[7] D. E. Radcliffe and J. Šimünek, “Soil Physics with HY-
DRUS Modeling and Applications,” CRC Press, Boca
Raton, 2010.
[8] C. C. Molling, “Precision Agricultural-Landscape Model-
ing System. Version 5. Combined User’s and Developer’s
Manual,” University of Wisconsin Board of Regents, Wis-
consin, 2008.
[9] C. C. Molling, J. C. Strikwerda, J. N. Norman, C. A.
Rodgers, R. Wayne, C. L. S. Morgan, G. R. Diak and J. R.
Mecikalski, “Distributed Runoff Formulation Designed
for a Precision Agricultural Landscape Modeling Sys-
tem,” Journal of the American Water Resources Associa-
tion, Vol. 41, No. 6, 2005, pp. 1289-1313.
doi:10.1111/j.1752-1688.2005.tb03801.x
[10] C. L. S. Morgan, “Quantifying Soil Morphological Prop-
erties for Landscape Management Applications,” Ph.D.
Dissertation, University of Wisconsin-Madison, Wiscon-
sin, 2003.
[11] H. Aksoy and M. L. Kavvas, “A Review of Hillslope and
Watershed Scale Erosion and Sediment Transport Mod-
els,” Catena, Vol. 64, No. 2-3, 2005, pp. 247-271.
doi:10.1016/j.catena.2005.08.008
[12] M. G. Schaap and F. J. Leij, “Using Neural Networks to
Predict Soil Water Retention and Soil Hydraulic Conduc-
tivity,” Soil and Tillage Research, Vol. 47, No. 1-2, 1998,
pp. 37-42. doi:10.1016/S0167-1987(98)00070-1
[13] W. Aimrun and M. S. M. Amin, “Pedo-Transfer Function
for Saturated Hydraulic Conductivity of Lowland Paddy
Soils,” Paddy Water Environment, Vol. 7, No. 3, 2009,
pp. 217-225. doi:10.1007/s10333-009-0165-y
[14] M. G. Schaap, F. J. Leij and M. T. van Genuchten, “Rosetta:
A Computer Program for Estimating Soil Hydraulic Pa-
rameters with Hierarchical Pedotransfer Functions,” Jour-
nal of Hydrology, Vol. 251, No. 3-4, 2001, pp. 163-176.
doi:10.1016/S0022-1694(01)00466-8
[15] L. Stroosnijder, “Measurement of Erosion: Is It Possi-
ble?” Catena, Vol. 64, No. 2-3, 2005, pp. 162-173.
doi:10.1016/j.catena.2005.08.004
[16] W. J. Rawles and D. L. Brakensiek, “Estimating Soil-
Water Retention from Soil Properties,” Journal of the Ir-
rigation and Drainage Division, Vol. 108, No. 2, 1982, pp.
166-171.
[17] A. B. McBratney, B. Minasny, S. R. Cattle and R. W.
Vervoort, “From Pedotransfer Functions to Soil Inference
Systems,” Geoderma, Vol. 109, No. 1-2, 2002, pp. 41-73.
doi:10.1016/S0016-7061(02)00139-8
[18] Y. Pachepsky, D. E. Radcliffe and H. M. Selim, “Scaling
Methods in Soil Physics,” CRC Press, New York, 2003.
[19] K. Parasuraman, A. Elshorbagy and B. C. Si, “Estimating
Saturated Hydraulic Conductivity in Spatially Variable
Fields Using Neural Network Ensembles,” Soil Science
Society of America Journal, Vol. 70, No. 6, 2006, pp.
1851-1859. doi:10.2136/sssaj2006.0045
[20] C. Gülser and F. Candemir, “Prediction of Saturated Hy-
draulic Conductivity Using Some Moisture Constants and
Soil Physical Properties,” Proceeding Balwois, Ohrid, 31
May 2008.
[21] R. Muñoz-Carpena, C. M. Regalado, J. Alvarez-Benedi
and F. Bartoli, “Field Evaluation of the New Philip-
Dunne Permeameter for Measuring Saturated Hydraulic
Conductivity,” Soil Science, Vol. 167, No. 1, 2002, pp. 9-
24. doi:10.1097/00010694-200201000-00002
[22] M. Mbonimpa, M. Aubertin, R. P. Chapuis and B. Bus-
sière, “Practical Pedotransfer Functions for Estimating the
Saturated Hydraulic Conductivity,” Geotechnical and Geo-
logical Engineering, Vol. 20, 2002, pp. 235-259.
doi:10.1023/A:1016046214724
[23] K. Kobayashi and M. U. Salam, “Comparing Simulated
and Measured Values Using Mean Squared Deviation and
Its Components,” Agronomy Journal, Vol. 92, No. 2, 2000,
pp. 345-352. doi:10.2134/agronj2000.922345x
[24] D. N. Moriasi, J. G. Arnold, M. W. Van Liew, R. L.
Bingner, R. D. Harmel and T. L. Veith, “Model Evalua-
tion Guidelines for Systematic Quantification of Accu-
racy in Watershed Simulations,” Transactions of the
ASABE, Vol. 50, No. 3, 2007, pp. 885-900.
[25] P. D. Colaizzi, P. H. Gowda, T. H. Marek and D. O. Por-

Test of the Rosetta Pedotransfer Function for Saturated Hydraulic Conductivity 212
ter, “Irrigation in the Texas High Plains: A Brief History
and Potential Reductions in Demand,” Irrigation and
Drainage, Vol. 58, No. 3, 2009, pp. 257-274.
doi:10.1002/ird.418
[26] NRCS, “Official Series Description,” 2008.
http://www2.ftw.nrcs.usda.gov/osd/dat/A/ACUFF.html
[27] C. Stumpp, S. Engelhardt, M. Hofmann and B. Huwe,
“Evaluation of Pedotransfer Functions for Estimating Soil
Hydraulic Properties of Prevalent Soils in a Catchment of
the Bavarian Alps,” European Journal of Forest Re-
search, Vol. 128, No. 6, 2009, pp. 609-620.
doi:10.1007/s10342-008-0241-7
[28] Y. Mualem, “New Model Evaluation Guidelines for Sys-
tematic Quantification of Accuracy in Watershed Simula-
tions,” Water Resources Research, Vol. 12, No. 3, 1976,
pp. 513-522. doi:10.1029/WR012i003p00513
[29] M. T. van Genuchten, “A Closed-Form Equation for Pre-
dicting the Hydraulic Conductivity of Unsaturated Soils,”
Soil Science Society American Journal, Vol. 44, No. 5,
1980, pp. 892-898.
doi:10.2136/sssaj1980.03615995004400050002x
[30] G. J. Bouyoucos, “Hydrometer Method Improved for Mak-
ing Particle Size Analyses of Soils,” Agronomy Journal,
Vol. 54, No. 5, 1962, pp. 464-465.
doi:10.2134/agronj1962.00021962005400050028x
[31] A. Klute, R. C. Dinauer, A. L. Page, R. H. Miller and D.
R. Keeney, “Methods of Soil Analysis. Part 1. Physical
and Mineralogical Methods,” Soil Science Society of Amer-
ica, Madison, 1986.
[32] Eijkelkamp, “Laboratory Permeameter. Operating Instruc-
tions,” 2008.
http://www.eijkelkamp.com/Portals/2/Eijkelkamp/Files/
Manals/M10902e%20Laboratory%20permeameters.pdf
[33] Eijkelkamp, “Sand/Kaolin Box,” 2005.
http://www.eijkelkamp.com/Portals/2/Eijkelkamp/Files/
Manuals/M10802e%20Sand%20kaolin%20box.pdf
[34] Eijkelkamp, “Pressure Membrane Apparatus,” 2005.
http://www.eijkelkamp.com/Portals/2/Eijkelkamp/Files/
Manuals/M10803e%20Pressure%20membrane.pdf