Int. J. Communications, Network and System Sciences, 2010, 3, 602-607
doi:10.4236/ijcns.2010.37080 Published Online July 2010 (http://www.SciRP.org/journal/ijcns/).
Using Bayesian Game Model for Intrusion Detection
in Wireless Ad Hoc Networks
Hua Wei, Hao Sun
Department of Applied Mathematics, Northwestern Polytechnical University, Xi'an, China
Received April 12, 2010; revised May 15, 2010; accepted June 22, 2010
Abstract
Wireless ad hoc network is becoming a new research fronter, in which security is an important issue. Usually
some nodes act maliciously and they are able to do different kinds of Denial of Service (Dos). Because of the
limited resource, intrusion detection system (IDS) runs all the time to detect intrusion of the attacker which is
a costly overhead. We use game theory to model the interactions between the intrusion detection system and
the attacker, and a realistic model is given by using Bayesian game. We solve the game by finding the
Bayesian Nash equilibrium. The results of our analysis show that the IDS could work intermittently without
compromising its effectiveness. At the end of this paper, we provide an experiment to verify the rationality
and effectiveness of the proposed model.
Keywords: Wireless Ad Hoc Networks, Game Theory, Intrusion Detection System, Bayesian Nash Equilibrium
1. Introduction
A wireless ad hoc network (WANET) is a collection of
mobile nodes in which the nodes communicate with each
other without the help of any fixed infrastructure [1].
Nodes within each other's radio range communicate di-
rectly via wireless links, while those that are far apart use
other nodes as relays. Because of the limited resource,
some nodes may act selfishness. Ad hoc network misbe-
havior maybe inflicted by malicious nodes, each of
which aims at harming the network operation; conse-
quently, mechanisms that enforce security present a par-
ticular challenge. In order to avoid the harm of malicious
nodes, one way is the use of an intrusion detection sys-
tem, which watches out for any intrusion and sets out an
alarm when an intrusion is detected. The intrusion detec-
tion and response mechanism is described in [2].
In recent years, we have seen researchers using game
theory in the area of ad hoc networks. It is a powerful
tool in that it can be used to model any system which
exhibits the characteristics of a game. In WANET, mo-
bile nodes typically have selfish motivations, lack of
cooperation among themselves, and have conflicting
interests with each other. These characteristics make
game theory (GT) a promising tool to model, analyze,
and design various aspects of WANET. We have given a
two-player game to model the interactions between an
intrusion detection system and an attacker in wireless ad
hoc network. Each defender is equipped with an intru-
sion detection system (IDS) in order to monitor the ac-
tiveness of an attacker.
The rest of the paper is organized as follows. Section 2
discusses related work. Section 3 describes the one-stage
game and multi-stage game, and Bayesian Nash equilib-
rium solutions are investigated. Section 4 presents nu-
merical examples to verify the effectiveness of the pro-
posed game. The conclusion of the paper is in section 5.
2. Related Work
Game theory has been successfully applied to many dis-
ciplines including economics, political science, and com-
puter science. Game theory usually considers a multi-
player decision problem where multiple players with
different objectives can compete and interact with each
other. In the context of intrusion detection, several game
theoretic approaches have been proposed to wired net-
works, sensor networks, and ad hoc networks.
Yenumula B. Reddy [3] discuss currently available
intrusion detection techniques, attack models using game
theory, and then propose a new framework to detect ma-
licious nodes in wireless sensor networks using zero sum
game approach for nodes in the forward data path. The
first part of the research provides the game model with
probability of energy required for transferring the data
packets. The second part derives the model to detect the
malicious nodes using probability of acknowledgement
at source. Yuhan Moon, Violet R. Syrotiuk [4] present
CCM-MAC, a cooperative CDMA-based multi-channel

H. WEI ET AL.603
medium access control (MAC) protocol for mobile ad
hoc networks (MANET) in which each node has one
half- duplex transceiver. They provide an analysis of the
maximum throughput of CCM-MAC and validate it
through simulation in MATLAB, and also compare the
throughput it achieves to IEEE 802.11, a multi-channel
MAC protocol, and a CDMA-based MAC protocol.
In [4] Hadi Otrok et al. address the problem of in-
creasing the effectiveness of an intrusion detection sys-
tem (IDS) for a cluster of nodes in ad hoc networks, and
formulate a zero-sum non-cooperative game between the
leader and intruder. They solve the game by finding the
Bayesian Nash equilibrium where the leader’s optimal
detection strategy is determined. Finally, empirical re-
sults are provided to support their solutions.
Yu Liu, Cristina Comaniciu and Hong Man [5] have
used static Bayesian game and dynamic Bayesian game
to model the interactions between attacker and defender
in ad hoc networks. They have shown that the static
game leads to a mixed-strategy Bayesian nash equilib-
rium when the defender’s belief of the attacker being
malicious is high, and the dynamic game has a mixed-
strategy Perfect bayesian equilibrium. In [6], they have
used game theory for developing efficient defense strate-
gies for a network with multiple IDSs. They have for-
mulated a non-zero-sum, noncooperative attacker/de-
fender game where the payoffs of players are non-strictly
competitive. They have showed that the game achieves at
least a Nash equilibrium that leads to a defense strategy
for the defender.
A two-player, non-cooperative, non-zero-sum game
has also been studied by Agah et al. [7] and Alpan and
Basar [8] to address attack-defense problems in sensor
networks. In their models, each player’s optimal strategy
depends only on the payoff function of the opponent and
the game is assumed to have complete information. [9-11]
have given the similar model, but the game is assumed to
have incomplete information.
Our model is similar to the ones mentioned in the
aforementioned works in that it is a two-player, non-
zero-sum and noncooperative game. However, our work
is not aimed at giving the best strategy of the defender.
In this paper, we have given a one-stage game and
multi-stage game. In the proposed works, the IDS of de-
fender runs all the time, which is a costly overhead for a
battery-powered mobile device since nodes have limited
resource. The results of our model show that the IDS
could work intermittently.
3. Bayesian Game
3.1. Game Model
In this section we present our game model. An IDS at-
tempts to detect intrusion from an attacker. Hence, we
may look at this as a game between two players, the IDS
and the attacker. The attacker is denoted by and IDS
is denoted by . The player ’s intent is to attack the
network without getting caught, whereas that of the
player is to detect intrusion when the attacker attacks.
There is no cooperation whatsoever between the two
players.
i
j i
j
Player has two types, regular that is denoted by
i
0
i


and malicious is denoted by 1
i

. Node’s type
is his private information and IDS is uncertain about its
opponent’s type. IDS has only one type, that is regular or
0
j


and it is common knowledge for both players.
To present our model, we make the following assump-
tions. An IDS needs not be running all the time during
which the wireless ad hoc network is up. The pure strat-
egy space of this player is denoted by
j
S= (Monitor t of
the time, Not monitor),


0, 1t
t
. The first strategy of
player depicts the situation when the IDS is active
for some percentage (denoted by ). For example, if the
IDS detects by monitoring the traffic, the IDS periodi-
cally monitors the traffic and the rest of the time, it sits
idle. Likewise, an attacker need not be trying to attack
100% of the time. The malicious type of player has
two pure strategies: Attack s of the time and Not attack,
j
i


0,s1. The regular type of player has one pure
strategy: Not attack. The two players choose their strate-
gies simultaneously at the beginning of the game, assum-
ing common knowledge about the game (costs and beliefs).
i
We first consider the scenario of the IDS. Tables 1-2
illustrate the payoff matrix of the game in strategic form.
In the matrix, represents the detection rate of the IDS,
represents the false alarm rate of the IDS, and
a
b


,0,1ab . In the Table 1(a), the payoff matrix for the
Table 1. The type of player is malicious. i
(a) Payoff matrix of IDS.
\ij (1) i
S (1)
i
S
(1)
i
S (21)(1 )d atsm tsltc
s
l

(2)
i
S d btn tc 0
(b) Payoff matrix of attacker.
\ ij (1) i
S (1)
i
S
(1)
i
S (12 )(1)a atsmtsl sc a
s
lsc
(2)
i
S 0 0
Table 2. The type of player is regular. i
\ij (1)
i
S (1)
i
S
(2)
i
S (0, )
d
btn tc (0, 0)

H. WEI ET AL. 604
player when player is malicious is given. m
denotes the overall gain of the player for detecting
the attack, and is the overall loss for not detecting the
attack during the whole lifetime. Costs of attacking and
monitoring are denoted by and during the
whole period. In our model, we assume that and
is reasonable since otherwise the player
does not have incentive to attack and the player does
not have incentive to monitor. The player monitors
t
of the time, the player attacks s of the time. The
probability of the player monitoring when the attack
is on is , during which the player gets a gain of
. Similarly, the probability of the player not
monitoring when the attack occurs is because of
which the player j loses an amount of . is
the cost incurred due to monitoring. The expected payoff
j
d
c
ts
i
i
j
i
d
c
j
)t
(1 
l
a
c
ml
j
j
)tsl tc
,a lc
tsm
i
j
s(1
d
of detecting the attack depends on the value of , which
is . When the player is not
active and there is an attack, so the payoff of the player
is
a
j(21)(1 )d atsm tsltc
j
s
l
d
btn tc n
i
. The entry at position (row 2, column 1) is
. is the overall loss incurred by the player
for the false detection. The rest of the entry of the
matrix is zero as the player plays Not attack.
j
The payoff matrix for the player when the player
is malicious is defined as shown in Table 1(b). In
contrast, the gain of player i is the loss of player ,
which is (1 – 2a)tsm + (1 – t)sl. The entry at (row 1.
column 2) is the same as in previous scenario. For the
other entries, when the player plays (Not at-
tack), his payoff is always .
i
i
j
i(2)
i
S
0
The payoff matrix for the player when it is regular
is given in Table 2. The player has only one strategy
when it is regular. The payoff of player i is always 0. If
player i ecides not to monitor, his payoff is 0; if he
decides to play Sj (1), he has the monitoring cost
and an expected loss due to the false alarm, so his
payoff is .
i
i
d
d
tc
btn
d
btn tc
3.2. One-Stage Game
The intent of both players is to maximize their own pay-
off. This implies that we assume that both players are
rational. Suppose player assigns a prior probability j
0

to player i is malicious. In the following, we use
Bayesian Nash equilibrium (BNE) to analyze the game
model, based on the assumption that is a common prior.
If player plays his pure strategy pair (Attack s of
the time if malicious, Not attack if regular), then the ex-
pected payoff of player is
i
j
0
((1))((1 )(1))
j
jd
ESatatsmtsltcsm


 
0
(1 )()


d
btntc

0
2))ES sl((
jj


So if 02
d
c
sl
bn
asm smbn




 , ,
then the best strategy of player is to play Monitor t of
the time. However, if player plays this strategy, At-
tack s of the time will not be the best strategy if player
is malicious, and he will transfer to play Not attack in-
stead. Hence, ((Attack s of the time if malicious, Not
attack if regular), Monitor t of the time,
((1)) ((2))
jj jj
ES ES
i
0
j
j

) is not a
BNE. If 02
d
c
m
bn
asm ssl

bn

 , ((Attack s of the time
if malicious, Not attack if regular), Not monitor, 0

) is
a BNE. Similarly, ((Not attack s of the time if malicious,
Not attack if regular), Not monitor, 0

) is not a BNE.
THEOREM 1: In the described game-theoretic model,
there is no pure-strategy BNE when 0

satisfies the
inequality
02
d
bn c
asm sm sl bn


.
We previously showed that no pure-strategy BNE ex-
ists for the game when 02
d
bn c
asm sm sl bn


. But
there is a mixed-strategy BNE.
Let be the probability with which the player
plays its first strategy. Hence, is the probability
with which it plays the second strategy. Similarly, let
be the probability with which the player plays its
first strategy. Hence, (1
p i
q
(1 )p
j
)q

is the probability with
which it plays the second strategy. Then the expected
payoff of player is
j
0
((1))((1 )(1))
j
jd
ESpaa tsmtsltctsm


 
00
(1)( )(1)( )

tc 
dd
pbtnbtn tc


0
2))ESpsl((
jj


From ((1)) (2))
jj
ES E(
jj
S

, we get that the malicious
type of player ’s equilibrium strategy is to play first
strategy with probability
i
*
0(2asm )
d
bn c
psm sl bn


 .
and the expected payoff of player is
i
((1))((1)(1 ))
ii a
ESq atsmatsmtsltc


(1 )()


a
qsl sc
((2)) 0
ii ES

H. WEI ET AL.605
From , we get that the equilib-
rium strategy of player is to play first strategy with
probability
((1))((2))
ii ii
ES ES
j
*
2
a
lc
qatmtm tl



.
THEOREM 2: In the described game-theoretic model,
the strategy pair ((Attack s of the time with probability
if malicious, Not attack if regular), Monitor t of
the time with probability ,
*
p
*
q0

) is a mixed-strategy
BNE.
The above described game is a static game, for which
the players maximize their utilities based on the payoff
matrix for the game. Due to the difficulty of assigning
accurate prior probabilities for player i’s type, we extend
the static to dynamic game, where the player j can update
his beliefs according to the Bayes’ rule.
3.3. Multi-Stage Game
The aforesaid one-stage game is static Bayesian game,
for which the player maximizes his payoff based on
a fixed prior about the maliciousness of his opponent.
The lifetime of the network could be broken down into
intervals of the time and our game could be used as a
repeated game over these intervals. So, we extend the
one-stage game to multi-stage game.
j
We assume that the one-stage game is repeatedly
played in each time period , where k = 0, 1, … An
interval of T seconds maybe selected for each stage game.
In order to get a simple model, we assume that T = 1.
The payoffs of the players in each stage game are the
same as in the proceeding one-stage game, and we as-
sume that there is no discount factor with respect to the
payoffs of the players. The extensive form of each stage
game can be represented in a similar manner as for the
static one-stage game.
k
t
In our model, the player 's type is known to all the
player while the player 's type is selected from the type
set ={malicious, regular}. Knowing that the player
's type is a private information. Bayesian equilibrium
[12] dictates that the player 's action depends on his
type
j
i
i

i

. By observing the behavior of the player , the
player can calculate the posterior belief evaluation
function
i
j
1(())
k
k
tii
at 
 using the following Bayes' rule
(())(())
(()) (())(()
k
k
k
i
ti ikiki
tiik
ti ikiki
at Pat
at at Pat

 

)



 (1)
where (())
k
tiik
at  0 and (() )
ik i
Pa t

is the prob-
ability that strategy is observed at this stage of
the game given the type
()
ik
at

of the player . From the
assumption of described game, we know that
i
(()1)( )
ik i
P atAttackapb  1p

 
(() 1)(1)a
ik i
PatNot Attackp  
(1 )(1)

bp
(() 0)
ik i
Pa tAttacka 


(() 0)1
ik i
PatNot Attackb 


LEMMA 1: the multi-stage game satisfies the four
Bayesian conditions (1)-(4).
1) Posterior beliefs are independent, and all types of
player have the same beliefs, and even unexpected
events will not change the independence assumption for
the type of the opponents.
j
2) Bayes’rule is used to update beliefs from
(()
k
tiik
at  ) to 11 (()
k
tiik
at 
) whenever possible.
3) The players do not signal what they do not know.
4) All players must have the same belief about the type
of another player.
Proof: condition (1) is trivially satisfied because
player has only one type. We can see that the multi-
stage game satisfies (2) from Equation (1). In our multi-
stage game context, player 's signal is part of attack
actions, thus (3) is satisfied. Because there are only two
players in the game at any stage, the condition (4) is sat-
isfied.
j
i
THEOREM 3: The multi-stage game has a perfect
Bayesian equilibrium (PBE).
At stage game , duo to the updated belief
k
t()


, the
probability p

is also updated continuously. From the
previous analysis of section 3.2, the malicious type of
player 's equilibrium strategy is to play his first strat-
egy with probability
i
()(2 )
d
bnc
pasm sm sl bn


 (2)
the equilibrium strategy of player is to play his
first strategy with probability
j
2
a
lc
qatm tm tl

 (3)
So the PBE of the game is given as (,,())pq 


,
with (,,())pq 


given by Equations (1)-(3).
4. Example
For each experiment, we assume that 1000ml

,
100n

. Figures 1 and 2 assume , 0.85 0.85ts 

,
5
d
c

, Figure 3 assumes , , 0.85t5
d
c0.9a

,
0.02b

, and Figure 4 assumes , 0.9s0.9t

,
0.95a

, 0.14b

. Figure 5 assumes , 0.9s0.5t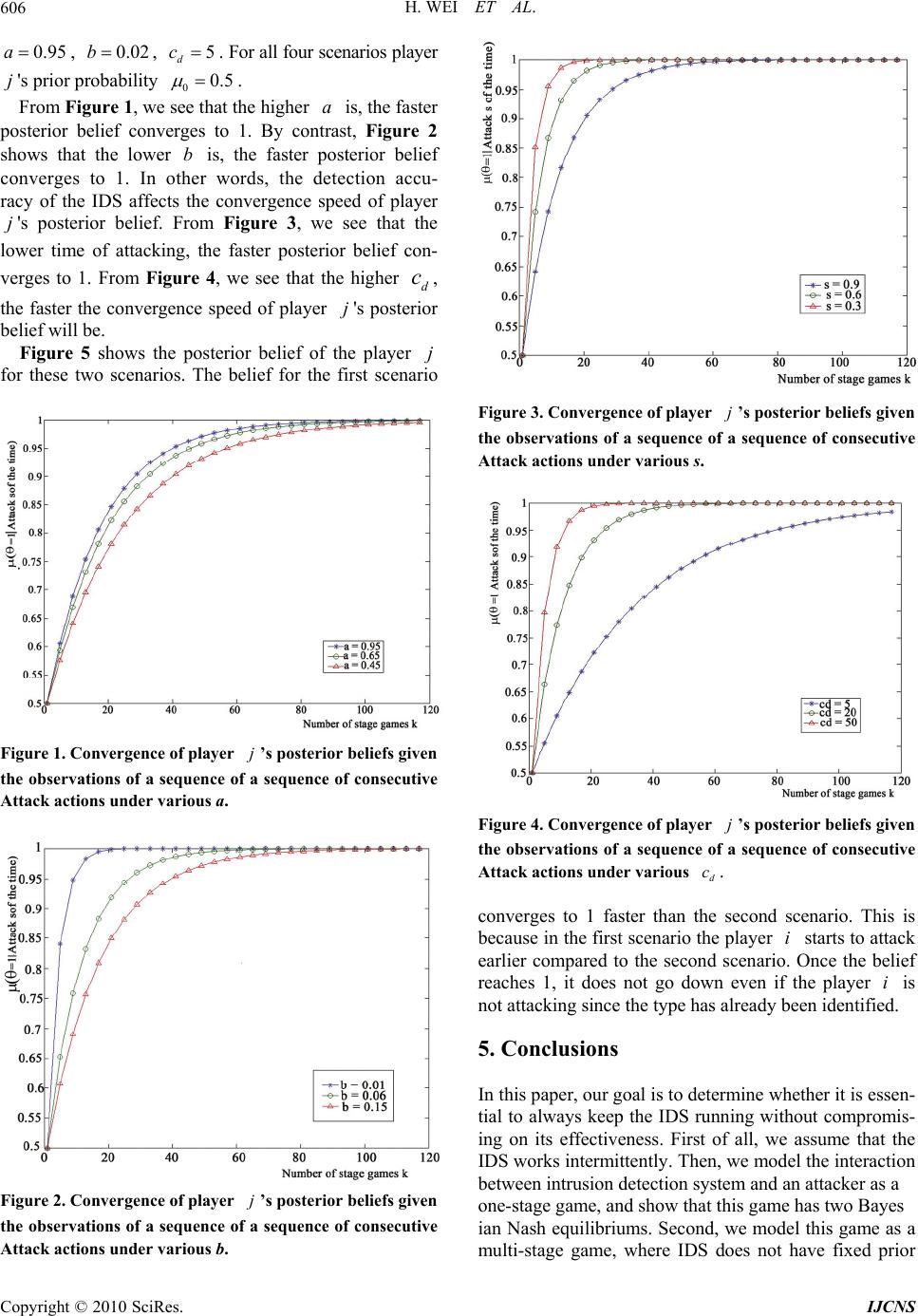

,

H. WEI ET AL. 606
0.95a
j
, , . For all four scenarios player
's prior probability
0.02b5
d
c
00.5


b
.
From Figure 1, we see that the higher is, the faster
posterior belief converges to 1. By contrast, Figure 2
shows that the lower is, the faster posterior belief
converges to 1. In other words, the detection accu-
a
racy of the IDS affects the convergence speed of player
's posterior belief. From Figure 3, we see that the
lower time of attacking, the faster posterior belief con-
verges to 1. From Figure 4, we see that the higher ,
j
d
c
the faster the convergence speed of player 's posterior
belief will be.
j
Figure 5 shows the posterior belief of the player
for these two scenarios. The belief for the first scenario
j
Figure 1. Convergence of player
j
’s posterior beliefs given
the observations of a sequence of a sequence of consecutive
Attack actions under various a.
Figure 2. Convergence of player
j
’s posterior beliefs given
the observations of a sequence of a sequence of consecutive
Attack actions under various b.
Figure 3. Convergence of player
j
’s posterior beliefs given
the observations of a sequence of a sequence of consecutive
Attack actions under various s.
Figure 4. Convergence of player
j
’s posterior beliefs given
the observations of a sequence of a sequence of consecutive
Attack actions under various .
d
c
converges to 1 faster than the second scenario. This is
because in the first scenario the player starts to attack
earlier compared to the second scenario. Once the belief
reaches 1, it does not go down even if the player is
not attacking since the type has already been identified.
i
i
5. Conclusions
In this paper, our goal is to determine whether it is essen-
tial to always keep the IDS running without compromis-
ing on its effectiveness. First of all, we assume that the
IDS works intermittently. Then, we model the interaction
between intrusion detection system and an attacker as a
one-stage game, and show that this game has two Bayes
ian Nash equilibriums. Second, we model this game as a
multi-stage game, where IDS does not have fixed prior

H. WEI ET AL. 607
Figure 5. Posterior belief.
probabilities about the type of its opponent and can up-
date its belief at the end of each stage of the game, and
show that this game has a mixed-strategy perfect Bayes-
ian equilibrium. The results of the proposed two games
show that IDS could work intermittently while getting
the same effectiveness.
6. Acknowledgements
The paper is supported by the National Natural Science
Foundation of China under Grant Nos.70871098 and
70901063.
7
. References
[1] R. Ramanathan and J. Redi, “A Brief Overview of Ad
Hoc Networks: Challenges and Directions,” IEEE Com-
munications Magzine, Vol. 40, No. 5, 2002, pp. 20-22.
[2] Y. G. Zhang and W. Lee, “Intrusion Detection in Wire-
less Ad-Hoc Networks,” Proceedings of the 6
th Annual
International Conference on Mobile Computing and Net-
working, Boston, 2000, pp. 275-283.
[3] Y. B. Reddy, “A Game Theory Approach to Detection
Mmalicious Nodes in Wireless Sensor Networks,” Pro-
ceedings of the 2009 Third International Conference on
Sensor Technologies and Applications, Athens, June
18-23, 2009, pp. 462-468.
[4] H. Otrok, N. Mohammed, L. Y. Wang, M. Debbabi and P.
Bhattacharya, “A Game-Theoretical Intrusion Detection
Model for Mobile Ad Hoc Networks,” Computer Com-
munications, Vol. 31, No. 4, 2008, pp. 708-721.
[5] Y. Liu, C. Comaniciu and H. Man, “A Bayesian Game
Approach for Intrusion Detetion in Wireless Ad Hoc
Networks,” Proceedings from the 2006 Workshop on
Game Theory for Communications and Networks, Pisa,
Italy, October 14, 2006, pp. 1-12.
[6] Y. Liu, H. Man and C. Comaniciu, “A Game Theoretic
Approach to Efficient Mixed Strategies for Intrusion De-
tection,” IEEE International Conference on Communica-
tions, Istanbul, 2006, pp. 2201-2206.
[7] A. Agah, S. K. Das, K. Basu and M. Asadi, “Intrusion
Detection in Sensor Networks: A Non-Cooperative Game
Approach,” Proceedings of the Third IEEE International
Symposium on Network Computing and Applications,
Boston, August-September 2004, pp. 343-346.
[8] T. Alpcan and T. Basar, “A Game Theoretic Approach to
Decision and Analysis in Network Intrusion Detection,”
Proceedings of the 42nd IEEE Conference on Decision
and Control, Maui, Hawaii, December 2003, pp. 2595-
2600.
[9] N. Marchang and R. Tripathi, “A Game Theoretical Ap-
proach for Efficient Deployment of Intrusion Detection
System in Mobile Ad Hoc Networks,” Proceedings of the
15th International Conference on Advanced Computing
and Communications, Guwahati, 2007, pp. 460-464.
[10] T. Poongothai and K. Jayara, “A Noncooperative Game
Approach for Intrusion Detection in Mobile Ad Hoc
Networks,” Proceedings of the 2008 International Con-
ference on Computing Communication and Networking,
St. Thomas, VI, December 18-20, 2008, pp. 1-4.
[11] A. Patcha and J.-M. Park, “A Game Theoretic Approach
to Modeling Intrusion Detection in Mobile Ad Hoc Net-
works,” Proceedings of the 2004 IEEE Workshop on In-
formation Assurance and Security, United States Military
Academy, West Point, NY, June 10-11, 2004, pp. 30-34.
[12] M. Willem, “Minimax Theorem,” Birkhauser, Boston,
1996.