Int. J. Communications, Network and System Sciences, 2012, 5, 557-568
http://dx.doi.org/10.4236/ijcns.2012.59066 Published Online September 2012 (http://www.SciRP.org/journal/ijcns)
Majority Voting Procedure Allowing Soft Decision
Decoding of Linear Block Codes on Binary Channels
Saïd Nouh, Achraf El Khatabi, Mostafa Belkasmi
SIME Lab, National School of Computer Science and Systems Analysis (ENSIAS),
Mohammed V Souissi University, Rabat, Morocco
Received July 3, 2012; revised July 30, 2012; accepted August 7, 2012
ABSTRACT
In this paper we present an efficient algorithm to decode linear block codes on binary channels. The main idea consists
in using a vote procedure in order to elaborate artificial reliabilities of the binary received word and to present the ob-
tained real vector r as inputs of a SIHO decoder (Soft In/Hard Out). The goal of the latter is to try to find the closest
codeword to r in terms of the Euclidean distance. A comparison of the proposed algorithm over the AWGN channel
with the Majority logic decoder, Berlekamp-Massey, Bit Flipping, Hartman-Rudolf algorithms and others show that it is
more efficient in terms of performance. The complexity of the proposed decoder depends on the weight of the error to
decode, on the code structure and also on the used SIHO decoder.
Keywords: Error Correcting Codes; Genetic Algorithms; HIHO Decoder; SIHO Decoder; Vote Procedure
1. Introduction
The current large development and deployment of wire-
less and digital communication encourages the research
activities in the field of error correcting codes. Codes are
used to improve the reliability of data transmitted over
communication channels susceptible to noise. Coding
techniques create codewords by adding redundant infor-
mation to the user information.
There are two classes of error correcting codes: con-
volutional codes and block codes. The class of block
codes contains two subclasses: nonlinear codes and linear
codes. The principle of a block code C(n, k) is as follows:
the initial message is cut out into blocks of length k. The
length of the redundancy is n – k and thus the length of
transmitted blocks is n. The main block codes are linear.
If the code C is linear then the code C(n, n – k) defined
by (1) is also linear with “.” denotes the scalar (dot)
product.
:0hC cCch

  (1)
The code C is called the dual code of C and each
equation of the form given by (1) is called an orthogonal
equation or a parity check equation.
There are two categories of decoding algorithms: Hard
decision and Soft decision algorithms. Hard decision
algorithms work on the binary form of the received in-
formation and generally they use the Hamming distance
as a metric to minimize [1]. In contrast, soft decision
algorithms work directly on the received symbols and
generally they use the Euclidian distance as a metric to
minimize [1].
The decoding category depends on the industrial re-
quests and the communication channel. When the chan-
nel allows to measure the reliabilities iin (float sym-
bols) of the sequence r of length n to decode the soft de-
cision decoders working on these reliabilities allow to
win generally about 2 dB more than the hard decision
decoders working on the binary form of r can do. This
difference between soft and hard decision decoders is
justified by the proportionality between each reliability
r
and the probability that the symbol rj is correct.
i
r
Even if the soft decision decoders are more efficient
than the hard decision decoders these latest are still an
interesting subject for many scientists and industries
thanks to their advantages. Some of those latest are listed
below:
 When only the binary form of the received word is
available as in the storage systems, the use of hard
decision decoders becomes the only solution.
 In [2] we have given an efficient method to find the
weight enumerator of a code which requires the use
of a hard decision decoder.
 If a code can be efficiently decoded by a hard deci-
sion decoder then an efficient soft decoding algorithm
of this code can be obtained by the Chasing technique
described in [3].
 Some cryptographic systems use hard decoders to
extract a noise added explicitly during the emission
C
opyright © 2012 SciRes. IJCNS

S. NOUH ET AL.
558
phase in order to decrypt the message.
The hard decision decoding problem is in general
NP-Hard. The wealth of the algebraic structure of some
codes allows simplifying this hardness as in the BCH
codes [4,5]. The famous permutation decoding algorithm
[6] is a generic decoder, applicable to all systematic
codes but it requires finding a PD-Set which is also a
NP-Hard problem [7]. Another generic decoder of linear
block codes is the Bit Flipping decoding algorithm (BF)
based on the verification of orthogonal equations which
was developed firstly for LDPC codes [8] and it is gen-
eralized thereafter for linear block codes but without en-
suring good error correcting performances [9].
In [10,11], the authors have applied artificial intelli-
gence to solve the decoding problem by genetic algo-
rithms in [10] and by neural networks in [11]. However
the authors of [12] have used a mathematical approach
based on Coset Decomposition and syndrome decoding.
On the other side the authors of [13] and [14] have
proposed a low complexity soft-Input Soft-Output mod-
ule to decode convolutional codes. They use classical
Viterbi algorithm and a module for computing softoutput
from the hard output of the Viterbi algorithm.
The purpose of this work is to find a generic efficient
hard decision decoding algorithm of linear block codes
by combining a vote procedure with a soft decision de-
coding. Majority voting procedure is done by a module
prior a soft decision decoder. Thus the efficiency of soft
decision decoding algorithms becomes exploitable in the
case of binary channels by creation of artificial reliabil-
ities with a vote using a reduced number of orthogonal
equations.
In the rest of this paper C(n, k, d) designate a linear
code of length n, dimension k, minimum distance d, error
correcting capability t, generated by a matrix G and it can
be checked by a matrix H and we note and
respectively the Hamming and the Euclidean
distance between two vectors x and y.

,dHx y

,dEx y
The remainder of this paper is structured as follows. In
Section 2 we present some decoding algorithms as re-
lated works. In Section 3 we present the proposed de-
coder and we make a comparison with other decoders.
Finally, a conclusion and a possible future direction of
this research are outlined in Section 4.
2. Related Works
In this section we present some hard decision decoding
algorithms with which we will compare our proposed
decoding scheme in the next section.
2.1. The Bit Flipping (BF) Decoding Algorithm
The matrix H has n columns and n – k rows or more, let
V be a vector of length n and h a binary word to decode.
The BF algorithm uses the following vote algorithm:
2
.1.1. The Vote Algorithm
Inputs:
- L a list a dual codewords (LC)
- M the number of dual codewords to use
- V a vector of length n.
- h a binary word of length n.
Outputs: V
Begin
for i from 1 to n do Vi0; end for;
for i from 1 to M do
u  ith element of L.
if (u.h≠0) then for i from 1 to n do
if (u
i=1) then VjVj+1;
end for;
end for;
End;
We have observed that when the vote is efficient, the
noised bits hi have a big value of votes Vi.
2.1.2. The Gallager’s Bit-Flipping Algorithm
The Gallager’s bit flipping algorithm [8] works as fol-
ow: l
Inputs:
- L: a list a dual codewords (LC)
- iter_max: the maximum number of iterations
- threshold: the number of failed parity check equations to
have for flipping.
- h: the received word.
Outputs: the decoded word h.
Begin
Continue true;
iter0;
For j from 1 to n do: zjhj;
While (iter < iter_max and Continue = true)
{iter  iter+1;
Continue = false;
Vote(h,L,V);
For j from 1 to n
If (Vj ≥ threshold) then
{ h
j 1-hj; Continue=true ;}
}
If (Continue=true) then For j from 1 to n hj zj;
End
This algorithm was developed firstly for decoding
LDPC codes [8], its generalization for linear codes requires
the use of a big number of parity check equations [9].
2.2. The Permutation Decoding Algorithm
The permutation decoding algorithm (PDA) was first
developed by Jessie McWilliams [6]. It can be used when
a certain number of permutations (automorphisms), leaving

S. NOUH ET AL. 559
the code invariant, is known. The PDA correct a word by
moving errors in the redundancy part of a permuted word,
the hardness of finding the automorphism group restricts
the use of this algorithm to codes with known stabilizers
like the use of the projective special linear group for ex-
tended quadratic residue (EQR) codes.
2.3. The Hartman Rudolph Algorithm
The Hartman Rudolph (HR) decoder [15] is a symbol by
symbol soft decision optimal decoding algorithm. It
maximizes the probability that a bit corresponding to a
symbol rj of the sequence r to decode is equal to 1 or 0.
Hartman and Rudolph have showed that this probability
depends on all the codewords of the dual code C gener-
ated by H. This algorithm has a high complexity because
it uses 2n–k dual codewords therefore it can be applicable
only in the case of linear codes with height rate. More
precisely it uses the formula (2) to decide if the mth bit of
the decoded word c’ is equal to 1 or 0.
2
'
11
'
1
0if 1
nk n
mjl
m
c
c









0
1otherwise
jl ml
c
l
n






1
0 otherwie

(2)
With the following notations:
 if
s
ij
ij






10
mrm
Pr r rm P
 The bit
j
l
c denotes the lth bit of the jth codeword of
the code C.
A hard version of this algorithm can be obtained by
using as inputs the binary form hi of the received sym-
bols ri as follow:

1, 2, 3,,:i in

 


1if 0
1o
therwise
i
r
h

 (3)
3. The Proposed ARDec Decoder
3.1. The Principle
The proposed ARDec decoder (Artificial reliabilities
based decoding algorithm) has the structure given in the
Figure 1. It uses a generalized parity check matrix H* to
compute artificial reliabilities of the binary received
word h.
Compute artificial
reliabilities of h
SIHO
Decoder
H
*
h
Figure 1. The proposed decoding algorithm ARDec scheme.
Let C(n, k, d) be the dual code of C. The ARDec de-
coder uses the vote algorithm described in the Section
2.1 to compute artificial reliabilities. In the case of BPSK
modulation, the bit 0 is represented by –1 and the bit 1 by
1 and ARDec works as follow:
Inputs:
- H* a generalized parity check matrix of C of M rows.
- h the binary word to decode.
Outputs: V
Begin
Vote(h, H*, V);
Balance (H*, V);
For i from 1 to n do:
if (h
i=1) then


ii
r=1 V+1

; else ii r= 1 V+1;
Use a SIHO decoder to find the codeword c having
the smallest Euclidean distance to r.
End
When the columns of the matrix H* doesn’t have the
same weight, we propose to balance the vote vector V by
the following Balance algorithm:
Inputs:
- H* a generalized parity check matrix of C of M rows.
- V a vector of voting values.
Outputs: V
Begin
For i from 1 to n do:


Wi
 
*
Wi+Hi j

1 End For
For i from 1 to n do:
For j from 1 to M do:
Wi ;
End For
End For
For i from 1 to n do:



Vi
Vi Wi  End For
End
3.2. ARDec Based on Genetic Algorithms:
ARDecGA
Genetic algorithms (GA) are heuristic search algorithms
premised on the natural selection and genetic [16,17], we
recall here some notions:
 Individual or chromosome: a potential solution of the
problem, it’s a sequence of genes.
 Population: a subset of the research space.
 Environment: the research space.
 Fitness function: the function to maximize/minimize.
 Encoding of chromosomes: it depends on the treated
problem, the famous known schemes of coding are:
binary encoding, permutation encoding, value encod-
ing and tree encoding.
 Three operators of evolution:
1) Selection: it allows selecting the best individuals to
insert in the intermediate generation and to create chil-

S. NOUH ET AL.
560
dren.
2) Crossover: For a pair of parents (p1, p2) it allows to
create two children ch1 and ch2 with a crossover prob-
ability pc.
3) Mutation: The genes of the individual are muted
according to the mutation probability pm.
The Maini algorithm [18], uses genetic algorithms to
decode linear codes, the first step is to sort the received
sequence r by reliabilities and to find a matrix G' of an
equivalent code and the permutation  which binds the
two codes. The information part


I
r of (r) con-
tains symbols with biggest reliabilities. A genetic algo-
rithm works on
 
I
r to find the codeword having
the smallest Euclidean distance from (r).
The genetic operators of the Maini algorithm are given
in [18] and we propose here a modification at the level of
the initial population and the crossover operator.
For the crossover operator we choose to cross indi-
viduals in one point m, but this latest is randomly chosen
between 1 and the length of the code.
For the initial population, we proceed as follow:
 Find h, the hard decision version of (r).
 Fix a value of pi the probability to inverse a bit of h.
 x ← h.
For j from 1 to n do:
1) Generate uniformly a random value x, 0 ≤ x ≤ 1.
2) If (x ≤ pi) then xi  xi  1.
The value of pi is chosen between 0.1 and 0.4.
For decoding a binary word, the sequence r of its arti-
ficial reliabilities can be created by the vote and balance
procedures. After that the permutation  is obtained by
sorting r. The ARDecGA algorithm based on the modi-
fied Maini decoder works on (r) as follow:
Inputs:
nce (r).
rations
hard version of (r).
st individual is
true) do
- The seque
- Ng: Number of gene
- Ni: Population size
- Ne: elite number
- pc: crossover probability
- pm: mutation probability
Outputs: the codeword c.
Begin
h  the
if (hC) then c h;
else
begin
Generate an initial population, of Ni individuals;
Each individual is a binary word of length k. The fir
the information part of h.
Ngen  1; continue true;
While (Ngen ≤ Ng and continue=
Compute the fitness of each individual a:
 

,
f
itness adE br, b is the codeword
by G'.
associated to the individual a in the code generated
 
ht ) then {cb If(

,dHb
continu e false}
end If
Sort the population by increasing order of fitness.
Copy the best Ne individuals (of small fitness) in the
intermediate population.
For i=Ne+1 to Ni do
Select two individuals; p1 and p2 among the
best individuals.
Cross and mute p1 and p2 to obtain ch1 and ch2
according to pc and pm.
Among ch1 and ch2, insert the best individual in
the intermediate population.
End for.
Ngen  Ngen+1.
End while.
If(continue=true) then
c the first individual in the population.
End If

1
cπc


end;
end
3.3. ARDec Based on OSD Algorithm of Order
M: ARDecOSDm
Thm of order m
Or et al.
[19 iabilities,
acode this last in an equivalent
c-encoding. In
tthe OSD, OSD, OSD2 and OSD3
decooder, they
h to good
e This algorithm requires
oerator matrix of the code, this characteristics
ade linear codes without restriction.
3eck
rix H
Tice of the generalized parity check matrix H* is a
key factor in the success of the ARDec decoder. For rep-
resenting a linear code for the soft decision Belief Pro-
showatrix should have the following
sider-
.
he ordered statistic decoding algorit
SDm is a SIHO decoder developed by Fossorie
]. It starts by sorting the received word by rel
ero deft that it passes t
ode by inversing in each time m bits and re
his paper we will use 0 1
ders as a module in our hard decision dec
eav a polynomial complexity and they yield
rror correcting performances.
nly the gen
llows its use to deco
.4. Construction of the Generalized Ch
*
Mat
he cho
pagation decoding algorithm, Yedidia et al. [20,21] have
ed that the check m
characteristics:
1) The number of ones in each row is small.
2) The number of ones in each column is large.
3) For all pairs of rows of the check matrix, the num-
ber of columns that have a one in both rows is small;
ideally zero or one.
In this work we will show that these characteristics are
good criteria for choosing H*. We use the algorithm
given in [2] for finding a list L of codewords from the
dual code of C, this list respect then the first characteristic
given above. Here we propose a genetic algorithm GA-GPC
for extracting H* from L. This algorithm tries to improve
the chosen generalized parity check matrix by con
ing the second and the third characteristics as fitness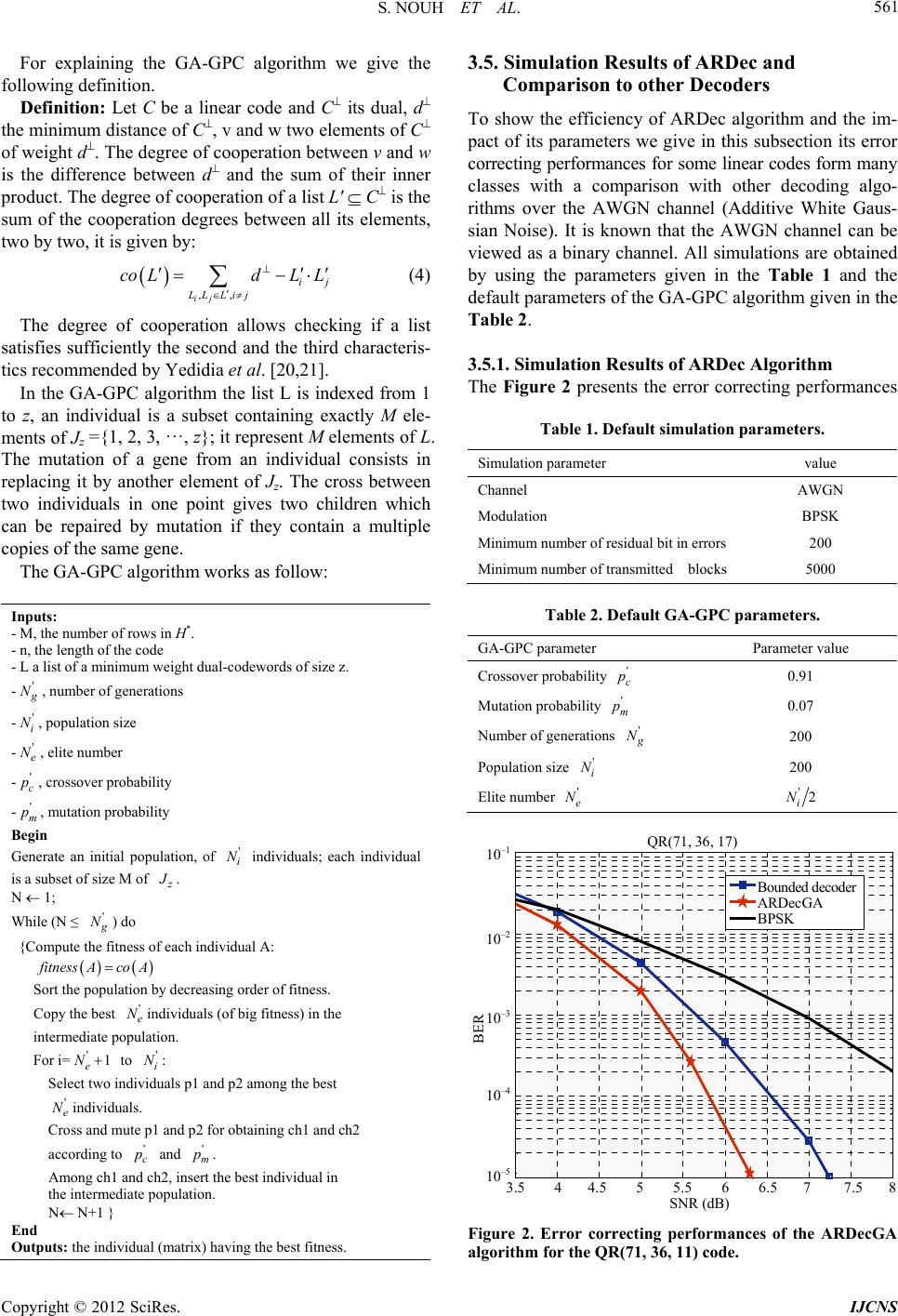

S. NOUH ET AL. 561
3.5. Simulation Results of ARDec and
r Decoders
Td the im-
p give in this subsection its error
correcting performances for some linear codes form many
clparison with other decoding algo-
rithmWGN channel (Additive White Gaus-
sn that the AWGN channel can be
vwnel. All simulations are obtained
bg the parameters given in the Table 1 and the
dG
T
3latiesults of A R D ec A l gorithm
Tting performances
ter ue
Fohe GA-GPC algorithm we give the
elements,
tw
operation allows checking if a list
sa
r explaining t
following definition.
Definition: Let C be a linear code and C its dual, d
the minimum distance of C, v and w two elements of C
of weight d. The degree of cooperation between v and w
is the difference between d and the sum of their inner
product. The degree of cooperation of a list L'  C is the
sum of the cooperation degrees between all its
o by two, it is given by:

,,
ij
ij
LLLij
co LdLL



 
 (4)
The degree of co
tisfies sufficiently the second and the third characteris-
tics recommended by Yedidia et al. [20,21].
In the GA-GPC algorithm the list L is indexed from 1
to z, an individual is a subset containing exactly M ele-
ments of Jz ={1, 2, 3, ···, z}; it represent M elements of L.
The mutation of a gene from an individual consists in
replacing it by another element of Jz. The cross between
two individuals in one point gives two children which
can be repaired by mutation if they contain a multiple
copies of the same gene.
The GA-GPC algorithm works as follow:
Inputs:
- M, the number of rows in H*.
- n, the length of the code
- L a list of a minimum weight dual-codewords of size z.
-'
g
N, number of generations
-'
i
N, population size
-'
e
N, elite number
-'
c
p
, crossover probability
-'
m
p
, mutation probability
Begin
Generate an initial population, of '
i
N individuals; each individual
is a subset of size M of
z
J
.
N  1;
While (N ≤ '
g
N) do
{Compute the fitness of each individual A:
 
f
itness Aco A
Sort the population by decreasing order of fitness.
Copy the best '
Nindividu
eals (of big fitness) in the
intermediate population.
='1
e
N to '
i
N:
Select two individuals p1 and p2 among the best
'
e
Nindividuals.
ross mute p1 and p2 for obtaining ch1 and ch2
ccoto '
c
For i
C
a
and
rding
Comparison to othe
o show the efficiency of ARDec algorithm an
act of its parameters we
asses with a com
s over the A
iaNoise). It is known
ieed as a binary chan
y usin
efault parameters of the GA-PC algorithm given in the
able 2.
.5.1. Si muon R
he Figure 2 presents the error correc
Table 1. Default simulation parameters.
Simulation parameval
Channel AWGN
Modulation BPSK
Minimum number of residual bit in errors 200
Minimum number of transmitted blocks 5000
.
Parameter value
p
and '
m
p
.
Among ch1 and ch2, insert the best individual in
the intermediate population.
N  N+1 }
End
Outputs: the individual (matrix) having the best fitness.
Table 2.efaultA- D GGPC parameters
GA-GPC parameter
Crossover probability '
c 0.91
p
Mutation probability m
'
p
0.07
Number of generations '
g
N 200
Population size '
i
N 200
Elite number '
e
N '2
i
N
3.5 44.5 55.5 66.5 77.5 8
10
-5
10
-4
10
-3
10
-2
10
-1
SNR (dB)
BER
QR(71,36,11)
Bounded decoder
ARDe cGA
BPSK
10
–1
10
–2
10
–3
10
–4
10
–5
Q
R
(
71, 36, 17
)
Bounded decode
r
ARDecGA
BPSK
3.5 4 4.5 5 5.5 6
SNR (dB)
BER
6.5 7.5 87
Fnces of thDecGA
lgorithm for the QR(71, 36, 11) code.
igure 2. Error correcting performae AR
a

S. NOUH ET AL.
562
of ARDece = 2, pc
=for the Quadratic RR(71,
3 to those of a bounde
dll configurations of of weight
lto (the error correctinability of
tdethe ARDecGA alhm allows
toore than the 2.3 dB ranteed by
tecoder, therefore 3.3 dB as ng gain is
o
In [22], authors have found a double circulant code
, 31, 12) which is optimal in the sense that it has
the maximum possible minimum distance for the length
62 and the dimension 31. The Figure 3 presents the error
correcting performances of ARDecOSD2 with M = 100
for this code and we have verified statistically that all
errors of weight less than or equal to 5 are corrected thus
about 2.6 dB as coding gain is obtained.
3.5.2. Impact of the Parameter M on ARDecGA
Algor ithm Performa nces
To show the impact of the parameter M on the error cor-
recting performances of the ARDecGA algorithm for a
DSC (Difference-Set Cyclic Code) code, we give in the
Figure 4 the simulation results for the DSC(73, 45, 10) code
with Ne = 2, Ng = 10, pc = 0.95, pm = 0.03 and Ni = 50.
The parameter M has an important effect on the effi-
ciency of ARDecGA algorithm. At BER = 10–4 there is
GA with M = 500, Ng = 50, Ni = 150, N
0.95, pm = 0.03
6, 11) compared
esidue code Q
d decoder (pseudo-
ecoder) which correct aerrors
ess than or equal 5g cap
his code). For this co,
win about 1 dB m
gorit
gua
he bounded dcodi
btained.
DCC(62
a
difference of more than 3 dB between M = 10 and M =
300 but the difference between M = 300 and M = 500 is
negligible.
3.5.3. Impact of the Parameter Ng on the ARDecGA
Performances
To show the impact of the number of generations Ng on
Figure 3. Error correcting performances of the ARDe-
2
the error correcting performances of the ARDecGA algo-
cOSD algorithm for a DCC(62, 31, 12) code.
rit
3.5.4. Impact of the Parameter Ni on the ARDecGA
To shf the population size Ni on the error
ive in the Figure 6 the simulation for the BCH(63, 30,
13) code with Ne = 2, M = 1000 and Ng = 100. For this
code 150 individuals in each generation are sufficient.
hm, we give in the Figure 5 the simulation for the
BCH(63, 30, 13) code with Ne = 2, M = 1000, pc=0.95,
pm = 0.03 and Ni = 300. For this code 20 generations are
sufficient.
Performances
ow the impact o
correcting performances of the ARDecGA algorithm, we
g
Figure 4. Impact of the parameter M on the ARDecGA er-
ror correcting performances for DSC(73, 45, 10) code.
Figure 5. Impact of the parameter Ng on the ARDecGA
error correcting performances fo r the BCH(63, 30, 13) code.

S. NOUH ET AL. 563
3.5.5. Impact of the Order m on the ARDecOSDm
Performances
To show the impact of the parameter m on the error cor-
recting performances of the ARDecOSDm algorithm we
give in the Figure 7 the simulation results for the QR(89,
45, 17) code with M = 1500. At BER = 10–5 there is a
gain of about 1.3 dB between the orders 0 and 3.
3.5.6. C omparison between ARDecOSD3 and
ARDecGA Algorithms
To compare the error correcting performances of the
ARDecOSD3 (M = 1000) and ARDecGA (Ni = 200, Ng = 50,
Ne = 2, pc = 0.95, pm = 0.03, M = 1000) algorithms we give
1234567
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
SNR (dB)
BCH(63
,
30
,
13)
Ni=6
Ni=50
Ni=100
Ni=150
Ni=200
BCH
(
63, 30, 13
)
10
0
–1
10
–2
10
–3
10
–4
10
–5
10
–6
10
BER
N
i=6
N
i=50
N
i=100
N
i=150
N
i=200
1 2 3 4 5 6 7
SNR
(
dB
)
Figure 6. Impact of the parameter Ni on the ARDecGA er-
ror correcting performances for the BCH(63, 30, 13) code.
3 4 5 6 7 8
10-6
10-5
10-4
10-3
10-2
10-1
100
SNR (dB)
BER
QR(89,45,17)
ARDecOSD0
ARDecOSD1
ARDecOSD2
ARDecOSD3
BPSK
QR(89, 45, 17)
10
0
–2
10
–6
10
–1
10
10
–3
10
–4
10
–5
ARDecOSD0
ARDecOSD1
ARDecOSD2
ARDecOSD3
BPSK
3 4 5 6 7 8
SNR (dB)
BER
Figure 7. Impact of the order m on the ARDecOSDm error
correcting performances for the QR(89, 45, 17) code.
in the Figure 8 the simulation results for the BCH(63, 39,
9) code. The ARDecGA is relatively better than the
ARDecOSD3 and it allows to win about 0.5 dB compared
to the Berlekamp-Massey decoder (BM) at BER = 10–5.
3.5.7. C omparison between ARDecGA and Hard
Decision Decoding Algorithm of OSMLD Codes
The vote technique is often used to decode linear code
with a particular structure like the class of the OSMLD
(One Step Logic Majority Decodable) codes which con-
tains the DSC(73, 45), DSC(273, 191) and BCH(15, 7)
codes. The famous known decoder of OSMLD code is
the majority logic decoder [23]. The Figure 9 presents a
comparison between error correcting performances of
Figure 8. Comparison between ARDecOSD3 and ARDecGA
performances for the BCH(63, 39, 9) code.
44.5 55.5 66.5 77.5 8
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
DSC(273,191,18)
SNR
(
dB
)
BER
ARDecGA
Logic Majority decoder
BPSK
DSC(273, 191, 18)
10
–1
10
–2
–5
ARDecGA
Logic Majority decoder
BPSK
10
–3
10
–4
10
10
–6
BER
4 4.5 5 5.5 6 6.5 7 7.5 8
SNR
(
dB
)
Figure 9. Comparison between ARDecGA and OSMLD de-
coder performances for DSC(273, 191, 18) code.

S. NOUH ET AL.
564
ARDecGA (M = 273, Ng = 50, Ni = 300, pc = 0.95, pm =
0.03, Ne = 2) and the majority logic decoder, it shows
that ARDecGA allows to win about 0.7 dB at BER =
10–5 than this classic decoder.
At BER = 10–5 the ARDecGA decoder allows to win
about 0.6 dB for the BCH(15, 7) code (Figure 10) and
0.9 dB for the DSC(73, 45) code (Figure 4).
3.5.8. C omparison be t w e en ARDecGA and G allager
Bit Flipping Algorithms
The Figure 11 presents a comparison between the error
correcting performances of ARDecGA (Ng = 6, Ni = 20,
pc = 0.95, pm = 0.03, Ne = 2) and the Bit Flipping Algo-
rithm (BF) applied to the BCH(63, 39, 9) code with the
2.5 3.54.55.5 6.5 7.5 8.5
9
10
-5
10
-4
10
-3
10
-2
10
-1
SNR (dB)
BCH(15,7,5)
BPSK
ARDecGA
HR (64)
HR (128)
HR (192)
HR (256)
10
–1
10
–2
10
–3
10
–4
10
–5
BCH(15, 7, 5)
2.5 3.5 4.5 5.5 6.5 7.5 8.5 9
SNR
(
dB
)
BPSK
ARDecGA
HR (64)
HR (128)
HR (192)
HR (256)
BER
Figure 10. Comparison between the performances of AR-
DecGA and HR decoders for the BCH(15, 7, 5) code.
44.5 55.5 66.5 77.
5
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
SNR (dB)
BCH(63
,
39
,
9)
BF M=450
ARDecGA
10–1
10–2
10–3
10–4
10–5
10–6
BCH
(
63
,
39
,
9
)
BF M=450
ARD ecG A
4 4.5 5 5.5 6 6.5 7 7.
SNR 5
(
dB
xed at 100 and the value of the threshold is optimized.
At BER = 10–5 the ARDecGA decoder allows to win
about 0.6 dB.
3.5.9. C omparison between ARDecGA and the Hard
Decision Hartman-Rudolf Algorithm
The Figure 10 presents a comparison between the error
correcting performances of ARDecGA algorithm (M =
10, Ng = 3, Ni = 8, pc = 0.95, pm = 0.03, Ne = 2) and the
Hartman Rudolf decoder (hard decision version) applied
to the BCH(15, 7, 5) code with the value of M as pa-
rameter. This figure shows that the ARDecGA decoder
with 10 vectors from C and 26 individuals in the genetic
algorithm allows to win more than 1 dB at BER = 10–4
compared to the HR decoder with 64, 128 and 192 vec-
tors from C. The ARDecGA decoder has the same per-
formances of the HR decoder when it uses all the 256
vectors.
e BCH(63, 39, 9) code there are 16777216 codewords
in its dual code BCH(63, 24, 14). Here, we propose to
use only the 450 codewords of the BCH(63, 24, 14)
code having the minimum weight 14 in the decoding by
the HR algorithm. The Figure 12 presents a comparison
between the performances of ARDecGA decoder (M =
450, Ng = 6, Ni = 20, Ne = 2, pc = 0.95, pm = 0.03) and the
Hartman Rudolf decoder (M = 450) applied to the
BCH(63, 39, 9) code. This figure shows that the
ARDecGA allows to win about 1 dB compared to the HR
decoder at BER = 10–5.
)
BER
Figure 11. Comparison between ARDecGA and BF error
correcting performances for the BCH(63, 39, 9) code.
same number of parity check equations M = 450. The
maximum number of iteration in the BF algorithm is
fi
When n – k increase, the hard decision version of the
Hartman-Rudolf algorithm becomes very complex. For
th
BCH(63
,
39
,
34567
8
10
-5
10
-4
10
-3
10
-2
10
-1
9)
SNR (dB)
HR
ARDecGA
BCH(63, 39, 9)
10
–1
10
–2
HR
ARDecGA
10
–3
10
–4
10
–5
3 4 5 6 7 8
SNR
(
dB
)
BE
R
Figure 12. Comparison between ARDecGA and HR perfor-
mances for the BCH(63, 39, 9) code.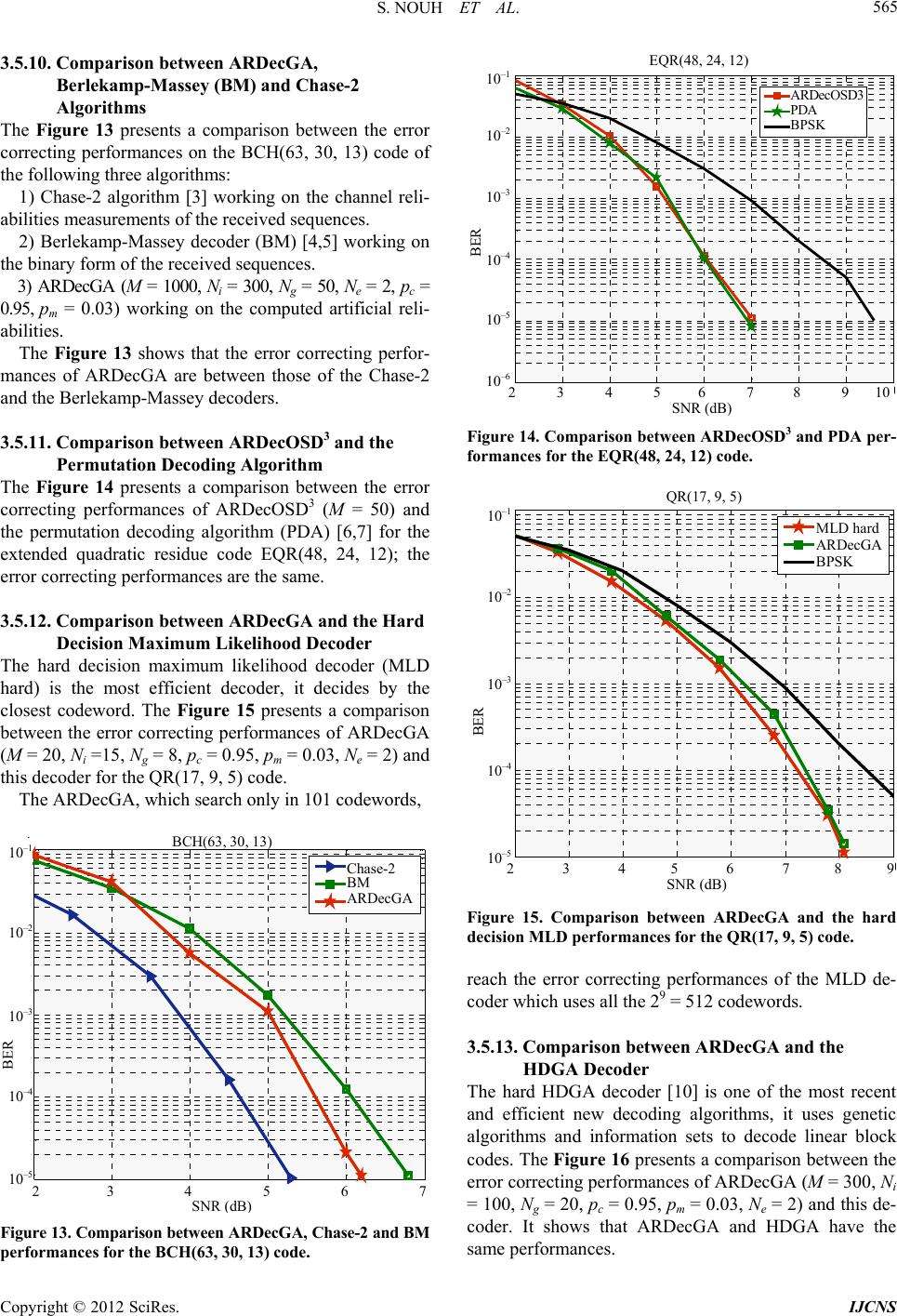

S. NOUH ET AL. 565
3.5.10. Comparison between ARDecGA,
Berlekamp-Massey (BM) and Chase-2
Algorithms
The Figure 13 presents a comparison between the error
correcting performances on the BCH(63, 30, 13) code of
the following three algorithms:
1) Chase-2 algorithm [3] working on the channel reli-
abilities measurements of the received sequences.
2) Berlekamp-Massey decoder (BM) [4,5] working on
th
ee code EQR(48, 24, 12); the
error correcting performances are the same.
3.5.12. Comparison between ARDecGA and the Hard
Decision Maximum Likelihood Decoder
The hard decision maximum likelihood decoder (MLD
hard) is the most efficient decoder, it decides by the
closest codeword. The Figure 15 presents a comparison
between the error correcting performances of ARDecGA
(M = 20, Ni =15, Ng = 8, pc = 0.95, pm = 0.03, Ne = 2) and
this decoder for the QR(17, 9, 5) code.
The ARDecGA, which search only in 101 codewords,
e binary form of the received sequences.
3) ARDecGA (M = 1000, Ni = 300, Ng = 50, Ne = 2, pc =
0.95, pm = 0.03) working on the computed artificial reli-
abilities.
The Figure 13 shows that the error correcting perfor-
mances of ARDecGA are between those of the Chase-2
and the Berlekamp-Massey decoders.
3.5.11. Comparison between ARDecOSD3 and the
Permutation Decoding Algorithm
The Figure 14 presents a comparison between the error
correcting performances of ARDecOSD3 (M = 50) and
the permutation decoding algorithm (PDA) [6,7] for the
xtended quadratic r sidue
23 4 5 6
7
10
-5
10
-4
10
-3
10
-2
10
-1
SNR
(
dB
)
BCH(63
,
30
,
13)
Chase-2
BM
ARDecGA
10
–1
10
–2
–4
1
10
–3
10
0
–5
BER
BCH
(
63
,
30
,
13
)
2 3 4 5 6 7
S
NR
(
dB
)
Chase-2
BM
ARD ecG A
Figure 13. Comparison between ARDecGA, Chase-2 and BM
performances for the BCH(63, 30, 13) code.
2 34 567 891
0
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
SNR
(
dB
)
BER
EQR(48,24,12)
ARDecOSD3
PDA
BPSK
10
–1
10
–2
10
–3
–6
10
–4
10
–5
10
EQR(48, 24, 12)
ARDecOS
D
3
PDA
BPS
K
BER
2 3 4 5 6 7 8 9 10
SNR
(
dB
)
Figure 14. Comparison between ARDecOSD3 and PDA per-
formances for the EQR(48, 24, 12) code.
2 3 45 67 8
9
10
-5
10
-4
10
-3
10
-2
10
-1
RQ(17,9,5)
SNR
(
dB
)
BER
MLD hard
ARDecGA
BPSK
10
–1
10
10
–3
10
–4
10
–5
–2
QR(17, 9, 5)
MLD hard
ARD ecG A
BPSK
BER
2 3 4 5 6 7 8 9
SNR (dB)
Figure 15. Comparison between ARDecGA and the hard
decision MLD performances for the QR(17, 9, 5) code.
reach the error correcting performances of the MLD de
3.5.13. Comparison between ARDecGA and the
HDGA Decoder
The hard HDGA decoder [10] is one of the most recent
and efficient new decoding algorithms, it uses genetic
algorithms and information sets to decode linear block
codes. The Figure 16 presents a comparison between the
error correcting performances of ARDecGA (M = 300, Ni
= 100, Ng = 20, pc = 0.95, pm = 0.03, Ne = 2) and this de-
coder. It shows that ARDecGA and HDGA have the
same performances.
-
coder which uses all the 29 = 512 codewords.

S. NOUH ET AL.
566
3.6. Complexity of ARDec
The complexity of ARDec is variable and it depends on
the following parameters:
 The parameter M.
 The code length n.
 The code dimension k.
 The weight of the error to decode.
 The complexity of the auxiliary SIHO decoder.
The Table 3 presents an upper bound of the complex-
ity of ARDecGA and ARDecOSDm and it gives those of
BM and HDGA algorithms. This table shows that the
complexity of ARDecGA is polynomial in n however the
one of ARDecOSDm is polynomial in nm. Both the com-
plexity of HDGA and the one of the BM algorithms are
polynomial in n2.
The Figure 17 shows a basic property of error cor-
ne codeword c in
e sphere of radius t (error correcting capability t of the
code) centered on h.
recting code in the ambient space. If h is a binary re-
ceived word then there exists at most o
th
1234567
10-5
10-4
10-3
10-2
10-1
100
SNR
(
dB
)
BER
BCH(63
,
45
,
7)
HDGA
ARDecGA
100
10–1
10–2
10–3
10–4
10–5
BCH(63, 45, 7)
1 2 3 4 5
SNR
6 7
(
dB
)
HDGA
ARD ecG A
BER
Figure 16. Comparison between ARDecGA and the hard
decision HDGA performances for the BCH(63, 45, 7) code.
Co
Table 3. Complexity of BM, HDGA and ARDec algorithms.
Decoder mplexity
ARDecOSDm Less than or equal to

OMn

1m
n


ARDecGA
Less than or equal to


log
ign i
OMn NNkN

 

ARDec based on SIHO decoder Less than or equal to
 
SIHO decoderOMn O
Berlekamp-Massey O(n2)
HDGA 

2log
ignn i
ON N kkN



c
1
c
2
c
3
c
4
c
5
c
6
h
c t
Figure 17. Basic property of error correcting codes.
In the decoding steps of h, the algorithm stops when
e codeword c at Hamming distance less than or equal
to t is found. This stop criterion allows reducing consid-
erably the complexity of ARDec. The Figure 18 shows
the average number of generations required to decode
errors of weight between 0 and 9 for the BCH(63, 30, 13)
code of error correcting capability t = 6 by the ARDec-
GA algorithm. It shows that the errors of weight less than
or equal to t – 1 are decoded in the first generation; the
errors of weight t requires about 2.86 generations at av-
erage and the errors of weight greater than t requires the
use of 100 generations because generally the stop crite-
rion isn’t verified in this case.
The Figure 18 shows that the use of only three gen-
erations allows to correct errors of weight less than or
equal to t (correctable errors) and justifies that ARDecGA
has in practice a small complexity comparing to the up-
per bound given in the Table 3.
When the number of generations N and the population
about 90% of err 7 and 46% of er-
rors of weight 8 for the B of error
apability equa
usion and Perspectives
In this paper we have preshard decision
ses the dual spce of
code C to compute artificial reliabilities of binary the
by a my voting procedure. The
ls with lowest reliabilities are moved in thre-
dundancy part of the word (h) by using a permutation
th
g
size Ni are sufficient the ARDecGA algorithm allows
orrecting some errors of weight more than t. The Figure c
19 shows that the use of ARDecGA with M = 1000, Ng =
100, pc = 0.95, pm = 0.03 and Ni = 300 allows the correc-
tion of ors of weight
CH(63, 30, 13) code
l to 6. correcting c
4. Concl
ented an efficient
uadecoding algorithm whicha linear
received word hajorit
symboe

S. NOUH ET AL. 567
1234 56789
10
0
10
1
10
2
Error weight
Average Ng
Average Number of generations
Average Number of generations
Average Ng
10
2
10
1
10
0
1 2 3 4 5 6 7
Error weight
8 9
Figure 18. Average number of generations for the BCH(63
30, , 13) code.
12 3 4 5 6 7 8
10
1
10
2
Error weight
correc
ti
on percen
t
age
(%)
correct ion percentage correction percentage
correction percentage (%)
1 2 3 4 5 6 7 8
Error weight
10
1
Figure 19. Correction percentage
10
2
for the BCH(63, 30, 13)
co
C. We have showed by
ty can be gained
SIHO decoder.
ing the Weight Enumerator of Binary Linear Block Codes,”
International Journal of Applied Research on Information
Technology and Computing, Vol. 2, No. 3, 2011, pp. 80-
93.
[3] D. Chase, “A Class of Algorithms for Decoding Block
Codes with Channel Measurement Information,” IEEE
Transactions on Information Theory, Vol. 18, No. 1, 1972,
pp. 170-181. doi:10.1109/TIT.1972.1054746
[4] J. L. Massey, “Shift-Register Synthesis and BCH Decod-
ing,” IEEE Transaction on Information Theory, Vol. 15,
No. 1, 1969, pp. 122-127.
[5] E. R. Berlekamp, “Algebraic Coding Theory,” Aegean
Park Press, Walnut Creek, 1984.
[6] F. J. MacWilliams, “Permutation Decoding of Systematic
Codes,” The Bell System Technical Journal, Vol. 63, No.
1, 1964, pp. 485-505.
[7] S. Nouh, M. Askali and M. Belkasmi, “Efficient Genetic
edia, 16-17 May 2012.
[8] R. G. Gallager, “Low-Density Parity-Check Codes,” IRE
Transactions on Information. Theory, Vol. 8, No. 1, 1962,
pp. 21-28. doi:10.1109/TIT.1962.1057683
de.
 which binds the two codes C and (C). The word (h)
contains generally a few noised symbols in its informa-
tion part which can be cleaned by a genetic algorithm or
by some test sequences of the OSD decoder. The simula-
tion results show that the ARDec decoder allows to cor-
rect all errors of weight less than or equal to the error
correcting capability of the code
simulation that more correcting capabili
by using a vote procedure and a powerful
REFERENCES
[1] G. C. Clarck and J. B. Cain, “Error-Correction Coding for
Digital Communication,” Plenum, New York, 1981.
[2] S. Nouh and M. Belkasmi, “Genetic Algorithms for Find-
Algorithms for Helping the Permutation Decoding Algo-
rithm,” International Conference on Intelligent Systems,
Mohamm
[9] R. H. Morelos-Zaragoza, “The Art of Error Correcting
Coding,” 2nd Edition, John Wiley & Sons, Hoboken, 2006.
[10] Azouaoui, I. Chana and M. Belkasmi “Efficient Informa-
tion Set Decoding Based on Genetic Algorithms,” Inter-
national Journal of Communications, Network and Sys-
tem Sciences, Vol. 5, No. 7, 2012, pp. 423-429.
[11] R. Sujan, et al., “Adaptive ‘Soft’ Sliding Block Decoding
of Convolutional Code Using the Artificial Neural Net-
Work,” Transactions on Emerging Telecommunications
Technologies, 2012.
[12] M. Sayed, “Coset Decomposition Method for Decoding
Linear Codes,” International Journal of Algebra, Vol. 5,
No. 28, 2011, pp. 1395-1404.
[13] M. Kerner and O. Amrani, “Iterative Decoding Using
Optimum Soft Input—Hard Output Module,” IEEE Tran s-
actions on Communications, Vol. 57, No. 7, 2009, pp.
1881-1885. doi:10.1109/TCOMM.2009.07.070167
[14] B. Cristea, “Viterbi Algorithm for Iterative Decoding of
[17] J. McCall, “Genetic Algorithms for Modelling and Opti-
mizationm” Jond Applied Mathe-
matics, Vol. 1222.
Parallel Concatenated Convolutional Codes,” Proceed-
ings of 18th European Signal Processing Conference,
Aalborg, 23-27 August 2010.
[15] C. R. P. Hartmann and L. D. Rudolph, “An Optimum
Symbol-by-Symbol Decoding Rule for Linear Codes,”
IEEE Transactions on Information Theory, Vol. 22, No. 5,
2009, pp. 514-517.
[16] D. E. Goldberg, “Genetic Algorithms in Search, Optimi-
zation and Machine Learning,” Addison Wesley, Reading,
1989.
urnal of Computational a
84, No. 1, 2005, pp. 205-
doi:10.1016/j.cam.2004.07.034
[18] H. Maini, K. Mehrotra, C. Mohan and S. Ranka, “Soft De-
cision Decoding of Linear Block Codes Using Genetic

S. NOUH ET AL.
568
near Block Codes Based on Ordered Statistics,” IEEE
Algorithms,” IEEE International Symposium on Informa-
tion Theory, Trondheim, 27 June-1 July 1994.
[19] M. P. C. Fossorier and S. Lin, “Soft Decision Decoding
of Li
Transactions on Information Theory, Vol. 41, No. 5, 1995,
pp. 1379-1396. doi:10.1109/18.412683
[20] J. S. Yedidia, J. Chen and M. Fossorier, “Generating Code
Representations Suitable for Belief Propagation Decod-
d M. Fossorier, “Representing
Algo
ing,” Tech. Report TR-2002-40, Mitsubishi Electric Re-
search Laboratories, Broadway, 2002.
[21] J. S. Yedidia, J. Chen an
Codes for Belief Propagation Decoding,” Proceedings of
IEEE International Symposium on Information Theory,
Yokohama, 29 June-4 July 2003, p. 176.
[22] A. Azouaoui, M. Askali and M. Belkasmi, “A Genetic
rithm to Search of Good Double-Circulant Codes,”
IEEE International Conference on Multimedia Comput-
ing and Systems Proceeding, Ouarzazate, 7-9 April 2011,
pp. 829-833.
[23] J. L. Massey, “Threshold Decoding,” M.I.T. Press, Cam-
bridge, 1963.