Int. J. Communications, Network and System Sciences, 2012, 5, 548-556
http://dx.doi.org/10.4236/ijcns.2012.59065 Published Online September 2012 (http://www.SciRP.org/journal/ijcns)
High Security Nested PWLCM Chaotic Map Bit-Level
Permutation Based Image Encryption
Qassim Nasir1, Hadi H. Abdlrudha2
1Department of Electrical and Computer Engineering, University of Sharjah, Sharjah, UAE
2Computer Science Department, Faculty of Information Technology, Petra Private University, Amman, Jordan
Received January 27, 2012; revised March 9, 2012; accepted July 25, 2012
ABSTRACT
Chaotic systems produce pseudo-random sequences with good randomness; therefore, these systems are suitable to efficient
image encryption. In this paper, a low complexity image encryption based on Nested Piece Wise Linear Chaotic Map
(NPWLCM) is proposed. Bit planes of the grey or color levels are shuffled to increase the encryption complexity. A
security analysis of the proposed system is performed and presented. The proposed method combine pixel shuffling, bit
shuffling, and diffusion, which is highly disorder the original image. The initial values and the chaos control parameters
of NPWLCM maps are derived from external secret key. The cipher image generated by this method is the same size as
the original image and is suitable for practical use in the secure transmission of confidential information over the Inter-
net. The experimental results of the proposed method show advantages of low complexity, and high-level security.
Keywords: Encryption; Chaos; Piecewise, Chaotic Maps; Security
1. Introduction
In recent years, and due to the development of multimedia
and information technology, digital images are shared over
the public communication networks. Therefore, there is
potential risk of vulnerable access to sensitive documents.
Image encryption and robust cryptographic become an
essential to protect these multimedia files from leakage.
Conventional cipher algorithms such as DES, IDEA. etc.
are not suitable for multimedia files due to public data
capacity, strong pixel correlation and high redundancy
which reduces the encryption performance [1]. The chaos
based multimedia files encryption is not new idea. Mat-
thew [2] was the fist step in this line of research. Large
amount of work using digital chaotic techniques to con-
struct cryptosystems has been studied and has attracted
more and more attention in the last years [3-19]. Re-
searchers are especially interested in enhancing the cha-
otic generators and the diffusion stage of the cryptosys-
tems. According to the classification of chaotic systems,
the security application of chaos can be divided into
analog chaotic secure communications utilizing continu-
ous dynamical systems [3] and digital chaotic cryptosys-
tems utilizing discrete dynamical systems.
Discrete chaotic system is easy to implement and has
good statistical properties, which can be used as random
number generator. Chaotic system is extremely sensitive
to parameters and initial conditions. If the system pa-
rameters or initial value is seen as the key, chaotic sys-
tems have become a good password system [4]. Recently
some researchers such as [5,6], they used two chaotic
maps to encrypt the image to enhance the security. Simi-
larly, Ashtiyani et al. [7] also employed chaotic maps
and other method to encrypt the images. Ahmad [8] in-
troduced a new method using two logistic chaotic maps
and a large enough external secret keys for image en-
cryption. This method exhibits a high security, but they
did not proof this method is robust or not to common
signal processing attacks. The scheme proposed in this
paper is based on two chaotic maps which can overcome
the periodicity of Arnold map and is more security; be-
sides, it is robust to the common signal attacks. The re-
searchers in [9,10], proved that logistic map, that was
widely used in the encryption domain, is not enough ran-
dom and uniform. Then, they propose to use other cha-
otic maps like Piece Wise Linear Chaotic Map (PWLCM).
In [11] and [12] presents a chaos-based cryptosystem for
secure transmitted images abased on a 2D chaotic map
which is used to shuffle the image pixel positions, ac-
companied with substitution (confusion) and permutation
(diffusion) operations on every block. A multiple rounds,
are combined using two perturbed chaotic PWLCM maps.
Indeed, to obtain better dynamical statistical properties
and to avoid the dynamical degradation caused by the
digital chaotic system working in a finite state, a pertur-
bation technique is used.
The objective of this research work is specially ori-
C
opyright © 2012 SciRes. IJCNS

Q. NASIR, H. H. ABDLRUDHA 549
ented towards using Nested PWLCM map based image
encryption schemes. Two enhancement measures in the
system efficiency have been proposed to the main com-
ponents of typical chaos-based image cryptosystems:
chaotic confusion and pixel diffusion processes. In the
first block confusion and shuffle of bit positions is per-
formed, while the other block is diffused by add and shift
algorithm. The resultant image is of high encryption se-
curity as diffusion is performed twice on the bit and byte
levels. Bit shuffling has been introduced by other re-
searchers such in Pixel Chaotic Shuffle (PCS) [13], Pixel
Shuffle (PS) [14] but the proposed method if a low com-
plexity one as it uses a simple NPWLCM.
The paper is organized as follows: Section 2 briefly
introduces the Nested PWLCM. Section 3 describes the
proposed encryption algorithm; the proposed system per-
formance measures and security analysis are given in
Section 4. And finally, we summarize our conclusions in
Section 5.
2. Nested PWLCM Chaotic Map
The general description of chaos is an unpredictable and
random-like long-term evolution that results from deter-
ministic nonlinear systems. The simplest class of chaotic
dynamic systems is one-dimensional chaotic map of the
form

1=, , nn
xfx 
=0,1, 2,n (1)
where the state variable x and the system parameter λ are
scalars, and f is a mapping function defined in the real
domain.
2.1. The Piecewise Linear Map [15]
This map is given by:
 


 
<0
1= 0
Bx nAx n
xn Bx nAx n




=0,1,2,n

(2)
where parameters A and B are chosen to be 1 and 1.998
respectively to generate chaos. This map is extensively
used for chaos generation due to its perfect properties
such as uniform invariant density function; exactness,
mixing and ergodicity; exponentially decaying correla-
tion function and simple realization in both hardware and
software [16]. Since the parameter A represents just a
scaling factor, the stochastic properties of the generated
bit sequence are dependent only on the parameter B,
which must assume values greater than 1 for the system
to be chaotic and not greater than 2 to avoid the state x(n)
being attracted to either +∞ or –∞ [17].
2.2. The Nested Piecewise Linear Chaotic Map
(NPWLCM)
The proposed Nested Piecewise Linear Chaotic Maps are
expressed as [18,19]:


  
44
1
44
110
=11<0
xnA xn
xn xnA xn




 



(3)


  
11
2
11
0
=<0
Bx nAx n
xn Bx nAx n








(4)


  
22
3
22
0
=<0
Bx nAx n
xn Bx nAxn








(5)


  
33
4
33
0
=<0
Bx nAx n
xn Bx nAxn






 (6)
where parameters A and B are chaos generation parame-
ters. The bifurcation diagram [19] of the NPWLCM
shows that when the control parameter B is 1.998, chaos
is still generated.
3. Encryption System Description
For image encryption, 2D or higher-dimensional chaotic
maps are naturally employed for a reason that the image
can be considered as a 2D array of pixels. Let’s assume
that the size of the plain image is N × M. If the image is
of gray levels then each pixel can be represented by 2G,
where G(= 8) is the number of bits per pixel. If the image
is of a color format, then it can represented by 3D di-
mension array of Red, Green, and Blue (RGB) levels.
Since images are composed of finite lattice called pixels,
the domain of the map f(.) is changed to the discretized
form Image permutation can be achieved through shuf-
fling the position of image bits and then pixels. It is nec-
essary to introduce a diffusion mechanism after the bit
permutation stage. The idea is to spread the influence of
every single pixel over the entire image. The complexity
evaluation is important to image encryption as well since
it always indicates the feasibility of encryption schemes.
Some special attentions should be given in terms of
computational speed, size and quality of the encrypted
images. The block diagram is composed of two processes:
chaotic confusion and pixel diffusion as shown in Figure
1.
In confusion module, each bit position at each column
in bit-plane is shuffled by using the pseudorandom se-
quence which is generated by NPWLCM chaotic map.
The change in the bit position at each pixel will modify
the pixel value. Thus the security of confusion module is
significantly improved due to introducing of diffusion ef-
fect throughout the bit-level permutation operation. More-
over, the overall security—level is further enhanced by
introducing another diffusion operation at the pixel—
level by using a simple Add and shift operations. To
achieve a satisfactory level of security the confusion-
diffusion operations are repeated (8 × m × n where m and

Q. NASIR, H. H. ABDLRUDHA
Cop IJCNS
550

1,4
,,
=0, =1
sort
NN
ki ki
x




1,8 1
=0, =0
,MN
ij
ij
n are the image width and high respectively) rounds it-
eration.
shuffled by using the indexing generated chaotic se-
quences. So each level will be shuffled using the follow-
ing formula by assuming the level matrix defined as The proposed image encryption is summarized by the
following steps:




B






1, 1,8
=0, =0, =1
:,1,= 1, 2
:,2,=3, 4
,,= :,3,=5,6
:,4,= 7,8
MN
'
ijk
Bsqkk
Bsqkk
ijk Bsqkk
Bsqkk




 
 


B
1
mask=& 7
i
T
:
1) The proposed image encryption process utilizes a
96 bit external secret key. This key is partitioned into
three 32 blocks. The chaotic sequence generation control
parameters (A, B), and the initial condition x(0) are de-
rived from this secret key blocks.
2) Generate four chaotic bit sequences by NPWLCM
using formulas (3 - 6). XOR post processing is used to
generate these random bit sequences. The shuffled bit-planes are shown in Figure 2.
3) Sort four chaotic binary sequences and generate
four new integer sequences by ordinal numbers corre-
sponding to the original sequences, such as
5) The permuted image is achieved by combining all
the 8 shuffled and confused bit-planes together
6) The pixels (Grey, or RGB) value will be diffused
using the following Add-Shift formula

1,4
=0, =1
,=
ki ki
sqi j

 .
4) Each bit-plane is shuffled separately by using the
sorting sequences generated in previous step as shown in
Figure 2. Thus the pixel value (Grey Levels bits, R-level
bits, G-level bits, Blue level bits) matrices are column

 
1
=mod 256
iii
XPXPT  



=mask 8mask
ii i
TXPXP 
Figure 1. Standard CHAOS based image encryption.
Figure 2. Bit indexing and shuffling within a row.
yright © 2012 SciRes.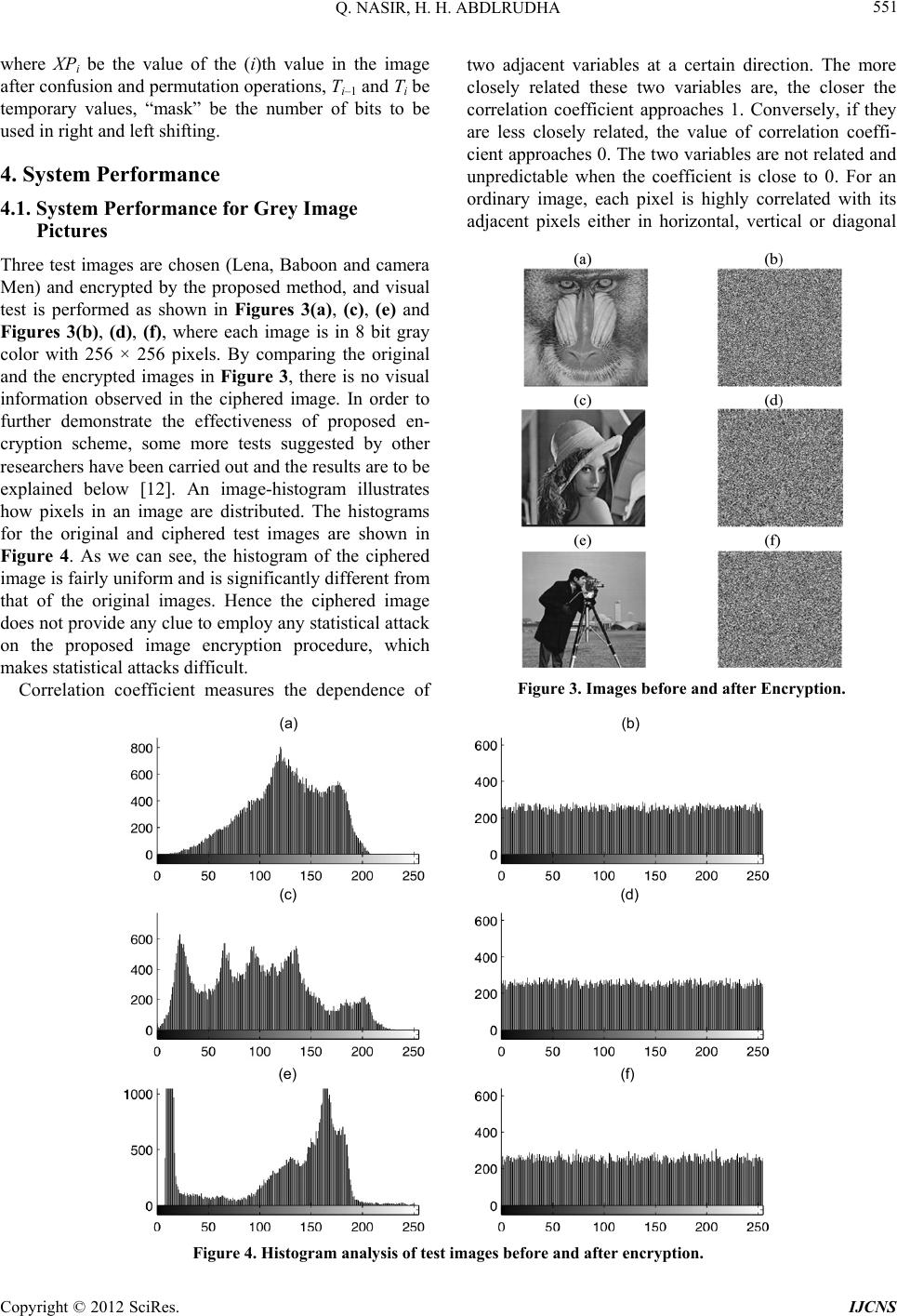

Q. NASIR, H. H. ABDLRUDHA 551
where XPi be the value of the (i)th value in the image
after confusion and permutation operations, Ti–1 and Ti be
temporary values, “mask” be the number of bits to be
used in right and left shifting.
4. System Performance
4.1. System Performance for Grey Image
Pictures
Three test images are chosen (Lena, Baboon and camera
Men) and encrypted by the proposed method, and visual
test is performed as shown in Figures 3(a), (c), (e) and
Figures 3(b), (d), (f), where each image is in 8 bit gray
color with 256 × 256 pixels. By comparing the original
and the encrypted images in Figure 3, there is no visual
information observed in the ciphered image. In order to
further demonstrate the effectiveness of proposed en-
cryption scheme, some more tests suggested by other
researchers have been carried out and the results are to be
explained below [12]. An image-histogram illustrates
how pixels in an image are distributed. The histograms
for the original and ciphered test images are shown in
Figure 4. As we can see, the histogram of the ciphered
image is fairly uniform and is significantly different from
that of the original images. Hence the ciphered image
does not provide any clue to employ any statistical attack
on the proposed image encryption procedure, which
makes statistical attacks difficult.
Correlation coefficient measures the dependence of
two adjacent variables at a certain direction. The more
closely related these two variables are, the closer the
correlation coefficient approaches 1. Conversely, if they
are less closely related, the value of correlation coeffi-
cient approaches 0. The two variables are not related and
unpredictable when the coefficient is close to 0. For an
ordinary image, each pixel is highly correlated with its
adjacent pixels either in horizontal, vertical or diagonal
Figure 3. Images before and after Encryption.
(a) (b)
(c) (d)
(e) (f)
Figure 4. Histogram analysis of test images before and after encryption.

Q. NASIR, H. H. ABDLRUDHA
552
direction. However, an efficient image cryptosystem
should show sufficiently low correlation in the adjacent
pixels and in all directions. The correlation distribution
of two adjacent pixels of the plain images and the cipher
images on the horizontally, vertical, and diagonal direc-
tions are shown in Figures 5-7. All adjacent pixels are
(a) (b)
(
c
)
(
d
)
(
e
)
(
f
)
Figure 5. Correlation of two horizontal, vertical and diagonal adjacent pixels—Baboon Test Image.
(a) (b)
(
c
)
(
d
)
(
e
)
(
f
)
Figure 6. Correlation of two horizontal, vertical and diagonal adjacent pixels—Lena Baboon Image.

Q. NASIR, H. H. ABDLRUDHA 553
(a) (b)
(c) (d)
(
e
)
(
f
)
Figure 7. Correlation of two horizontal, vertical and diagonal adjacent pixels—Camera Test Image.
selected and then the pixel value on the location (x + 1, y)
over the value on (x, y) in the case of horizontal direction.
Similar tests are done for pixel vale on (x, y + 1) over (x,
y) for vertical, and pixel value on (x + 1, y + 1) over (x, y)
in case of diagonal as shown in the Figures 5-7 for the
sampled images (Lena, baboon, and camera man). To
quantify and compare the correlations of adjacent pixels,
the correlation coefficient rxy of each adjacent pair is
calculated for the plain and ciphered images using the
following formulas:


cov ,
=
xy
x
y
x
y
DD
r (7)


   
cov ,=
x
yExExyEy

(8)
1
1
=
L
i
i
Ex x
L
 (9)
 
2
L
xi
DxEx
=1
1
=
i
L (10)
where x and y are gray scale values of two adjacent pix-
els in the image, and L denotes the total number of sam-
ples (number of pixels in the image).
The results of the correlation coefficients for horizon-
tal, vertical and diagonal adjacent pixels for the plain
image and its cipher image are given in Table 1. It is
clear from Figures 5-7 and Table 1 that the strong cor-
Table 1. Correlation coefficients for two adjacent pixels in
the original and encrypted images.
Corr.Baboon Lena Camera
Orig.lEncry.Orig.l Encry. Orig.lEncry.
Horiz.0.846 –0.020 0.9471 –0.0159 0.92010.0202
Vert.0.811–0.0440.9665 –0.020 0.9443–0.077
Diag.l0.717–0.0330.899 0.014 0.907–0.050
relation between adjacent pixels in plain image is greatly
reduced in the cipher image produced by the proposed
chaos based encryption scheme.
Two common measures can be used to measure en-
cryption performance such as number of pixels change
rate (NPCR) and the unified average changing intensity
(UACI) which measures the normalized mean difference
between the plane and ciphered images. Let the plane,
and the ciphered image denoted by P and C [12]. Define
a bipolar array, D, with the same size as the images P
and C. D(i, j) is determined as follows:
  
1if, ,
,=
0 elsewhere
PijCij
Dij

 (11)
The NPCR is defined as


,
,
N
PCR =100
ij
Dij

(12)
N 
M

Q. NASIR, H. H. ABDLRUDHA
554
where M and N are the width and height of the P or C.
While The UACI measures the average intensity of dif-
ferences between the plain image and the ciphered image.
UACI is defined as follows [12]:


11
=0 =0
1
UACI=255
MN
ij
Cij
MN
 
 12
,,
100
Cij

(13)
Table 2 summarizes the mean value of NPCR and
UACI between the original image and the ciphered im-
age for the Grey Images. The NPCR and UACI are high
enough to say that the two images are very different.
Information Entropy will be used to measure the en-
cryption performance as it is defined to express the degree
of uncertainties in the system. It is well known that the
entropy Hm of a message source m can be calculated as:

21
=0
=
G
mi
i
Hp

2
1
log
i
mpm




(14)
where p(mi) represents the probability of symbols (mi), G
= number of gray level (= 8). If a source emits 28 symbols
with equal probabilities, then source entropy Hm is equal
to 8. Actually, given that a practical information source
seldom generates random messages, in general its en-
tropy is smaller than the ideal one. If the entropy of en-
crypted images is less than, but approaching eight, it will
reduce the probability of successful restoration of images
by interceptors. On the contrary, if the entropy is more
than eight, then interceptors easily decode the encrypted
images. Table 3 shows that the entropy of the encrypted
images using the proposed encryption scheme is close to
theoretical value 8. This means that information leakage
in the encryption process is negligible and the encryption
system is secure upon the entropy attack.
4.2. System Performance for Color Image
Pictures
Figures 8 and 9 demonstrate that the proposed encryp-
tion algorithm change the RGB histogram to be uniform
which is required by any encryption method. Table 4
summarizes the mean value of NPCR and UACI for Lena
color image compared with PCS and PS. The proposed
method has NPCR higher than 99.6.
Table 2. NPCR and UACI between original and ciphered
images.
Image NPCR UACI
Baboon 99.6003 27.3953
Lena 99.6292 28.505
Camera Man 99.5682 31.0874
Table 3. Entropy of the ciphered images.
Image Entropy
Baboon 7.9975
Lena 7.9975
Camera Man 7.9966
Figure 8. Lena color image and RGB intensity Histogram Analysis.

Q. NASIR, H. H. ABDLRUDHA 555
Figure 9. Encrypted Lena color image and RGB intensity histogram analysis.
Table 4. Mean value of NPCR and UACI test for color Lena
Image with dif ferent encryption methods.
Encryption NPCR% UACI%
NPWLCM 99.632 99.631 99.594 33.104 30.637 27.621
PCS [13] 99.42 99.6 99.54 27.78 27.6624.94
PS [14] 99.26 99.45 99.13 21.41 23.42 15.08
5. Conclusion
In this paper, an image encryption scheme based on
Nested Piece Wise Linear Chaotic Map (PWLCM) is
proposed. The system is stream cipher architecture. The
NPWLCM chaos control parameters (A, B) and initial
values x(0) of the maps are derived from an external
password (secret key). The diffusion and confusion are
conducted on the bit as well as on the pixel level and the
method is applicable for both gray and color images.
Detailed security analysis of the proposed scheme is pre-
sented which show a high security performance measures.
The correlation coefficients of the encrypted images are
below 0.07 for all test images and in all directions. In
addition, high values (more than 99%) of NPCR and
UACI of 27% - 33% prove its ability to resist against
pixel changes attacks. Based on the results, we conclude
that the proposed simple NPWLCM is suitable for real
time secure image transmission over public networks.
Implementation of the proposed encryption scheme on
DSP chip is one of our future directions.
REFERENCES
[1] S. Lian, “A Block Cipher Based on Chaotic Neural Net-
works,” Neurocomputing, Vol. 72, No. 4-6, 2009, pp. 1296-
1301. doi:10.1016/j.neucom.2008.11.005
[2] R. Matthews, “On the Derivation of a Chaotic Encryption
Algorithm,” Cryptologia, Vol. 13, No. 1, 1989, pp. 29-42.
doi:10.1080/0161-118991863745
[3] Z. Li and D. Xu, “A Secure Communication Scheme Us-
ing Projective Chaos Synchronization,” Chaos, Solitons
and Fractals, Vol. 22, No. 2, 2004, pp. 477-481.
doi:10.1016/j.chaos.2004.02.019
[4] F.-Y. Wang and G.-W. Cui, “A New Image Encryption
Algorithm Based on the Logistic Chaotic System,” The
3rd IEEE International Conference on Computer Science
and Information Technology (ICCSIT), Chengdu, 9-11
July 2010, pp. 192-194.
[5] C. M. Li and L. X. Hong, “A New Image Encryption
Scheme Based on Hyperchaotic Sequences,” IEEE Inter-
national Workshop on Anti-Counterfeiting, Security, Iden-
tification, Xiamen, 16-18 April 2007, pp. 237-240.
[6] Y. Cheng, S. Yang and S.-F. Li, “Image Encryption of
Multiple Keys Method Based on Chaotic Maps,” First In-
ternational Conference on Pervasive Computing Signal
Processing and Applications (PCSPA), Harbin, 17-19 Sep-
tember 2010, pp. 891-894. doi:10.1109/PCSPA.2010.220
[7] M. Ashtiyani, P. M. Birgani and H. M. Hosseini, “Chaos-
Based Medical Image Encryption Using Symmetric Cry-
ptography,” The 3rd International Conference on Infor-
mation and Communication Technologies: From Theory
to Applications, Damascus, 7-11 April 2008, pp. 1-5.

Q. NASIR, H. H. ABDLRUDHA
556
[8] M. Ahmad, C. Gupta and A. Varshney, “Digital Image
Encryption Based on Chaotic Map for Secure Transmis-
sion,” International Multimedia Signal Processing and
Communication Technologies, Aligarh, 14-16 March 2009,
pp. 292-295. doi:10.1109/MSPCT.2009.5164233
[9] D. Socek, S. Li, S. S. Magliveras and B. Furht, “En-
hanced 1-D Chaotic Key Based Algorithm for Image En-
cryption,” First International Conference on Security and
Privacy for Emerging Areas in Communications Networks,
Athens, 5-9 September 2005, pp. 406-407.
[10] G. Alvarez, F. Montoya, M. Romera and G Pastor, “Cry-
ptanalysis of an Ergodic Chaotic Cipher,” Physics Letters
A, Vol. 311, No. 2-3, 2003, pp. 172-179.
doi:10.1016/S0375-9601(03)00469-9
[11] A. Awad, S. E. Assad, Q. Wang, C. Vladeanu and B. Bak-
hache, “Comparative Study of 1-D Chaotic Generators for
Digital Data Encryption,” International Journal of Com-
puter Science, Vol. 35, No. 4, 2008, pp. 483-488.
[12] A. Awad, “A New Chaos-Based Cryptosystem for Secure
Transmitted Images,” IEEE Transactions on Computers,
No. 99, 2011, p. 1.
[13] C. X. Zhu, Z. G. Chen and W. W. Ouyang, “A New Im-
age Encryption Algorithm Based on General Chen’s Cha-
otic System,” Journal of Central South University of
Technology, Vol. 37, No. 6, 2006, pp. 1142-1148.
[14] C. K. Huang and H. H. Nein, “Multi Chaotic Systems
Based Pixel Shuffle for Image Encryption,” Optics Com-
munication, Vol. 282, No. 11, 2009, pp. 2123-2127..
[15] A. Abid, Q. Nasir and A. Elwakil, “Implementation of an
Encrypted Wireless Communication System Using Nested
Chaotic Maps,” International Journal of Bifurcation and
Chaos, Vol. 20, No. 12, 2010, pp. 4087-4096.
doi:10.1142/S0218127410027957
[16] S. Li, G. Chen and X. Mou, “On the Dynamical Degrada-
tion of Digital Piecewise Linear Chaotic Maps,” Interna-
tional Journal of Bifurcation and Chaos, Vol. 15, No. 10,
2005, pp. 3119-3151. doi:10.1142/S0218127405014052
[17] T. Addabbo, M. Alioto, A. Fort, S. Rocchi and V. Vignoli,
“A Feedback Strategy to Improve the Entropy of a Chaos-
Based Random Bit Generator,” IEEE Transactions on
Circuits and Systems, Vol. 53, No. 2, 2006, pp. 326-337.
doi:10.1109/TCSI.2005.856670
[18] M. Drutarovsky and P. Galajda, “ Chaos-Based True Ran-
dom Number Generator Embedded in a Mixed-Signal Re-
configurable Hardware,” Journal of Electrical Engineer-
ing, Vol. 57, No. 4, 2006, pp. 218-225.
[19] A. M. Abid, “An Implementation of Chaotic Encryption
in Wireless Voice Transmission,” M.Sc. Thesis, University
of Sharjah, Sharjah, 2009.